CVC Lite: HOWTO Write a Decision Procedure in CVC Lite

The master source file for a theory should be called theory_foo.cpp. Typically, a new theory needs its own set of proof rules, which are implemented as three files: foo_proof_rules.h, foo_theorem_producer.h, and foo_theorem_producer.cpp. The first one is the abstract interface to the rules, which the untrusted DP code can #include. The other two files implement this abstract API, and comprise the trusted part of the code. All these files should be placed in src/theory_foo.

Naming Convensions

A theory may define several methods for creating expressions in theory_foo.h. Typically, they are named as barExpr(), bazExpr(), etc. For instance, theory_arith.h defines plusExpr(), minusExpr(), etc. These functions are most useful if they are declared as non-member functions (not part of the class TheoryFoo), since then they can be called directly by the CVC Lite library users.

It is also convenient to define testers like isBar() and isBaz(), which return true for the corresponding expressions. For example, theory_arith.h defines isPlus(), isMinus(), etc.

General Guidelines

There are several important guidelines for writing proof rules specific to your theory:

Every method, variable, class, or type should have a doxygen-style comment with at least a brief description:

//! Convert Blah expression to Baz value
Baz Blah2Baz(const Blah& b);

Imagine telling such a description to your colleague who has very faint idea of what you are coding. If a brief description does not make sense to him/her, or the function does something non-trivial or non-obvious, add a longer description:

//! Convert Blah expression to Baz value
!
 * Recursively descend into Blah, collect every Foo-leaf, order them in
 * the descending order of Baz-ability, and wrap into the Baz expression.
 * 
 * \param b is a non-trivial Blah value (otherwise we assert-fail).
 
Baz Blah2Baz(const Blah& b);

Often it is convenient to keep the brief description in the *.h file, and the long description in the corresponding *.cpp file.

The only exceptions are the Theory API methods, for which no documentation is necessary, since these are already documented in theory.h.

Adding New Theory

Before You Start...

Next, write down all the definitions mathematically and phrase the scope of the new theory in terms of a logic with a particular signature (the set of predefined interpreted and uninterpreted symbols that belong to this theory). Make sure this signature is disjoint from all the other theories (this is very important, since CVC Lite is based on Nelson-Oppen combination result, and requires signatures to be disjoint).

Your decision procedure should decide inconsistency of a set of formulas in the above logic. Make sure you actually know an algorithm for that. While it is possible to add undecidable or incomplete theories to CVC Lite (and we already have some), those should only be used for a very good reason. Otherwise, make sure you know that your algorithm is sound, complete, and terminating.

Take the above algorithm and make it an online one. That is, your algorithm should be able to accept a new formula at any point in time, and perform some incremental computation to take that formula into account. This is usually the most complicated step as far as the math is concerned. I will explain this step in detail in section Theory API below.

If you are adding your theory to the official CVC Lite code base, discuss your ideas on cvcl-devel mailing list! Yes, do it, I mean it. If you do not, we will notice your sneaky additions right away, and will ask many difficult questions in public. So, you may as well just announce it yourself.

Configure and Makefiles

File src/vcl/vcl.cpp is the only source file in the core of CVC Lite that you really need to touch in order to add a new theory. If you have to do something else, you are either doing it wrong, or there better be a very good reason for it, which you thoroughly discussed on cvcl-devel.

Now you are all set for compiling your new code, except that there is no code to compile yet...

Header File: theory_foo.h

Declaration of TheoryFoo class is required. Kinds and functions for creating new expressions are only needed if you want the end-user of CVCL library to be able to create expressions from your theory and/or refer to their kinds directly. This is not always desirable. For instance, you may want to generate special terms or predicates that only make sense as temporary storage of information for your theory. The DARK_SHADOW and GRAY_SHADOW operators are good examples from the arithmetic theory. You have no clue what I'm talking about? That's right, you get it.

Kinds, Expressions, and Types

In code, the new symbols and operators translate into new kinds of expressions. That is, new kinds and new values of the Expr class.

A kind is a natural number which uniquely determines what sort of expression it is (variable, uninterpreted function symbol, specific operator like plus, minus, a type expression, etc.). Kinds are also used to define your theory's signature, and hence, they must be unique to your theory.

In the simplest case, a kind represents the entire expression or type. Examples are simple types (like REAL and INT) and some constants (e.g. TRUE and FALSE).

More typically, however, a kind represents an operator (PLUS, MINUS, ...), and children of an expression of that kind are the arguments of that operator.

Finally, some kinds are used by more complex expressions with additional non-term attributes. For example, REC_LITERAL is used by record expressions { f1=e1, f2=e2, ... } whose children are the values of the fields (e1, e2, ...), and an additional attribute is the vector of field names: (f1, f2, ...). Other examples are quantifiers and lambda-terms. Such expressions require not only a new kind declaration, but also a special subclass of ExprValue (see below).

Kind Declaration

//! Local kinds of TheoryFoo
typedef enum {
  FOO_TYPE = 3500,   //!< Type FOO for the elements of this theory
  BAR,               //!< The binary (x | y) operator, where x,y: FOO
  BAZ,               //!< Unary buzz(x) predicate
  BLEAH              //!< An internal auxiliary term
} FooKind;

Notice, that the numbering in this example starts from 3500. This can be any integer which ensures that the new kinds do not clash with the existing kinds in other theories. Pick a random one, see if your kinds don't clash with others. You can check this either by inspecting src/include/kinds.h (the cental declaration of core kinds) and all the other theories, or compile and run cvcl to see if you get an error message about kinds registered twice.

The above type declaration of FooKind can be either in src/include/theory_foo.h (usually the best place), or in some header file in src/theory_foo/ directory, depending on whether you want to expose your kinds to the end library user or not. In the latter case, do not forget to add that header file to the HEADERS variable in your Makefile.in (see the previous section).

Kind Registration

getEM()->newKind(FOO_TYPE, "FOO");
getEM()->newKind(BAR, "||");
....

The string in the second argument is for printing the kind by the pretty-printer, and also for parsing, that is, turning a string back into a number (the kind).

New Expression Subclasses

An expression subclass is a subclass of ExprValue. You can declare it where appropriate in your theory files, using the same judgement as for the kinds. The new subclass needs to be registered with ExprManager by calling registerSubclass() method.

size_t computeHash() const;
size_t getMMIndex() const;
int isGeneric() const { return getMMIndex(); }
bool isGeneric(int idx) const { return (idx == getMMIndex()); }
// Syntactic equality of two expressions
bool operator==(const ExprValue& ev2) const;
// Make a clean copy of itself using the given memory manager
ExprValue* copy(MemoryManager* mm, ExprIndex idx = 0);

void* operator new(size_t, MemoryManager* mm) {
  return mm->newData();
}
void operator delete(void*) { }

Subclasses may overload other virtual methods of ExprValue as needed. For instance, arity(), getKids(), getXXXAttr(), etc. Some standard attribute access functions can also be overloaded, e.g. getString(), getRational().

However, you should not overload testers such as isRecord(), isVar() and such (unless you really know what you are doing), since the core relies on specific properties of the corresponding subclasses.

For example, let us say that the auxiliary term BLEAH in TheoryFoo needs a string attribute, which is a part of expression, but is not a child (and not even a term in the logic), and an integer attribute which is not part of the expression (e.g. it is needed for marking expressions during the algorithm run). An example of a new subclass for this expression is the following:

  class BleahExpr: public ExprValue {
  private:
    string d_str; //!< Data field; defines the value of expression
    int d_int;    //!< An attribute
    size_t d_MMIndex; //!< The registration index for ExprManager
  public:
    //! Constructor
    BleahExpr(ExprManager* em, const string& str,
	      size_t mmIndex, ExprIndex idx = 0)
     : ExprValue(em, ARRAY_VAR, idx), d_str(str),
       d_int(0), d_MMIndex(mmIndex) { }
    
    //! String attribute (part of expression)
    const std::string& getString() const { return d_str; }

    //! Integer attribute (not part of expression)
    int& getIntAttr(int idx) { return d_int; }
    size_t getIntAttrSize() const { return 1; }
    
    ExprValue* copy(MemoryManager* mm, ExprIndex idx = 0) const {
      return new(mm) BleahExpr(d_em, d_str, d_MMIndex, idx);
    }
    
    size_t computeHash() const {
      return PRIME*ExprValue::hash(BLEAH)+s_charHash(d_str.c_str());
    }

    size_t getMMIndex() const { return d_MMIndex; }
    size_t isGeneric() const { return getMMIndex(); }
    bool isGeneric(size_t idx) const { return (idx == getMMIndex()); }

    // Only compare the string, not the integer attribute
    bool operator==(const ExprValue& ev2) const {
      if(ev2.getMMIndex() != d_MMIndex) return false;
      return (d_str == ev2.getString());
    }

    void* operator new(size_t, MemoryManager* mm) {
      return mm->newData();
    }
    void operator delete(void*) { }
  };

Registration of this subclass generates a memory manager index, which must be stored somewhere, usually in a class variable of TheoryFoo, say d_bleahIdx of type size_t. Registration in this case should be done in the constructor of TheoryFoo:

d_bleahIndex = getEM()->registerSubclass(sizeof(BleahExpr));

The approved and recommended way of creating expressions of BLEAH kind is the following:

Expr bleahExpr(const string& s) {
  BleahExpr av(d_em, s, d_BleahIndex);
  return newExpr(&av);
}

Expr bleah = bleahExpr("cow moo"), b2 = bleahExpr("asdfqwerty");
bleah.getIntAttr(0) = 42;
if(bleah != b2)
  cout << bleah.getString() << b2.getIntAttr(0) << endl;

Note that it is impossible to define a non-member expression creation function for BleahExpr, since the memory manager index is stored in the class-local variable of TheoryFoo. And don't even think of using a static variable to work around this limitation.

In general, you should NEVER store anything in a static variable, since it may violate thread-safety of the library. Before you ever think of using a static variable for anything, think what happens if someone creates two copies of the system (with two different sets of expression and memory managers). Is it safe to share this variable among several system instances? In the case of the memory manager index, the answer is definitely not.

One possible fix for this problem is to bind the memory manager to the kind(s) that the subclass uses. Let us know if you really need this feature, and it will be implemented.

Constructor and API Methods

TheoryFoo(VCL* vcl);

TheoryFoo::TheoryFoo(VCL *vcl): Theory(vcl, "Foo") {
  d_rules = createProofRules(vcl); // instantiate our own rules

  // Register new local kinds with ExprManager
  getEM()->newKind(FOO_TYPE, "FOO");
  getEM()->newKind(BAR, "||");
  getEM()->newKind(BAZ, "BAZ");
  getEM()->newKind(BLEAH, "BLEAH");

  // Register our expression subclass
  d_bleahIndex = getEM()->registerSubclass(sizeof(BleahExpr));

  vector<int> kinds;
  kinds.push_back(FOO_TYPE);
  kinds.push_back(BAR);
  kinds.push_back(BAZ);
  kinds.push_back(BLEAH);

  registerTheory(this, kinds);
}

  void assertFact(const Theorem& e);
  void checkSat(bool fullEffort);
  void computeType(const Expr& e);

  Theorem rewrite(const Expr& e);
  void setup(const Expr& e);
  void update(const Theorem& e, const Expr& d);
  ExprStream& print(ExprStream& os, const Expr& e);
  Expr parseExprOp(const Expr& e);

  void addSharedTerm(const Expr& e);
  Theorem solve(const Theorem& e);
  void notifyInconsistent(const Theorem& thm);
  Expr computeTCC(const Expr& e);

The next section describes these API methods in more detail. You are also strongly encouraged to read the documentation on each of these methods.

Theory API: The Very Important Invariants

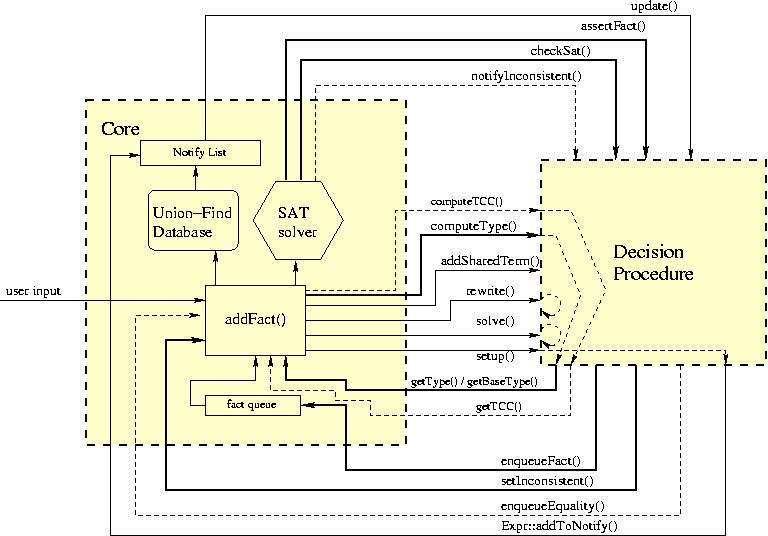
High-Level Information Flow

The chart below shows the flow of information to and from the decision procedure, and which parts of the core are responsible for collecting and generating it. Thick lines represent the most important methods, and dashed lines represent methods used only for very special occasions.

The most straightforward path of information, once it gets to the core through the external user input, is the following. First, all the relevant terms are typechecked (computeType() method). This method implements a step in the recursive typechecking algorithm, where the current expression is typechecked based on its structure and the types of its children. Typechecking of children is done by calling getType() or getBaseType(). The latter computes the largest supertype of the expression; for instance, the exact type of x may be a subrange 0..5, which is a subtype of INT, but its base type is REAL. Exact and base types are cached on expressions, and are computed on demand.

An important property of computeType() is that it must not only compute the exact type of the expression, but also verify that all subexpressions are type-correct, relative to their base types. For instance, x = y has type BOOLEAN, and it is only type-correct if getBaseType(x) == getBaseType(y). If this property is violated, TypecheckException must be thrown with the appropriate message. Note, that the exact types of x and y may be different, and even disjoint.

After the type checking, Type Correctness Conditions (TCCs) are generated and checked. TCC is a formula which is true if and only if any partial function in the original formula is used safely according to the Kleene semantics. That is, every partial function is either applied only to the arguments in its domain, or its value does not influence the value of the formula.

TCCs are computed recursively by computeTCC() and getTCC() methods, very similar to computing the types. If your theory does not introduce partial functions explicitly (like division in arithmetic), then you do not need to re-implement computeTCC() in your theory; the default implementation will do the job.

TCCs have a nice property that if they are true in the current context, then the corresponding user formulas can be safely interpreted by the total 2-valued models. Hence, computeTCC() is the only Theory API method that deals with partiality. All other methods consider any formula to be total (no partial functions) and 2-valued (only TRUE or FALSE, no undefined values.

Once TCC has been proven valid in the current context, the new fact (formula) goes to the SAT solver, and if it is a literal (atomic formula or its negation), it is submitted to the decision procedure through assertFact(). The decision procedure processes this fact, updates its internal data structures, and possibly reports a contradiction (setInconsistent()) or new facts (enqueueFact(), and in special cases, enqueueEquality()). This completes the main loop of information flow.

Note, that both enqueueFact() and setInconsistent() deliver information to the same place in the core, except that reporting the conflict bypasses the queue, and is taken care of immediately, rather than after all the previously enqueued facts are processed. This is the primary reason for having these two functions separated (as opposed to having only enqueueFact()).

Inside this main loop, rewrite() and solve() are called to transform (or simplify) the facts before they reach the rest of the core. Normally, these functions do not have side-effects (except for caching results), and return new (simplified) facts through their return values.

When the SAT solver runs out of facts, and the context is still satisfiable, it calls checkSat() with fullEffort==true. At this point, the decision procedure must determine whether all the information it has seen so far makes the context satisfiable or not w.r.t. its theory. Just like in the case of assertFact(), it may either report a contradiction, or enqueue a new fact. If any new fact is enqueued, it starts the main loop again. If checkSat() does not generate any new facts and does not find a contradiction, the core stops and reports the context to be satisfiable.

Method checkSat() is also called every time the fact queue becomes empty, before the SAT solver asserts a new splitter. In this case, the fullEffort argument is set to false, and the decision procedure is not required to do anything. Many DPs, however, choose to perform some relatively inexpensive checks to detect inconsistencies and/or new facts, which increases performance. Similarly, if a new fact is enqueued, the main loop continues (without the SAT solver asserting new splitters) until the queue is empty.

In CVC Lite, every term (non-formula expression) has a canonical representative in the union-find database. This database represents the equivalence classes of terms w.r.t. logical equality. All the terms in the formulas passing through the core are simplified by replacing them with their canonical representatives.

Often, a decision procedure wants to be notified when a subexpression changes its canonical representative. For instance, if the DP has seen an term 2*x+3*y, and x has changed its representative to y+2, then it is important to conclude that 2*x+3*y == 2*(y+2) + 3*y == 5*y+4. For this purpose, the core maintains the notify list data structure, which is interfaced through setup() and update() methods.

Every term in the core must be setup, and as a part of that process, the method setup() of the appropriate DP is called. Here the decision procedure has a chance to register notification requests related to the given expression. These requests are added to the notify lists of the relevant expressions using Expr::addToNotify() member method.

Normally, a DP wants to be notified when immediate children of the expression change. For instance, for an expression 2*x, if the variable x changes, the arithmetic DP wants to be notified about it. Therefore, in the setup(2*x) call, it adds 2*x to the notify list of x by calling x.addToNotify(this, 2*x). The first argument (this) is the reference to the current Theory subclass.

Later, when x changes its canonical representative, say, to y+2, its notify list is consulted, and the update(x==y+2, 2*x) call is made. The first argument is a directed equality informing the DP of what has changed, and the second is the expression for which this change is relevant. In this particular example, update() will enqueue a new fact: 2*x==2*y+4.

Similarly, when 2*x+3*y is being setup, its immediate children (2*x and 3*y) get the entire expression added to their notify lists. Later, when 2*x changes its canonical representative to 2*y+4 due to the previous update() call, another update() call is made with 2*x==2*y+4 for 2*x+3*y, and a new fact is enqueued: 2*x+3*y==5*y+4, and so on.

Note, that the notify list mechanism is not restricted to only immediate children. For instance, for high-degree monomials in non-linear arithmetics (e.g. x^2*y) it makes sense to register them with all factors (in this case, x, x^2, y, and x*y) which are not necessarily subexpressions of the original monomial (x^2*y).

Finally, sometimes a decision procedure may want to know that the current context has become inconsistent, and this what notifyInconsistent() call is for. To date, only the quantifier theory uses it to find out which instantiations were useful in producing a conflict. Most likely, you do not need it.

Backtracking Data Structures

The trick used in CVC Lite is actually quite simple and elegant: DP does not have to know about backtracking, it indeed works under the assumption that facts can only be added to the context. However, all of its internal state must be stored in backtracking data structures, which backtrack automatically with the core.

Such backtracking data structures are called context-dependent objects (CDO). There are currently three pre-defined context-dependent data structures: CDO (context-dependent object, cdo.h), CDList (backtracking stack, cdlist.h), and CDMap (backtracking map, similar to STL map, cdmap.h).

Class CDO is a templated class for any C++ class which can be cleanly copied with operator=() and copy constructor, and which have the default constructor (this is how these objects are saved and restored on backtracking). CDO is best suited for individual variables (array indices, Expr or Theorem variables, etc.).

Class CDList is a backtracking stack, and its API is very similar to that of STL vector. You can push_back() elements onto the stack, check the size() of the stack, and look up individual elements with operator[]. You cannot, however, modify or remove elements from the list. Keep in mind, that the size of the list may change between the API method calls, which means, you should keep any persistent indices to the list in backtracking variables (CDO).

Class CDMap is a templated class very similar to STL map. You can add new key-value pairs to it, you can modify the value under a key, but you cannot remove a pair from the map.

Let me repeat this again: all persistent data in a decision procedure MUST be stored in backtracking data structures! There are some rare exceptions to the rule (like storing the Expr representing the value "0" to avoid re-building it), but generally, you do not even want to know about backtracking. It is all done under the hood, and you should not care.

Variables and Foreign Terms (i-Leaves)

What CVC Lite knows as a "variable" has nothing to do with what a decision procedure considers a "variable." These two are not very much related.

A variable (or an i-leaf) from the DP point of view is either a CVC Lite variable, or a shared term from some other theory. For instance, in 2*arr[idx]-3*y, the subterm arr[idx] belongs to the theory of arrays, and therefore, is a variable (an i-leaf) as far as the theory of arithmetic is concerned. Similarly, y is a variable in the theory of arithmetic, because it is also a CVC Lite variable.

Such a definition does not provide a direct test for an i-leaf. Instead, you have to check whether this term is one of "yours" (one that your theory knows about), which is usually determined by the expression kind. If not, then it is a variable, as far as your theory is concerned.

But never make any assumptions about an i-leaf; it can be any expression whatsoever, and Expr::isVar() tester will not necessarily return true for it. In other words, there is no such thing as a variable in your theory. There are only terms you cannot recognize, which you treat as variables.

Methods Reimplemented in a Subclass

assertFact()

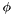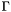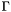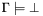Mathematically, the asserted fact $\phi$ is added to the logical context $\Gamma$ , and the job of the decision procedure is to check whether $\Gamma$ is satisfiable or not; in other words, we are solving the problem $\Gamma\models\bot$ .

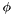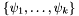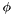When the decision procedure receives a new fact $\phi$ , it may either save this fact in its internal database for later processing, or may immediately process it, and possibly derive new facts $\{\psi_1,\ldots,\psi_k\}$ from $\phi$ and submit them back to the core (enqueueFact()).

In the case when the set of derived facts is equisatisfiable with the original fact 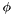$\phi$ , the decision procedure does not need to keep 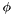$\phi$ in its database; the completeness will still be preserved.

For instance, if the DP receives r1=r2, where r1 and r2 are records with fields f1 and f2, then the two facts r1.f1=r2.f1 and r1.f2=r2.f2 (equalities of the individual fields) together are logically equivalent to the original fact r1=r2, and therefore, enqueuing them is sufficient for preserving completeness. The original fact need not be saved.

checkSat(bool fullEffort)

This call is your last warning: if you do not act now, the whole system will stop and notify the user. However, the worst that can happen is that CVC Lite becomes incomplete (it may report InValid when the query is actually valid). It still remains sound, however. That is, the Valid answer will still be correct.

When fullEffort is false, the DP may choose to do as much or as little work as it wants.

setup()

Whenever the canonical representative of any t_i changes in the union-find database, a corresponding call to update() will be made, and the DP will have a chance to re-process the expression e to keep it up-to-date.

update()

Also, the new equalities that update() derives must be submitted through enqueueEquality() call. This also means that the right-hand side of the submitted equalities must be fully simplified. See enqueueEquality() for more information.

addSharedTerm()

When such a term appears in the system, the core notifies both theories about the term.

Completeness of the CVC Lite framework relies on the invariant that decision procedures propagate all the equalities between shared terms that can be derived in the current logical context.

Often, the algorithms in DPs are designed to propagate all the equalities automatically (over all terms, including shared). In this case, addSharedTerm() need not be re-implemented.

In some cases, however, the DP has to take extra effort to satisfy the above invariant, and it is more efficient to restrict this extra effort only to the set of shared terms. In this case, addSharedTerm() needs to collect the set of shared terms in a database (which, of course, has to be backtrackable), and use it in the checkSat() call.

rewrite(Expr e)

This function can assume that all the immediate children of e are already completely simplified and rewritten. The same property must hold for the result of the rewrite.

Another invariant that rewrite() has to preserve is that if the result of a rewrite is an equality (you return e<=>(e1==e2)), then in the resulting equality e1 >= e2 w.r.t. operator>=(Expr, Expr), the fixed total ordering on all expressions given by the expression manager. This invariant is important for termination of the simplifier, since equalities in CVC Lite are used as (directed) rewrite rules, replacing the left-hand side (e1) with the right-hand side (e2).

The core will call the rewrite() function iteratively on the right-hand side of the result, until the expression does not change. However, if the rewriting algorithm can guarantee that in a particular case no further rewrites from this theory will change the expression, the result can be flagged as a normal rewrite. In this case, the core will not call rewrite() again, resulting in better performance. The property that the expression indeed does not change with further rewrites is checked in the "debug" build, and any violation triggers assertion failures with ``Simplify Error 1'' and ``Simplify Error 2'' messages.

It is important to understand that the iterative call to rewrite() only applies to the top-level node, and not to subexpressions. That is, if rewrite() changes the subexpressions (and not only the top-level operator), then it may violate another invariant that all the children of the result are completely rewritten and simplified. If this invariant cannot be guaranteed, then rewrite() needs to call simplifyThm() method explicitly.

Theorem TheoryFoo::rewrite(const Expr& e) {
  Theorem res;
  if(isBar(e)) {
    res = reflexivityRule(e); 
    res.getRHS().setRewriteNormal();  // No more rewrites needed
  } else {
    // May need to rewrite several times
    res = < do real work >
  }
  return res;
}

solve(Theorem e)

According to Clark Barrett's Ph.D. thesis, only one theory is allowed to have a solver. In CVC Lite, such theory is the theory of arithmetic. The restriction to a single solver in CVC Lite is somewhat relaxed, and several theories can have their own solvers, provided that the solved form that such a secondary solver generates is also a solved form w.r.t. the theory of arithmetic. This is the only asymmetric and non-local invariant in the core of Theory API.

computeType()

When computing a type of an expression e, this method determines which DP owns the expression, and calls the appropriate computeType() method, which is expected to check the expression for type consistency, and return the exact type of the expression. The return type is then cached as an attribute on the expression e for a fast look-up in the subsequent calls to getType().

Each decision procedure must implement computeType() method for all of its operators. For example, the theory of records has an operator for constructing record literals, for extracting a field of a record, and for updating a field of a record. This means that computeType() needs to be able to compute the types for these three operators, and verify that all subexpressions are of expected types.

Since subtypes in CVC Lite are handled by TCCs, type consistency at this stage is only checked with respect to the base types, which is returned by getBaseType() method provided by the base Theory class. For example, if a record expression e has a field foo of type INT, and the expression is a record update e WITH .foo := t, where t is of type REAL, then this expression is considered well-typed, since the base types of both INT and REAL is REAL.

computeTCC()

For example, an expression x/y is undefined when y=0, and is defined otherwise. Therefore, 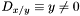$D_{x/y}\equiv y\ne 0$ .

notifyInconsistent()

print()

The recursive call to the global pretty-printer is implemented through the overloaded operator<< for ExprStream. Read the documentation on ExprStream class before coding.

Once coded, test your printer code! Print all the kinds of expressions from your theory, make the expressions large and complex, interspersed with terms from other theories, etc. Make sure it both looks good, and CVC Lite can read every term it prints.

ExprStream&
TheoryFoo::print(ExprStream& os, const Expr& e) {
  switch(os.lang()) {
  case PRESENTATION_LANG:
    switch(e.getKind()) {
    case ARROW:
      os << "[" << push << e[0] << space << "-> " << e[1] << push << "]";
      break;
    case EQ:
      os << "(" << push << e[0] << space << "= " << e[1] << push << ")";
      break;
    case NOT: os << "NOT " << e[0]; break;
    .................
    default:
      // Print the top node in the default LISP format, continue with
      // pretty-printing for children.
      e.print(os);
    }
    break; // end of case PRESENTATION_LANGUAGE
  case INTERNAL_LANG:
    ..................
    break; // end of case INTERNAL_LANG
  default:
    // Print the top node in the default LISP format, continue with
    // pretty-printing for children.
    e.print(os);
  }
  return os;
}

parseExprOp()

Methods Provided by Theory API

enqueueFact()

Other exceptions include facts derived by the update() function, which may be reported through enqueueEquality().

setInconsistent()

This method is used for more efficient processing of the derived contradiction, bypassing the fact queue.

simplifyThm() and simplify()

Be careful! This method may call your own rewrite(Expr e) method recursively.

enqueueEquality()

In CVC Lite, equalities are treated as directional, meaning that left-hand side is always being replaced by the right-hand side. This means that if in the expression d there is a subexpression e1, then it must be replaced by e2. It also means that the resulting expression d2 must be reported to be equal to the original one as d==d2, and not the other way around.

Since the core may occasionally swap equalities submitted through enqueueFact() (for termination reasons), it is important to submit the above equality by-passing the swapping engine. This is where enqueueEquality() is useful.

Invariant: enqueueEquality() expects the argument to be a Theorem of the form e1==e2, where e2 is a fully simplified expression in the current context. That is, e2 == simplify(e2). You are responsible for maintaining this invariant in your decision procedure.

inconsistentThm() and inconsistent()

isTerm()

isLiteral()

isAtomic()

This method is relatively expensive when called for the first time, but it caches the result in the Expr attributes, so the amortized complexity tends to be rather low.

updateHelper()

This function is convenient to use inside update() for rewriting d, the expression being updated. However, it only works when the changed subexpression in d is its immediate child.

getType()

getTCC()

parseExpr()

Proof Rules: The Trusted Core

A proof rule is a function which takes premises (previously generated theorems) and other parameters, and generates a new theorem. The implementation of proof rules comprises the trusted core of CVC Lite, and the soundness of the tool relies entirely on the soundness of this core. In other words, no matter what the bulk of the code does, if CVC Lite derives the validity of a particular fact, it is guaranteed that that theorem is indeed valid, provided the trusted implementation is correct and sound.

For this reason, it is prudent to keep the trusted core reasonably small, and more importantly, keep each proof rule clean and simple, so that the correctness of the rule itself (mathematically) and its implementation can be easily verified by manual inspection.

For the same reason, every rule must be thoroughly documented. It's a very good idea to include a LaTeX formula for the proof rule that a function implements. Keep in mind that reverse-engineering the mathematical meaning of a proof rule is a daunting task, especially if the code is rather long and complex.

Hierarchy of Classes

Important: the _CVCL_TRUSTED_ symbol must be defined only in *.cpp files, and never in *.h, to prevent accidental inclusion of theorem_producer.h, and thus, inadvertently making large portions of code trusted.

Exporting the proof rules to the untrusted code (class TheoryFoo) is implemented through the custom API in foo_proof_rules.h (abstract class FooProofRules), whose pure methods are the proof rules. This header file does not include theorem_producer.h, and therefore, is suitable for inclusion by untrusted code.

The implementation of FooProofRules consists of the implementation API: foo_theorem_producer.h (class FooTheoremProducer, inherits from FooProofRules and TheoremProducer), and the implementation proper in foo_theorem_producer.cpp.

Normally, theorem_producer.h is included from foo_theorem_producer.h (to declare FooTheoremProducer as a subclass of TheoremProducer), and foo_theorem_producer.h is included from foo_theorem_producer.cpp:

// File foo_proof_rules.h
class FooProofRules {
....
};

// File foo_theorem_producer.h
#include "theorem_producer.h"

class FooTheoremProducer: public FooProofRules, public TheoremProducer {
....
};

// File foo_theorem_producer.cpp
#define _CVCL_TRUSTED_
#include "foo_theorem_producer.h"
....

In order for the theory code to use the proof rules, a pointer to FooProofRules is declared in the TheoryFoo class:

// File theory_foo.h

class FooProofRules;
class TheoryFoo: public Theory {
......
  FooProofRules* d_rules;
  //! Create an instance of FooProofRules class
  FooProofRules* createProofRules(VCL* vcl);
.....
};

Since instantiating FooProofRules requires creating a new object of class FooTheoremProducer, which belongs to trusted part of the code, the implementation of createProofRules() method needs to be in foo_theorem_producer.cpp, rather than in theory_foo.cpp. This is the only exception to the rule that everything declared in a X.h file must be implemented in the corresponding X.cpp file in CVC Lite.

// File foo_theorem_producer.cpp
......
FooProofRules* TheoryFoo::createProofRules(VCL* vcl) {
  return new FooTheoremProducer(vcl);
}
.....

In the TheoryFoo() constructor, the class variable d_rules is initialized by calling createProofRules():

// File theory_foo.cpp
.....
TheoryFoo::TheoryFoo(VCL* vcl): Theory(vcl, "Foo") {
.....
  d_rules = createProofRules(vcl);
.....
}

// Destructor: destroy the proof rules class
TheoryFoo::~TheoryFoo() { delete d_rules; }
.....

Implementing a Proof Rule

There is a special macro CHECK_SOUND(cond, message) for checking the soundness conditions. If the condition cond does not evaluate to true, then a SoundException is thrown with the message string.

For efficiency, the user may decide to skip the soundness checks. In order to honor this decision, all soundness checks must be supressed when the CHECK_PROOFS macro evaluates to false:

if(CHECK_PROOFS) {
  CHECK_SOUND(denominator != 0,
              "TheoryArith: Division rule: denominator == 0");
}

Soundness checks play the most important role in making CVC Lite sound. Your implementation must guarantee that if all soundness checks pass, then the rule is indeed sound to apply, and the theorem you generate at the end is indeed a theorem. Soundness checks include verifying that the premises (Theorems given as arguments) are of the expected format, and all the additional parameters satisfy all the side conditions of the proof rule.

Soundness checks must be complete and self-sufficient (bullet-proof) within the rule; that is, no matter how the rule is called and with which arguments, there should be no way for the rule to generate an invalid theorem. Even if the untrusted code which calls the rule does all the necessary checks, you have to do them again inside the rule. This is the whole point of the code being trusted: it cannot go wrong, no matter what happens outside. In case of CVC Lite, this means that any non-null Theorem object represents a valid theorem, no matter how this theorem was generated.

The main component of a Theorem object is a formula (returned by Theorem::getExpr()), which is valid in the appropriate logical context. The logical context is defined by the set of assumptions carried along in the Theorem object. 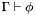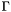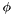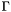Mathematically, a theorem object represents a sequent $\Gamma\vdash\phi$ , where $\Gamma$ is the set of assumptions (formulas assumed to be true), and $\phi$ is the theorem itself, the formula which logically follows from $\Gamma$ .

$\frac{\Gamma_1\vdash\phi_1\quad\cdots\quad\Gamma_n\vdash\phi_n} {\Gamma_1,\ldots,\Gamma_n\vdash\psi}$

where the assumptions of the conclusion are the union of all the assumptions from the premises.

The easiest way to compute the set of assumptions for the conclusion is to use the overloaded method merge() provided by the theorem.h API. This way you do not have to bother about the internal representation of assumptions. Keep in mind, that CVC Lite may be running in the mode without assumptions (for efficiency), which can be queried by withAssumptions() method:

Theorem fooRule(const Theorem& prem1, const Theorem& prem2) {
.....
Assumptions a;
if(withAssumptions())
  a = merge(prem1, prem2);
....
}

If the rule accepts more than two premises, you can merge assumptions by passing the vector of all premises to the merge() method.

When there is only one premis, the simplest way is to make a clean copy of the assumptions from the premis:

if(withAssumptions())
  a = premis.getAssumptionsCopy();

Occasionally, one needs to remove assumptions from the set, as in the following rule:

$\frac{\Gamma_1\vdash\alpha\quad \Gamma_2, \alpha\vdash\phi} {\Gamma_1, \Gamma_2\vdash\phi}\mbox{Cut}$

Theorem cutRule(const Theorem& alpha, const Theorem& phi) {
.....
Assumptions a;
if(withAssumptions())
  a = (phi.getAssumptions() - alpha.getExpr()) + alpha.getAssumptions();
....
}

Remember, however, that due to the internal representation used in CVC Lite, removing an assumption is quite expensive, while merging is very cheap.

Also, if the soundness of your rule relies on the presence (or absence) of certain assumptions in premises, the first thing you need to check for is that withAssumptions() returns true (otherwise there is no way to determine the soundness of the rule, so it should not be called in the mode without assumptions).

In the above rule, if the assumption 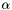$\alpha$ were required to be present for soundness of the rule, one could check it as follows:

const Expr& alphaExpr = alpha.getExpr();
const Assumptions& phiAssump = phi.getAssumptionsRef();
if(CHECK_PROOFS) {
  CHECK_SOUND(withAssumptions(),
              "TheoryFoo::cutRule: called without assumptions!");
  CHECK_SOUND(!phiAssump[alphaExpr].isNull(),
              "TheoryFoo::cutRule: alpha is not an assumption of phi");
}

It is extremely important that assumptions are computed correctly when withAssumptions() returns true, since assumptions are used by the SAT solver in the core framework, and are absolutely crucial for the results to be correct (or sound). Remember, that assumptions represent the logical context where the theorem is true, and if they are not computed properly, the entire theorem may become invalid.

Each Theorem object carries a proof of itself in the form of a Proof object.

Proofs are relatively expensive to generate (they take up extra space and somewhat slow down the rule execution), and therefore, it is the user's privilege to turn them off. For this reason, all proof generation code must be guarded by the method withProof(), similarly to withAssumptions().

CVC Lite uses a version of Natural Deduction as its logical basis, and exploits the idea of Curry-Howard isomorphism to represent proofs as terms over function symbols representing proof rules. A ``type'' of a proof term is the formula (theorem) derived by the corresponding proof. The correctness of a proof in this framework corresponds to the proof term being ``well-typed.''

The TheoremProducer API provides an overloaded method newPf() for building proof terms. The first argument of (almost) any newPf() version is the name of the proof rule (string), and the rest are the arguments (parameters as Expr values, and the proofs of the rule's premises).

The key idea in building a proof term for the rule is to provide enough information in the proof term to be able to re-run the rule again with exactly the same arguments.

$\frac{\Gamma_1\vdash x < y \quad \Gamma_2\vdash y < z} {\Gamma_1, \Gamma_2\vdash x < z}\mbox{project}$

Theorem projectRule(const Theorem& xLTy, const Theorem& yLTz) {
.....
Proof pf;
if(withProof()) {
  vector<Expr> exprs;
  vector<Proof> pfs;
  exprs.push_back(xLTy.getExpr());  exprs.push_back(yLTz.getExpr());
  pfs.push_back(xLTy.getProof());  pfs.push_back(yLTz.getProof());
  pf = newPf("project", exprs, pfs);
}
.....
}

It is a very good idea to describe the proof object arguments in the proof rule documentation (doxygen comments) in foo_proof_rules.h file.

Note, that the proof object does not carry around any information about the assumptions. This is because all the assumptions are present implicitly as ``types'' of bound proof variables in LAMBDA-terms. I skip the description of this issue in the current version of this document, as it is rather subtle, and there is a 99% chance that you do not need to know that for your DP.

Finally, creating the resulting theorem in the proof rule is usually done by calling newTheorem(conclusionExpr, a, pf), where a is the Assumptions variable, and pf is the proof term.

There is a special class of proof rules called rewrite rules in CVC Lite. These are proof rules without premises (axioms) whose conclusion is of the form expr1 = expr2 or frm1 <=> frm2. These rules are so ubiquitous in the system that there is a special optimized constructor for the corresponding theorems: newRWTheorem(expr1, expr2, a, pf).

Note: the Theorem object constructed by the rewrite rule has a different internal representation from the "normal" Theorem object. Therefore, constructing a rewrite theorem with newTheorem(expr1.eqExpr(expr2), a, pf) will result in a run-time error. Make sure that if your theorem is a rewrite theorem (an equality = or equivalence <=>), then it must be constructed using the newRWTheorem() method.

I did not mention anything about computing the expression for the conclusion of the rule, but it should be fairly obvious how to do this. Remember, that each proof rule should be coded as concisely and as cleanly as possible, to ensure the effectiveness of manual inspection. Remember, this is a trusted part of the code. Keep It Simple, Stupid. :-)