A multiresolution analysis (MRA) for a space L is tower of subspaces
together with a scaling function (or "father wavelet")
such that
The above definition can be generalized in several ways. We can replace condition 2 by an apparently more general condition:
(x-j):j
} is a Riesz basis.
for an
MRA. See [3] (p. 21) for some
basic facts about Riesz basis, and more generally the
concept of a frame.
We can also work with functions f(x) over 
d (d=1,2,...).
Then (following [Strichartz]) we can replace
by a lattice 
d. Then the scaling property
can be replaced by
where M is a linear transformation of
d satisfying
M and all the eigenvalues 
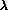of M
satisfy |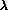|>1. In this case |detM| is an integer m
2
and /M is a group of order m. In the simplest
case, =d is the unit lattice and M=2I with m=2d.
These conditions for MRA are also not independent:
thus, [2] shows that condition 3
(separation) is implied by conditions 1 and 2*.
Assuming that the Fourier transform of has
the property that |F()(y)| is continuous at y=0.
Then
NOTATION: in the literature, there are two conventions
for indexing the tower of subspaces in an MRA. Mallat
uses the convention ViVi-1 while our notation
follows Daubechies. Let us write V-i for Vi
so that we have ViVi-1, to get an indexing
consistent with Mallat. The naturalness of each
indexing scheme (Vi or Vi) can be explained this
way. If you are more interested in the analysis of
signals, then the Mallat convention makes more sense.
That is, you begin with a signal f=f0V0, and you
can produce successively coarser approximations
f1V1, f2V2, etc. Following Mallat,
we call the superscript i in Vi the "scale" of fi,
and this is the inverse of the "resolution".
If you want to do signal synthesis,
then you begin with a signal f=f0V0
and by adding more details, you can refine it
to f1V1, f2V2, etc.
