Prev Up Next
Go backward to MULTIRESOLUTION ANALYSIS
Go up to Top
Go forward to APPENDIX A: MATHEMATICAL BACKGROUND

DILATION EQUATION

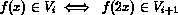
The scaling property

and the fact that {(t-j): j} is an orthogonal basis for V0 implies that
is an orthogonal basis for Vi. EXERCISE: show this.

In general, for any function g(x) and j,k, we define

Then the above shows that {j,k: k} is an orthogonal basis for Vj.

Restricting attention to V1, this means

for some ck's. This is called the dilation equation. We can of course obtain ck as the projection of onto sqrt(2)(2x-k),

Let us now derive several properties of the ck's.

PROPERTY I, ORTHOGONALITY.

For each m,
In proof, use the fact that (x)(x-m)dt=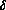(m), and substitute the dilation equation for (x) and for (x-m).

PROPERTY II, NORMALITY.

Proof sketch: use the fact that 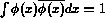and substitute the dilation equation for (x).

PROPERTY III, DILATION IN FOURIER DOMAIN:

Dilation in the Fourier domain is expressed by
where
where we write hk for 2-1/2ck. In proof, we just take the Fourier transform of both sides of the dilation equation to give us
The transformation of this infinite sum to the above formula () actually require justification (see [3], p.54).

Iterating this, we obtain

Note that
by the normalization assumption
We may also assume 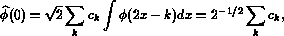. Hence
This infinite product is defined if H(0)=1. Even if H(0)1, the infinite product may be well defined (because of fortuitious cancellation: see [Collela] in [1])

Other remarks:


1. H(omega) is a trigonometric polynomial if the ck's are zero for |k|>N (some N).
2. The case where ck=0 for |k|>N can be shown to lead to a unique compact solution (t) to the dilation equation. [Show]
3. The dilation equation can be viewed as a fixed point operator, and it can be used to compute (t). It is easy to see from this iteration that the solution (t) is supported in the interval [N,-N].
4. It is instructive to illustrate all the above equations with the case of Haar functions where c0=c1=(1)/(sqrt(2)).
Chee Yap

Prev Up Next