 (x) and its
corresponding Haar wavelet
(x) and its
corresponding Haar wavelet 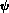 (x):
(x):
To have a concrete example as we introduce the
abstract framework later, we describe Haar wavelets.
Here is a picture of a Haar scaling function  (x) and its
corresponding Haar wavelet
(x) and its
corresponding Haar wavelet 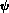 (x):
(x):
[FIGURE]
First consider the space V0![]() L of all piecewise
constant functions f(x)
with breakpoints at integer values of x.
Clearly, f(x) can be written as a superposition of
integer translates of the Haar scaling function:
L of all piecewise
constant functions f(x)
with breakpoints at integer values of x.
Clearly, f(x) can be written as a superposition of
integer translates of the Haar scaling function:
Thus the set {
 (x-j) : j
(x-j) : j
The functions
forms an orthogonal basis for Vi. It becomes orthonormal if we use
 instead.
instead.
Now let us consider the relationship among these subspaces. Clearly, we have
Consider the orthogonal complement Wi of Vi in Vi+1,
By definition, a function g(x)
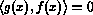 for all f(x)
for all f(x)forms a basis for Wi.
EXERCISE: what are the breakpoints and support functions
for  i,j and
i,j and 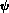 i,j?
i,j?
Next, we can repeatedly expand the above equation to yield
In fact, we can continue this expansion for negative indices to yield
We note two other properties. Intuitively, it is clear that a function f(x)
is dense in L. Second, note that
where 0 is only the identically zero function.