Wavelets are special functions that can be used to represent
other functions.
The functions of interest to us are real functions.
They can be one dimensional functions f(x) such as sound waves,
or two dimensional function f(x,y) such as images.
In order to have nice mathematical properties, we usually
restrict the functions to some nice function spaces such as
L1(
) or L2(2). In the following, let L
denote the class of functions under discussion (which
may be taken L2() unless otherwise noted).
A set
B
L
is called a
basis for L if every function
f
L
can be expressed as a `superposition' (linear combination)
of functions in B,
In particular, B is called a wavelet basis when it is constructed in a special way and comprises of wavelets. This idea of forming suppositions goes back to the French engineer Joseph Baptiste Fourier (1807) who asserted that any function f(x) with a period 2
can be written as
the superposition
Here, the basis functions are (1)/(2), sinix and cosix for i=1,2,....
We view x as the `time' (or space, depending on
application) dimension of the function f(x).
Then each term ajcosjx + bj sinjx (j
0)
in the above superposition can be viewed as a `frequency' component
of f(x). In fact, aj, bj is easily seen to be equal
the following integrals:
[Show this!] So a periodic function f(x) may be represented in the frequency domain by the discrete set of coefficients {aj, bj: j
0}.
More generally, a function f(x)L (not necessarily
periodic) can be represented in
the frequency domain by its Fourier transform which is
defined (see NOTES)
as follows:
It is easy to recover f(x) from
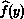using the Fourier inversion formula,
The study of this transform leads to the subject of Fourier or Harmonic analysis.
Despite the importance and success of this kind of
`frequency' analysis, the use of sines and cosines as
basis is unsatisfactory for analysing functions f(x)
that are `localized' in x (for instance a musical note f(x)
is localized in time).
Clearly, sines and cosines are not localized in this
sense. We want basis functions
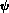i(x) that decay rapidly with | x |.
One can introduce `windowed Fourier transform' to
analyze local signals. But wavelets turn out to give
a better alternative because it fits in the general
framework of superposition of functions.
In retrospect, the
first wavelet basis was already introduced by Alfred Haar (1909).
Grossman and Morlet (1980) defined wavelets in quantum physics.
But it was after Mallat's introduction of multiresolution analysis
in 1985 that the subject took off.
There are many excellent books on Wavelets and popular wavelet articles on the web. Some references used in these notes are Koornwinder (ed.) [3], Hernández-Weiss [2] and Benectto-Frazier [1].
, and 
denote the set of integers, reals and
complex numbers, respectively.
The support of a function f(x) is the set supp(f):={x: f(x)
0}.
The Kronecker delta function is 
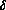(m)=1 if m=0,
and 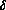(m)=0 for m0.
For any interval [a,b], the characteristic
function chi[a,b](x) is 1 iff a
xb, and 0 otherwise.
The integration 
f(x)dx of a function fL is
assume to range over unless otherwise stated.
Likewise, in a summation SUMk ck where k is an integer,
it is assumed that k range over all integers .
The inner product of functions f,gL is just
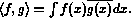Note that functions in L have complex values in general,
and
here indicates complex conjugation:
,
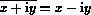where i=sqrt(-1).
Also, | f| is defined to be
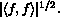We say f and g are orthogonal if
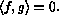We should remember that functions in L2() are
defined up to a set of measure zero.
See Appendix A for more mathetical preliminaries.
