![\[\Gamma\models\phi,\]](form_44.png)
Contents
Mathematically, CVC Lite solves a problem of validity of a formula in a given logical context (that's why it is called validity checker):
![\[\Gamma\models\phi,\]](form_44.png)
where 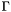 is a set of formulas which define the logical context, and
is a set of formulas which define the logical context, and 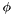 is the formula being tested for validity under
is the formula being tested for validity under 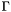 .
.
If the formula is proven valid, CVC Lite can produce a proof and a subset of the assumptions 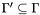 which were used in that proof, so that
which were used in that proof, so that 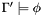 . If the formula is invalid, then additional formulas are added to
. If the formula is invalid, then additional formulas are added to  which are consistent with
which are consistent with  , but imply the negation of
, but imply the negation of  . This set of formulas is called a counterexample.
. This set of formulas is called a counterexample.
CVC Lite can be used in two modes: as a C/C++ library, and as a command-line executable (implemented as a command-line interface to the library). This manual mainly describes the command-line interface.
Download the distribution tarball, say, cvcl-2.0.0.tar.gz, and unpack it:
gunzip -c cvcl-2.0.0.tar.gz | tar xf -
This will create a directory cvcl-2.0.0. Then compile:
cd cvcl-2.0.0 ./configure make
By default, CVC Lite compiles the debugging version, which is slow, but has many internal checks, and is good for reporting bugs. You can change the build type by configuring with the following parameters:
./configure --with-build=optimized make
Optimized build is nearly 10 times as fast as the "debug" build, at the expense of not being as rigorous with self-testing, which is probably the best choice for most users. Other build types include gprof, gcov, etc. For more configure options, run ./configure --help.
Finally, install it system-wide:
make install
This installs the executable cvcl and the library libcvclite.a and/or libcvclite.so in the standard system directories (normally /usr/local/lib and /usr/local/bin), and the library header files in /usr/local/include/cvcl. User applications then can include cvcl headers by
#include "cvcl/vc.h"
cvcl. It reads the input (a sequence of commands) from standard input and prints the results on standard output. Errors and some other messages (e.g. debugging traces) are printed on standard error.
Typically, the input to cvcl is saved in a file and redirected to the executable, or given on a command line:
# Reading from standard input: cvcl < input-file.cvc # Reading directly from file: cvcl input-file.cvc
Notice that, for efficiency, CVC Lite uses input buffers, and the input is not always processed immediately after each command. Therefore, if you want to type the commands interactively and receive immediate feedback, use the +interactive option (can be shortented to +int):
cvcl +int
Run cvcl -h for more information on the available options.
Any text after a character '%' and to the end of the current line is a comment:
%%% This is a CVC Lite comment
REAL, INT, subranges (both are subtypes of REAL), BOOLEAN, BITVECTOR(n) and uninterpreted types declared by the user:
% subrange type finite_range: TYPE = [-2..10]; % Uninterpreted types: T, T1: TYPE;
All the uninterpreted types are assumed to be infinite and disjoint.
The example above also shows how to introduce named types. A type name (finite_range) is semantically equivalent to the corresponding type definition ([-2..10]), and can be used interchangeably (with the exception of uninterpreted types, which do not have unnamed equivalents). In general, any type can be given a name:
name : TYPE = type_definition;
The compound types are tuples, records, functional types, and arrays:
% Tuples (can be nested)
tuple_type: TYPE = [REAL, array_type, [[-2..10], INT] ];
% Records
record_type: TYPE = [# number: INT, value: REAL,
database: ARRAY INT OF REAL #];
% Function types
fun_type: TYPE = INT -> REAL;
binary_function_type: TYPE = (REAL, BOOLEAN) -> BOOLEAN;
% Array types:
array_type: TYPE = ARRAY [0..100] OF REAL;
infinite_array_type: TYPE = ARRAY INT OF REAL;
Note, that the syntax for function types has changed in 2.0 version (it used to be [T1 -> T] and [[T1,T2] -> T3]). The new version will recognize the old syntax, and will accept it if you specify +old-func-syntax command line option.
CVC Lite supports subtypes, which are declared as follows:
T: TYPE; pred: T -> BOOLEAN; % subT is a subtype of T: subT: TYPE = SUBTYPE(pred);
where pred is a predicate (a function taking a type T as an argument and returning a BOOLEAN value). For example, a type of positive real numbers can be declared as follows:
posReal: TYPE = SUBTYPE(LAMBDA (x:REAL): x > 0);
a, b, c: INT; x,y,z: REAL; f: REAL -> REAL;
Constant declarations can also be used as named expressions:
expr: INT = 5+3*c; rational_const: REAL = 3/4;
Here expr is now identical to 5+3*c, and can be used interchangeably in the later expressions. Named expressions are often useful for shared subexpressions (expressions used several times in different places), which makes the input more concise.
It is important to note that named expressions are processed very efficiently by CVC Lite. It is much more efficient to associate a complex expression with a name directly rather than to introduce an uninterpreted constant and later assert that it is equal to the same expression. This point will be explained in more detail later in section Commands.
Literals are expressions like 5 (arithmetic number), TRUE and FALSE (Boolean constants), and expressions of compound types constructed directly out of its components:
% Tuple and record expressions: tuple_expr: [REAL, INT] = (2/3, -4); record_expr: [# key: INT, value: REAL #] = (# key := 4, value := y+1/2 #); % Functions: func: REAL -> REAL = LAMBDA (x: REAL): 2*x+3; func_bin: (REAL, INT) -> REAL = LAMBDA (x: REAL, i:INT): i*x-1; array_lit: ARRAY INT OF REAL = ARRAY (x: INT): x+1;
More complex expressions involve operators and interpreted (predefined) functions. First, we cover the general operators such as conditionals and local variable bindings (LET operator).
% Conditional expression
e1: REAL =
IF x > 0 THEN y
ELSIF x >= 1 THEN z
ELSIF x > 2 THEN w
ELSE 2/3 ENDIF;
% LET operator
e2: REAL =
LET x1: REAL = 5,
x2: REAL = 2*x1 + 7/2,
x3: INT = 42
IN
(x1 + x2) / x3;
CVC Lite has the usual arithmetic operators: +, - (both unary and binary), *, /, <, >, <=, >=.
Components of tuples and records can be accessed using the `.' (dot) operator:
x: [REAL,INT,BOOLEAN]; first: REAL = x.0; r: [# key: INT, value: REAL #]; z: REAL = r.value;
Array access:
a: ARRAY [0..100] OF REAL; idx: [0..100]; elem: REAL = a[idx];
Tuples, records and arrays can be updated using the WITH operator. The resulting expression is a new tuple, record or array, respectively, with the corresponding element (or several elements) replaced by a new value:
% Records Rec: TYPE = [# key: INT, value: REAL #]; r: Rec; r1: Rec = r WITH .value := 8; % Tuples Tup: TYPE = [REAL,REAL]; t: Tup; t1: Tup = t WITH .1 := 2/3; % Update the second field (numbering starts from 0) % Arrays Arr: TYPE = ARRAY [0..100] OF REAL; a: Arr; % Updating two elements at once a1: Arr = a WITH [10] := 2/3, [42] := 3/2;
Updates to a nested component can be combined in a single WITH operator:
Cache: TYPE = ARRAY [0..100] OF [# addr: INT, data: REAL #]; State: TYPE = [# pc: INT, cache: Cache #]; s0: State; s1: State = s0 WITH .cache[10].data := 2/3;
Application of functions and predicates (interpreted and uninterpreted) is written in the usual way:
f: REAL -> REAL; % uninterpreted unary function g: (REAL, INT) -> BOOLEAN; % uninterpreted binary predicate b: BOOLEAN = g(f(5), -11);
Logical operators include equality = and disequality /=, propositional connectives AND, OR, XOR, =>, <=>, and quantifiers:
quant: BOOLEAN = FORALL (x,y: REAL, i,j,k: INT): i>=0 AND i+x > y
=> EXISTS (z: REAL): x < z AND z < y;
x : BITVECTOR(32);
Bit-vector variables (or terms) of length 0 are not allowed. Bit-vector constants can be represented in binary or hexadecimal format. The rightmost bit is called the least significant bit (LSB), and the leftmost bit is the most significant bit(MSB). The index of the LSB is 0, and the index of the MSB is n-1 for an n-bit constant. This convention naturally extends to all bit-vector expressions. Following are some examples of bit-vector constants:
0bin0000111101010000, and the corresponding hex representation is 0hex0f50.
The Bit-vector implementation in CVC Lite supports a very large number of functions and predicates. The functions are categorized into word-level functions, bitwise functions, and arithmetic functions.
Let t1,t2,...,tm denote some arbitrary bitvector terms.
Word-level functions:
Name Symbol Example
==========================================
Concatenation @ t1@t2@...@tm
Extraction [i:j] x[31:26]
left shift << 0bin0011 << 3 = 0bin0011000
right shift >> x[24:17] >> 5
0bin1000 >> 3 = 0bin0001
sign extension SX(bv,n) SX(0bin100, 5) = 0bin11100
Bitwise functions: Name Symbol Example ========================================== bitwise AND & t1&t2&...&tm bitwise OR | t1|t2|...|tm bitwise NOT ~ ~t1 bitwise XOR BVXOR BVXOR(t1,t2) bitwise NAND BVNAND BVNAND(t1,t2) bitwise NOR BVNOR BVNOR(t1,t2) bitwise XNOR BVXNOR BVXNOR(t1,t2)
Arithmetic functions: Name Symbol Example ========================================== bitvector add BVPLUS BVPLUS(n,t1,t2,...,tm) bitvector mult BVMULT BVMULT(n,t1,t2) bitvector sub BVSUB BVSUB(n,t1,t2) bitvector unary minus BVUMINUS BVUMINUS(t1)
In bit-vector arithmetic functions
CVC Lite also supports conditional terms (IF cond THEN t1 ELSE t2 ENDIF), where cond is boolean term, t1 and t2 can be bitvector terms. This allows us to simulate multiplexors. An example is:
x,y : BITVECTOR(1); QUERY(x = IF 0bin0=x THEN y ELSE BVUMINUS(y));
Following is the list of predicates supported:
Predicates:
Name Symbol Example
=======================================
equality = x=y
less than BVLT BVLT(x,y)
less than or
equal to BVLE BVLE(x,y)
greater than BVGT BVGT(x,y)
greater than
equal to BVGE BVGE(x,y)
CVC Lite requires that in the formula x=y, x and y are expressions of
the same length. No such restrictions are imposed on the other predicates.
Following are some example CVC Lite input formulas involving bit-vector expressions
Example 1 illustrates the use of arithmetic, word-level and bitwise NOT operations:
x : BITVECTOR(5); y : BITVECTOR(4); yy : BITVECTOR(3); QUERY( BVPLUS(9, x@0bin0000, (0bin000@(~y)@0bin11))[8:4] = BVPLUS(5, x, ~(y[3:2])) );
Example 2 illustrates the use of arithmetic, word-level and multiplexor terms:
bv : BITVECTOR(10); a : BOOLEAN; QUERY( 0bin01100000[5:3]=(0bin1111001@bv[0:0])[4:2] AND 0bin1@(IF a THEN 0bin0 ELSE 0bin1 ENDIF)=(IF a THEN 0bin110 ELSE 0bin011 ENDIF)[1:0] );
Example 3 illustrates the use of bitwise operations:
x, y, z, t, q : BITVECTOR(1024); ASSERT(x=~x); ASSERT(x&y&t&z&q = x); ASSERT(x|y = t); ASSERT(BVXOR(x,~x)=t); QUERY(FALSE);
Example 4 illustrates the use of predicates and all the arithmetic operations:
x, y : BITVECTOR(4); ASSERT(x=0hex5); ASSERT(y = 0bin0101); QUERY( BVMULT(8,x,y)=BVMULT(8,y,x) AND NOT(BVLT(x,y)) AND BVLE(BVSUB(8,x,y), BVPLUS(8, x, BVUMINUS(x))) AND x = BVSUB(4, BVUMINUS(x), BVPLUS(4, x,0hex1)) );
Example 5 illustrates the use of shift functions
x, y : BITVECTOR(8); z, t : BITVECTOR(12); ASSERT(x=0hexff); ASSERT(z=0hexff0); QUERY(z = x << 4); QUERY((z >> 4)[7:0] = x);
For invalid inputs, the COUNTEREXAMPLE command can be used to generate appropriate counterexamples. The generated counter example is essentially a bitwise assignment to the variables in the input.
ASSERT -- add a formula to the current logical context 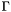
QUERY -- check if the formula is valid in the current logical context: 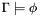
TRANSFORM -- simplify given expressionPRINT -- parse and print back the given expressionPUSH -- push the scope levelPOP -- pop the scope levelPOPTO -- pop to the given scopeWHERE -- print all the assumptions in the current logical contextCOUNTEREXAMPLE -- print the counterexample to the last (failed) QUERYTRACE -- turn on tracing for a given flag (for debugging)UNTRACE -- turn off tracing for a given flagOPTION -- set/unset a command line flagDUMP_PROOF -- dump the proof of the last (successful) QUERYDUMP_ASSUMPTIONS -- dump the assumptions used in the proof of the last (successful) QUERYDUMP_TCC -- dump the TCC for the last formula in ASSERT or QUERYDUMP_TCC_ASSUMPTIONS -- dump assumptions used in the proofs of the TCC for the last ASSERT or QUERYDUMP_TCC_PROOF -- dump the proof of the TCC for the last ASSERT or QUERYDUMP_CLOSURE -- convert the last (successful) QUERY into an implication (assumptions => query) and print this formulaDUMP_CLOSURE_PROOF -- dump the proof of the closure of the last (successful) QUERYECHO -- print the given stringWhile many of the commands are either self-explanatory or easy to understand by trying them out, there are a few commands and their combinations worth mentioning specially.
ASSERT <formula>;
Adds a new formula to the current logical context 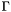 .
.
PUSH saves the current logical context 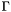 on the stack.
on the stack.
POP restores the context 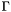 from the top of the stack, and pops it off the stack. Any changes to the logical context (by ASSERT or other commands) between the matching PUSH and POP operators are flushed, and the context is completely restored to what it was right before the PUSH.
from the top of the stack, and pops it off the stack. Any changes to the logical context (by ASSERT or other commands) between the matching PUSH and POP operators are flushed, and the context is completely restored to what it was right before the PUSH.
PUSH and POP commands can be nested to an arbitrary depth.
QUERY <formula>;
Checks if the formula is valid in the current logical context:
![\[\Gamma\models\phi.\]](form_48.png)
When the answer is "Valid", the logical context does not change. However, if the answer is "InValid", then the current logical context is augmented with new atomic formulas C such that the entire context 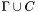 remains logically consistent, but
remains logically consistent, but 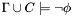 . In other words, C becomes a counterexample for
. In other words, C becomes a counterexample for 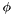 .
.
This counterexample can be printed out using WHERE or COUNTEREXAMPLE commands. In the current release, both commands produce the same output (they print the entire logical context). In the future, COUNTEREXAMPLE will become more selective, and will only print those formulas from the context which are sufficient for a counterexample.
Since QUERY may modify the current context, if you need to check several formulas in a row in the same context, it is a good idea to surround QUERY command by PUSH and POP in order to preserve the current context:
PUSH; QUERY <formula> POP;
Note on Completeness: Counterexample is only guaranteed to satisfy the above property for the logical fragment with a complete decision procedure. Since CVC Lite supports quantifiers and non-linear intereger arithmetic, it is inherently incomplete. Therefore, the ``counterexample'' C might not necessarily be a counterexample, but simply a set of additional formulas from which CVC Lite could not prove the queried formula, and gave up.
DUMP_PROOF DUMP_ASSUMPTIONS
Print out a proof of the latest QUERY (if it was successfully proven), and the assumptions (formulas) from the current logical context used in the proof.
Note, that DUMP_PROOF uses free proof variables for the proofs of assumptions without defining them, and therefore, is not necessarily the best way to check the proofs. See DUMP_CLOSURE_PROOF.
DUMP_CLOSURE DUMP_CLOSURE_PROOF
If the last QUERY successfully proved a formula 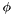 using only a subset
using only a subset 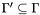 of the current logical context, then
of the current logical context, then DUMP_CLOSURE prints a formula
![\[\bigwedge\Gamma'\Rightarrow\phi,\]](form_51.png)
which is now valid by itself, independent of the logical context, and DUMP_CLOSURE_PROOF prints out a proof of that formula.
This eliminates the problem of undefined proof variables from DUMP_PROOF. In addition, the proofs of all the relevant TCCs are incorporated into the proof of the closure using a 3-valued implication introduction rule. See the next section on Partial Functions and TCCs for details.
x/y = x/y always true (valid)? What about the case when y=0?
CVC Lite supports partial using Type Correctness Conditions, or TCCs for short. A TCC for a formula or a term t is a formula 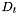 such that
such that 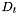 is true if and only if the term
is true if and only if the term t is defined.
For example, the expression x/y is defined when y/=0, and therefore, 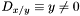 . Similarly, the entire equality
. Similarly, the entire equality x/y=x/y has exactly the same TCC.
Not all terms and subformulas need to be defined in order for a formula to have a well-defined meaning. For instance, a formula
![\[y\ne 0 \Rightarrow x/y = x/y\]](form_53.png)
is always true, even when y=0, since then the antecedent of the implication becomes false, and the value of the conclusion becomes irrelevant (in particular, it may be undefined).
More formally, CVC Lite adopts a Kleene version of the 3-valued semantics. Under this semantics, undefined value "propagates" up through the terms and predicates (so they are strict), but the logical connectives and if-then-else operators allow irrelevant subterms and subformulas to be undefined (they are non-strict).
For example, an expression f(x/(y+1), 42) is undefined for y=-1, but the expression
IF y > 0 THEN f(x/(y+1), 42) ELSE 0 ENDIF
is always defined, provided f is a total function. Similarly, the formula
![\[(x/y < x/y) \Rightarrow y = 0\]](form_54.png)
is a valid formula, since the antecedent is always false (and hence, the formula is always true) except when y=0, in which case the antecedent is irrelevant (and, in fact, it is undefined). This formula might look bizarre at first, but it is consistent with the classical (total) first-order logic, and with our general mathematical intuition (think what a high school math teacher would say about it!).
Division is not the only partial function in CVC Lite. User-defined functions can be partial if they are defined on a subtype. For example, INT is a subtype of REAL, and any subrange is a subtype of INT. Therefore, an uninterpreted function
f: [0..100] -> INT;
is a partial function defined only on integer values from 0 to 100. It is possible, however, to apply this function to a term of type REAL, and the formula may still make sense. For example:
x: [5..10]; y: REAL; ASSERT y+1/2 = x; ASSERT f(y+3/2) < 15;
is a perfectly reasonable sequence of assertions (from the mathematical point of view), and therefore, is accepted by CVC Lite. However, changing the order of these assertions becomes problematic:
x: [5..10]; y: REAL; ASSERT f(y+3/2) < 15; ASSERT y+1/2 = x;
This will result in a TCC failure, since at the time of the first ASSERT it is not yet known that y+3/2 is an integer between 0 and 100. CVC Lite enforces a rule that the TCC for a formula in ASSERT or QUERY is valid in the current logical context. It will not "look into the future" for possible justification of a failed TCC. Think of it as an extension of the well-known programming paradigm: an object must be defined before its use; similarly, a formula must make mathematical sense in the context it appears.
Whenever an ASSERT or QUERY command is executed, the corresponding TCC is first checked for validity in the current context (before the formula is added to the logical context). If the TCC is proven valid, then the formula itself is added to the context (in ASSERT) or checked for validity (in QUERY).
The command DUMP_TCC prints out the TCC for the latest ASSERT or QUERY, and DUMP_TCC_PROOF produces the corresponding proof (assuming TCC has been proven successfully).
The proofs of the corresponding TCCs are also used in the proof of the closure of a valid formula (see DUMP_CLOSURE_PROOF in the previous section).
 1.4.4
1.4.4