CVCL::ArithTheoremProducer Class Reference

#include <arith_theorem_producer.h>

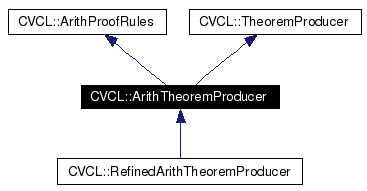
Inheritance diagram for CVCL::ArithTheoremProducer:

[legend]Collaboration diagram for CVCL::ArithTheoremProducer:

[legend]List of all members.

Public Member Functions

ArithTheoremProducer (TheoremManager *tm, TheoryArith *theoryArith)
Constructor.
Expr rat (Rational r)
Create Expr from Rational (for convenience).
Type realType ()
Type intType ()
Expr darkShadow (const Expr &lhs, const Expr &rhs)
Construct the dark shadow expression representing lhs <= rhs.
Expr grayShadow (const Expr &v, const Expr &e, const Rational &c1, const Rational &c2)
Construct the gray shadow expression representing c1 <= v - e <= c2.
virtual Theorem uMinusToMult (const Expr &e)
==> -(e) = (-1) * e
virtual Theorem minusToPlus (const Expr &x, const Expr &y)
==> x - y = x + (-1) * y
virtual Theorem canonUMinusToDivide (const Expr &e)
-(e) ==> e / (-1); takes 'e'
virtual Theorem canonDivideConst (const Expr &c, const Expr &d)
(c) / d ==> (c/d), takes c and d
virtual Theorem canonDivideMult (const Expr &cx, const Expr &d)
(c * x) / d ==> (c/d) * x, takes (c*x) and d
virtual Theorem canonDividePlus (const Expr &e, const Expr &d)
(+ c ...)/d ==> push division to all the coefficients.
virtual Theorem canonDivideVar (const Expr &e, const Expr &e)
x / d ==> (1/d) * x, takes x and d
virtual Expr simplifiedMultExpr (std::vector< Expr > &mulKids)
virtual Expr canonMultConstMult (const Expr &c, const Expr &e)
virtual Expr canonMultConstPlus (const Expr &e1, const Expr &e2)
virtual Expr canonMultPowPow (const Expr &e1, const Expr &e2)
virtual Expr canonMultPowLeaf (const Expr &e1, const Expr &e2)
virtual Expr canonMultLeafLeaf (const Expr &e1, const Expr &e2)
virtual Expr canonMultLeafOrPowMult (const Expr &e1, const Expr &e2)
virtual Expr canonCombineLikeTerms (const std::vector< Expr > &sumExprs)
virtual Expr canonMultLeafOrPowOrMultPlus (const Expr &e1, const Expr &e2)
virtual Expr canonMultPlusPlus (const Expr &e1, const Expr &e2)
virtual Theorem canonMultMtermMterm (const Expr &e)
virtual Theorem canonPlus (const Expr &e)
Canonize (PLUS t1 ... tn).
virtual Theorem canonMult (const Expr &e)
Canonize (MULT t1 ... tn).
virtual Theorem canonInvertConst (const Expr &e)
virtual Theorem canonInvertLeaf (const Expr &e)
virtual Theorem canonInvertPow (const Expr &e)
virtual Theorem canonInvertMult (const Expr &e)
virtual Theorem canonInvert (const Expr &e)
==> 1/e = e' where e' is canonical; takes e.
virtual Theorem canonDivide (const Expr &e)
Canonize t1/t2.
virtual Theorem canonMultTermConst (const Expr &c, const Expr &t)
t*c ==> c*t, takes constant c and term t
virtual Theorem canonMultTerm1Term2 (const Expr &t1, const Expr &t2)
t1*t2 ==> Error, takes t1 and t2 where both are non-constants
virtual Theorem canonMultZero (const Expr &e)
0*t ==> 0, takes 0*t
virtual Theorem canonMultOne (const Expr &e)
1*t ==> t, takes 1*t
virtual Theorem canonMultConstConst (const Expr &c1, const Expr &c2)
c1*c2 ==> c', takes constant c1*c2
virtual Theorem canonMultConstTerm (const Expr &c1, const Expr &c2, const Expr &t)
c1*(c2*t) ==> c'*t, takes c1 and c2 and t
virtual Theorem canonMultConstSum (const Expr &c1, const Expr &sum)
c1*(+ c2 v1 ...) ==> (+ c' c1v1 ...), takes c1 and the sum
virtual Theorem canonPowConst (const Expr &pow)
c^n = c' (compute the constant power expression)
virtual Theorem canonFlattenSum (const Expr &e)
flattens the input. accepts a PLUS expr
virtual Theorem canonComboLikeTerms (const Expr &e)
combine like terms. accepts a flattened PLUS expr
virtual Theorem constPredicate (const Expr &e)
e0 @ e1 <==> true | false, where @ is {=,<,<=,>,>=}
virtual Theorem rightMinusLeft (const Expr &e)
e[0] @ e[1] <==> 0 @ e[1] - e[0], where @ is {=,<,<=,>,>=}
virtual Theorem plusPredicate (const Expr &x, const Expr &y, const Expr &z, int kind)
x @ y <==> x + z @ y + z, where @ is {=,<,<=,>,>=} (given as 'kind')
virtual Theorem multEqn (const Expr &x, const Expr &y, const Expr &z)
x = y <==> x * z = y * z, where z is a non-zero constant
virtual Theorem multIneqn (const Expr &e, const Expr &z)
Multiplying inequation by a non-zero constant.
virtual Theorem flipInequality (const Expr &e)
"op1 GE|GT op2" <==> op2 LE|LT op1
Theorem negatedInequality (const Expr &e)
Propagating negation over <,<=,>,>=.
Theorem realShadow (const Theorem &alphaLTt, const Theorem &tLTbeta)
Real shadow: a <(=) t, t <(=) b ==> a <(=) b.
Theorem realShadowEq (const Theorem &alphaLEt, const Theorem &tLEalpha)
alpha <= t <= alpha ==> t = alpha
Theorem finiteInterval (const Theorem &aLEt, const Theorem &tLEac, const Theorem &isInta, const Theorem &isIntt)
Finite interval for integers: a <= t <= a + c ==> G(t, a, 0, c).
Theorem darkGrayShadow2ab (const Theorem &betaLEbx, const Theorem &axLEalpha, const Theorem &isIntAlpha, const Theorem &isIntBeta, const Theorem &isIntx)
Dark & Gray shadows when a <= b.
Theorem darkGrayShadow2ba (const Theorem &betaLEbx, const Theorem &axLEalpha, const Theorem &isIntAlpha, const Theorem &isIntBeta, const Theorem &isIntx)
Dark & Gray shadows when b <= a.
Theorem expandDarkShadow (const Theorem &darkShadow)
Theorem expandGrayShadow0 (const Theorem &grayShadow)
GRAY_SHADOW(v, e, c, c) ==> v=e+c.
Theorem splitGrayShadow (const Theorem &grayShadow)
G(x, e, c1, c2) ==> (G1 or G2) and (!G1 or !G2).
Theorem expandGrayShadow (const Theorem &grayShadow)
G(x, e, c1, c2) ==> e+c1 <= x AND x <= e+c2.
Theorem expandGrayShadowConst (const Theorem &grayShadow)
Optimized rules: GRAY_SHADOW(a*x, c, c1, c2) ==> [expansion].
Theorem grayShadowConst (const Theorem &g)
|- G(ax, c, c1, c2) ==> |- G(x, 0, ceil((c1+c)/a), floor((c2+c)/a))
Rational constRHSGrayShadow (const Rational &c, const Rational &b, const Rational &a)
Implements j(c,b,a).
Theorem lessThanToLE (const Theorem &less, const Theorem &isIntLHS, const Theorem &isIntRHS, bool changeRight)
Theorem intVarEqnConst (const Expr &eqn, const Theorem &isIntx)
Theorem eqElimIntRule (const Theorem &eqn, const Theorem &isIntx, const std::vector< Theorem > &isIntVars)
Equality elimination rule for integers:
$\frac{\mathsf{int}(a\cdot x)\quad \mathsf{int}(C+\sum_{i=1}^{n}a_{i}\cdot x_{i})} {a\cdot x=C+\sum_{i=1}^{n}a_{i}\cdot x_{i} \quad\equiv\quad x=t_{2}\wedge 0=t_{3}}$
See the detailed description for explanations.
$\frac{\Gamma\models ax=t\quad \Gamma'\models\mathsf{int}(x)\quad \{\Gamma_i\models\mathsf{int}(x_i) | x_i\mbox{ is var in }t\}} {\Gamma,\Gamma',\bigcup_i\Gamma_i\models \exists (y:\mathrm{int}).\ x=t_2(y)\wedge 0=t_3(y)}$
See detailed docs for more information.
Theorem isIntConst (const Expr &e)
return e <=> TRUE/FALSE for e == IS_INTEGER(c), where c is a constant
Theorem equalLeaves1 (const Theorem &e)
Theorem equalLeaves2 (const Theorem &e)
Theorem equalLeaves3 (const Theorem &e)
Theorem equalLeaves4 (const Theorem &e)
Theorem diseqToIneq (const Theorem &diseq)
x /= y ==> (x < y) OR (x > y)

Static Public Member Functions

static bool greaterthan (const Expr &, const Expr &)

Private Member Functions

Auxiliary functions for eqElimIntRule()

Methods that compute the subterms used in eqElimIntRule()

Rational modEq (const Rational &i, const Rational &m)
Compute the special modulus: i - m*floor(i/m+1/2).
Expr create_t (const Expr &eqn)
Create the term 't'. See eqElimIntRule().
Expr create_t2 (const Expr &lhs, const Expr &rhs, const Expr &t)
Create the term 't2'. See eqElimIntRule().
Expr create_t3 (const Expr &lhs, const Expr &rhs, const Expr &t)
Create the term 't3'. See eqElimIntRule().
void sumModM (std::vector< Expr > &summands, const Expr &sum, const Rational &m, const Rational &divisor)
Takes sum = a_0 + a_1*x_1+...+a_n*x_n and returns the vector of similar monomials (in 'summands') with coefficients mod(a_i, m). If divide flag is true, the coefficients will be mod(a_i,m)/m.
Expr monomialModM (const Expr &e, const Rational &m, const Rational &divisor)
Compute the special modulus: i - m*floor(i/m+1/2).
void sumMulF (std::vector< Expr > &summands, const Expr &sum, const Rational &m, const Rational &divisor)
Compute the special modulus: i - m*floor(i/m+1/2).
Expr monomialMulF (const Expr &e, const Rational &m, const Rational &divisor)
Compute the special modulus: i - m*floor(i/m+1/2).
Rational f (const Rational &i, const Rational &m)
Compute floor(i/m+1/2) + mod(i,m).
Expr substitute (const Expr &term, ExprMap< Expr > &eMap)
Compute the special modulus: i - m*floor(i/m+1/2).

Private Attributes

TheoryArith * d_theoryArith

Detailed Description

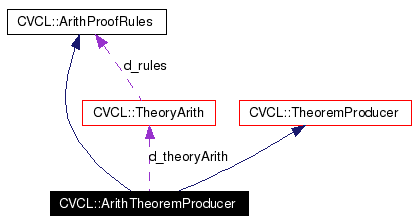
Definition at line 40 of file arith_theorem_producer.h.

Constructor & Destructor Documentation

CVCL::ArithTheoremProducer::ArithTheoremProducer ( TheoremManager * tm,

TheoryArith * theoryArith

) [inline]

Constructor.

Definition at line 74 of file arith_theorem_producer.h.

Member Function Documentation

Rational ArithTheoremProducer::modEq ( const Rational & i,

const Rational & m

) [private]

Compute the special modulus: i - m*floor(i/m+1/2).

Definition at line 2019 of file arith_theorem_producer.cpp.
References CVCL::floor(), CVCL::Rational::toString(), and CVCL::TRACE.
Referenced by f(), and monomialModM().

Expr ArithTheoremProducer::create_t ( const Expr & eqn ) [private]

Create the term 't'. See eqElimIntRule().

Definition at line 1959 of file arith_theorem_producer.cpp.
References CVCL::Expr::getRational(), CVCL::isMult(), CVCL::isPlus(), monomialModM(), CVCL::multExpr(), CVCL::plusExpr(), rat(), sumModM(), CVCL::Rational::toString(), and CVCL::Expr::toString().

Expr ArithTheoremProducer::create_t2 ( const Expr & lhs,

const Expr & rhs,

const Expr & t

) [private]

Create the term 't2'. See eqElimIntRule().

Definition at line 1978 of file arith_theorem_producer.cpp.
References CVCL::Expr::getRational(), CVCL::isPlus(), CVCL::Expr::isRational(), monomialModM(), CVCL::plusExpr(), rat(), sumModM(), and CVCL::Rational::toString().

Expr ArithTheoremProducer::create_t3 ( const Expr & lhs,

const Expr & rhs,

const Expr & t

) [private]

Create the term 't3'. See eqElimIntRule().

Definition at line 1998 of file arith_theorem_producer.cpp.
References CVCL::Expr::getRational(), CVCL::isPlus(), CVCL::Expr::isRational(), monomialMulF(), CVCL::plusExpr(), rat(), sumMulF(), and CVCL::Rational::toString().

void CVCL::ArithTheoremProducer::sumModM ( std::vector< Expr > & summands,

const Expr & sum,

const Rational & m,

const Rational & divisor

) [private]

Takes sum = a_0 + a_1*x_1+...+a_n*x_n and returns the vector of similar monomials (in 'summands') with coefficients mod(a_i, m). If divide flag is true, the coefficients will be mod(a_i,m)/m.

Referenced by create_t(), and create_t2().

Expr ArithTheoremProducer::monomialModM ( const Expr & e,

const Rational & m,

const Rational & divisor

) [private]

Compute the special modulus: i - m*floor(i/m+1/2).

Definition at line 2055 of file arith_theorem_producer.cpp.
References CVCL::Expr::arity(), CVCL::Expr::getKids(), CVCL::Expr::getRational(), CVCL::isMult(), CVCL::Expr::isNull(), modEq(), CVCL::multExpr(), rat(), CVCL::Expr::toString(), CVCL::Rational::toString(), and CVCL::TRACE.
Referenced by create_t(), and create_t2().

void CVCL::ArithTheoremProducer::sumMulF ( std::vector< Expr > & summands,

const Expr & sum,

const Rational & m,

const Rational & divisor

) [private]

Compute the special modulus: i - m*floor(i/m+1/2).

Referenced by create_t3().

Expr ArithTheoremProducer::monomialMulF ( const Expr & e,

const Rational & m,

const Rational & divisor

) [private]

Compute the special modulus: i - m*floor(i/m+1/2).

Definition at line 2103 of file arith_theorem_producer.cpp.
References f(), CVCL::isMult(), CVCL::multExpr(), rat(), and CVCL::Rational::toString().
Referenced by create_t3().

Rational ArithTheoremProducer::f ( const Rational & i,

const Rational & m

) [private]

Compute floor(i/m+1/2) + mod(i,m).

Definition at line 2028 of file arith_theorem_producer.cpp.
References CVCL::floor(), modEq(), and CVCL::Rational::toString().
Referenced by monomialMulF().

Expr ArithTheoremProducer::substitute ( const Expr & term,

ExprMap< Expr > & eMap

) [private]

Compute the special modulus: i - m*floor(i/m+1/2).

Definition at line 2120 of file arith_theorem_producer.cpp.
References CVCL::Expr::begin(), CVCL::Expr::end(), CVCL::ExprMap< Data >::end(), CVCL::ExprMap< Data >::find(), CVCL::isMult(), CVCL::isPlus(), and CVCL::plusExpr().

Expr CVCL::ArithTheoremProducer::rat ( Rational r ) [inline]

Create Expr from Rational (for convenience).

Reimplemented in CVCL::RefinedArithTheoremProducer.
Definition at line 78 of file arith_theorem_producer.h.
References CVCL::TheoremProducer::d_em, and CVCL::ExprManager::newRatExpr().
Referenced by canonCombineLikeTerms(), canonComboLikeTerms(), canonDivideConst(), canonDivideMult(), canonDividePlus(), canonDivideVar(), canonInvertConst(), canonInvertLeaf(), canonInvertMult(), canonInvertPow(), canonMultConstConst(), canonMultConstMult(), canonMultConstTerm(), canonMultLeafLeaf(), canonMultLeafOrPowMult(), canonMultOne(), canonMultPowLeaf(), canonMultPowPow(), canonMultZero(), canonPowConst(), canonUMinusToDivide(), create_t(), create_t2(), create_t3(), darkGrayShadow2ab(), darkGrayShadow2ba(), expandGrayShadow(), expandGrayShadowConst(), grayShadowConst(), intVarEqnConst(), lessThanToLE(), minusToPlus(), monomialModM(), monomialMulF(), rightMinusLeft(), simplifiedMultExpr(), and uMinusToMult().

Type CVCL::ArithTheoremProducer::realType ( ) [inline]

Definition at line 79 of file arith_theorem_producer.h.
References d_theoryArith, and CVCL::TheoryArith::realType().

Type CVCL::ArithTheoremProducer::intType ( ) [inline]

Definition at line 80 of file arith_theorem_producer.h.
References d_theoryArith, and CVCL::TheoryArith::intType().

Expr CVCL::ArithTheoremProducer::darkShadow ( const Expr & lhs,

const Expr & rhs

) [inline]

Construct the dark shadow expression representing lhs <= rhs.

Definition at line 82 of file arith_theorem_producer.h.
References d_theoryArith, and CVCL::TheoryArith::darkShadow().
Referenced by darkGrayShadow2ab(), and darkGrayShadow2ba().

Expr CVCL::ArithTheoremProducer::grayShadow ( const Expr & v,

const Expr & e,

const Rational & c1,

const Rational & c2

) [inline]

Construct the gray shadow expression representing c1 <= v - e <= c2.
Alternatively, v = e + i for some i s.t. c1 <= i <= c2
Definition at line 88 of file arith_theorem_producer.h.
References d_theoryArith, and CVCL::TheoryArith::grayShadow().
Referenced by darkGrayShadow2ab(), darkGrayShadow2ba(), finiteInterval(), grayShadowConst(), and splitGrayShadow().

Theorem ArithTheoremProducer::uMinusToMult ( const Expr & e ) [virtual]

==> -(e) = (-1) * e

Implements CVCL::ArithProofRules.
Reimplemented in CVCL::RefinedArithTheoremProducer.
Definition at line 63 of file arith_theorem_producer.cpp.
References CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), rat(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::minusToPlus ( const Expr & x,

const Expr & y

) [virtual]

==> x - y = x + (-1) * y

Implements CVCL::ArithProofRules.
Reimplemented in CVCL::RefinedArithTheoremProducer.
Definition at line 72 of file arith_theorem_producer.cpp.
References CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), rat(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::canonUMinusToDivide ( const Expr & e ) [virtual]

-(e) ==> e / (-1); takes 'e'
Canon Rule for unary minus: it just converts it to division by -1, the result is not yet canonical:
Implements CVCL::ArithProofRules.
Definition at line 83 of file arith_theorem_producer.cpp.
References CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), rat(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::canonDivideConst ( const Expr & c,

const Expr & d

) [virtual]

(c) / d ==> (c/d), takes c and d
Canon Rules for division by constant 'd'
Implements CVCL::ArithProofRules.
Definition at line 93 of file arith_theorem_producer.cpp.
References CVCL::TheoremProducer::d_hole, CVCL::Expr::getRational(), CVCL::isRational(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), rat(), CVCL::Expr::toString(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::canonDivideMult ( const Expr & cx,

const Expr & d

) [virtual]

(c * x) / d ==> (c/d) * x, takes (c*x) and d

Implements CVCL::ArithProofRules.
Definition at line 113 of file arith_theorem_producer.cpp.
References CVCL::Expr::getRational(), CVCL::isMult(), CVCL::isRational(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), rat(), CVCL::Expr::toString(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::canonDividePlus ( const Expr & e,

const Expr & d

) [virtual]

(+ c ...)/d ==> push division to all the coefficients.
The result is not canonical, but canonizing the summands will make it canonical. Takes (+ c ...) and d
Implements CVCL::ArithProofRules.
Definition at line 142 of file arith_theorem_producer.cpp.
References CVCL::Expr::arity(), CVCL::Expr::begin(), CVCL::Expr::end(), CVCL::isPlus(), CVCL::isRational(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), CVCL::plusExpr(), rat(), CVCL::Expr::toString(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::canonDivideVar ( const Expr & e,

const Expr & e

) [virtual]

x / d ==> (1/d) * x, takes x and d

Implements CVCL::ArithProofRules.
Definition at line 166 of file arith_theorem_producer.cpp.
References CVCL::Expr::getRational(), CVCL::isRational(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), rat(), CVCL::Expr::toString(), and CVCL::TheoremProducer::withProof().

bool ArithTheoremProducer::greaterthan ( const Expr & ,

const Expr &

) [static]

Definition at line 2146 of file arith_theorem_producer.cpp.
References CVCL::Expr::arity(), CVCL::Expr::begin(), CVCL::Expr::end(), CVCL::Expr::getKind(), CVCL::Expr::getRational(), CVCL::Expr::isRational(), CVCL::MULT, CVCL::PLUS, CVCL::POW, and CVCL::RATIONAL_EXPR.
Referenced by MonomialLess::operator()().

Expr ArithTheoremProducer::simplifiedMultExpr ( std::vector< Expr > & mulKids ) [virtual]

Definition at line 202 of file arith_theorem_producer.cpp.
References CVCL::multExpr(), and rat().
Referenced by canonMultConstMult(), canonMultLeafLeaf(), canonMultLeafOrPowMult(), canonMultPowLeaf(), and canonMultPowPow().

Expr ArithTheoremProducer::canonMultConstMult ( const Expr & c,

const Expr & e

) [virtual]

Definition at line 215 of file arith_theorem_producer.cpp.
References CVCL::Expr::arity(), CVCL::Expr::begin(), CVCL::Expr::end(), CVCL::Expr::getKind(), CVCL::Expr::getRational(), CVCL::Expr::isRational(), CVCL::MULT, rat(), simplifiedMultExpr(), and CVCL::Expr::toString().
Referenced by canonMultMtermMterm().

Expr ArithTheoremProducer::canonMultConstPlus ( const Expr & e1,

const Expr & e2

) [virtual]

Definition at line 237 of file arith_theorem_producer.cpp.
References CVCL::Expr::arity(), CVCL::Expr::begin(), canonMultMtermMterm(), d_theoryArith, CVCL::Expr::end(), CVCL::Expr::getKind(), CVCL::Expr::getOp(), CVCL::Theorem::getRHS(), CVCL::Expr::isRational(), CVCL::PLUS, and CVCL::Theory::substitutivityRule().
Referenced by canonMultMtermMterm().

Expr ArithTheoremProducer::canonMultPowPow ( const Expr & e1,

const Expr & e2

) [virtual]

Definition at line 256 of file arith_theorem_producer.cpp.
References CVCL::Expr::getKind(), CVCL::Expr::getRational(), CVCL::POW, CVCL::powExpr(), rat(), and simplifiedMultExpr().
Referenced by canonMultMtermMterm().

Expr ArithTheoremProducer::canonMultPowLeaf ( const Expr & e1,

const Expr & e2

) [virtual]

Definition at line 296 of file arith_theorem_producer.cpp.
References CVCL::Expr::getKind(), CVCL::Expr::getRational(), CVCL::POW, CVCL::powExpr(), rat(), and simplifiedMultExpr().
Referenced by canonMultMtermMterm().

Expr ArithTheoremProducer::canonMultLeafLeaf ( const Expr & e1,

const Expr & e2

) [virtual]

Definition at line 335 of file arith_theorem_producer.cpp.
References CVCL::powExpr(), rat(), and simplifiedMultExpr().
Referenced by canonMultMtermMterm().

Expr ArithTheoremProducer::canonMultLeafOrPowMult ( const Expr & e1,

const Expr & e2

) [virtual]

Definition at line 363 of file arith_theorem_producer.cpp.
References CVCL::Expr::arity(), CVCL::Expr::begin(), CVCL::Expr::end(), CVCL::Expr::getKind(), CVCL::Expr::getRational(), CVCL::MULT, CVCL::POW, CVCL::powExpr(), rat(), and simplifiedMultExpr().
Referenced by canonMultMtermMterm().

Expr ArithTheoremProducer::canonCombineLikeTerms ( const std::vector< Expr > & sumExprs ) [virtual]

Definition at line 435 of file arith_theorem_producer.cpp.
References CVCL::Expr::arity(), CVCL::Expr::begin(), canonMultMtermMterm(), CVCL::Expr::end(), CVCL::Expr::getKind(), CVCL::Expr::getRational(), CVCL::Theorem::getRHS(), CVCL::Expr::isRational(), CVCL::MULT, CVCL::multExpr(), CVCL::plusExpr(), and rat().
Referenced by canonMultLeafOrPowOrMultPlus(), canonMultPlusPlus(), and canonPlus().

Expr ArithTheoremProducer::canonMultLeafOrPowOrMultPlus ( const Expr & e1,

const Expr & e2

) [virtual]

Definition at line 516 of file arith_theorem_producer.cpp.
References CVCL::Expr::begin(), canonCombineLikeTerms(), canonMultMtermMterm(), CVCL::Expr::end(), CVCL::Expr::getKind(), and CVCL::PLUS.
Referenced by canonMultMtermMterm().

Expr ArithTheoremProducer::canonMultPlusPlus ( const Expr & e1,

const Expr & e2

) [virtual]

Definition at line 535 of file arith_theorem_producer.cpp.
References CVCL::Expr::begin(), canonCombineLikeTerms(), canonMultMtermMterm(), CVCL::Expr::end(), CVCL::Expr::getKind(), and CVCL::PLUS.
Referenced by canonMultMtermMterm().

Theorem ArithTheoremProducer::canonMultMtermMterm ( const Expr & e ) [virtual]

Implements CVCL::ArithProofRules.
Definition at line 559 of file arith_theorem_producer.cpp.
References CVCL::Expr::arity(), CVCL::Expr::begin(), canonMultConstConst(), canonMultConstMult(), canonMultConstPlus(), canonMultLeafLeaf(), canonMultLeafOrPowMult(), canonMultLeafOrPowOrMultPlus(), canonMultOne(), canonMultPlusPlus(), canonMultPowLeaf(), canonMultPowPow(), canonMultZero(), d_theoryArith, CVCL::Expr::getKind(), CVCL::Expr::getRational(), CVCL::Theorem::getRHS(), CVCL::isMult(), CVCL::Expr::isRational(), CVCL::MULT, CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), CVCL::PLUS, CVCL::POW, CVCL::RATIONAL_EXPR, CVCL::Theory::reflexivityRule(), CVCL::Expr::toString(), and CVCL::TheoremProducer::withProof().
Referenced by canonCombineLikeTerms(), canonInvertMult(), canonMult(), canonMultConstPlus(), canonMultLeafOrPowOrMultPlus(), and canonMultPlusPlus().

Theorem ArithTheoremProducer::canonPlus ( const Expr & e ) [virtual]

Canonize (PLUS t1 ... tn).

Implements CVCL::ArithProofRules.
Reimplemented in CVCL::RefinedArithTheoremProducer.
Definition at line 725 of file arith_theorem_producer.cpp.
References CVCL::Expr::begin(), canonCombineLikeTerms(), CVCL::Expr::end(), CVCL::Expr::getKind(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), CVCL::PLUS, and CVCL::TheoremProducer::withProof().
Referenced by CVCL::RefinedArithTheoremProducer::canonPlus().

Theorem ArithTheoremProducer::canonMult ( const Expr & e ) [virtual]

Canonize (MULT t1 ... tn).

Implements CVCL::ArithProofRules.
Definition at line 759 of file arith_theorem_producer.cpp.
References CVCL::Expr::arity(), CVCL::Expr::begin(), canonMultMtermMterm(), CVCL::Expr::end(), CVCL::Expr::getKind(), CVCL::Theorem::getRHS(), CVCL::MULT, CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), and CVCL::TheoremProducer::withProof().
Referenced by canonDivide().

Theorem ArithTheoremProducer::canonInvertConst ( const Expr & e ) [virtual]

Definition at line 778 of file arith_theorem_producer.cpp.
References CVCL::Expr::getRational(), CVCL::isRational(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), rat(), CVCL::Expr::toString(), and CVCL::TheoremProducer::withProof().
Referenced by canonInvert().

Theorem ArithTheoremProducer::canonInvertLeaf ( const Expr & e ) [virtual]

Definition at line 795 of file arith_theorem_producer.cpp.
References CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), CVCL::powExpr(), rat(), and CVCL::TheoremProducer::withProof().
Referenced by canonInvert().

Theorem ArithTheoremProducer::canonInvertPow ( const Expr & e ) [virtual]

Definition at line 808 of file arith_theorem_producer.cpp.
References CVCL::Expr::getKind(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), CVCL::POW, CVCL::powExpr(), rat(), CVCL::Expr::toString(), and CVCL::TheoremProducer::withProof().
Referenced by canonInvert().

Theorem ArithTheoremProducer::canonInvertMult ( const Expr & e ) [virtual]

Definition at line 828 of file arith_theorem_producer.cpp.
References CVCL::Expr::arity(), canonInvert(), canonMultMtermMterm(), CVCL::Expr::getKind(), CVCL::Theorem::getRHS(), CVCL::MULT, CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), rat(), CVCL::Expr::toString(), and CVCL::TheoremProducer::withProof().
Referenced by canonInvert().

Theorem ArithTheoremProducer::canonInvert ( const Expr & e ) [virtual]

==> 1/e = e' where e' is canonical; takes e.

Implements CVCL::ArithProofRules.
Definition at line 852 of file arith_theorem_producer.cpp.
References canonInvertConst(), canonInvertLeaf(), canonInvertMult(), canonInvertPow(), CVCL::Expr::getKind(), CVCL::MULT, CVCL::PLUS, CVCL::POW, CVCL::RATIONAL_EXPR, and CVCL::Expr::toString().
Referenced by canonDivide(), and canonInvertMult().

Theorem ArithTheoremProducer::canonDivide ( const Expr & e ) [virtual]

Canonize t1/t2.

Implements CVCL::ArithProofRules.
Definition at line 875 of file arith_theorem_producer.cpp.
References canonInvert(), canonMult(), d_theoryArith, CVCL::DIVIDE, CVCL::Expr::getKind(), CVCL::Theorem::getRHS(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), CVCL::Expr::toString(), CVCL::Theory::transitivityRule(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::canonMultTermConst ( const Expr & c,

const Expr & t

) [virtual]

t*c ==> c*t, takes constant c and term t

Implements CVCL::ArithProofRules.
Definition at line 894 of file arith_theorem_producer.cpp.
References CVCL::isRational(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), CVCL::Expr::toString(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::canonMultTerm1Term2 ( const Expr & t1,

const Expr & t2

) [virtual]

t1*t2 ==> Error, takes t1 and t2 where both are non-constants

Implements CVCL::ArithProofRules.
Definition at line 909 of file arith_theorem_producer.cpp.
References CVCL::Expr::toString().

Theorem ArithTheoremProducer::canonMultZero ( const Expr & e ) [virtual]

0*t ==> 0, takes 0*t

Implements CVCL::ArithProofRules.
Definition at line 923 of file arith_theorem_producer.cpp.
References CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), rat(), and CVCL::TheoremProducer::withProof().
Referenced by canonMultMtermMterm().

Theorem ArithTheoremProducer::canonMultOne ( const Expr & e ) [virtual]

1*t ==> t, takes 1*t

Implements CVCL::ArithProofRules.
Definition at line 932 of file arith_theorem_producer.cpp.
References CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), rat(), and CVCL::TheoremProducer::withProof().
Referenced by canonMultMtermMterm().

Theorem ArithTheoremProducer::canonMultConstConst ( const Expr & c1,

const Expr & c2

) [virtual]

c1*c2 ==> c', takes constant c1*c2

Implements CVCL::ArithProofRules.
Definition at line 942 of file arith_theorem_producer.cpp.
References CVCL::Expr::getRational(), CVCL::isRational(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), rat(), CVCL::Expr::toString(), and CVCL::TheoremProducer::withProof().
Referenced by canonMultMtermMterm().

Theorem ArithTheoremProducer::canonMultConstTerm ( const Expr & c1,

const Expr & c2,

const Expr & t

) [virtual]

c1*(c2*t) ==> c'*t, takes c1 and c2 and t

Implements CVCL::ArithProofRules.
Definition at line 961 of file arith_theorem_producer.cpp.
References CVCL::Expr::getRational(), CVCL::isRational(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), rat(), CVCL::Expr::toString(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::canonMultConstSum ( const Expr & c1,

const Expr & sum

) [virtual]

c1*(+ c2 v1 ...) ==> (+ c' c1v1 ...), takes c1 and the sum

Implements CVCL::ArithProofRules.
Definition at line 982 of file arith_theorem_producer.cpp.
References CVCL::Expr::begin(), CVCL::Expr::end(), CVCL::Expr::getKind(), CVCL::isRational(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), CVCL::PLUS, CVCL::plusExpr(), CVCL::Expr::toString(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::canonPowConst ( const Expr & pow ) [virtual]

c^n = c' (compute the constant power expression)

Implements CVCL::ArithProofRules.
Definition at line 1006 of file arith_theorem_producer.cpp.
References CVCL::Expr::arity(), CVCL::Expr::getKind(), CVCL::Expr::getRational(), CVCL::Rational::isInteger(), CVCL::Expr::isRational(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), CVCL::pow(), CVCL::POW, rat(), CVCL::Expr::toString(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::canonFlattenSum ( const Expr & e ) [virtual]

flattens the input. accepts a PLUS expr

Implements CVCL::ArithProofRules.
Definition at line 1029 of file arith_theorem_producer.cpp.
References CVCL::Expr::begin(), CVCL::Expr::end(), CVCL::Expr::getKind(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), CVCL::PLUS, CVCL::plusExpr(), CVCL::Expr::toString(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::canonComboLikeTerms ( const Expr & e ) [virtual]

combine like terms. accepts a flattened PLUS expr

Implements CVCL::ArithProofRules.
Definition at line 1057 of file arith_theorem_producer.cpp.
References CVCL::ExprMap< Data >::begin(), CVCL::Expr::begin(), CVCL::ExprMap< Data >::count(), CVCL::ExprMap< Data >::end(), CVCL::Expr::end(), CVCL::isMult(), CVCL::isPlus(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), CVCL::plusExpr(), rat(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::constPredicate ( const Expr & e ) [virtual]

e0 @ e1 <==> true | false, where @ is {=,<,<=,>,>=}

Parameters:

e takes e is (e0@e1) where e0 and e1 are constants

Implements CVCL::ArithProofRules.
Definition at line 1120 of file arith_theorem_producer.cpp.
References CVCL::Expr::arity(), CVCL::TheoremProducer::d_em, CVCL::EQ, CVCL::ExprManager::falseExpr(), CVCL::GE, CVCL::Expr::getKind(), CVCL::Expr::getRational(), CVCL::GT, CVCL::isRational(), CVCL::LE, CVCL::LT, CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), CVCL::Expr::toString(), CVCL::ExprManager::trueExpr(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::rightMinusLeft ( const Expr & e ) [virtual]

e[0] @ e[1] <==> 0 @ e[1] - e[0], where @ is {=,<,<=,>,>=}

Implements CVCL::ArithProofRules.
Definition at line 1160 of file arith_theorem_producer.cpp.
References CVCL::EQ, CVCL::GE, CVCL::Expr::getKind(), CVCL::Expr::getOp(), CVCL::GT, CVCL::LE, CVCL::LT, CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), rat(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::plusPredicate ( const Expr & x,

const Expr & y,

const Expr & z,

int kind

) [virtual]

x @ y <==> x + z @ y + z, where @ is {=,<,<=,>,>=} (given as 'kind')

Implements CVCL::ArithProofRules.
Definition at line 1179 of file arith_theorem_producer.cpp.
References CVCL::EQ, CVCL::GE, CVCL::GT, CVCL::LE, CVCL::LT, CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::multEqn ( const Expr & x,

const Expr & y,

const Expr & z

) [virtual]

x = y <==> x * z = y * z, where z is a non-zero constant

Implements CVCL::ArithProofRules.
Definition at line 1199 of file arith_theorem_producer.cpp.
References CVCL::Expr::eqExpr(), CVCL::Expr::getRational(), CVCL::Expr::isRational(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::multIneqn ( const Expr & e,

const Expr & z

) [virtual]

Multiplying inequation by a non-zero constant.
z>0 ==> e[0] @ e[1] <==> e[0]*z @ e[1]*z
z<0 ==> e[0] @ e[1] <==> e[1]*z @ e[0]*z
for @ in {<,<=,>,>=}:
Implements CVCL::ArithProofRules.
Definition at line 1214 of file arith_theorem_producer.cpp.
References CVCL::GE, CVCL::Expr::getKind(), CVCL::Expr::getOp(), CVCL::Expr::getRational(), CVCL::GT, CVCL::Expr::isRational(), CVCL::LE, CVCL::LT, CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), CVCL::Expr::toString(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::flipInequality ( const Expr & e ) [virtual]

"op1 GE|GT op2" <==> op2 LE|LT op1

Implements CVCL::ArithProofRules.
Definition at line 1243 of file arith_theorem_producer.cpp.
References CVCL::isGE(), CVCL::isGT(), CVCL::LE, CVCL::LT, CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), CVCL::Expr::toString(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::negatedInequality ( const Expr & e ) [virtual]

Propagating negation over <,<=,>,>=.
NOT (op1 < op2) <==> (op1 >= op2)
NOT (op1 <= op2) <==> (op1 > op2)
NOT (op1 > op2) <==> (op1 <= op2)
NOT (op1 >= op2) <==> (op1 < op2)
Implements CVCL::ArithProofRules.
Definition at line 1264 of file arith_theorem_producer.cpp.
References CVCL::GE, CVCL::GT, CVCL::isGT(), CVCL::isIneq(), CVCL::isLE(), CVCL::isLT(), CVCL::Expr::isNot(), CVCL::LE, CVCL::LT, CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), CVCL::Expr::toString(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::realShadow ( const Theorem & alphaLTt,

const Theorem & tLTbeta

) [virtual]

Real shadow: a <(=) t, t <(=) b ==> a <(=) b.

Implements CVCL::ArithProofRules.
Definition at line 1294 of file arith_theorem_producer.cpp.
References CVCL::Theorem::getExpr(), CVCL::Expr::getKind(), CVCL::Theorem::getProof(), CVCL::isLE(), CVCL::isLT(), CVCL::LT, CVCL::merge(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newTheorem(), CVCL::Theorem::toString(), CVCL::TheoremProducer::withAssumptions(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::realShadowEq ( const Theorem & alphaLEt,

const Theorem & tLEalpha

) [virtual]

alpha <= t <= alpha ==> t = alpha
takes two ineqs "|- alpha LE t" and "|- t LE alpha" and returns "|- t = alpha"
Implements CVCL::ArithProofRules.
Definition at line 1332 of file arith_theorem_producer.cpp.
References CVCL::Theorem::getExpr(), CVCL::Theorem::getProof(), CVCL::isLE(), CVCL::merge(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), CVCL::Theorem::toString(), CVCL::TheoremProducer::withAssumptions(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::finiteInterval ( const Theorem & aLEt,

const Theorem & tLEac,

const Theorem & isInta,

const Theorem & isIntt

) [virtual]

Finite interval for integers: a <= t <= a + c ==> G(t, a, 0, c).

Implements CVCL::ArithProofRules.
Definition at line 1367 of file arith_theorem_producer.cpp.
References CVCL::Theorem::getExpr(), CVCL::Theorem::getProof(), grayShadow(), CVCL::isIntPred(), CVCL::isLE(), CVCL::isPlus(), CVCL::isRational(), CVCL::merge(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newTheorem(), CVCL::Expr::toString(), CVCL::TheoremProducer::withAssumptions(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::darkGrayShadow2ab ( const Theorem & betaLEbx,

const Theorem & axLEalpha,

const Theorem & isIntAlpha,

const Theorem & isIntBeta,

const Theorem & isIntx

) [virtual]

Dark & Gray shadows when a <= b.
takes two integer ineqs (i.e. all vars are ints) "|- beta <= b.x" and "|- a.x <= alpha" and checks if "1 <= a <= b" and returns (D or G) and (!D or !G), where D = Dark_Shadow(ab-1, b.alpha - a.beta), G = Gray_Shadow(a.x, alpha, -(a-1), 0).
Implements CVCL::ArithProofRules.
Definition at line 1434 of file arith_theorem_producer.cpp.
References CVCL::Expr::arity(), b, darkShadow(), CVCL::Theorem::getExpr(), CVCL::Theorem::getProof(), CVCL::Expr::getRational(), grayShadow(), CVCL::isIntPred(), CVCL::isLE(), CVCL::isMult(), CVCL::merge(), CVCL::minusExpr(), CVCL::multExpr(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newTheorem(), rat(), CVCL::Expr::toString(), CVCL::Theorem::toString(), CVCL::TheoremProducer::withAssumptions(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::darkGrayShadow2ba ( const Theorem & betaLEbx,

const Theorem & axLEalpha,

const Theorem & isIntAlpha,

const Theorem & isIntBeta,

const Theorem & isIntx

) [virtual]

Dark & Gray shadows when b <= a.
takes two integer ineqs (i.e. all vars are ints) "|- beta <= b.x" and "|- a.x <= alpha" and checks if "1 <= b < a" and returns (D or G) and (!D or !G), where D = Dark_Shadow(ab-1, b.alpha - a.beta), G = Gray_Shadow(b.x, beta, 0, b-1).
Implements CVCL::ArithProofRules.
Definition at line 1520 of file arith_theorem_producer.cpp.
References CVCL::Expr::arity(), b, darkShadow(), CVCL::Theorem::getExpr(), CVCL::Theorem::getProof(), CVCL::Expr::getRational(), grayShadow(), CVCL::isIntPred(), CVCL::isLE(), CVCL::isMult(), CVCL::merge(), CVCL::minusExpr(), CVCL::multExpr(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newTheorem(), rat(), CVCL::Expr::toString(), CVCL::Theorem::toString(), CVCL::TheoremProducer::withAssumptions(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::expandDarkShadow ( const Theorem & darkShadow ) [virtual]

takes a dark shadow and expands it into an inequality.
Implements CVCL::ArithProofRules.
Definition at line 1608 of file arith_theorem_producer.cpp.
References CVCL::Theorem::getAssumptionsCopy(), CVCL::Theorem::getExpr(), CVCL::Theorem::getProof(), CVCL::isDarkShadow(), CVCL::leExpr(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newTheorem(), CVCL::Expr::toString(), CVCL::TheoremProducer::withAssumptions(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::expandGrayShadow0 ( const Theorem & grayShadow ) [virtual]

GRAY_SHADOW(v, e, c, c) ==> v=e+c.

Implements CVCL::ArithProofRules.
Definition at line 1626 of file arith_theorem_producer.cpp.
References CVCL::Theorem::getAssumptionsCopy(), CVCL::Theorem::getExpr(), CVCL::Theorem::getProof(), CVCL::isGrayShadow(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), CVCL::Expr::toString(), CVCL::TheoremProducer::withAssumptions(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::splitGrayShadow ( const Theorem & grayShadow ) [virtual]

G(x, e, c1, c2) ==> (G1 or G2) and (!G1 or !G2).
Here G1 = G(x,e,c1,c), G2 = G(x,e,c+1,c2), and c = floor((c1+c2)/2).
Implements CVCL::ArithProofRules.
Definition at line 1654 of file arith_theorem_producer.cpp.
References CVCL::floor(), CVCL::Theorem::getAssumptionsCopy(), CVCL::Theorem::getExpr(), CVCL::Theorem::getProof(), CVCL::Expr::getRational(), grayShadow(), CVCL::isGrayShadow(), CVCL::Rational::isInteger(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newTheorem(), CVCL::Expr::toString(), CVCL::TheoremProducer::withAssumptions(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::expandGrayShadow ( const Theorem & grayShadow ) [virtual]

G(x, e, c1, c2) ==> e+c1 <= x AND x <= e+c2.

Implements CVCL::ArithProofRules.
Definition at line 1687 of file arith_theorem_producer.cpp.
References CVCL::Theorem::getAssumptionsCopy(), CVCL::Theorem::getExpr(), CVCL::Theorem::getProof(), CVCL::Expr::getRational(), CVCL::isGrayShadow(), CVCL::Rational::isInteger(), CVCL::leExpr(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newTheorem(), rat(), CVCL::Expr::toString(), CVCL::TheoremProducer::withAssumptions(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::expandGrayShadowConst ( const Theorem & grayShadow ) [virtual]

Optimized rules: GRAY_SHADOW(a*x, c, c1, c2) ==> [expansion].
Implements three versions of the rule:

$\frac{\mathrm{GRAY\_SHADOW}(ax,c,c1,c2)} {ax = c + i - \mathrm{sign}(i)\cdot j(c,i,a) \lor GRAY\_SHADOW(ax, c, i-\mathrm{sign}(i)\cdot (a+j(c,i,a)))}$

where the conclusion may become FALSE or without the GRAY_SHADOW part, depending on the values of a, c and i.
Implements CVCL::ArithProofRules.
Definition at line 1721 of file arith_theorem_producer.cpp.
References CVCL::abs(), b, constRHSGrayShadow(), CVCL::TheoremProducer::d_em, CVCL::Expr::eqExpr(), CVCL::ExprManager::falseExpr(), CVCL::Theorem::getAssumptionsCopy(), CVCL::Theorem::getExpr(), CVCL::Theorem::getProof(), CVCL::Expr::getRational(), CVCL::GRAY_SHADOW, CVCL::isGrayShadow(), CVCL::Rational::isInteger(), CVCL::isMult(), CVCL::Expr::isRational(), CVCL::isRational(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), CVCL::TheoremProducer::newTheorem(), CVCL::Expr::orExpr(), rat(), CVCL::Expr::toString(), CVCL::TheoremProducer::withAssumptions(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::grayShadowConst ( const Theorem & g ) [virtual]

|- G(ax, c, c1, c2) ==> |- G(x, 0, ceil((c1+c)/a), floor((c2+c)/a))
In the case the new c1 > c2, return |- FALSE
Implements CVCL::ArithProofRules.
Definition at line 1789 of file arith_theorem_producer.cpp.
References CVCL::ceil(), CVCL::TheoremProducer::d_em, d_theoryArith, CVCL::ExprManager::falseExpr(), CVCL::floor(), CVCL::Theorem::getAssumptionsCopy(), CVCL::Theorem::getExpr(), CVCL::Theorem::getProof(), CVCL::Expr::getRational(), grayShadow(), CVCL::isGrayShadow(), CVCL::Rational::isInteger(), CVCL::Expr::isRational(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newTheorem(), rat(), CVCL::TheoryArith::separateMonomial(), CVCL::Expr::toString(), CVCL::TheoremProducer::withAssumptions(), and CVCL::TheoremProducer::withProof().

Rational ArithTheoremProducer::constRHSGrayShadow ( const Rational & c,

const Rational & b,

const Rational & a

)

Implements j(c,b,a).
accepts 3 integers a,b,c and returns (b > 0)? (c+b) mod a : (a - (c+b)) mod a
Definition at line 1831 of file arith_theorem_producer.cpp.
References CVCL::Rational::isInteger(), and CVCL::mod().
Referenced by expandGrayShadowConst().

Theorem ArithTheoremProducer::lessThanToLE ( const Theorem & less,

const Theorem & isIntLHS,

const Theorem & isIntRHS,

bool changeRight

) [virtual]

Takes a Theorem(\alpha < \beta) and returns Theorem(\alpha < \beta <==> \alpha <= \beta -1) where \alpha and \beta are integer expressions
Implements CVCL::ArithProofRules.
Definition at line 1849 of file arith_theorem_producer.cpp.
References CVCL::Theorem::getExpr(), CVCL::Theorem::getProof(), CVCL::isIntPred(), CVCL::isLT(), CVCL::leExpr(), CVCL::merge(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), rat(), CVCL::Expr::toString(), CVCL::TheoremProducer::withAssumptions(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::intVarEqnConst ( const Expr & eqn,

const Theorem & isIntx

) [virtual]

Parameters:

eqn is an equation 0 = a.x or 0 = c + a.x

isIntx is a proof of IS_INTEGER(x)

Returns:
the theorem 0 = c + a.x <==> x=-c/a if -c/a is int else return the theorem 0 = c + a.x <==> false.
It also handles the special case of 0 = a.x <==> x = 0
Implements CVCL::ArithProofRules.
Definition at line 1903 of file arith_theorem_producer.cpp.
References CVCL::Expr::arity(), CVCL::TheoremProducer::d_em, d_theoryArith, CVCL::Expr::eqExpr(), CVCL::ExprManager::falseExpr(), CVCL::Theorem::getAssumptionsCopy(), CVCL::Theorem::getExpr(), CVCL::Theorem::getProof(), CVCL::Expr::getRational(), CVCL::Rational::isInteger(), CVCL::isIntPred(), CVCL::isMult(), CVCL::isPlus(), CVCL::Expr::isRational(), CVCL::isRational(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), rat(), CVCL::TheoryArith::separateMonomial(), CVCL::Expr::toString(), CVCL::TheoremProducer::withAssumptions(), and CVCL::TheoremProducer::withProof().

Theorem CVCL::ArithTheoremProducer::eqElimIntRule ( const Theorem & eqn,

const Theorem & isIntx,

const std::vector< Theorem > & isIntVars

) [virtual]

Equality elimination rule for integers:
$\frac{\mathsf{int}(a\cdot x)\quad \mathsf{int}(C+\sum_{i=1}^{n}a_{i}\cdot x_{i})} {a\cdot x=C+\sum_{i=1}^{n}a_{i}\cdot x_{i} \quad\equiv\quad x=t_{2}\wedge 0=t_{3}}$
See the detailed description for explanations.
$\frac{\Gamma\models ax=t\quad \Gamma'\models\mathsf{int}(x)\quad \{\Gamma_i\models\mathsf{int}(x_i) | x_i\mbox{ is var in }t\}} {\Gamma,\Gamma',\bigcup_i\Gamma_i\models \exists (y:\mathrm{int}).\ x=t_2(y)\wedge 0=t_3(y)}$
See detailed docs for more information.
This rule implements a step in the iterative algorithm for eliminating integer equality. The terms in the rule are defined as follows:

$\begin{array}{rcl} t & = & C+\sum_{i=1}^na_{i}\cdot x_{i}\\ t_{2}(y) & = & -(C\ \mathbf{mod}\ m+\sum_{i=1}^{n}(a_{i}\ \mathbf{mod}\ m) \cdot x_{i}-m\cdot y)\\ & & \\ t_{3}(y) & = & \mathbf{f}(C,m)+\sum_{i=1}^{n}\mathbf{f}(a_{i},m)\cdot x_{i} -a\cdot y\\ & & \\ m & = & a+1\\ & & \\ \mathbf{f}(i,m) & = & \left\lfloor \frac{i}{m} +\frac{1}{2}\right\rfloor +i\ \mathbf{mod}\ m\\ & & \\ i\ \mathbf{mod}\ m & = & i-m\left\lfloor\frac{i}{m} +\frac{1}{2}\right\rfloor \end{array}$

All the variables and coefficients are integer, and a >= 2.

Parameters:

eqn is the equation ax=t:
$a\cdot x = C + \sum_{i=1}^n a_i\cdot x_i.$

isIntx is a Theorem deriving the integrality of the LHS variable: IS_INTEGER(x)

isIntVars is a vector of Theorems deriving the integrality of all variables on the RHS

Implements CVCL::ArithProofRules.

Theorem ArithTheoremProducer::isIntConst ( const Expr & e ) [virtual]

return e <=> TRUE/FALSE for e == IS_INTEGER(c), where c is a constant

Parameters:

e is a predicate IS_INTEGER(c) where c is a rational constant

Implements CVCL::ArithProofRules.
Definition at line 2365 of file arith_theorem_producer.cpp.
References CVCL::TheoremProducer::d_em, CVCL::ExprManager::falseExpr(), CVCL::Expr::getRational(), CVCL::isInt(), CVCL::Rational::isInteger(), CVCL::isIntPred(), CVCL::isRational(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), CVCL::Expr::toString(), CVCL::ExprManager::trueExpr(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::equalLeaves1 ( const Theorem & e ) [virtual]

Implements CVCL::ArithProofRules.
Definition at line 2382 of file arith_theorem_producer.cpp.
References CVCL::Theorem::getAssumptions(), CVCL::Theorem::getProof(), CVCL::Theorem::getRHS(), CVCL::MULT, CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), CVCL::PLUS, CVCL::RATIONAL_EXPR, CVCL::TheoremProducer::withAssumptions(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::equalLeaves2 ( const Theorem & e ) [virtual]

Implements CVCL::ArithProofRules.
Definition at line 2414 of file arith_theorem_producer.cpp.
References CVCL::Theorem::getAssumptions(), CVCL::Theorem::getProof(), CVCL::Theorem::getRHS(), CVCL::MULT, CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), CVCL::PLUS, CVCL::RATIONAL_EXPR, CVCL::TheoremProducer::withAssumptions(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::equalLeaves3 ( const Theorem & e ) [virtual]

Implements CVCL::ArithProofRules.
Definition at line 2446 of file arith_theorem_producer.cpp.
References CVCL::Theorem::getAssumptions(), CVCL::Theorem::getProof(), CVCL::Theorem::getRHS(), CVCL::MULT, CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), CVCL::PLUS, CVCL::RATIONAL_EXPR, CVCL::TheoremProducer::withAssumptions(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::equalLeaves4 ( const Theorem & e ) [virtual]

Implements CVCL::ArithProofRules.
Definition at line 2478 of file arith_theorem_producer.cpp.
References CVCL::Theorem::getAssumptions(), CVCL::Theorem::getProof(), CVCL::Theorem::getRHS(), CVCL::MULT, CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newRWTheorem(), CVCL::PLUS, CVCL::RATIONAL_EXPR, CVCL::TheoremProducer::withAssumptions(), and CVCL::TheoremProducer::withProof().

Theorem ArithTheoremProducer::diseqToIneq ( const Theorem & diseq ) [virtual]

x /= y ==> (x < y) OR (x > y)
Used in concrete model generation
Implements CVCL::ArithProofRules.
Definition at line 2509 of file arith_theorem_producer.cpp.
References CVCL::Theorem::getAssumptions(), CVCL::Theorem::getExpr(), CVCL::Theorem::getProof(), CVCL::gtExpr(), CVCL::Expr::isEq(), CVCL::Expr::isNot(), CVCL::ltExpr(), CVCL::TheoremProducer::newPf(), CVCL::TheoremProducer::newTheorem(), CVCL::orExpr(), CVCL::Expr::toString(), CVCL::TheoremProducer::withAssumptions(), and CVCL::TheoremProducer::withProof().

Member Data Documentation

TheoryArith* CVCL::ArithTheoremProducer::d_theoryArith [private]

Definition at line 41 of file arith_theorem_producer.h.
Referenced by canonDivide(), canonMultConstPlus(), canonMultMtermMterm(), darkShadow(), grayShadow(), grayShadowConst(), intType(), intVarEqnConst(), and realType().

The documentation for this class was generated from the following files:

Generated on Thu Apr 13 16:57:46 2006 for CVC Lite by

1.4.4