#include <theory_arith_old.h>
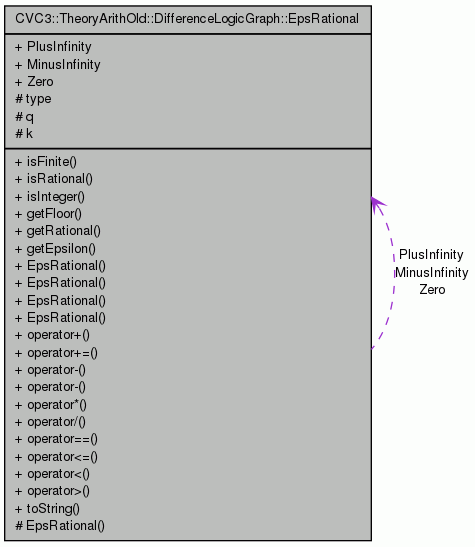
Public Member Functions
- bool isFinite () const
- bool isRational () const
- bool isInteger () const
- Rational getFloor () const
- Rational getRational () const
- Rational getEpsilon () const
- EpsRational ()
- EpsRational (const EpsRational &r)
- EpsRational (const Rational &q)
- EpsRational (const Rational &q, const Rational &k)
- EpsRational operator+ (const EpsRational &r) const
- EpsRational & operator+= (const EpsRational &r)
- EpsRational operator- (const EpsRational &r) const
- EpsRational operator- ()
- EpsRational operator* (const Rational &a) const
- EpsRational operator/ (const Rational &a) const
- bool operator== (const EpsRational &r) const
- bool operator<= (const EpsRational &r) const
- bool operator< (const EpsRational &r) const
- bool operator> (const EpsRational &r) const
- std::string toString () const
Static Public Attributes
- static const EpsRational PlusInfinity
- static const EpsRational MinusInfinity
- static const EpsRational Zero
Protected Types
- enum RationalType { FINITE, PLUS_INFINITY, MINUS_INFINITY }
Protected Member Functions
Protected Attributes
Detailed Description
EpsRational class ecapsulates the rationals with a symbolic small  added. Each rational number is presented as a pair
added. Each rational number is presented as a pair  , where
, where  is treated symbolically. The operations on the new rationals are defined as
is treated symbolically. The operations on the new rationals are defined as
Note that the operations on the infinite values are not defined, as they are never used currently. Infinities can only be asigned or compared.
Definition at line 473 of file theory_arith_old.h.
Member Enumeration Documentation
Type of rationals, normal and the two infinities
Definition at line 478 of file theory_arith_old.h.
Constructor & Destructor Documentation
| CVC3::TheoryArithOld::DifferenceLogicGraph::EpsRational::EpsRational | ( | RationalType | type | ) | [inline, protected] |
Private constructor to construt infinities.
Definition at line 492 of file theory_arith_old.h.
| CVC3::TheoryArithOld::DifferenceLogicGraph::EpsRational::EpsRational | ( | ) | [inline] |
The blank constructor
Definition at line 559 of file theory_arith_old.h.
Referenced by operator*(), operator+(), operator-(), and operator/().
| CVC3::TheoryArithOld::DifferenceLogicGraph::EpsRational::EpsRational | ( | const EpsRational & | r | ) | [inline] |
Copy constructor
Definition at line 562 of file theory_arith_old.h.
| CVC3::TheoryArithOld::DifferenceLogicGraph::EpsRational::EpsRational | ( | const Rational & | q | ) | [inline] |
Constructor from a rational, constructs a new pair (q, 0).
- Parameters:
-
q the rational
Definition at line 569 of file theory_arith_old.h.
| CVC3::TheoryArithOld::DifferenceLogicGraph::EpsRational::EpsRational | ( | const Rational & | q, |
| const Rational & | k | ||
| ) | [inline] |
Constructor from a rational and a given epsilon multiplier, constructs a new pair (q, k).
- Parameters:
-
q the rational k the epsilon multiplier
Definition at line 578 of file theory_arith_old.h.
Member Function Documentation
| bool CVC3::TheoryArithOld::DifferenceLogicGraph::EpsRational::isFinite | ( | ) | const [inline] |
Returns if the numbe is finite.
Definition at line 499 of file theory_arith_old.h.
Referenced by CVC3::TheoryArithOld::computeTermBounds(), CVC3::TheoryArithOld::getLowerBound(), CVC3::TheoryArithOld::getUpperBound(), CVC3::TheoryArithOld::hasLowerBound(), and CVC3::TheoryArithOld::hasUpperBound().
| bool CVC3::TheoryArithOld::DifferenceLogicGraph::EpsRational::isRational | ( | ) | const [inline] |
Returns if the number is a plain rational.
- Returns:
- true if rational, false otherwise
Definition at line 506 of file theory_arith_old.h.
References k.
| bool CVC3::TheoryArithOld::DifferenceLogicGraph::EpsRational::isInteger | ( | ) | const [inline] |
Returns if the number is a plain integer.
- Returns:
- true if rational, false otherwise
Definition at line 513 of file theory_arith_old.h.
References CVC3::Rational::isInteger(), k, and q.
Referenced by CVC3::TheoryArithOld::DifferenceLogicGraph::tryUpdate().
| Rational CVC3::TheoryArithOld::DifferenceLogicGraph::EpsRational::getFloor | ( | ) | const [inline] |
Returns the floor of the number 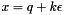 using the following fomula
using the following fomula
![\[ \lfloor \beta(x) \rfloor = \begin{cases} \lfloor q \rfloor & \text{ if } q \notin Z\\ q & \text{ if } q \in Z \text{ and } k \geq 0\\ q - 1 & \text{ if } q \in Z \text{ and } k < 0 \end{cases} \]](form_277.png)
Definition at line 526 of file theory_arith_old.h.
References CVC3::Rational::isInteger(), k, and q.
| Rational CVC3::TheoryArithOld::DifferenceLogicGraph::EpsRational::getRational | ( | ) | const [inline] |
Returns the rational part of the number
- Returns:
- the rational
Definition at line 541 of file theory_arith_old.h.
References q.
Referenced by CVC3::TheoryArithOld::DifferenceLogicGraph::addEdge(), CVC3::TheoryArithOld::DifferenceLogicGraph::getValuation(), and CVC3::TheoryArithOld::DifferenceLogicGraph::tryUpdate().
| Rational CVC3::TheoryArithOld::DifferenceLogicGraph::EpsRational::getEpsilon | ( | ) | const [inline] |
Returns the epsilon part of the number
- Returns:
- the epsilon
Definition at line 548 of file theory_arith_old.h.
References k.
Referenced by CVC3::TheoryArithOld::DifferenceLogicGraph::addEdge(), CVC3::TheoryArithOld::DifferenceLogicGraph::getValuation(), and CVC3::TheoryArithOld::DifferenceLogicGraph::tryUpdate().
| EpsRational CVC3::TheoryArithOld::DifferenceLogicGraph::EpsRational::operator+ | ( | const EpsRational & | r | ) | const [inline] |
Addition operator for two EpsRational numbers.
- Parameters:
-
r the number to be added
- Returns:
- the sum as defined in the class
Definition at line 586 of file theory_arith_old.h.
References DebugAssert, EpsRational(), FINITE, k, q, and type.
| EpsRational& CVC3::TheoryArithOld::DifferenceLogicGraph::EpsRational::operator+= | ( | const EpsRational & | r | ) | [inline] |
Addition operator for two EpsRational numbers.
- Parameters:
-
r the number to be added
- Returns:
- the sum as defined in the class
Definition at line 598 of file theory_arith_old.h.
References DebugAssert, FINITE, k, q, and type.
| EpsRational CVC3::TheoryArithOld::DifferenceLogicGraph::EpsRational::operator- | ( | const EpsRational & | r | ) | const [inline] |
Subtraction operator for two EpsRational numbers.
- Parameters:
-
r the number to be added
- Returns:
- the sum as defined in the class
Definition at line 611 of file theory_arith_old.h.
References DebugAssert, EpsRational(), FINITE, k, q, and type.
| EpsRational CVC3::TheoryArithOld::DifferenceLogicGraph::EpsRational::operator- | ( | ) | [inline] |
Unary minus operator
Definition at line 620 of file theory_arith_old.h.
References DebugAssert, FINITE, k, q, and type.
| EpsRational CVC3::TheoryArithOld::DifferenceLogicGraph::EpsRational::operator* | ( | const Rational & | a | ) | const [inline] |
Multiplication operator EpsRational number and a rational number.
- Parameters:
-
a the number to be multiplied
- Returns:
- the product as defined in the class
Definition at line 634 of file theory_arith_old.h.
References DebugAssert, EpsRational(), FINITE, k, q, and type.
| EpsRational CVC3::TheoryArithOld::DifferenceLogicGraph::EpsRational::operator/ | ( | const Rational & | a | ) | const [inline] |
Division operator EpsRational number and a rational number.
- Parameters:
-
a the number to be multiplied
- Returns:
- the product as defined in the class
Definition at line 645 of file theory_arith_old.h.
References DebugAssert, EpsRational(), FINITE, k, q, and type.
| bool CVC3::TheoryArithOld::DifferenceLogicGraph::EpsRational::operator== | ( | const EpsRational & | r | ) | const [inline] |
Equality comparison operator.
Definition at line 653 of file theory_arith_old.h.
| bool CVC3::TheoryArithOld::DifferenceLogicGraph::EpsRational::operator<= | ( | const EpsRational & | r | ) | const [inline] |
Less than or equal comparison operator.
Definition at line 658 of file theory_arith_old.h.
References FatalAssert, FINITE, k, MINUS_INFINITY, PLUS_INFINITY, q, and type.
| bool CVC3::TheoryArithOld::DifferenceLogicGraph::EpsRational::operator< | ( | const EpsRational & | r | ) | const [inline] |
Less than comparison operator.
Definition at line 683 of file theory_arith_old.h.
| bool CVC3::TheoryArithOld::DifferenceLogicGraph::EpsRational::operator> | ( | const EpsRational & | r | ) | const [inline] |
Greater than comparison operator.
Definition at line 688 of file theory_arith_old.h.
| std::string CVC3::TheoryArithOld::DifferenceLogicGraph::EpsRational::toString | ( | ) | const [inline] |
Returns the string representation of the number.
- Returns:
- the string representation of the number
Definition at line 695 of file theory_arith_old.h.
References FatalAssert, FINITE, k, MINUS_INFINITY, PLUS_INFINITY, q, CVC3::Rational::toString(), and type.
Referenced by CVC3::TheoryArithOld::DifferenceLogicGraph::getEdgeTheorems(), CVC3::TheoryArithOld::getLowerBound(), CVC3::TheoryArithOld::getUpperBound(), and CVC3::TheoryArithOld::DifferenceLogicGraph::tryUpdate().
Member Data Documentation
The type of this rational
Definition at line 481 of file theory_arith_old.h.
Referenced by isFinite(), operator*(), operator+(), operator+=(), operator-(), operator/(), operator<=(), and toString().
The rational part
Definition at line 484 of file theory_arith_old.h.
Referenced by getFloor(), getRational(), isInteger(), operator*(), operator+(), operator+=(), operator-(), operator/(), operator<=(), operator==(), and toString().
The epsilon multiplier
Definition at line 487 of file theory_arith_old.h.
Referenced by getEpsilon(), getFloor(), isInteger(), isRational(), operator*(), operator+(), operator+=(), operator-(), operator/(), operator<=(), operator==(), and toString().
const TheoryArithOld::DifferenceLogicGraph::EpsRational TheoryArithOld::DifferenceLogicGraph::EpsRational::PlusInfinity [static] |
The infinity constant
Definition at line 551 of file theory_arith_old.h.
Referenced by CVC3::TheoryArithOld::getUpperBound().
const TheoryArithOld::DifferenceLogicGraph::EpsRational TheoryArithOld::DifferenceLogicGraph::EpsRational::MinusInfinity [static] |
The negative infinity constant
Definition at line 553 of file theory_arith_old.h.
Referenced by CVC3::TheoryArithOld::computeTermBounds(), and CVC3::TheoryArithOld::getLowerBound().
const TheoryArithOld::DifferenceLogicGraph::EpsRational TheoryArithOld::DifferenceLogicGraph::EpsRational::Zero [static] |
The zero constant
Definition at line 555 of file theory_arith_old.h.
Referenced by CVC3::TheoryArithOld::getLowerBound(), and CVC3::TheoryArithOld::getUpperBound().
The documentation for this class was generated from the following files:
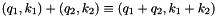

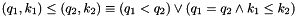
 1.7.3
1.7.3