Figure 1:

I'm writing to disagree with your proposed solution to the first Sand Counter problem, from November. You suggest that, if he can always tell how many grains of sand I removed, then that establishes that he can really count the sand.
That does not establish his ability to count the grains on a ratio scale (a scale with a real zero), only on an interval scale (a scale with an arbitrary but consistent zero). For example, if his unrevealed count is consistently off by 100 grains, he will still always report accurate differences between two separate unrevealed counts.
My colleague Richard Cole has made the following observations on January 30, 2015.
This is a nice problem, but I think your proposed solution is not optimal. I can do 10 with six edges (assuming you allow distance 1 connections) and n with about 3/4n edges.
With solution A,B,C,D,E,F,G,H,I,J (10), use the links A --> C --> F --> J, G --> H --> I, D-->E (and distances as imposed by the solution, i.e., 2, 3, 4, 1, 1, 1,).
For the size n problem, suppose n is odd. Then do one link of length floor{(n-1)/2} from 1 to (n+1)/2 (using number names). Now do a link from (n+1)/2 + 1 to n and from n to 1. Proceed in this way, putting in longest links in each of the halves created by the first link, as well as connections to an already placed person, until n/2 people are placed. Then the remainder can be fixed by longest links without the need for connections to an already placed person.
But the solution to the 10 player problem suggests there may be still cleverer approaches.
Hi Dennis,
Regarding the February puzzle ("Take Your Seats"), I think two hints
suffice when n=5:
B==A+1
E==C+2
and five hints when n=9:
D==A+3
F==D+2
E==B+3
H==G+1
I==H+1
(here == means congruence mod n).
But I have no idea about lower bounds or optimality.
Nice problem! -- Don
Richard Manion pointed out that the column shows four solutions but only three questions. There wasn't room for the fourth question, but here it is.
Sometimes, stability depends on wealth and the willingness to take risk. Suppose that we have four entities all having force 1 and all having wealth 6. If, say, E1, E2, and E3 form a coalition to defeat E4, then they divide E4's wealth, but now one of them will be the target of the other two. We say an entity E is risk-ready if it's willing to agree to an attack that might later expose E to an attack. Otherwise, we say E is risk-averse.
4. Wealth can change the calculus: suppose all entities are risk-ready and have force 1, but E1 has wealth 6, E2 has 7, E3 has 8 and E4 has 9. What will happen?
Guenter Rote (rote@inf.fu-berlin.de) vastly improved our solution (and clarified the question:) here. Here are some clarifications and assumptions for making the problem more specific:
Figure 1:

We address the grid squares as (x,y) from (0,0) (lower left corner) to (499,499), where x is the horizontal coordinate.
At time t=50, we build a horizontal end-to-end wall of length 500 at height y=512, and wait till the wall is hit at some time t0+½, where t0≤50+2×512−1=1073. After it is hit, we build horizontal walls of length 10 with the left endpoints at (x,y) =(0,510), (10,509), (20,508), …, (490,461), in a staggered fashion, one wall at each step t0+1, t0+2, …, t0+50.
Figure 2: 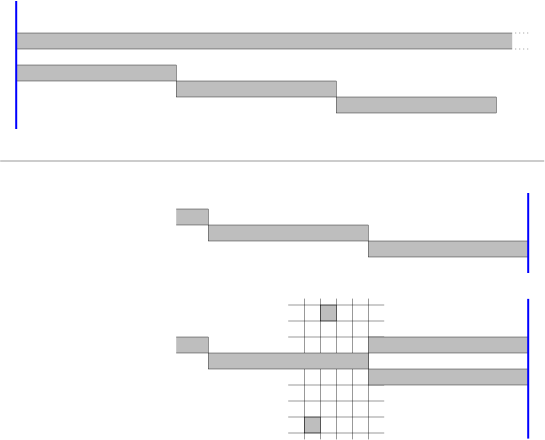
If the puck is below the long wall, it will hit one of these short walls immediately after it is built. In that case, there are 12 potential locations of the puck and we can capture it quickly. We only show a solution for the last wall at y=461, which is hit at time t0+½+50. (The other cases are a bit more tricky, but more time is available to finish in these cases.) We build a facing wall and two detection bricks, as shown in Figure 2. By listening whether the puck makes one or two pauses after exiting through the corners, we can identify its position and cage it, after something like 23 additional steps, but there is certainly room for improvement in this endgame. More substantial savings are possible by placing the walls with a horizontal offset of 11 instead of 10, for example.
If no second hit occurred by time t0+½+50, we know that the puck is in the upper half. We have wasted 50 steps, but on the other hand, we know that t0≤50+2×487−1=1023. This stronger bound exactly balances the wasted time. We construct horizontal walls with their left endpoints at (x,y) =(0,564), (10,565), (20,566), …, (490,613), and the procedure runs exactly like in the lower half. The total time until the puck is confined is perhaps around 1073+50+23∼1146, with an error margin of one or two.
If it is an issue that we partially dismantle a completely built wall, we could build the initial wall of length 500 in portions of 10 bricks at a time. The case that the initial wall is put on top of the puck has not been discussed, but this is actually a lucky advantage: we know that the puck must be in a position as if it had just hit the wall, and we can immediately start the second phase without waiting.
If left alone, the puck follows one of 501 closed loops. 499 loops are tilted rectangles, and two are the diagonals of the field. Each loop is traversed in 1000 steps. If we place a wall anywhere, it will intercept 6 of these loops, unless it touches the boundary or straddles a diagonal. If we wait 1000 time steps after placing the wall, we are sure that the puck was not on one of these loops, and we should place the wall somewhere else.
Figure 3: 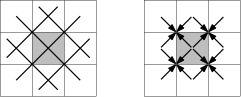
We put the wall on the 83 positions (3,1), (9,1), (15,1), …, (495,1) and wait 1000 units.
Figure 4: 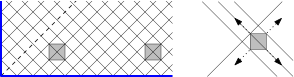
After 83 failed rounds of length 1000, at time 83001, only 3 potential tracks are left: two diagonal tracks, and one close to a diagonal. We place the wall near the center at (250,249) and wait, see Figure 4. After at most 501 steps, the puck must have hit the wall, and then it can be in one of 4 possible places and directions. After trying to block its way three times, we know precisely where it is, and we can confine it as described at the beginning.
Georgi Guliashvili vinmesmiti@gmail.com
proposed the following:
Th - Time hour
Tm - Time minute
Ah - Alarm hour
Am - Alarm minute
M - should ring that number of minutes away
---
Mh = M / 60 (Rounded down)
Mm = M % 60
F(A,T,m,R) = min( (A - (T + m) ) % R, (R - (A - (T + m) ) ) % R)
Answer = F(Ah, Th, Mh, 24) + F(Am, Tm, Mm, 60)
---
Suppose we want to take a 30 minute nap and the time is 15:18 and the alarm is set to 14:50.
So:
Th - 15
Tm - 18
Ah - 14
Am - 50
Mh = 0
Mm = 30
F(50, 18, 30, 60) = min( (50 - (18 + 30) ) % 60, (60 - (50 - (18 + 30) ) ) % 60) = min(2, 58) = 2
F(14, 15,0,24) = min( (14 - (15 + 0) ) % 24, (24 - (14 - (15 + 0) ) ) % 24) = min(23, 1) = 1
Answer = 3
Earl Roethke earl.roethke@siemens.com
pointed out that the warm-up has a two move solution:
F moves from 3 to 6
C moves from 9 to 3
which does work out nicely.
My colleague Ernie Davis suggested the following:
For upstart question 1, you can prove that for some graphs there is nothing better than one-player-stays-put. Suppose it is the complete graph (all pairs of nodes are connected), so that all nodes look the same. Now we can imagine that at the beginning, each player draws a map, chooses an order he's going to explore, and labels the nodes A--Z on his map. Now an adversary comes along and changes the nodes on player 1's map so that he won't meet player 2 until as late as possible; of course there is no way that player 1 can detect that anything has been changed. In the "one-player-stays-put" strategy, the adversary can at most fiddle things so that moving player hits the stationary player on move N; if both players move, the adversary can do better than that.
The algorithm for the adversary is as follows. Let Q[T] be the physical node where player 2 will be at time I; let Z[T] be the letter that player 1 has assigned for time T; and let P[U] be the adversary's mapping of player 1's letter U to a physical node. Then
Then
for (U=1 .. N) {
W[U] = { Q[T] | Z[T] = U } // the places where 2 will be when 1 is
} // at U
renumber the U's in descending order of |W[U]|;
for (U = 1 .. N)
P[U] = any node which is not equal to P[1] ... P[U-1]
and not an element of W[U];
It is easily shown that if there are at most N different times T, then in each step of the second loop of the algorithm, the adversary has at least one option until U=N.
I presented this problem at the banquet of ICLP16 -- 32nd International Conference on Logic Programming. Two of the participants gave some nice solutions though not to the second upstart.
Neng-Fa Zhou wrote:
"Dear Dennis,
"Thank you for the entertaining puzzles. In order to show that logic
programming can offer entertaining solutions, I wrote programs (in Picat)
for solving the card puzzle:
http://picat-lang.org/exs/shasha_cards1.pi
http://picat-lang.org/exs/shasha_cards2.pi
"Be aware that the second part of the problem, i.e., finding the minimum k, is time consuming. I hope that other LP people can offer better and more entertaining solutions.
"Best regards,
Neng-Fa"
Then Ingmar Dasseville wrote.
"Hi,
"I also found the puzzles very entertaining. I took some time to try to compete with Neng-Fa's programs.
"Here is an IDP version of the shasha_cards_1: http://dtai.cs.kuleuven.be/krr/idp-ide/?src=1f49baf8fb785706cff6d63d8f98ab62
"For shasha_cards_2 I took a different approach and modelled a problem which is harder for me to win (and easier to model). I take the answer for that as an upperbound. And subsequently I prove that this answer is optimal.
"Instead of: for each opponent order: can we find an insertion of our cards
I modelled: can we find an insertion of our cards, so that no matter what
the numbers on our opponents card will be, that we will still win.
win(x) <- on(x) >= k and (forall y: k =< y =< 8 => win(x+y)).
meaning that in the model, if we find a card larger than K, we will only
consider it winning, if all numbers between k and 8 lead to a win:
http://dtai.cs.kuleuven.be/krr/idp-ide/?src=ca9fb22da79dd2c0b6ef62b8ff63a5ff
"This problem is easily solved by our system in a very short time. Minimizing k leads to an upper bound of k=3. But of course it could be possible that our winning strategy depends on the order of our opponents cards, so we still want to prove that k = 2 is impossible
"So we're left with finding an ordering of 28 cards (2-8), so that each insertion of 1's still leads to a loss. For this I wrote a Haskell program to see check a particular candidate. In this program I check whether [3,3,3,3,4,4,4,4,5,5,5,5,6,6,6,6,7,7,7,7,8,8,8,8] can be extended to a win using only four 1's. Which it can't. https://goo.gl/YrUzE3
"So through the combination of the IDP and the Haskell Program we can conclude that k = 3. And both can be run in a matter of seconds. (The 3 code snippets are runnable online)
"Ingmar"
Matthew Sheby pointed out that in the four different case, another possible distribution of rubies is 13, 17, 0. This by itself doesn't change the best answer which is still 12.
Also, in case it's not clear, there is no order in the boxes, so when the text says "first box", this just means one of the three boxes. Thus, for example, a possible left-to-right configuration is 17, 0, 13.
Josef Tkadlec proposed a variant in which "the boxes are arranged left to right and you are told that each next box has at least as many rubies as the one to its left." For example, for b=3 boxes one can prove that you can guarantee 3/7 of all the rubies (and not more), by asking for (1/7, 2/7, 3/7) from the respective boxes. "
Richard Cole pointed out a better solution to the first challenge problem: connect the 4 R's in the middle two rows with 3 edges, and connect the top row corner R to the middle ones with a 4th edge. Do the mirror image for the B's. Swap the single isolated B on the top row with the single isolated R on the bottom row.
Chris Achenbach found another solution that uses six bridges (edges)
and two swaps.
Swap (2,1) with (2,2)
Swap (2,3) with (2,4)
2 Roads form a cross: (3,1)--(4,2) and (4,1)--(3,2)
2 Roads form a cross: (3,2)--(4,3) and (4,2)--(3,3)
2 Roads form a cross: (3,3)--(4,4) and (4,3)--(3,4)
He has also created a
game based on it.
John Tate pointed out that the second warm-up doesn't work as written because babab matches part of Y. In fact, Y should be bbaababba.
David Abrahamson pointed out a negative answer to the upstart: X = a. Obviously, Y = b is no less expensive.
Here is a corrected version of the article with a better upstart. http://cs.nyu.edu/cs/faculty/shasha/papers/stringwarscorrected.doc
Jie Wu of Temple University was the first to show that my lower bound was foolish. Even if only one site out of 20 has a certain partition, the number of sites that contain that partition can double after each time step.
Here is a corrected version with that bug fixed: http://cs.nyu.edu/cs/faculty/shasha/papers/bounceblockchainfinal_corrected.doc
Mark Kaminsky decreased the cognitive load on listeners compared to
my encoding.
He suggested a base-5 approach:
Thus, the following table will cover the hours:
101 00:00
1011 01:00
10111 02:00
101111 03:00
1011111 04:00
1101 05:00
11011 06:00
110111 07:00
1101111 08:00
11011111 09:00
11101 10:00
111011 11:00
1110111 12:00
11101111 13:00
111011111 14:00
111101 15:00
1111011 16:00
11110111 17:00
111101111 18:00
1111011111 19:00
1111101 20:00
11111011 21:00
111110111 22:00
1111101111 23:00
As the two sets of chimes with one silence are distinctive, we need
not do anything further at the hour (e.g. 22:00). For the other fifteen minute
intervals, we can add:
01 x:15
011 x:30
0111 x:45
Mark calculates the time as follows:
If I have figured out how you are counting the timing, the first
and second pentary digits will each average about two seconds
(I'll pretend that we are using 24:00 to simplify my calculations;
the actual average will be slightly lower):
1 0 seconds
11 1 second
111 2 seconds
1111 3 seconds
11111 4 seconds
Then there is another two seconds for the silence between digits, so we have six seconds average to chime the hour.
The four quarter hours will take:
x:00 0 seconds
x:15 2 seconds
x:30 3 seconds
x:45 4 seconds
for an average of 2.25 seconds.
Thus, the average duration is about 8.25 seconds.
Here is my solution for the optimal chimes puzzle: https://gist.github.com/afrozenator/bd01d5d039ebce0121ad9d0b85df41e3 I get an average time of 6.7seconds with my encoding for Chime Upstart, with the encoding being just a simple enumeration of all sequences following the rules sorted according to the time they take, so for k=1 the 96 sequences are: (the code will output this when run) Chimes: ['1', '11', '111', '101', '1111', '1011', '1101', '11111', '10111', '11011', '11101', '10101', '111111', '101111', '110111', '111011', '101011', '111101', '101101', '110101', '1111111', '1011111', '1101111', '1110111', '1010111', '1111011', '1011011', '1101011', '1111101', '1011101', '1101101', '1110101', '1010101', '11111111', '10111111', '11011111', '11101111', '10101111', '11110111', '10110111', '11010111', '11111011', '10111011', '11011011', '11101011', '10101011', '11111101', '10111101', '11011101', '11101101', '10101101', '11110101', '10110101', '11010101', '111111111', '101111111', '110111111', '111011111', '101011111', '111101111', '101101111', '110101111', '111110111', '101110111', '110110111', '111010111', '101010111', '111111011', '101111011', '110111011', '111011011', '101011011', '111101011', '101101011', '110101011', '111111101', '101111101', '110111101', '111011101', '101011101', '111101101', '101101101', '110101101', '111110101', '101110101', '110110101', '111010101', '101010101', '1111111111', '1011111111', '1101111111', '1110111111', '1010111111', '1111011111', '1011011111', '1101011111'] Chime times: [0, 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 9, 9, 9] Average chime time: 6.697917 The reasoning is that, any time is equally probable, so it is useless to do something like a Huffman code - so just plain enumeration of the rule abiding sequences and sorting on time and cutting off at 96 will do. Similarly for k=2,3,4,5 the times are: k t 1 6.698 2 2.958 3 2.156 4 1.750 5 1.635 giving a graph that looks like this, I'm guessing it is O(1/k^2) My scheme increases the cognitive load on the Medievaliana citizens, but will hopefully save them some time.
Matthew points out that Afroz's solution assumes that a single chime sequence has a duration of zero whereas it should have one. However, he agrees with the approach. In addition, he has python code for up to 96 different chime codes.
I think we found a slightly better solution than Mohiuddin's. Using the scoring scheme of 1 chime == 1 second and gap == 2 seconds, we evaluated the average duration of 4 different schemes: - a basic scheme that picks up the first 96 unique binary codes that satisfy the requirements - your published solution - Mohiuddin's published solution - a variant of Mohiuddin's where I replaced the decimal value 341 with the value 2047. These schemes respectively have average durations of 9.5, 10.5, 9.333333, and 9.3125 seconds. Mohiuddin's algorithm appears correct except perhaps the scoring scheme being different makes a slight difference or they cut off their algorithm a little too early and did not let it discover 2047 as a better selection. The better solution in binary is: ['1', '11', '111', '101', '1111', '1011', '1101', '11111', '10111', '11011', '11101', '10101', '111111', '101111', '110111', '111011', '101011', '111101', '101101', '110101', '1111111', '1011111', '1101111', '1110111', '1010111', '1111011', '1011011', '1101011', '1111101', '1011101', '1101101', '1110101', '1010101', '11111111', '10111111', '11011111', '11101111', '10101111', '11110111', '10110111', '11010111', '11111011', '10111011', '11011011', '11101011', '10101011', '11111101', '10111101', '11011101', '11101101', '10101101', '11110101', '10110101', '11010101', '111111111', '101111111', '110111111', '111011111', '101011111', '111101111', '101101111', '110101111', '111110111', '101110111', '110110111', '111010111', '101010111', '111111011', '101111011', '110111011', '111011011', '101011011', '111101011', '101101011', '110101011', '111111101', '101111101', '110111101', '111011101', '101011101', '111101101', '101101101', '110101101', '111110101', '101110101', '110110101', '111010101', '11111111111', '1111111111', '1011111111', '1101111111', '1110111111', '1010111111', '1111011111', '1011011111', '1101011111']
Here is their code.
I said "we" above as my daughter got quite excited to learn "binary numbers" and enthusiastically participated in the whole exercise. She is 12. Best Regards Nagendra and Ananya
Cliff McCullough found a better solution to the warm-up. He writes: "The solution in ACM stated to paddle at 4km/hr on the black segment (3km/hr) first. The land speed would be 1km/hr and the black segment is 1km so the paddler reaches the mid-point in 1 hr. Since the paddler can then only due 2km/hr the red segments (2km) must be taken and at a land speed of 0.5km/hr that will take another 4 hrs. So total time is 5hr.
"I believe there is a faster route.
"If the paddler follows all the red segments it will only take 4hrs.
"In the first hour the paddler paddles at 4km/hr and has a land speed of 2.5km/hr. Thus the paddler will cover 2.5km which takes the paddler 0.5k into the second set of red segments. The remaining 1.5km is then done at 0.5km/hr which takes 3hrs. So the total time is 4hr."
Upstart: Generalize the above solution to k candidates all with approximately equal support. Each person should have a probability of no more than p of actually supporting the candidate he or she mentions. The goal is for the effective sample size to be 100.
Matthew Sheby proposed the following analysis if the candidates all have exactly popularity 1/k.
"Take the k candidates and sort them in descending order by popularity. The most popular choice polls in the sample set with a probability >= 1/k . (If not, then that wouldn't be the most popular choice.) With a sample size of 100 pollees, then there are at least (100/k) true answers picking that most popular choice. According to the terms of the problem, one wants to add y pollees so that the percentage any given pollee likes their mentioned candidate is <= p. Assuming the answers are all stigmatic if publicized, we want to split these extra people up evenly across all the candidates, so there would be ( y /k ) random number generator-based answers added per candidate. As a result, we can set p == ((100/k)/((100/k) + (y/k))). Solving for y, we see that the number of candidates falls out and we get y = (100 * (1-p)/p). Since we're dealing with people, make that ceil(100 * (1- p )/ p )."
When one candidate A has the most support, he proposes: "If A is the support of the most popular candidate, then 0 <= 1/k <= A <= p <= 1. If x is the number of extra people needed for polling, then x = ceil(100kA(1/p)(1-p))."
You said "The most straightforward way would be for all decisions to be made by referendum, but that is impractical, because governments make thousands of decisions per day and the public simply does not have the necessary information. ".
We have all assumed that statement to be true, but is it necessarily true? At least for major decisions?
Representative government apparently dates to the Roman republic, when it was realized that everyone could not participate directly in government decisions. Wikipedia (https://en.wikipedia.org/wiki/Representative_democracy) discusses some problems and alternatives. However, direct democracy apparently existed in the Medieval period, in the "folk mote" (for example, "Mediaeval London" by Walter Besant; http://www.gutenberg.org/files/57803/). The town where I resided for many years (Leverett, Mass) has a direct town meeting where every resident can appear, talk, and vote.
However, it is no longer true that it is not possible for everyone to vote on an individual issue. The internet, and so on, now make it technically possible for everyone who is interested to participate on a case-by-case basis. There are technical difficulties of course, but those need to be solved regardless.
What would such a system look like, and what would be the implications?
I imagine a system where, for major government decisions, every citizen who felt him/herself interested in the topic, could participate in the vote INSTEAD OF conducting the vote by the elected representatives. In other words this would not be a survey but would be a binding vote.
Benefits:
1. Instead of choosing a representative who will vote on future issues in the way we wish, we will know what each issue is at the time we make our vote.
2. Instead of choosing a representative who will putatively agree with our opinions on all topics, we can decide on each topic individually.
3. Those individuals who are interested in a particular topic can inform themselves (see 6. below) about it and participate in the vote, while those not interested can abstain. For example, on a proposal for some new public building in Brooklyn, someone in Albany may not care at all while someone in Brooklyn may care a lot. However, the person in Albany may have a brother-in-law who will bid on the construction. Nothing would prevent that person in Albany from participating. Thus the vote, and indeed the number of voters who participate, would provide fine-grained and real-time (in the sense of the moment when the vote occurred) information about the popularity of the issue.
4. Potential for corruption would decrease. Currently each representative is a single-point-of-failure in the democratic process. There would be less to gain in "buying" a representative, so presumably the temptation to do so would decrease.
5. Similarly to point 4, the benefits of a representastive to being re-elected would decrease, so the campaigning costs to the candidates could (maybe) decrease.
The above assumes that elected representatives would still exist. What would their role be?
6. Their current research activities would continue, but the research results would be made public (probably in both summary and detailed form). Any doubtful claims could in principle be fact-checked by public and private agencies.
7. They would still seek to be representative of the opinions of their constituencies.
8. They would continue to vote on some matters.
The above is only a summary of my thoughts which are, to a large extent, engendered by recent commentary and events exposing weaknesses in the current practice of democracy.
"... In the solution to the second question, where Alice goes first but Bob must bet more chips than Alice, ... if Bob bet one chip on each of the numbers Alice did not bet on, as in the proposed solution, and two chips on 17 of the numbers Alice did bet on, his odds would be 19/36. Alice's odds in this scenario would be 17/36, but she would be better off placing all 36 chips on 36 different numbers. That way, Bob could still bet one chip on the number Alice did not bet on and two chips each on 17 other numbers. Putting his last chip on one of Alice's other numbers would not improve his odds, but it would reduce Alice's odds since neither of them would win if the ball rolled to that number."
"Here's the solution I came up with: If Bob goes last , here are the situations I've found where he's sure to win: s >= 3* sum(1 to k) If we have k = 2, then each person is able to play a total of 2 cards, for a total value of 3. For all numbers less than 8, Alic and Carol can conspire to make it so that Bob cannot play his last card. But when we hit 9 (which is 3*sum(1 to k), Alice and Carol have to accumulate 3 (sum(1 to k)) tokens each, by virtue of playing all their cards. Bob has played all his cards but one, but because there are a total of 9 tokens (3*sum(1 to k)) left, the card he has left must be the exact number of tokens left, thus winning the game. This is generalizable for all higher k as well. Thus, s can equal 3* sum(1 to k)
"If it were a n-player game, Bob would need s >= n * sum(1 to k).
"Any s > 3*sum(1 to k) Bob is sure to win as well, as all three players play their final card, having sum(1 to k) tokens left, and there are still tokens in the middle of the table up for grabs. Alice loses, as she cannot play any cards, Carol loses, since she cannot play any cards, By virtue of the rules, all other players have lost, so that means Bob wins.
"What I cannot prove yet is if there are any solutions s < 3*sum(1 to k). I suspect no, because I believe that for every card that Bob can play, there is a deterministic moveset that Alice and Carrol can play to counteract him, but I don't have the math for that yet."
I'm Owen Parish (oparish4@gmail.com), and I've been reading 'The Puzzling Adventures of Dr Ecco' by Dennis Shasha. I've discovered improved solutions for the 'Offshore Oil Well' set of puzzles from that book.
An oil well requires 0.1 barrel of water to run per minute, and it will produce 1 barrel of oil per minute. It can only store 10 barrels of water in its water drums, and it can only store 100 barrels of oil in its oil drums. A pipeline is required to pump water in, and to pump oil out. It cannot do both at once, and it takes 6 minutes for the oil to finish flowing through the pipeline after it stops being pumped along it, and 6 minutes for water to flow through the pipeline once the water pumping process begins.
Assuming both sets of drums are full to begin with:
The most efficient method is to pump out oil to create a deficit, switch to pumping water such that the water arrives just as the water drums are empty, fill them to maximum capacity, then switch back to pumping oil. The deficit in the oil will have been filled up during this interval.
X = Pipeline capacity
Y = Deficit of oil created
A = Time spent pumping water in
B = Time spend pumping oil out
0.1 barrel of water is used up each minute; The excess water fills up the drums over a period of A minutes:
(X - 0.1) * A = 10
1 barrel of oil is produced each minute; The excess oil being emptied creates the deficit over a period of B minutes:
(X - 1) * B = Y
When the water drums are full they will run the well for 100 minutes. If it takes 12 minutes to switch to pumping water, this means we can spend 88 minutes creating the oil deficit.
B = 100 - 12 = 88
The deficit of oil is 1 barrel per minute spent pumping water in, plus 12 more for the switching process.
Y = A + 12
A = Y - 12
Substituting:
(X - 0.1) * (Y - 12) = 10
(X - 1) * 88 = Y
Y = 88X - 88
(X - 0.1) * (88X - 88 - 12) = 10
(X - 0.1) * (88X - 100) = 10
88X^2 - 100X - 8.8X + 10 = 10
88X^2 - 100X - 8.8X = 0
88X^2 - 108.8X = 0
As X must exceed 0:
88X - 108.8 = 0
88X = 108.8
X = 108.8/88
A = 10/(108.8/88 - 0.1) = 10/(108.8/88 - 8.8/88) = 10/(100/88) = 880/100 = 8.8
Y = 8.8 + 12 = 20.8
So, the pipeline capacity needs to be 108.8/88 barrels per minute, the oil pumping interval needs to be 88 minutes, the water pumping interval needs to be 8.8 minutes, and the oil deficit will be 20.8 barrels.
This is 1.24 (2 dp), so a slightly better solution than 1.25.
T:0 - Oil Drums: 100 - Water Drums: 10 - Pipeline: Empty - Oil pumping started
T:88 - Oil Drums: 79.2 - Water Drums: 1.2 - Pipeline: Full - Oil pumping finished, with 108.8 barrels of oil pumped
T:94 - Oil Drums: 85.2 - Water Drums: 0.6 - Pipeline: Empty - Water pumping started
T:100 - Oil Drums: 91.2 - Water Drums: 0 - Pipeline: Full - Water being pumped
T:108.8 - Oil Drums: 100 - Water Drums: 10 - Pipeline: Empty - Water pumping finished, with 10.88 barrels of water pumped
The size of the water drums has a greater impact per barrel capacity, so they should be expanded.
Y = Deficit of oil created
A = Time spent pumping water in
B = Time spend pumping oil out
C = New water drum capacity
0.1 barrel of water is used up each minute; The excess water fills up the drums over a period of A minutes:
(1.2 - 0.1) * A = 1.1 * A = C
1 barrel of oil is produced each minute; The excess oil being emptied creates the deficit over a period of B minutes:
(1.2 - 1) * B = 0.2 * B = Y
When the water tanks are full they will run the well for C * 10 minutes. We still need to allow 12 minutes for the switching operations.
B = (C * 10) - 12
The deficit of oil is 1 barrel per minute spent pumping water in, plus 12 more for the switching process.
Y = A + 12
A = Y - 12
Substituting:
C = (Y - 12) * 1.1
C = 1.1Y - 13.2
C = 1.1(0.2 * B) - 13.2
C = 0.22B - 13.2
C = 0.22((C * 10) - 12) - 13.2
C = 2.2C - 2.64 - 13.2
C = 2.2C - 15.84
15.84 = 2.2C - C = 1.2C
C = 15.84/1.2 = 13.2
A = 13.2/1.1 = 12
Y = 12 + 12 = 24
B = (13.2 * 10) 12 = 132 - 12 = 120
So, the new water drum capacity needs to be 13.2 barrels, the oil pumping interval needs to be 120 minutes, the water pumping interval needs to be 12 minutes, and the oil deficit will be 24 barrels.
T:0 - Oil Drums: 100 - Water Drums: 13.2 - Pipeline: Empty - Oil pumping started
T:120 - Oil Drums: 76 - Water Drums: 1.2 - Pipeline: Full - Oil pumping finished, with 144 barrels of oil pumped
T:126 - Oil Drums: 82 - Water Drums: 0.6 - Pipeline: Empty - Water pumping started
T:132 - Oil Drums: 88 - Water Drums: 0 - Pipeline: Full - Water being pumped
T:144 - Oil Drums: 100 - Water Drums: 13.2 - Pipeline: Empty - Water pumping finished, with 14.4 barrels of water pumped