Input X: D by N matrix consisting of N data items in D dimensions.
Output Y: d by N matrix consisting of d < D dimensional embedding
coordinates for the input points.

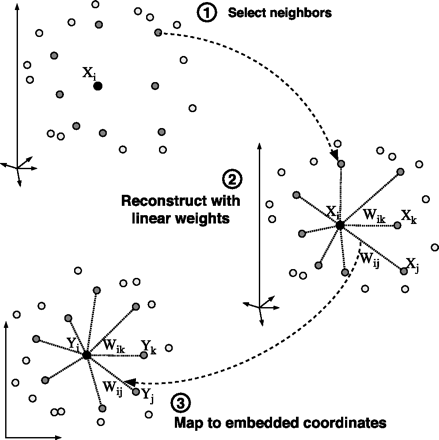
for i=1:N compute the distance from Xi to every other point Xj find the K smallest distances assign the corresponding points to be neighbours of Xi end
for i=1:N create matrix Z consisting of all neighbours of Xi [d] subtract Xi from every column of Z compute the local covariance C=Z'*Z [e] solve linear system C*w = 1 for w [f] set Wij=0 if j is not a neighbor of i set the remaining elements in the ith row of W equal to w/sum(w); end
create sparse matrix M = (I-W)'*(I-W) find bottom d+1 eigenvectors of M (corresponding to the d+1 smallest eigenvalues) set the qth ROW of Y to be the q+1 smallest eigenvector (discard the bottom eigenvector [1,1,1,1...] with eigenvalue zero)
[a] Notation
Xi and Yi denote the ith column of X and Y
(in other words the data and embedding coordinates of the ith point)
M' denotes the transpose of matrix M
* denotes matrix multiplication
(e.g. M'*M is the matrix product of M left multiplied by its transpose)
I is the identity matrix
1 is a column vector of all ones
[b] This can be done in a variety of ways, for example above we compute
the K nearest neighbours using Euclidean distance.
Other methods such as epsilon-ball include all points within a
certain radius or more sophisticated domain specific and/or
adaptive local distance metrics.
[c] Even for simple neighbourhood rules like K-NN or epsilon-ball
using Euclidean distance, there are highly efficient techniques
for computing the neighbours of every point, such as KD trees.
[d] Z consists of all columns of X corresponding to
the neighbours of Xi but not Xi itself
[e] If K>D, the local covariance will not be full rank, and it should be
regularized by seting C=C+eps*I where I is the identity matrix and
eps is a small constant of order 1e-3*trace(C).
This ensures that the system to be solved in step 2 has a unique solution.
[f] 1 denotes a column vector of all ones