



Next: Support Routines
Up: Complementarity and Nondegeneracy
Previous: Primal and dual nondegeneracy
The condition number of an SDP is defined in [7] and its
significance is discussed there. Briefly, the condition number of an
SQLP is defined as the condition number of the Jacobian of
the function to which Newton's method is applied in defining the
XZ+ZX search direction, evaluated at the solution.
This quantity is 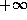 if and only if the solution of the SQLP
fails to satisfy the strict complementarity or primal or dual nondegeneracy
conditions. The routine is
if and only if the solution of the SQLP
fails to satisfy the strict complementarity or primal or dual nondegeneracy
conditions. The routine is
- sqlcond.m
- Given the data of an SQLP and the solutions
 and
and 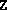 , this routine verifies the optimality conditions and
computes a lower bound (in the 1-norm) of the condition number of
an SQLP. The calling sequence
, this routine verifies the optimality conditions and
computes a lower bound (in the 1-norm) of the condition number of
an SQLP. The calling sequence is:
is:
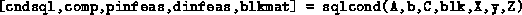
In exact arithmetic, the routine would return the value
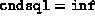 (
( 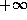 ) if and only if
strict complementarity or primal or dual nondegeneracy are violated.
A large value of cndsql is a strong indication of
that at least one of these three conditions fails to hold.
This routine takes a long time to execute compared to
pcond.m and dcond.m, and can therefore be
used only for small problems, but its advantage
is that no tolerance is required to determine ranks.
) if and only if
strict complementarity or primal or dual nondegeneracy are violated.
A large value of cndsql is a strong indication of
that at least one of these three conditions fails to hold.
This routine takes a long time to execute compared to
pcond.m and dcond.m, and can therefore be
used only for small problems, but its advantage
is that no tolerance is required to determine ranks.
In order to use sqlcond on a diagonally constrained SDP or
a Lovász 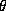 problem, the user must ensure that
problem, the user must ensure that 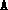 ,
, 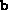 and
and
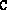 have been constructed, by first calling the
appropriate script (dsdp.m or lsdp.m) with
have been constructed, by first calling the
appropriate script (dsdp.m or lsdp.m) with 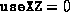 and
and 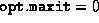 .
.
Madhu Nayakkankuppam
Wed Jun 25 18:01:54 EDT 1997
 is:
is:
![]()
 is:
is:
![]()
![]() problem, the user must ensure that
problem, the user must ensure that ![]() ,
, ![]() and
and
![]() have been constructed, by first calling the
appropriate script (dsdp.m or lsdp.m) with
have been constructed, by first calling the
appropriate script (dsdp.m or lsdp.m) with ![]() and
and ![]() .
.