



Next: The condition number
Up: Complementarity and Nondegeneracy
Previous: Strict complementarity
Primal and dual nondegeneracy conditions are defined for SDP's in
[6]. It is important to realize that these conditions are
defined with respect to the specified block structure (see [7]),
so that they reduce to standard LP conditions in the special case that
all blocks are one. The extensions of these concepts to SQLP's
will be discussed in [3]. See also
the comments in the codes for the definitions.
The most important of these can be accessed
using Matlab's help command. The routines are:
- pcond.m
- Given the constraints of an SQLP,
its block structure and a primal feasible point,
this routine tests for primal degeneracy. The
calling sequence is:
[cndp,Dsize,D] = pcond(A,blk,X,tol)
where 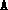 ,
,  ,
,  are structures as earlier and
tol is a tolerance used to decide whether
components of
are structures as earlier and
tol is a tolerance used to decide whether
components of  are or are not on the boundary of their cones.
In exact arithmetic, the routine would return the value
are or are not on the boundary of their cones.
In exact arithmetic, the routine would return the value
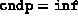 (
( 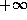 ) if and only if the problem is primal degenerate at
) if and only if the problem is primal degenerate at  .
A large value of cndp is a strong
indication that the problem is primal degenerate.
Type help pcond for the definition, as well as an explanation
of the output parameters Dsize and D.
.
A large value of cndp is a strong
indication that the problem is primal degenerate.
Type help pcond for the definition, as well as an explanation
of the output parameters Dsize and D.
- dcond.m
- Given the constraint matrix of an SQLP,
the block structure and a dual feasible point,
this routine tests for dual degeneracy. The calling sequence
is:
[cndd,Bsize,B] = dcond(A,blk,Z,tol)
where 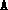 ,
,  ,
,  are structures as earlier and
tol is a tolerance used to decide whether
components of
are structures as earlier and
tol is a tolerance used to decide whether
components of 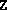 are or are not on the boundary of their cones.
In exact arithmetic, the routine would return the value
are or are not on the boundary of their cones.
In exact arithmetic, the routine would return the value
 (
( 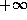 ) if and only if the problem is dual degenerate at
) if and only if the problem is dual degenerate at 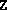 .
A large value of cndd is a strong
indication that the problem is dual degenerate.
Type help dcond for the definition, as well as an explanation
of the output parameters Bsize and B.
.
A large value of cndd is a strong
indication that the problem is dual degenerate.
Type help dcond for the definition, as well as an explanation
of the output parameters Bsize and B.
As a rough guide,
if  (
( 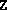 ) passed to pcond.m (dcond.m)
is the solution of an SQLP solved with the default parameter
values in setopt.m, and if
) passed to pcond.m (dcond.m)
is the solution of an SQLP solved with the default parameter
values in setopt.m, and if 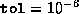 , then a
value exceeding, say
, then a
value exceeding, say 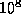 , for cndp (cndd)
is indicative of primal (dual) degeneracy.
Avoid setting tol too small, especially if strict
complementarity does not hold, in which case try values larger
than
, for cndp (cndd)
is indicative of primal (dual) degeneracy.
Avoid setting tol too small, especially if strict
complementarity does not hold, in which case try values larger
than 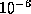 .
.
Primal (dual) nondegeneracy
implies the uniqueness of dual (primal) solutions. The converse is
true if strict complementarity holds [6].
Before calling pcond.m or dcond.m for a
diagonally constrained SDP or a Lovász 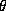 problem,
the user must ensure that
problem,
the user must ensure that 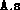 ,
, 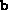 and
and
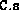 have been constructed. This can easily be done by calling the
appropriate script (dsdp.m or lsdp.m) with
have been constructed. This can easily be done by calling the
appropriate script (dsdp.m or lsdp.m) with 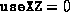 and
and 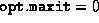 . Upon termination of the script, the variables
will be defined in the Matlab workspace.
. Upon termination of the script, the variables
will be defined in the Matlab workspace.




Next: The condition number
Up: Complementarity and Nondegeneracy
Previous: Strict complementarity
Madhu Nayakkankuppam
Wed Jun 25 18:01:54 EDT 1997
![]() ,
, ![]() ,
, ![]() are structures as earlier and
tol is a tolerance used to decide whether
components of
are structures as earlier and
tol is a tolerance used to decide whether
components of ![]() are or are not on the boundary of their cones.
In exact arithmetic, the routine would return the value
are or are not on the boundary of their cones.
In exact arithmetic, the routine would return the value
![]() (
( ![]() ) if and only if the problem is primal degenerate at
) if and only if the problem is primal degenerate at ![]() .
A large value of cndp is a strong
indication that the problem is primal degenerate.
Type help pcond for the definition, as well as an explanation
of the output parameters Dsize and D.
.
A large value of cndp is a strong
indication that the problem is primal degenerate.
Type help pcond for the definition, as well as an explanation
of the output parameters Dsize and D.
![]() ,
, ![]() ,
, ![]() are structures as earlier and
tol is a tolerance used to decide whether
components of
are structures as earlier and
tol is a tolerance used to decide whether
components of ![]() are or are not on the boundary of their cones.
In exact arithmetic, the routine would return the value
are or are not on the boundary of their cones.
In exact arithmetic, the routine would return the value
![]() (
( ![]() ) if and only if the problem is dual degenerate at
) if and only if the problem is dual degenerate at ![]() .
A large value of cndd is a strong
indication that the problem is dual degenerate.
Type help dcond for the definition, as well as an explanation
of the output parameters Bsize and B.
.
A large value of cndd is a strong
indication that the problem is dual degenerate.
Type help dcond for the definition, as well as an explanation
of the output parameters Bsize and B.