



Next: Complementarity and Nondegeneracy
Up: Specialized Routines
Previous: Diagonally constrained SDP's
A specialized solver to compute the Lovász 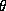 function of an
undirected graph is also available. As in the diagonally
constrained case, such
an SDP may be solved more efficiently by the XZ method than the
XZ+ZX method, as long as the number of edges in the graph is not too large.
The driver script is lsdp.m and the
specialized function is flsdp.m. The five steps involved in
setting up and solving a problem are again similar to Section 3,
except for the following important differences:
function of an
undirected graph is also available. As in the diagonally
constrained case, such
an SDP may be solved more efficiently by the XZ method than the
XZ+ZX method, as long as the number of edges in the graph is not too large.
The driver script is lsdp.m and the
specialized function is flsdp.m. The five steps involved in
setting up and solving a problem are again similar to Section 3,
except for the following important differences:
- These routines solve a specialized SDP, not an SQLP.
The quadratic and linear parts of the SQLP are assumed to be empty.
- The k-th constraint matrix
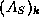 ,
, 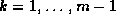 , is
, is
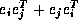 , where (i,j) is the kth edge in the graph,
and
, where (i,j) is the kth edge in the graph,
and 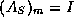 , with
, with 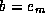 .
These should not be constructed explicitly. The user must instead
provide an edge list G (a matrix with as many rows
as there are edges and 2 columns, with each row of this matrix
defining an edge of the graph (listing its two vertices))
and a weight list w (a vector with one component for each
vertex of the graph, specifying the weight for that vertex).
The cost matrix
.
These should not be constructed explicitly. The user must instead
provide an edge list G (a matrix with as many rows
as there are edges and 2 columns, with each row of this matrix
defining an edge of the graph (listing its two vertices))
and a weight list w (a vector with one component for each
vertex of the graph, specifying the weight for that vertex).
The cost matrix 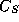 is defined by
is defined by
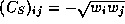 (and is not constructed explicitly).
The optimal value of this SDP is actually
the negative of the value of the
(and is not constructed explicitly).
The optimal value of this SDP is actually
the negative of the value of the 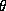 function of the graph.
function of the graph. - The routine lsetopt.m sets the options in the structure
opt just as dsetopt.m does.
- The initialization routine for the variables is called
linit.m, which expects the variables G
and w to be available in the Matlab workspace.
- Like dsdp.m, the script lsdp.m requires the parameter
useXZ to be available, and calls the
specialized solver flsdp.m
only if useXZ equals 1 (the default value set by lsetopt.m).
Otherwise, it calls fsql.m to solve the problem by
the XZ+ZX method, after constructing the matrices
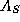 and
and 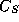 and
the vector b and setting the structures
and
the vector b and setting the structures 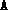 and
and 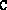 and the vector
and the vector 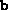 accordingly.
accordingly. -
The problems that fall into this class are graph problems
that usually require the graph to be connected. Hence, this
specialized solver have been purposefully designed to work with a
single block only. If validate is set to 1,
flsdp.m checks to see if the graph is connected and
prints a warning if it is not.
- The user who wants a function interface can bypass the
script by typing
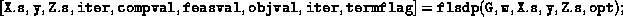
- When the output parameter
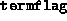 has the value 3, the
meaning is slightly different from the XZ+ZX case. Here,
has the value 3, the
meaning is slightly different from the XZ+ZX case. Here,  means that the Schur complement matrix, which is symmetric and
mathematically positive definite for the
XZ method, was numerically indefinite or singular, i.e. Matlab's
chol routine failed or generated a zero diagonal element.
Also, the termination code
means that the Schur complement matrix, which is symmetric and
mathematically positive definite for the
XZ method, was numerically indefinite or singular, i.e. Matlab's
chol routine failed or generated a zero diagonal element.
Also, the termination code  is not used.
is not used.
Appendix B contains sample Matlab sessions that illustrate
the use of dsdp.m and lsdp.m on these special types
of problems.




Next: Complementarity and Nondegeneracy
Up: Specialized Routines
Previous: Diagonally constrained SDP's
Madhu Nayakkankuppam
Wed Jun 25 18:01:54 EDT 1997
![]() function of an
undirected graph is also available. As in the diagonally
constrained case, such
an SDP may be solved more efficiently by the XZ method than the
XZ+ZX method, as long as the number of edges in the graph is not too large.
The driver script is lsdp.m and the
specialized function is flsdp.m. The five steps involved in
setting up and solving a problem are again similar to Section 3,
except for the following important differences:
function of an
undirected graph is also available. As in the diagonally
constrained case, such
an SDP may be solved more efficiently by the XZ method than the
XZ+ZX method, as long as the number of edges in the graph is not too large.
The driver script is lsdp.m and the
specialized function is flsdp.m. The five steps involved in
setting up and solving a problem are again similar to Section 3,
except for the following important differences:
![]()