Diagonally constrained SDP's

  For the case of diagonally constrained problems (for example, MAX-CUT relaxations), the Schur complement equations can be formed and solved very efficiently using the XZ search direction [4, 5]. The specialized routines dsdp.m and fdsdp.m take advantage of this. As before, the five steps involved in setting up and solving a problem are: preparing the data, setting the options, initializing the variables, invoking the solver, and interpreting the output. These are similar to those described in Section 3, except for the following important differences:

• These routines solve a specialized SDP, not an SQLP. The quadratic and linear parts of the SQLP are assumed to be empty.
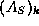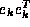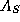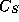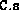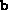• The k-th constraint matrix is assumed to be , where is the k-th unit vector (a vector of all zeros, except a 1 at the k-th position), so the matrix should not be stored explicitly. The user must provide the cost matrix (stored in the field ) and the primal constraint right-hand side b, stored in . The fields and 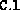are assumed to be empty, and are ignored. No structure 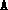is needed.
• There is a special initialization routine called dsetopt.m which sets the options to default values. The default value for reltol is larger than that used by setopt.m, since the XZ method generally cannot achieve the same high accuracy as the XZ+ZX method. Also the default value for tau is 0.99 (instead of 0.999) since the XZ method performs poorly with values of tau close to one.
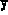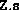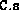• There is a special initialization routine called dinit.m which initializes , , . It expects that and 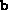are available in the Matlab workspace.
• The script dsdp.m uses an additional parameter called useXZ, which when set to 1 (this is the default set by dsetopt.m) solves the problem by the specialized code fdsdp.m using the XZ method. When useXZ is set to 0, the specialized code is not used, but instead dsdp.m calls fsql.m to solve the problem using the XZ+ZX method, after constructing the matrix 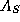explicitly and setting the structure 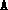accordingly. The latter usually provides more accurate solutions, but at substantially increased computation time.
• The problems that fall into this class are graph problems that usually require the graph to be connected, and hence will usually be applied to problems with a single block. They do not use the validate parameter, i.e. no check is made to ensure block structure compatibility. Nevertheless, a few simple consistency checks are always made on the data.
• The user who wants a function interface can bypass the script dsdp.m by typing

  

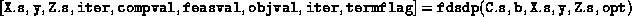
• When the output parameter 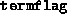has the value 3, the meaning is slightly different from the XZ+ZX case. Here, means that the Schur complement matrix, which is symmetric and mathematically positive definite for the XZ method, was numerically indefinite or singular, i.e. Matlab's chol routine failed or generated a zero diagonal element. Also, the termination code is not used.