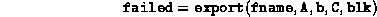
SDPpack's interface to ASCII data is provided via the two routines export.m and import.m. The calling sequence for export.m is
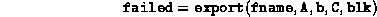
where fname is the name of the file (string) to
which the data must be exported. The data will be stored in one of the
formats described in Appendix A. If  is sparse, then the
format in Table 3 is used, otherwise that in
Table 2 is used. If the data was successfully
exported, export.m returns 0, otherwise 1. The calling
sequence for import.m is
is sparse, then the
format in Table 3 is used, otherwise that in
Table 2 is used. If the data was successfully
exported, export.m returns 0, otherwise 1. The calling
sequence for import.m is
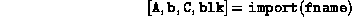
where fname is the name of a file (string) containing an SDP in one of the two formats described in Appendix A.
The three routines plotgap.m, plotfeas.m and plotobj.m plot the gap, the primal and dual infeasibilities, and the primal and dual objectives respectively, as a function of the iteration count. Several other miscellaneous features are available via the auxiliary routines described below. More information is available by typing help routine_name from within Matlab.
lam = blkeig(X,blk)
For example, (strict) complementarity is easily checked by typing
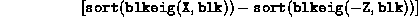
where 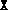 and
and 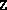 are the computed solutions of an SDP.
(The sorting operation does not preserve the block structure.)
are the computed solutions of an SDP.
(The sorting operation does not preserve the block structure.)
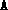 ), the block structure (blk) and a primal feasible point
), the block structure (blk) and a primal feasible point
 , this routine can be used to test for primal degeneracy. The
calling sequence is:
, this routine can be used to test for primal degeneracy. The
calling sequence is:
[cndprimal,D] = primalcond(A,blk,X,eigtol)
where eigtol is a tolerance used in computing the
rank of 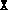 . A large value of cndprimal is a strong
indication that the problem is primal degenerate [4] (type
help primalcond for the definition).
. A large value of cndprimal is a strong
indication that the problem is primal degenerate [4] (type
help primalcond for the definition).
 ), the block structure (blk) and a dual feasible
), the block structure (blk) and a dual feasible
 , this routine tests for dual degeneracy. The calling sequence
is:
, this routine tests for dual degeneracy. The calling sequence
is:
[cnddual, B] = dualcond(A,blk,Z,eigtol)
where eigtol is a tolerance used in computing the
rank of 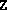 . A large value of cnddual is a strong
indication that the problem is dual degenerate [4] (type
help dualcond for the definition).
. A large value of cnddual is a strong
indication that the problem is dual degenerate [4] (type
help dualcond for the definition).
If 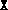 (
(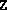 ) passed to primalcond.m (dualcond.m)
is the solution of an SDP solved with the default parameter values in
setpars.m, and if
) passed to primalcond.m (dualcond.m)
is the solution of an SDP solved with the default parameter values in
setpars.m, and if 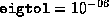 , then a value
exceeding, say
, then a value
exceeding, say 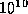 , for cndprimal (cnddual)
is indicative of primal (dual) degeneracy. Primal (dual) degeneracy
implies the nonuniqueness of dual (primal) solutions. The converse is
true if strict complementarity holds [4].
, for cndprimal (cnddual)
is indicative of primal (dual) degeneracy. Primal (dual) degeneracy
implies the nonuniqueness of dual (primal) solutions. The converse is
true if strict complementarity holds [4].
 and
and  , this routine verifies the optimality conditions and
computes a lower bound (in the 1--norm) of the condition number of
an SDP [5]. The calling sequence is:
, this routine verifies the optimality conditions and
computes a lower bound (in the 1--norm) of the condition number of
an SDP [5]. The calling sequence is:
[cndjac,dgap,pinfeas,dinfeas,blockmat] = sdpcond(A,b,C,blk,X,y,Z)
A large value of cndjac is a strong indication of degeneracy (primal, dual or both), or that the solution violates strict complementarity. This routine takes a long time to execute compared to primalcond.m and dualcond.m, but the advantage over primalcond.m and dualcond.m is that no tolerance is required.
To use these routines to examine the degeneracy or conditioning
properties of a Lovász  function problem or of a diagonally
constrainted SDP, the user must ensure that the data
function problem or of a diagonally
constrainted SDP, the user must ensure that the data 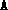 ,
, 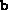 and
and
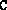 have been constructed. This can easily be done by calling the
appropriate script (lsdp.m or dsdp.m) with
have been constructed. This can easily be done by calling the
appropriate script (lsdp.m or dsdp.m) with 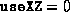 and
and 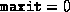 . Upon termination of the script, these variables
will be defined in the Matlab workspace.
. Upon termination of the script, these variables
will be defined in the Matlab workspace.
K = skron(M,N,blk)
This routine is called only by sdpcond.m.
[Anew,bnew,flag] = preproc(A,b,rkthresh)
where rkthresh is a small threshold
(e.g. 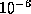 ) used to determine the rank of
) used to determine the rank of  .
.
 (see Section 3.1).
(see Section 3.1).
 problems. There is also a routine to create SDP's
with solutions of prescribed rank. These routines are discussed
below.
problems. There is also a routine to create SDP's
with solutions of prescribed rank. These routines are discussed
below.
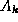 is assumed to be
is assumed to be 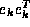 , where
, where 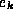 is the k--th unit
vector (a vector with all zeros, except a 1 in the k--th
position). The routine generates
is the k--th unit
vector (a vector with all zeros, except a 1 in the k--th
position). The routine generates 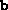 and
and 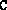 randomly. This
problem can be solved with the specialized routines dsdp.m
and fdsdp.m (see Section 4), which do not
require
randomly. This
problem can be solved with the specialized routines dsdp.m
and fdsdp.m (see Section 4), which do not
require 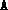 to be explicitly stored.
to be explicitly stored.
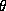 function of a random graph with
n vertices and expected edge density approximately dsty.
The vertices are given random weights. A warning is printed if
the graph is disconnected. The specialized routine lsdp can
be used to solve this problem (see Section 4).
function of a random graph with
n vertices and expected edge density approximately dsty.
The vertices are given random weights. A warning is printed if
the graph is disconnected. The specialized routine lsdp can
be used to solve this problem (see Section 4).
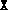 having rank
r, and a dual solution
having rank
r, and a dual solution  having rank s. This
routine does not have the provision to handle multiple blocks, so here,
blk is just a single number. This is particularly useful for
creating degenerate test problems, or problems with a non--strictly
complementary solution.
having rank s. This
routine does not have the provision to handle multiple blocks, so here,
blk is just a single number. This is particularly useful for
creating degenerate test problems, or problems with a non--strictly
complementary solution.
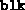 ) and the number of constraints (m) are
available in the Matlab workspace, and creates an SDP which has no
strictly feasible primal solution.
) and the number of constraints (m) are
available in the Matlab workspace, and creates an SDP which has no
strictly feasible primal solution.
In addition to these routines, the convert subdirectory contains scripts that will convert SDP data to a format recognized by some other popular codes. In particular, there are scripts to_sp, to_lmitlbx and to_sdpa which convert SDP data in the Matlab workspace to formats recognized by SP [6], Matlab's LMI Toolbox, and SDPA [7] respectively. Typing help routine_name within Matlab provides some more information on the correspondence between SDPpack variables and those used by the other codes. This is merely to encourage users to try other codes on the benchmark problems in Appendix C (available from the SDPpack web page). These routines may not be supported in future releases.