



Next: Lovász function
Up: Specialized Routines
Previous: Specialized Routines
For the case of diagonally constrained problems (for example, MAX--CUT
relaxations), the Schur complement equations can be formed and solved
very efficiently using the XZ search direction [2,3]
(sometimes called the KSH/HRVW/M direction in the literature.)
The specialized routines dsdp.m and fdsdp.m take
advantage of this. As before, the five steps involved in setting up and
solving a problem are: preparing the data, setting the parameters,
initializing the variables, invoking the solver, and interpreting the
output. These are almost identical to the description in
Section 3, except for the following important differences:
- The k--th constraint matrix
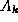 is assumed to be
is assumed to be 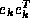 , where
, where 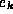 is the k--th unit vector (a vector of all zeros,
except a 1 at the k--th position), so the matrix
is the k--th unit vector (a vector of all zeros,
except a 1 at the k--th position), so the matrix 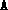 does not
have to be stored explicitly. The user must provide the cost matrix
does not
have to be stored explicitly. The user must provide the cost matrix
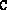 and the primal constraint right-hand side
and the primal constraint right-hand side 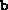 .
.
- There is a special initialization routine called
dsetpars.m which sets the parameters to default values. The
default value for reltol is larger than that used by
setpars.m, since the XZ method generally cannot achieve the
same high accuracy as the XZ+ZX method. Also the default value for
tau is
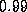 (instead of
(instead of 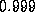 ) since the XZ method performs
poorly with values of tau close to one.
) since the XZ method performs
poorly with values of tau close to one.
- There is a special initialization routine called
dinitvars.m which initializes the variables. It expects that
the variables C and
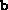 are available in the Matlab workspace.
are available in the Matlab workspace.
- The script dsdp.m uses an additional parameter called
useXZ, which when set to 1 (this is the default set by
dsetpars.m) solves the
problem by the specialized code fdsdp.m using the XZ method.
When useXZ is set to 0, the specialized code is not used, but
instead dsdp.m calls fsdp.m to solve the problem using
the XZ+ZX method, after constructing the matrix
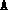 explicitly.
The latter usually provides more accurate solutions, but at substantially
increased computation time.
explicitly.
The latter usually provides more accurate solutions, but at substantially
increased computation time.
-
The problems that fall into this class are graph problems
that usually require the graph to be connected. Hence, these
specialized solvers have been purposefully designed to work with a
single block only. Consequently, they do not use the validate
parameter, but automatically make a few simple consistency checks on
the data.
- The user who wants a function interface can bypass the script dsdp.m
by typing:
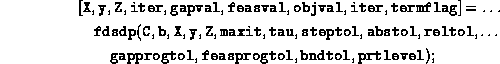
- When the output parameter
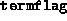 has the value 3, the
meaning is slightly different from the XZ+ZX case. Here,
has the value 3, the
meaning is slightly different from the XZ+ZX case. Here,  means that the Schur complement matrix, which is symmetric for the
XZ method, was numerically indefinite or singular, i.e. Matlab's
chol routine failed or generated a zero diagonal element.
means that the Schur complement matrix, which is symmetric for the
XZ method, was numerically indefinite or singular, i.e. Matlab's
chol routine failed or generated a zero diagonal element.




Next: Lovász function
Up: Specialized Routines
Previous: Specialized Routines
Madhu Nayakkankuppam
Fri Mar 28 00:48:56 EST 1997
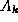 is assumed to be
is assumed to be 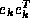 , where
, where 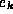 is the k--th unit vector (a vector of all zeros,
except a 1 at the k--th position), so the matrix
is the k--th unit vector (a vector of all zeros,
except a 1 at the k--th position), so the matrix 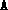 does not
have to be stored explicitly. The user must provide the cost matrix
does not
have to be stored explicitly. The user must provide the cost matrix
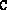 and the primal constraint right-hand side
and the primal constraint right-hand side 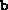 .
.
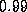 (instead of
(instead of 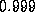 ) since the XZ method performs
poorly with values of tau close to one.
) since the XZ method performs
poorly with values of tau close to one.
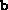 are available in the Matlab workspace.
are available in the Matlab workspace.
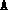 explicitly.
The latter usually provides more accurate solutions, but at substantially
increased computation time.
explicitly.
The latter usually provides more accurate solutions, but at substantially
increased computation time.
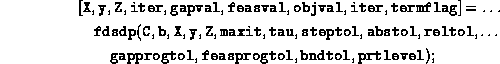
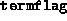 has the value 3, the
meaning is slightly different from the XZ+ZX case. Here,
has the value 3, the
meaning is slightly different from the XZ+ZX case. Here,  means that the Schur complement matrix, which is symmetric for the
XZ method, was numerically indefinite or singular, i.e. Matlab's
chol routine failed or generated a zero diagonal element.
means that the Schur complement matrix, which is symmetric for the
XZ method, was numerically indefinite or singular, i.e. Matlab's
chol routine failed or generated a zero diagonal element.