Introduction to Computer Science
2014-15 Fall
Allan Gottlieb
Tuesday Thursday 11:00-12:15
Room 101 CIWW

Start Lecture #1

Chapter 0 Administrivia

I start with chapter 0 so that when we get to chapter 1, the numbering will agree with the text.

0.1 Contact Information

0.2 Course Web Page

There is a web site for the course. You can find it from my home page, which is http://cs.nyu.edu/~gottlieb

0.3 Textbook

The course text is Liang, Introduction to Java Programming (Brief Version), Tenth Edition (10e)

0.4 Email, and the Mailman Mailing List

0.5 Grades

Grades are based on the labs and exams; the weighting will be approximately
25%*LabAverage + 30%*MidtermExam + 45%*FinalExam (but see homeworks below).

0.6 The Upper Left Board

I use the upper left board for lab/homework assignments and announcements. I should never erase that board. Viewed as a file it is group readable (the group is those in the room), appendable by just me, and (re-)writable by no one. If you see me start to erase an announcement, let me know.

I try very hard to remember to write all announcements on the upper left board and I am normally successful. If, during class, you see that I have forgotten to record something, please let me know. HOWEVER, if I forgot and no one reminds me, the assignment has still been given.

0.7 Homeworks and Labs

I make a distinction between homeworks and labs.

Labs are

Homeworks are

0.7.1 Homework Numbering

Homeworks are numbered by the class in which they are assigned. So any homework given today is homework #1. Even if I do not give homework today, the homework assigned next class will be homework #2. Unless I explicitly state otherwise, all homeworks assignments can be found in the class notes. So the homework present in the notes for lecture #n is homework #n (even if I inadvertently forgot to write it to the upper left board).

0.7.2 Doing Labs on non-NYU Systems

You may develop (i.e., write and test) lab assignments on any system you wish, e.g., your laptop. However, ...

0.7.2.1 Testing Your Labs on i5.nyu.edu

I feel it is important for CS majors to be familiar with basic client-server computing (related to cloud computing) in which one develops on a client machine (for us, most likely one's personal laptop), but runs on a remote server (for us, i5.nyu.edu). This requires three steps.

  1. Obtaining an account on i5.
  2. Copying files (the lab) from your system to i5.
  3. Logging into i5 and running the lab.

I have supposedly given you each an account on i5.nyu.edu, which takes care of step 1. Accessing i5 is different for different client (laptop) operating systems.

0.7.3 Obtaining Help with the Labs

Good methods for obtaining help include

  1. Asking me during office hours (see web page for my hours).
  2. Asking the mailing list.
  3. Asking another student, but ...
    Your lab must be your own.
    That is, each student must submit a unique lab. Naturally, simply changing comments, variable names, etc. does not produce a unique lab.

0.7.4 Computer Language Used for Labs

Your labs must be written in Java.

0.8 A Grade of Incomplete

The rules for incompletes and grade changes are set by the school and not the department or individual faculty member.

The rules set by CAS can be found in here. They state:

The grade of I (Incomplete) is a temporary grade that indicates that the student has, for good reason, not completed all of the course work but that there is the possibility that the student will eventually pass the course when all of the requirements have been completed. A student must ask the instructor for a grade of I, present documented evidence of illness or the equivalent, and clarify the remaining course requirements with the instructor.

The incomplete grade is not awarded automatically. It is not used when there is no possibility that the student will eventually pass the course. If the course work is not completed after the statutory time for making up incompletes has elapsed, the temporary grade of I shall become an F and will be computed in the student's grade point average.

All work missed in the fall term must be made up by the end of the following spring term. All work missed in the spring term or in a summer session must be made up by the end of the following fall term. Students who are out of attendance in the semester following the one in which the course was taken have one year to complete the work. Students should contact the College Advising Center for an Extension of Incomplete Form, which must be approved by the instructor. Extensions of these time limits are rarely granted.

Once a final (i.e., non-incomplete) grade has been submitted by the instructor and recorded on the transcript, the final grade cannot be changed by turning in additional course work.

0.9 Academic Integrity Policy

This email from the assistant director, describes the departmental policy.

  Dear faculty,

  The vast majority of our students comply with the
  department's academic integrity policies; see

  www.cs.nyu.edu/web/Academic/Undergrad/academic_integrity.html
  www.cs.nyu.edu/web/Academic/Graduate/academic_integrity.html

  Unfortunately, every semester we discover incidents in
  which students copy programming assignments from those of
  other students, making minor modifications so that the
  submitted programs are extremely similar but not identical.

  To help in identifying inappropriate similarities, we
  suggest that you and your TAs consider using Moss, a
  system that automatically determines similarities between
  programs in several languages, including C, C++, and Java.
  For more information about Moss, see:

  http://theory.stanford.edu/~aiken/moss/

  Feel free to tell your students in advance that you will be
  using this software or any other system.  And please emphasize,
  preferably in class, the importance of academic integrity.

  Rosemary Amico
  Assistant Director, Computer Science
  Courant Institute of Mathematical Sciences

The university-wide policy is described here

0.10 An Introduction with a Programming Prerequisite

How weird is this?

The formal prerequisite for 0101 is 0002, which teaches the Python programming language. (I had a tiny, insignificant, part in the development of Python when I first arrived at NYU, 30+ years ago.) (Grayed out material is not part of the official course.)

If instead of taking 0002, you have programmed in some other language (say C/C++), that is fine.

If, however, you are already a wizard Java programmer (or even a mere expert), you are taking the wrong course—you would be wasting somebody's money and, more significantly, wasting much of your time.

0.11 Important Downloads

0.11.1 Programs for Remote Access

As mentioned above you will occasionally need to access a remote computer, specifically i5.nyu.edu. To do this you will need two programs on your local machine, one to copy files to/from the remote computer, the other to log in to the other computer. For Unix and MacOS, the programs are scp and ssh and should be already on your computer. For Windows, you should download WinSCP and PuTTY right away.

The JDK and the Eclipse IDE

The Java Development Kit is needed to compile and run Java programs. Many students find an Integrated Development Environment very helpful in writing and debugging Java programs. The IDE we will use is called Eclipse.

Instructions for getting the JDK and Eclipse are here.

Chapter 1 Introduction to Computers, Programs, and Java

1.1 Introduction

This course, indeed the CS major sequence, emphasizes software, i.e., computer programs, rather than hardware, i.e., the physical components of a computer.

We teach a little hardware in 201, Computer Systems Organization, giving a high-level, non-detailed view, and present much more in 436, the Computer Architecture elective.

In general, the NYU course sequence offers a top-down view: we first show you how to program in high-level languages such as Java and Python, later we present the assembly language that is essentially the language understood by the computer itself, and later still we describe the how the electronic components in a computer are able to actually execute these programs.

Many (I think most) universities follow this approach. Others provide a bottom-up sequence beginning with the components, then low-level (assembly) languages, and then high-level languages.

1.2 What is a Computer?

Computers store and process data.

Modern computers store the programs on the same media as the data.

Figure 1.1 in the book is quite dated: It shows the design of 1980s computers. Modern machines do not have a single bus over which all information must travel. Compare the diagrams in sections 1.3 and 1.3.6 of my OS class notes

1.2.1 Central Processing Unit (CPU)

The CPU contains the electronic components that actually execute the instructions given to the computer.

First of all the CPU decodes the instruction (i.e., determines what is to be done, for example add the contents of two CPU memory units called registers and place the result in another register). Other instructions require the CPU to access additional components of the computer, e.g., the central memory.

In addition to determining the action needed, the CPU performs many of the operations required. For example the ALU (Arithmetic/Logic Unit) portion of the CPU contains an adder and thus performs the register add mentioned above.

1.2.2 Bits and Bytes (and Words)

Within a computer all data is stored as a sequence of bits, each of which can take on one of two values. Computers today mostly represent numbers as words, each consisting of 32 or 64 bits.

A 32-bit word can take on 232 (approximately 4 billion) different values.

I very much believe that you should remember just one value, 210=1024. Then you can deduce that
    232 = 22*230 = 4*23*10 = 4*210*210*210 = 4*1024*1024*1024,
which is a little more than 4*1000*1000*1000 = 4,000,000,000 (4 billion).

Modern computers cannot access a single bit of memory. They can access a single word and most computers (including all those we shall consider) can access a smaller unit called a byte or octet, which consists of 8 bits.

Since a byte is the smallest unit of memory that can be addressed (i.e., referred to directly), modern computers are called byte-addressable.

Since the bytes can be accessed in any order (not just sequentially in order byte #1, byte #2, ...), the memory is said to support random access and is called random access memory or RAM.

Kilo-, Mega-, Giga-, Tera-

This is actually a little controversial. If we use base 10 the prefixes correspond to thousands, millions, billions, and trillions. If, instead, we use base 2 they correspond to 210=1024, 220=10242, 230=10243, and 240=10244. Both of these are used. For example, a gigabyte of disk contains 109 bytes; whereas a gigabyte of RAM contains 230 bytes.

It is clearly nonsensical that an 80GB disk cannot hold 10 copies of the data contained in an 8GB RAM. Nonetheless, it is true. In fact, the proper terminology is that the disk contains only 80GiB (abbreviating 80 gibibytes) not 80GB. However common usage is still 80GB.

1.2.4 Storage Devices

Computers can access any byte in RAM quite quickly, which is wonderful. However, there are at least four problems with RAM.

  1. Energy / Heat.
    It is trivial to buy, power, and cool a 4TB disk; But I believe a 4GB RAM uses a few watts so a 4TB RAM would use kilowatts, a significant heat source.
  2. Limited size / Cost.
    Today's (personal) computers have a few gigabytes GBs of RAM.
    Although a gigabyte of RAM is huge by historical standards, it is still insufficient to hold all the data we want on a computer system. For example, my (lavishly equipped) laptop has 8GB, which can store one movie in standard definition (one DVD) but not one hi-def movie (one blu-ray).
    Quite related to capacity is the question of cost. In August 2014 a quick Google search shows a 4TB disk for about $130 and a 4GB RAM module for about $50 or about 400 times more expensive per byte.
  3. Volatile.
    RAM does not maintain its contents when the power is shut off and hence is not suitable for storing permanent data. Hard drives, various types of CDs, and flash storage do maintain their contents without power.
  4. Non-transportable.
    RAM cannot be moved easily from one machine to another. You would lose the data present (due to volatility) and if done often or carelessly, might damage the device. Some disk drives (called external disks) can be transported, but CDs and flash drives are much better in this regard.

Disk Drives

When compared to RAM, disks provide several hundred times more bytes per dollar, generate much less heat are non-volatile, and many (so called external disks) are readily transported from machine to machine.

However, disks are not byte addressable (i.e., you can't refer to an individual byte store on a disk). Instead the smallest addressable unit is called a sector, which is typically 512 bytes (very new disks have larger sectors). Disks form the primary storage medium for most computer systems that are at least as big as a laptop.

CDs

The book's words are a little confusing. CDs come in basically three flavors: read-only, write-once, and rewritable. (In this course CDs refer to data CDs; audio CDs organize the data stored in a different manner). DVDs and Blu-ray are (for us) simply higher density CDs (in 202 you will learn that the filesystems stored on DVDs differs from those of CDs).

Flash Drives

Flash drives are physically small storage units (some are often called thumb drives due to their size and shape). Unlike disks and CDs, flash drives have no moving parts and are thus much faster. Like disks they are not byte addressable; their smallest accessible unit is called a block.

Blocks can be rewritten a large number of times. However, the large number is not large enough to be completely ignored.

Flash drives are often called solid-state disks (SSDs).

Tape Drives

These are becoming less important and we will not discuss them.

1.2.5 Input and Output Devices

Note the CPU-centric terminology. Devices that primarily produce output, such as mice and keyboards, are called input devices, and devices that primarily accept input such as monitors are called output devices.

How does a keyboard send an 'X' as opposed to an 'x'?

How does moving a mouse, cause the pointer to move?

Screen resolution and dot pitch of a monitor are defined correctly in the book, but the statements about quality and clarity are too simplistic; the size of the monitor must be considered as well.

1.2.6 Communication Devices

We will not study these.

1.3 Programing Languages

I assume you have written at least a few programs (perhaps in 0002) and thus know a little about at least one programming language.

1.3.1 Machine Language

At the level of the hardware every program is just a sequence of 1s and 0s. If you take the computer architecture elective (and I hope you do), you will learn how to combine a (large) bunch of NOTs, ANDs, and ORs into an elementary processor that can execute machine language.

1.3.2 Assembly Language

Assembly language is basically a more convenient way to express machine language. For example most computers have an instruction that says to add register #4 to register #3 and put the result in register #1. In the MIPS assembly language used in our computer architecture class this would be written as add $1,$3,$4 In MIPS machine language this would be written as 00000000011001000000100000100000.

If you are curious, those 32 bits are logically (but not physically) broken in to fields
000000 00011 00100 00001 00000 100000
type   src1  src2  reslt shift func
Type=0 means an all-register instruction, the next three fields give the register numbers, shift is not used for add, funct=32 means add.

An assembler translates assembly language into the corresponding machine code.

1.3.3 High Level Languages

Languages like Java, Python, C, etc, unlike machine language, are designed to be understood by humans not a specific computer. Computers cannot execute programs in these languages directly and they cannot be simply translated line by line into machine code as can much of assembly language. Instead a sophisticated software translation/execution system is needed.

Compilers vs Interpreters

In some cases a single program, called a compiler, does the complete translation into machine language. In other cases the compiler produces assembly language, which an assembler then converts to machine language.

A third possibility, one commonly used for Java, is that the compiler translates the high level language into another language, in the case of Java this second language is called Java bytecode. Another program, called the JVM or Java Virtual Machine, executes this bytecode, either by compiling it to machine language, or by interpreting it directly.

An interpreter is a system that accepts a program as input and executes it directly. One interpreter you all know is the processor in your computer. This (hardware) interpreter reads machine language. The JVM is a software interpreter (i.e., it is itself a program). It reads and executes instructions in the Java byte code.

Another interpreter is the calculator on your phone; another is a text to speech translator.

1.4 Operating Systems

An operating system (OS) is a software system that raises the level of abstraction provided by the hardware to a more convenient virtual machine that other software can then use. For example, when we write programs accessing disk files, we do not worry about (or even have knowledge of) how the data is actually stored on the disk. Indeed, they very concept of a file is foreign to a disk and is an abstraction provided by the OS.

The OS also acts as a resource manager permitting multiple users to share the hardware resources.

Naturally much more detail is provided in my OS class notes. A short summary is in section 1.1 of those notes.

1.4.1 Controlling and Monitoring System Activities

1.4.2 Allocating and Assigning System Resources

1.4.3 Scheduling Operations

1.A Connecting to a Remote Computer

As mentioned above, you should all have accounts on i5.nyu.edu. Your username and password on i5 is the same as on home.nyu.edu. You may need to access i5 for some of the labs (which have not yet been assigned).

If your personal computer runs MS Windows, you should have downloaded (or will very soon download) two important free apps: putty and winscp. You should then be able to connect to i5.nyu.edu.

If your personal computer runs MacOS, discover how to bring up a terminal window (a.k.a. a command window). MacOS already has the command needed to access i5, type ssh <username>@i5.nyu.edu, where <username> is your username.

I will demo the use of remote computing when everyone has had a chance to get the programs needed.

1.5 Java, the World Wide Web, and Beyond

Java is a very popular, modern, general purpose, programming language. It comes with an extensive standard library that aids in writing graphical programs, especially those, called applets, that are invoked from browsers, e.g., firefox.

Java has extensive support for the modern software development methodology called object-oriented programming.

Java is a full-featured, and thus large, programming language. In its entirety, Java is not simple; but, in the beginning at least, we will be able to avoid most of the tricky parts.

1.6 The Java Language Specification, API, JDK, and IDE

Any programming language needs a detailed, precise specification describing the syntax and semantics of the language. It is basically the rules that determine a legal Java program. We will not need this level of precision.

Changing the specification essentially changes the language. The Java spec is stable.

The Application Program Interface (API) is defined by the standard library that comes with Java. It is comparatively easy to extend the API—write another library routine—and this does occur.

There are several versions of Java; we use Java SE 1.7, which we will just call Java.

Start Lecture #2

Remark: I forgot do show the home page last time.

The programs used to compile and run Java programs are part of the Java Development Toolkit (JDK).

Instead of using the JDK, one can use an Integrated Development Environment (IDE). Several IDEs are available. I will mostly use the JDK, but will show how to use the Eclipse IDE. You may develop your labs using either the JDK or an IDE, but the final product must be a Java program that can be run with just the JDK.

The various IDEs are all slightly different; whereas the JDKs (in principle) all accept the same language and produce the same results.

You may develop you lab assignments on any Java system you wish. However, we shall run you program using a Java SDK so you should test your program that way as well. I shall give examples of SDK usage (it is very easy).

1.7 A Simple Java Program

// Hello world in the C programming language
#include <stdio.h>
void main(int argc, char *argv[]) {
    printf("Hello, world.\n");
}

// Hello world in Java
public class Hello {
    public static void main (String[] args) {
    System.out.println("Hello, world.");
    }
}

On the right we see a simple Java program that prints the sentence Hello, world.. This program must be contained in the file named Hello.java.

For comparison, the corresponding C program is directly above the Java program. I put this program in a file called hello.c, but it could have been in a file called xyzzy.c (the .c is important).

Although they may look different, these two programs are basically the same. We now discuss the Java version, line by line.

  1. This line is a comment and is, in a sense, not part of the program. It is there to aid anyone reading the program. A comment begins with two consecutive slashes and ends at the end of the line.
  2. This line introduces the class named Hello. Java is case sensitive and, by convention, class names are capitalized. We will have much more to say about classes later. Now we just note that they can contain data (this simple class does not) and methods (this class has the method main()). Methods in Java are akin to procedures in other programming languages.
    Hello is public, which means it can be accessed from any other class. Many simple .java files contain just a single public class. In that case the file must be named X.java, where X is the name of the class.
    The { at the end of the line marks the beginning of the body of the class.
  3. This line introduces the method main(). The name main() is special. When a program is run (by the command java), the system begins by executing the main() method. This line tells us several things about main(): The { at the end of the line marks the beginning of the body of the method.
  4. This line (the bulk of the body of main()) invokes the method println, which is part of the field out in the class System.out.
  5. This line ends the method main().
  6. This line ends the class Hello.

1.B (GUI) Displaying Text in a Message Dialog Box

  // Hello world in Java -- gui version
  public class HelloGui {
    public static void main (String[] args) {
      javax.swing.JOptionPane.showMessageDialog(null, "Hello, world.");
    }
  }

Java comes with a large library of predefined functions. The top example on the right shows how just changing the output function causes a dialog box to be produced. Naturally, this code only works on a graphical display.

A difficulty is that actually explaining how the dialog box appears on the screen is quite complicated, involving widgets, fill-rectangle, and other graphics concepts.

1.C A Pedantic Version of Hello.java

  // Hello world in Java -- pedantic version
  public class HelloPedantic {
    public static void main (String[] args) {
      java.lang.System.out.println("Hello, world.");
    }
  }

In fact, our original Hello example used a shortcut. The class System is actually found in the package java.lang (which is searched automatically by javac). The code on the right shows the program without using the shortcut.

1.D Review Questions

These have answers on the web in the companion. See the book for details. I tried it and it works.

If you cannot understand an answer, ask! A good question for the mailing list.

Homework: 1.1, 1.3.

For the benefit of those students who may not yet have the book, here are the problems.

1.1 (Displaying three messages) Write a program that displays

  Welcome to Java
  Welcome to Computer Science
  Programming is fun

1.3 (Displaying a pattern) Write a program that displays the following pattern:


      J     A     V     V    A
      J    A A     V   V    A A
  J   J   AAAAA     V V    AAAAA
   J J   A     A     V    A     A

Unless otherwise stated homeworks are from the Programming Exercises at the end of the current chapter. They are not from the Review Questions.

1.8 Creating, Compiling and Executing a Java Program

Creating a Java Program

A Java program is created using a text editor. I use emacs. Others use vim, textedit, notepad, or a variety of alternatives. Another possibility is the editor included with a Java IDE such as eclipse.

Compiling a Java Program

Java programs are compiled using a Java compiler. The standard compiler included with a JDK is called javac. To compile our Hello program, located in the file Hello.java, one would write

  javac Hello.java

Javac translates Java into an intermediate form normally called bytecode. This bytecode is portable. That is the bytecode produced on one type of computer can be executed on a computer of a different type.

The bytecode is placed in a so-called class file, in this case the file Hello.class

Our C version of Hello, if contained in the file Hello.c, could be compiled via the command

    cc -o Hello Hello.c

The resulting file Hello is not portable. Instead it has instructions suitable for one specific machine type (and software system).

The Java Virtual Machine (JVM)

Portability of Java bytecode has been obtained by defining a virtual machine on which to run the bytecode. This virtual machine is called the JVM, Java Virtual Machine.

Each platform (hardware + software, e.g., Intel x86 + MacOS or SPARC + Solaris) on which Java is to run includes an interpreter of this virtual machine. Somewhat ambiguously, the emulator of the Java Virtual Machine is itself also called the JVM.

The penalty for this portability is that executing bytecode by the (typically software) JVM is not as efficient as executing non-portable, so-called native, code tailored for a specific machine.

Executing a Java Program

Since essentially no hardware/OS can execute Java bytecode directly, another program is run and is given the bytecode as data. This program is typically included in any Java IDE. When using the JDK the program is called java (lower case).

For our example the bytecode located in the file Hello.class is executed via the JDK command

  java Hello

(Note that we must write Hello and not Hello.class.)

1.9 Programming Style and Documentation

1.9.1 Appropriate Comments and Comment Styles

There are three types of Java comments.

  1. // comments the rest of the line
  2. /* ... */ comments the material ...
  3. /** ... */ uses javadoc

I will use only the first form, but you may use any of the three.

To learn about javadoc, which is quite cool, see the reference in the book.

1.9.2 Proper Indentation and Spacing

You should all be familiar with proper indenting to show the meaning of the program since Python requires it.

1.9.3 Block Styles

I use the end-of-line style but many prefer the next-line style. You may use either (see the book for examples of next-line style).

1.10 Programming Errors

I wish I could write a few words or pages (or books) that would show you how to avoid making errors and how to find and fix error made by others.

Instead, it will be a semester-long effort: We will write programs in class, which will doubtless have errors that we can fix together.

Homework: 1.7

1.10.1 Syntax Errors

1.10.2 Runtime Errors

1.10.3 Logic Errors

1.10.4 Common Errors>

1.11 Developing Java Programs Using NetBeans

We will use Eclipse instead

1.11.1 Creating a java Project

1.11.2 Creating a java Class

1.11.3 Compiling and Running a Class

1.12 Developing Java Programs Using Eclipse

Make sure most students have already downloaded Eclipse before starting.

In general you can either follow the book or some of the help in Eclipse itself

1.12.1 Creating a java Project

Click File → New → Java Project. This should bring up a dialog box.

I agree with Liang that it is wise to select Use project folder as root for sources and class files.

1.12.2 Creating a java Class

Click File → New → Class. There is also a button for this (it has a `C').

You can select the option to automatically generate the header line for the main program. Naturally, you don't do this for a class that does not contain the main program.

Somehow Liang forgot to say that you then type in the rest of the class definition.

1.12.3 Compiling and Running a Class

When you save the class (Cntl-S), Eclipse automatically compiles it.

To run the project you can click a button, type the f11 function key, or can right click the class name in the Package Explorer pane then click on Run as → Java Application.

Chapter 2 Elementary Programming

2.1 Introduction

2.2 Writing Simple Programs

I prefer to choose examples not from the book so that you wind up with two examples instead of one done twice.

A Primitive Program for Solving Quadratic Equation

Let's solve quadratic equations Ax2 + Bx + C = 0. Computational problems like this often have the form

  1. Get the input
  2. Compute the output
  3. Print the results
  4. Do it again.

For this simple version we will hard-wire the input (thereby avoiding step 1) and not do it again (thereby avoiding 4).

Question: What is the input?
Answer: The three coefficients A, B, and C.

Question: How are the results computed?
Answer: -B +- sqrt(B2-4AC)

Question: What about sqrt of a negative number?
Answer: What about it? Mathematically, you get complex numbers. We will choose A, B, C avoiding this case. A real program would check.

public class Quadratic1 {
    public static void main (String[] args) {
        double a, b, c;     // double precision floating point
        a = 1.0;
        b = -3.0;
        c = 2.0;
        double discriminant = b*b - 4.0*a*c;
        // We assume discriminant >= 0 for now
        double ans1 = (-b + Math.pow(discriminant,0.5))/(2.0*a);
        double ans2 = (-b - Math.pow(discriminant,0.5))/(2.0*a);
        System.out.println("The roots are " + ans1 + " and " + ans2);
    }
}

The program is on the right. Note the variables are declared to have type double. This is the normal declaration for real numbers in Java.

We can assign values to variables either when we declare them or separately. Both are illustrated in the example.

Note that the first two lines and the last two lines are the same as in the first example.

Question: How does the println work? In particular, what are we adding?
Answer: The + is overloaded. X+Y means add if X and Y are numbers; it means concatenate if X and Y are strings.

But in the program we have both strings and numbers.
When the operands are mixed, numbers are converted (coerced) to strings.

The name double is historical. On early systems real numbers were called floating point because the decimal point was not in a fixed location but instead could float. This way of writing real numbers is akin to scientific notation. The keyword double signifies that the variable is given double the amount of storage as is given to a variable declared to be float.

2.3 Reading Input from the Console

A Less Primative Program for Solving Quadratic Equations

Our previous quadratic solver was quite primitive. In order to solve a different quadratic equation it was necessary to change the program, recompile, and re-run.

In this section we will save the first two steps, by having the program read in the coefficients A, B, and C. Later we will use a loop to enable one run to solve many quadratic equations.

On the right is the less primitive program written in a pedantic style. Below that we show the program as it would normally be written.

public class Quadratic2Pedantic {
  public static void main (String[] args) {
    double a, b, c;
    double discriminant, ans1, ans2;
    java.util.Scanner getInput;
    getInput = new java.util.Scanner(java.lang.System.in);
    a = getInput.nextDouble();
    b = getInput.nextDouble();
    c = getInput.nextDouble();
    discriminant = b*b - 4.0*a*c;
    // We assume discriminant >= 0 for now
    ans1 = (-b + Math.pow(discriminant,0.5))/(2.0*a);
    ans2 = (-b - Math.pow(discriminant,0.5))/(2.0*a );
    java.lang.System.out.println("The roots are " + ans1
                                 + " and " + ans2);
  }
}

Note the following new features in this program.

On the right we see the program rewritten in a style that would normally be used.

import java.util.Scanner;
public class Quadratic2 {
  public static void main (String[] Args) {
    Scanner getInput = new Scanner(System.in);
    double a = getInput.nextDouble();
    double b = getInput.nextDouble();
    double c = getInput.nextDouble();
    double discriminant = b*b - 4.0*a*c;
    // We assume discriminant >= 0 for now
    double ans1 = (-b + Math.pow(discriminant,0.5))/(2.0*a);
    double ans2 = (-b - Math.pow(discriminant,0.5))/(2.0*a);
    System.out.println("The roots are " + ans1 + " and
                       " + ans2);
  }
}

The above explanation is way more complicated that the program itself! For now, but not for later, it is fine to just remember how to read doubles. Other methods in the Scanner class include nextInt(), nextBoolean(), and next(). The last method finds the next token (roughly the next string).

Homework: 2.1, 2.5

For those without the book.

2.1: Write a program that reads Celsius degrees (in double), converts it to Fahrenheit, and displays the result. The formula is F=(9/5)C+32.

2.5: Write a program that reads in the subtotal and the gratuity rate, then computes the gratuity and the total.

2.4 Identifiers

These are the names that appear when writing a program. Examples include variable names, method names, and object names, and class names. There are rules (really conventions) for the names.

2.5 Variables

As we have said classes contain data (normally called fields) and methods. Fields are examples of variables, but we haven't seen any fields yet. Note that the various doubles above are not (directly) members of the class Quadratic2. Instead, they are part of the main() method, which itself is a member of the class.

Later we shall learn that there are two kinds of fields, static and non-static.

Another kind of variable is the local variable, which is a variable declared inside a method. We have seen several, e.g. discriminant.

The final kind of variable is the parameter. We have seen one example so far, the args parameter always present in the main() method.

Note that discriminant is not a parameter. The variable in Math.pow() corresponding to discriminant is the parameter. In general variables are classified by how they are declared, not by how they are used.

2.6 Assignment Statements and Assignment Expressions

Many programming languages have assignment statements, which in Java are of the form

variable = expression ;

Executing this statement evaluates the expression and places the resulting value in the variable.

This ability to change the value of a variable (so called mutable state) is a big deal in programming language design. Proponents of functional languages believe that imperative languages, such as Java, are harder to understand due to the changing state.

Java, like the C language on which the Java syntax is based, also includes assignment expressions, which are of the form

  variable = expression

(NO semicolon). An assignment expression evaluates the RHS (right hand side) expression, assigns the value to the LHS variable, and then returns this value as the result of the assignment expression itself.

  System.out.println(x = Math.pow(2,0.5));
  


  a = b = c = 0;
  



  a = 1 + (b = 2 + (c = 0));

The first example evaluates the square root of 2, assigns the value to x, and then passes this value to println.

The second example first performs c=0, which results in c becoming 0 and the value 0 returned. This 0 is then assigned to b and returned, where it is assigned to a. Note the right to left evaluation.

The third example is ugly, confusing, and not recommended. It works as follows: c=0 is evaluated assigning 0 to c and returning 0. Then 2+0 is evaluated to 2, assigned to b, and returned. Then 1+2 is evaluated to 3, assigned to a, and discarded.

Java, again like C, uses = for assignment and == to test if two values are equal. Another common choice is to use := for assignment and = to test for equality.

Start Lecture #3

2.7: Named Constants

We have seen constant numbers and constant strings. But these were literal constants; that is the value itself was used (e.g., 2 or "Hello, world.").

A string constant like "Hello, world." is certainly descriptive, but a numeric constant like 2 is not (does its usage signify that we are computing base 2, that our computer game program is playing 2-handed cribbage, or what?). In addition, if we wanted to change either constant, we would need to change all relevant occurrences.

Instead of explicitly writing the 2 or "Hello, world." at each occurrence, we can defined a named constant (a.k.a. a symbolic constant) for each value.

  final int NUMBER_BASE = 2;
  final int CRIBBAGE_HANDS = 2;
  final String MSG = "Hello, world.";

The first two lines on the right could be used in a two-handed cribbage program that somehow relied on base 2 representations. Then if the program was to be extended to 4-handed cribbage as well, we would have a clue where to look.

The final keyword says that definition gives the final value this identifier will have. That is, the identifier will not be assigned a new value. It is read-only or constant.

2.8 Naming Conventions

Java has conventions for the capitalization of various names. These are universally followed for names in the language itself. Although they are probably not required for user-defined names, you definitely should follow them. They enable you to tell at a glance whether a name is used for a variable, a method, a class, or a constant.

2.9 Numeric Data Types and Operations

2.9.1 Numeric types

Numerical values in Java come in two basic types, corresponding to mathematical integers and real numbers. However each of these come in various sizes.

Mathematical integers have four Java types.

Mathematical real numbers have two Java types

The difference between the four integer types is the amount of memory used for each value. As the name suggests a byte is stored in a single byte. A short is stored in two bytes; an integer is stored in four; and a long is stored in eight.

Similarly, a float is stored in four bytes and a double is stored in eight.

For integers, allocating more storage permits a wider range of values.

Floating point is more complicated. The extra storage is used to extend the range of both the fractional part and the exponent. Recall that floating point numbers are represented in what is essentially scientific notation, so they contain both a fractional part and an exponent (unlike customary scientific notation, the exponent represents a power of 2 not 10).

2.9.2 Reading Numbers from the Keyboard

  Scanner getInput = new Scanner(System.in);
  byte b = getInput.nextByte()

We have already seen nextDouble(). There are analogous methods for the other 5 numeric possibilities, namely nextByte(), nextShort(), nextInt(), nextLong(), nextFloat(), nextDouble()

2.9.3 Numeric Operators

Java, like essentially all languages, defines +, -, *, and / to be addition, subtraction, multiplication, and division.

  (-1) % 5 == -1
  (-1) modulo 5 == 4

Java defines % to be the remainder operator. Some people (and some books and some web pages) will tell you that Java defines % to be the mathematical modulo operator.
DON'T believe it!
Remainder and modulo do agree when you have positive arguments, but not in general.

2.10 Numeric Literals

Literals are constants that appear directly in a program. We have already seen examples of both numeric and string literals.

2.10.1 Integer Literals

Normally integers are interpreted as decimal (base 10). However, if the literal begins with 0 followed by a digit, the value is interpreted as octal (base 8). If it begins with 0x or 0X, it is interpreted as hexadecimal (base 16). If it begins with 0b or 0B, it is interpreted as binary (base 2). Otherwise, it is interpreted as decimal (base 10).

Question: What is the use of base 8 and base 16 for us humans with 10 fingers (i.e, digits)?
Answer: Getting at individual bits.

An integer literal is considered an int unless it ends with an l or an L, in which case it is considered to be a long. It is better to use L since l looks like 1.

2.10.2 Floating-Point Literals

public class Floating {
  public static void main (String[] args) {
    System.out.println(10 / 3);
    System.out.println(10D / 3);
  }
}

Real numbers are always decimal. If the literal ends with an f or an F, it is considered a float. By default a real literal is a double, but this can be emphasized by ending it with a d or a D. Note that, if the literal ends with an f, F, d, or D, it is floating point even if it does not have a decimal point.

Question: what is printed by the program on the right?

Scientific Notation

Literals such as 6.02×1023 (Avogadro's number) can also be expressed in Java (and most other programming languages). Although the exact rules are detailed, the basic idea is easy: First write the part before the × then write an e or an E (for exponent) then write the exponent. So Avogadro's number would be 6.02E23. Negative exponents get a minus sign (9.8E-3).

The details concern the optional + in the exponent, the optional trailing d, D, f, or F for and the ability to omit the decimal point if it is at the right.

2.11 Evaluating Expressions and Operator Precedence

This is quite a serious subject if one considers arbitrary Java expressions. In general, to find the details, one should search the web using site:sun.com. This leads to the Java Language Specification http://java.sun.com/docs/books/jls/third_edition/html/j3TOC.html . The chapter on expressions http://java.sun.com/docs/books/jls/third_edition/html/expressions.html is 103 pages according to print preview on my browser!

For now we restrict ourselves to arithmetic expressions involving just +, -, *, /, %, (, and ). In particular, we do not now consider method evaluation. In this case the rules are not hard and are very similar to the rules you learned in algebra.

  1. Evaluate (innermost) parenthesized parts first and then erase the parentheses.
    So 3*(5+2) == 3*7 == 21).
  2. Within a parenthesized part evaluate all *, /, % in one left-to-right pass.
    So (7 * 4 % 5) + 12 = 3 + 12 == 15
  3. Within a parenthesized part, after doing *, /, %, do all +, - in one left-to-right pass.
    So (8 - 3 + 2) / (1 + 2 - 7) == 7 / -4 = -1

The last step also illustrated integer division, which in Java rounds towards zero.

Note that the above discussed binary operators (i.e they operate on two values). Java has unary operators as well, e.g., unary -, which are evaluated first. So
5 + - 3 == 5 + (-3) == 2   and   - 5 + - 3 == (-5) + (-3) == -8

Unary + is defined as well, but doesn't do much. Unary (prefix) operators naturally are applied right to left
So 5 - - - 3 == 2 and 5 + + + + 3 == 8

WARNING!!

+ + x is very different from ++ x. The same holds for - - versus --. This will be made clear in section 2.14.

2.12 Case Study: Displaying the Current Time

I don't like repeating in class programs that are in the book but will make a partial exception here since obtaining the current time is important and is easy in Java.

  public class CurrentTime {
    public static void main(String[] args) {
      long seconds = System.currentTimeMillis() / 1000;
      long minutes = seconds / 60;
      long hours   = minutes / 60;
      System.out.print("GMT is now " + hours%24 + ":" +);
      System.out.println(minutes%60 + ":" + seconds%60);
    }
  }

System.currentTimeMillis() returns the number of milliseconds since midnight January 1, 1970. From this we can calculate the number of completed seconds/minutes/hours very easily. A little more thought shows how to calculate the current hour, etc.

The program is on the right. One point is that the times returned by System.currentTimeMillis() are for GMT.

Question: Why would calculating the month/day/year be harder?

2.12 (Alternate): Computing How long Ago

It is no fun to just do one from the book so we also do a silly version of a program to tell how long it is from one date to another. For example from 1 July 1980 to 5 September 1985 is 5 years, 2 months and 4 days.

Such a program would actually be useful. However, we will do a silly version since we don't yet know about arrays and if-then-else.

  1. We pretend that all months have 30 days and hence that a year has 30×12=360 days.
  2. We require that the user give the later date first. Actually we call it today's date, but it can be any date providing it is later than the second date.
// Silly version of How Long Ago
import java.util.Scanner;
public class HowLongAgo {
  public static void main (String[] args) {
    final int MONTH_DAYS = 30; // ridiculous
    final int YEAR_DAYS = 12*MONTH_DAYS; // equally ridiculous
    Scanner getInput = new Scanner(System.in);

    System.out.println("Enter today's day, month, and year");
    int day = getInput.nextInt();
    int month = getInput.nextInt();
    int year = getInput.nextInt();
    System.out.println("Enter old day, month, and year");
    int oldDay = getInput.nextInt();
    int oldMonth = getInput.nextInt();
    int oldYear = getInput.nextInt();

    // Compute total number of days ago
    int deltaDays = (day-oldDay) + (month-oldMonth)*MONTH_DAYS
        + (year-oldYear)*YEAR_DAYS;

    // Convert to days / months / years
    int yearsAgo = deltaDays / YEAR_DAYS;
    int monthsAgo = (deltaDays % YEAR_DAYS) / MONTH_DAYS;
    int daysAgo = (deltaDays % YEAR_DAYS) % MONTH_DAYS;

    System.out.println ("The old date was " + yearsAgo +
                " years " + monthsAgo + " months and "
                + daysAgo + " days ago.");
  }
}

The program (on the right) performs this task in four steps.

  1. Prompt for and read in the input (the longest step).
  2. Compute the total number of days between the two dates.
  3. Convert the days into years/months/days. This uses the remainder operator % and should be studied.
  4. Print the output.

Note that monthsAgo is not the total number of months ago since we have already removed the years.

I computed the three values in the order days, months, years, which is from most significant to least significant. You can instead compute the values in the reverse order (least to most significant). To see an example, read the book's solution.

Splitting a combined value into parts is actually quite useful. Consider splitting a 3-digit number into its three digits. For example, given six hundred fifteen, we want 6, 1, and 5. This is the same problem as in our program but YEAR_DAYS is 100 and MONTH_DAYS is 10.

Question: How would you convert a number into millions, thousands, and the rest?
Answer: Set YEAR_DAYS = 1,000,000 and MONTH_DAYS = 1,000.

Question: How would you convert dollars into hundreds, twenties, and singles?
Answer: Set YEAR_DAYS to 100 and MONTH_DAYS to 20.

Question: How would an operating system convert a virtual address into segment number, page number, and offset?
Answer: Set YEAR_DAYS to the number of bytes in a segment and ... oops wrong course (and real OSes do it differently).

Homework: 2.7 Write a program that prompts the user to enter the number of minutes and then calculates the (approximate) number of years and days it represents. Assume all years have 365 days.

2.13 Augmented Assignment Operators

Statements like x = x + y; are quite common and several languages, including Java and C, have a shorthand form x += y;.

Similarly Java et al. has -=, *=, /=, and %=. Note that there is NO space between the arithmetic operator and the equal sign.

2.14 Increment and Decrement Operators

An especially common operation is x = x + 1; and Java and friends have an especially short form x++. Similarly, we have x-- (but NOT ** or // or %%). Note that there is NO space between the two arithmetic operators. If you write x * + + y, you are requesting two unary additions (followed by one multiplication) not one ++ operator (followed by a multiplication).

As we just saw x++ can be part of an expression rather than the entire expression by itself. In this case, a question arises. Is the value used in the remainder of the expression the old (un-incremented) value of x, or the new (incremented) value? Both are useful and both are provided.

  x  = 5;
  y1 = x++ + 10;
  y2 = ++x + 10;
  y3 = x-- + 10;
  y4 = --x + 10;

Consider the code sequence on the right where all 5 variables are declared to be ints.

  1. The first line simply sets x to 5.
  2. The second line clearly increments x to 6, but is y1 set to 5+10 or 6+10? Answer: x++ is a post-increment, that is the increment is done after the value of x is supplied to the remaining expression. Thus y1 becomes 5+10=15. As a mnemonic hint the ++ comes after the x and the increment comes after the value of x is returned.
  3. The third line clearly increments x to 7, but this time we have a pre-increment (the ++ comes before the x and the increment is done before the value of x is returned. Thus y2 becomes 7+10=17.
  4. The rules for -- are the same as for ++ so the fourth line clearly decrements x to 6. It is a post-decrement, occurring after the value of x is returned. Thus y3 becomes 7+10=17.
  5. Clearly the last line decrements x back to 5. It is a pre-decrement occurring before the value of x is returned. Thus y4 becomes 5+10=15;

Since there were two increments and two decrements, we expect x to end with the same value as it had in the beginning ... and it does.

On the board show how to calculate the index for queues (rear++ and front++) and for stacks (top++ and --top). What about moving all four ++ and -- operators to the other side?

2.15 Numeric Type Conversions

What happens if we try to add a short to an int? How about multiplying a byte by a double?

Even simpler perhaps, how about assigning an integer value to a real variable, or vice versa?

The strict answer is that you can't do any of these things directly; instead, one of the values must be converted to the other type.

Sometimes this conversion happens automatically (but it does happen). Other times it must be explicitly requested, and some of these requests fail.

Coercion vs. Type Casting

When the programming language automatically converts a value of one type (e.g. int) to another type (e.g., double), we call the conversion a coercion.

When the programmer explicitly requests the conversion, we call it type casting.

Widening vs. Narrowing

Any short value is also a legal int. Similarly any float value is a legal double.

Conversions of this kind are called widenings since the new type in a sense is wider (takes more bits to represent) than the old. Similarly, the reverse conversions are called narrowing.

Java will perform widening coercions but not narrowing coercions. To perform a narrowing conversion (note conversion, not coercion), the programmer must use an explicit cast. This is done by writing the target type in parenthesis.

public class Test {
  public static void main (String[] args) {
    long a = 1234567890123L;   // one trillion plus
    int b;
    double x;
    float y;
    // b = a;  won't compile; coercions cannot narrow
    b = (int)a;    // narrowing cast
    x = a;
    y = a;
    System.out.println(a+ " " +b+ " " +x+ " " +y);
  }
}

javac Test.java; java Test
1234567890123 1912276171 1.234567890123E12 1.23456795E12

The code on the right illustrates these points. Two problems have arisen and a third would have occurred for a larger a.

  1. The narrowing from a to b was disastrous: 1234567890123 has become 1912276171. Not all 64-bit values fit in 32 bits. No wonder Java won't do the coercion and requires you to explicitly do the type cast!
  2. The coercion from a to y resulted in some loss of precision. A (32-bit) float uses some bits for the exponent so does not have as many available for the mantissa as does a 32-bit int, which has no exponent. So a very large int would not fit and a is larger that the largest int. Note that this can lead to a loss of precision but not to a completely wrong answer as in the previous case.
  3. The coercion from long to double was successful in this case, but in other examples could lose precision. A 64-bit double has more than enough mantissa bits to exactly represent any int, but not enough for largest long. Although a was larger than any int, it is very far from the largest long, so no precision was lost.

Wider Range vs. Wider Numbers

The last example showed that Java will coerce a 64-bit long into a 32-bit float. Clearly the 32-bit number is narrower than the 64-bit number, but the coercion is permitted.

The justification is that the range of possible floats (vastly) exceeds the range of possible longs, so the coerced value will be approximately equal to the original, only some precision will be lost.

2.16 Software Development Process

2.16 (Alternate) Case Study: Computing Compound Interest

Say you have a bank account with $1000 that pays 3% interest per year and want to know what you will have after a year.

import java.util.Scanner;
public class CompoundInterest {
  public static void main (String[] args) {
    Scanner getInput = new Scanner(System.in);
    double origBal = getInput.nextDouble();
    double interestRate = getInput.nextDouble();
    int n = getInput.nextInt();   // numberCoumpoundings
    double finalBal = origBal*Math.pow(1+interestRate/n,n);
    System.out.println(finalBal);
  }
}
javac CompoundInterest.java; java CompoundInterest
1000. .03 1
1030.0

java CompoundInterest
1000. .03 2
1030.2249999999997

java CompoundInterest
1000. .03 12
1030.4159569135068

java CompoundInterest
1000. .03 100000
1030.4545293116412

java CompoundInterest
1000. .03 1000000
1030.4545335307425

The program on the right is fairly straigtforward, given what we have done already. First we read the input data: the original balance, the (annual) interest rate, and the number of compoundings.

Then we compute the final balance after one year. We could do k years by changing the exponent from n to k*n.

Finally, we print the result.

The only interesting line is the computation of finalBal. Let's read it carefully in class to check that it is the same as the formula above.

Make sure you see the coercions that occurs in the division and addition.

We show five runs, the first one is for so called simple interest (only compounded once). We did this above and sure enough we again get $1030 for 3% interest on $1000.

The second is semi-annual compounding. Note that we do not need to recompile (javac).

The third is monthly compounding.

The fourth and fifth suggest that we are approaching a limit.

Start Lecture #4

Remark: Let's do 3.16 (a demo of eclipse) now.

2.17 Case Study: Counting Monetary Units

We already did a simpler version of this.

Let's do the design of a more complicated version: Read in a double containing an amount of dollars and cents, e.g., 123456.23 and print the number of twenties, tens, fives, singles, quarters, dimes, nickels, pennies.

There is a subtle danger here that we will ignore (the book doesn't even mention it). A number like 1234.1 cannot be represented exactly as a double since 0.1 cannot be written in base 2 (using a finite number of bits) just as 1/3 cannot be written as a decimal.

Remark: The above paragraph is indeed correct.

Ignoring the danger, the steps to solve the problem are

  1. Read the data.
  2. Convert the dollars and cents to an integer number of pennies.
  3. Find the number of twenties and subtract the corresponding number of pennies.
  4. Find the number of tens and subtract the corresponding number of pennies.
  5. ...
  6. Find the number of nickels and subtract the corresponding number of pennies.
  7. What is left is the number of pennies.
  8. Print the results.

Let's start this in class. One solution is here.

2.18: Common Errors and Pitfalls

Read this section. They are indeed common errors. We will keep writing programs and gain experience in recognizing, correcting, and then avoiding errors.

Chapter 3 Selections

3.1 Introduction

Essentially all computer languages have a way to indicate that some statements are executed only if a certain condition holds.

Java syntax is basically the same as in C. I consider it OK but not great.

3.2 boolean Data Type

We have seen four integer types (byte, short, int, and long), two real types (float and double), and a character type (char). These 7 types are called primitive.

Java has one more primitive type (boolean), used to express truth and falsehood.

Comparison Operators
Operator  Name
==equal to
!=not equal to
<less than
<=less than or equal to
>greater than
>=greater than or equal to

Mathematicians, when discussing Boolean algebra, capitalize Boolean since it is named after a person, specifically the logician George Boole. Java does not capitalize boolean.
Why?
Answer: Because boolean is a primitive type and Java does not capitalize the names of primitive types.

Note: We will learn that in Java, classes are also types, but not primitive types. As we know, class names are capitalized.

There are two boolean constants, true and false.

There are 6 comparison operators that are used to compare values in an ordered type (a type in which values are ordered). So we can compare ints with ints, doubles with doubles, and chars with chars. The result of a comparison is a boolean, namely true or false.

If values from different (ordered) types are being compared, one must be converted to the type of the other. Again this can be via coercion or type casting

int i = 1, j = 2;
boolean x, y = true, z;
x = i == j; // false
z = i < j; // true

On the right we see some simple uses of booleans. The one point to note is the distinction between = and == in Java.
The single = is the assignment operator that causes the value on the RHS to be placed into the variable on the LHS.
The double == is the comparison operator that evaluates its LHS and RHS, compares the results, and yields either true or false.

booleans are boring without if statements, which we learn next.

3.3 if Statements (a.k.a if-then Statements)

Found in basically all languages. We will see that the C/Java syntax for if permits the notorious dangling else problem (which is why I consider it not great).

if (boolean expression) {
  one or more statements;
}

The simplest form of if statement is shown on the right.

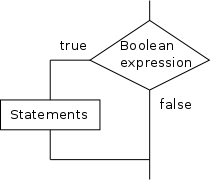
if-then

The semantics (meaning) of an if statement (sometimes called an if-then or a one-way if statement) is simple and is the same as in many other languages.

Odd or Even?

  ... (what did I leave out?)
  Scanner getInput = new Scanner(System.in);
  int x = getInput.nextInt();
  if (x%2 == 1) {
      System.out.println("Odd");
  }
  if (x%2 == 0) {
      System.out.println("Even");
  }
  ... (what did I leave out?)

On the right we see an (incomplete) simple program illustrating the use of an if statement.

For practice, let's begin by filling in the parts I omitted at the top and bottom.

Notice the useful tests: x%2==0 means that x is even; x%2==1 means that x is odd.

The second test on the right is redundant since, if an integer x is not odd, it must be even.
Wrong!
Question: Why is it wrong?

3.4 Two-Way if-else Statements (a.k.a. if-then-else Statements)

if (boolean expression) {
    one or more statements;
} else {
    one or more statements;
}

Often if is used to choose between two actions, one to be executed when the Boolean expression is true and the other to be executed when the Boolean expression is false.

The skeleton code for this if-then-else construct is shown on the right. The previous simpler skeleton is normally called an if-then even though Java (and C) do not actually employ a then keyword.

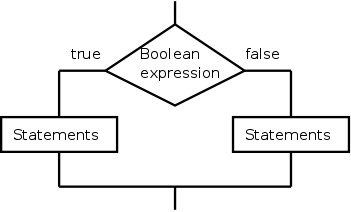
if-then-else

As the name suggests, the semantics of an if-then-else is to do the then or the else depending on the if. Specifically,

Omitting the {}

if (boolean expression)
    exactly one statement


if (boolean expression)
    exactly one statement
else
    exactly one statement


if (boolean expression) {
    one or more statements
} else
    exactly one statement

If any of the three blocks (the then block in the if-then statement, the then block in the if-then-else statement, or the else block in the if-then-else statement) consists of only one statement, its surrounding {} can be omitted.

On the right we see three of the four cases where the {} can be omitted.
Question:What is the remaining possibility?
Answer: The then block has exactly one statement and no {} while the else block has one or more statements and does have the {}.

Experienced Java programmers would almost always omit such {}, but it is probably better for beginners like us to leave them in for a while so that all if-then's and all if-then-else's have the same visual structure. There is an exception, see below.

3.5 Nested if and Multi-Way if-else Statements

The statement(s) in either the then block or the else block can include another if statement, in which case we say the two if statements are nested.

if (be1) { // be is Boolean expr
    if (be2) {
        ss1 // ss is statement(s)
    } else {
        ss2
    }
} else {
    if (be3) {
        ss3
    } else {
        ss4
    }
}

On the right we see three if statements, with the second and third nested inside the first.

If be1, the Boolean expression of the outside if statement evaluates to true, the second if statement is executed. If instead be1 is false, the third if statement executes.

There are eight possible truth values for the three Boolean expressions (be1–be3), but only four possible actions (ss1–ss4).
Question: Why?
Answer: Because for be1==true the value of be3 is irrelevant and for be1==false, the value of be2 is irrelevant.

Question: What are the values of be1..be3 if ss1 is executed? Similarly, for ss2, ss3, and ss4.

Selecting One of Several Possibilities

if (be1) {
    ss1
} else {
    if (be2) {
        ss2
    } else {
        if (be3) {
            ss3
        } else {
            ssDefault
        }
    }
}

Often deeply nested if-then-else's have the nesting only in the else part. This gives rise to code similar to that shown on the right.

Be sure you understand why this is not the same as separate (non-nested) if statements.

One trouble with the code shown is that it keeps moving to the right and, should there be many condition, you either get very wide lines or only have a few columns to use.

This is one situation where it pays even for beginners to make use of the fact that the {} can be omitted when they enclose exactly one statement. To make use of this possibility, you must realize that an if statement, in its entirety, is only one statement. For example, the entire nested if structure on the right is only one statement, even though it may have hundreds of statements inside its many {} blocks. Similarly, each of the nested ifs is just one statement.

if (be1) {
    ss1
} else if (be2) {
    ss2
} else if (be3) {
    ss3
} else {
    ssDefault
}

As a result we can remove the { and } from else { if ... } and convert the above to the code on the right.

Please read the code sequence carefully and understand why it is the same as the one above.

Note that the indenting is somewhat misleading as the symmetric placement of ss1, ss2, s3, and ssDefault suggests that they have equal status. In particular, since be1==true implies that ss1 gets executed, you might think that be3==true implies that ss3 gets executed. But that is wrong! Be sure you understand why it is wrong (hint: what if all the boolean expressions are true?).

Again be sure you can determine the truth values of be1..be3 if ss1..ss3 or ssDefault is executed.

Indeed this pattern with all the statements in the then block is so common that some languages (but not Java) have a keyword elif that is used in place of the else if above.

Other languages require an explicit then and an explicit ending to an if statement, most commonly end if. In that case no {} are ever needed for if statements.

Homework: 3.7 and 3.9.

3.8 Common Errors and Pitfalls

Don't forget the {} when you have more that one statement in the then block or else block. I recommend that, while you are learning Java, you use {} for each ss even if it is just one statement (except for the else if situation illustrated just above).

Don't mistakenly put a ; after the boolean expression right before the then block.

Don't write if (be==true). Instead, write the equivalent if (be). Although the first form is not wrong; it is poor style.

Don't test floating point values for exact equality. Often floating-point numbers are a little off for reasons such as "0.2 cannot be expressed exactly in floating point". (Since the mantissa of a floating point number is in binary, there is no way to express 1/5 exactly, just as there is no way to express 1/3 exactly in a base 10 mantissa.

The Notorious Dangling else

if (be1)
    if (be2)
        s2
else
    s1

The indenting on the right mistakenly suggests that should be1 evaluate to false, s1 will be executed. That is WRONG. The else in the code sequence is part of the second (i.e., inner) if, the one containing be2.
Question: How did I know that?
Answer: The Java (and C) rule is that an else pairs with the nearest unfinished if.

  if (be1)
      if (be2)
          s2
      else
          s1

A consequence of this rule is that the code above should be written as shown on the right, to make clear that s1 is executed if be1 evaluates to true AND be2 evaluates to false.

In a language like Python that enforces proper indentation, no such misleading information can occur.

In a language such as Ada with an explicit end if, the problem does not arise.

if (be1) {        if (be1) {
    if (be2) {        if (be2) {
        s2               s2
    }                 } else {
} else {                  s1
    s1               }
}                 }

On the right, I have added {} to make the meaning clear. The code on the far right has the same semantics as the dangling else code above. There is no ambiguity: the outer then has not yet ended when we get to the else (just match the braces) so the else must be part of the inner if.

The code on the near right has the semantics that the original indentation above mistakenly suggested. Again there is no ambiguity: The inner if was terminated by the second } (the inner if is part of the outer if's then block). Hence the else must be part of the outer if.

Silly Redundancies

  boolean even;        boolean even = number%2 == 0;
  if (number%2 == 0)
      even = true;
  else
      even = false;

  boolean b1;          boolean b1;
  int x, y;            int x, y;
  ...                  ...
  if (b1) {            if (b1) {
      x = 5;               x = 5;
      y = 10;          } else {
  } else {                 x = 20;
      x = 20;          }
      y = 10;          y = 10;
  }

These are not wrong, but add complexity to the code.

In both examples on the right, the far right code is simpler and hence clearer and preferred to the corresponding longer code on the near right.

In the first example the boolean expression is exactly the value we want to place into even, so do so directly, not via an if-then-else.

In the second example the redundant code is assigning the same value (specifically 10) to the same variable (specifically b2) in both the then and else arms. Thus, we can factor it out and just write it once outside the if-then-else.

3.7 Generating Random Numbers

Read

3.7 (Alternate) Generating Random Numbers

The class Math contains a method random() that returns a random double between 0 and 1 excluding 1.

By comparing this random with a fixed value between 0 and 1, you can execute the then-block a fixed percentage of the time.

3.7.A Wanna Play?

  import java.util.Scanner;
  ...
  System.out.println ("Do you want to play?");
  System.out.println ("Type 1 for yes 0 for no.");
  if (getInput.nextInt() == 1) {
      System.out.println("How many dollars do you want to bet?");
      int bet = getInput.nextInt();
      if (Math.random() <= 0.4)
          System.out.println("You win " + bet + " dollars!");
      else
          System.out.println("You lose.  Pay me " + bet + " dollars.");
  }
  ...

The program on the right is a trivial betting game

A key to the program is the Math.random() method in the Java library.

Note that the test we employ means that 40% of the time, the user wins and 60% of the time the user loses.

A real program would let you play many times without re-running the program. We will soon (chapter 5) learn how to write loops to enable this to happen.

Question: How come I had to import the Scanner class, but didn't have to import the Math class?
Ans: The Math class is in java.lang, which is automatically searched by javac; whereas the Scanner class is in java.util, which is not automatically searched so must be mentioned explicitly.

I left some parts out (indicated by ...), let's fill them in.

A working version is here.

3.8 Case Study: Computing Body Mass Index

Read.

3.8 (Alternate) Case Study: A Real Quadratic Equation Solver

Let's fix some problems with our previous solution to solving the quadratic equation Ax2+Bx+C=0.

  1. We shamefully divided by 2A without checking if A==0. In that case we don't have a quadratic equation at all!
  2. If A!=0 (i.e., a real quadratic) we need to handle the three cases of positive, negative, and zero discriminant separately

Let's start this in class. One possible program is here.

Start Lecture #5

3.9 Problem: Computing Taxes

Let's start this one in class as well. Handout sheet with tax table. A scan of the table is here.

The input is the filing status and the income; the output is the amount tax that is due.

3.10 Logical Operators

Boolean Operators
OperatorName
!not
&&and
||or
^exclusive or

Like most computer languages, Java permits Boolean expressions to contain so-called "logical operators". These operators have Boolean expressions as both operands and results.

The table on the right shows the four possibilities. The not operator is unary (takes one operand) and returns the opposite Boolean value as result.

The and operator is binary and returns false unless both operands are true.

The (inclusive) or operator is binary and returns true unless both operands are false. That is, the meaning of || is one or the other or both.

The exclusive or operator is binary and returns true if and only if exactly one operand is true. That is, the meaning of ^ is one or the other but not both. Note that ^ can also be thought of as not equal, but remember that the operands are Booleans not numbers.

Precedence of Logical, Comparison, and Arithmetic Operators

The logical operators have lower precedence than the comparison operators, which in turn have lower precedence than the arithmetic operators. In particular,
      x!=0 && 1/x < y+2   is evaluated as   (x!=0) && ( (1/x) < (y+2) )
which is normally what you want.

Short-Circuit Evaluation of && and ||

Since a&&b=false if either (or both) a==false or b==false, once we know that one of the operands to && is false, we need not evaluate the other.

Java makes use of this observation and ensures that, if the left operand of && is false, then the right operand is not evaluated. This, so-called short-circuit evaluation of a&&b saves a little time but, much more importantly, guarantees that
x!=0 && 1/x < y+2 will never divide by zero.

Similarly, if the left operand of || is true, the right operand is not evaluated.

3.11 Case Study: Determining Leap Year

As you probably know a day is the time it takes the earth to rotate about its axis, and a year is the time it takes for the earth to revolve around the sun.

By these definitions a year is a little less than 365.25 days. To keep the calendars correct (meaning that, e.g., the vernal equinox occurs around the same time each year), most years have 365 days, but some have 366.

A very good approximation, which will work up to at least the year 4000 and likely much further is as follows (surprisingly, we are not able to predict exactly when the vernal equinox will occur far in the future; see wikipedia).

Let's write in class a program that asks for the year and replies by saying if the year is a leap year. One solution is in the book.

3.12 Case Study: Lottery

The book has an interesting lottery game. The program generates a random 2-digit number and accepts another 2-digit number from the user.

Lets write some of this in class. Recall that Math.random() returns a random double between 0 and 1, possibly 0 but not 1. Since math.Random() is in java.lang we do not have to import it.

A full solution is in the book.

3.13 switch Statements

We have seen how to use if-then-else to specify one of a number of different actions, with the chosen action determined by a series of Boolean expressions.

Often the Boolean expressions consist of different values for a single (normally arithmetic) expression.

switch(expression) {
  case value1: stmts1
  case value2: stmts2
  ...
  case valueN: stmtsN
  default:  defaultStmts
}

For example we may want to do one action if i+j is 4, a different action if i+j is 8, a third action if i+j is 15, and a fourth action if i+j is any other value. In such cases the switch statement, shown on the right, is appropriate.

When a switch statement is executed, the expression is evaluated and the result specifies, which case is executed.

The semantics of switch are somewhat funny. Specifically, given the visual similarity with if-then-else, one might assume that after stmts1 is executed, control transfers to the end of the switch. However, this is wrong: Unless explicitly directed, control flows from one case to another.

The semantics of the C/Java switch closely resemble those of an assembler-level jump table and the computed goto of Fortran.

switch (expression) {
  case value1: stmts1
               break;
  case value2: stmts2
               break;
  ...
  case valueN: stmtsN
               break;
  default:  def-stmts
}

It is quite easy to explicitly transfer control from the end of one case to the end of the entire switch. Java, again borrowing from C, has a break statement that serves this purpose.

We see on the right the common form of a switch in which the last statement of each case is a break.

When a break is executed within a switch, control breaks out of the switch. That is, execution proceeds directly to the end of the switch. In particular, the code on the right will execute exactly one case or the default.

Homework: 3.11.

Homework: Write a program that reads in 3 doubles and determines if they can be the three side lengths of a triangle. This means make sure that the sum of any two is greater than the third.

3.14 Conditional Expressions

Recall that Java has +=, which shortens x=x+5 to x+=5. Java has another shortcut, the tertiary operator ?...:, which can be used to shorten an if-then-else.

bool-expr ? expr1 : expr2

if (x==5)
  y = 2;
else
  y = 3;

y = x==5 ? 2 : 3;

The general form of the so-called conditional expression is shown on the top right. The value of the entire expression is either expr1 or expr2, depending on the value of the Boolean expression bool-expr.

For example, the middle right if-then-else can be replaced by the bottom right assignment statement containing the equivalent conditional expression.

Note that this is not limited to arithmetic and can often be used to produce grammatically correct output. For example, consider the following example

  System.out.println ("Please input " + n + " number" + ((n==1) ? "." : "s."));

I realize this looks weird; be sure you see how it works.

Homework: Redo 3.7, this time using ? : to print the grammatically correct results.

3.15: Operator Precedence and Associativity

Operator Precedence in
decreasing order
OperatorAssociativity
var++, var--Left-to-right
+,- (unary), ++var, --varRight-to-left
(type)Right-to-left
!Left-to-right
*,/,%Left-to-right
+,- (binary)Left-to-right
<,<=,>,>=Left-to-right
==,!=Left-to-right
^Left-to-right
&&Left-to-right
||Left-to-right
?: (tertiary)Right-to-left
=,+=,-=,*=,/=,%=Right-to-left

The table on the right lists the operators we have seen in decreasing order of precedence. This order of precedence means that, in the absence of parentheses, if an expression contains two operators from different rows of the table, the operator in the higher row is done first.

The second column gives the associativity of the operators. If an expression contains two operators from the same row and that row has left-to-right associativity, the left operator is done first. Similarly if the row has right-to-left associativity, the right operator is done first. As with precedence, parentheses can be used to override this default ordering.

Not many programmers have the entire table memorized (not to mention the fact that there are other operators we have not yet encountered). Instead, they use parenthesis even when their use might not be necessary due to precedence and associativity.

However, it is wise to remember the precedence and associativity of some of the frequently used operators. For example, one should remember that *,/,% are executed before (binary +,-) and that both groups have left-to-right associativity. It would clutter up a program to see an expression like
((x*y)/z)/(((-x)+z)-y) rather than the equivalent (x*y/z)/(-x+z-y)

Homework: Write a java program that reads four integers. If any two (or any three, or all four) are equal, just print an error message. If all four are distinct, print the 2nd largest.

Homework: Contemplate but do NOT write a java program that first reads 11 integers. If any two (or any three, or ..., or all eleven) are equal, just print an error message. If all eleven are distinct, print the 6th largest (i.e., the middle value). There must be a better way! There is.

3.16 Debugging

Demo a little of the Eclipse debugger. For example try quadratic3. Don't forget to set a breakpoint before inputing the values.

Chapter 4 Mathematical Functions, Characters, and Strings

4.1 Introduction

4.2 Common Mathematical Functions

  public class PiAndE {
      public static void main(String[] args) {
          System.out.println("pi=" + Math.PI + " and e=" + Math.E);
      }
  }

The Math class contains many important methods and two important constants. We have already used a few methods from the class and will use several more this semester. The constants, E (the base of the natural logarithm) and PI (the ratio of a circle's perimeter to its diameter) are shown on the right. As you can see, since the Math class is a part of the java.lang package and the latter is searched automatically by javac, you do not need any import in order to use elements of the class. 

public static double sin(double theta)
public static double cos(double theta)
public static double tan(double theta)
public static double asin(double x)
public static double acos(double x)
public static double atan(double x)

public static double toDegrees(double radians)
public static double toRadians(double degrees)

4.2.1 Trigonometric Methods

The Math class has support for basic trigonometry.

The six methods on the upper right compute the three basic trig functions and their inverses. In all cases, the angles are expressed in radians.

The two methods below them are used to convert to and from degrees.

4.2.2 Exponent Methods

public static double pow(double a, double b)
public static double sqrt(double a)

public static double log(double x)
public static double exp(double x)

public static double log10(double x)

The first routine on the right computes ab. Since the special case of square root, where b=.5 is so widely used it has its own function, which is given next.

Mathematically, logs and exponentials based on Math.E are more important than the corresponding functions using base 10. They come next.

The base 10 exponential is handled with pow, but there is a special function for the base 10 log as shown.

4.2.3 The Rounding Methods

Given a floating point value, one can think of three integer values that correspond to this floating point value.

  1. The floor, i.e., the greatest integer not greater than.
  2. The ceiling, i.e., the least integer not less than.
  3. The nearest integer. What about ties?
public static double floor(double x)
public static double ceil(double x)
public static double rint(double x)

The Math class has three methods that correspond directly to these mathematical functions, but return a type of double. They are shown on the right. For the third function, ties are resolved toward the even number so rint(-1.5)==rint(-2.5)==-2.

public static int round(float x)
public static long round(double x)

In addition Math has an overloaded method round() that rounds a floating point value to an integer value. The two round method are distinguished by the type of the argument (standard practice for overloaded methods). Given a float, round() returns an int. Given a double, round() returns a long.

This choice prevents the loss of precision, but of course there are many floats and doubles (e.g., 10E30) that are too big to be represented as an ints or longs.

4.2.4 The min, max, and abs Method

These three methods are heavily overloaded, they can be given int, long, float, or double arguments (or, for min and max one argument of one type and the other of another type).

4.2.5 The random Method

We have already used Math.random() several times in our examples. As mentioned random() returns a double x satisfying 0≤x<1.

To obtain a random integer n satisfying m≤x<n you would write m+(int)((n-m)*Math.random()). For example, to get a random integer 10≤x<100 (i.e., a 2-digit number), you write 10+(int)(90*random()).

Start Lecture #6

Remark: Complete 3.12; didn't do it last time.

4.3 Character Data Type and Operations

  char c = 'x';
  String s = "x";
  s = c;   // compile error

  char apostrophe = '\'';

The char (character) datatype is used to hold a single character. A literal char is written as a character surrounded by single quotes.

Question: What do you do if you want the character '?
Answer: Escape it with a backlash as shown.

4.3.1 Unicode and ASCII code

Java's char datatype uses 16-bits to represent a character, thereby allowing 216=65,536 different characters. This size was inspired by the original Unicode, which was also 16 bits. The goal of Unicode was that it would supply all the characters in all the world's languages.

However, 65,536 characters proved to be way too few; Unicode has since been revised to support many more characters (over a million), but we won't discuss how it was shoehorned into 16-bit Java characters. It turns out that the character 'A' has the 16-bit value 0000000000100001 (41 in hex, 65 in decimal).

There are two ways to write this character. Naturally 'A' is one, but the other looks wierd, namely '\u0041'. This representation consists of a backslash, a lower case u (presumably for unicode), and exactly 4 hexadecimal digits. I don't like this terminology—to me digit implies base 10—but it is standard.

So 'A' is the 4*16+1=65th character in the Unicode set.

public class As {
  public static void main(String[] Args) {
    System.out.println("A\u0041\u0041A \u0041");
  }
}

javac As.java; java As
AAAA A

The two character representations can be mixed freely, as we see on the right.

In the not so distant past, computers (at least US computers) used the 7-bit ASCII code (rather nationalistically, ASCII abbreviates American Standard Code for Information Interchange). The 65th ASCII character is also 'A'. All the letters, digits, etc are in both ASCII and unicode and are in the same position in each code (65 for A). It might be right that the 127 ASCII codes make up the first 127 unicode characters and are at the same position, but I am not sure.

Although it will not be emphasized in this course, it is indeed wonderful that alphabets from around the world can be represented.

4.3.2 Escape Sequences for Special Characters

Esc SeqBecomes
\"Double quote
\\Backslash
\'Single quote
\tTab
\nNewline
\bBackspace
\fFormfeed
\rReturn

As we have seen the double quote character (") is used to begin and end a string.

Question: What do we do if we want a double quote (") to be part of a string?
Ans: We use an escape sequence beginning with \. In particular we use \" to include a " inside a string.
Question: But then how do we get \ itself?
Answer: We use \\ (of course).

On the right is a list of Java escape sequences. The ones above the line are more commonly used than the ones below.

4.3.3 Casting (Really Converting) Between char and Numeric Types

I believe a better heading would be converting between char and numeric types. Recall that a conversion performed automatically by Java is called a coercion; one specified explicitly by the user is call a cast.

public class Test {
  public static void main (String[] args) {
    int i;
    short s;
    byte b;
    char c = 'A';
    i = c;
    s = c;
    b = c;
    System.out.println(c + " " + i + " " + s + " " + b);
  }
}

The code on the right has two errors. Clearly a (16-bit) char might not fit into an (8-bit) byte. The second, more subtle, problem is that the (16-bit) char also might not fit into a (16-bit) short. The reason is is that a short is signed, whereas char is not so the latter can be about twice as large.

Hence (implicit) coercions will not occur and the program on the right will not compile. You may write casts such as b=(byte)c; that will compile, but will produce wrong answers if the actual value in the char c does not fit in the byte b.

Similarly, integer values may be cast into chars, but again Java will not coerce them.

4.4 The String Type

In Java a String (note the capital S) is very different from a double, short, or char. Whereas all the latter are primitive types, String is actually a class and hence the String type is a reference type.

So what?

It actually is an important, indeed crucial, distinction, but not yet. Remember that Java was not designed as a teaching language, but as a heavy-duty production language. Once consequence is that doing some simple things (reading an integer, writing a trivial main program, declaring a string) use fairly sophisticated concepts.

For now we just want to learn how to declare String variables, write String constants, assign Strings, and concatenate Strings. Fortunately, we can do all of these tasks without having to deal with the complications. Later we will learn much, much more about classes.

"This is A string"
"This is \u0041 string"

String s1, s2;
s1 = "A string";
String s3 = "Another string";
s2 = s1 + " " + s3;
s2 += " and more";

A string
A string Another string and more
Another string

The top line on the right shows a String constant.
The syntax is very simple: a double quote, some characters, a double quote.
The second line is the same String constant, but using the alternate representation for writing the character 'A'.

The next group contains legal Java statements.

The last group of lines show the output when we println() each of the three strings.

    String s1 = "A1", s2 = "A2";
    s1 += " " + s2;
    s1 += s1;
    System.out.println(s1);

Homework: What would be the output when the program on the right is run? I omitted the boilerplate at the beginning and end of nearly every program.

String Methods

As mentioned a Java String is an object and objects can contain (or be associated with) data and methods. A method associated with an object is called an instance method. A method associated with a class (such as Math.random()) is called a static method or a class method.

All the methods in Math are static methods. Every main() method that we have defined is a static method; it is associated with the class in which it is defined.

By default, when you define a method you get an instance method; that is why the definition of every main() method needs to contain the static keyword.

4.4.1 Getting String Length

  String s1 = "string1";
  String s2 = "";
  int i;
  i = String.length(s1); // does not compile
  i = s1.length();          // correct.  i=7
  i = s2.length();          // correct.  i=0
  i = "string7".length();   // correct.  i=7

One instance method defined in the String class is length. Since it is an instance method it is associated with a specific String object, not with the class itself. That explains why the fourth line on the right is wrong and the fifth is correct.

Note that length() takes no arguments; instead it accesses the String object to which it is associated.

As the last example illustrates, Java permits you to apply length() to a String literal.

Once you get accustomed to its syntax, the length() method works as expected.

4.4.2 Getting Characters from a String

  String s = "abcd";
  char i = s.charAt(2); // i == 'c'
  char j = s.charAt(0); // j == 'a'
  char k = s.charAt(s.length()-1); // k = 'd'
  char l = s.charAt(s.length()); // ALWAYS illegal

Another instance method defined on Strings is charAt(), which takes an int argument. s.charAt(i) returns the ith character in the String s. As illustrated on the right indexing starts at zero, and thus the last character in a String s is at position s.length()-1.

We will see later that arrays are also indexed starting at zero.

4.4.3 Concatenating Strings

  String s1 "voo";
  String s2 "doo";
  String s3 = s1.concat(s2);
  String s4 = s1 + s2;

As illustrated on the right, the String instance method concat() takes a String argument (in addition to the base string to which it is associated). s1.concat(s2) returns the String formed by concatenating s2 at the end of s1.

Since string concatenation is so common in Java programming, a shortcut has been defined and you can simply use the plus sign. In particular, on the right both s3 and s4 become the String "voodoo".

Coercing numbers to Strings

  int x = 5;
  double y = 3.4;
  System.out.println("x="+x);
  System.out.println("y="+y);

  x=5
  y=3.4

We have seen Java statements similar to the code on the right. At first it looks like we are adding a number to a string, which is crazy. We just learned that + can be used for concatenating strings, but that doesn't seem to help the code on the right since, although the left operand is a String, the right operand is an int.

What really happens is another Java coercion. If an int (or long or double, etc) is found where a String is needed, the former is automatically converted (i.e., coerced) to the later.

As you would expect s1+=s2 is permitted and is the same as s1=s1+s2, whether s1 and s2 are both Strings, both numbers, or one of each.

4.4.4 Converting Strings

  String s1 = " Abcd*E FG ";
  String s2 = s1.toLowerCase();
  String s3 = s1.toUpperCase();
  String s4 = s1.trim();
  System.out.println("-" + s2 + "-");
  System.out.println("-" + s3 + "-");
  System.out.println("-" + s4 + "-");
   
 - abcd*e fg -
 - ABCD*E FG -
 -Abcd*E FG-

Three more String instance methods are toLowerCase, toUpperCase, and trim. The first one works as expected, the value returned is the same as the original, but all capital letters are now lower case. The second one capitalizes all lower case letters, and the third removes leading and trailing whitespace (essentially blanks, tabs, and newlines).

On the right, we see all three methods in action. The purpose of the "-" in the println()s is to make visible any leading and trailing whitespace. Note that interior whitespace is not removed by trim() and that non-alphabetic characters are left alone by all three methods.

Note that none of the methods we have seen in section 4.4 alter the base string to which they are associated. In particular, the code on the right does not change s1.

4.4.5 Reading a String from the Console

We have already used the Scanner class found in java.util to read ints. Specifically, we used the nextInt() method. The Scanner class also contains a next() method, which will read and return the next token. For now we can think of a token as a string without whitespace.

  String s1 = getInput.next();
  String s2 = getInput.next();
   
     now  -+*is*  the time for

If the code on the upper right is executed and the line on the lower right is entered at the keyboard, then s1 will become the string "now" and s2 will become the string
"-+*is*".

The nextLine() Instance Method

What should we do if we care about the whitespace? We have seen that both next() and nextInt() skip over whitespace and this is also true for nextLong(), nextDouble(), etc.

The solution is the nextLine() method that reads and returns an entire line from the keyboard, i.e., all the text up to (but not including) the next newline (the enter key on the keyboard).

You should not mix usage of nextLine() with the other nextFoo() methods for reasons having to do with the implementation of the Scanner class.

4.4.6 Reading a Character from the Console

Armed with nextLine(), it is easy to read a character: just use nextLine() to read the line into a String and the apply charAt(0). Indeed, by varying the argument to charAt(), you can extract each character.

4.4.7 Comparing Strings

Testing for Equality

Question: How do we test if two Strings s1 and s2 are equal?
Answer: Is this a joke? Just use s1 == s2
Wrong! 

  String s1="AABB", s2="AA", s3="BB";
  String s4 = s2 + s3;
  System.out.println(s1 == s4);
  System.out.println(s1.equals(s4));

The code on the right prints false and then true. So s1!=s2, but s1.equals(s2) is true.

Since the corresponding use of i1==i2 does not have this strange behavior, something is different for Strings. The difference is that a String is an object but an int is not. Objects have different semantics; we will learn much more about this later in the course.

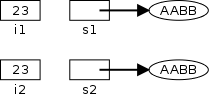
ref-semantics

For now we just note that == tests if the Stringss reference the same object, whereas equals() tests if the referenced objects have the same value. Perhaps the diagrams on the right will help.

The two ints themselves each have the value 23. The technical term is that ints have value semantics. The two strings themselves each reference an object and those objects have the same value (Strings have reference semantics).

Very roughly speaking, for both ints and Strings, == simply looks inside the boxes and checks if the contents are equal.
For the ints, the contents are equal, both are 23.
For the Strings, the contents are not equal, they are references to (i.e., point at) different objects.

For a String, equals() goes further. It follows the reference and looks inside the oval (i.e. examines the object) and checks if the values are equal.

Start Lecture #7

Remark: ITS says everyone added to the class should have an account on i5.nyu.edu. Please let me know if you do not.

Remark: Lab 1 assigned and is due in one week.

Testing for Inequality

The != operator works the same as ==, it tests if the two operands are the same object. !s1.equals(s2) works as expected; it is the negation of s1.equals(s2)

Testing for Greater Then, etc

The operators > >= < <= are not defined since there is no concept of one reference being larger than another. Instead, one uses the compareTo() method, which returns an int.

s1.compareTo(s2) returns a negative int if the value of the object referenced by s1 is less than the value of the object referenced by s2. It returns zero if the values are equal and returns a positive int if the value of the object referenced by s1 is greater than the value of the object referenced by s2.

Other String Comparisons

The String class has many other methods, for example you can ignore case during comparisons.

Check This Out

4.4.8 Obtaining Substrings

  String substring(int start, int end)
  String substring(int start)
   
   
   

We have already seen charAt(), which returns a specified char in a given String. In addition, there are two (overloaded) substring() instance methods as shown on the right.

The first method, which takes two arguments, gives the substring starting at the position specified by the first argument and ending just before the position specified by the second argument. 

  String s = "1 23 45 67   ";
  System.out.println("->"+s.substring(1,2)+"<-");
  System.out.println("->"+s.substring(1,5)+"<-");
  System.out.println("->"+s.substring(2,2)+"<-");
  System.out.println("->"+s.substring(3)+"<-");
   
  -> <-
  -> 23 <-
  -><-
  ->3 45 67   <-

The second method, which takes one argument, gives the substring starting at the position specified by the argument and extending to the end of the original string. Thus, for any String s and int n,
s.substring(n) is the same as s.substring(n,s.length())

On the right are several examples using the
    String s = "1 23 45 67 ".
The first example on the right starts as position 1 (which is the second character since the first is at position 0) and ends just before position 2. So it returns the substring containing just the character at position 1.

The definition implies that, if the two arguments are equal (and less than the length of the string, and non-negative), the result is the empty string.

What is Meant by Overloaded?

We just noted that substring() is overloaded. What does this mean?

Java has many instances of overloaded methods, that is two or more methods with the same name. We have already seen examples, such as Math.abs(). The overloading of + to mean either integer addition, real addition, or concatination is a closely related concept. Moreover, Java permits you to define new overloaded methods as well.

Question: How does Java decide which one of the overloaded methods to invoke?
Answer: It checks the signatures of the method definitions, i.e., the number and types of the parameters, and chooses the one that matches the current argument list. (That is good enough for now, but in reality one must also consider coercions.)

4.4.9 Finding a Character or a Substring in a String

The basic method is index(). If given a char as argument, it returns the first position of the character in the string or -1 if the character is not present. Similarly, if the argument is a String, index() returns -1 or the first position where the argument string occurs in the base string.

There are variants that look for the last match, not the first, and that only start looking at a specified position in the string.

4.4.10 Conversion between Strings and Numbers

  int i    = Integer.parseInt(s);
  double d = Double.parseDouble(s);

Of course, not all Strings, e.g., "abcxyz", can be viewed as numbers. But a String such as "145" can be converted to an int or double by the expressions on the right. Similarly a String such as "432.54" can be converted to a double by the second line on the right.

Note that these are static methods (they have a class name in front and take the object to work on as an argument). In addition we have Byte.parseByte(s), Short.parseShort(s), etc.

Question: Why is it Integer.parseInt() and not int.parseInt()
Answer: int is not a class. Look up wrapper in the book index or in these notes.

4.5 Case Studies

4.5.1 Case Study: Guessing Birthdays

Read

4.5.2 Case Study: Converting a Hexadecimal Digit to a Decimal Value

Read

4.5.3 Case Study: Revising the Lottery Program using Strings

Read

4.5 (Alternate) Case Study: A Crippled Palindrome Checker

A palindrome is a string that reads the same right to left as left to right. For example "abcba", "xx", " 12 21 ", "", and " gft tfg " are all palindromes; whereas "abc", " zz", "123123" are all not palindromes.

   Scanner getInput = new Scanner(System.in);
   System.out.println("Enter an 6 or 7 character string");
   String s67 = getInput.nextLine();
   System.out.println("The string is ->" + s45 + "<-");
   int first=0, last=s67.length()-1;
   if (s67.length() != 6  && s67.length() != 7)
       System.out.println("String has wrong length");
   else if (s67.charAt(first++) != s67.charAt(last--))
       System.out.println("Not a palindrome");
   else if (s67.charAt(first++) != s67.charAt(last--))
       System.out.println("Not a palindrome");
   else if (s67.charAt(first++) != s67.charAt(last--))
       System.out.println("Not a palindrome");
   else
       System.out.println("Palindrome!");

The idea is to begin by comparing the first and last characters. If they are unequal, the string is not a palindrome. If instead they are equal, then compare the second and next-to-last characters. Keep going. If you use up all the characters or if there is just one left, then you have a palindrome.

We have a problem!

Since we have not yet studied loops, there is no way for us to keep going. That is why the checker is crippled. In particular, I added the requirement that the input string must be either 6 or 7 characters long (and checked the input for validity).

For a 6 or 7 character sequence it is enough to compare the first to the last, the second to the next-to-last and the third to the next-to-next-to-last.

Note how I tested three different pairs of characters using the (textually) identical test three times.

Question: Why did I use nextLine() instead of next()?
Ans: In case the string contains blanks.
Question: How come 3 tests (involving 6 characters) were enough to determine if a 7-character string is a palindrome?
Ans: For odd length strings, the middle character is in the same position both forwards and backwards. For example in a 7-character string the 4th character from the front is also the 4th character from the rear.

4.6 Formatting Console Output

A comparatively recent addition to Java is the C-like printf method. (It was added in Java 2 Standard Edition 5; we are using J2SE 7).

System.out.printf(format, item1, item2, ..., item n);

The first point to make is that printf() takes a variable number of arguments, as indicated on the right. The required first argument, which must be a string, indicates how many additional arguments are needed and how those arguments are to be printed.

Wherever the first argument contains a %, the value of the next argument is inserted (a double %% is printed as a single %).

System.out.printf("i = %d and j = %d", i, j);
System.out.printf("x = %f and y = %e", x, y);

The first line on the right prints the integer values of x and y.
The second line prints two real values, the second using scientific notation.

Common Specifiers
SpecifierOutput
%bBoolean
%cCharacter
%dInteger
%fFloating Point
%eScientific Notation
%sString

The table on the right gives the most common specifiers. Although Java will perform a few coercions automatically (e.g., an integer value will be coerced to a string if the corresponding specifier is %s), most conversions are illegal. For example

  int i;    double x;    int one=1, two=2;
  System.out.printf("Both %f and %d are bad\n", i, x);
  System.out.printf("%d plus %d is %d\n", one, two, one+two); // OK

You could find out which coercions are OK, but I very much suggest that instead you do not use any. That is, use %f and %e only for floats and doubles; use %d only for the four integer types; use %s only for Strings, etc.

Width and Precision

System.out.printf("%d\n%d\n",45,7);
 
45
7
 
45
 7
 
System.out.printf("%2d\n%2d\n",45,7);
 
System.out.printf("%2d\n%2d\n",45,789);
 
45
789

Note that %d uses just enough space to print the actual number; it does not pad with blanks. If you print integers of different lengths one per line using %d they won't line up properly. For example, the printf() on the right will produce the first output, not the second.

To remedy this problem you can specify a minimum width between the % and the key-letter. For example the second printf() does produce the second output.

But what would happen if we tried to print 543 using %2d? There are two reasonable choices.

  1. Print something like ** the way some spread sheets display a value if the containing cell is too narrow.
  2. Use three columns.

Java chooses the second option. So the bottom printf() produces the bottom output.

These same considerations apply to the other 5 specifiers in the table: if the value is not as wide as the specified width, the value is right justified and padded on the left with blanks.

For the real number specifiers %f and %e one can specify the precision in addition to the (minimum) width. This is done by writing the width, then a period, and then the precision between the % and the letter.

For example %6.2 means that the floating-point value will be written with exactly 2 digits after the decimal point and if the result (including a minus sign if needed) is less than 6 characters, the value will be padded with blanks on the left.

Left Justification

As we have seen, when the width is specified (with or without precision), the value is right justified if needed and padded on the left with blanks. This is normally just what you want for numbers, but not for strings.

For all specifiers (numbers, strings, etc) Java supports left justification as well, padding on the right with blanks. Simply put a minus sign right before the width as in %-9f, %-10.2e, or %-7s.

Chapter 5 Loops

5.1 Introduction

As you know from Python, loops are used to execute the same block of code multiple times. There are several kinds of Java loops: The while (and do-while) are fairly general; the for is most convenient when the loops are counting, but can be used (abused?) in quite general ways.

5.2 The while Loop

 
while (BooleanExpression) {
  statements
}

Some early languages (notably early Fortran) did not have a while loop, but essentially all modern languages (including modern versions of Fortran) do.

The idea of a while loop is that the body is executed while (i.e, as long as) the Boolean expression is true.

while

The semantics are fairly simple:

  1. The Boolean expression is tested. If it is false, the while loop ends.
  2. If the BE is true, the statements in the loop body are executed.
  3. The process repeats from the beginning.

The flowchart on the right illustrates these simple semantics.

Note that if the Boolean expression is false initially, the loop body (the statements in the diagram) are not executed at all. We shall see in the next section a different kind of loop in which the body is executed at least once.

Note: right after the while loop is executed, the BE is FALSE.
Please don't get this wrong.

 
while ((i=getInput.nextInt) >= 0) {
  // process the non-negative i
}

For example, when (really if and when) the loop on the right ends (assuming no EOF), the value of i is negative!

Let us write a program that adds two non-negative numbers just using ++ and --. One solution is here.

This is actually how one defines addition starting with Peano's postulates

5.2.1 Case Study: Guessing Numbers

The program picks a random integer between 0 and 100 inclusive (101 possibilities). The user repeatedly guesses until they are correct. For each guess, the program states higher, lower, or correct.

Let's do this in class; one solution is in the book, another is here.

5.2.2 Loop Design Strategies

There are four parts to a loop and hence 4 tasks for the programmer to accomplish.

  1. Initialization (e.g., i = 0;)
  2. Continuation test (e.g., i < 10)
  3. Body
  4. Update for next iteration (e.g., i++)

As you have seen in Python and we shall see in Java, loops can be quite varied. For one thing the body can be almost arbitrary. For now let's assume that the body is the quadratic equation solver that we have written in class. Currently it just solves one problem and then terminates. How can we improve it to solve many quadratic equations?

final int N=10;
int i = 0;
while (i<N) {
  // input a, b, c
  // solve one equation
  i++;
}
 
int n=getInput.nextInt();
int i = 0;
while (i<n) {
  // input a, b, c
  // solve one equation
  i++;
}
 
// input a, b, c
while (a!=0 || b!=0 || c!=1) {
  // solve one equation
  // input a, b, c
}
 
while (true) {
  // input a, b, c
  if (a==0 && b==0 && c==1) {
    break;
  }
  // solve one equation
}

There are at least four techniques, each of which can be applied to many different problems.

  1. Hardwire the count.
    The code on the upper right has the count (10) within the code itself.
    This can also be done by running the loop backwards: initializing i=10; testing i>0, and decrementing i--.
  2. Read the count.
    We can input n rather that hardwiring it. This is illustrated in the second code sequence on the right. As with the hardwired count, one variable suffices if you run the loop backwards. For these first two possibilities a for loop would be more convenient than a while (see section 5.4).
  3. Use a sentinel, that is, choose a special input, which will never be used for a real computation (say a and b both equal zero, and c equals 1 in our quadratic equation solver) and, if an input is this sentinel, the loop terminates.
  4. Check for EOF (end of file).
    If, instead of using one of the nextX() methods in the Scanner class, we used the read() method in the System.in object, the program could detect when the EOF is reached. In this way, we can continue to input problems and solve them until there are none remaining. A very simple example is in the optional 4.2.A; however, this requires a concept (exceptions) that we will not cover for quite a while.

5.2.3 Case Study: Multiple Subtraction Quiz

5.2.3 (Alternate) Case Study: Improving the Quadratic Solver

On the right (and here) is the code for an improved quadratic equation solver, one that solves many equations in one run. This program illustrates several of the points made above.

// The next line is for hardwiring; we are reading the count
// final int count = 10;
Scanner getInput = new Scanner(System.in);
System.out.println("Solving quadratic equations ax^2 + bx + c");
System.out.println("How many equations are to be solved?");
int count = getInput.nextInt();
while (count-- > 0) {
  System.out.println("Enter real numbers a, b, c");
  double a = getInput.nextDouble();
  double b = getInput.nextDouble();
  double c = getInput.nextDouble();
  if (a == 0)
    if (b != 0)
      System.out.println("One real root: " + -c/b);
    else if (c == 0) // note a and b are zero
      System.out.println("Trivial: all values are roots!");
    else
      System.out.println("Inconsistant: no roots!");
  else { // a != 0
    double discriminant = b*b - 4.0*a*c;
    if (discriminant < 0)
      System.out.println("The roots are complex");
    else if (discriminant == 0)
      System.out.println("One (double) root: " + -b/(2*a));
    else {                  // discriminant > 0
      double ans1 = (-b + Math.pow(discriminant,0.5))/(2.0*a);
      double ans2 = (-b - Math.pow(discriminant,0.5))/(2.0*a);
      System.out.println("Two roots: " + ans1 + " and " + ans2);
    }
  }
}
  1. Commented out is a line that would have been used to hardwire the count.
  2. As written, the count is read in. Thus the first two alternatives in 4.2.2 are shown.
  3. By executing
       while(count-- > 0)
    we ensure that the loop body, which inputs and solves one quadratic equation, is executed exactly count times. Be sure you understand why count-- was used, and why --count would not work.
  4. Notice how the code as written clearly separates the work of inputting and solving an equation from the work of ensuring that we solve the correct number of equations. The former is the loop body; the latter the Boolean expression.
  5. When we learn Java methods, we will see that we could pull the entire loop body out into a separate method. This method would read a, b, c, solve the equation, and print the results.
  6. Alternatively we could write a method
      solve(a,b,c)
    that would solve one equation and print the results. This method would be called from the body of the loop right after the values of a, b, and c have been read.

Start Lecture #8

Remark: I am planning a 5 point absolute gift on lab2 that requires you to ssh to i5.nyu.edu since I know of no one who has been unable to access i5.nyu.edu.

5.2.4 Controlling (i.e., Ending) a Loop with a Sentinel Value

On the right is a simple program to sum n numbers. Since it does not make sense to sum a negative number of numbers, we let n<0 be the sentinel that ends the program.

  Scanner getInput = new Scanner(System.in);
  while (true) {
    System.out.println("How many numbers do you want to add?");
    int n = getInput.nextInt();
    if (n < 0) {
      break;
    }
    System.out.printf("Enter %d numbers: ", n);
    int i = 0;
    double sum = 0;
    while (i++ < n) {
      double x = getInput.nextDouble();
      sum += x;
    }
    System.out.printf("The sum of %d values is %f\n", n, sum);
  }

There are again a few points to note.

  1. while(true) gives an non-ending loop since the Boolean expression is always true. So there must be some other way the loop ends.
  2. This is an n and 1/2 times loop: The first part of the body is executed one more time than the second part.
  3. break is used to break out of the loop, see section 5.9.
  4. This example illustrates a nested loop, that is, a loop inside a loop.
  5. The inner loop is itself a simple loop that sums n numbers.
  6. The outer loop is needed since we want to sum n numbers several times, with possibly different values for n each time.

5.2.A Ending a Loop with an EOF (End of File)

  public class UseEOF {
      public static void main(String[] args)
             throws java.io.IOException {
          final int EOF = -1;
          int c;
          while ( (c = System.in.read()) != EOF)
              System.out.printf("%c",c);
      }
  }

On the right is a very simple loop that is terminated by EOF (end-of-file). However, it does use an advanced feature of Java, namely exceptions.

The read()method either returns the next byte (an integer in the range 0..255) from System.in or it returns -1 to signify an end of file. (If an I/O error occurs an exception is thrown.)

The Java library did the heavy lifting (the EOF technique); enabling my program to use the simpler sentinel technique.

5.2.5 Input and Output Redirections

Note: This section has very little to do with Java; it illustrates a very useful feature of modern operating systems that apply to all programs.

As you know System.in is normally the keyboard and System.out is normally the display. However, they can be redirected to be an ordinary file in the file system. When System.in is redirected to a file f, input is taken from f instead of from the keyboard, and when System.out is redirected to a file g, output goes to g.

For example the program UseEOF with the mysterious implementation, simply copies all its input to its output.

I copied it to i5 so we can run it (ignore how it works).

If we type simply  java UseEOF,  then whatever we type will appear on the screen.

If we type instead  java UseEOF <f,  then the file f will appear on the screen.

Similarly  java UseEOF <f >g copies the file f to the file g.

5.3 The do-while Loop

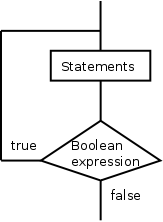
do-while

As we have seen a while loop repeatedly performs a test-action sequence: first a BE is tested and then, if the test passes, the body is executed.

In particular, if the test fails initially, the body is not executed at all.

Most of the time, this is just what is wanted; however, there are occasions when we want the body to be first and the test second. In such situations we use a do-while loop.

do {
  stmts
} while (BE);

Note that unlike the behavior we have seen for while loops a do-while loop is guaranteed to execute its body at least once.

We see the code skeleton for this loop on the near right and the flowchart on the far right.

5.3.A Converting a Positive Integer to a String

  public static void main(String[] args) {
      Scanner getInput = new Scanner(System.in);
      System.out.println("Enter an UNSIGNED integer");
      int n = getInput.nextInt();
      String s = new String();  // empty string
      do {
          String digit = (n % 10) + "";
          s = s.concat(digit);
      } while ((n /= 10) > 0);
      getInput.close();
      System.out.println("The answer is ->" + s + "<-");
  }

The code on the right is the beginning of a program to convert an integer to a string. Limitations of the program include first that it does not permit a leading plus or minus sign, and second it only does one conversion and then quits. We could easily fix these two problems.

What if we wanted to produce the reversed string. For example, given as input of integer 123, we want "321". There are at least 3 possible ways to do this.

  1. You could simply use digit.concat(s) instead of s.concat(digit).
  2. We could extract the digits from left to right instead of right to left. The hard part is to know where to start. If you knew the numbers were 4 digits you would begin with the quotient and remainder when divided by 1000.
  3. Later we will learn about the StringBuilder class, which contains a reverse() method that can do the reversal in one line.
    StringBuilder sb = (new StringBuilder(s)).reverse();
    (Naturally, we would then println() sb not s).

5.4 The for Loop

for

Recall the four components of a loop as stated in 5.2.2

  1. Initialization (e.g., i = 0;)
  2. Continuation test (e.g., i < 10)
  3. Body
  4. Update for next iteration (e.g., i++)

On the right we show a flowchart illustrating these four components. This particular flowchart is representative of a while loop.

Homework: Draw the corresponding flowchart for a do-while loop.

Components 1, 2, and 4 of a loop can all be written in one for statement. After the word for comes a parenthesize list with three elements separated by semicolons. The first component is the initialization, the second the test, and the third the update to prepare for the next iteration.

The first code shown on the right presents the for loop corresponding to the example mentioned in the list of loop components given just above. Indeed, this is a common usage of for, to have a counter step through consecutive values.

for(i=0; i<10; i++){
  body
}
 
for(int i=0; i<10; i++)
 
for(i=0, j=n; i*j < 100;  i++, j--)
 
for( ; ; )

The second for on the right shows that the loop variable can be declared in the for itself. One effect of this declaration is that the variable, i in this case, is not visible outside the loop. If there was another declaration of i inside another loop, the two variables named i would be unrelated.

It is also possible to initialize and update more than one variable as the third example shows, although this is much less common.

Finally, the various components can be omitted, in which case the omitted item is essentially erased from the flowchart. For example, if the first component is omitted, there is no initialization performed; if the middle item is omitted there is no test; and, if the third item is omitted there is no update. So the last, rather naked, for, similar to a while(true), will just keep executing the body until some external reason ends the loop (e.g., a break).

Homework: 5.1 5.5, 5.9

5.5 Which Loop to Use?

They are equivalent. Any loop written with one construct can be written with either of the other two.

The for loop puts all the non-body in one place. If these pieces are small, e.g., for(i=0;i<n;i++), this is quite convenient. If they are large and or complicated, the while form is generally easier to read.

Much of this is personal preference. I don't believe there is a right or wrong answer.

5.6 Nested Loops

We have already done a nested loop in section 4.2.4.

It is essentially the same as in Python or any other programming language. The inner loop is done repeatedly for each execution of the outer loop.

for (int i=0; i<n-1; i++) {
  for (int j=i+1; j<n; j++) {
    // if the ith element exceeds the jth,
    // swap them
  }
}

For example, once we learn about arrays, we will see that the code on the right is a simple (but, alas, inefficient) way to sort an array into increasing order (i.e., smallest element first).

The ith iteration of the outer loop ensures that the ith element is correct. This is accomplished by swapping the ith element with any subsequent element that is smaller.

5.7 Minimizing Numeric Errors

This concerns the hazards of floating point arithmetic. Although we will not be emphasizing numeric errors, two general points can be made.

  1. When comparing floating point values do not use equality (or inequality) testing. Either
  2. When adding many floating point values try to add the smaller ones first.

5.8 Case Studies

5.8.1 Case Study: Finding the Greatest Common Divisor

Given two positive integers, the book just tries every integer from 1 up to the smaller input and chooses the largest integer that divides both of the inputs.

Let try a different way to get the GCD. Keep subtracting the smaller from the larger until both are equal, at which point you have the GCD.

(54, 36) → (18, 36) → (18, 18) → 18.
(7, 6) → (1, 6) → (1, 5) → ... → (1, 1) → 1.

We are repeating an action so the program will have a loop. This leads to two questions.

  1. What is the loop body?
  2. What is the loop ending condition.

Let's do this program in class. A solution is here.

5.8.2 Case Study: Predicting the Future Tuition

Read.

Start Lecture #9

5.8.3 Case Study: Converting Decimals to Hexadecimals

Although the program is not very instructive, familiarity with hexadecimal notation is useful in computer science, especially when considering computer design and architecture.

The idea in the conversion is to repeatedly find the quotient and remainder when dividing by 16. The remainder is the low order hex digit and the quotient is used to find the other digits, using the same procedure. We used a similaar technique before when making change using $20s, $10s, $5s, $1s, quarters, dimes, nickels, and pennies. That time we produced the digits from left to right (largest to smallest); now we go from right to left (low order to high order). 

import java.util.Scanner;
public class DecToHex {
    public static void main(String[] args) {
        Scanner getInput = new Scanner(System.in);
        System.out.println("Enter an unsigned positive integer.");
        int dec = getInput.nextInt();  // we assume positive
        String hex = "", hexDigit;
        while (dec !=0 ) {           // fails if dec==0 initially
            int rem = dec % 16;      // remainder
            dec = dec / 16;          // quotient
            switch(rem) {
            case 10: hexDigit = "A"; break;
            case 11: hexDigit = "B"; break;
            case 12: hexDigit = "C"; break;
            case 13: hexDigit = "D"; break;
            case 14: hexDigit = "E"; break;
            case 15: hexDigit = "F"; break;
            default: hexDigit = "" + rem;
            }
            hex = hexDigit + hex;
        }
        System.out.println(hex);
    }
}

For example, to convert 1000 to hex, the quotient and remainder are 62 and 8.
So 8 is the low order hex digit and we next work on 62.
The quotient and remainder are 3 and 14. So 14 is the next hex digit and we next work on 3. The quotient and remainder are 0 and 3. So 3 is the next hex digit and the zero tells us to stop.

Thus the 3 hex digits are 3 14 8. How should we write 14? The convention is to use A for 10, B for 11, ... F for 15 so 14 is E and the final answer is 3E8.

My program used a switch to convert the individual hex digit to the required string. There are other ways using Java library routines. See the book for an example.

monteCarlo

5.8.A Case Study: Monte Carlo Simulation to Calculate Pi

Calculate π by randomly dropping darts on a unit square and seeing what percentage land within inside the inscribed circle. The percentage inside is approximately proportional to the ratio of the area of the circle to the area of the square. The approximation improves with more points. Since we know the area of the square and the percentage of points that fell inside and outside, we can solve for the area of the circle.

Do in class. One solution is here.

5.9 Keywords break and continue

We have already seen break for breaking out of a switch statement.

When break is used inside a loop, it does the analogous thing: namely it breaks out of the loop. That is execution transfers to the first statement after the loop. This works for any of the three forms of loops we have seen: while, do-while, and for.

In the case of nested loops, the break just breaks out of the innermost loop.

There is an alternate form of break that can be used to break out of many levels of looping or to break out of other constructs as well.

The continue statement can be used only inside a loop. When executed, it continues the loop by ending the current iteration of the body and proceeding to the next iteration. Specifically:

  1. In a while loop, a continue transfers control to the test at the top of the loop.
  2. In a do-while loop, a continue transfers control to the test at the bottom of the loop.
  3. In a for loop, a continue transfers control to the update at the bottom of the loop (from where control transfers to the test at the top).

5.10 Case Study: Checking Palindromes

A palindrome is a string that reads the same from left to right as from right to left. Note that blanks count. For example the following are palindromes.

In section 4.5 (Alternate) we developed a crippled palindrome checker, crippled because officially we did not know about loops. Now we can do it right.

The program on the right, queries the user for a string and then checks if it is a palindrome. Note the following points.

  import java.util.Scanner;
  class DemoPalindrome {
    public static void main (String[] Args) {
      Scanner getInput = new Scanner(System.in);
      while (true) {
        System.out.println("Type a string, use !!EXIT!! to exit");
        String s = getInput.nextLine();
        if (s.equals("!!EXIT!!"))
          break;

        boolean isPalindrome = true;  // updated if proved wrong
        int lo = 0;
        int hi = s.length()-1;
        while (lo < hi) {   // this works for *all* s even s=""
          if (s.charAt(lo) != s.charAt(hi)) {
            isPalindrome = false;
            break;
          }
          lo++;   hi--;
        }
        if (isPalindrome)
          System.out.println("->" + s + "<- is a palindrome.");
        else
          System.out.println("->" + s + "<- is not a palindrome.");
      }
      getInput.close();
    }
  }
  1. The instance method getInput.nextLine() reads the entire next line as a string and strips off the final newline. By using this function instead of getInput.next(), we permit the input to contain blanks or to be the empty string.
  2. Names such as isPalindrome are commonly used for boolean variables or methods that return whether a property holds.
  3. We initialize isPalindrome before the loop and correct it if we find evidence within the loop that we were wrong. Thus after the loop isPalindrome is correct.
  4. The while(lo<hi) loop successfully handles the case where s has an odd or even number of characters (including the one character case). It also handles the case where s is the empty string containing no characters.
  5. Note that the first break ends the outer loop; whereas the second ends an inner loop.
  6. The getInput.close() keeps Eclipse happy.

Question: How can you write the final if-then-else as a one-liner using the tertiary operator ?: and the printf() method?
Answer: Do in class but note that this is not necessarily an improvement.

5.11 Case Study: Displaying Prime Numbers

We want to compute the first N primes. Unlike the book, we will

  1. Input N, not have it hardwired.
  2. Try divisors up to only the square root of the candidate prime.

Although the second improvement does make the program much faster for large primes, it is still quite inefficient compared to the best methods, which are very complicated and use serious mathematics.

Start it in class.

Homework: Write this program in Java and test it for N=25.

Chapter 6 Methods

6.1 Introduction

Like all modern programming languages, Java permits the user to abstract a series of actions, give it a name, and invoke it from several places.

Many programming languages call the abstracted series of actions a procedure, a function, or a subroutine. Java, and some other programming languages, call it a method.

We have seen methods already, namely main().

6.2 Defining a Method

We know how to define a method since we have repeatedly defined the main() method. The general format of a method definition is.

    modifiers returnType name (list of parameters) { body }

For now we will always use two modifiers public static.

The main() method had returnType void since it did not return a value. It also had a single argument, an array of Strings.

The returnType and parameters will vary from method to method.

public static int myAdd(int x, int y) {
  return x+y;
}

On the right we see a very simple method that accepts two int parameters and returns an int result. Note the return statement, which ends execution of the method and optionally returns a value to the calling method.

The type of the value returned will be the returnType named in the method definition.

6.3 Calling a Method (that Returns a Value)

We have called a number of methods already. For example getInput.nextInt(), Math.pow(), Math.random(). There is very little difference between how we called the pre-defined methods above and how we call methods we write.

One difference is that if we write a method and call it from a sibling method in the same class, we do not need to mention the class name.

public class DemoMethods {
  public static void main(String[]) {
    int a = getInput.nextInt();
    int b = getInput.nextInt();
    System.out.println(myAdd(a,b));
  }
  public static int myAdd(int x, int y) {
    return x+y;
  }
}

On the right we see a full example with a simple main() method that calls the myAdd() method written above. You can mention the class name if you like. so the argument to println() could have been DemoMethods.myAdd(a,b)

Method such as myAdd() that return a value are used in expressions the same way as variables and constants are used, except that they contain a (possibly empty) list of parameters. They act like mathematical functions. Indeed, they are called functions in some other programming languages.

Note that the names of the arguments in the call do NOT need to agree with the names of the parameters in the method definition.

Homework: 6.1, 6.3.

Call Stacks

  public class CallStack {
    public static void main(String[] args) {
        int ans = f(4);
        System.out.println(ans);
    }
 
    public static int f(int x) {
        int ans = g(x+1) + 10;
        return ans;
    }
 
    public static int g(int y) {
        int ans = h(y+3) + 100;
        return ans;
    }
 
    public static int h(int z) {
        int ans = 1000 * z;
        return ans;
    }
  }

Assume f() calls g() and then g() calls f(). The LIFO (Last In, First Out) semantics of method invocation means that, when h returns, control goes back to g, not to f.

Method invocation and return achieves this semantics as follows. Use Eclipse to show some of this.

6.4 void Method Example

public class DemoMethods {
  public static void main(String[]) {
    int a = getInput.nextInt();
    int b = getInput.nextInt();
    printSum(a,b);
  }
  public static void printSum(int x, int y) {
    System.out.println(x+y);
  }
}

Methods that do not return a value (technically their return type is void) are invoked slightly differently. Instead of being part of an expression, void methods are invoked as standalone statements. That is, the invocation consists of the method name, the argument list, and a terminating semicolon.

An example is the printSum() method invoked by main() in the example on the right.

Homework: 6.9.

6.5 Passing Parameters by Values

Referring to the example above, the arguments a,b in main() are paired with the parameters x,y in printSum in the order given, a is paired with x and b is paired with y.

passByValue

The result is that x and y are initialized to the current values in a and b. Note that this works fine if an argument a or b is a complex expression and not just a variable. So printSum(4,a-8) is possible.

The parameters, however, must be variables.

A crucial point, that is sometimes confusing is that Java is a pass-by-value language (a.k.a. call-by-value).

public class DemoPassByValue {
  public static void main(String[]) {
    int a;
    int b = 6;
    int c = 7;
    tryToAdd(a,b,c);
  }
  public static void tryToAdd(int x, int y, int z) {
    x = y + z;
  }
}

This means that, at method invocation, the values in the arguments are transmitted to the corresponding parameters, but, at method return, the final values of the parameters are not, repeat NOT, repeat NOT sent back to the parameters.

For example the code on the right does not set a to 13.

When we learn about objects and their reference semantics, we will need to revisit this material.

6.6 Modularizing Code

Programs are often easier to understand if they are broken into smaller pieces. When doing so, the programmer should look for self-contained, easy to describe pieces.

public class DemoModularizing {
  public static void main(String[] args) {
    // input 3 points (x1,y1), (x2,y2), (x3,y3)
    double perimeter = length(x1,y1,x2,y2) +
      length(x2,y2,x3,y3) + length(x3,y3,x1,y1);
    System.out.println(perimeter);
  }
  public static length(double x1, double y1,
                       double x2, double y2) {
    return Math.sqrt((x2-x1)*(x2-x1) + (y2-y1)*(y2-y1));
  }
}

Another advantage is the ability for code reuse. In the very simple example on the right, we want to calculate the perimeter of a triangle specified by giving the (x,y) coordinates of its three vertices.

Recall that the perimeter is the sum of the lengths of the three sides and the length of a line is the square root of the sum of the squares of the difference in coordinate values.

Without modularization, we would have one large formula that was the sum of the three square roots.

As written on the right, I abstracted out the length calculation, which in my opinion, makes the code easier to understand.

Less trivial examples are the methods in the Math class. Imagine writing a geometry package and having to code the square root routine each time it was used.

6.7 Case Study: Converting Hexadecimals to Decimals

Read.

6.7 (Alternate) Case Study: A Modularized Monte Carlo Approximation of Pi 

public class Pi {
  public static void main (String[] args) {
    final long NUM_BALLS = (long)1.0E11; // could read this in
    long inside = 0;                     // number in circle
    double x, y;
    System.out.println("     Dropped      Inside  Estimate of pi");
    for (long dropped=1; dropped<=NUM_BALLS; dropped++) {
      x = Math.random();
      y = Math.random();
      inside += (dist(x,y,0.5,0.5)<0.5) ? 1 : 0;
      if (interesting(dropped))
        System.out.printf("%12d%12d%14.10f\n",
           dropped,inside,estimate(dropped,inside));
    }
  }
  public static double dist(double x1, double y1,
                            double x2, double y2) {
    return Math.sqrt((x1-x2)*(x1-x2) + (y1-y2)*(y1-y2));
  }
  public static double estimate(long dropped, long inside) {
    return 4.0*((double)inside / (double)dropped);
  }
  public static boolean interesting(long x) {
    double l10 = Math.log10(x);  // Power of 10 == l10 an integer
    return Math.abs(l10 - Math.rint(l10)) < 1.0E-14;
  }
}

javac Pi.java  && time java Pi
     Dropped      Inside  Estimate of pi
           1           1  4.0000000000
          10           9  3.6000000000
         100          82  3.2800000000
        1000         780  3.1200000000
       10000        7806  3.1224000000      
      100000       78634  3.1453600000      
     1000000      786032  3.1441280000      
    10000000     7853077  3.1412308000
   100000000    78539849  3.1415939600
  1000000000   785396741  3.1415869640
 10000000000  7853941114  3.1415764456
100000000000 78539619440  3.1415847776
real    222m10.434s
user    168m54.970s
sys       0m35.810s

On the right we see a modularized version of the Monte Carlo method of approximating π discussed in section 4.8.3.

Recall that we simply drop darts onto the unit square and keep track of what proportion lie inside the inscribed circle. This proportion is approximately equal to the ratio of the area of the circle to the area of the square.

We then treat the ratios as exactly equal and solve the resulting equation for π

I wrote this program in a top down fashion (see 6.11) starting with main() and defining a new method whenever there was anything to figure out.

This generated three methods: dist() used to see if the ball was inside the circle, estimate() to calculate the current approximation, and interesting() to decide if the current estimate is worth printing (the hardest part of the program).

Below the program we see the output when it is run.

I used a utility on my system to determine the execution time required. We see that the program ran for 222 minutes. For 169 minutes the program was itself executing; for 36 minutes, the operating system was executing on the program's behalf. For the remaining time, some other program must have been running or this program was blocked doing I/O.

6.8 Overloading Methods

A very nice feature of Java and other modern languages is the ability to overload method names.

public class DemoOverloading {
  public static void main(String[] args) {
    System.out.printf ("%d %f %f\n", max(4,8),
                       max(9.,3.), max(9,3.));
  }
  public static int max(int x, int y) {
    return x>y ? x : y;
  }
  public static double max(double x, double y) {
    return x>y ? x : y;
  }
  public static double max(int x, double y) {
    return ((double) x)>y ? x : y;
  }
}

Of course if you use a method named max and another named min each with two integer arguments, Java is not confused and invokes max when you write max and invokes min when you write min.

All programming languages do that.

But now look on the right and see three methods all named max, one returning the maximum of two ints one returning the maximum of two doubles, and the third returning (as a double) the max of an int and a double.

When compiling a method definition javac notes the signature of the method, which for overloading consists of the method name, the number of parameters, and the type of each parameter.

When an overloaded method is called, the method chosen is the one with signature matching the arguments given at the call site.

Technical fine points: Java will coerce a 9 to a double if needed. But if an overloaded method has two signatures, one requiring coercion and the other not, the second is chosen. If the overloaded method has two signature, each with two parameters, having types so that one would require coercing the first argument and the other would require coercing the second argument, the program does not compile.

6.9 the Scope of Variables

The scope of a declaration is the portion of the program in which the declared item can be referenced.

The rules for scope vary from language to language.

In Java a block is a group of statements enclosed in {}. For example, the body of most loops, the body of most then and else clauses of an if, and the body of a method are all blocks. (One statement bodies of then clauses, else clauses, and loops can be written without {} and then are not blocks).

A variable declared inside a method is called a local variable.

In Java the scope of a local variable begins with its declaration and continues to the end of the block containing the declaration.

We have seen an exception: if the initialization portion of a for statement contains a declaration, that local variable has scope from the declaration to the end of the loop body.

Similarly, a parameter in a method definition is a local variable and its scope extends from the parameter declaration to the end of the method body.

6.9.A Nested vs Non-nested Blocks

On the right we see two skeletons. The near right skeleton contains two blocks block1 and block2, neither of which is nested inside the other.

something { |   something {
  block1    |     start of block3
}           |     something {
something { |       block4
  block2    |     }
}           |   }

In this case it is permitted to declare two variables with the same name, one in block1 and one in block2. These two variables are unrelated. That is, the situation is the same as if they had different names.

On the far right we again see two blocks, but this time block4 is nested inside block3. In this situation it is not permitted to have the same variable name declared in both blocks. Such a program will not compile.

Some languages do permit a local variable to be redeclared in a nested block. When that occurs, the outer declaration is hidden when execution is in the inner block. This is sometimes called a hole in the scope of the outer declaration.

6.10 Case Study: Generating Random Characters

Let's do one slightly different from the book's.

Print N (assumed an even number) random characters, the odd ones lower case and the even ones upper case.

public class RandomChars {
  public static void main(String[] args) {
    final int n = 1000;     // assumed EVEN
    for(int i=0; i<n/2; i++) {
      System.out.printf("%c", pickChar('a'));
      System.out.printf("%c", pickChar('A'));
    }
  }
  public static char pickChar(char c) {
    return (char)((int)(c)+(26*Math.random()));
  }
}

The program on the right is surprisingly short. The one idea used to create it was the choice of the pickChar() method. This method is given a character and returns a random character between the given argument and 26 characters later. So, when given 'a, it returns a random lower case character and, when given 'A, it returns a random upper case character.

Remember that in Unicode, the representation used for Java chars, lower case (so called latin) letters are contiguous as are upper case letters.

Be sure you understand the value returned by pickChar().

Homework: 6.17, 6.35. It doesn't affect the homework, but there is an typo in the problem. The given formula is valid only for a regular pentagon (one with all sides equal and all angles equal), not a general pentagon.

Start Lecture #10

Remark: The tutoring hours slightly changed. See the CS website (go to education>undergrad and then at the bottom is Undergraduate Tutoring.

6.11 Method Abstraction and Stepwise Refinement

One big advantage of methods is that users of a method do not need to understand how the method is implemented. The user needs to know only the method signature (parameters, return value, thrown exceptions) and the effect of the method.

Although I remember enough calculus to derive the Taylor series for sine, that might not be the best way to implement sin(). Moreover, I would need to work very hard to produce an acceptable implementation of atan(). Nonetheless, I would have no problem writing a program accepting a pair (x,y) representing a point in the plane and producing the corresponding (r,θ) representation. To do this I need to just use atan(), not implement it.

As mentioned previously, when given a problem that by itself is too complicated to figure out directly, it is often helpful to break it into pieces. A very simple example was in the previous section. Separating out pickChar() made the main program easy and pickChar itself was not very hard.

6.11.1 Top-Down Design

topDownDesign

We haven't done anything large enough to really illustrate top-down design. The idea is to keep dividing the problem into smaller subproblems until you reach a size small enough to implement directly. That is, you first specify a few methods that would enable you to write the main() method. On the right we see a calendar example from the book. The input consists of two integers, the year and the month number. Given this input, the program is to print a calendar for the specified month.

The first diagram on the right shows the beginning of the top-down design process. We have decided the overall problem of printing a calendar has two (very unequal sized) parts: reading the input and printing the desired month.

The first task is simple enough to implement; the second is more complicated and we again divide it.

The process is repeated until we believe each box can be implemented without further refinement.

The figure on the right (a very slightly modified version of figure 6.11 from the 10e) shows this design philosophy applied to the calendar problem.

You can guess the functionality of most of the methods from their name (an indication of good naming). The startDay is the day of the week (an integer) the specified month begins. Also getTotalNumberOfDays requires explanation. It calculates the number of days from 1 January 1800 to the first day of the month read from the input.

6.11.2 Top-Down or Bottom-Up Implementation

Given a fleshed out design as in the diagram, we now need to implement all the boxes. There are two styles top-down and bottom-up.

In the first, you perform a pre-order traversal of the design. That is, you start by implementing the root calling the (unimplemented) child methods as needed.

In order to test what you have done before you are finished, you implement stub versions of the methods that have been called but not yet implemented. For example, the stub for a void method such as printMonthBody might do nothing or might just System.out.println("printMonthBody called");.

Stubs for non-void methods need to return a value of the correct type, but that value need not be correct.

In a bottom-up approach, you perform a post-order traversal of the design tree. That is, you implement only boxes all of whose children have been implemented (we are ignoring recursive procedures here). In the beginning this means you implement a leaf of the tree.

Since you implement the main program last, you need to write test programs along the way to test what you have implemented so far.

6.11.3 Implementation Details

Read. In particular read over the full implementation of printCalendar.java

6.11.4 Benefits of Stepwise Refinement

The benefits below, very similar to the book's presentation, are valid, but depend on a wise refinement. It is by no means trivial to decide how to break up a large project.

The Whole is Harder than the Sum of Its Parts

Often a large program seems more complicated than the collection of its parts. For example, the calendar printing program sounds formidable, but each of the pieces mentioned above do not appear frightening. Reducing the total difficulty leads to

Easier, Developing, Debugging, and Testing

Reuse

Sometimes when you break up a problem, you find the same piece occurring in several places. You might have implemented it multiple times if you worked on the whole problem but when broken up you see the same method appearing and implement it only once. Often this involves generalizing the method to cover the multiple use cases.

For example a geometry project would likely need to often calculate the distance between two points, or the area of a triangle given the coordinates of its three vertices.

For large projects considerable effort is often expended to find a good decomposition into pieces, in particular one that exhibits much reuse.

With a wise decomposition you may isolate pieces that can be subsequently reused (with perhaps some modification) in future programs.

Easier for Team Projects

It is much harder for 10 people to work on one large project that for 5 groups of 2 to work on 5 smaller subjects

Chapter 7 Single-Dimensional Arrays

7.1 Introduction

7.2 Array Basics

Arrays are an extremely important and popular data structure that are found in essentially all programming languages. An array contains multiple elements all of the same type.

In this chapter we restrict ourselves to 1-dimensional (1D) arrays, which are essentially lists of values of a given type. The next chapter presents the more general multi-dimensional array.

In Java the ith element of a 1D array named myArray is referred to as myArray[i]. Note the square brackets [].

7.2.1 Declaring Array Variables

main(String[] args)

In the example on the right, which we have used in every program we have written, the only parameter args is a 1D array of Strings.

Note the syntax, first the base type (the type of each element of the array), then [], and finally the name of the array.

double[] y;

When the array is not a parameter as above, but is instead a locally declared variable, the syntax is essentially identical and is shown on the right. The only difference being a semicolon added at the end.

7.2.2 Creating Arrays

double[] x;
x = new double[10];
 
double[] x = new double[10];

There is an important difference between declaring scalars as we have done many times previously and declaring an array. When the scalar is declared, it is ready to be used (i.e., to be given a value). For an array another step is needed.

The declaration double[] x, declares x but does not reserve space for any of the elements x[i]. This must either be done separately as shown on the top right or written together as shown on bottom right.

The "Reference"

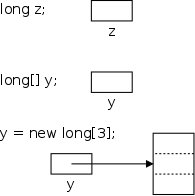
declare-1D

As illustrated in the diagram on the right, the declaration long z; allocates space for the variable z. We could initialize z in the declaration or assign z a value later; in either case the place to put the value is already there.

Similarly, the declaration long[] y creates space for y itself. But it does not create space for the individual y[i]. The variable y itself is a reference (pointer) to the actual space for the array.

The new operator allocates space for all the array elements and returns a reference (pointer) to it. In the example on the right space is allocated for 3 longs. The equal sign as usual indicates an assignment statement; in this case it assigns to to y the value returned by new, which is a reference (i.e. pointer) to the newly allocated space. The effect is that the array y can hold 3 elements, each a long.

In Java the first element always has index 0, so y consists of y[0], y[1], y[2].

Comparison with Objects

We do not officially know about objects, but recall that java.util.Scanner is a class and getInput is an element of that class, i.e. an object. Also an array is an object.

  Scanner getInput = new Scanner(System.in);
   
  Scanner getInput;
  getInput = new Scanner(System.in);

On the top right is our standard definition of the getinput object. This is actually another Java shortcut for the full two line form shown below. So we see that, as for arrays, arbitrary objects must be both declared and also created (the latter again uses new).

7.2.3 Array Size and Default Values

  int m[];
  m = new int[10];
  // use m
  m = new int[22];

The size of an array is fixed; it cannot be changed. But you can create a new array and assign it to a previously used array variable as shown on the right.

To retrieve the size of a 1D array arr is easy, just write arr.length. For example x.length would be 10 for the example above.

Note that length is a property of an array not a method call. In particular, it is written length not length().

A difference between arrays and scalars is that when the array is created (using the new operator), initial values are given to each element.

7.2.4 Accessing Array Elements

for (int i=0; i<x.length; i++) {
  x[i] = 34;
}

As suggested above, elements of a 1D array are accessed by giving the array name, then [, then a value serving as index, and finally a ]. For example, the code on the right, sets every element of the array x to 34.

Note the use of .length.

7.2.5 Array Initializers

Creating an integer array containing the values 1, 8, 29, and -2 is logically a three step procedure.

  int[] arr;
  arr = new int[4];
   
  int[] arr = new int[4];
   
  int[] arr;
  arr = new int[4];
  arr[0]=1; arr[1]=8; arr[2]=29; arr[3]=-2;
   
  int[] A = {1,8,29,-2};
  1. Declare the array.
  2. Create the array with room for 4 elements.
  3. Place the given 4 values into the 4 slots.

We have already seen how the first two steps can be combined into one Java statement. For example see the first two sections of code on the right.

In fact the Java programmer can write one statement that combines all three steps. The third code group on the right, which has each step as one statement, can be written much more succinctly as shown on the fourth group.

Note that the usage of curly brackets as shown is restricted to initialization and a few other situations, you cannot use {1,8,29,-2} in other places.

7.2.6 Processing Arrays

Very often arrays are used with loops, one iteration of the loop corresponding to one entry in the array.

  int[] a = new int[10];
  int[] b = new int[10];
  int[] c = new int[10];
  for (int i=0; i<a.length; i++) {
      b[i] = 2*i;
      c[i] = i+100;
      a[i] = b[i] + c[i];   // 3i+100
      System.out.printf("a[%d]=%d b[%d]=%2d c[%d]=%d\n",
                        i, a[i], i, b[i], i, c[i]);
  }

In particular for loops are often used since they provide the most convenient syntax for stepping through a range of values. The first entry of a Java array is always index 0; hence, the last entry of an array A is A.length-1.

For example the simple code on the right steps through three arrays, setting the value of two of them and calculating from these values the value of the third.

7.2.7 For-each Loops (or Enhanced For Loops)

We have seen several short-cuts provided by Java for common situations. Here is another. If you want to loop through an array accessing, but not changing, the ith element during the ith iteration, you can use the for-each variant of a for loop.

for(int i=0; i<a.length; i++) {    for(double x: a) {
  // use (NOT modify) a[i]           // use (NOT modify) x
}                                  }

Assume that a has been defined as an array of doubles. Then instead of the standard for loop on the near right, we can use the shortened, so-called for-each variant on the far right. The shorten variant executes the body once for each element of the array.

7.3 Case Study: Analyzing Numbers

Read

7.3 (Alternate) Case Study: The Mean and the Standard Deviation

Given n values, x0, ..., xn-1, the mean (often called average and normally written as μ) is the sum of the values divided by n.
The variance is the average of the squared deviations from the mean. That is, [(x0-μ)2 + ... + (xn-1-μ)2]/n
Finally the standard deviation is the square root of the variance.

  final int N = getInput.nextInt();
  System.out.printf("Enter the %d numbers\n", n);
  double[] x = new double[N];
  double sum=0;
  for (int i=0; i<n; i++) {
      x[i] = getInput.nextDouble();
      sum += x[i];
  }
  double mean = sum / n;
  double diffSquared=0;   // std dev is sqrt(diffSquared/n)
  for (double z : x)
      diffSquared += Math.pow(z-mean,2);
  System.out.printf("Mean is %f; standard deviation is %f\n",
                    mean, Math.sqrt(diffSquared/n));

A Java program to calculate the mean and standard deviation is on the right.

Note that the first loop, which assigns values to the x array, must use the conventional for loop; whereas, the second loop, which only uses the values already in x can employ the for-each variant.

Note that if we just wanted the mean, we would not use an array. We need it here since we need to reuse the input values after we have computed the mean.

The normal rules apply concerning the need for {}. Since the second loop has a one-line body, the {} can be omitted.

public class DeckOfCards {
  public static void main(String[] args) {
    int[] deck = new int[52];
    String[] suits = {"Spades", "Hearts", "Clubs",
                      "Diamonds"};
    String[] ranks = {"Ace", "2", "3", "4", "5", "6",
      "7", "8", "9", "10", "Jack", "Queen", "King"};
    // Initialize cards
    for (int i = 0; i < deck.length; i++)
      deck[i] = i;
    // Shuffle the cards
    for (int i = 0; i < deck.length; i++) {
      // Generate an index randomly
      int index = (int)(Math.random() * deck.length);
      // Swap deck[i] and deck[index]
      int temp = deck[i];
      deck[i] = deck[index];
      deck[index] = temp;
    }
    // Display the shuffled deck
    for (int i = 0; i < 4; i++) {
      String suit = suits[deck[i] / 13];
      String rank = ranks[deck[i] % 13];
      System.out.println("Card number " + deck[i]
         + ": " + rank + " of " + suit);
    }
  }
}

7.4 Case Study: Deck of Cards

Let's look at this example from the book with some care. I downloaded it from the companion web site. You can download all the code examples.

The idea is to have a deck of cards represented by an array of 52 integers, the ith entry of the array represents the ith card in the deck.

How does an integer represent a card?
First of all the integers are themselves chosen to be between 0 and 51. Given an integer c (for card), we divide c by 13 and look at the quotient and remainder. The quotient (from 0..3) represents the suit of the card and the remainder (from 0..12) represents the rank.

Look at the String arrays; they give us a way to print the name of the card given its integer value by using the quotient and remainder.

The deck initialized to be in order starting wit the Ace of Spades and proceeding to the King of Diamonds (Liang must not be an avid card player).

Notice how the deck is shuffled: The card in deck[i] is swapped with one from a random location. This can move a single card multiple times. Pay particular attention to the 3 statement sequence used to swap two values; it is a common idiom.

Liang printed the first 4 cards; I print the entire deck. The last loop, rewritten as a one-liner, is shown below.

  for (int C : deck)
      System.out.printf("Card number %2d: %s of %s\n", C, ranks[C%13], suits[C/13]);

7.5 Copying Arrays

array1

Serious business. We can no longer put off learning about reference semantics.

Consider the situation on the near right. We have created two arrays each capable of holding 5 integers. The first has been initialized; the second has not. We now wish to make the second array a copy of the first.

Note that the array name is not the array itself. Instead it points to (technically, refers to) the contents of the array. One consequence is that the size of array1 does not depend on the number of elements in the array, which turns out to be quite helpful later on.

If we simply execute array1 = array2;, we get the situation in the upper right. We have copied the reference (i.e., the pointer) contained in array1 so that this same reference is contained in array2.

As a result both arrays refer to the same content, which is normally not what is desired. In this state, changing the contents of one array, changes the other.

Be sure you see why array2 = array1; gives the depicted situation and be sure you see why now changing either array1[3] or array2[3] changes the other as well.

If the goal is to get the situation shown in the lower right, you need a loop such as
    for (int i = 0; i <array1.length; i++) {
        array2[i] = array1[i];
    }
to copy each entry of array1 to the corresponding entry of array2.

After the loop is executed and we have the picture in the lower right, the arrays are still independent: changing one does not change the other.

Start Lecture #11

Remarks:

  1. Lab 3 assigned.
  2. Vote next class on midterm day.

7.5.A Why Didn't This Happen Before???

int a, b;
a = 5;
b = a;
b = 10;

Look at the simple code on the right. According to the picture with arrays, after we execute b=a;, both a and b will refer to the same value, namely 5. Then when we execute b=10;, both a and b will refer to the same value, namely 10.

But this does NOT happen. Instead, b==10, but a==5 as we expected.

Why?

val-vs-ref

The technical answer is that primitive types, for example int, have value semantics; whereas, arrays (and objects in general) have reference semantics.

Looking at the diagram on the right, which shows explicitly the memory used for variable array1 and for the array itself, we see that the variable array1 refers to (or points at) a block of memory locations that are the containers for the values of the various array1[i]. In contrast, the int variables a and b ARE the containers where the values 5 and 10 are stored. With primitive types such as int, there are no pointers or references involved.

When you change a or b, you change the value; when you change array1, you change the reference (pointer).

7.6 Passing Arrays to Methods

There are two cases to consider, passing an element of an array and passing the entire array. I will first cover passing an element since I believe that case is easier.

7.6.A Passing Array Elements

There is very little to say about passing an element of a one dimensional array as an argument. The element is simply a value of the base type of the array.

On the right is the simple printSum() method that we saw earlier. It accepts two integer parameters and prints their sum.

public static void main(String[] args) {
    int[] x = {5, 10, -1, 25};
    printSum(x[2],x[1]);
}
public static void printSum(int x, int y) {
    System.out.println(x+y);
}

The main() method defines and initializes an array x containing 4 ints, and then invokes printSum(x[2],x[1]).

The printSum() method will add the two values and print the sum just as if it was invoked via printSum(-1,10);

7.6.B Passing an Entire Array as an Argument

 
public static void printArray(int[] a) {
    for (int ai : a)
        System.out.println(ai);
}

The printArray() method on the right has an (entire) int array as parameter. To call the method is easy: printArray(b) where b is a one-dimensional array of integers. The argument b of the caller is assigned to the parameter a of printarray(). Note that the types must match: the argument in the caller must be of type int[], i.e., an array of ints. As written printArray() accepts a 1D array of any size.

In this example, the called method (printArray()) does not alter its parameter. The only subtlety in passing an entire array is analyzing the behavior when the called method does change a component of the parameter, which we study next.

Updating a Component of an Array Parameter

The error-prone part of this situation is melding Java's pass-by-value method invocation with its reference semantics for arrays. However, it is not tricky and there are no new rules or exceptions; you must simply apply pass-by-reference semantics and reference semantics.

  public static void BumpZerothEntry(int[] a) {
      a[0]++;
  }
  public static void main(String[] args) {
      int[] b = {5, 10, -1, 25};
      BumpZerothEntry(b);
  }

Assume we have a method, such as BumpZerothEntry() that accepts an array parameter a and updates at least one component. As shown on the right, the main() method invokes BumpZerothEntry() with argument b, an integer array.

At the point of the method call, the value in b is copied to a, but, as we know, when the method returns, any current value in a is NOT copied back to b. This rule still holds for arrays; NO change.

Remember that copying the value from b to a does not mean that the individual array elements are copied; just the reference is copied.

array-param

The diagram at the right show the configuration when the method is called.

Due to pass-by-value semantics, even if the called method changes the value in the parameter a, the value in the argument b would not change; it would remain a pointer to the 4-element structure shown. For example, if the called method executed a = new int[8];, then the arrow from the a box would change and would now point to a tall rectangle with 8 slots. The b arrow would NOT change.

Now lets return to the code above. The called method does not change the value in the parameter a, the parameter remains a pointer to the 4-element structure. Naturally, the argument b also does not change.

Now consider what does happen. The called method executes a[0]+=1;, which changes not the value in a (a pointer), but instead changes the value in a cell pointed to by a. Since the same cells are pointed to by both b and a, a cell point to by the argument b has changed.

Hence when the method returns, the value in b[0] is now 6.

Summary: The call above does not (indeed, cannot) change the value of b, but it can and does change the value of an individual b[i].

Repeat: Pass-by-value is pass-by-value; arrays are references; nothing has changed.

Homework: 7.1. Write a program that reads student scores, calculates the best score, and then assigns grades based on the following scheme.

The program prompts the user to enter the number of students, then prompts the user to enter all of the scores, and concludes by displaying the grades.

Notes:

Updating a Component of an Array Parameter: Example

public static void main(String[] args) {
    int   xScalar =  5 ;
    int[] yArray  = {5};
    int[] zArray  = {5};
    System.out.printf("xScalar=%d   yArray[0]=%d   zArray[0]=%d\n",
                      xScalar,      yArray[0],     zArray[0]);
    tryToChange(xScalar, yArray[0], zArray);
    System.out.printf("xScalar=%d   yArray[0]=%d   zArray[0]=%d\n",
                      xScalar,      yArray[0],     zArray[0]);
}
 
public static void tryToChange(int scalar, int component, int[] array) {
    scalar    = 10;       // will NOT change argument
    component = 10;       // will NOT change argument
    array[0]  = 10;       // WILL     change a COMPONENT of argument
}
 
xScalar=5   yArray[0]=5   zArray[0]=5
xScalar=5   yArray[0]=5   zArray[0]=10

The code on the right shows 3 attempts to change a 5 to a 10. Two fail; the third is successful.

  1. The first attempt passes a scalar to a method, which updates the corresponding parameter. This is hopeless since Java is a pass-by-value language.
  2. The second attempt passes an array component to the method, which again updates the corresponding parameter. This is hopeless since Java is a pass-by-value language.
  3. The third attempt passes an array itself to the method, which does not, repeat NOT attempt to modify the corresponding parameter (that would be hopeless since Java is a pass-by-value language). Instead the method modifies a component of the passed array, which succeeds.

Anonymous Arrays

Java also has anonymous arrays, i.e., arrays without a name. So you can write printArray(new int[]{1,5,9}); However, you cannot use {1,5,9} as an array constant wherever you want. It can be used only when initializing a new array (and a few other places).

7.7 Returning an Array from a Method

We have seen how arrays can be passed into a method. They can also be the result of a method as shown on the right. Note the following points about reverse (which returns an array that has the same elements as its input but in reverse order).

public static int[] reverse(int[] a) {
    int[] ans = new int[a.length];
    for (int i=0; i<a.length; i++)
        ans[a.length-1-i] = a[i];
    return ans;
}

Note: One night I was editing my magazine column and needed a function to reverse a number. Since I just taught it a few hours previously in 101, I actually wrote one of those routines that is all library method calls. Then, for fun I made it an ugly one-liner. Here is the result.

    public static int reverse (int n) {
        // StringBuilder sb = new StringBuilder(Integer.toString(n));
        // return Integer.parseInt(sb.reverse().toString());
        return Integer.parseInt(new StringBuilder(Integer.toString(n)).reverse().toString());
    }

7.8 Counting the Occurrences of Each Letter

Read

Homework: 7.3 Write a program that reads integers between 1 and 100 and counts the occurrences of each. Assume the input ends with 0.

7.8 (Alternate) Case Study: Histogram of Math.random()

If Math.random() is any good, about 1/10 of the values should be less than 0.1, about 1/10 between 0.1 and 0.2, etc. That is a very mild test. Indeed, devising a good test for randomness is not so easy. 

System.out.printf("How many random numbers? ");
Scanner getInput = new Scanner(System.in);
int numRandom = getInput.nextInt();
int[] count = {0,0,0,0,0,0,0,0,0,0};
double[] limit = {0.0,0.1,0.2,0.3,0.4,0.5,0.6,
                  0.7,0.8,0.9,1.0};
for(int i=0; i<numRandom; i++) {
    double y = Math.random();
    for (int j=0; j<10; j++)
        if (y < limit[j+1]) {  // one will succeed
            count[j]++;
            break;
        }
}
for (int j=0; j<10; j++) {
    System.out.printf("The number of random numbers "
          + "between %3.1f and %3.1f is %d\n",
          limit[j], limit[j+1], count[j]);
}

The program on the right tests how well Math.random() performs by having Math.random() generate a bunch of random numbers and counting how many fall in each 0.1 range.

Note the following points.

The program can be downloaded from here.

Let's compile and run it for different number of random numbers and see what happens.

7.9 Variable-Length Argument Lists

We have used System.out.printf() which has a variable number of arguments.

public static void main(String args[]) {
    printMax(34, 3, 3, 2, 56.5);
    printMax(new double[]{1, 2, 3});
}
public static void printMax(double... numbers) {
    if (numbers.length == 0) {
        System.out.println("No argument passed");
        return;
    }
    double ans = numbers[0];
    for (int i = 1; i < numbers.length; i++)
        if (numbers[i] > ans)
            ans = numbers[i];
    System.out.println("The max value is " + ans);
}

Java permits the last parameter to correspond to a varying number of arguments, but all of these arguments must be of the same type. The corresponding argument, although declared differently, is treated as an array of that type.

The example on the right is from the book.

Pay attention to the parameter of printMax. Java uses ellipses to indicate varargs. In this case a variable number of double arguments are permitted and will all be assigned to the array double... numbers. Also permitted (and illustrated) is actually passing an array of double's.

Other non-vararg parameters could have preceded the double... numbers parameter.

  public static int getRandom(int... numbers)

Homework: 7.13. Write a method that returns a random number between 1 and 54, excluding the numbers passed in the argument. The method header is shown on the right.

7.10 Searching Arrays

 
public static int search(int[] a, int val)

Given an integer array a and a value val, find an index i such that A[i]==val. The method header is on the right

Question: What if there is more than one i that works?
Answer: Normally, we just report one of them, specifically the first one.

Question: What if none work?
Answer: We must indicate this in some way, often we return -1, which cannot be an index (all Java arrays have index starting at 0).

Question: What if we want to search integers and also search strings?
Answer: We define two overloaded searches (or we learn about generics).

7.10.1 The Linear Search Approach

public static int linearSearch(int[] A, int val) {
    final int NOT_FOUND = -1;
    for (int i=0; i<A.length; i++)
        if (A[i] == val)
            return i;
    return NOT_FOUND;
}

There is an obvious solution: Try A[0], if that fails try A[1], etc. If they all fail return -1. This is shown on the right.

The only problem with this approach is that it is slow if the array is large. If the item is found, it will require on average about n/2 loop iterations for an array of size n and if the item is not found, n iterations are required.

  public static int[] eliminateDuplicates(int[] numbers)

Homework: 7.15. Write a method that returns a new array by eliminating the duplicate values in the array. Use the header line on the right. Write a test program that reads in ten integers, invokes the method, and displays the result.

7.10.2 The Binary Search Approach

If the array is unsorted, there is nothing better than the above. But of course if we are doing many searches it pays to have the array sorted.

mid = (hi + lo) / 2; // 1.
if (A[mid]==val)
    return mid;      // 2.
else if (A[mid]<val)
    lo = mid + 1;    // 3.
else // A[mid]>val
    hi= mid-1;       // 4.

public static int binarySearch(int[]A, int val) {
    final int NOT_FOUND = -1;
    int lo = 0;
    int hi = A.length -1;
    int mid = (hi+lo)/2;
    while (lo <= hi) { // 5
        // above if-then-else
    }
    return NOT_FOUND;  // 6
}

Given a sorted array, we can preform a divide and conquer attack. Assume the array is sorted in increasing order (smallest number first).

  1. Try the middle element.
  2. If it is the desired value, done.
  3. If the middle is smaller than desired, restrict to the bottom half.
  4. If the middle is larger than desired, restrict to the top half.
  5. Repeat the above.
  6. If you restrict to the empty set, the desired element is not there.

Although the routine is easy to understand conceptually it is also notoriously easy to get wrong, (e.g. setting lo=mid instead of low=mid+1).

7.11 Sorting Arrays

Sorting is crucial. As we just saw, fast searching depends on sorting.

There are many sorting algorithms; we will learn only two, both are bad. That is, both take time proportional to N2, where N is the number of values to be sorted. Good algorithms take time proportional to N*logN. This doesn't matter when N is a few hundred, but is critically important when N is a few million.

Moreover, serious sorting does not assume that all the values are in memory at once.

We treat sorting more extensively in Data Structures (102).

Having said all this, sorting is important enough that it is quite worth our while to learn some algorithms. Naturally, it also helps us learn to translate algorithms into Java.

Start Lecture #12

Remark: Vote for midterm date.

7.11.A Selection Sort (Alternate Version—Bubble Sort)

The basic idea in both the 10e and bubble sort is that you start by ensuring that the smallest element is in the first slot (a[0]) and then repeat for the rest of the array (a[1]...a[a.length-1]).

for (int j=1; j<a.length; j++)
    if (a[j] < a[0]) { // a[0] not min
        temp = a[0]; // so swap with a[j]
        a[0] = a[j]; // swapping takes
        a[j] = temp; // 3 instructions
    }

The difference between the selection sort in 10e and the bubble we will do is how each algorithm gets the minimum element into a[0]. The code on the right shows the simple method used by bubble sort. The code in the book is slightly more complicated and perhaps slightly faster (both are bad, i.e., N2, sorts).

What remains is to wrap the code with another loop to find the 2nd smallest element and put it in a[1], etc.

Let's do that in class.

7.11.2 Insertion Sort

for (i=1; i<A.length; i++)
  // Insert a[i] correctly into a[0]..a[i-1]

Insertion sort is well described by the code on the right. A key point to note is that at each iteration a[0]...a[i-i] is already sorted.

The remaining question is how do we insert a[i] into a[0]..a[i-1] maintaining the sorted order?

In looking for the correct place to put a[i], we could either start with a[0] and proceed down the array or start with a[i-1] and proceed up the array. We do the latter?

Why?

Consider an example where i is 8 and the right place to put a[i] is in slot a[4]. Where are we going to put a[4]?
Answer: It must go in a[5]. Then where does a[5] go?
Answer: in a[6].

Thus we need to move the higher elements before we can move the lower. We can easily do this while searching for the correct spot to put a[i], providing we are traveling from higher to lower indices.

public static void insSort(int[] a) {
    for (int i=1; i<a.length; i++) {
        int ai = a[i];
        int j = i-1;
        while (j>=0 && ai<a[j]) {
            a[j+1] = a[j];
            j--;
        }
        a[j+1] = ai;
    }
}

The code on the right deserves a few comments since it's brevity belies its subtlety.

Homework: Write a method that accepts an array of single-digit integers and prints out the elements in sorted order with a count of how many times each appeared. For example if the array contains. 1,5,2,3,8,2,1,5,5 you would print
1 appears 2 times
2 appears 2 times
3 appears 1 time
5 appears 3 times
8 appears 1 time

7.12 The Arrays Class

The book notes that Java has many predefined methods for arrays. In particular java.util.Arrays.sort(a) would have sorted the array a (for any primitive type, thanks to overloading).

The best place to see all the methods (and classes, and more) that are guaranteed to be in all Java implementations is http://download.oracle.com/javase/7/docs/api/ (I use http://java.sun.com/javase/7/docs/api/).

7.13 Command-Line Arguments

We know that the main() method has a single parameter, which is an array of String's. However, we have not yet made use of this. Technically, we have used it all the time; we just had the empty array.

7.13.1 Passing Strings to the main() Method

Recall that, if we have a program Prog.java, we compile it with the command javac Prog.java and run the result with the command java Prog.

To transmit command-line arguments to Prog.java, there is no change to the compilation, but we run the program differently. Specifically, we add the arguments after the name of the program.

Say we want to give Prog three arguments, one integer and two strings. In particular, assume the arguments are: 25, arg 8, and last. We would write

          java Prog 25 "arg 8" last

Several comments are needed on the syntax (specifically the quotes) and then we can discuss what happens.

  1. Although we think of 25 as an integer and we write it as an integer, arg[0] is a String. Indeed, the jvm passes all arguments as strings.
  2. The last argument last does not have quotes. This is correct. It would also be correct to write "last". In either case the main() method would receive a string of length 4.
  3. The second argument "arg 8" does have quotes. This is necessary since arg 8 would be two arguments. To repeat, quotes are needed if the argument contains spaces; they are optional if the argument does not have spaces.

So what does this do? Specifically, what happens to the 25 "arg 8" last
Assume Prog.java contains the line

         public static void main(String[] args) {

Then the effect is the same as if args was declared and initialized as follows.

         String[] args = {"25", "arg 8", "last"}

A common use of command line arguments is to specify a file for the program to use. For example when we write javac Joe.java we are invoking the progam javac and telling it to process the file Joe.java. However, we do not yet know how to process files in Java so our example below does not use file names as arguments.

7.13.2 Case Study: Calculator

The code on the right (only slightly modified from the book) is for a trivial calculator that can do one operation, providing the operation is +, -, ., or /.
Question: Why do we use . for multiply instead of *?
Answer: The character * has a special meaning when used to specify an argument to a program (it means all the files in the current directory).

There are a few additional points to say about the program on the right.

public static void main(String[] args) {
  if (args.length!=3 || args[1].length()!=1) {
    System.out.println(
      "Usage: java Calculator operand1 [+-./] operand2");
    System.exit(1);
  }
  int ans;
  char operator = args[1].charAt(0);
  switch (operator) {
    case '+': ans = Integer.parseInt(args[0]) +
                    Integer.parseInt(args[2]);
              break;
    case '-': ans = Integer.parseInt(args[0]) -
                    Integer.parseInt(args[2]);
              break;
    case '.': ans = Integer.parseInt(args[0]) *
                    Integer.parseInt(args[2]);
              break;
    case '/': ans = Integer.parseInt(args[0]) /
                    Integer.parseInt(args[2]);
              break;
    default:  System.out.printf("Illegal operator %c\n",
                                operator);
              System.exit(1);
  }
  System.out.printf("%s %c %s = %d\n",
                     args[0], operator, args[2], ans);
}
  1. The program takes three arguments: two operands surrounding one operator. the first operand becomes args[0], the operator becomes args[1], and the second operand becomes args[2].
  2. Note the error checking for the right number of arguments and that the operator is just one character. Also note length vs. length().
  3. System.exit() terminates the job. The integer argument gives the status, but we will not make use of that value. Often zero is used for normal termination and a nonzero argument is used for abnormal termination.
  4. In recent versions of java, a switch can be based on an integer, a character, or a string, so I didn't have to convert args[1] to a character.
  5. As mentioned before, in addition to Character, java has wrapper classes for all the primitive types. The Integer class contains a class method parseInt() that converts a String to an int.
  6. An alternate implementation would be to calculate operand1 and operand1 before the switch (using Integer.parseInt)).

Chapter 8 Multidimensional Arrays

8.1 Introduction

As we have seen, a one-dimensional array corresponds to a list of values all of the same type. Similarly, a two-dimensional array corresponds to a table of such values and an array of higher dimension correspond to an analogous higher dimensional table.

8.2 Two-Dimensional Array Basics

8.2.1 Declaring Variables of Two-Dimensional Arrays and Creating Two-Dimensional Arrays

As with one-dimensional arrays, there are three steps in declaring and creating arrays of higher dimension.

double [][] m; // m for Matrix
m = new double [2][3];
m[0][0]=4.1; m[0][1]=3; m[0][2]=4;
m[1][0]=6.1; m[1][1]=8; m[1][2]=3;
 
double [][] m = new double [2][3];
m[0][0]=4.1; m[0][1]=3; m[0][2]=4;
m[1][0]=6.1; m[1][1]=8; m[1][2]=3;
 
double [][] m = {
  {4.1, 3, 4},
  {6.1, 8, 3}
};

double [][] m = {{4.1, 3, 4}, {6.1, 8, 3}};
  1. Declare the array.
  2. Create the array.
  3. Initialize the array (optional).

These can be done separately or can be combined.

On the right we see that, as with 1D-arrays, there are three possibilities: Each of the three steps can be done separately, the first two can be combined, or all three can be combined. I wrote the third possibility twice using different spacings.

Arrays like this one are often called rectangular due to rectangular appearance they have if all the entries with a given first index are written in a row as I did on the right. These 2D-arrays correspond to mathematical matrices.

In fact not all 2D Java arrays are rectangular. Instead, a 2D array in Java is really a 1D array of 1D arrays (of possibly differing lengths) as we shall see in the next few sections.

8.2.2 Obtaining the Lengths of Two-Dimensional Arrays

The simple diagram on the right is very important. It illustrates what is meant by the statement that Java 2D arrays are really 1D arrays of 1D arrays. That is, Java 1D arrays can have elements that are themselves 1D arrays.

2d-matrix

The m in the diagram is the same as in the example code above.

Note first of all, that we again have reference semantics for the arrays. Specifically, m refers to (points to) the 1D array of length two in the middle of the diagram. Similarly m[0] refers to the top right 1D array of size 3. However, m[0][0] is a primitive type and thus it IS (as opposed to refers to) a double.

Next note that there are three 1D arrays in the diagram (m, m[0], and m[1]) of lengths, 2, 3, and 3 respectively. As with the 1D arrays of the preceding chapter you obtain the length of these three 1D arrays using .length, specifically, m.length, m[0].length, and m[1].length. The difference between m and the others is that each element of m is of type double[]; whereas each element of m[0] and each element of m[1] is of type double.

Finally, note that you cannot write m[1,0] for m[1][0], further suggesting that Java does not have 2D arrays as a native type.

8.2.3 Ragged Arrays

ragged

One advantage of having 1D arrays of 1D arrays rather than true 2D arrays is that the inner 1D arrays can be of different lengths. For example, on the right, m is an array of length 2, m[0] is an array of length 3, and m[1] is an array of length 1.

A written text, such as these notes, that does not have its right margin aligned is said to have ragged right alignment. Since the right hand boundary of the component 1d arrays look somewhat like ragged right text, arrays such as m are called ragged arrays.

double [][] m = { {3.1,4,6},  {5.5} };

double [][] m;
m = new double [2][]; // the 2 is needed
m[0] = new double [3];
m[1] = new double [1];
m[0][0]=3.1; m[0][1]=4; m[0][2]=6;
m[1][0]=5.5;

There are several ways to declare, create, and initialize a ragged array like M. The simplest is all at once as on the upper right.

The most explicit is the bottom code. Note how clear it is that M has length 2, m[0] has length 3, and m[1] has length 1.

Intermediates are possible. For example the first two lines can be combined. Another possibility is to combine the initialization of m[0] with its creation.

8.3 Processing Two-Dimensional Arrays

 
for (int i=0; i<n; i++) {  | for (int i=0; i<m.length; i++) {
  for(int j=0; j<m; j++) { |   for (int j=0; j<m[i].length; j++) {
    // process m[i][j]     |     // process m[i][j]
  }                        |     }
}                          |   }

On the far right is the generic code often used when processing a single 2D array (I know 2D arrays are really 1D arrays of 1D arrays). This code works fine for ragged and non-ragged (i.e., rectangular) arrays. Note that the bound in the inner loop depends on i.

When the array is known to be rectangular (the most common case) with dimensions r (for row) and c (for column), the simpler looking code on the near right is often used.

8.3.A Some Examples

The Types of a 2D Matrix and its Components

  public static void main(String[] args) {
    double[][] m = { {1,2,3}, {4,5,6} };
    method1(m);
    method2(m[1]);
    method3(m[1][1]);
  {
  public static void method1(????? x) {}
  public static void method2(????? x) {}
  public static void method3(????? x) {}

The code fragment on the right shows the declaration of a 2D array m and its use in three method invocations.

In the first invocation the entire array is passed; in the second we pass one of the rows1; in the third we pass a single entry.

Question? What should the ????? be in the three method definitions that follow?

Note: There is no way to refer to an entire column of the array; indeed, defining a column is problematic for ragged arrays.

Start Lecture #13

Remark: The midterm will be thursday 23 october 2014. A practice exam is on the web site.

Remark: According to http://cs.nyu.edu/webapps/fall2014/Undergraduate/final_exams our final is CSCI-UA.0101-002 Tuesday, December 16, 2014 10:00AM - 11:50AM CIWW 201

Declaring, Allocating, and Reading an n×m Rectangular Array

  int n = getInput.nextInt();
  int m = getInput.nextInt();
  float[][] arr = new float[n][m];
  for (int i = 0; i<n; i++)
    for (int j = 0; j<m; j++)
      arr[i][j] = getInput.nextFloat();

The code to define and read a 2D rectangular array is straightforward and is shown on the right.

Note that, although you could have declared the array before knowing its bounds, you need the bounds before doing the allocation (invoking new).

Max, Min, and sum of a Rectangular n by m Array

  double[][] matrix;
  // compute and/or read matrix
  double maximum = matrix[0][0];
  double minimum = matrix[0][0];
  double sum = 0;
  for (int i=0; i<n; i++)
    for (int j=0; j<m; j++) {
      if (matrix[i][j] > maximum)
        maximum = matrix[i][j];
      if (matrix[i][j] < minimum)
        minimum = matrix[i][j];
      sum += matrix[i][j];
    }

These are quite easy since the computation for each element of the matrix is independent of all other elements. The idea is simple, use 2 nested loops to index through all the all the elements. The loop body contains the computation for the generic element.

The code fragment on the right shows three parts of the program.

  1. First matrix is declared to be a 2D array of doubles.
  2. The allocation and initializing/reading of the matrix is not shown. The previous section shows how this can be done.
  3. Next we show the declaration and initialization of the desired results.
  4. Finally, the computation loop is given.

For a possibly ragged array of unknown size, simply replace n by matrix.length and replace m by matrix[i].length.

Calculating Non-Independent Array Elements

We have dealt with computations of arrays where computing each element is an independent event. But that is not always the case.

  double[] arr = new double[n+1];
  arr[0] = 0;
  for (int i=1; i<=n; i++)
     arr[i] = arr[i-1] + getInput.nextDouble();

On the right we read n and then n doubles. We compute a 1D array arr where the ith element is the sum of the first i elements read.

Naturally, more complicated examples are possible. For example, similar to the above you could be given a 2D rectangular array and compute a new array of the same shape where the (i,j) entry of the new array equals the product of old entries (i,j), (i,j+1), (i,j+2), ... . That is the new entry is the product of the old entry and all the old entries below it.

Declaring, Allocating, and Reading a Ragged Array

  5
  4  11. 12. 13. 14.
  2  21. 22.
  1  31.
  7  41. 42. 43. 44. 45. 46. 47.
  7  51. 52. 53. 55. 55. 56. 57.

   
  11. 12. 13. 14. 55.
  21. 22.
  31.
  41. 42. 43. 44. 45. 46. 47.
  51. 52. 53. 55. 55. 56. 57.

Suppose we want to read in the ragged array of floats shown on the near right. It is drawn to indicate that it has 5 rows, the first with 5 columns, the second with 2, the third with 1, the fourth and fifth with 7.

Somehow, we must convey this size/shape information to the program. Often this is done with counts as shown above on the far right.

public static void main(String[] args) {
    Scanner getInput = new Scanner(System.in);
    int n = getInput.nextInt(); // n rows (constant)
    int m;                      // m cols (varies)
    float[][] arr = new float[n][];
    for (int i = 0; i < n; i++) {
        m = getInput.nextInt();   // num cols this row
        arr[i] = new float[m];
        for (int j = 0; j < m; j++)
            arr[i][j] = getInput.nextFloat();
    }

The Java program on the right reads data in the format shown above and allocates all the relevant arrays (remember that a 2D array with 5 rows is really six 1D arrays).

We first read n, the number of rows and allocate arr, a 1D array each of whose n components is a 1D array of floats.

Then, for each of the n rows we read m,the number of columns and allocate a 1D array of floats, to hold the elements of the row

Finally, we are able to actually read and store the actual elements of the array.

Read this carefully to be sure you understand how the ragged array was declared, created, and initialized.

Initializing a (Possibly Ragged) Array with Random Integers from 1 to N

// declare and create (with new) arr
for (int i=0; i<arr.length; i++)
    for (int j=0; j<arr[0].length; j++)
        arr[i][j] = 1 + (int)((n)*Math.random());

We use the nested loop construction appropriate for ragged arrays. The (one-line) loop body uses the technique we learned how to scale the values from Math.random() to produce numbers from 1 to n.

8.4 Passing Two-Dimensional Arrays to Methods

Read

8.4.A Matrix Multiply

public static void matrixMult (double [][] b,
                double [][] b, double [][] c) {
  // check that the dimensions are legal
  for (int i=0; i<a.length; i++)
    for (int j=0; j<a[0].length; j++) {
      a[i][j] = 0;
      for (int k=0; k<C.length; k++)
        a[i][j] += b[i][k]*c[k][j];
    }
}

Remark: Write the formula on the board. I do not assume you have memorized the formula. If it is needed on an exam, it will be supplied.

For multiplication the matrices must be rectangular. Indeed, if we are calculating A=B×C, then B must be an n×p matrix and C must be a p×m matrix (note the two ps). Finally, the result A must be an n×m matrix.

The code on the right does the multiplication, but it omits the dimensionality checking. Note that this checking would involve loops (to ensure that the arrays are not ragged).

Since the first parameter is an array, the values stored in the array will be visible in the corresponding argument of the calling method.

An alternative implementation would be to have the caller supply the array bounds and have the called program trust that the arrays are of the size specified. Then the method definition would begin

public static void matrixMult (int n, int m, int p, double [][] A, double [][] B, double [][] C) {
  // A is an n by m matrix, B is n by p matrix, C is a p by m matrix

A full program including input/output is here.

Homework: 8.13.

8.5 Problem: Grading a Multiple-Choice Test

Read

8.6 Problem: Finding a Closest Pair

Read

8.6 (Alternate): Choosing an Intermediate Airport Hub

For this problem we join the Flat Earth Society so that we can calculate flight distances using the simple (but inaccurate) formula
      sqrt( (x2-x1)2) + (y2-y1)2)

Assume you are given a set of (x,y) pairs that represent the coordinates of airport hubs that you like. These are fixed so you can hardwire them.

public static void main (String[] args) {
  final double [][] points = {  {0,0}, {3,4}, {1,9}, {-10,-10} };
  System.out.println("Input 4 doubles for start and end points");
  Scanner getInput = new Scanner(System.in);
  double [] start = {getInput.nextDouble(),getInput.nextDouble()};
  double [] end = {getInput.nextDouble(), getInput.nextDouble()};

  int minIndex = 0;
  double minDist = dist(start, points[0]) + dist(points[0], end);
  for (int i=1; i<points.length; i++)
    if (dist(start,points[i])+dist(points[i],end) < minDist) {
      minIndex = i;
      minDist = dist(start,points[i])+dist(points[i],end);
    }
  System.out.printf("Intermediate hub number %d (%f,%f) %s%f\n",
            minIndex, points[minIndex][0], points[minIndex][1],
            " is the best.  The distance is ", minDist);
}
public static double dist(double [] p, double [] q) {
  return Math.sqrt((p[0]-q[0])*(p[0]-q[0])+
                   (p[1]-q[1])*(p[1]-q[1]));
}

Read in two (x,y) pairs S and E representing the starting and ending airports of a flight you want to make and find which hub P of those given minimizes the total trip consisting of traveling from S to P and from P to E.

Note the following aspects of the solution on the right.

8.7: Problem: Sudoku

Not as interesting as the title suggests. The program in this section just checks if an alleged solution is correct.

8.8: Multidimensional (i.e., Higher Dimensional) Arrays

double x[][][] = {
    { {1,2,3,4}, {1,2,0,-1}, {0,0,-8,0} },
    { {1,2,3,4}, {1,2,0,-1}, {0,0,-8,0} }
                 };

There is nothing special about the two in two-dimensional arrays. We can have 3D arrays, 4D arrays, etc.

On the right we see a 3D array x[2][3][4]. Note that both x[0] and x[1] are themselves 2D arrays.

8.8.1 Case Study: Daily Temperature and Humidity

double[][][] data =
    new double[numDays][numHours][2];

double[][] temperature =
    new double[numDays][numHours];
double[][] humidity =
    new double[numDays][numHours];

The three dimensional array data on the upper right holds the temperature and humidity readings for each of 24 hours during a 10 day period.
data[d][h][0] gives the temperature on day d at hour h.
data[d][h][1] gives the humidity on day d at hour h.

I do not like this data structure since the temperature and humidity are really separate quantities so I believe the second data structure is better (the naming is improved).

8.8.1 (Alternate) Case Study: A Data Structure for Predicting Weather

 
double[][][] temperature =
  new double[numLatitudes][numLongitudes][numAltitudes];

On the right we see a legitimate 3D array that was used in a NASA computer program for weather prediction. The temperature is measured at each of 20 altitudes sitting over each latitude and longitude.

8.8.2 Problem: Guessing Birthdays

A cute guessing game. The Java is not especially interesting, but you might want to figure out how the game works.

Homework: 8.7

Remark: End of material on midterm.

Remark: Answers to homework are on the web. You need a password to get them. The ch 8 solutions are not yet readable. I will make them readable tuesday after class.

Remark: Lab 4 is on the web but is not due until 30 oct.

Chapter 9: Objects and Classes

9.1 Introduction

Object-oriented programming (OOP) has become an important methodology for developing large programs. It helps to support encapsulation so that different programming teams can work on different aspects of the same large programming project.

Java has good support for OOP.

In Java, OOP is how gui programs are usually developed.

9.2 Defining Classes for Objects

An object is an entity containing both data (called fields in Java) and actions (called methods in Java). Two examples would be a circle in the plane and a stack of dishes.

For a circle, the data could be the radius and the (x,y) coordinates of the center. Actions might include, moving the center, changing the radius, computing the area, or (in a graphical setting) changing the color in which the circle is drawn.

For a stack (of dishes), the data could include the contents (plates) and the current top of stack pointer (the top plate). Actions might include pushing an element on to the top of the stack (putting a new plate on top) and popping the top element off (taking the top plate).

In Java, objects of the same type, e.g., many circles, are grouped together in a class.

It might be useful to think of a class as a factory, one that produces objects of a certain type. Then issuing a new operation is akin to placing your order (which is filled immediately).

Public class LongStack {
  int top = 0;
  long[] theStack;
  void push(long elt) {
    theStack[top++] = elt;
  }
  long pop() {
    return theStack[--top];
  }
}

On the right is the beginnings of a class for stacks containing Java long's. The fields in the class are top and theStack; the methods are push() and pop().

Unlike local variables, which we have seen many times before, a field is not local to (i.e., inside of) a method.

Three obvious problems with this class are.

  1. The array theStack is declared but is not created (there is no new operation).
  2. It is an error to pop an empty stack (we would reference theStack[-1], but this condition is not checked for.
  3. It is an error to push a full stack (we would reference theStack[theStack.length]), but this condition is not checked for.

Given a class, a new object is created by instantiating the class. Indeed, an object is often called an instance of its class.

Many classes supply one or more special method called constructors that Java invokes automatically whenever an object is instantiated. Although a constructor can in principle perform any action, normally its task is to allocate and initialize the fields. For example, a longStack constructor would create the array theStack.

Start Lecture #14

Remark: Answers to the practice midterm are on the web.

9.3 Example: Defining Classes and Creating Objects

public class TestCircle1 {
  // Main method
  public static void main(String[] args) {
    // Create a circle with radius 5.0
    Circle1 myCircle = new Circle1(5.0);
    System.out.println("The area of the circle of radius "
      + myCircle.radius + " is " + myCircle.getArea());

    // Create a circle with default radius 1
    Circle1 yourCircle = new Circle1();
    System.out.println("The area of the circle of radius "
      + yourCircle.radius + " is " + yourCircle.getArea());

    // Modify circle radius
    yourCircle.radius = 100;
    System.out.println("The area of the circle of radius "
      + yourCircle.radius + " is " + yourCircle.getArea());
  }
}
 
// Define the circle class with two constructors
class Circle1 {
  double radius;
 
  /** Construct a circle with radius 1 */
  Circle1() {
    radius = 1.0;
  }
 
  /** Construct a circle with a specified radius */
  Circle1(double newRadius) {
    radius = newRadius;
  }
 
  /** Return the area of this circle */
  double getArea() {
    return radius * radius * Math.PI;
  }
}

On the right is an example from the book. Note several points.

  1. There are two classes here. The top one is like many others we have seen in that it contains just the main() method. Since this class is public the file is named TestCircle1.java.
  2. The main method instantiates the second class Circle1 twice, thereby creating two Circle1 objects.
  3. In the first instantiation the radius is given; the second time it is not. Different constructors (named Circle1()) are called for the two cases (see below).
  4. The resulting objects myCircle and yourCircle can now be used in the main() method. For example both have their area computed and one has its radius changed.
  5. The Circle1 class is not public. It can only be used in this file (really this package). A single file can have only one (non-nested) public class; that class determines the name of the file.
  6. The class Circle1 has one field and three methods.
  7. The first two methods, also named Circle, are constructors due to their name being the same as the name of the class.
  8. Since the constructors are overloaded, their signatures are used to tell them apart. Both constructors serve the same purpose, they initialize the radius field.
  9. The third method getArea looks simple, we know the area of a circle is πr2, but ...

Class Fields and Methods vs. Instance Fields and Methods

A method can be declared static. The main() method in the class TestCircle is an example. Such a method is called a class method or static method and is associated with the class as a whole. In contrast a non-static method, called an instance method, is associated with an individual object. The Circle1 class has one instance method, no class methods, and two constructors.

Thus when the two Circle1 objects are created, each gets its own getArea() method.

In a like manner a field can be declared to be static (none are in this example) in which case it is called a class field (or sometimes a static field) and there is only one that is shared by all objects instantiated from the class.

A field not declared to be static is called an instance field and each object gets its own copy; changing one, does not affect the others. An object instantiated from a class is often called an instance of the class.

Putting this together we see that when the main() class invokes getArea() it must specify which getArea() is desired, i.e., which object's getArea() should be invoked. So myCircle.getArea() invokes the getArea() associated with myCircle and hence when this invocation of getArea() mentions radius (an instance field) it gets the radius associated with myCircle.

UML (Unified Modeling Language) Diagrams for Our Circles

The Unified Modeling Language (UML) is a standardized format for depicting classes and objects (and other things). It is not a formal part of this course, but we need some way to describe a class and its objects so I will used UML.

circle1-uml

On the far right we see the UML diagram for the Circle class. The top line gives the class name, the next group gives the fields (i.e., the data elements) and the last group gives the methods.

On the near right we show the UML diagram for the two objects we created of type Circle1.

Note that, unlike Java, UML puts the types of the fields and methods after the name.

9.3.A: A Two-File Program

public class TV {
  int channel = 1; // Default channel is 1
  int volumeLevel = 1; // Default volume level is 1
  boolean on = false; // By default TV is off
  public TV() {}
  public void turnOn() {
    on = true;
  }
  public void turnOff() {
    on = false;
  }
  public void setChannel(int newChannel) {
    if (on && newChannel >= 1 && newChannel <= 120)
      channel = newChannel;
  }
  public void setVolume(int newVolumeLevel) {
    if (on&&newVolumeLevel>=1 && newVolumeLevel<=7)
      volumeLevel = newVolumeLevel;
  }
  public void channelUp() {
    if (on && channel < 120)
      channel++;
  }
  public void channelDown() {
    if (on && channel > 1)
      channel--;
  }
  public void volumeUp() {
    if (on && volumeLevel < 7)
      volumeLevel++;
  }
  public void volumeDown() {
    if (on && volumeLevel > 1)
      volumeLevel--;
  }
}

public class TestTV {
  public static void main(String[] args) {
    TV tv1 = new TV();
    tv1.turnOn();
    tv1.setChannel(30);
    tv1.setVolume(3);

    TV tv2 = new TV();
    tv2.turnOn();
    tv2.channelUp();
    tv2.channelUp();
    tv2.volumeUp();

    System.out.println("tv1's channel is "
      +tv1.channel+" and volume level is "
      +tv1.volumeLevel);
    System.out.println("tv2's channel is "
      +tv2.channel+" and volume level is "
      +tv2.volumeLevel);
  }
}
tv-uml

Above and to the right we see another simple class defined and used as well as the corresponding UML diagram. This example (from the book), separates the definition and use into separate files, which is very common. Each file has one public class that determines the name of the file.

Again note that the instance methods are referred to as objectName.methodName.

The plus signs in the UML indicate that the methods are public.

To compile and run this program you would type.

  javac TestTV.java TV.java
  java TestTV

The last line could not have been java TV since you must invoke the file that has the main() method.

9.4 Constructing Objects Using Constructors

We have seen constructors above. Note the following points.

The purpose of many constructors is to (allocate and) initialize the object being created via new.

Normally, a class provides a constructor with no parameters (as well as possibly other constructors with one or more parameters). This constructor is often called the no argument or no-arg constructor.

If the class contains NO constructors at all, the system provides a no-arg constructor with empty body. Thus the no-arg constructor in class TV could have been omitted.

9.4A LongStack Revisited

class LongStack {
  int top = 0;
  long[] theStack;
  LongStack() {
    theStack = new long[100];
  }
  LongStack(int n) {
    theStack = new long[n];
  }
  void push(long elt) {
    if (top>=theStack.length)
      System.out.println("No room to push!");
    else
      theStack[top++] = elt;
  }
  long pop() {
    if (top<=0) {
      System.out.println("Nothing to pop!");
      return -99;  // awful!!
    }
    return theStack[--top];
  }
}
public class DemoLongStack {
  public static void main (String[] args) {
    long x = 333, y = 444;
    LongStack myLStk = new LongStack(4);
    System.out.printf("Before: x=%d and y=%d\n", x, y);
    myLStk.push(x);
    myLStk.push(y);
    x = myLStk.pop();
    y = myLStk.pop();
    System.out.printf("After:  x=%d and y=%d\n", x, y);
  }
}

Before: x=333 and y=444
After:  x=444 and y=333

Now that we know a little more about constructors, we can add them to class LongStack, and, while we are at it, put in some error checks. The revised code is on the right.

If we knew about Java exceptions, it would be good to utilize them for these error checks. In particular, returning a -99 is awful.

The default stack, i.e., the one created with the no-arg constructor, has room for 100 elements. The user can, however, specify the size when invoking new and then the other constructor will be called.

Note that LongStack is no longer a public class. With no public (or private or protected) declaration, the default is that LongStack is visible within the current package.

Packages are important for large programs and will be discussed a little later. For now you can think of LongStack as a public name but, since the file has only one real public class (DemoLongStack), it must be named DemoLongStack.java.

The main() method declares a longStack and uses it a little. Below the code, we see the output produced, which indeed exhibits stack-like (LIFO) semantics.

Note especially the command myLStk.push(x), which we now discuss.

When compared to most programming languages something looks amiss with this statement. The purpose of the command is to push x on to the stack myLStk and hence should be written something like push(x,myLStk). Similarly, the purpose of x=myLStk.pop() is to pop the stack myLStk and place the value into x. So it should be something like x=pop(myLStk).

However, in Java, and other object-oriented languages, it is written as shown in DemoLongStack. The asymmetry between x and myLStk is deliberate. The point is that the LongStack object myLStk contains not only data (in this case top and theStack) but the methods push() and pop() as well.

In terms of the factory analogy (which should not be taken too literally), the LongStack factory has a service department that works on LongStacks, in particular it can push longs onto one of its LongStacks.

We have previously seen this dotted notation (object dot methodName). For example, getInput.nextInt().

If push() were a class method instead of an instance method, then an invocation would include the stack as a parameter, perhaps LongStack.push(x,myLStk).

9.5 Accessing Objects via Reference Variables

Recall the serious business we mentioned in section 7.5 when discussing copying arrays. Liang finally comes to grips with it here.

9.5.1 Reference Variables and Reference Types

As with arrays, variables for objects contain references to the objects not the objects themselves.

Naturally, if a class ClassBig has many large fields, objects of the class are large. Similarly, if ClassSmall has just one int as a field, objects of this class are small. However, an important technical point to note is to consider

  ClassBig big = new ClassBig();   ClassSmall small = new ClassSmall();

Then big and small are the same size. Neither contains an object; instead each contains a reference to an object (i.e., a pointer, which is essentially an address). You don't need a bigger address label to send a letter to a mansion than to a studio apartment.

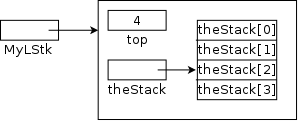
ref-types

The diagram on the right illustrates the situation right after main() executes

  LongStack myLStk = new LongStack(4);

We see that myLStk refers to (points at) the new object.

We also see that the object has three pieces.

  1. There is the int top, which is a primitive type so actually contains the value.
  2. There is the one dimensional array theStack which is a reference to a bunch of longs, currently it references 4 longs.
  3. There is the block of 4 long themselves. Since long is a primitive type these four cells will contain values. If theStack were instead an array of 4 objects or an array of 4 arrays, the cells would be references.

The above is very important. It is a key tenant of Java that primitive types have value semantics and that both arrays and objects have reference semantics.

We will learn later that, for each primitive type, there is a corresponding class with a similar name (but naturally with reference, not value, semantics). Specifically, the names are Byte, Short, Integer, Long, Boolean, Character, Float, Double.

9.5.2 Accessing an Object's Data and Methods

After creation, methods and data fields within objects are referenced using dot notation as mentioned above and illustrated by getInput.nextInt(), myLStk.pop(), and myLStk.top.

Note that the name before the dot is a variable containing (a reference to) an object. It is not a class as in Math.PI or Math.random(). (You can tell right away, because it begins with a lower case letter.)

Also note that the fields and methods just mentioned do not have the static modifier. We shall see static fields later and have seen many static methods already. Fields and methods that are not static are called instance fields (or instance variables) and instance methods.

If in the DemoLongStack example above, the main() method created two LongStack's, each one would have its own top, theStack, push(), and pop().

static methods and fields are associated with a class (that is why the name before the dot is a class). In contrast, instance methods and fields are associated with an object (that is why the name before the dot is (a reference to) an object).

9.5.3 Reference Data Fields and the null Value

As I mentioned several lectures ago, Java assigns default values to many variables, but I do not use or recommend learning the default values. I always (try to remember to) explicitly initialize the variables at their declaration or ensure that they are assigned a value before there value is requested.

Nonetheless there is one default you will need to recognize as it will indicate a fairly common error. If you declare an object or array but do not create it (with new), then it receives the default value (really default reference or default pointer) null. If you then attempt to use the object, you can get a NullPointerException.

Here is an example from the LongStack class above.

  1. If the class definition contained no constructors, then Java would have supplied the default (no-nothing) no-arg constructor. The main() method would not compile since it contains new LongStack(4), which does not match the no-arg constructor (the only constructor present).
  2. If, in addition. the new invocation was changed to not specify the size, the program would compile and the default, do-nothing no-arg constructor would be called. The result would be that theStack would be declared but not created. Then, when the first push is invoked, a NullPointerException would be raised because theStack contains null.

9.5.4 Differences between Variables of Primitive Types and Reference Types 

int[][] c = { {4,5,6}, {7,8,9} };
int[] a = c[0];
int[] b = a;
b[1] = 999;
System.out.println(a[1]);
System.out.println(c[0][1]);
 
class C {
    int a;
}
public class Test {
  public static void main(String[] args) {
    // C c1 = new C(),  c2 = new C();
    C c1 = new C(),  c2;
    c1.a = 1;
    c2 = c1;
    c2.a = 99;
    System.out.println("c1.a=" + c1.a);
  }
}

This section of the book finally gives the pictures showing that reference types only point to values; they do not contain values. All this applies equally well to arrays where we previously discussed it.

The Story with Arrays

The top example on the right illustrates reference semantics for arrays. Both values printed are 999.

The Story with Objects

The bottom (one-file, two-class) example illustrates reference semantics for objects. The value printed is 99. If the commented out line is used instead of the line below it, the printed value is still 99.

The Stories are Very Similar

In both cases we have two references pointing to the same thing. This is often called an alias. If you use one of the references to change the thing, the other reference sees the change.

Start Lecture #15

Midterm Exam

Start Lecture #16

9.6 Using Classes from the Java Library

A significant strength of Java is its very extensive class library.

9.6.1 The Date Class

Let's use this opportunity as an excuse for reviewing how to obtain information from http://java.sun.com/javase/7/docs/api.

The 10e mentions two constructors and three methods (toString(), getTime(), and setTime()).

If you knew that Date was in java.util you could restrict the classes, but let's not and use the default of all classes.

The same two constructors are present as in the 10e (along with several that are deprecated). The methods are there as well, together with many others (some deprecated).

  import java.util.Date;
  Date myDate = new Date();
  System.out.println(myDate.toString());

Don't forget the syntax of objectName.methodName. On the right is a simple example.
Question: How would the example have differed without the import?
Answer: Date would have been java.util.Date twice in the declaration/creation.

9.6.2 The Random Class

Again use the web and find the constructors and methods.

9.6.3 The Point2D Class

Let's write some of this ourselves.

The class contains:

Homework: 9.3.

Start Lecture #17

9.7 Static Variables, Constants, and Methods

We have now seen several methods in classes that are associated with objects. For example myDate.toString() invokes the toString() method that is associated with the object myDate. If we had also declared another Date, say yourDate, then myDate.toString() would be a different method from yourDate.toString().

This is a good thing since the string version of myDate is different from the string version of yourDate (unless myDate and yourDate happen to refer to the exact same time).

Similarly, we have seen several data fields defined in classes that are associated with each instance of the class. For example, the top of each instance of LongStack is unique.

This is also good. If you have several LongStack's, you don't expect their top's to be equal and surely pushing one LongStack should not affect the top of any other LongStack.

class ShortStack {
  int top = 0;
  short[] theStack;
  ShortStack() {
    theStack = new short[100];
  }
  ShortStack(int n) {
    theStack = new short[n];
  }
  // Maintain total number of items stacked
  static int totalStacked = 0; // should be pvt
  static int getTotalStacked() {
    return totalStacked;
  }
  void push(short elt) {
    if (top>=theStack.length)
      System.out.println("No room to push");
    else
      theStack[top++] = elt;
    totalStacked++;
  }
  short pop() {
    if (top<=0) {
      System.out.println("Nothing to pop.");
      return -99;  // awful!!
    }
    totalStacked--;
    return theStack[--top];
  }
}
 
public class DemoShortStack {
  public static void main (String[] args) {
    ShortStack mySStk1 = new ShortStack(4);
    ShortStack mySStk2 = new ShortStack();
    mySStk1.push((short)12);  mySStk1.push((short)13);
    mySStk2.push((short)22);  mySStk2.push((short)23);
    System.out.printf("Before pops: stacked=%d\n",
              ShortStack.getTotalStacked());
    short x = mySStk1.pop();
    short y = mySStk1.pop();
    System.out.printf("After pops:  x=%d, y=%d %s%d\n",
              x, y, "and stacked=",
              ShortStack.getTotalStacked());
  }
}

Before pops: stacked=4
After pops:  x=13, y=12 and stacked = 2

9.7.A Static Variables

Sometime having separate instances of each method and field for each object is not what we want. On the right we see ShortStack. I derived it from LongStack, by first replacing all long's with short's.

Then I decided to keep track of the total number of items currently stacked on all the ShortStack's. This single variable totalStacked is incremented by every push(), no matter which ShortStack is being pushed, and is decremented by every pop(). We indicate that there is one totalStacked associated with the entire class ShortStack rather than one totalStacked associated with each instance of shortStack (i.e., one associated with each object) by declaring totalStacked to be static.

A variable like totalStacked that is associated with the class and not with each instance is called a static variable or a class variable.

Unlike instance variables that are referred to as objectName.variableName, static variables are referred to as className.variableName.

9.7.B Static Methods

I could have printed totalStacked in the main() method, but did not. Instead, I had the class define a static method getTotalStacked() that returns the value of totalStacked and had main() call getTotalStacked(). (We will see the reason for doing this shortly when we study Visibility Modifiers just below.)

We could have writen getTotalStacked() as an instance method, so that there would be one associated with each object of type ShortStack. However, that would be a little silly and misleading (but would work) since the method just returns the value of a class field and hence all instances of the method do the same thing. Hence we declare getTotalStacked() to be static so that there is only one getTotalStacked() method for the entire class. That is, we make it a class method or static method.

We have already used static methods, e.g. Math.random(). Note that the name is className.methodName(), which explains the name ShortStack.getTotalStacked() in DemoShortStack.main().

9.7.C Static Variables Are Fields, Not Local Variables

Recall that variables like top and totalStacked that are declared in a class but not inside a method are called fields or data fields. Hence top is called an instance data field or instance field and totalStacked is called a static data field or static field.

Also, variables declared within a method are called local variables. Since they are associated with an individual method invocation (i.e., their lifetime is that of a single invocation.) and not with an object or the class in general, such variables cannot be given the static modifier.

9.7.D Static Methods Do Not Reference Instance Entities Directly

A static method cannot access instance fields or instance methods of its class. Indeed, it would not make any sense to do so: An instance entity is associated with a specific object in the class; whereas, the static method is associated with the class as a whole so there is no specific instance entity for it to choose.

9.7.E Don't Tell Anyone

One more point, one that will reveal a great secret. Since a class method is dependent only on its class and not on any object of the class, we can define and use a class method even if no objects of the class have been created. At long last we can understand

   public static void main (String[] args)

which must be used in every Java program.

9.8 Visibility Modifiers

Some of our classes, data fields, and methods have been public and some have not. What gives?
There are actually four possibilities, of which we have used two.

  1. public
  2. private
  3. protected
  4. default (unspecified), which is package-private or package-access

(Top level classes, i.e., classes not inside any other class, can not be declared private or protected.)

9.8.A public and private

An entity (a class, a field, or a method) that is declared to be public can be accessed from any class.

An entity that is declared to be private is accessible only within its own class.

public class DemoPubPvt {
    public static void main(String[] args) {
        C1 c1 = new C1();
        int sum = c1.pub + c1.pvt;
    }
}
public class C1 { // C1.java
    public  int pub = 1;
    private int pvt = 1;
}

Look at the example on the right and note the following.

9.8.B Why Use Private?

Recall that ShortStack declares totalStacked to be private. Why?

This declaration prevents other classes from accessing the variable, which has the great advantage that the author of the original class can be sure that no other class either changes the variable or depends on how the variable is implemented.

In such cases it is common to supply an accessor method (a.k.a. a getter, ugh) such as getTotalStacked() to supply the current value to a user of the class.

Sometimes the author also supplies a setter method that alters the value. An advantage of private in this case is that the setter can also check the value for legality.

9.8.C Packages and Default Visibility

Java includes the notion of a package, which is a collection of classes. A .java file can begin with a line
      package packageName;
which declares all the classes in the file to be in the package packageName.

If you use Eclipse, you may get package statements as the first line of your files.

Packages are very important for large programs, but less so for the small ones we will write.

None of our .java files have needed a package statement. In such cases Java places the classes declared in the file into the so called default package.

If an entity is declared without a visibility modifier (public, private, or protected), then the entity has package visibility, which means it is visible in all classes belonging to the same package that the entity belongs to. We will assume (as is often the case) that all the .java files in a given directory that do not have package statement, belong to the same package. In particular if you use the default package (as I have done) all entities without a visibility modifier are visible to all .java files in the current directory.

9.8.D protected

The protected visibility modifier comes into play only when there are subclasses and inheritence so we defer it to Chapter 11.

9.8.E The Bottom Line (for now)

Until we learn about subclasses and protected, our use of modifers will be fairly simple (in part because we are not learning about packages).

  1. Each .java file will have one top-level public class.
  2. The main() method must be declared public and will be in a top-level public class.
  3. Use private for entities that should not be visible outside the current class.
  4. For other entities the public visibility modifier and no visibility modifier have the same effect.

Homework: 9.7

9.9 Data Field Encapsulation

9.9.A Improving ShortStack

class ShortStack {
  int top = 0;
  short[] theStack;

class ShortStack {
  private int top = 0;
  private short[] theStack;
  int getTop() {
    return top;
  }

On the upper right we see the beginning of the ShortStack class we saw previously. In the second group, we added private visibility modifiers, which improves the class considerably. Why?

  1. Users of ShortStack must not alter top. Altering top would distroy the LIFO semantics required for a stack. If we wished to give the user read-only access to top, we could supply a getTop() accessor method as shown at the bottom.
  2. Since users of ShortStack have no access to theStack, the ShortStack programmer can change the implementation to not use a single array. In general, you want to make public the published interface to the class, and keep private the implementation details.

Improving the Circle1 Class

public class Circle2 {
  private double radius = 1;
  private static int numberOfObjects = 0;

  public Circle2() {
    numberOfObjects++;
  }
  public Circle2(double newRadius) {
    radius = newRadius;
    numberOfObjects++;
  }

  public double getRadius() {
    return radius;
  }
  public static int getNumberOfObjects() {
    return numberOfObjects;
  }
  public double getArea() {
    return radius * radius * Math.PI;
  }

  public void setRadius(double newRadius) {
    radius = (newRadius >= 0) ? newRadius : 0;
  }
}

Until we learn about packages and subclasses, we need only distinguish public and private. Both protected and the default package-private are equivalent to public in the absence of subclasses and packages.

On the right we see an improved circle class, now called Circle2.

Start Lecture #18

Remark: Comment on labs and midterm grades.

Remark: The final exam date has been posted by the department, and appears on the class home page.

9.10 Passing Objects to Methods

class ShortStack {
  private int top = 0;
  private short[] theStack;
  private static int totalStacked = 0;
  ShortStack() {
    theStack = new short[100];
  }
  ShortStack(int n) {
    theStack = new short[n];
  }
  static int getTotalStacked() {
    return totalStacked;
  }
  int getTop() {
    return top;
  }
  void push(short elt) {
    if (top>=theStack.length)
      System.out.println("No room to push");
    else
      theStack[top++] = elt;
    totalStacked++;
  }
  short pop() {
    if (top<=0) {
      System.out.println("Nothing to pop.");
      return -99;  // awful!!
    }
    totalStacked--;
    return theStack[--top];
  }
}
public class DemoShortStack2 {
  public static void main (String[] args) {
    ShortStack mySStk1 = new ShortStack(4);
    ShortStack mySStk2 = new ShortStack();
    mySStk1.push((short)12);  mySStk1.push((short)13);
    mySStk2.push((short)22);  mySStk2.push((short)23);
    System.out.printf("Before pops: stacked=%d\n",
                      ShortStack.getTotalStacked());
    short x = mySStk1.pop();
    short y = mySStk1.pop();
    System.out.printf("After pops:  x=%d, y=%d %s%d\n",
                      x, y, "and stacked=",
                      ShortStack.getTotalStacked());
    System.out.println("Printing and emptying stack #1");
    printAndEmptyShortStack(mySStk1);
    System.out.println("Printing and emptying stack #2");
    printAndEmptyShortStack(mySStk2);
  }
  public static void printAndEmptyShortStack(ShortStack SStk){
    System.out.printf("%d items stacked, %d in this stack.\n",
                      ShortStack.getTotalStacked(),
                      SStk.getTop());
    for (int i=1; SStk.getTop()>0; i++)
      System.out.printf("Item #%d is %d\n", i, SStk.pop());
    System.out.println();
  }
}

Before pops: stacked=4
After pops:  x=13, y=12 and stacked=2
Printing and emptying stack #1
2 items stacked, 0 in this stack.

Printing and emptying stack #2
2 items stacked, 2 in this stack.
Item #1 is 23
Item #2 is 22

As with arrays, passing an object to a method actually passes a reference (pointer) to the object.

The book illustrates this with one of the circle classes. You should read that.

For variety) we consider our ShortStack class.

As illustrated on the right, I have included several improvements and enhancements that I will describe just below. Although I wrote both classes, it is useful to think of the ShortStack class as written by the author and to think of DemoShortStack as written by the user.

The simplest improvement is that the data fields top, theStack and totalStacked are now private. As mentioned previously, this prevents the user from modify these variables, which makes the author's job easier.

Accessors are provided for top and totalStacked giving the user read-only access to the variables.

In addition to the author's enhancements to ShortStack the user added a method printAndEmptyShortStack(). Since the methods of needed for its implementation are all public, printAndEmptyShortStack() is as easy for the user to write as it would be for the author. Since it is a rather specialized method, the author didn't think it worthwhile to include in the general-purpose ShortStack class.

The printAndEmptyShortStack() method has one parameter; it is of type ShortStack. The method is invoked just as if the parameter was a primitive type or an array. As always it is passed by value so changes the method makes to the argument itself are not visible to the caller upon return. However, as with an array, the parameter is a reference, which the method can use to access and possibly change the object itself.

Note the use of the accessor functions getTotalStacked() and getTop(). Specifically, note that, since getTotalStacked() is a class method, it is referenced as className.methodName(), namely ShortStack.getTotalStacked(). In contrast, since getTop() is an instance method, it is referenced as objectName.methodName, namely SStk.getTop().

Passing a Reference by Value??

How can you pass a reference (an object is a reference) by value? I thought values were for primitive types, not for references.

That does sound bad but yes the reference is passed by value, it is copied from the argument to the parameter and is not copied back (standard call-by-value semantics)

This is exactly the same as passing an array, which we did earlier.

To repeat what I said earlier, there is nothing special about passing an object or an array, you just must remember that all arguments are pass-by-value and that arrays and objects are references.

A Snapshot During Execution

The diagram on the right shows the situation when main() has called printAndEmptyShortStack() for the first time and the loop is just starting.

shortStack2

For technical reasons, covered in elective courses in compilers and comparative programming languages, objects themselves are stored in a region of memory separate from local variables. This region is normally called the heap.

The variables local to a method are stored in a region called the stack (yes, it does have stack-like FIFO properties).

These variables disappear when the method returns, and their size is known when the program is written. Neither of these properties are assured for entities stored in the heap.

Although this separation of stack from heap is quite important for efficiency, we will not emphasize it in this course.

The diagram illustrates value semantics for the int and short variables x, y, and i. Specifically the memory locations assigned to these variables contain the current value of the variable (this so called value semantics holds for all primitive types).

In contrast, consider the local variables SStk and mySStk1, which are declared to be objects. In this example all objects are ShortStack's. These have reference semantics. The memory assigned to one of these variables contains only a pointer to the object and not the object itself.

Also note the call-by-value semantics. The contents of the argument myStk1 is copied into the parameter SStk.

9.11 Array of Objects

array-of-objs

To understand arrays of objects we just combine the semantics of arrays with the semantics of objects. Consider the diagram on the right.

9.1.A Creating a 1D Array of Objects

To create a 1D array of objects, you must execute new to create the array and then need a loop of news to create the individual objects.

  String[] strArray;
  strArray = new String[8];
  for (int i=0; i<8; i++)
    strArray[i] = new String("xyz");

Compare the code on the right to the previous diagram for a1o. The first line creates just the reference to the array (the box labeled a1o). The second line creates the block of references for the array itself (in the previous diagram this was a block of two references; now it is a block of 8 references) and stores a reference to this block in the item created by the first line. The loop then creates the 8 objects and stores references to them in the block created in line 2.

Remark: Lab 5 is available, it is due 13 Nov.

9.1.B Creating a 2D Array of Objects

 
 
  String[][] strArray2;
  strArray2 = new String[3][];
  for (int i=0; i<3; i++) {
    strArray2[i] = new String[4];
    for (int j=0; j<4; j++)
      strArray2[i][j] = new String("xyzzy");
  }

Creating a 2D array requires even more news. The code on the right creates a 3×4 array of strings and should be compared with a2o in the diagram above, which created a 2×2 array of objects.

We need to create the reference StrArr corresponding to a20 (no new required). We need to create the block of 3 1D arrays (one new) and assign this to strArray2. We need a loop to create a block of references and make StrArray point to it and then need a double-nested loop to create the objects and have the String variables point to them.

9.12 Immutable Objects and Classes

An object is called immutable if, once created, it cannot be changed.

Let me be clearer about that. When we say the object cannot be changed, we mean the data fields of the object cannot be changed.

For example, any String object is immutable (its only data field is the sequence of characters that constitute the string). A class, such as String, all of whose objects are immutable is also called immutable.

In contrast a StringBuilder can change after construction, as we have seen. So the StringBuilder class is mutable

What must we do to write an immutable class?

Naturally, we must make all the data fields private and no public method can change a data field. Such methods are often called mutators. But that is not enough!

The reason I am covering this (admittedly subtle) material is not that we desperately need immutable classes, but instead to give more practice in understanding objects and reference semantics

An Immutable Class: NoChanges

public class NoChanges {
  private int x;
  public NoChanges(int z) {
    x = z;
  }
  public int getX() {
    return x;
  }
}

Looking to the right, clearly the class NoChanges is immutable: the only data field is x, which cannot be directly accessed (it is private). With the accessor getX() we can find the value of x, but cannot change it. Thus once we create a NoChanges object with say

      NoChanges nc =  new NoChanges(5).

then the x component of this NoChanges object has the value 5 and will never change.

But of courses the variable nc can be assigned to another NoChanges object.

A Mutable Class: Changes

public class Changes {
  public int a;
  public int b;
  public Changes(int r, int s) {
    a = r;   b = s;
  }
}

In contrast, the class Changes is not immutable (it is mutable). For example, consider the code below

  Changes c = new Changes (5,6);
  c.a = 9;

This example has changed the object c by changing its first component from 5 to 9.

A Harder Example: Class Maybe

public class Maybe {
  private Changes c;
  public Maybe(int w) {
    c = new Changes (w,w);
  }
  public Changes getC() {
    return c;
  }
}
 
public static void main (String[] args) {
  Maybe mb = new Maybe(12);
  mb.c.a = 1;        // Will not compile
  mb.getC().a = 1;   // Works fine
}

The interesting case is class Maybe. At first (and even second) glance it looks like class NoChanges. Indeed each line of Maybe looks like the corresponding line of NoChanges. The only difference is the initialization of c. But just as with NoChanges, we do not give the user access to c (it is private) and the accessor lets us only find c's current value, not change it.

But there is a difference! The variable c is of type Changes, which is an object and hence has reference semantics. Also the object to which we now have a reference is itself mutable. Therefore the accessor has returned a reference that enables us to change the value of the components.

Code to exploit this hole is shown in the bottom frame on the right.

This should remind you of passing an array to a method. The method cannot change the array itself (since Java is pass-by-value), but it can use the array (with its reference semantics) to make changes to the components of the array.

There are three requirements for a class to be immutable.

  1. All data fields must be private.
  2. No mutator methods.
  3. No accessor method returns a reference to a mutable data field.

Again, the point of this exercise is not so much to learn about immutable objects, but to again come to grips with reference semantics, which are crucial to understanding Java.

9.13 The Scope of Variables

There are two kinds of variables found in a class.

  1. Data fields.
  2. Variables (including parameters) declared inside a method withing the class.

If a local variable has the same name as a data field, the field name is hidden (i.e., not directly accessible) in that method. For this reason as well as for increased clarity, it is not recommended (but is permitted) to use the same name for both a class variable and a non-parameter local variable.

We shall see next section that it is common to have parameters with the same name as fields.

9.14 The this Reference

The special name this is used in several ways with respect to objects and classes. We see two of them below on the right as well as an illustration of a few other points. Although the code is quite simple, it warrants careful study.

The class C contains an instance field i, a class field si, two constructors, an accessor (a.k.a. a get method or getter (ugh)), two mutators (a.k.a set methods or setters), one for setting each of the two fields, and a main() method.

public class C {
  int i;
  static int si = 4;
 
  C (int i) {
    this.i = i;
  }
  C () {       // no-arg constructor
    this(8);
  }
 
  int getI () { // hides nothing
    return i;
  }
 
  void setI (int i) { // instance field
    this.i = i;
  }
  void setSi (int si) { // class field
    C.si = si;
  }
 
  public static void main (String[] args) {
    C c = new C();
    System.out.println(c.i);
  }
}

9.14.1 Using this to Reference Hidden Data Fields

9.14.2 Using this to Invoke a Constructor

As is often the case, the no-arg constructor of class C performs the same actions as the 1-arg constructor, but with a default value. Thus we would like to have the no-arg constructor invoke the other constructor, but there is no name we can use for the constructor. Hence, Java defines this() to serve such a purpose.

In fact any constructor (even on with arguments) can use this() to invoke another overload constructor in the same class, providing this() is the first statement in the constructor.

Chapter 10 Object-Oriented Thinking

10.1 Introduction

We have seen already several differences when using objects. With instance methods one of the parameters is the object itself and is written differently. For example given a String s1, we get its length via s1.length() rather than length(s1). However, designing (large) systems using objects as centerpieces (so called object-oriented design) has deeper differences from conventional design than the essentially syntactic change in length().

10.2 Class Abstraction and Encapsulation

Class abstraction is the separation of how a class is used from how a class is implemented.

How to use a given class is described by the class specification, also called is public interface. In Java classes, public fields and the signatures of public methods form the interface. (Recall that a method's signature consists of its name and the number and type of its parameters.)

In contrast, private fields, private methods, and the bodies of public methods are not part of the specification, but are part of the implementation.

When looked at from the user's point of view, the knowledge needed to create and use a class's objects is all contained in the specification. In that way a class encapsulates the knowledge needed to create and uses its objects.

We sometimes call a class an abstract data type or ADT. Really the full class is the data type and the public interface abstracts this data type to just those parts that a user needs.

Yet another name is information hiding, the implementation of the class is hidden from the users of the class.

In summary, how to use a given class is described by the class specification. In the next section we discuss an example.

Java supports Objected Oriented Programming, whose three pillars are Abstraction/Encapsulation, Inheritance, and Polymorphism (often with dynamic dispatch). In this section we will study the first pillar, the next chapter covers the other two.

10.2.1 An Example: Using (Without Understanding) Heron's Formula

public class Point {
  private double x, y;
  public Point(double x, double y) {
    this.x = x;
    this.y = y;
  }
  public double getX() { return x; }
  public double getY() { return y; }

  public double distTo(Point q) {
    return Math.sqrt( Math.pow(x-q.x(), 2) +
                      Math.pow(y-q.y(), 2) );
  }
}
public class Triangle {
  private Point p1, p2, p3;
  public Triangle (Point p1, Point p2, Point p3) {
    this.p1 = p1;
    this.p2 = p2;
    this.p3 = p3;
  }
  public double perimeter() {
    return p1.dist(p2) + p2.dist(p3) + p3.dist(p1);
  }
  public double area() {
    double semi = perimeter() / 2;
    return Math.sqrt((semi-p1.dist(p2)) * (semi-p2.dist(p3)) *
                     (semi-p3.dist(p1)) * semi);
  }
}

On the right we have two public classes (from two .java files) Point and Triangle. Let's see what users need to know and what they do not need to know in order to successfully use the classes.

Obviously they need to know the names of the classes Point and Triangle since they are in the public interface. They do not need to know the names and types of the fields (they are private). They do need to know that you create a Point by giving the (only) constructor two doubles. They do not need to know how the point is actually constructed.

For example, the author could change the implementation to use polar coordinates (radius and angle) internally but still support an x-y interface. The author would replace the fields x and y with fields r and theta. However, the constructor would still accept x-y coordinates and convert them to polar coordinates, which would be stored in the r and theta fields.

point-uml

The important point is that users would need take NO action. Indeed they would not even need to be told of the change.

They do need to know the method name distTo() and that it takes a Point as argument to calculate the distance from the base point to the given point. They do not have to know the distance formula (but they probably do remember it from analytic geometry).

The Point UML is on the right. Note the use of minus signs to indicate private fields. Similarly plus signs are used to indicate public methods and public constructors.

triangle-uml

For Triangle, they need to know that the constructor requires three Points (the vertices), but again not that we store the points as the fields (we could change the implementation to use another representations without affecting the user).

They need to know the method name perimeter() if they wish to calculate the perimeter and area() if they wish to calculate the area. They do not need to know the implementations. For perimeter(), this is no great savings given the distTo() method, but for area() it is a savings since most users probably do not know Heron's formula.

10.3 Thinking in Objects

Organizing programs around object, often enables modifications to be easily performed, especially additions.

  private String color = new String(); // empty string
  public Triangle (Point p1, Point p2, Point p3, String color) {
    this.p1 = p1;
    this.p2 = p2;
    this.p3 = p3;
    this.color = color
  }

For example, if we wish to associate an optional color with each triangle (say another part of the program draws the shapes on the screen), we would add another field and a corresponding accessor and mutator method as shown on the right.

The old constructor (as well as old programs using it) is still valid and results in a triangle with the empty string as color. That is the reason we initialized color in the declaration.

  private String color;
  public Triangle (Point p1, Point p2, Point P3) {
    this(p1, p2, p3, ""); // the modified old constructor
  }
  public Triangle (Point p1, Point p2, Point P3, String Color) {
    // the new constructor as above
  }

An alternate implementation would be to remove the initialization from the declaration, and change the old constructor to call the new constructor giving it an empty string as the color parameter.

This implementation again illustrates using this() to have one constructor invoke another one in the same class. Normally, as on the right, the invoked constructor has more parameters than does the invoker.

With graphics it is often important to know the depth of an object so that the program can determine what is visible. We could again add another private field, say depth, give it a default value and define another constructor to set it (or another two constructors, one with color and one without).

10.4 Class Relationships

We have looked at designing individual classes. In this section, we consider relationships between classes. However, a very important relationship, inheritance, will not be discussed until next chapter.

10.4.1 Association

Association is a general concept that helps in documenting the relation between classes. The book's example using three classes Courses, Students, and Faculty is illustrative and familiar to us.

The relations between the three classes can be represented diagrammatically as follows.

assoc-uml

The diagram asserts that:

  1. From 3 to 120 students can Take (i.e., be enrolled in) a course.
  2. One faculty member can Teach a course and when doing so has the role of Teacher.
  3. Students can take an arbitrary number of courses.
  4. A faculty member can teach 0 to 5 courses.

In Java we use fields and methods to implement associations. For example consider the following skeleton implementation.

Public Class Student {         Public class Course {                 Public class Faculty {
  private Course[] courseL;      private Student[] classL;             private Course[] courseL;
  public void                    private Faculty faculty;              public void
      addC(Course c) {...}       public void addS(Student s) {...}         addC(Course c) {...}
                                 public void setF(Faculty f) {...}

As shown above each student has a list of courses they are taking; each course has one faculty member and a list of students enrolled; and each faculty member has list of courses they are teaching.

Clearly, this is only the beginning. For example, students can drop courses, faculty can submit grades, courses and students have names, etc.

Redundant Information

As shown above some information is stored redundantly. For example if alexa is taking physics then:

  1. The Student object alexa will be a member of the classL array in the course object physics.
  2. The Course object physics will be in the courseL array in the Student object Alexa.

Having the same information stored twice has the advantage that you can easily find all the courses that Alexa is taking as well as all the students taking physics.

The disadvantages are that:

  1. More storage is used.
  2. Adding a student to a course involves two actions.
  3. Whenever data is redundant, you must insure consistency.

This Example is Crazy and Can't Possibly Work! ... Or Can It?

This is mathematically hopeless! The student object alexa is part of the course object physics (since it is a member of physics.classL), and physics is part of alexa (since it is a member of alexa.courseL). So alexa is a part of physics and physics is a part of alexa, which says they are equal; but they are not.

Question: How can this work?
Answer: Reference Semantics!

10.4.2 Aggregation and Composition

Sometimes we have a stronger, asymmetric relationship between two classes. For example, an object of type A might have an object of type B in it, where we think of the A object owning the B object. This relationship is normally called a has-a relationship. Examples.

  1. A resident has a social security number.
  2. A resident has an address.
  3. A car has a vin number.
  4. A student has a transcript.
  5. An employee has a supervisor.

The terminology used is that the owner is called the aggregating object and its class is called the aggregating class. The subject is called the aggregated object and its class is called the aggregating class.

Note that it is possible for one subject to have two owners; for example two residents can have the same address. If, however, owners are unique (e.g., only one car can have a given vin number), then the aggregation is called a composition.

aggregation

On the right we see the pictorial (uml) representation. The solid diamond represents composition and the hollow diamond aggregation. The diagram indicates that up to 5 residents can have the same address.

  public class Resident {
    private SSN ssn;
    private Address address;
  }

When implementing composition or mere aggregation, the subject is made a field in the object class, e.g., the Resident class would have two fields, one for the ss# and one for the address. The Address class may have several fields, e.g., zip code, street name, street number, apartment.

  public class Employee {
    private SSN ssn;
    private Employee[] supervisor;
  }

It is possible for the subject and object to be members of the same class. For example, both an Employee's supervisor is probably also an Employee. Moreover a an employee may have multiple supervisors. As shown on the right an array is then used.

Once again we have Java code that looks impossible; how can an Employee object contain an array of Employee objects? Once again the answer is reference semantics.

10.5 Case Study: Designing the Course Class

  public class Course {
    private String courseName;
    private Student[] student;
    private int numStudents = 0;
    private int capacity; 
    private static int totalEnrollment;
 
    public Course(String courseName, int capacity) {
      this.courseName = courseName;
      student = new Student[capacity]
    }
 
    public Course(String courseName) {
      this(courseName, 100);  // default capacity
    }
 
    public void addStudent(Student student) {
      if (numStudents < capacity)
        this.student[numStudents++] = student;
        totalEnrollment++;
      }
      // else learn about exceptions and raise one
    }
 
    // getter's for the four private fields
 
    public void dropStudent (Student student) {
      // Homework, but not all of 10.9 (CS-102)
    }
  }

You should read this section in the book.

On the right is slightly altered version of Liang's development. Note the following points.

  1. All the fields are private. This use of private is quite common. We discussed its advantages before.
  2. I added the static field totalEnrollment which gives the total enrollment in all the courses created. Make sure you understand why it must be static.
  3. The book does not explicitly initialize numStudents; presumably Java does it automatically. I do not recommend relying on default initialization since I find the explicit initialization a form of documentation and not all programming languages do these automatic initializations.
  4. Liang creates the Student array together with the declaration and thus must give the length. My first constructors obtains the length from the user; my second constructor uses a default and invokes the first constructor by using this(). Such pairs of constructors are common.
  5. I added the beginning of an error check to addStudent().

Homework: Write dropStudent(), which is not hard, but don't do all of 10.9.

Start Lecture #19

10.6 Designing a Class for Stacks

We already did stacks. There is very little substantive difference between our ShortStack and Liang's StackOfIntegers.

  1. Liang's push() never overflows. Instead, it doubles the stack size. These are the same semantics as the Stack class supplied in the Java library. In 102 we will do a slightly fancier version of this.
  2. A boolean method empty() is supplied; again as in the library. Many would use the name isEmpty() instead.
  3. An integer peek() method returns the top of stack without removing it from the stack (also in the library).

10.7 Processing Primitive Data Type Values as Objects

For performance reasons, the Java primitive types (int, char, etc) are not objects. Reference semantics requires an extra level of indirection.

10.7.A Wrapper Classes

Since the full power of object orientation requires objects, Java defines, for each primitive type, a corresponding, so called, wrapper class with a very similar name (but capitalized of course since it is a class). For example, Character is the wrapper class for char. Also present are Boolean, Byte, Short, Integer, Long, Float, and Double.

Do remember that the wrapper classes provide objects, and thus have reference semantics.

It is easy to obtain the Character corresponding to a given char: The Character class provides a constructor for just this purpose. Thus, new Character('a') produces the Character object corresponding to the char 'a'. This Character object contains one field, namely a char containing 'a'.

There are corresponding constructors for the other wrapper classes.

  public class Test {
    public static void main(String[] args) {
      Integer i = new Integer(1);
      Integer j = new Integer(2);
      Integer iPlusJ = new Integer(0);
      System.out.printf("Before i=%d, j=%d and iPlusJ=%d\n",
                        i, j, iPlusJ);
      iPlusJ = i + j;
      System.out.printf("After  i=%d, j=%d and iPlusJ=%d\n",
                        i, j, iPlusJ);
    }
  }
   
  javac Test.java  && java Test
  Before i=1, j=2 and iPlusJ=0
  After  i=1, j=2 and iPlusJ=3

All the wrapper classes are immutable; you cannot alter a constructed object. This is not a severe restriction seem since a variables can be changed to point to different objects.

The code on the right is illustrative.

The expression new Integer(0) produces an immutable object that contains the int 0. This object can never contain another value. The variable iPlusJ initially contains a reference to the object just constructed. The addition produces an new object containing the int 5, and the assignment statement places a reference to that object in the variable iPlusJ as we can see from the output produced.

10.7.B The Numeric Wrapper Classes

The six numeric wrapper classes, Byte, Short, Integer, Long, Float, and Double, are all similar. Each contains six instance methods byteValue(), shortValue(), intValue(), longValue(), floatValue(), and doubleValue() that return the field value converted to the corresponding primitive type.

Each also contains two constructors, one with parameter the corresponding primitive type (e.g., a byte parameter for the Byte constructor), and one with parameter a String so for example you can write either new Double(12.3) or new Double("12.3").

Like many other classes, each numeric wrapper class contains a static toString() method that converts the internal value to a string.

There are many other methods as well; see the online Java library documentation for more information.

10.7.C The Non-numeric Character and Boolean Wrapper Classes

The Character Class

   
  boolean isDigit(char c)
  boolean isLetter(char c)
  boolean isLetterOrDigit(char c)
  boolean isLowerCase(char c)
  boolean isUpperCase(char c)
   
  char toLowerCase(char c)
  char toUpperCase(char c)

Perhaps the part of the Character class most useful to us is the collection of static methods that operate on char's (not Character's).

On the right we see seven of these class methods. As an example to test if the char c is a digit, you would write

  if (Character.isDigit(c))

Note the consistent naming: the prefix is is used for a test, and the prefix to is used for a conversions.

Homework:

  1. (Checking SSN) Write a program that prompts the user to enter a social security number in the format
    DDD-DD-DDDD, where D is a digit. The program prints "Valid SSN" for a valid social security number and "Invalid SSN" for an invalid social security number.
  2. (Occurrence of each digit in a string) Write a method that counts the occurrences of each digit in a string using the following header     public static int[] count(String s)
    The method counts how many times each digit appears in the string. The return value is an array of 10 ints, each of which holds the count for a digit. For example, after executing int[] counts = count("21323AB0");
    counts[0] is 1, counts[1] is 1, counts[2] is 2, counts[3] is 2, and the other six are 0.

The Boolean Class

This class supplies a few methods, but I am not sure we will use any of them.

10.8 Automatic Conversion Between Primitive Types and Wrapper Class Types

The previous section illustrated both an advantage and slight annoyance with the wrapper classes Float, Long, etc. when compared to the corresponding primitive data types (float, long, etc).

The advantage is that, since the wrappers are classes, they can make use of the object oriented features (many of which we have not yet seen).

Short[] s = {new short[5], new short[7], new short[-3]};
 
short[] s = {5, 7, -3};
 
Short[] s = {5, 7, -3};

The minor annoyance is the relative wordiness of the first line on the right when compared to the second line. In most cases the annoyance can be avoided because Java will automatically convert between the primitive type and the corresponding wrapper class as shown in the third line.

Conversion to the wrapper class is called boxing and the reverse conversion is called unboxing.

Assessment of Wrappers

The wrapper classes do work but it would be nicer if we didn't have to deal with them. The reason they are there is that, due to efficiency considerations, the primitive types are not classes and hence cannot make use of the properties of objects. With the addition of autoboxing and autounboxing in newer versions of Java, the wrapper classes are not as cumbersome to use.

10.9 The BigInteger and BigDecimal classes

BigInteger

A BigInteger can be arbitrarily large. This is accomplished increasing the amount of memory devoted to a BigInteger as needed when its absolute value increases.

  public static void main (String[] arg) {
    BigInteger factorial50 = BigInteger.ONE;
    for (int i=2; i<=50; i++)
      factorial50 = factorial50.multiply(new BigInteger(i+""));
    System.out.println(factorial50);
  }

The program on the right could not be written using longs or Longs since the result (50!) is too big.

It is clearly awkward to write, but it does work and gives the correct result for 50!

Since I am sure you want to know the answer and don't want to wait until you get back to your textbook to look it up, I placed it here, together with a bonus.

10.10 The String Class

In Java a String is an object. Thus, like a ShortStack, a String has reference semantics.

In some languages a string is an array of characters. Although in Java an array of char's is similar to a String (e.g., both have reference semantics), they are not the same (e.g., you do not use [] to extract a char from a String).

BigDecimal

In a similar a BigDecimal can be used to evaluate a decimal with an unbounded precision.

Naturally, 1/3 can not be represented with any number of digits and an attempt to perform that calculation with BigDecimals will not terminate and will eventually throw an ArithmeticException.

For such situations java supplies an overloaded divide method in which you specify a maximum number amount of precision, thereby guaranteeing termination and preventing the above exception.

10.10.1 Constructing a String

As shown on the right, String's can be created several ways.

System.out.println("A string");
 
 
String s0;
 
 
String s1 = new String();
 
 
String s2 = new String("A string");
if (s2 != "A string")
  System.out.println("Outrageous");

char[] ca = {'c','h','a','r','s'};
String s3 = new String(ca);
  1. The first example shows a string literal. This is an object but there is no variable containing it (really, we should say referring to it).
  2. The next example declares a string variable but creates no string (similar to int[] a;). This variable cannot be used until it is assigned a value.
  3. Next we use the String constructor with no parameters. This produces (a reference to) the empty string, which is assigned to s1. Unlike s0, s1 is ready to be used.
  4. There is another String constructor, which has a String parameter. This constructor produces a new object with the same contents as the parameter. That is, a copy is made of the object, which can give surprising results (see 10.2.2, below).
  5. There is a third constructor that has a character array as parameter and produces a string with those characters.

10.10.2 Immutable Strings and Interned Strings

String objects are immutable, they cannot be changed. However, a string variable is mutable and can reference different string objects at different times.

String str1 = "joe";
String str2 = "linda";
str1 = "linda";

On the right we have two String objects: "joe" and "linda", and two String variables: str1 and str2. The objects cannot change but we have changed the str1 variable.

String Literals are Interned

Java creates only one copy of each string literal, even if you write it several times. Thus after the code above is executed, there is only one object "linda". The technical term is that the literal is interned.

When are Strings Equal (==)?

if (str2 == str1)  // Yes
  System.out.println("Of course.");

String str3 = new String("linda");
if (str3 != str1)  // Yes !!
  System.out.println("Outrageous!");
if (str3 != "linda")  // Yes !!
  System.out.println("Outrageous!");

String str4 = new String(str1);
if (str1 != str4)  // Yes !!
  System.out.println("Outrageous!");

javac Test.java  &&  java Test
Of course
Outrageous!
Outrageous!
Outrageous!

After the three statements above, both str1 and str2 refer to this one literal. That is, str1 and str2 contain the same reference and, as indicated to the right they of course compare equal (==).

However, when you create a string using the one-argument constructor as done on the right, a copy is made, that is you get a NEW string. Since str3 refers to this copy it is NOT equal (!=) to either str1, str2 or "linda", which seems outrageous!

Equally outrageous is the situation with str4

These last two paragraph seem very bad. We have three String variables str1, str3, and str4, each of which would print the same string linda, but they are not equal. Fortunately, there is more to this chapter.

10.10.A String Comparisons

The problem we just had was that we were comparing the references and not the values they referred to. To do the latter we need to use a method in the String class that we discussed earlier in 4.4.7.

boolean equals (Object anObject)
 
String s1 = "joe";
String s2 = new String(s1);
if ("joe".equals(s1)) // YES
  System.out.println("Of course");
if ("joe".equals(s2)) // YES
  System.out.println("Of course");
if (s1.equals(s2)) // YES
  System.out.println("Of course");
 
Of course
Of course
Of course

On the right we see the equals() method. Technically, it has an Object as parameter, but for now pretend that the only permitted Object is a String.

Something looks wrong! How come equals has only one parameter. Surely, we want to see if two strings are equal. The answer is that equals() is an instance method and thus is attached to a string object, which it then compares to its parameter.

We see examples of the usage on the right. Note that, in these examples both if(s1 == s2) and if("joe" == s2) would be NO.

There are other string comparison methods defined, e.g., one that ignores case and one (compareTo() that distinguishes less than from greater than (see section 4.4.7).

10.10.3 (Converting,) Replacing, and Splitting Strings

 
  String toLowerCase()
  String toUpperCase()
  String trim()
  String replace(char old, char new)
  String replaceFirst(String old, String new)
  String replaceAll(String old, String new)
  String[] split(String delim)
 
  String[] ans = "ab cd e".split(" ");
 
  ans[0]=="ab"  ans[1]=="cd"  ans[2]=="e"

The instance methods on the right are well described by their names except perhaps for trim() and split.

trim() removes leading and trailing blanks.

split() is quite nice, splitting the original string at the specified delimiter returning the pieces as an array.

For example, executing the statement shown in the middle right, declares ans to be an array of strings having three elements. These elements are shown on the bottom right.

10.10.4 Matching, Replacing and Splitting by Patterns.

Many of the string arguments in the preceding section are interpreted as regular expressions, which can be quite useful. For example the regular expression *\.java would match any string that ended in .java.

In addition to the methods in 10.10.3, we note matches(), which is like equals() except that its string argument is interpreted as a regular expression.

10.10.B Finding a Character or a Substring in a String

  int indexOf(char c)
  int indexOf(String s)

The two methods on the right find the first occurrence of the character or string in the object. They return -1 if the character or string does not occur.

There are variants that look for the first occurrence after a specified position, the last occurrence, or the last occurrence before a specified index. They all return -1 if the search is unsuccessful.

10.10.5 Converting between Srrings and (Character) Arrays

We have already seen the String(char[] charArray) constructor. The inverse operation is provided by the toCharArray() method.

  char[] ca = "Joseph".toCharArray();
  String s1 = new String(ca);
 
  String s2 = new String("Joseph".toCharArray());

For example, the first code snippet initializes s1 to Joseph in a complicated way, using the character array ca as an intermediary.
The second (one-line, no intermediary) snippet, is perhaps even more complicated.

10.10.6 Converting Characters and Numeric Values to Strings

So far we have see constructors and instance methods. No we will see two class methods, one of which is heavily overloaded.

The class method String.valueOf() converts many data types into strings. Note again that this is a class (i.e., static) method so is associated with the class String and not with any specific string. It is heavily overloaded; there are versions with a char argument, a char[] argument, a double argument, an int argument, a boolean argument, and others as well.

10.10.7 Formatting Strings

The other class method is String.format(). It takes the same arguments as System.out.printf() but, instead of printing the result, it returns it as a String.

String s = String.format("6.2f",3.78);

For example, the statement on the right sets s equal to "  3.78".

10.11 The StringBuilder and StringBuffer Classes

Java has 3 classes whose objects are strings, namely String, StringBuilder, and StringBuffer.

  1. String is the simplest, most efficient, and most limited of the three classes. The limitation is that a String object cannot be changed after it has been created.
    Do not forget, however, that a String variable can change during execution, first referencing one String object and then referencing another
  2. StringBuilder is more complicated: The resulting objects can be changed after construction, as we shall see.
  3. StringBuffer is yet more complicated as it supports multi-tasking, a very important property, but one we shall not discuss. For that reason we will not mention StringBuffer again.

10.11.1 Modifying Strings in the StringBuilder

  class Test {
    public static void main (String[] Args) {
      StringBuilder sB = new StringBuilder("Hello");
      String s = new String ("Hello");
      System.out.printf("s is \"%s\" and sB is \"%s\"\n", s, sB);
      System.out.printf("The lengths of s and sB are %d and %d\n",
                s.length(), sB.length());
      System.out.printf("The capacity of sB is %d\n", sB.capacity());
      s = s.concat(", world.");
      sB.append(", world.");
      System.out.printf("s is \"%s\" and sB is \"%s\"\n", s, sB);
    }
  }
  s is "Hello" and sB is "Hello"
  The lengths of s and sB are 5 and 5
  The capacity of sB is 21
  s is "Hello, world." and sB is "Hello, world."

Superficially a String s and a StringBuilder sB appear to act the same. Indeed, a quick glance at the code on the right suggests that StringBuilder adds nothing.

In this case, however, looks can be deceiving. Specifically, s.concat() and sB.append() are really quite different because the String referenced by s is immutable; whereas, the StringBuilder referenced by sB is not.

The expression sB.append(", world") actually appends the argument onto the object referenced by sB. It does not copy the original contents of that object.

In contrast s.concat(", world") does not, indeed cannot change the string referenced by s. What happens is that

  1. this string is copied
  2. the argument is appended to the copy
  3. a reference is returned to the copy

When we assign the resulting reference to s, s now refers to the copy and, the original is inaccessible (assuming no other variable contains a reference to the original).

There are other StringBuilder instance methods that permit insertions and modifications in the middle of the object as well as deletion of parts of the object. One could write String methods to do the same, but they would be a complicated and would be slower for large strings since they would involve copying.

There are other methods as well.

Why Does this Matter?

For our programs it hardly matters at all. The real advantage of StringBuilder is that these manipulations are done on the original, with no copy being made. For strings of length a few dozen, making copies is no big deal (unless done very many times). However, for much larger strings, the copying can become expensive.

10.11.2 The toString, capacity, length, setLength, and charAt Methods

All of these are instance methods. As expected sb.toString() returns the String equivalent of the StringBuilder sb, sb.length() returns the length, and sb.charAt() returns the character at the position specified by the argument.

The capacity() instance method is less obvious. A Java StringBuilder object is generally bigger than its current length (this larger size is called the capacity). The capacity() method returns the current capacity. That way it is easy for the system to append characters. Except for efficiency considerations, we can ignore capacity since the JVM will extend the StringBuilder whenever needed.

You can also reduce the length of a StringBuilder (eliminating characters at the end) or increase its length (padding with null characters) by using the setLength() method.

10.11.3 Case Study: Ignoring Nonalphanumeric Characters When Checking Palindromes

The book's solution is basically an exercise in using a few of the methods. The basic steps are

  1. Read in a String s.
  2. Create an empty StringBuilder sb
  3. Using Character.isLetterOrDigit(s.charAt), append only the letters and digits to sb.
  4. Convert this back to a String s1.
  5. Convert s1 to a StringBuilder sb1
  6. Reverse sb1 and convert it back to a String s2.
  7. The answer is s2.equals(s1)

The reason for converting back to String's is that (surprisingly?) I don't think StringBuilder has an equals() or compareTo() method.

I did this without a StringBuilder, but it is less efficient since Strings are immutable so my solution involves more copying

Homework: (Sorting characters in a string) Write a method that returns a sorted string using the following header.

      public static String sort(String s)

For example, sort("acb") returns "abc"

Start Lecture #20

Chapter 11 Inheritance and Polymorphism

11.1 Introduction

As mentioned previously the three main principals of object oriented programming are abstraction/encapsulation, inheritance, and polymorphism. We studied abstraction/encapsulation in the previous chapter; now we cover the remaining two principals.

The idea of inheritance, which is fundamental in object-oriented programming, is that sometimes classes B and C are refinements of class A (that is, each has all the fields and methods of A plus some more) and it is silly to have to reproduce in B and C all of A. Actually it is worse than silly, it is a bad idea since it then adds the requirement of keeping the all the implementations of A consistent. Instead, we make B and C are subclasses of A and then all the methods and fields of A are inherited by both B and C.

geo-objs-1

For example, we could have a GeometricObject class with a field giving the color in which to draw the object. We could then define three subclasses, Point, Quadrilateral and Triangle, each of which would automatically inherit the color field from GeometricObject. These subclasses can have additional fields not contained in their parent. For example, the Point class has x,y coordinates as fields.

The three subclasses could be independent of each other, except for the fields they each inherit from their common parent. That is, they do not inherit from each other. However, in this case, Triangles and Quadrilaterals each aggregate Points (they have a has-a relationship): The Triangle class has three Points as fields and the Quadrilateral class has four. Finally, Triangle would have an area() method using Heron's formula from the previous chapter; whereas Quadrilateral needs a more complicated formula (especially if we allow non-convex figures).

It is possible (indeed common) to have subclasses of subclasses. For example, we have a Rectangle subclass of Quadrilateral. Rectangle adds height and width fields and overrides Quadrilateral's area() method with a much simpler formula.

An important point to notice is that a triangle is a geometric object, a quadrilateral is a geometric object, a point is a geometric object and a rectangle is a quadrilateral. We often find this is-a relation between subclass and superclass (just as the composition/aggregation relation between classes ofter involves a has-a relation between the objects).

11.2 Superclasses and Subclasses

The terminology for the situation in the previous section is that GeometricObject is called a superclass, a parent class, or a base class. Triangle, Quadrilateral, and Point are each called a subclass, a child class, an extended class, or a derived class of GeometricObject.

Similarly Rectangle is a subclass of Quadrilateral.

Consider the example on the right.

public class GeometricObject {
  String color;
  GeometricObject(String color) {
    this.color = color;
  }
  GeometricObject() { GeometricObject("black"); }
}
 
public class Point extends GeometricObject {
  double x;
  double y;
  Point (double x; double y) {
    this.x = x;    // points are black
    this.y = y;
  }
}
 
public class Quadrilateral
     extends GeometricObject {
  private Point p1, p2, p3, p4;
  // constructors
  double area() {
    // complicated formula for area
  }
  // more
}
 
public class Rectangle extends Quadrilateral {
  private double width, height;
  // constructors
  double area() {
    return width * height;
  }
  // more
}
  1. We first define the GeometricObject class. This very general class would include quadrilaterals, circles, triangles, etc. There is not much data that is common to all these kinds of objects so the GeometricObject class has very few data fields. We define only the color, which might be used in drawing the object. As written the color can be modified by any client, which is not a good idea and is improved below.
  2. We then define a Point class, which extends GeometricObject and is used in Quadrilateral. I assert that every point is black, but it is not yet clear how this is done.
  3. Next we have the definition of the Quadrilateral class, which is a subclass of GeometricObject. We shall see in section 11.14 that the Point's p1,...,p4 should be protected rather than private so that the subclass Rectangle has access to these fields.
  4. Note that Quadrilateral is not declared to be a subclass of Point. Although a quadrilateral has a point, it is not true that every quadrilateral IS A point. The is-a relationship is normally needed for a subclass to be appropriate. A quadrilateral is a geometric object.
  5. Finally, we have the class Rectangle. Note that Rectangle redefines the area() method. This action is referred to as overriding as opposed to overloading, which we have seen before. The distinction between these two possibilities is discussed in section 11.5.

A Terminology Comment

Note that a Rectangle object contains more fields than does a Quadrilateral object, which in turn contains more fields than a GeometricObject object. So each Rectangle object is bigger than a Quadrilateral object. Indeed the fields of the latter are a subset of the fields of the former. So the name subclass seems backwards! Liang points this out at the bottom of page 415.

However, I do NOT believe the naming is backwards!

A subclass is called a subclass because each object in the subclass is also a member of the superclass. Thus the set of objects in the subclass is a subset of the set of objects in the superclass.

public, private, and protected

We know that a public item is visible everywhere and a private one is visible only in the class in which it is defined.

A child class is not special in this regard. It sees the public parts of its parent, but is blind to the private parts. We will soon learn about protected visibility which extends visibility to children but not to unrelated classes.

When to Use Subclasses (is-a Relations)

As mentioned previously subclasses are used to model is-a relationships. However, not all is-a relationships should be modeled with a subclass. Do not use a subclass if the would be parent has fields not appropriate for the child. As Liang mentions a square is a rectangle, but a Square class does not need fields representing height and width so should not be a subclass of Rectangle.

No Multiple Inheritance

Some languages, notably C++, permit a child to inherit from multiple parents; however Java does not.

Area of a Quadrilateral

quadrilateral

We mentioned above that there is a complicated formula for the area of a quadrilateral. Just for fun, not part of the course, I worked it out.

Assume the 4 points p1, p2, p3, and p4 are given in an order so that the resulting edges do not cross each other. I shall always assume the quadrilateral is convex as shown in the diagram on the right. Draw one of the diagonals, say connecting p1 and p3.

It is easy to get the lengths of each side as the square root of delta-x squared + delta-y squared. So in the diagram we know all the sij.

Now the quadrilateral is composed of two triangles and we know the side lengths for each triangle. There is a cute formula for the area of any triangle with side lengths a, b, and c. Let s be the semiperimeter s=(a+b+c)/2, then the area of the triangle is the square root of s(s-a)(s-b)(s-c).

This analysis enables us to compute the complicated formula for the quadrilateral area mention above.

11.3 Using the super Keyword

Recall that this refers to the current object. In an analogous way super refers to the superclass of the current class. It is used to

11.3.1 Calling Superclass Constructors

When we create a new object, a constructor is called. Recall that class Point is a child of class GeometricObject. Suppose we construct a point object pt1. The Point constructor is called and produces/initializes the data fields x, y in pt1.

But the Point object pt1 contains, in addition to its own data, the Color data field in GeometricObject. How is this created/initialized?

The answer is that constructors in the subclass invokes a constructor in the superclass. In our case, constructors in Point invoke a constructor in GeometricObject.

How is this done?

A wrong way would be to have the Point constructor invoke new GeometricObject(). That would create a new GeometricObject object rather than creating/initializing a part of the current Point object.

Indeed it is an error to mention the superclass constructor inside a subclass; instead super() is used.

public class Rectangle extends Quadrilaterial {
  private double width, height;
  public Rectangle (Point p1, Point p2,
                    Point p3, Point p4) {
    super(p1, p2, p3, p4);
    height = p1.distTo(p2); // a convention
    width = p2.distTo(p3);
  }
}
 
public class Quadrilateral extends GeometricObject {
  Point p1, p2, p3, p4;
  public Quadrilateral (Point p1, Point p2,
                        Point p3, Point P4) {
    super("blue"); // quads are blue
    this.p1 = p1;
    this.p2 = p2;
    this.p3 = p3;
    this.p4 = p4;
  }
}

On the right we see a part of an improved Rectangle class and below it part of the base class Quadrilateral. Although not explicitly included in the class, a derived class inherits the fields from its base. Thus a Rectangle object has 4 Point fields that must be created/initialized by the constructor (as well as the double fields width and height.

Were there no inheritance involved, the Rectangle constructor would have 4 assignment statements using this to define/initialize the four points. However, the points are not declared in Rectangle so cannot be referenced by this. Instead we invoke super() to have a constructor in the base class Quadrilateral do the necessary work.

The idea is that the constructors in a derived class deal with the fields introduced in the derived class; dealing with the fields inherited from the base class is left to the base class constructors, furthering abstraction/encapsulation.

When super() is used in a constructor, it must be the first statement. The idea is that you must first construct the base class object before you add the refinements supplied by the subclass.

You might wonder why these same considerations don't apply to Point as they did to Rectangle. After all, Point is a derived class (its parent is GeometricObject).

The answer is that they do apply; a default super() has been supplied by Java, as will be explain in the next section.

11.3.2 Constructor Chaining

As we have seen a few lectures ago, one constructor can invoke another (overloaded) constructor in the same class by employing this() as it first statement We have just seen that a constructor in a derived class can utilize super() as its first statement to invoke a constructor in the base class. If a constructor in a derived class does neither of these actions, Java itself supplies a no-arg super() as the first statement of the constructor.

The upshot of the above paragraph is that, if A is derived from B, which in turn is derived from C, any A constructor will, as its first action, invoke a B constructor, which, as its first action, will invoke an C constructor.

Thus the real actions will be performed in the order C, B, A, i.e., from base to derived. This naturally applies as well when there are more than 3 classes.

For example, consider the class tree on the right, which represents the parent-child relations in our geometry example.

geometry-tree

The process of applying constructors from base to derived is called constructor chaining.

11.3.3 Calling Superclass Methods

The keyword super can be used to reference superclass methods as well as superclass constructors. Normally the superclass method would be available in the subclass without any decoration. However, if the superclass and subclass both have a method with the same name, prepending super. references the method in the superclass whereas the naked name references the method in the subclass. We see an example in the next section

You might think that if a method in Rectangle wanted to invoke a method called f() in GeometricObject it could say super.super.f(), but no, just one super. is permitted.

11.4 Overriding Methods

 
public class Parent {
  int f() { return 1; }
  int g() { return 10; }
}
 
public class Child extends Parent {
  int f() { return 100; }
  int h() { return f()+2*super.f()+g(); }
}
 
public  class Test {
  public static void main(String[] args) {
    Parent p = new Parent;
    Child c  = new Child;
    System.out.println(c.h());
    System.out.println(c.f()+c.g());
  }
}
 
 
112
110

Consider the example on the right. The parent class defines two methods f() and g(). The child class defines two methods f() and h().

For a parent object nothing about the child class is known. So f() means the f() in the parent class, the same for g(), and there is no h().

For a child object the situation is more interesting since everything in the parent that is not private is known in the child. So g() means the g() in the parent and h() means the h() in the child, but what about f()?

The rule is that a naked f() means the f() in the child. However, the f() in the parent can be obtained as super.f(). That is why the first line printed, c.h(), is 100+2*1+10.

What about usage in the class Test, a client of the child class. In the client, super cannot be used so c.f() in the example invokes the f() in the child. Since g() occurs only in the parent c.g() refers to that g(), which explains why the second line printed is 100+10.

What about static Methods?

The example above used instance methods in both the parent and child. If a method f() in the child overrides f() in the parent, you must have either both static or neither static.

If they are both static then

11.5 Overriding vs. Overloading

It is important to understand the distinction between overriding, which we just learned, and overloading, which have seen previously.

An Overriding Example

public class Base {
  public void f(double x) {
    System.out.printf("Base says x=%f\n", x);
  }
}
public class Derived extends Base {
  public void f(double x) {
    System.out.printf("Derived says x=%f\n", x);
  }
}
public class Test {
  public static void main(String[] Args) {
    Derived d = new Derived();
    d.f(5.0);
    d.f(5);
  }
}
Derived says x=5.000000
Derived says x=5.000000

The first frame on the right demonstrates overriding. Both the base class and the derived class define an instance method f(). The key point, which makes this an overriding example is that both f()'s have the same signature (i.e, the same number and types of parameters) and the same return type.

In such a case, the method in the derived class overrides the method in the base class, which means that, for objects of the derived class, only the method defined in the derived class is visible (the method in the base class is hidden from the objects in the derived class).

In the example, both d.f(5.0) and d.f(5) invoke the f() in the child class. In the second case the 5 is coerced from int to double.

An Overloaded Example

 
public class Derived extends Base {
  public void f(int x) {
    System.out.printf("Derived says x=%d\n", x);
  }
}
Base says x=5.000000
Derived says x=5

The second example is almost the same, but with a key difference. Both Base and Test are unchanged; however the f() in Derived is changed so that it's parameter is of type int (and the printf() now uses %d not %f).

This tiny change has a large effect. The f() in the derived class no longer has the same signature as the f() defined in the base. Thus, both are available (i.e., f() is overloaded).

For this reason d.f(5) invokes f() in the derived class;
whereas, d.f(5.0) invokes f() in the base.

11.5.1 Confirming Overriding

If you place @Override just before a method definition, the compiler will check that this method does indeed override a method in a parent class.

11.A Quadrilateral and Friends Improved

geo-objs-1

Let's look at a larger example. I have filled in some of the details for the geometric objects sketched above.

Recall the hierarchy of classes we have defined. It is illustrated on the right.

Geometric Object

 
public class GeometricObject {
  protected String color;
  public GeometricObject(String color) {
    this.color = color;
  }
  public GeometricObject() { this("black"); }
}

The Geometric Object sits at the top of the hierarchy. It is a simple class with only a single data field, color, which has protected visibility. This visibility (officially presented in section 11.14) means that subclasses may modify color. The Rectangle class uses this ability to construct red rectangles..

Point

public class Point extends GeometricObject {
  private double x, y;
  public Point(double x, double y) {
    this.x = x;   // points are black
    this.y = y;
  }
  public double getX() { return x; }
  public double getY() { return y; }
  public void setX(double y) { this.x = x; }
  public void setY(double y) { this.y = y; }
  public double distTo (Point p) {
    return Math.sqrt(Math.pow(this.x-p.x,2) +
                     Math.pow(this.y-p.y,2));
  }
}

Next we have Point. As expected, a point is defined by two real numbers, the x and y coordinates.

Note that the constructor implicitly invokes the no-arg constructor of GeometricObject() and hence points are black.

After the standard getters and setters, we have the instance method distTo(), which is used by other classes below and eventually be used for the correct area of triangles and quadrilaterals.

Quadrilateral

 
public class Quadrilateral extends GeometricObject {
  protected Point p1, p2, p3, p4;
  public Quadrilateral (Point p1,Point p2,Point p3,Point P4) {
    super("blue");   // ordinary quads are blue
    this.p1 = p1;    
    this.p2 = p2;    // should check that
    this.p3 = p3;    // these points form
    this.p4 = p4;    // a *convex* figure
  }
  public double area() {
    return 123.4;    // A stub, need the complicated formula
  }
}

For us a quadrilateral is simply 4 points.

Since we want blue quads, we cannot use the no-arg super(), but must supply our own color.

We definitely should check the points for convexity.

This version of the code has a stub area() method. The use of stubs during program development is fairly common.

Rectangle

public class Rectangle extends Quadrilateral {
  private double width, height;
  public Rectangle(Point p1, Point p2, Point p3, Point p4) {
    super(p1, p2, p3, p4);
    color = "red";
    height = p1.distTo(p2);  // convention
    width = p2.distTo(p3);
    // should check really a rectangle (how?)
  }
 
  public Rectangle(Point p1, Point p3) { // Parallel to axes
    super(p1, new Point(p1.getX(), p3.getY()), 
          p3, new Point(p3.getX(), p1.getY()));

    color = "red";
    width  = Math.abs(p1.getX() - p3.getX());
    height = Math.abs(p1.getY() - p3.getY());
    // Nothing to check; the angles are definitely 90 deg,
    // which is why this constructor does not invoke the first
  }
 
  public double getWidth() { return width; }
  public double getHeight() { return height; }
  public double area() {
    return width * height;
  }
}

A rectangle is a quadrilateral with each angle 90 degrees. Since the vertices of the rectangle are the vertices of the underlying quad, we need to pass these via super().

The second constructor, can be used in the common case where the sides of the rectangle are parallel to the coordinate axes. In this case only a pair of points is needed; they form opposite vertices of the rectangle; the other two vertices are calculated from these two, which guarantees that do have a rectangle.

We want red rectangles. Since there is no way to invoke the super.super constructor, we set the color explicitly, utilizing its protected visibility.

Rectangles have well defined widths and heights, which are calculated by the constructor and made available via accessors methods.

Triangle

public class Triangle extends GeometricObject {
  protected Point p1, p2, p3;
  public Triangle (Point p1, Point p2, Point p3) {
    super("green");   // triangles are green
    this.p1 = p1;    
    this.p2 = p2;
    this.p3 = p3;
  }
  public double area() {
    return 12.3;   // A stub, need the complicated formula
  }
}

For us a triangle is simply 3 points.

Since we want green triangles, we cannot use the no-arg super(), but must supply our own color.

This version of the code has a stub area() method. The use of stubs during program development is fairly common.

Testing

public class TestGeo {
  public static void main (String[] args) {
    Point origin = new Point(0.0,0.0);
    Point p1 = new Point(0.0,0.0);
    Point p2 = new Point(1.0,0.0);
    Point p3 = new Point(1.0,1.0);
    Point p4 = new Point(0.0,1.0);
    
    Quadrilateral quad = new Quadrilateral (p1,p2,p3,p4);
    Rectangle rect1 = new Rectangle (p1,p2,p3,p4);
    Rectangle rect2 = new Rectangle (origin, new Point(1.,4.));
    Triangle tri = new Triangle (origin, p2, new Point(1.,2.));

    System.out.printf("quad: area=%f, color=%s\n",
                      quad.area(), quad.color);
    System.out.printf("rect1: width=%f, height=%f, color=%s\n",
                      rect1.getWidth(), rect1.getHeight(), rect1.color);
    System.out.printf("rect2: width=%f, height=%f, area=%s\n",
                      rect2.getWidth(), rect2.getHeight(), rect2.area());
    System.out.printf("tri: area=%f, color=%s\n",
                      tri.area(), tri.color);
  }
}
 
quad: area=123.400000, color=blue
rect1: width=1.000000, height=1.000000, color=red
rect2: width=1.000000, height=4.000000, area=4.0
tri: area=12.300000, color=green

Testing class hierarchies is a slow process. You have to test each class separately and then need to worry about interactions between them.

There are certainly more things to test. For one thing, we did not print out the x,y coordinates of the points in the objects we constructed. This absence is especially bad for rect2, where two of the points have their x,y coordinates computed by the constructor.

One thing our limited testing did show is that we get the wrong area for quadrilaterals and for triangles, which is not surprising since we have only stubs for the corresponding area() methods.

An interesting text would be to compare the areas of quad and rect1 after the stub areas have been replaced by the correct formulas. The figures are congruent, but their areas are computed using different formulas.

Weaknesses

One weakness is naturally the area stubs.

Perhaps the biggest gap is that, if the points of a quadrilateral are given in the wrong order, the quadrilateral's sides will intersect each other. A better program would check that the sides do not intersect. We will ignore this subtlety and always make sure to give the points in the right order and that the resulting figure is convex.

Questions

  1. Where in the class tree should we put a new class Circle?
  2. Where in the class tree should we put a new class Square?
  3. Where in the class tree should we put a new class Ellipse?
  4. Where in the class tree should we put a new class Parallelogram?

Start Lecture #21

11.6 The Object Class and its toString Method

You would think from looking at a class definition beginning

  public class TopLevel {

with no extends clause that this class has no parent. That, however, is wrong.

Any class without an extends clause, whether defined in the Java library or by you and me, actually extends the built in class java.lang.Object.

Hence, any method defined in Object is available to all classes, unless it is overridden.

One interesting instance method defined in Object is toString(), which when applied to an object, produces a string describing the object. The actual description given is the class name, followed by @ followed by the memory address of the object. The class name is certainly useful, the memory address at least enables us to distinguish one object from another.

One advantage of having a toString() method defined for all objects is that other methods can count on its existence. For example the various print methods (e.g., printf(), println(), etc) use this to coerce objects to strings. Thus if obj is any object at all,
    printf("The object is %s\n", obj);
is guaranteed to work.

I use the automatic application of toString() in the next section and in the 2nd version of the geometry classes below.

11.7 Polymorphism

We have already seen encapsulation/abstraction and inheritance, which are major constituents of object oriented programming. We now turn our attention to polymorphism (and dynamic binding/dispatch), the third major constituent).

Say we are clients (i.e., users) of the geometry classes and want to print the color. The author doesn't want to add this print to the geometry classes themselves since it is useful only for us and not to all geometry users.

  public static void printColor(GeometricObject geoObj) {
    System.out.printf("The color of %s is %s\n",
                   geoObj, geoObj.getColor());
  }

The author does modify GeometricObject to add a get method for the color and then we write ourselves the simple method on the right. Now if we call the method with any GeometricObject all is well.

But we actually don't have variables of type GeometricObject; instead we have variables of various subtypes such as Rectangle or Point. Thus the natural call PrintColor(rect1) would be a type error, we are passing a Rectangle as the argument and the method has a GeometricObject as its parameter.

But no it is not an error!

A variable of a supertype (the type defined by a superclass) can always refer to an object of any of its subtypes. This concept of polymorphism can also be stated in terms of objects as: An object of a subclass can be used anywhere that an object of its superclass could be used.

In section 11.B we see an enhanced version of the geometry example that includes printColor() and a few polymorphic calls.

11.8 Dynamic Binding

How should we implement printArea() in our geometry classes?

It would be a one-line method in the Rectangle class, namely

    void printArea() { System.out.printf("The area of %s is %f\n", this, this.area()); }

(Recall that the Rectangle class already has the method area() and toString(), inherited from Object, is invoked automatically by the %s in printf().

But the exact same (character for character) one-line method printArea() would be perfect in the class Quadrilateral since Quadrilateial has an area() method and also inherits toString() from Object.

Similarly, the exact same method would work for Triangle.

Once we put a trivial area() method in Point (it always returns 0), the exact same printArea() method would work there as well.

So is that the solution, cut-and-paste the identical method in all these classes? It would work, but it sure seems ugly. More significantly, it is a maintenance burden to remember to update all the versions should a change be desired in the future.

Try 1

Since GeometricObject is at the top of our geometry class hierarchy, why not put printArea() there? Since all the geometric classes extend GeometricObject, this has the effect of placing printArea() in all of them.

Hence when, for example, we write rect1.printArea(), we will invoke the printArea() written in GeometricObject. Since the object in question is rect1, when printArea() issues this.area(), the area() in Rectangle will be called as desired.

Success!
The code is in section 11.B.

You might have worried that, since printArea() is an instance method in GeometricObject it expects its this object to be a GeometricObject and not a Rectangle. But this fear is ungrounded, thanks to polymorphism!

You also might worry that this.area() would refer to the area() in GeometricObject and not the area() in Rectangle. Read on.

Try 2

Let's say that we don't want to add printArea() to any of the geometry classes since it is somewhat special purpose. Our clients will probably have different ways of printing. So we write the following one-line method in the TestGeo class.

  static void myPrintArea(GeometricObject geoObj) {
    System.out.printf("My area of %s is %f\n", geoObj, geoObj.area());
  }

Then, in the main() method, we write myPrintArea(rect1).

At first glance this looks unlikely to compile since we have a type mismatch. The argument given to myPrintArea() is a Rectangle, but the parameter is a GeometricObject. However, we know that polymorphism will save us. The parameter of type GeometricObject can legally point to an object of type Rectangle.

At second glance, it looks like it will work, but poorly. When compiling myPrintArea(), Java will see geoObj.area() where geoObj is of type GeometricObject and will thus always invoke the area() method in the class GeometricObject no matter what class the actual argument is in (assume for the moment we put a dummy area() in GeometricObject). This is bad, we have different formulas for the area of points, general quadrilaterals, and rectangles.

Failure.

Wrong! It actually works great.

We now have to understand how.

Declared Type vs. Actual Type

As we know well, Java requires that, prior to using a variable, we must declare it to be of a specific type (int, Object, Point, etc).

Previously, we have called the type in the declaration, simply the type of the variable. But now, in the presence of objects and polymorphism, we need to make a finer distinction and refer to the type in the declaration as the declared type of the variable.

When the declared type is a primitive such as int or char, there is very little more to say. The variable will always contain a value of its (declared) type. Recall that a double x=3; first converts the 3 to a double, which is then stored in x. The variable x always contains a value of its (declared) type double.

When the declared type is class, (e.g., String, or Rectangle), the situation is more interesting. First, we remember that a variable of declared type Quadrilateral never contains a Quadrilateral. It often does contain a reference to a Quadrilateral, but never contains the object itself (reference vs. value semantics).

Moreover, a variable of declared type Quadrilateral can, due to polymorphism, at times contain a reference to a Quadrilateral, and at other times a reference to a Rectangle, and at other times a reference to a Triangle.

The type of the object to which a variable refers is called the variable's actual type. Note that the actual type of a variable can change during execution of the program.

How the Second Implementation Works

Recall the situation. We have a method myPrintArea() that has one parameter geoObj, whose declared type is GeometricObject. We call this method in several places with arguments of various geometric types, sometimes the argument is a Rectangle, other times it is a Triangle and other times it is yet another type. The myPrintArea() method contains a call of geoObject.area(). We previously concluded that, since the type of geoObject is GeometricObject, the call would always be to the area() method in GeometricObject.

We are wiser now and can question this conclusion. If myPrintArea() was called with an argument that referenced a Rectangle, then geoObj will indeed have declared type GeometricObject, but it will have actual type Rectangle.

Thus the question becomes, Does the method invocation geoObj.area() select the area() method to call based on the declared type of geoObj or on its actual type?. Another wording of this same question is, does geoObj.area()use static dispatch (declared type) or dynamic dispatch (actual type)?.

The answer in Java is that is uses dynamic dispatch, and hence our second implementation does indeed work. This situation is illustrated in section 11.B.

In C++ static dispatch is used by default but dynamic dispatch can be chosen by declaring the method to be virtual.

11.9 Casting Objects and the instanceof Operator

Recall the situation for converting one primitive type to another. Java performs safe type conversions (called coercions) automatically, but will not perform unsafe conversions, unless told told by an explicit cast.

int    i1=1,  i2=2,  i3=3;
double d1=1., d2=2., d3=3.E50;
d1 = i1;
d1 = (double)i1;
// i2 = d2;      Compile-time error
i2 = (int)d2; // Fine
i3 = (int)d3; // Gives wrong answer

Referring to the code on the right we see illustrations of the various conversion possibilities

Upcasting and Downcasting

geometry-tree

We now want to understand the corresponding actions for objects in the class hierarchy. In this situation the terminology is upcasting and downcasting.

The familiar diagram on the right motivates the names.

Upcasting refers to a conversion from a class lower in the diagram to a class higher in the diagram (really there is the class Object above GeometricObject).

Downcasting refers to a conversion from a class higher in the diagram to one lower in the diagram.

The code below is the rough analogue for objects of the code above for primitive types. Note that the variable p2 after initialization has declared type Parent, but actual type Child. This situation is not present with primitive types since those variables always contain a value of the declared type of the value. In contrast variables of any object type contain a reference to an object whose type can be a subtype of the declared type of the variable.

 
public class Parent {...}
public class Child extends Parent {...}
Parent p1 = new Parent();
Parent p2 = new Child(); // NOT Parent()
Parent p3 = new Parent();
Child  c1 = new Child();
Child  c2 = new Child();
Child  c3 = new Child();
p1 = c1;
p1 = (Parent) c1;
//   c2 = p2;        Compile-time error
c2 = (Child)p2;   // Fine
c3 = (Child)p3;   // Run-time error

Referring to the code we see

The general rules are (compare with primitive types above):

Using the instanceof Operator to Avoid the Run-time Error

We have just seen that downcasting with an explicit cast will compile but might fail at run-time depending on the actual type of the variable at that time.

What should we do to avoid this run-time error?

public class Parent {...}
public class Child extends Parent {...}
Parent p;
Child  c;
// much code involving p

if (p instanceof Child)
  c = (Child) p;

The code on the right gives one technique. The omitted code could be complicated and, depending on various values that are known only at run time, might result in the actual type of p being either Parent or Child.

We wish to do the downcast only if legal, i.e., only if the actual type of p is Child (or a descendant of Child). The instanceof operator is defined for exactly this purpose. It returns true if the object on the left is in the class on the right (or a descendant of that class).

Who Needs All This?

Why would I want to upcast and why would I ever want to try to downcast to something not matching the actual type of the variable.

Consider some sort of container class, i.e., a class each of whose instance is some collection of GeometricObject's. For example consider

Each of these three examples illustrates a container for GeometricObject's. Let's say in some geometry program you have the array geoObjArr into which you have placed various geometric objects, some points, some rectangles, some quadrilaterals, etc.

If you try something like geoObjArr[i].height, you will get a compile-time error since geoObjArr[i] has declared type GeometricObject, which has no height field.

A naked assignment to a variable of declared type Rectangle will not compile, so you need an explicit cast to do the downcasting. But this operation will give a run-time error if the actual type of geoObjArr[i] is not a Rectangle (or a descendant).

Thus you need an if statement with instanceof as shown above.

Start Lecture #22

Remark: Lab 6 assigned.

11.B Quadrilateral and Friends (version 2)

geo-objs-1

This section expands further on our running example of geometric objects, whose (unchanged) class hierarchy is on the right.

Compilable Code

A compilable and less cramped version of this code is here. It contains some features that we have not yet learned.

GeometricObject

public class GeometricObject {
  protected String color;
  GeometricObject(String color) {
    this.color = color;
  }
  GeometricObject() { GeometricObject("black"); }
 
  public String getColor() {
    return color;
  }
  public void setColor (String color) {
    this.color = color;
  }
       
  public void printArea() {
    System.out.printf("The area of %s is %f\n",
                      this, this.area());
  }
  public double area() {
    System.out.printf("Error: Must override area in %s\n",
                      this);
    return 0;
  }
}

The color is protected. This visibility means that (ignoring packages) only GeometricObjects and its subclasses can access the color. However, we do wish to give read-only access to all clients (i.e., to all classes) and thus supply a public getColor().

Supplying a public set method might not be a good idea but is not the same as making color public (see below).

The printArea() method should not be invoked for a plain geometricObject but is define here so that it is available in subclasses where it is applicable.

A general geometricObject does not have a well-defined area. The area() method should be abstract, but we have not yet learned how.

Interface vs Implementation for color

Supplying both get- and set- methods seems the same as declaring color to be public. There is a difference, however. These two methods promise our clients that they can access the color using the name of the color, but in the future we may wish to implement the color differently format (e.g., using RGB triples). As defined here we have that flexibility since we know no other class can assume that color is a string. If we do change the format, we must change the accessor and mutator methods to convert the user's color name to the internal RGB format.

Point

public class Point extends GeometricObject {
  protected double x, y;
  public Point(double x, double y) {
    this.x = x;   // points are black
    this.y = y;
  }
  public double getX() {
    return x;
  }
  public double getY() {
    return y;
  }
  public void setY(double y) {
    this.y = y;
  }
  public void setY(double y) {
    this.y = y;
  }
  public double distTo (Point p) {
    return Math.sqrt(Math.pow(this.x-p.x,2)+
                     Math.pow(this.y-p.y,2));
  }
  public double area() {
    return 0;
  }
}

In this class the fields (the x,y coordinates of the points) are protected so that subclasses, but not clients can access the fields.

As mentioned previously supplying public methods to get and set methods does not prevent the author from changing the implementation (say by using r,θ coordinates instead of x,y).

An area() method has been added. It is standard in geometry to declare a point to have zero area. For motivation think of a point as a circle with 0 radius or if you prefer the limit of a circle as the radius approaches zero.

Remember that a Point has a Color, inherited from GeometricObject. Although you don't see a reference to super() inside Point, Java has supplied a call to the no-arg constructor.

It would be good to add another constructor, one that takes a Point as parameter.

Quadrilateral

public class Quadrilateral extends GeometricObject {
  protected Point p1, p2, p3, p4;
  public Quadrilateral (Point p1, Point p2, Point p3, Point p4) {
    // should check pts form convex quadrillateral in this order
    this.p1 = p1;
    this.p2 = p2;
    this.p3 = p3;
    this.p4 = p4;
  }
  public double area() { // use triangle semiperimeter formula
    double diag  = p1.distTo(p3);
    double s12   = p1.distTo(p2);
    double s23   = p2.distTo(p3);
    double s34   = p3.distTo(p4);
    double s41   = p4.distTo(p1);
    double semi1 = (s12 + s23 + diag) / 2;
    double semi2 = (diag + s34 + s41) / 2;
    return Math.sqrt(semi1*(semi1-s12)*(semi1-s23)*(semi1-diag))+
           Math.sqrt(semi2*(semi2-s34)*(semi2-s41)*(semi2-diag));
  }
}
  1. The fields are protected and should have an accessor method, possibly one that returns an array of four Points.
  2. The promised method to compute the area of a general quadrilateral has been added.
  3. Again, it would be good to have a constructor that accepts a quadrilateral as its parameter.
  4. More difficult would be to have the original constructor check that the points are given in the correct order. For a start you can find the intersection of the line p1-p2 with the line p3-p4. This intersection should not be between p1 and p2. If it is between them, swap the points p1 and p2. That should fix it.

Rectangle

public class Rectangle extends Quadrilateral {
  private double width, height;
  public Rectangle(Point p1, Point p2, Point p3, Point p4) {
    super(p1, p2, p3, p4);
    width = p1.distTo(p2);
    height = p2.distTo(p3);
    // should check that all angles are right angles
  }
  public Rectangle(Point p1, Point p3) { // parallel to axes
    super(p1, new Point(p3.x,p1.y), p3, new Point(p1.x,p3.y));
    width = Math.abs(p1.x-p3.x);
    height = Math.abs(p1.y-p3.y);
    // Nothing to check
  }
  public double getWidth() {
    return width;
  }
  public double getHeight() {
    return height;
  }
  public double area() {
    return width * height;
  }
}
  1. Don't forget that a Rectangle is a Quadrilateral and hence also a GeometricObject. Thus a Rectangle has a number of fields and methods beyond what is shown in its own class.
  2. A rectangle has a width and height. We define the width as going from the first to the second point.
  3. The first constructor, which is given 4 points, should check that the angles are all 90 degrees, for example by calculating the slopes of the sides.
  4. The second constructor, which produces a rectangle with sides parallel to the axes, only needs two points and by construction has all right angles.
  5. Since Rectangle extends Quadrilateral, the former inherits an area() method from the later.
  6. However, the area of a rectangle is much easier and faster to compute as base*height, so we override (not just overload) the general method with a one specialized for rectangles.

Testing

The summary is that there is a great deal to test, much more than is shown. As mentioned in class, testing / correcting / maintaining a serious software project typically requires much more time and effort than designing and programming the system

The code on the right is inadequate for full testing, but does illustrate some of the Java features we just learned.

TestQuad

public class TestQuad {
  public static void main (String[] args) {
    Point origin = new Point(0.0,0.0);
    Point p1 = new Point(1.0,0.0);
    Point p2 = new Point(1.0,1.0);
    Point p3 = new Point(0.0,1.0);
    Point p4 = new Point(5.0,5.0);
    Quadrilateral quad1 = new Quadrilateral
             (origin, p3, new Point(5.,0.), new Point(5.,-8.));
    Rectangle rect1 = new Rectangle (origin,p1,p2,p3);
    Rectangle rect2 = new Rectangle (origin, new Point(1.0,4.0));
    Rhombus rhom1 = new Rhombus(origin,p1,p2,p3);
    p1.printArea();
    printColor(rhom1);  // Polymorphic call (section 11.7)
    printColor(rect1);  // Polymorphic call
    quad1.printArea();  // Inherited method (section try 1)
    rect2.printArea();  // Inherited method
    myPrintArea(rhom1); // Dynamic binding/dispatch (sec try 2)
    myPrintArea(p4);    // Dynamic binding/dispatch
    quad1 = rect1;      // Implicit casting (section 11.9)
    quad1.printArea();  // Dynamic binding/dispatch
  }
  public static void printColor(GeometricObject geoObj) {
    System.out.printf("The color of %s is %s\n",
                      geoObj, geoObj.getColor());
  }
  public static void myPrintArea(GeometricObject geoObj) {
    System.out.printf("My area of %s is %f\n",
                      geoObj, geoObj.area());
  }
}
// Output
The area of Point@4830c221 is 0.000000
The color of Rhombus@2ce83912 is blue
The color of Rectangle@41fae3c6 is blue
The area of Quadrilateral@3e7ffe01 is 22.500000
The area of Rectangle@44fd13b5 is 4.000000
My area of Rhombus@2ce83912 is 1.000000
My area of Point@4318f375 is 0.000000
The area of Rectangle@41fae3c6 is 1.000000
  1. The first non-constructor invoked prints the area of a Point. Naturally the area is 0.
  2. More interesting is the Point@4830c221 that is printed as the %s conversion of the Point itself. The (hexadecimal) number after the @ is the memory address of the point. The only use we can make of the address, is to tell if two references are to the same point.
  3. Printing colors is polymorphic. We pass a Rhombus or Rectangle to a method that expects a GeometricObject. All is well since an object of a subtype can be used anywhere an object of a supertype is needed, a form of upcasting.
  4. One way to print areas is to use printArea() defined in GeometricObject, and inherited by all its subclasses.
  5. When quad1.printArea() invokes printArea(), the internal call this.area() invokes area() in Quadrilateral. Similarly rect2.printArea() calls area() in Rectangle.
  6. Another way to print areas is to use myPrintArea() in the client. Rhomb1 refers to a Rhombus and this is copied to the geoObj parameter, a legal (upcasting) assignment. Due to dynamic dispatch, geoObj.area() invokes area() in Rhombus (not in GeometricObject).
  7. Similarly myPrintArea(p4) eventually invokes area() in Point.
  8. Finally, after quad1 is assigned a Rectangle, quad1.printArea() invokes area() in Rectangle.

11.B.1 Adding a Circle Class

On the board let's develop a Circle class with data fields center and radius.

  1. The normal constructor is given the center point and the radius.
  2. Another constructor just gets the center and gives a default radius of 1.
  3. Another constructor just gets the radius and supplies the center at the origin.
  4. The final constructor gets neither and supplies both defaults.
  5. Circles are pink, not black.
  6. Have an instance method for area.
  7. Have a class method that returns a largest circle created so far.

Homework: 11.1. UML diagram not required. The area formula they references is the same one I used in the Quadrilateral class. The filled data field is in the book's GeometricObject but not in ours. You may ignore it.

Homework: Use cut and paste to extract our geometry classes from the notes. Better is to get the compilable and neater version linked at the beginning of section 11.B. Add your Triangle class from the homework above, and the Circle class we developed to these files and incorporate your tests of Triangle and Circle into our TestQuad (which should be named TestGeom).

11.10 The Object's equals() Method

public boolean equals (Object obj) {
  return (this == obj);
}

String s1= new String("xy");
String s2= new String("xy");
System.out.printf("%b %b\n",
                  s1==s2, s1.equals(s2));

public boolean equals(Object obj) {
  if (obj instanceof Circle)
    return radius == ((Circle)obj).radius;
  return false;
}

In addition to toString(), which we learned earlier, the Object class has an instance method equals(), shown on the right.

Note carefully that obj1.equals(obj2) checks if the variables are ==, which means that both variable refer to the same object. Often you want equals() to return true if the two objects have the same contents. For example the String class overrides equals() so that the middle code on the right prints false true.

If the bottom code is placed in the Circle class then, Circle c1,c2; with equal radii will result in ci.equals(c2) yielding true.

An Illustrative Technical Point: Overriding vs. Overloading

class GeometricObject {
  // Fields and methods omitted
}
class Circle extends GeometricObject {
  double radius;
  public Circle (double radius) {
    this.radius = radius;
  }
  public boolean equals (Circle c) {
    return radius == c.radius;
  }
  // Other fields and methods omitted
}
public class TestOverload {
  public static void main(String[] args) {
    GeometricObject g1 = new Circle(11.0);
    GeometricObject g2 = new Circle(11.0);
    Circle  c1         = new Circle(11.0);
    Circle  c2         = new Circle(11.0);
    System.out.printf("c1.equals(c2)=%b\n", c1.equals(c2));
    System.out.printf("c1.equals(g2)=%b\n", c1.equals(g2));
    System.out.printf("g1.equals(c2)=%b\n", g1.equals(c2));
    System.out.printf("g1.equals(g2)=%b\n", g1.equals(g2));
  }
}
javac TestOverload.java  && java TestOverload
c1.equals(c2)=true
c1.equals(g2)=false
g1.equals(c2)=false
g1.equals(g2)=false


class GeometricObject {
  // Fields and methods omitted
}
class Circle extends GeometricObject {
  double radius;
  public Circle (double radius) {
    this.radius = radius;
  }
  public boolean equals (Object o) {
    if (o instanceof Circle)
      return radius == ((Circle) o).radius;
    return false;
  }
  // Other fields and methods omitted
}
public class TestOverride {
  public static void main(String[] args) {
    GeometricObject g1 = new Circle(11.0);
    GeometricObject g2 = new Circle(11.0);
    Circle  c1         = new Circle(11.0);
    Circle  c2         = new Circle(11.0);
    System.out.printf("c1.equals(c2)=%b\n", c1.equals(c2));
    System.out.printf("c1.equals(g2)=%b\n", c1.equals(g2));
    System.out.printf("g1.equals(c2)=%b\n", g1.equals(c2));
    System.out.printf("g1.equals(g2)=%b\n", g1.equals(g2));
  }
}
javac TestOverride.java  && java TestOverride
c1.equals(c2)=true
c1.equals(g2)=true
g1.equals(c2)=true
g1.equals(g2)=true

The equals() code on the right, looks simpler that the one above and seems to do the same job: When two circles are compared, their radii are checked.

Look at the main() procedure. Four variables are declared, two GeometricObjects and two Circles. Each of the variables is initialized to a Circle with radius 11.0.

Since each variable refers to a different object, they would all yield false if compared using ==.

However, we are comparing them using the equals() method.

The Question

The question is which equals() method is invoked, the one in Object, which requires that the same object is referenced, or the one in Circle, which requires only that the radii are equal.

The Answer

A key difference between the equals() in 11.10 and the simpler one on the upper right is the former overrides the equals() defined in Object since both have the same signature; whereas the latter has a different signature and thus yields two overloaded implementation of equals().

The Key Java Fact

In the overloaded case, the choice of which equals() to invoke depends on the declared type of the argument. In the overriding case the choice depends on the actual type of the argument.

Since the simpler equals() method overloads (not overrides) the one in Object, it is the declared types of the variables that are relevant and only the first invocation c1.equals(c2) uses the equals() defined in circle.

If we change the definition of equals() in Circle to the one in 11.10, the situation changes dramatically. For clarity, we also changed the class name to TestOverride

Now the two equals() definitions have the same signature so the one in Circle overrides the one in GeometricObject.

As a result the choice of method implementation defends on the actual type (i.e., the type of the referenced object), not on the declared type (of the referencing variable).

Since all four variables g1, g2, c1, c2 reference objects with type Circle, each of the four invocations, executes the equals() in Circle. Thus only the radii are compared and the comparison yields true in all four cases.

11.11 The ArrayList Class

arrayList

It is straightforward to create an array of objects; just do it, but see the next section. The fancy ArrayList permits all sorts of extra operations. If you look on http:java.sun.com, you will find that there are even more goodies than the book suggests, as well as some nifty performance guarantees. Another example of the justly-deserved fame accorded the Java libraries.

On the right is a UML diagram for part of ArrayList. The <E> indicates that the class is generic, i.e., you can apply it to get an array of Strings, Circles, etc. We also see that it is found in java.util.

11.11.A Pros and Cons of ArrayList

When we first learned arrays, we dealt with arrays of primitive types (int, double, etc). In that case everything works well. However for arrays of classes (Strings, Objects, Circles, etc.), there are complications.

It is easy to dismiss ArrayList, it is more complicated to use than a simple array. However, there are serious advantages, including the following.

  1. An ArrayList is never full. If you try to add an element to an ArrayList that has no space remaining, the ArrayList grows automatically. (If you remove many elements the Arraylist remains large but can be manually shrunk.)
  2. It runs faster than a linked list implementation (another data structure that holds an unbounded number of elements).
  3. It plays well with generics. Generics permit one to write a single class that can act as a stack of integers, a stack of strings, a stack of circles, etc. We may touch on generics in 101; they are a serious subject in 102. A weakness of Java is that it does not fully support generic arrays. But the ArrayList is itself generic.
    When I taught generics in 102, I avoided ArrayList, but would not do that again.

The only real disadvantage of ArrayList is that you can't use the convenient array syntax a[i]. Instead, to access the analogue of a[i] you write a.get(i) and to set that element to b, you write a.set(i,b). That is, getters and setters meet arrays.

If we do generics in 101 to the point of needing a generic array, we will do it with Arraylist

11.12 Useful Methods for Lists

Converting Between Arrays and ArrayLists

These conversions can be done with a loop, but in fact there are methods in the library that permit each to be done in one line.

To convert an array of Circles Circle[] circArray, to an ArrayList, you write
    ArrayList<Circle> circArrList = new ArrayList<>(Arrays.asList(circArray);
The static method asList() in the Arrays class converts an array into a list and ArrayList has a constructor that accepts a list.

To convert the other way you write
    Circle[]circArray = new Circle[circArrList.size();]
    cirArrList.toArray(circArray);
The instance method toArray() in ArrayList does the conversion.

Question: How can toArray() put the answer into circArray since the latter is an argument and Java is pass-by-value (no exceptions).
Answer: Reference semantics.

11.13 Case Study: A Custom Stack Class

Shows how to use the ArrayList class to design a stack class that holds arbitrary objects.

This section does not show the full power of ArrayList. The real advantage is not just that you can have an ArrayList<Object> into which you can place arbitrary Objects (although that is perfect for heterogeneous lists), but that using generics and Arraylist<E> you can write ONE stack class that can be used for stacks of Objects, stacks of Circles, stacks of Strings, etc. The key point is that if this one generic stack class is used to construct a stack of Circles, Java will not permit you to push a String onto that stack.

11.14 The protected Data and Methods

Since we will not be studying packages (and they are primarily useful for large projects and libraries, which we are not writing), for us the rules are simple.

For a (top-level) class itself (we will not be writing nested classes), the only legal modifiers are public and the default (no modifier)

Most of our classes will be public.

For members of a class (i.e., for fields and method)

11.15 Preventing Members from Being Extended and Overriden

We have seen the final keyword use for constants. It has other analogous uses as well.

  1. A final class cannot be extended.
  2. A final method cannot be overridden.

Chapter 12 Exception Handling

12.1 Introduction

We have seen several places where errors do not occur until run time. For example, a full LongStack might receive a push() request. Another example, this one from geometry, would occur if a Rhombus constructor detects that the given points do not yield a quadrilateral with all sides equal.

In Java, situations like this are often handled with exceptions, which we now study.

12.2 Exception-Handling Overview

double s12 = p1.distTo(p2);
if (s12!=p2.distTo(p3) || s12!=p3.distTo(p4) || s12!=p4.distTo(p1)) {
  System.out.println("Error: Rhombus with unequal sides");
  System.exit(5);       // an exception would be better
}
sidelength = s12;

double s12 = p1.distTo(p2);
try {
  if (s12!=p2.distTo(p3) || s12!=p3.distTo(p4) || s12!=p4.distTo(p1))
    throw new Exception("Rhombus with unequal side");
  sidelength = s12;
}
catch (Exception ex) {
  System.out.println("Error: Rhombus with unequal sides");
  System.exit(5);
}

A rhombus is a quadrilateral with four equal length sides. The top frame on the right shows part of a Rhombus constructor that checks if the lengths are equal. The Java class extends quadrilateral (but for now ignore the Color field).

The frame below it shows one way to accomplish the same task using an exception. This small code segment introduces four Java terms: try, throw, catch, and Exception.

The keywords try and catch each introduce a block of code, which are related as follows.

In the example code, if all the side lengths are equal, sidelength is set. If they are not all equal an exception in the class Exception is thrown, sidelength is not set, an error message is printed and the program exits.

This behavior nicely mimics that of the original, but is much more complicated.
Question: Why would anyone use it?

Start Lecture #23

12.2.A Exception-Handling Advantages

The answer to the above question is that using exceptions in the manner of the previous section to more-or-less exactly mirror the actions without an exception is not a good idea.

A problem that exceptions helps us solve is the following. The author of the geometry package does not know what the author of the client wants to do when an error occurs. Without any such knowledge the package author might have to terminate the run as there was no better way to let the client know that a problem occurred.

The better idea is for the package to detect the error, but let the client decide what to do.

std-rhomb 
 public Rhombus (Point p, double sideLength, double theta) {
   super (p,
          new Point(p.x+sideLength*Math.cos(theta),
                    p.y+sideLength*Math.sin(theta)),
          new Point(p.x+sideLength*(Math.cos(theta)+1.),
                    p.y+sideLength*Math.sin(theta)),
          new Point(p.x+sideLength, p.y));
   this.sideLength = sideLength;
 }
 
 double s12 = p1.distTo(p2);
 if (s12!=p2.distTo(p3) || s12!=p3.distTo(p4) ||
     s12!=p4.distTo(p1))
   throw new Exception ("Rhombus with unequal sides.");
 sideLength = s12;
 
 
 
 try {
   rhom1 = new Rhombus(origin,origin,p2,p3);
 }
 catch (Exception ex) {
   System.out.printf("rhom1 error: %s  Use unit square.\n",
                     ex.getMessage());
   rhom1 = new Rhombus (origin, 1.0, Math.PI/2.0);
 }

The first step is to add a rhombus constructor having parameters a point, a side-length, and an angle and producing the rhombus shown in the diagram on the right (if Θ=Π/2, the rhombus is a square).

The constructor itself is in the 2nd frame.

This enhancement has nothing to do with exceptions and should have been there all along. You will see below how this standard rhombus is used by the client when she mistakenly attempts to construct an invalid rhombus.

The next step, shown in the 3rd frame, is to have the regular rhombus constructor throw an exception, but not catch it.

The client code is in the last frame. We see here the try and catch. In this frame the client uses the original 4-point rhombus constructor, but the points chosen do not form a rhombus. The constructor detects the error and raises (throws in Java-speak) an exception. Since the constructor does not catch this exception, Java automatically re-raises it in the caller, namely the client code, where it is finally caught. This particular client chooses to fall back to a unit square.

It is this automatic call-back that exceptions provide that the original code does not.

12.A Quadrilateral and Friends (version 3)

There is not much difference between versions 2 and 3. A compilable, less cramped implementation is here.

public abstract class GeometricObject { // Will learn about abstract
  protected String color = "blue";
  public void printArea() {
    System.out.printf("The area of %s is %f\n", this, this.area());
  }
  public String getColor() {
    return color;
  }
  public void setColor(String color) {
    this.color = color;
  }
  public abstract double area();        // Must be overridden
  }
}

public class Point extends GeometricObject {
  protected double x, y;
  public Point(double x, double y) {
    this.x = x;
    this.y = y;
  }
  public double distTo (Point p) {
    return Math.sqrt(Math.pow(this.x-p.x,2)+Math.pow(this.y-p.y,2));
  }
  public double area() {
    return 0;
  }
  public double getX() {
    return this.x;
  }
  public double getY() {
    return this.y;
  }
}

public class Quadrilateral extends GeometricObject {
  protected Point p1, p2, p3, p4;
  public Quadrilateral (Point p1, Point p2, Point p3, Point p4) {
    // should check these points for a convex quadrillateral in this order
    this.p1 = p1;
    this.p2 = p2;
    this.p3 = p3;
    this.p4 = p4;
  }
  public double area() { // diagonal gives 2 triangles; use semiperimeter formula
    double diag  = p1.distTo(p3);
    double s12   = p1.distTo(p2);
    double s23   = p2.distTo(p3);
    double s34   = p3.distTo(p4);
    double s41   = p4.distTo(p1);
    double semi1 = (s12 + s23 + diag) / 2;
    double semi2 = (diag + s34 + s41) / 2;
    return Math.sqrt(semi1 * (semi1-s12) * (semi1-s23) * (semi1-diag))  +
        Math.sqrt(semi2 * (semi2-s34) * (semi2-s41) * (semi2-diag));
  }
}

public class Rhombus extends Quadrilateral {
  private double sideLength;
  public Rhombus (Point p1, Point p2, Point p3, Point p4) throws Exception {
    super(p1, p2, p3, p4);
    double s12 = p1.distTo(p2);
    if (s12!=p2.distTo(p3) || s12!=p3.distTo(p4) || s12!=p4.distTo(p1))
      throw new Exception ("Rhombus with unequal sides.");
    sideLength = s12;
  }
  public Rhombus (Point p, double sideLength, double theta) {
    super (p,
           new Point(p.x+sideLength*Math.cos(theta), p.y+sideLength*Math.sin(theta)),
           new Point(p.x+sideLength*(Math.cos(theta)+1.), p.y+sideLength*Math.sin(theta)),
           new Point(p.x+sideLength, p.y));
    this.sideLength = sideLength;
  }
  public double getSideLength() {
    return sideLength;
  }
}

public class Rectangle extends Quadrilateral {
  private double width, height;
  public Rectangle(Point p1, Point p2, Point p3, Point p4) {
    super(p1, p2, p3, p4);
    width = p1.distTo(p2);
    height = p2.distTo(p3);
    // should check that all angles are right angles via slopes neg recip
    // or check both widths equal, both heights equal, both diags equal
  }
  public Rectangle(Point p1, Point p3) { // Sides parallel to the axes
    super(p1, new Point(p3.x,p1.y), p3, new Point(p1.x,p3.y));
    width = Math.abs(p1.x-p3.x);
    height = Math.abs(p1.y-p3.y);
    // Nothing to check
  }
  public double getWidth() {
    return width;
  }
  public double getHeight() {
    return height;
  }
  public double area() {
    return width * height;
  }
}

public class Circle extends GeometricObject {
  private Point center;
  private double radius;
  private static double maxRadius = -1;
  private static Circle maxCircle = null;
  public Circle(Point center, double radius) throws Exception {
    if (radius < 0)
        throw new Exception ("Circle with negative radius.");
    circleNoException(center, radius);
  }
  private void circleNoException(Point center, double radius) {
    this.center = center;
    this.radius = radius;
    this.color  = "pink";
    if (radius > maxRadius) {
      maxRadius = radius;
      maxCircle = this;
    }
  }
  public Circle(double radius) throws Exception{
    this(new Point(0.,0.), radius);
  }
  public Circle(Point center) { // No exception possible
    circleNoException(center, 1.0);
  }
  public Circle() { // No exception possible
    circleNoException(new Point(0.,0.), 1.0);
  }
  public Point getCenter() {
    return this.center;
  }
  public double getRadius() {
    return this.radius;
  }
  public double area () {
    return Math.PI * radius * radius;
  }
  public static Circle largestCircle() {
    if (maxRadius < 0)
      System.out.println("No circles created, so maximum circle is null");
    return maxCircle;
  }
  public boolean equals(Object obj) {
    if (obj instanceof Circle)
      return radius == ((Circle)obj).radius;  // Only radius counts
    return false;
  }
}

public class TestQuad {
  public static void main (String[] args) throws Exception {
    Point origin = new Point(0.0,0.0);
    Point p1 = new Point(1.0,0.0);
    Point p2 = new Point(1.0,1.0);
    Point p3 = new Point(0.0,1.0);
    Point p4 = new Point(5.0,5.0);
    Quadrilateral quad1 = new Quadrilateral(origin, p3, new Point(5.,0.), new Point(5.,-8.));
    Rectangle rect1 = new Rectangle (origin,p1,p2,p3);
    Rectangle rect2 = new Rectangle (origin, new Point(1.0,4.0));
    Rhombus rhom1;
    try {
      rhom1 = new Rhombus(origin,origin,p2,p3);
    }
    catch (Exception ex) {
      System.out.printf("rhom1 error: %s  Using unit square.\n", ex.getMessage());
      rhom1 = new Rhombus (origin, 1.0, Math.PI/2.0);
    }
    p1.printArea();
    printColor(rhom1);      // Polymorphic call (section 11.7)
    printColor(rect1);      // Polymorphic call
    quad1.printArea();      // Inherited method (section first try)
    rect2.printArea();      // Inherited method
    myPrintArea(rhom1);     // Dynamic binding/dispatch (section second try)
    myPrintArea(p4);        // Dynamic binding/dispatch
    quad1 = rect1;      // implicit casting (section 11.9)
    quad1.printArea();      // dynamic binding/dispatch
    Circle c1 = new Circle();
    Circle c2 = new Circle(2.);
    Circle c3 = new Circle();
    System.out.println(c3.equals(c1));
    Circle c = Circle.largestCircle();
    c.printArea();
    System.out.println(c.getColor());
    GeometricObject geo1 = new Rectangle(origin, p2);
    GeometricObject geo2 = new Rhombus(origin, new Point(3,4), new Point(8,4), new Point(5,0));
    System.out.println(geo1.area());
  }
  public static void printColor(GeometricObject geoObj) {
    System.out.printf("The color of %s is %s\n", geoObj.toString(), geoObj.getColor());
  }
  public static void myPrintArea(GeometricObject geoObj) {
    System.out.printf("My area of %s is %f\n", geoObj.toString(), geoObj.area());
  }
}

rhom1 error: Rhombus with unequal sides.  Using unit square.
The area of Point@40a0dcd9 is 0.000000
The color of Rhombus@2ce83912 is blue
The color of Rectangle@41fae3c6 is blue
The area of Quadrilateral@3e7ffe01 is 22.500000
The area of Rectangle@44fd13b5 is 4.000000
My area of Rhombus@2ce83912 is 1.000000
My area of Point@4318f375 is 0.000000
The area of Rectangle@41fae3c6 is 1.000000
true
The area of Circle@2e471e30 is 12.566371
pink
1.0

12.3 Exception Types

Our use of exceptions so far has just been to create one of our own. Specifically, we threw a new Exception. Every exception is an object and thus is a member of some class. So our exception was a member of the class Exception.

Many of the Java library methods can throw exceptions as well. For example, the Scanner constructor we use to create a Scanner object will throw an exception in the FileNotFoundException class if the argument to the Scanner constructor names a file that does not exist.

exception-tree

The diagram on the right shows the class tree for exceptions.

As always, Object is the root of the tree and naturally has many children in addition to Throwable, which is shown. As the name suggests, the Throwable class includes objects that can be thrown, which are exceptions.

From our simplified point of view, there are three important classes of pre-defined exceptions, namely Error, Exception, and RuntimeException. They are highlighted in the diagram.

  1. System errors throw exceptions in the Error class (or one of its descendents). There is very little we can say or do about these exceptions. Fortunately, they rarely occur.
  2. Many errors throw exceptions in the Exception class (or one of its descendents). One example, given above, is that the Scanner constructor can throw an exception in the FileNotFoundException subclass of the IOException subclass of the Exception class. Also our geometry program throws an exception in the Exception class.
  3. The RuntimeException subclass of the Exception class is singled out for a reason explained in Section 12.5.1.

12.4 More on Exception Handling

12.4.1 Declaring Exceptions

Java divides exceptions into two groups: checked exceptions and unchecked exceptions. Referring to the diagram above, red exceptions are unchecked, blue exceptions are checked.

More precisely, I write exception for the concept and Exception for the class of exceptions shown in blue. Then exceptions in either the Error or RuntimeException are unchecked. Those in the Exception class but not in the RuntimeException class are checked.

The difference for us between checked and unchecked exceptions is that any method that might throw a checked exception must declare this fact in its header line. For example consider the following constructor from the Rhombus class

public Rhombus (Point p1, Point p2, Point p3, Point p4) throws Exception {
  super(p1, p2, p3, p4);
  double s12 = p1.distTo(p2);
  if (s12!=p2.distTo(p3) || s12!=p3.distTo(p4) || s12!=p4.distTo(p1))
    throw new Exception ("Rhombus with unequal sides.");
  sideLength = s12;
}

Please note two important points.

  1. The declaration asserts that this method might throw the exception. There is no guarantee that the method will throw the exception.
  2. The declaration asserts that this method might throw the exception. That is, we assert that executing the method might cause the exception to be thrown, and that the method does not itself catch the exception. If the method handles the exception internally, then the header does not list the exception.

The purpose of this declaration is to alert users (clients) of the method that the exception may be raised while executing the client code since the throw is not caught internally and thus would propagate to the caller.

For example, the main() method in version 3 above, has header line

  public static void main (String[] args) throws Exception

Note that by examining only the code in main(), you will find no statement that directly throws an exception.

The point is that main() calls the rhombus() constructor, which throws and does not catch an exception. Thus if the exception is in fact thrown by rhombus(), Java will automatically re-throw it in main().

An important point of this declaration is that if you read a method header line and do not see throws, then you can be sure that calling that method will not result in a checked exception being thrown by your call.

12.4.2 Throwing Exceptions

Throwing an exception is easy; just throw it. But first you need to create an object in some subclass of throwable (i.e., a member of Error, Exception, or a descendant of one of these).

public class Test {
  public static void main(String[]Args) throws Exception {
    throw new Exception();
    throw new BufferOverflowException;
  }
}

public class MyException extends Exception {}
public class Test {
  static MyException myE = new MyException();
  public static void main(String[]args) throws MyException {
    throw myE;
  }
}

The first frame shows two examples of throwing predefined exceptions. Since BufferOverflowException is a subclass of RuntimeException (a red box), it does not appears in the throws clause.

The second frame shows an example of creating a custom exception class and throwing an instance of this class. If MyException extended a red box rather than the blue one, the throws in the method header would not be needed.

12.4.3 Catching Exceptions

Catching an exception is a two step procedure involving try and catch blocks.

It is an compile time error for a statement not in a try block to throw a checked exception that is not declared in the method header.

If an unchecked exception occurs in a statement not within a try block, the exception is not caught by this method. Instead, the current method ends and the same unchecked exception is raised in the statement that called the method. If the current method is the main method, the program is terminated.

  try {
    statements;
  }
  catch (Exception1 ex1) {
    handler for Exception1;
  }
  catch (Exception2 ex2) {
    handler for Exception2;
  }
  ...
  catch (ExceptionN exN) {
    handler for ExceptionN;
  }
  statements after the catches

To catch an exception you must first delimit a sequence of statements with a try block, as shown on the right.

If no exception occurs within the try block, the corresponding catch blocks are ignored.

If an exception does occur within the try block, the corresponding catch blocks are searched to see if one catches this class of exception. If such a block is found, its handler is executed followed by the statements after the catches.

If no catch block matches, the exception is NOT caught and once again, the current method is ended and the exception is re-raised in the statement that called the method.

Order of Catch Blocks

The order of the catch blocks is significant as they are checked for matching in the order they are written.

Note that if a catch block is declared to handle exceptions in a class C, it also catches exceptions in any descendant class of C.

As a result, if a later catch block handles a subclass of a prior cache block, the later catch block can never be executed. Indeed, it is compile-time error to list cache blocks in this nonsensical order

An Example

Draw on the board a deeper example with f() calling g() calling h(), handlers in various places, and h() raising various exceptions.

12.4.4 Getting Information from Exceptions

So far, inside catch (Exception ex) we have not used the object ex at all. Moreover sometimes in a throw we have included a string, which again we have not used.

The key to using the exception object and the string included with the throw is to employ one of the methods supplied by the class throwable. Two useful instance methods are getMessage(), which is used in our geometry program and printStackTrace().

Our geometry program uses getMessage(), which returns the string argument passed to the throw clause. As its name suggests printStackTrace prints a trace of the call stack (main called joe, joe called sam, sam threw an exception).

12.4.5 Example: Declaring, Throw, and Catching Exceptions

You should read the book's example. Here is an example from our geometry classes.

public class Rhombus extends Quadrilateral {
  private double sideLength;
  public Rhombus (Point p1, Point p2, Point p3, Point p4) throws Exception {
    super(p1, p2, p3, p4);
    double s12 = p1.distTo(p2);
    if (s12!=p2.distTo(p3) || s12!=p3.distTo(p4) || s12!=p4.distTo(p1))
      throw new Exception ("Rhombus with unequal sides.");
    sideLength = s12;
  }
  public Rhombus (Point p, double sideLength, double theta) {
    super (p,
           new Point(p.x+sideLength*Math.cos(theta), p.y+sideLength*Math.sin(theta)),
           new Point(p.x+sideLength*(Math.cos(theta)+1.), p.y+sideLength*Math.sin(theta)),
           new Point(p.x+sideLength, p.y));
    this.sideLength = sideLength;
  }
  public double getSideLength() {
    return sideLength;
  }
}
 
public class TestQuad {
  public static void main (String[] args) {
    Point origin = new Point(0.0,0.0);
    Point p1 = new Point(1.0,0.0);
    Point p2 = new Point(1.0,1.0);
    Point p3 = new Point(0.0,1.0);
    Point p4 = new Point(5.0,5.0);
    Rhombus rhom1;
    try {
      rhom1 = new Rhombus(origin,origin,p2,p3);
    }
    catch (Exception ex) {
      System.out.printf("rhom1 error: %s  Using unit square.\n", ex.getMessage());
      rhom1 = new Rhombus (origin, 1.0, Math.PI/2.0);
    }
  }
}
 
rhom1 error: Rhombus with unequal sides.  Using unit square.

The constructor call inside the try is clearly not a rhombus since one side has length zero and the other three are not zero. Hence the constructor throws (but does not catch) a new Exception.

The main method executes the constructor inside a try block so, if the exception is thrown, the catch block is checked and sure enough the only catch there matches. Hence ex becomes the new Exception.

The handler first prints the message included in the throw (via ex.getMessage() and then announces that it will use a unit square instead. The unit square is obtained by invoking the other rhombus constructor that takes, one point, the side length and base angle. This handler cannot raise an exception.

Since the exception thrown by the first invocation of the Rhombus() constructor, is caught and the catch block cannot raise an exception, main() cannot raise an exception and hence its header line does not mention exceptions.

The full example (version 3) of main() constructs several objects. Some of the constructions can raise exceptions that main() does not catch. Hence its header line does announce that an exception can be thrown.

Homework: 12.1.

Homework: Do 12.3 two ways.

  1. Check the index with an if statement to see if Out of Bounds.
  2. Always reference the array and catch the ArrayIndexOutBoundsException. Print the error msg in the catch block.

12.5 The finally Clause

In addition to throw and catch blocks there is occasionally a finally block that gets executed in any case. Consider the example on the right (there can be many catch blocks).

try {
  try block
}
catch (something) {
  catch block
}
catch (somethingElse) {
finally {
  finally block
}
the rest
  1. If no exceptions occur in the try block, the catch blocks are skipped, the finally block is executed, and then the rest.
  2. If an exception occurs in the try block that is caught in a catch block, the rest of the try block is skipped, the matching catch block is executed, the finally block is executed, and then the rest.
  3. If an exception occurs in the try block that is not caught in a catch block, the rest of the try block is skipped, the finally block is executed, and the exception is re-raised in the caller of the method.
  4. Even if the try block contains a return statement, it is still true that if the try block begins, the corresponding finally block will also be started.

12.6 When to Use Exceptions

As mentioned above, it is often silly to use an exception as a complicated if statement. Exceptions are useful when the throw and catch are in separate routines as this usage takes advantage of the automatic up-call that exceptions provide and simple code does not.

12.7 Rethrowing Exceptions

try {
  statements;
}
catch (SomeException ex) {
  statements
  throw ex
}

A catch block can re-throw the exception it has just caught so that the exception is also handled in the caller.

Typical syntax is shown on the right.

12.8 Chained Exceptions

Another possibility is that a catch block for one exception can throw a different exception.

12.9 Defining Custom Exception Classes

Most of the exceptions raised either have no argument or have a string as an argument. The exception in the Rhombus class has a string argument.

public class MyException extends Exception {
  MyException(int code, String str) {
    super(String.format("MyException: (code=%d) %s\n", code, str));
  }
}
 
// Some code
if (something-bad)
  throw new MyException(22, "Something bad happened");

However, you can define your own subclass of the Exception class (say MyException) and have a MyException constructor take whatever arguments you want.

The example on the right takes an integer code in addition to the usual string. It uses String.format() to combine the two arguments into a single string that is then passed to the Exception() constructor.

12.10 The File Class

In Java reading and writing files is divided into two tasks.

  1. First we need to name the file in question. For this we use the File class.
  2. Second we need to perform the actual input and output, creating the file if necessary. For this there are several classes that can be used. In this chapter we will learn PrintWriter and (an old friend) Scanner.

The File class is used to construct a File object from a file name and to perform certain operations on the object. However, it is not used to create a file, to read a file, or to write a file.

File(String pathname)
File(String parent, String child)
File(File parent, String child)

The primary form of the File constructor is the first one shown on the right. This form accepts a single String fn as parameter and constructs a file object corresponding to the file with name fn.

This file may or may not exist and the constructor does not create the file in any case. The name may be relative (to the current directory) or may be absolute. One downside of absolute addresses is that they are OS dependent.

Some boolean Instance Methods

The File class includes exists(), canRead(), canWrite(), isDirectory(), isFile, isAbsolute(), and isHidden().

Their names describe well their actions.

Some String Instances Methods Returning Portions of the Name

The File class includes getName(), getPath(), and getParent().

They return respectively the file name without any directories, the full file name, and the full file name of the parent.

Some Utility Instance Methods

Start Lecture #24

12.A Some Graphics: Running Processing With Eclipse

Professor Klukowska's Instructions for setting up processing are here. Let's follow the instructions and set up processing in eclipse.

Then look at my example using pieces from our GeometricObjects. Explain how setup() and loop() get executed. Also explain how the applet gets passed to the geometry package via the variable canvas.

Documentation on processing is on the home page processing.org.

12.11 File Input and Output

Once we have a File object, we can actually perform input/output on the corresponding file in the file system.

One complication is that the I/O operation can fail. For example, you might try to read from a file that doesn't exits or write to a file for which you do not have the needed permissions. The technical term is that an I/O exception can occur. Since this is a checked exception, we cannot ignore it. For now we simply add throws java.io.IOException to the header line for any method that (directly or indirectly) invokes I/O.

12.11.1 Writing Data Using PrintWriter

The first step in writing data to a file is to create a PrintWriter object, which in turn needs a File object. We can create both at once with

    java.io.PrintWriter output = new java.io.PrintWriter(new java.io.File("x.text"));

If the above looks too imposing, use some import statements.

    import java.io.PrintWriter;
    import java.io.File;
    PrintWriter output = new PrintWriter(new File("x.text"));

Indeed since we will be throwing java.io.IOException as well, we might want to import all of java.io via import java.io.*

  import java.io.*;
  public class CheckDir {
    public static void main(String[] arg) throws IOException {
      File tmpDir = new File("/tmp");
      System.out.println("/tmp exists: " + tmpDir.exists());
      File newDir = new File(tmpDir, "new");
      System.out.println("/tmp/new exists: " + newDir.exists());
      newDir.mkdir();
      System.out.println("/tmp/new exists: " + newDir.exists());
      File newFile = new File(newDir, "newFile");
      System.out.println("/tmp/new/newFile exists: " + newFile.exists());
      PrintWriter putOutput = new PrintWriter(newFile);
      System.out.println("/tmp/new/newFile exists: " + newFile.exists());
      putOutput.printf("Let\'s print a two %d\n", 2);
      putOutput.close();
    }
  }
   
  /tmp exists: true
  /tmp/new exists: false
  /tmp/new exists: true
  /tmp/new/file exists: false
  /tmp/new/file exists: true

Now we can use output the way we have used System.out in the past. For example we can write output.println("hi");

After all the data has been sent to the PrintWriter object, its close() instance method must be called.

For example, let's step through the program on the right line by line.

On my system there is a directory /tmp that is used to hold unimportant files that can be deleted at any time. In order to get the output shown, /tmp/new must not exist when the program is run.

Beware!

The constructor for Printwriter takes a File argument. If the corresponding file does not exist, it is created.

If the corresponding file does exist, the current file is deleted without warning and an empty file is created in its place. Forewarned is forearmed.

12.11.2 Closing Resources Automatically Using try-with-resources

Start Lecture #25

Remark: Look at geoProcessing to see two definitions of moving a quad left.

12.11.3 Reading Data Using Scanner

We have used the Scanner class many times, but always with System.in, which is predefined to correspond to the keyboard. In order to obtain a Scanner capable of reading from the file named existing.text we write (assuming the necessary import's have been executed.

  Scanner input = new Scanner(new File ("existing.text"));

You can also write this declaration (and the one above for PrintWriter) in two steps.

   File f = new File("existing.text");
   Scanner input = new Scanner(f);
    

12.11.4 How Does Scanner Work?
12.11.4 (my title) What Does Scanner Do?

Remark: I found the book somewhat confusing at the end of this section. It seems to suggest that the behavior is different when you change from an input file to input from the keyboard.

Token-Reading Methods and nextLine()

import java.util.Scanner;
import java.util.Date;
import java.io.File;
public class Test {
  public static void main (String[] Args) throws Exception {
    Scanner input = new Scanner (new File ("t.txt"));
    Scanner getInput = new Scanner (System.in);
    String s1 = input.next();
    String s2 = input.next();
    String line = input.nextLine();
    System.out.printf("s1=\"%s\"  and  s2=\"%s\"\n", s1, s2);
    System.out.printf("line=\"%s\"\n", line);
    s1 = getInput.next();
    s2 = getInput.next();
    line = getInput.nextLine();
    System.out.printf("s1=\"%s\"  and  s2=\"%s\"\n", s1, s2);
    System.out.printf("line=\"%s\"\n", line);
  }
}
 
File t.txt contains one line (ending with a newline)
   34   567   |<-- the line ends here
 
I entered the same characters from the keyboard
 
s1="34"  and  s2="567"
line="   "
s1="34"  and  s2="567"
line="   "

The instance methods nextByte(), nextShort(), nextInt(), nextLong(), nextFloat(), nextDouble(), and next() are often referred to as token-reading methods. They all work basically the same and depend on the value of the delimiter, which by default is equal to whitespace. Although there are other characters often considered whitespace and one can change the delimiter, for now just think of delimiter as meaning any non-empty mixture of blanks, tabs, and newlines. Then the token-reading methods work as follows.

  1. They start at the current position of the file (think of System.in for now as just another file).
  2. They read and discard any delimiters found at this position.
  3. They read the next characters up to but not including any delimiters that follow.
  4. The characters just read are converted into a byte, short, etc. (The method next() produces a String, which you might not consider a conversion.)
  5. That is it! In particular, any delimiters that follow the converted characters have not been read. The current position of the file is the first of these delimiters.

The nextLine() method is different and is not considered token-reading. It acts as follows.

  1. All the characters starting with the current position (even if it is a delimiter) and continuing up to and including the next newline are read.
  2. The newline is discarded.
  3. The remaining characters, including any delimiters, are formed into a string, which is returned.

12.11.5 Case Study: Replacing Text

import java.io.*;
import java.util.*;
public class ReplaceText {
  public static void main(String[] args) throws Exception {
    if (args.length != 4) {
      System.out.printf("Usage: java ReplaceText %s\n",
                    "sourceFile targetFile oldStr newStr");
      System.exit(0);
    }
    File sourceFile = new File(args[0]);
    if (!sourceFile.exists()) {
       System.out.println("Source file " + args[0] +
                          " does not exist");
       System.exit(0);
    }
    File targetFile = new File(args[1]);
    if (targetFile.exists()) {
      System.out.println("Target file " + args[1] +
                         " already exists");
      System.exit(0);
    }
    Scanner input = new Scanner(sourceFile);
    PrintWriter output = new PrintWriter(targetFile);
    while (input.hasNext()) {
      String s1 = input.nextLine();
      String s2 = s1.replaceAll(args[2], args[3]);
      output.println(s2);
    }
    input.close();
    output.close();
  }
}

The program on the right illustrates many of the concepts we have just learned and is worth some study.

The program is executed with four command-line arguments, the first two are file names and the second two are strings (technically, all command-line arguments are Strings; the first two strings are interpreted by the program as names of files).

The program copies the first file to the second replacing all occurrences of the third argument with the fourth argument.

  1. Note the error checking. It checks for the correct number of arguments, checks that the old file exists, and checks that the new file does not exist.
  2. Note how it uses args[i] for the command line arguments, and don't forget that the first index is 0.
  3. The while loop keeps reading lines until end-of-file (EOF).
  4. The loop body writes the lines read to the new file after doing the replacement.
  5. Finally, the files are closed.

Remark: The real work is done in the one statement beginning String s2, in particular by the library method replaceAll(). The rest of the code is essentially just checking and preparing for the library call. It is not uncommon for the actual work to be done by a small portion of the code your write.

12.11.A Copying a File

Note that if we erase the last two arguments from the previous program, what remains is a file copy routine. If we then remove the error checks (not advisable), we see how easy java makes it for us to deal with files.

Homework: 12.15.

12.12 Reading Data from the Web

Presumably it is much more difficult to read a file located somewhere on the web than it is to read a file on the local machine.

  public class ReadURL {
    public static void main(String[] arg) {
      try {
        java.net.URL url = new java.net.URL(arg[0]);
        java.util.Scanner getInput = 
                  new java.util.Scanner(url.openStream());
        while (getInput.hasNext()) {
          System.out.println(getInput.nextLine());
        }
      }
      catch (java.net.MalformedURLException ex) {
        System.out.println("Bad URL, did you forget http:// ?");
      }
      catch (java.io.IOException  ex) {
        System.out.println("Bad file, does it exist?");
      }
    }
  }

However, that is not so. Indeed, reading and writing are the same, we use Scanner and Printwriter.

The difference is that instead of using a java.io.File object to specify the file, we use a java.net.URL object.

Indeed, the program on the right does exactly that. Moreover, it illustrates catching several exceptions and treating them differently. A lazy and hence shorter solution would have been to just say that main method throws Exception (since the two kinds of exceptions caught are subclasses of Exception).

Let's run it and spy on my desktop allan.cs.nyu.edu and on google.com. You can play with this if you like; it is here.

12.13 Case Study: Web Crawler

This is cute, but would be better in 102 where we really study depth-first search

Chapter 13 Abstract Classes and Interfaces

13.1 Introduction

We shall soon see that it is sometimes useful to define methods without bodies (called abstract methods) just to act as placeholders for real methods that will override this abstract method.

13.2 Abstract Classes

13.2.1 Why Abstract Methods?

public class GeometricObject {
  protected String color = "blue";
  public void printArea() {
    System.out.printf("The area of %s is %f\n",
                      this, this.area());
  }
  public String getColor() {
    return color;
  }
  public double area() {
    System.out.printf("Error: area not overridden in %s\n",
                      this);
    return 0;
  }
}

Consider the area() methods sprinkled throughout our geometry example. In particular, consider the area() method defined in the GeometricObject class as shown on the right. The code on the right is similar to the geometry classes we have studied.

The method certainly does not compute the area and the important point is that there is no way it can compute the area of a GeometricObject itself since the only field guaranteed to exist is the color.

The reason for including area() here was twofold.

  1. It reminds us that all the geometric objects we plan to actually construct (rectangles, circles, etc) do have areas so we should be overriding this area() method with one in each subclass.
  2. It allows container classes of geometric objects to have the area computed for each contained object.

So What Was Wrong, i.e. Why Abstract Methods

The problem with the area() method in the GeometricObject class is that it only reminds us to override area() in each class derived from GeometricObject. We want more than a reminder, we want a guarantee.

Another advantage of abstract methods is that they permit us to have interfaces, which we will very briefly touch on soon.

Defining an Abstract area() Method

public abstract class GeometricObject {
  protected String color = "blue";
  public void printArea() {
    System.out.printf("The area of %s is %f\n",
                      this, this.area());
  }
  public String getColor() {
    return color;
  }
  public abstract double area(); // MUST be overridden
}

On the right we see a reimplementation of GeometricObject as an abstract class, with area() an abstract method. Note that this method has no body and cannot be called.

The compiler insures that this abstract method is overridden in the subclasses of GeometricObject.

Since this class contains an abstract method, the class must itself be declared abstract, as we have done on the first line.

You can declare a variable of type GeometricObject, but you cannot construct an object of the class. Specifically, you can no longer write new GeometricObject, since GeometricObject is now abstract.

Thus a variable of declared type GeometricObject can never have actual type GeometricObject. Instead, the object referred to by the variable must be a member of a subclass of GeometricObject. Specifically a GeometricObject variable can contain a reference to a Rectangle, a Point, a Circle, etc. In all these cases the abstract area() method in GeometricObject is overridden and becomes a concrete (i.e., non-abstract) method.

13.2.2 Interesting Points about Abstract Classes.

  1. Any nonabstract class (also know as a concrete class) extending an abstract class (e.g. Circle extending GeometricObject) must override all abstract methods with concrete methods. In other words any concrete class must have no accessible abstract methods.
  2. An abstract class can have constructors. They are applied (via super) from constructors in a concrete subclass.
  3. There are no abstract objects, i.e. you cannot apply new directly to any abstract constructor
  4. It is permitted to have an abstract class with no abstract methods.
  5. A subclass of a concrete can be abstract. For example, Object is concrete but its subclass GeometricObject is abstract.
  6. Although you cannot create abstract objects, you can use an abstract type when defining arrays or other containers. For example the following is legal.
          GeometricObject[] geoObj = new GeometricObject[10];
          geoObj[0] = new Circle(10.);
          geoObj[2] = new Point(3.,4.);
  7. A subclass can override a concrete method and make it abstract.

13.3 Case Study: the Abstract Number Class

We have already studied the 6 so-called numeric wrapper classes Byte, Short, Integer, Long, Float, and Double. As mentioned all of these classes have the following 6 methods defined: byteValue(), shortValue(), intValue(), longValue(), floatValue(), and doubleValue().

All six of the above classes are subclasses of Number, which defines abstract methods corresponding to the 6 XValue() methods just mentioned. In addition, BigDecimal and BigInteger are subclasses of Number

One advantage is that you can have an array (or another container) of Numbers that contains Integers, Doubles, etc.

13.4 Case Study: Calendar and GregorianCalendar

Java defines an Abstract class Calendar, which defines a more customary representation of a date (e.g., month, day, year, hour, min, sec). One could imagine subclasses corresponding to Gregorian calendars, lunar calendars, and Jewish calendars, but only the first is currently in the java API.

To give an idea of what is common across calendars, the Boolean method after() is concrete in Calendar (it tells if the calendar object is later in time than the argument). However computeTime() and computeFields(), which convert the customary time representation to/from the number of milliseconds after 1 Jan 1950, must be abstract since the fields and their meanings differ for Gregorian, lunar, and Jewish calendars.

13.5 Interfaces

If all methods in a class are abstract and all data fields are constants (public static final in Java), the class is called an interface.

Imagine that you want to write a class MyClass that extends two base classes ClassA and ClassB. That is, a MyClass object has all the data fields of both ClassA and ClassB (plus any others you add to MyClass). Also MyClass starts with all the methods of the two base classes (minus any that are overridden in MyClass, plus any new methods added in MyClass).

public class MyClass extends ClassA, ClassB {
    statements;
}

You would try to write the class as shown on the right. This is called multiple inheritance since MyClass inherits from multiple base classes. However, Java does not support multiple inheritance (although some languages, notably C++, do support it).

One question with multiple inheritance is what to do if two base classes include methods with the same signature but different bodies.

public class MyClass
       implements InterfaceA, InterfaceB {
    statements;
}

Java does support a somewhat similar notation. If ClassA and ClassB are very simple, specifically if they each consist of just constants and abstract methods, then they are called interfaces, say InterfaceA and InterfaceB, and MyClass can be defined as shown on the right. Since all methods in an interface are abstract and hence body-free, the question mentioned just above for multiple inheritance cannot arise.

13.6 The Comparable<T> Interface

package java.lang;
public interface Comparable<T> {
  public abstract int compareTo(T o);
}

As shown on the right the Comparable interface consists of just one (abstract) method, compareTo().

Many classes in the java library implement this interface, which means that they supply an integer valued compareTo() instance method having one parameter, a T.

The class T is called the formal generic type and is filled in when the class implementing compareTo() is declared. For example the definition of the String class contains
    public class String implements Comparable<String> {
This means that String contains an instance method
    public int compareTo(String s) {

If the instance object is less than the argument object, the value returned is negative; if the two are equal, the value returned is 0; and if the instance object is greater than the argument object, the value return is positive.

  public final class String 
  extends object
  implements Serializable, Comparable<String>, CharSequence

If we access the online Java documentation, we can see the actual header line, which is on the right. So String implements three interfaces. More interesting is the <String> appended to Comparable. This is an manifestation of Java generics, introduced in Java 1.5 (1.7/1.8 is current). Generics serve several purposes. Here they signify that a String can only be compared to another String, not an arbitrary object.

Start Lecture #26

13.6.A Case Study: Sorting Student Records

public class Student implements Comparable<Student> {
  public int    stuId;
  public String name;
  public Student(int stuId, String name) {
    this.stuId = stuId;
    this.name  = name;
  }
  public int compareTo(Student stu) {
    return name.compareTo(stu.name);
  }
}
 
import java.util.Scanner;
import java.io.File;
import java.io.FileNotFoundException;
public class TestStudent {
  public static void main(String[]args)
         throws FileNotFoundException {
    Scanner getInput = new Scanner(new File("stu.db"));
    int n = getInput.nextInt();
    Student[] student = new Student[n];
    for (int i=0; i<n; i++) {
      int    stuId   = getInput.nextInt();
      String name    = getInput.next();
      student[i] = new Student(stuId, name);
    }
    sort(n, student);
    System.out.printf("Sorted by name\n");
    for (int i=0; i<n; i++) {
      System.out.printf("%s\t%3d\n", student[i].name,
                        student[i].stuId);
    }
  }
  public static void sort(int n, Student[] student) {
    for (int i=0; <n-1; i++)
      for (int j=i+1; j<n; j++)
        if (student[i].compareTo(student[j]) > 0) {
          Student tmpStudent = student[i];
          student[i] = student[j];
          student[j] = tmpStudent;
        }
  }
}
 
10
1   Robert
2   John
3   Alice
4   Jessica
5   Sam
6   Sarah
7   Mary
8   Judy
9   Alice
10  Harry
 
Sorted by name
Alice     3
Alice     9
Harry    10
Jessica   4
John      2
Judy      8
Mary      7
Robert    1
Sam       5
Sarah     6

The example on the right illustrates a class extending Comparable as well as reviewing a number of concepts we have learned previously.

The top frame shows a very simple Student class that implements the Comparable interface. The class contains

The second frame shows a test program using the Student class. The first loop reads in student IDs and names from a database file stu.db (shown in the third frame) and calls the Student() constructor to create the entries in the student array.

After the student records are read into the student array, the sort routine is invoked.

Note that this sort of Students, is nearly identical to a corresponding sort of ints or Strings. When we find two Students out of order, we use the standard three statement idiom to put them in order.

Finally the records are printed, to verify that they are now in sorted order.

The third frame contains the stu.db file. This file begins with a count of the number of students followed by the records themselves, one per line.

Finally, the fourth frame is the output of the TestStudent program. As expected, the records are now sorted by the name field. Since the name Alice appeared in two input records, it also appears twice in the output. Since the sort used is stable, the relative order of the two Alice records is preserved.

Using java.util.Arrays.sort() Instead

Since the Student class above implements Comparable<Student>, we do not need to write our own sort. We can remove the sort() method and then replace the line
    sort(n, student);
with
    java.util.Arrays.sort(student)
and the library routine does the sorting for us.

13.6.B Case Study: Comparable Circles

  public class ComparableCircle extends Circle 
         implements Comparable<ComparableCircle> {
   
    public ComparableCircle(Point center, float radius,
                                          int color) {
      super(center, radius, color);
    }
    public ComparableCircle(Point center, float radius) {
      super(center, radius);
    }
   
    public int compareTo(ComparableCircle c) {
      return (int)(radius - c.radius);
    }
  }

Our Circle class does not implement Comparable since it has no compareTo() method.

So we extend the class and call the result ComparableCircle as you see on the right.

Not only can we invoke the useful compareTo() method ourselves, but we can use several items from the java library that require comparable classes. For example we could sort an array of ComparableCircles without writing our own sort routine; instead we would use java.util.Arrays.sort().

Note the subtraction in the compareTo() on the right rather than the if-then-else in the book. Either is fine but I wanted to illustrate that the values need not be +1, 0, -1.

In fact, we could have defined ComparableCircle to implement Comparable<Circle>.

13.7 Example: The Cloneable Interface

13.8 Interfaces vs. Abstract Classes

As mentioned previously, Java does not support multiple inheritance, but a class can implement multiple interfaces. This is not as complex since interfaces are extremely simple classes.

13.9 Case Study: The Rational Class

In mathematics, the set of fractions is referred to as the rational numbers. Every rational number is the quotient of two integers. Normally one keeps rational numbers in lowest terms (e.g., 2/5 rather than 14/35). The book gives an interesting case study, which you might enjoy; I did. (Inspired by this case study I wrote for fun BigRational.java; where the numerator and denominator are BigIntegers, again in lowest terms.)

13.10 Class Design Guidelines

13.10.1 Cohesion

A class should describe a single entity. So having a class CircleAndTriangle does not sound like a good idea.

But you might say that circles and triangles are related; they both have areas and perimeters and perhaps colors. This suggests that they should both be derived from a common ancestor, not that they should be one class.

13.10.2 Consistency

Follow the Java naming and style conventions (see this short section in the book for a brief review).

13.10.3 Encapsulation

Most fields should be private to ease maintenance and modifiability, you can't easily change the meaning of a data field to which the users have access. You should provide get and set methods as appropriate. In general, only expose to the user (i.e., make public) items whose meaning you guarantee will not change.

13.10.4 Clarity

Read.

13.10.5 Completeness

Read. A good example is the String class. It is not likely that any one application would use all the methods, but it is good that they are there. This way the implementation cost is amortized over many uses.

13.10.6 Instance vs. Static

Declare data fields to be static if the value is constant for all objects in the class. Static fields should not be set via a constructor. For one thing, there may not be any objects created when the field is used (in a static method).

Some methods do not need any object of the class. For example, our friend, the main() method, has this property. Such methods must be declared static as there is no object to which they can be attached.

Instance methods can reference both instance and class fields, as well as both instance and class methods.

Class methods can reference class methods and fields, but cannot reference instance methods and fields (what object would the instance method or field refer to?).

13.10.7 Inheritance vs. Aggregation

Inheritance corresponds to an is-a relationship; aggregation corresponds to a has-a relationships

13.10.8 Interfaces vs. Abstract Classes

Abstract classes are an example of inheritance so again are normally based on an is-a relationship. Interfaces are for weaker relationships, typically a property that can be possessed by a number of different classes (e.g., comparable).

Chapter 14 JavaFX Basics

Chapter 15 Event-Driven Programming and Animations

Chapter 16 JavaFX Controls and Multimedia

Chapter 17 Binary I/O

Chapter 18 Recursion

18.1 Introduction

A method is recursive if it directly or indirectly calls itself. So if the method f() invokes f(), we call f() recursive. Also if f() invokes g() and g() invokes f(), we call both f() and (g) recursive.

For an example consider two mathematical functions f() and g() defined on the integers by these three rules.

  1. f(n) = 0               if n≤0
  2. f(n) = f(n-1) + g(n-1) if n>0
  3. g(n) = f(n) + 1        for all n

For example let's compute f(3)

f(3) =                f(2)                    +                          g(2)
     =     f(1)         +              g(1)   +               f(2)        +             1
     = f(0) +    g(0)   +     f(1)        + 1 +     f(1)        +               g(1)  + 1
     =  0   + f(0) + 1  + f(0) +    g(0)  + 1 + f(0) +    g(0)  +    f(1)         + 1 + 1
     =  0   +  0   + 1  +  0   + f(0) + 1 + 1 +   0  + f(0) + 1 + f(0) + g(0)     + 1 + 1
     =  0   +  0   + 1  +  0   +   0  + 1 + 1 +   0  +   0  + 1 +   0  + g(0)     + 1 + 1
     =  0   +  0   + 1  +  0   +   0  + 1 + 1 +   0  +   0  + 1 +   0  + f(0) + 1 + 1 + 1
     =  0   +  0   + 1  +  0   +   0  + 1 + 1 +   0  +   0  + 1 +   0  +   0  + 1 + 1 + 1
     =  7

0    0
1    1
2    3
3    7
4   15
5   31
6   63
7  127
8  255
9  511

public class FG {
  public static void main(String[]arg) {
    for (int i=0; i<10; i++)
      System.out.printf("%2d %4d\n",
                        i, f(i));
  }
  public static int f(int n) {
    if (n <= 0)
      return 0;
    return f(n-1) + g(n-1);
  }
  public static int g(int n) {
    return f(n) + 1;
  }
}

The program is quite simple and is shown on the right together with the output produced.

What is surprising is that it works! After all when we invoke f(3), this sets n=3 and invokes f(2), which sets n=2. So now in the same method, namely f(), the same variable, namely n, has two different values at the same time, namely 3 and 2.

How can this be?

Actually, the situation gets even worse when we consider the call of f(9), and worse still when we remember that f() calls g(), which in turn calls f(). There will be very many values for n in f() at the same time.

18.2 Case Study: Computing Factorials

public class Factorial {
  public static void main(String[]arg) {
    System.out.printf(" n Recursive  Iterative\n");
    for (int i=-1; i<10; i++)
      if (i<0)
        System.out.printf("(%d)! is not defined!!\n", i);
      else
        System.out.printf("%2d %8d  %8d\n",
                          i, recFac(i), iterFac(i));
  }
  public static int recFac(int n) {
    if (n <= 1)
      return 1;
    else
      return n * recFac(n-1);
  }
  public static int iterFac(int n) {
    int fact=1;
    for (int i=2; i<=n; i++)
      fact = fact * i;
    return fact;
  }
}

 n Recursive  Iterative
 (-1)! is not defined!!
 0        1         1
 1        1         1
 2        2         2
 3        6         6
 4       24        24
 5      120       120
 6      720       720
 7     5040      5040
 8    40320     40320
 9   362880    362880

Factorial is a very easy function to compute either with or without recursion. It is normally written using ! rather than the usual parenthesized notation. That is, instead of factorial(7), we usually write 7!

For a positive integer n, n! is defined to be

  1 * 2 * 3 * ... * n

For example 5! = 1 * 2 * 3 * 4 * 5 = 120

If instead of viewing n! as multiplying from 1 up to n, we view it as multiplying from n down to 1, we see that the definition is the same as defining (recursively).

  n! = n * (n-1)!

It is conventional to define 0! = 1.

Sometimes factorial is defined to be 1 for negative numbers as well, but I believe it is more common to consider factorial undefined for negative numbers.

The program on the right computes factorial twice, once with each definition. The factorial methods would return 1 if given a negative argument, but the main program declares this to be an error.

As in the previous section, perhaps the most interesting question is "How can the Java program possible work with n having so many different values at the same time?".

The Call Stack for Factorial

On the board show the stack growing and shrinking when computing recFact(4).

18.3 Case Study: Computing Fibonacci Numbers

public class Fibon {
  public static void main(String[]arg) {
    System.out.printf(" n Recursive  Iterative\n");
    for (int i=-1; i<8; i++)
      if (i<0)
        System.out.printf("Fibonacci undefined for %d\n", i);
      else
        System.out.printf("%2d %8d  %8d\n",
                          i, recFibon(i), iterFibon(i));
  }
  public static int recFibon(int n) {
    if (n <= 1)
      return 1;
    else
      return recFibon(n-1) + recFibon(n-2);
  }
  public static int iterFibon(int n) {
    int a=1, b=1, c=1;
    for (int i=2; i<=n; i++) {
      c = a + b;
      a = b;
      b = c;
    }
    return c;
  }
}

 n Recursive  Iterative
 Fibonacci is not defined for -1
 0        1         1
 1        1         1
 2        2         2
 3        3         3
 4        5         5
 5        8         8
 6       13        13
 7       21        21

The Fibonacci sequence is normally defined recursively by the following two rules.

  1. f(0) = f(1) = 1
  2. f(n) = f(n-1) + f(n-2) for n>1

From the formulas above, we see that the sequence begins

  1, 1, 2, 3, 5, 8, 13, ...

The limiting ratio f(n)/f(n-1) as n approaches infinity is called the golden mean and comes up in a number of mathematical and biological settings.

The code for both recursive and iterative solutions is on the right.

Again the methods will calculate Fibonacci values for negative n, but the main() method correctly flags it as an error.

Draw on the board the diagram showing all the recursive calls that occur when you invoke recFib(4).

I must note that the recursive version is horribly inefficient. On my laptop an execution of iterFibon(50) is essentially instantaneous, but recFibon(50) did not finish in a minute.

This inefficiency is due to the many recursive calls required. For example recFibon(39) made well over 204 million recursive calls to arrive at the answer of 102,334,155.

18.4 Problem Solving Using Recursion

It is important when designing a recursive solution, that you avoid infinite recursion where the method f() always calls itself. There must be a so called base case that can be solved directly. For example, in the factorial problem, we specified that 0!=1.

Another requirement is that when you are not in a base case, the recursive calls bring you closer to the base case, so that you eventually reach a base case. For example, in the factorial problem, if n>0, then we define n! = n*(n-1)!, which means that when trying to compute factorial for n, we need to compute factorial for n-1. Since the base case is n=0, n-1 is closer to the base case than is n.

Often the base case occurs for a small value of an integer parameter, (e.g., n for factorial or Fibonacci, the length for many string problems, array bounds for some array problems, etc). Then, if the recursive call has a smaller value of the parameter than the original, it is closer to the base case.

Thus, many times the high-level structure of a recursive solution is

  if (the parameters fit the base case)
     return the solution directly
  else
     call the method recursively with a smaller parameter value
     return the answer using the answer from the recursive call

Here is an (inefficient, overly complex) method of adding non-negative integers that uses the above pattern.

public static int sum(int x, int y) {
   if (y == 0) then
      return x
   return sum(x,y-1) + 1;
}

Multiple Base Cases

Sometimes we have more than one base case. For example consider the isPalindrome() procedure on the right. Recall that a string is a palindrome if it reads the same from left to right as from right to left.

public static boolean isPalindrome(String s) {
  if (s.length() <= 1) // base cases 1a and 1b
    return true;
  if (s.charAt(0) == x.charAt(s.length()-1)) // base case 2
    return false;
  return isPalindrome(s.substring(1,s.length()-1));
}

The first base case is that an empty string or a string of length one is always a palindrome.

The second base case is that if the first and last characters are not equal, then the string is not a palindrome.

If neither base case applies than the original string is a palindrome if and only if the substring omitting the first and last characters (a smaller problem closer to the first base case) is a palindrome.

An Alternate Interpretation

The above code is from the book. I might prefer to view the solution with only two base cases as follows.

public static boolean isPalindrome(String s) {
  if (s.length() <= 1) // base case
    return true;
  return (s.charAt(0)==x.charAt(s.length()-1)) &&
         isPalindrome(s.substring(1,s.length()-1));
}

The base cases are that empty and length 1 strings are palindromes.

If we are not in a base case, the original string is a palindrome if and only if (1) the first and last characters are the same and (2) the substring omitting these two characters is a palindrome. This interpretation gives rise to the code on the right.

18.5 Recursive Helper Methods

Sometimes it is easier or more efficient to solve a more general problem. For example, an inefficiency in the above palindrome program is that at each recursive call it builds a new string when in fact all that we need to do is to restrict our attention to a contiguous portion of the original string.

public static boolean isPalindrome(String s, int lo, int hi) {
  if (hi <= lo)
    return true;    // base cases
  return (s.charAt(lo)==s.charAt(hi)) &&
         isPalindrome(s, lo+1, hi-1);
}

So instead of asking if a string is a palindrome, we as a more general question: is the portion of the string from position lo to position hi a palindrome and then recursively restrict the range lo...hi, while keeping the same string. This program is shown on the right.

One objection to the last program is that it is more awkward for the user who must now invoke the program as isPalindrome(s,0,s.length()-1). In other words, the helper program may have helped the implementer (in this case to make their program more efficient), but is sure didn't help the user who much preferred writing isPalindrome(s).

public static boolean isPalindrome(String s) {
  return isPalindrome(s, 0, s.length()-1));
}

To answer this objection, we write a second isPalindrome() method that meets the user's expectation and properly invokes the first isPalindrome() method. The code is shown on the right. Note that the method name isPalindrome() is overloaded: If invoked with just a string argument, the second version is called; if invoked, with a string and two integers, the first version is called.

Remark: Chris Nelson points us at an infinite recursive game http://insideastarfilledsky.net/. Chris adds

The description of the game isn't perfect on the front page but the bullets points page answers a question about the term "infinite": http://insideastarfilledsky.net/bulletPoints.php
I watched the trailer and you can see the recursion. In particular the part entitled Wait, where are you now? is reminiscent of the questions one asks when trying to understand a recursive method.

18.5.1 Recursive Selection Sort

18.5.2 Recursive Binary Search

18.A Binary Trees: A Recursive Data Structure

tree

On the right is an preliminary look at an important data structure, much studied in 102: a binary tree.

These trees have two kinds of nodes: interior nodes drawn as squares, and leaves drawn as circles. Each interior node has one or two children (hence the name binary; in 102 we also study general trees with interior nodes having many children). Each leaf has no child. A node also contains data, in this case a character.

If we look closely, we see that the tree on the right has no node with exactly one child. A tree in which all nodes have either two or zero children is called a proper binary tree.

public class Tree {
  char data;
  Tree left;
  Tree right;
  Tree(char data, Tree left, Tree right) {
    this.data  = data;
    this.left  = left;
    this.right = right;
  }
  Tree (char data) {  // construct a leaf
    this(data, null, null);
  }
}

The code on the right is a Java class for the binary tree data structure. Note that we use the name Tree when the object is in fact a single node of a tree (the justification for this terminology will be soon clear).

We see that a Tree has three components, two Tree's and a char, which seems crazy! How can a Tree contain two Tree's? For one thing how can a Tree be large enough to hold two trees?

The answer is an old friend (enemy?), reference semantics. The variables left and right do not contain trees, but instead contain references to trees. Recall that all references are the same (modest) size. Thus a Tree object contains two references to Tree's and a char.

For a leaf the references are null For an interior node, the references are not null, but point to actual trees.

Informally, you can think of a tree (i.e., a tree node) as it is shown in the diagram. That is, you can view a node as containing two arrows and a character, with arrows corresponding to null references drawn differently (or omitted).

Start Lecture #27

Remark: A practice final is on the web page.

18.A.1 Constructing, Counting, and Traversing a Binary Tree

The program on the right first constructs the tree in the diagram above, then counts the nodes in the tree and finally traverses the tree in three different orders.

public class Tree {
  char data;
  Tree left;
  Tree right;
  Tree(char data, Tree left, Tree right) {
    this.data  = data;
    this.left  = left;
    this.right = right;
  }
  Tree (char data) {  // constructs a leaf
    this(data, null, null);
  }
  public static void main(String[]arg) {
    Tree t1 = new Tree('A');
    Tree t2 = new Tree('B');
    t1 = new Tree('C',t1,t2);
    t2 = new Tree('D');
    Tree t3 = new Tree('S',t1,t2);
    t1 = new Tree('a');
    t2 = new Tree('n');
    t1 = new Tree('E',t1,t2);
    t2 = new Tree('G');
    t1 = new Tree('0',t1,t2);
    t1 = new Tree('1',t3,t1);
    System.out.printf("The tree has %d nodes\n",
                      count(t1));
    System.out.printf("\nPreorder Traversal\n");
    t1.preOrderTraverse();
    System.out.printf("\n\nPostorder Traversal\n");
    t1.postOrderTraverse();
    System.out.printf("\n\nInorder Traversal\n");
    t1.inOrderTraverse();
  }
  public static int count(Tree t) {
    if (t == null)
      return 0;
    return 1 + count(t.left) + count(t.right);
  }
  public void visit() {
    System.out.printf("%c ", this.data);
  }
  public void preOrderTraverse() {
    if (this==null)             // base case
      return;
    this.visit();
    if (this.left != null)
      this.left.preOrderTraverse();
    if (this.right != null)
      this.right.preOrderTraverse();
  }
  public void postOrderTraverse() {
    if (this==null)             // base case
      return;
    if (this.left != null)
      this.left.postOrderTraverse();
    if (this.right != null)
      this.right.postOrderTraverse();
    this.visit();
  }
  public void inOrderTraverse() {
    if (this==null)             // base case
      return;
    if (this.left != null)
      this.left.inOrderTraverse();
    this.visit();
    if (this.right != null)
      this.right.inOrderTraverse();
  }
}

There are 11 nodes in the tree

Preorder Traversal
1 S C A l l 0 1 a n G

Postorder Traversal
A l C l S a n 1 G 0 1

Inorder Traversal
A C l S l 1 a 1 n 0 G

Constructing

First let us concentrate on how the beginning of the main() method uses both constructors to create the desired tree, which I have redrawn here for convenience.

tree

To create an interior node, we use the first constructor and thus need to supply two child trees in addition to the data. This means we must construct both children before constructing their parent. Hence, the tree must be constructed from the bottom up.

To construct a leaf we use the second constructor and thus supply only the data item, which in this small example is simply a character. The left and right fields are set to null by the first constructor.

In main() I deliberately reused the Tree variables t1,t2,t3 as I believe it is instructive to see which tree nodes must be remembered to enable constructing other nodes.

On the board execute each line of main() showing the variable name, the reference, and the referred to Tree. As execution proceeds, we see why we called the objects referred to by t1,t2,t3 trees not nodes.

Counting

With recursion available counting is a very easy, very short program. Without recursion it would be considerably more challenging. The idea for counting is that the number of nodes in any (nonempty) tree is 1 (for the root) plus the number in the left subtree (a recursive call of the same routine) plus the number in the right subtree (another recursive call of the same routine).

The base case is that the number of nodes in an empty tree is zero. A reference to an empty tree has the value null.

Traversing

In a tree traversal all the tree nodes are visited. In the three traversals we study, each node is visited exactly once. In general, what to do during a visit is specified by the user method visit(). In our example, visit() consists simply of printing the node's character data item.

How do we ensure we visit each node (exactly once) and in what order should we visit them? The key to the first question is that traversing a node has three tasks, visit the node, traverse the left subtree (a recursive call) and traverse the right subtree (another recursive call).

Three orderings are common: pre-order, post-order, and in-order. In all three, a left child is traversed before its right sibling. The pre/post/in refers to when a node is visited in relation to traversing its children.

On the board, without looking at the code, manually perform all three traversals for the tree above. Then repeat the exercise for a non-proper binary tree.

Homework: For each of the trees below, determine the order of node visitation for all three traversals.

traversal-hw

18.6 Case Study: Finding the Directory Size

Now that we understand trees and how to recursively walk through them, we can solve a number of problems. We will look at a familiar structure, the file system tree.

import java.io.File;
import java.util.Scanner;
public class DirOrFileSize {
  public static void main(String[] args) {
    System.out.print("Enter a directory or a file: ");
    Scanner input = new Scanner(System.in);
    String directory = input.nextLine();
    System.out.printf("There are %d bytes.\n",
                      getSize(new File(directory)));
  }
  public static long getSize(File file) {
    if (! file.isDirectory())  // Base case, 1 file
      return file.length();
    else { // All files and subdirectories
      long size = 0; // Total size from here down
      File[] files = file.listFiles();
      for (int i = 0; i < files.length; i++)
        size += getSize(files[i]);
      return size;
    }
  }
}

In this tree the interior nodes are the directories and the leaves are the simple files. In 202 you will learn that file system trees are more complicated than this and actually are often not trees.

Note that a directory can have any number of files and sub-directories so some interior nodes have more than 2 children. Thus we do not have a binary tree and cannot use inorder traversal.

Since the trees are not binary, the data structure in 18.A cannot be used. However this is not our problem. The authors of java.io.File must have taken 102 or equivalent in order to write that class. We are just clients of the class and do not need to look under the covers to see how it is implemented.

The program on the right reads in a file or directory name and prints the total size of all the files there. Specifically, if given a file it gives the size of the file; whereas, if given a directory, it prints the size of all the files under that directory (which includes files under subdirectories of the directory).

The base case is a simple file, in which case the size is obtained by calling the length() instance method in the File class.

When encountering a directory, getSize() sums the sizes of all the files and subdirectories in the given directory. Note that this involves many recursive calls, one for each file and subdirectory. Much of the work is done by the library method listFiles() that conveniently constructs and returns an array of Files, giving the contents of the directory.

18.6.A Listing Files in or Under a Directory

dir-tre

Consider the file system tree on the right, where boxes are directories and circles are ordinary files.

The program below, when run on this file system, produces the output on the lower right.

Note that the items within the a directory appear below it and are indented. All the work is done by the second (recursive) listFiles(). Its first parameter is the file or directory to list and the second argument is the indentation to use.

We overload listFiles() as a convenience to the user.

The base case is when the first argument is a file, which is simply listed using the File.getName() library routine.

 
T
  E
  F
    b
    y
    A
      a
  x
  y
  D

import java.io.File;
import java.util.Scanner;
public class ListFiles {
  public static void main(String[] args) {
    System.out.print("Enter a directory or a file: ");
    Scanner getInput = new Scanner(System.in);
    String dirOrFile = getInput.next();
    listFiles(new File(dirOrFile));
  }
  public static void listFiles(File dirOrFile) {
    listFiles(dirOrFile, "");
  }
  public static void listFiles(File dirOrFile, String indent) {
    System.out.println(indent + dirOrFile.getName());
    if (! dirOrFile.isDirectory())
      return; // base case -- simple file
    File[] dirOrFiles = dirOrFile.listFiles();
    for (int i = 0; i < dirOrFiles.length; i++)
      listFiles(dirOrFiles[i], indent + "  ");
    return;
  }
}

When given a directory, listFiles() finds all the files and subdirectories and then calls itself recursively on each one giving an indentation 2 greater than its own indentation.

The algorithm is actually a preorder traversal extended to non-binary trees.

Homework: Compute the postorder traversal of the above tree. Note that there is no inorder traversal defined since this is not a binary tree and we wouldn't know when to visit the parent.

18.B Case Study: Binary Search Trees

search-tree

Assume we have a binary tree, whose data component is an int (or any class that extends comparable. Also assume that the tree is sorted in the sense that, for any node all the data to the left is less than the data at the node and all the data to the right is greater than the data at the node.

Such a tree is called a binary search tree. An example is drawn on the right.

Let's say we want to search the tree to see if the number 18 is present (it is) and then we want to search to see if 35 is present (it isn't).

In each case we could use one of our traversal methods and have visit check to see if the desired data item is present.

But we can do much better.

Once we have examined the root we know right away that there is no need to check the right subtree for 18 and no need to check the left subtree for 35.

This will be covered in great detail in 102. An important point is that we would prefer bushy trees, that is, trees which have many leaves (this will be made precise in 102). We can search such trees in time log(N), where N is the number of nodes.

boolean search (Binsrchtree tree, int value) {
  if (tree==null)
    return false;
  if (value==tree.data)
    return true;
  if (value<tree.data)
    return search(tree.left, value);
  return  search(tree.right, value);
}

The (untested) code on the right illustrates the idea of eliminating half the tree at each step since it never searches both left and right subtrees.

The interesting question is how do we add and remove items from this tree and keep the crucial property
left subtree < node < right subtree.

18.C Case Study: Game Trees (Min-Max Search)

game-tree

On the right we see a representative game tree, a key data structure in many 2-person computer games such as chess and checkers. Placing the numbers in the leaves and then searching the tree constitutes is how such programs choose their next move.

For the moment, ignore the numbers in the nodes and assume it is the computer's turn to move. The root of the tree represents the current game position. The arcs leaving a node represent the possible moves from the corresponding position. In the given diagram, there are only two possible moves from each position; in real games this so-called branching factor is much larger and the tree correspondingly much wider.

Since the tree has three levels below the root we are considering three half-moves (i.e., moves by one side). Specifically the arcs leaving the root represent the possible moves of the computer and the two nodes below the root are the resulting position. The arcs leaving these nodes represent the possible replies of the opponent and the bottom row of arcs represent our possible rejoinders to these replies. We have chosen to stop after three half-moves; real programs go deeper.

Since we are not considering any further moves the nodes at depth 3 are leaves. Now for the numbers. Another key component of a game program is the static board evaluator, a method that evaluates how favorable the board position is for the computer. Those are the numbers in the leaves. So the computer would most prefer to be in the position with label 10 and least prefer the position with label -20.

Since the third row of arrows represent the computer's move, it will choose the ones that lead to higher score. Those (maximized) values are the numbers in the bottommost row of internal nodes.

Since the middle row of arrows are the oponent's moves, the choice will be the minimum, which gives the numbers in the middle row of internal nodes.

Finally, the top row of arrows are again the computer's moves so the maximum is computed and that is the value in the root.

As a result of this analysis, the computer will make the right-hand move and expects that the game will have a value of 4. The arcs in magenta represent the computer's belief of the game continuation and the magenta arc is called the principal variation.

18.D Case Study: Evaluating Expressions in Prefix Form

// Evaluate expressions in prefix form
// 1.  A double
// 2.  op Expr Expr (op = + - * /)
import java.util.Scanner;
public class EvalExpr {
  static Scanner getInput = new Scanner(System.in);
  public static void main (String[] args)
                          throws Exception{
    System.out.print("Enter an expression: ");
    System.out.println("Answer: " + evalNextExpr());
  }
  static double evalNextExpr() throws Exception {
    if (getInput.hasNextDouble())
      return getInput.nextDouble();
    String s = getInput.next();
    if (s.length()!=1)
      throw new Exception ("Invalid expression.");
    char c = s.charAt(0);
    if (c == '+')
      return evalNextExpr() + evalNextExpr();
    if (c == '-')
      return evalNextExpr() - evalNextExpr();
    if (c == '*')
      return evalNextExpr() * evalNextExpr();
    if (c == '/')
      return evalNextExpr() / evalNextExpr();
    throw new Exception ("Invalid expression.");
  }
}

We normally write expressions using infix form, where the operator is placed in between the operands. For example, 6+4. We have precedence rules so that 6+4*3=18.

Two other forms are used, prefix form and postfix form. One of these is called Polish and the other reverse Polish, but I forget which is which.

In prefix form the operator is placed before the two operands and in suffix form the operator is placed after the two operands.

There is no concept of precedence since there is only one way to evaluate +6*4 3

The program on the right makes the simplifying assumption that spaces are placed after each token. For example the previous expression would be written + 6 * 4 3

Note how short this program is; I suspect it would be quite a bit longer and harder if we didn't have recursion available. In particular the line
return evalNextExpr()+evalNextExpr();
(and the equivalent ones with +,-,*,/) would be more difficult.

18.7 Problem: Towers of Hanoi

Illustrating the Problem

Show demo on emacs.

public class Hanoi {
  public static void main(String[]args) {
    movePile (Integer.parseInt(args[0]),"left","right",
                                        "middle","");
  }
  public static void movePile (int n, String from, String to,
                               String aux, String indent) {
    if (n > 0) {    // n==0 is base case, do nothing
      movePile (n-1, from, aux, to, indent+"  ");
      System.out.printf ("%sMove disk (#%d) from %s to %s\n",
                         indent, n, from, to);
      movePile (n-1, aux, to, from, indent+"  ");
    }
  }
}

Solving the Problem

Although the problem might seem difficult, it is actually simple once the following (recursive) key is recognized.

To move an n-disk pile from one peg to a second peg

  1. Move the top n-1 disks to the third peg
  2. Move the (now) top disk to the second peg
  3. Move the n-1 disks from the third peg to the second peg

18.8 Problem: Fractals

18.9 Recursion vs. Iteration

Both recursion and iteration are control-flow techniques. That is both determine when other statements are executed.

In theory, they are equivalent: any program using one of them can be converted to using the other.

It is normally rather easy to convert iteration into recursion, but is rarely done for languages like Java where recursion carries extra overhead,

It is in general quite difficult to convert a recursive method into an iterative one, except for ...

18.10 Tail Recursion

If a method calls itself only once and this call is the last action of the method, we have tail recursion.

In this case it is easy to convert the method to use a form of iteration.

Very roughly speaking, the reason recursion is difficult to eliminate is that an extra stack frame is needed to hold the values of the local variables in the new invocation. When this invocation terminates, the new frame is dropped and the old frame, corresponding to the caller, is used.

With tail recursion the called method can use the frame of the caller because the caller has nothing left to do and hence no longer needs its frame.

Some compliers automatically convert tail recursion into iteration. This is most common in languages emphasizing recursion such as lisp.

Converting Recursion into Tail Recursion

int recursiveFactorial(int n) {
  if (n == 0)
    return 1
  return n * recursiveFactorial(n-1);
}

int tailRecFactorial(int n) {
  tailRecFactorial(n, 1);
}
int tailRecFactorial(int n, int value) {
  if (n == 0)
    return value;
  return tailRecFactorial(n-1, n*result)
}

Because tail recursion can be readily converted to iteration, it is advantageous to arrange for only one recursive call with that call the last action of the method

The code on the right illustrates one such conversion.

The top version is our familiar recursive implementation of factorial. It is not tail recursive since after the recursive call is performed the caller must still do a multiplication. Close, but no cigar!

The bottom version has cleverly pushed the multiplication into the recursive call so that it is now performed before the recursion takes place not after. This minor change would permit several compilers (not for Java) to convert the program into iteration.

The End: Good luck on the final!