Representation

We need some generic representation for objects that allows us to model not just motorbikes but any object category. This representation must be able to cope with the various issues highlighted above. We choose to model objects as a constellation of parts. The two cars below looks quite different, but notice that the circles pick out regions that are similar in both their appearance and relative positions within the image. By modeling both the location and appearance of these consistent regions across a set of training images for a category, we obtain a model of the category itself. Our approach is a direct continuation of work at Caltech [Burl,Weber] on this problem, but many other people have adopted similar methods for the problem [Amit,Felzenszwalb].

The obvious issue is how do we find these distinctive regions in the first place. Given that no manual selection is possible, we rely upon an interest operator to identify a whole set of regions in the image, of which we hope a subset may be distinctive and thus potentially useful in representing the category. The particular interest operator we use is that of Kadir & Brady [Kadir]. It works by finding regions that are salient over both scale and location. Below are some motorbike images from our training set (we only show six but in reality we used hundreds). The output of the Kadir and Brady operator is shown. The red crosses indicate the centre of the region and the green circles indicate the radius.

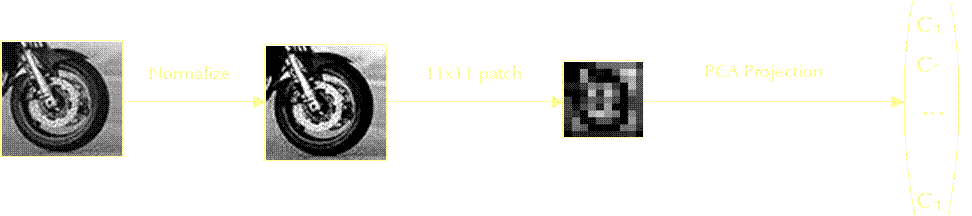
We model three properties of the regions: location, scale and appearance. For location we take the centre of each region and it's radius gives the scale. The representation for appearance is a little more complicated. Taking each patch in turn, we first chop out a square around the centre at the appropriate scale. We then normalize the pixel intensities to give us invariance to differences in illumination. We the rescale the region to a small (typically 11x11) patch. This patch is then projected, using PCA into a 15-dimensional sub-space. This gives us a low-dimensional vector-space representation of appearance that we can model more easily than the original region.

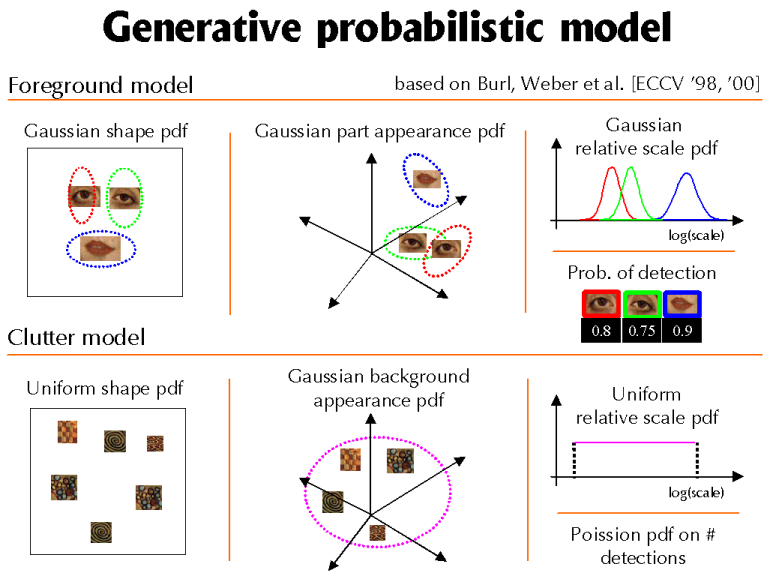
We have now described how we represent the regions within the image. We now describe the generative probabilistic model we use to model their properties. Our model has a fixed number of parts (typically 5-7) which model the properties of regions on the object (the foreground model) and a clutter model which models the remaining regions in the background of the image. In the figure below, we show a toy 3 part model for faces:

• The relative location of the parts is modeled by a joint Gaussian density. Translation and scale invariance is achieved by conditioning on the first part of the model. The remaining regions are assumed to occur uniformly and independently over the image, so are modeled with a uniform density.

• The appearance of each part is modeled by a Gaussian in the 15-dimensional PCA space. The intuition here is that similar looking patches will fall within a similar region of the space and can be modeled effectively by a Gaussian density. The background regions are also modeled by a fixed Gaussian density.

• The scale of each part is also modeled by a Gaussian, with the background regions assumed to be distributed uniformly over scales.

• To handle occlusion, we model the probability of each part being present.

• Finally, we model the number of background detections expected in the image with a Poisson distribution.

My varying the parameters in this model we hope to be able to represent a wide range of object categories. In the next section, we consider how we might estimate the parameters that give a good representation of the category.

References:

Y. Amit and D. Geman. A computational model for visual selection. Neural Computation, 11(7):1691–1715, 1999.

P. Felzenszwalb and D. Huttenlocher. Pictorial structures for object recognition. In Proc. CVPR, pages 2066-2073, 2000.

M. Burl, M.Weber, and P. Perona. A probabilistic approach to object recognition using local photometry and global geometry. In Proc. ECCV, pages 628–641, 1998.

M. Weber, M. Welling, and P. Perona. Unsupervised learning of models for recognition. In Proc. ECCV, pages 18–32, 2000.