Next: Conclusions Up: Order of Magnitude Comparisons Previous: Finite order of magnitude

The first-order theory

Our final result asserts that if the om-space is rich enough then the full first-order language of order-of-magnitude distance comparisons is decidable. Specifically, if the collection of orders of magnitude is dense and unbounded above, then there is a decision algorithm for first-order sentences over the formula, ``od(W,X) << od(Y,Z)'' that runs in time O(4ⁿ (n!)² s) where n is the number of variables in the sentence and s is the length of the sentence.

The basic reason for this is the following: As we have observed in corollary 4, a cluster tree T determines the truth value of all constraints of the form ``od(a,b) << od(c,d)'' where a,b,c,d are symbols in the tree. That is, any two instantiations of T in any two om-spaces agree on any such constraint. If we further require that the om-spaces are dense and unbounded, then a much stronger statement holds: Any two instantiations of T over such om-spaces agree on any first-order formula free in the symbols of T over the relation ``od(W,X) << od(Y,Z)''. Hence, it suffices to check the truth of a sentence over all possible cluster trees on the variables in the sentence. Since there are only finitely many cluster trees over a fixed set of variables (taking into account only the relative order of the labels and not their numeric values), this is a decidable procedure.

Let L be the first-order language with equality with no constant or function symbols, and the single predicate symbol ``much_closer(a,b,c,d)''. It is easily shown that L is as expressive as the language with the function symbol ``od'' and the relation symbol <<.

Definition 7: An om-space O with orders of magnitude D is dense if it satisfies the following axiom:

A.9: For all orders of magnitude d₁ << d₃ in D, there exists a order of magnitude d₂ in D such that d₁ << d₂ << d₃.

O is unbounded above if it satisfies the following:

A.10: For every order of magnitude d₁ in D there exists d₂ in D such that d₁ << d₂.

If D is the collection of orders of magnitude in the hyperreal line, then both of these are satisfied. In axiom [A.9], if 0 << d₁ << d₃, choose d₂ =sqrt (d₁ d₃), the geometric mean. If 0 = d₁ << d₃, choose d₂ = d₃ d where d << 1. In axiom [A.10] choose d₂ = d₁ / d where 0 < d << 1.

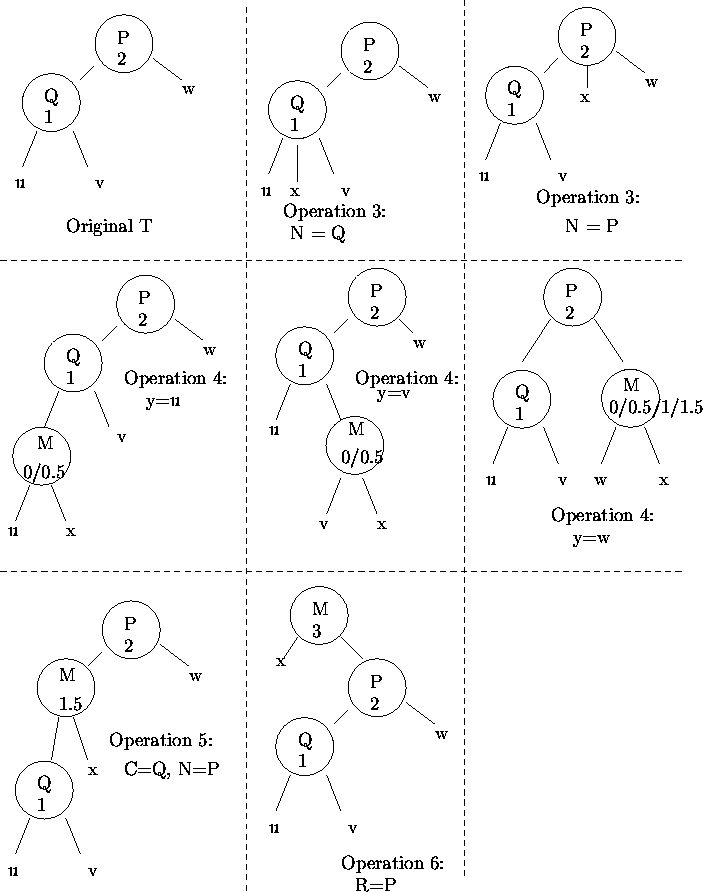
Definition 8: Let T be a cluster tree. Let l₀=0, l₁, l₂ ... l_kbe the distinct labels in T in ascending order. An extending label for T is either (a) l_i for some i; (b) l_k+1 (note that l_k is the label of the root); (c) (l_i-1 + l_i)/2 for some i between 1 and k.

Note that if T has k distinct non-zero labels, then there are 2k+2 different extending labels for T.

Definition 9: Let T be a cluster tree. Let x be a symbol not in T. The cluster tree T' extends T with x if T' is formed from T by applying one of the following operations (a single application of a single operation).

1.: T is the null tree and T' is the tree containing the single node x.
2.: T consists of the single node for symbol y. Make a new node M, make both x and y children of M, and set the label of M to be either 0 or 1.
3.: For any internal node N of T (including the root), make x a child of N.
4.: Let y be a symbol in T, and let N be its father. If N.label <> 0, create a new node M with an extending label for T such that M.label < N.label. Make M a child of N, and make x and y children of M.
5.: Let C be an internal node of T other than the root, and let N be its father. Create a new node M with an extending label for T such that C.label < M.label < N.label. Make M a child of N and make x and C children of M.
6.: Let R be the root of T. Create a new node M such that M.label = R.label + 1. Make R and x children of M. Thus M is the root of the new tree T'.

(See Figure 3.)

**Figure 3:** Extensions of a cluster tree
$\begin{figure}\begin{center} \par\setlength{\unitlength}{0.00083333in} \begingr... ...fault}{\mddefault}{\updefault}w}}}}} \end{picture}} \par\end{center}\end{figure}$

Note that if T is a tree of n symbols and at most n-1 internal nodes then

There are n-1 ways to carry out step 3.
There are n possible ways to choose symbol y in step 4, and at most 2n-2 for the label on M in each.
There are at most n-2 different choices for C in step 5, and at most 2n-3 choices for the label on M in each.
There is only one way to carry out step 6.

Hence, there are less than 4n² different extensions of T by x. (This is almost certainly an overestimate by at least a factor of 2, but the final algorithm is so entirely impractical that it is not worthwhile being more precise.)

Definition 10: Let T be a cluster tree, and let p be a formula of L open in the variables of T. T satisfies p if every instantiation of T satisfies p.

Theorem 4: Let T be a cluster tree. Let p be an open formula in L, whose free variables are the symbols of T. Let O be an om-space that is dense and unbounded above. Algorithm decide(T,p) returns true if T satisfies p and false otherwise.


function decide(T : cluster tree; p : formula) return boolean
convert p to an equivalent form  in which  the only logical symbols in p are 
              not, and, exists, = (equals) and variable names, 
       and the only non-logical symbol is the predicate ``much_closer''. 
case
    p has form X=Y: return (distance(X,Y,T) = 0); 
    p has form ``much_closer(W,X,Y,Z)'': return distance(W,X,T) < distance(Y,Z,T)); 
    p has form not q: return not(decide(T,q)) 
    p has form q and r: return(decide(T,q) and decide(T,r)) 
    p has form exists_X a;
      if for some extension T' of T by X, decide(T',a) = true 
	   then return true
           else return false endif endcase 
end decide

function distance(X,Y : symbol; T : cluster tree) return integer 
N := the common ancestor of X and Y in T; 
return(N.label)  
end distance

The proof of theorem 4 is given in the appendix.

Running time: As we have remarked above, for a tree T of size k there are at most 4k² extensions of T to be considered. The total number of cluster trees considered is therefore bounded by the product from k=1 to n of 4k², which is 4ⁿ (n!)². It is easily verified that the logical operators other than quantifiers add at most a factor of s where s is the length of the sentence. Hence the running time is bounded by O(4ⁿ (n!)² s).

A key lemma, of interest in itself, states the following:

Lemma 28: Let T be a cluster tree. Let p be an open formula in L, whose free variables are the symbols of T. Let O be an om-space that is dense and unbounded above. If one instantiation Z of T in O satisfies p then every instantiation of T in O satisfies p.

That is, either p is true for all instantiations of T or for none. The proof is given in the appendix.

It should be observed that the above conditions on O in lemma 28 are necessary, and that the statement is false otherwise. For example, let O be the om-space described in example I, section 3, of polynomials over an infinitesimal d. Then O is not unbounded above; there is a maximum order-of-magnitude O(1). Let T be the starting tree of Figure 3 (upper-left corner). Let p be the formula ``exists X od(V,W) << od(W,X)'', free in V and W. Then the valuation { U -> d, V -> 0, W -> 1} satisfies T but not p, whereas the valuation { U -> d², V -> 2 d², W -> d} satisfies both T and p.

Next: Conclusions Up: Order of Magnitude Comparisons Previous: Finite order of magnitude