Input X: D by N matrix consisting of N data items in D dimensions.
Output Y: d by N matrix consisting of d < D dimensional embedding coordinates for the input points.

1. Find neighbours in X space [b,c].

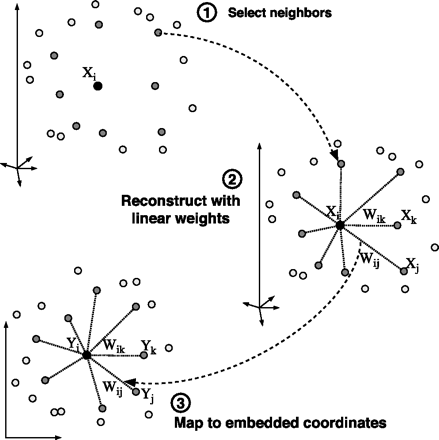
   for i=1:N
     compute the distance from Xi to every other point Xj
     find the K smallest distances 
     assign the corresponding points to be neighbours of Xi
   end
   

2. Solve for reconstruction weights W.

   for i=1:N
     create matrix Z consisting of all neighbours of Xi [d]
     subtract Xi from every column of Z
     compute the local covariance C=Z'*Z [e]
     solve linear system C*w = 1 for w [f]
     set Wij=0 if j is not a neighbor of i
     set the remaining elements in the ith row of W equal to w/sum(w);
   end
   

3. Compute embedding coordinates Y using weights W.

   create sparse matrix M = (I-W)'*(I-W)
   find bottom d+1 eigenvectors of M
     (corresponding to the d+1 smallest eigenvalues) 
   set the qth ROW of Y to be the q+1 smallest eigenvector
     (discard the bottom eigenvector [1,1,1,1...] with eigenvalue zero)
   

Notes

[a] Notation
    Xi and Yi denote the ith column of X and Y
      (in other words the data and embedding coordinates of the ith point)
    M' denotes the transpose of matrix M
    * denotes matrix multiplication
      (e.g. M'*M is the matrix product of M left multiplied by its transpose)
    I is the identity matrix
    1 is a column vector of all ones

[b] This can be done in a variety of ways, for example above we compute 
    the K nearest neighbours using Euclidean distance. 
    Other methods such as epsilon-ball include all points within a 
    certain radius or more sophisticated domain specific and/or
    adaptive local distance metrics.

[c] Even for simple neighbourhood rules like K-NN or epsilon-ball 
    using Euclidean distance, there are highly efficient techniques 
    for computing the neighbours of every point, such as KD trees. 

[d] Z consists of all columns of X corresponding to 
    the neighbours of Xi but not Xi itself

[e] If K>D, the local covariance will not be full rank, and it should be 
    regularized by seting C=C+eps*I where I is the identity matrix and 
    eps is a small constant of order 1e-3*trace(C). 
    This ensures that the system to be solved in step 2 has a unique solution.

[f] 1 denotes a column vector of all ones