 |
Let P be a finite set of points in an om-space. If the distances between different pairs of points in P are of different orders of magnitude, then the om-space imposes a unique tree-like hierarchical structure on P. The points will naturally fall into clusters, each cluster C being a collection of points all of which are much closer to one another than to any point in P outside C. The collection of all the clusters over P forms a strict tree under the subset relation. Moreover, the structure of this tree and the comparative sizes of different clusters in the tree captures all of the order-of-magnitude relations between any pair of points in P. The tree of clusters is thus a very powerful data structure for reasoning about points in an om-space, and it is, indeed, the central data structure for the algorithms we will develop in this paper. In this section, we give a formal definition of cluster trees and prove some basic results as foundations for our algorithms.
Definition 2: Let P be a finite set of points in an om-space. A non-empty subset C subset P is called a cluster of P if for every x,y in C, z in P-C, od(x,y) << od(x,z). If C is a cluster, the diameter of C, denoted ``odiam(C)'', is the maximum value of od(x,y) for x,y in C.
Note that the set of any single element of P is trivially a cluster of P. The entire set P is likewise a cluster of P. The empty set is by definition not a cluster of P.
Lemma 1: If C and D are clusters of P, then either C subset D, D subset C, or C and D are disjoint.
Proof: Suppose not. Then let x in C intersect D, y in C-D, z in D-C. Since C is a cluster, od(x,y) << od(x,z). Since D is a cluster, od(x,z) << od(x,y). Thus we have a contradiction. Q.E.D.
By virtue of lemma 1, the clusters of a set P form a tree. We now develop a representation of the order of magnitude relations in P by constructing a tree whose nodes correspond to the clusters of P, labelled with an indication of the relative size of each cluster.
Definition 3: A cluster tree is a tree T such that
For any node N of T, the field ``N.symbols'' gives the set of symbols in the leaves in the subtree of T rooted at N, and the field ``N.label'' gives the integer label on node N.
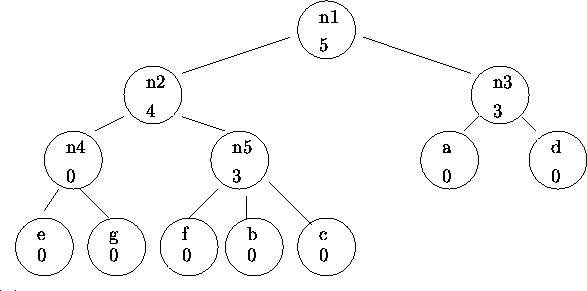
Thus, for example, in Figure 1, n3.label = 3 and n3.symbols = {a,d}; n1.label = 5 and n1.symbols = {a,b,c,d,e,f,g}.
As we shall see, the nodes of the tree T represent the clusters of a set of points, and the labels represent the relative sizes of the diameters of the clusters.
Definition 4: A valuation over a set of symbols is a function mapping each symbol to a point in an om-space. If T is a cluster tree, a valuation over T is a valuation over T.symbols. If N is any node in T and Z is a valuation over T, we will write Z(N) as an abbreviation for Z(N.symbols).
We now define how a cluster tree T expresses the order of magnitude relations over a set of points P.
Definition 5: Let T be a cluster tree and let Z be a valuation over T. Let P =Z(T), the set of points in the image of T under Z. We say that Z satisfies T (read Z satisfies or instantiates T) if the following conditions hold:
The following algorithm generates an instantiation Z given a cluster tree T:
procedure instantiate(in T : cluster tree; O : an om-space)
return : array of points indexed on the symbols of T
variable G[N] : array of points indexed on the nodes of T;
Let k be the number of internal nodes in T;
Choose d0 = 0 << d1 << d2 << ... << dk to be k+1 different orders of magnitude;
/* Such values can be chosen by virtue of axiom A.7 */
pick a point x in O;
G[root of T] := x;
instantiate1(T,O, d1 ... dk, G);
return the restriction of G to the symbols of T.
end instantiate.
instantiate1(in N : a node in a cluster tree; O : an om-space;
d1 ... dk : orders of magnitude;
in out G : array of points indexed on the nodes of T)
if N is not a leaf then
let C1 ... Cp be the children of N;
x1 := G[N];
q := N.label;
pick points x2 ... xp such that
for all i,j in 1 ... p, if i <> j then od(xi, xj) = dq;
/* Such points can be chosen by virtue of axiom A.8 */
for i = 1 ... p do
G[Ci] := xi;
instantiate1(Ci, O, d1 ... dk, G);
endfor
endif end instantiate1.
Thus, we begin by picking orders of magnitude corresponding to the values of the labels. We pick an arbitrary point for the root of the tree, and then recurse down the nodes of the tree. For each node N, we place the children at points that all lie separated by the desired diameter of N. The final placement of the leaves is then the desired instantiation.
Lemma 2: If T is a cluster tree and O is an om-space, then instantiate(T,O) returns an instantiation of T.
The proof is given in the appendix.
Moreover, it is clear that any instantiation Z of T can be generated as a possible output of instantiate(T, O). (Given an instantiation Z, just pick G[N] at each stage to be Z of some symbol of N.)
Note that, given any valuation Z over a finite set of symbols S, there exists a cluster tree T such that T.symbols = S and Z satisfies T. Such a T is essentially unique up to an isomorphism over the set of labels that preserves the label 0 and the order of labels.