
#include <theory_arith_new.h>
Inheritance diagram for CVC3::TheoryArithNew:


Definition at line 41 of file theory_arith_new.h.
typedef Hash::hash_map<Expr, Theorem> CVC3::TheoryArithNew::TebleauxMap [private] |
Definition at line 609 of file theory_arith_new.h.
typedef std::set<Expr> CVC3::TheoryArithNew::SetOfVariables [private] |
Definition at line 613 of file theory_arith_new.h.
typedef Hash::hash_map<Expr, SetOfVariables> CVC3::TheoryArithNew::DependenciesMap [private] |
Definition at line 614 of file theory_arith_new.h.
typedef std::set<ExprBoundInfo> CVC3::TheoryArithNew::BoundInfoSet [private] |
A set of BoundInfo objects
Definition at line 634 of file theory_arith_new.h.
typedef Hash::hash_map<Expr, Theorem> CVC3::TheoryArithNew::TebleauxMap [private] |
Definition at line 613 of file theory_arith_new.mine.h.
typedef std::set<Expr> CVC3::TheoryArithNew::SetOfVariables [private] |
Definition at line 617 of file theory_arith_new.mine.h.
typedef Hash::hash_map<Expr, SetOfVariables> CVC3::TheoryArithNew::DependenciesMap [private] |
Definition at line 618 of file theory_arith_new.mine.h.
typedef std::set<ExprBoundInfo> CVC3::TheoryArithNew::BoundInfoSet [private] |
A set of BoundInfo objects
Definition at line 638 of file theory_arith_new.mine.h.
enum CVC3::TheoryArithNew::NormalizationType [private] |
Type of noramlization GCD = 1 or just first coefficient 1
Definition at line 808 of file theory_arith_new.h.
enum CVC3::TheoryArithNew::NormalizationType [private] |
Type of noramlization GCD = 1 or just first coefficient 1
Definition at line 812 of file theory_arith_new.mine.h.
| TheoryArithNew::TheoryArithNew | ( | TheoryCore * | core | ) |
Definition at line 1052 of file theory_arith_new.cpp.
References assertedExprCount, consistent, createProofRules(), d_buffer, d_bufferIdx, d_diseq, CVC3::TheoryArith::d_intType, CVC3::TheoryArith::d_realType, d_rules, CVC3::DARK_SHADOW, CVC3::DIVIDE, CVC3::GE, CVC3::Theory::getEM(), CVC3::GRAY_SHADOW, CVC3::GT, IF_DEBUG, CVC3::INT, CVC3::INTDIV, CVC3::IS_INTEGER, CVC3::LE, CVC3::LT, CVC3::MINUS, CVC3::MOD, CVC3::MULT, CVC3::NEGINF, CVC3::ExprManager::newKind(), CVC3::PLUS, CVC3::POSINF, CVC3::POW, CVC3::RATIONAL_EXPR, CVC3::REAL, CVC3::REAL_CONST, CVC3::Theory::registerTheory(), CVC3::SATISFIABLE, CVC3::ContextObj::setName(), CVC3::SUBRANGE, and CVC3::UMINUS.
| TheoryArithNew::~TheoryArithNew | ( | ) |
Definition at line 1137 of file theory_arith_new.cpp.
References d_inequalitiesLeftDB, d_inequalitiesRightDB, and d_rules.
| CVC3::TheoryArithNew::TheoryArithNew | ( | TheoryCore * | core | ) |
| CVC3::TheoryArithNew::~TheoryArithNew | ( | ) |
Check the term t for integrality.
Definition at line 68 of file theory_arith_new.cpp.
References CVC3::Expr::getType(), CVC3::IS_INTEGER, isIntegerDerive(), CVC3::isReal(), and CVC3::Theory::typePred().
Referenced by isInteger(), processFiniteInterval(), processSimpleIntEq(), and rafineIntegerConstraints().
A helper method for isIntegerThm().
Check if IS_INTEGER(e) is easily derivable from the given 'thm'
Definition at line 76 of file theory_arith_new.cpp.
References CVC3::Expr::arity(), CVC3::Theory::getCommonRules(), CVC3::Theorem::getExpr(), CVC3::Expr::isAnd(), and CVC3::Theorem::isNull().
Referenced by isIntegerThm().
| bool CVC3::TheoryArithNew::isInteger | ( | const Expr & | e | ) | [inline, private] |
Check the term t for integrality (return bool).
Definition at line 145 of file theory_arith_new.h.
References isIntegerThm(), and CVC3::Theorem::isNull().
Referenced by assertFact(), assignVariables(), checkSatInteger(), computeType(), doSolve(), pickIntEqMonomial(), processFiniteInterval(), processFiniteIntervals(), processRealEq(), and solve().
| bool TheoryArithNew::kidsCanonical | ( | const Expr & | e | ) | [private] |
Check if the kids of e are fully simplified and canonized (for debugging).
Definition at line 94 of file theory_arith_new.cpp.
References CVC3::Expr::arity(), canon(), CVC3::debugger, std::endl(), CVC3::Debug::getOS(), IF_DEBUG, and CVC3::Theory::isLeaf().
Canonize the expression e, assuming all children are canonical.
Compute a canonical form for expression e and return a theorem that e is equal to its canonical form. Note that canonical form for arith expressions is of the following form:
b + a_1 x_1 + a_2 x_2 + ... + a_n x_n (ONE SUM EXPRESION)
or just a rational b (RATIONAL EXPRESSION)
where a_i and b are rationals and x_i are arithmetical leaves (i.e. variables or non arithmetic terms)
Implements CVC3::TheoryArith.
Definition at line 123 of file theory_arith_new.cpp.
References CVC3::Expr::arity(), CVC3::ArithProofRules::canonDivide(), CVC3::ArithProofRules::canonMult(), CVC3::ArithProofRules::canonPlus(), CVC3::ArithProofRules::canonPowConst(), CVC3::TheoryArith::canonThm(), d_rules, DebugAssert, CVC3::DIVIDE, CVC3::Expr::getKind(), CVC3::Theorem::getRHS(), CVC3::isRational(), CVC3::MINUS, CVC3::ArithProofRules::minusToPlus(), CVC3::MULT, CVC3::PLUS, CVC3::POW, CVC3::Theory::reflexivityRule(), CVC3::Theory::substitutivityRule(), CVC3::Expr::toString(), CVC3::TRACE, CVC3::Theory::transitivityRule(), CVC3::UMINUS, and CVC3::ArithProofRules::uMinusToMult().
Referenced by canonSimplify(), kidsCanonical(), pivotRule(), processFiniteInterval(), and rewrite().
Canonize and reduce e w.r.t. union-find database; assume all children are canonical.
Definition at line 246 of file theory_arith_new.cpp.
References canon(), DebugAssert, CVC3::Theory::find(), CVC3::Theorem::getRHS(), CVC3::Expr::hasFind(), CVC3::Theory::simplifyExpr(), CVC3::Expr::toString(), CVC3::TRACE, and CVC3::Theory::transitivityRule().
Referenced by canonPred(), canonPredEquiv(), and canonSimplify().
Composition of canonSimplify(const Expr&) by transitivity: take e0 = e1, canonize and simplify e1 to e2, return e0 = e2.
Definition at line 157 of file theory_arith_new.h.
References canonSimplify(), CVC3::Theorem::getRHS(), and CVC3::Theory::transitivityRule().
Canonize predicate (x = y, x < y, etc.).
accepts a theorem, canonizes it, applies iffMP and substituvity to derive the canonized thm
Definition at line 279 of file theory_arith_new.cpp.
References CVC3::Expr::arity(), canonSimplify(), DebugAssert, CVC3::Theorem::getExpr(), CVC3::Theory::iffMP(), CVC3::Theory::substitutivityRule(), and CVC3::Theorem::toString().
Referenced by addToBuffer(), doSolve(), processFiniteInterval(), processRealEq(), and processSimpleIntEq().
Canonize predicate like canonPred except that the input theorem is an equivalent transformation.
Definition at line 295 of file theory_arith_new.cpp.
References CVC3::Expr::arity(), canonSimplify(), DebugAssert, CVC3::Theorem::getRHS(), CVC3::Theory::substitutivityRule(), CVC3::Theorem::toString(), and CVC3::Theory::transitivityRule().
Referenced by normalize(), and rewrite().
Solve an equation and return an equivalent Theorem in the solved form.
Psuedo-code for doSolve. (Input is an equation) (output is a Theorem)
Definition at line 331 of file theory_arith_new.cpp.
References canonPred(), CVC3::ArithProofRules::constPredicate(), CVC3::Debug::counter(), d_rules, DebugAssert, CVC3::debugger, CVC3::Theorem::getExpr(), IF_DEBUG, CVC3::Theory::iffMP(), isInteger(), CVC3::isRational(), CVC3::Theorem::isRewrite(), normalize(), processIntEq(), processRealEq(), MiniSat::right(), CVC3::ArithProofRules::rightMinusLeft(), CVC3::Theory::setIncomplete(), CVC3::Theory::symmetryRule(), CVC3::Theorem::toString(), and CVC3::TRACE.
Referenced by solve().
takes in a conjunction equivalence Thm and canonizes it.
accepts an equivalence theorem whose RHS is a conjunction, canonizes it, applies iffMP and substituvity to derive the canonized thm
Definition at line 318 of file theory_arith_new.cpp.
picks the monomial with the smallest abs(coeff) from the input
pick a monomial for the input equation. This function is used only if the equation is an integer equation. Choose the monomial with the smallest absolute value of coefficient.
Definition at line 388 of file theory_arith_new.cpp.
References DebugAssert, isInteger(), CVC3::isMult(), CVC3::isPlus(), CVC3::isRational(), MiniSat::min(), and MiniSat::right().
Referenced by processSimpleIntEq().
processes equalities with 1 or more vars of type REAL
input is e1=e2<==>0=e' Theorem and some of the vars in e' are of type REAL. isolate one of them and send back to framework. output is "e1=e2 <==> var = e''" Theorem.
Definition at line 420 of file theory_arith_new.cpp.
References canonPred(), d_rules, DebugAssert, CVC3::EQ, CVC3::Theory::getBaseType(), CVC3::Theorem::getLHS(), CVC3::Theorem::getRHS(), CVC3::Theory::iffMP(), isInteger(), CVC3::Theory::isLeaf(), CVC3::Theory::isLeafIn(), CVC3::isMult(), CVC3::isPlus(), CVC3::isRational(), CVC3::isReal(), MiniSat::left(), CVC3::ArithProofRules::multEqn(), CVC3::ArithProofRules::plusPredicate(), CVC3::TheoryArith::rat(), MiniSat::right(), CVC3::Theorem::toString(), and CVC3::TRACE.
Referenced by doSolve().
processes equalities whose vars are all of type INT
input is e1=e2<==>0=e' Theorem and all of the vars in e' are of type INT. isolate one of them and send back to framework. output is "e1=e2 <==> var = e''" Theorem and some associated equations in solved form.
Definition at line 642 of file theory_arith_new.cpp.
References CVC3::CommonProofRules::andElim(), CVC3::Expr::arity(), DebugAssert, CVC3::Theory::getCommonRules(), CVC3::Theorem::getExpr(), CVC3::Expr::isAnd(), CVC3::Expr::isFalse(), CVC3::Theorem::isRewrite(), processSimpleIntEq(), solvedForm(), CVC3::Expr::toString(), and CVC3::TRACE.
Referenced by doSolve().
One step of INT equality processing (aux. method for processIntEq()).
| eqn | is a single equation 0 = e |
Definition at line 507 of file theory_arith_new.cpp.
References CVC3::CommonProofRules::andIntro(), CVC3::Expr::arity(), CVC3::Expr::begin(), canonPred(), d_rules, DebugAssert, CVC3::Expr::end(), CVC3::EQ, CVC3::ArithProofRules::eqElimIntRule(), CVC3::Theory::getCommonRules(), CVC3::Theorem::getExpr(), CVC3::Theorem::getLHS(), CVC3::Expr::getRational(), CVC3::Theorem::getRHS(), CVC3::Theory::iffMP(), CVC3::ArithProofRules::intVarEqnConst(), isIntegerThm(), isIntx(), CVC3::isMult(), CVC3::isPlus(), CVC3::Expr::isRational(), CVC3::Theorem::isRewrite(), CVC3::ArithProofRules::multEqn(), pickIntEqMonomial(), CVC3::ArithProofRules::plusPredicate(), CVC3::TheoryArith::rat(), MiniSat::right(), separateMonomial(), CVC3::CommonProofRules::skolemize(), CVC3::Theory::symmetryRule(), CVC3::Expr::toString(), and CVC3::TRACE.
Referenced by processIntEq().
Take an inequality and isolate a variable.
Update the statistics counters for the variable with a coeff. c.
Definition at line 805 of file theory_arith_new.cpp.
References d_countLeft, d_countRight, CVC3::Rational::toString(), and CVC3::TRACE.
Referenced by addToBuffer(), and updateStats().
| void TheoryArithNew::updateStats | ( | const Expr & | monomial | ) | [private] |
Update the statistics counters for the monomial.
Definition at line 818 of file theory_arith_new.cpp.
References CVC3::Expr::getRational(), separateMonomial(), and updateStats().
| void TheoryArithNew::addToBuffer | ( | const Theorem & | thm | ) | [private] |
Add an inequality to the input buffer. See also d_buffer.
Definition at line 826 of file theory_arith_new.cpp.
References CVC3::Expr::begin(), canonPred(), d_buffer, d_rules, CVC3::Expr::end(), CVC3::Theorem::getExpr(), CVC3::Theory::iffMP(), CVC3::isPlus(), CVC3::isRational(), CVC3::ArithProofRules::rightMinusLeft(), CVC3::TRACE, and updateStats().
Separate monomial e = c*p1*...*pn into c and 1*p1*...*pn.
Implements CVC3::TheoryArith.
Definition at line 941 of file theory_arith_new.cpp.
References CVC3::Expr::arity(), DebugAssert, CVC3::Expr::getKids(), CVC3::isMult(), CVC3::isPlus(), CVC3::isRational(), CVC3::Expr::isRational(), CVC3::multExpr(), CVC3::TheoryArith::rat(), CVC3::Expr::toString(), and CVC3::TRACE.
Referenced by findRationalBound(), lessThanVar(), processSimpleIntEq(), and updateStats().
Definition at line 929 of file theory_arith_new.cpp.
References DebugAssert, CVC3::isRational(), separateMonomial(), and CVC3::Expr::toString().
| bool CVC3::TheoryArithNew::isStale | ( | const Expr & | e | ) | [private] |
Check if the term expression is "stale".
| bool CVC3::TheoryArithNew::isStale | ( | const Ineq & | ineq | ) | [private] |
Check if the inequality is "stale" or subsumed.
| void CVC3::TheoryArithNew::projectInequalities | ( | const Theorem & | theInequality, | |
| bool | isolatedVarOnRHS | |||
| ) | [private] |
| void TheoryArithNew::assignVariables | ( | std::vector< Expr > & | v | ) | [private] |
Definition at line 1395 of file theory_arith_new.cpp.
References CVC3::Theory::assignValue(), d_graph, findBounds(), CVC3::Theory::findExpr(), CVC3::Theory::inconsistent(), CVC3::Rational::isInteger(), isInteger(), CVC3::TheoryArith::rat(), CVC3::TheoryArithNew::VarOrderGraph::selectSmallest(), and CVC3::TRACE.
Referenced by computeModelBasic().
| void TheoryArithNew::findRationalBound | ( | const Expr & | varSide, | |
| const Expr & | ratSide, | |||
| const Expr & | var, | |||
| Rational & | r | |||
| ) | [private] |
Definition at line 1326 of file theory_arith_new.cpp.
References DebugAssert, CVC3::Theory::findExpr(), CVC3::Expr::getRational(), CVC3::isRational(), separateMonomial(), and CVC3::Expr::toString().
Referenced by findBounds().
Definition at line 1344 of file theory_arith_new.cpp.
References d_inequalitiesLeftDB, d_inequalitiesRightDB, DebugAssert, findRationalBound(), CVC3::isLT(), MiniSat::left(), MiniSat::right(), CVC3::CDList< T >::size(), CVC3::Rational::toString(), and CVC3::TRACE.
Referenced by assignVariables().
| Theorem CVC3::TheoryArithNew::normalizeProjectIneqs | ( | const Theorem & | ineqThm1, | |
| const Theorem & | ineqThm2 | |||
| ) | [private] |
Take a system of equations and turn it into a solved form.
Takes a vector of equations and for every equation x_i=t_i substitutes t_j for x_j in t_i for all j>i. This turns the system of equations into a solved form.
Assumption: variables x_j may appear in the RHS terms t_i ONLY for i<j, but not for i>=j.
Definition at line 681 of file theory_arith_new.cpp.
References CVC3::CommonProofRules::andIntro(), CVC3::ExprMap< Data >::begin(), DebugAssert, CVC3::debugger, CVC3::ExprMap< Data >::end(), CVC3::Theory::getCommonRules(), IF_DEBUG, substAndCanonize(), CVC3::TRACE, CVC3::Debug::trace(), and TRACE_MSG.
Referenced by processIntEq().
Substitute all vars in term 't' according to the substitution 'subst' and canonize the result.
ASSUMPTION: 't' is a fully canonized arithmetic term, and every element of subst is a fully canonized equation of the form x=e, indexed by the LHS variable.
Definition at line 733 of file theory_arith_new.cpp.
References CVC3::Expr::arity(), CVC3::TheoryArith::canonThm(), CVC3::ExprMap< Data >::empty(), CVC3::ExprMap< Data >::end(), CVC3::ExprMap< Data >::find(), CVC3::Theory::isLeaf(), CVC3::Theory::reflexivityRule(), CVC3::Theory::substitutivityRule(), and CVC3::TRACE.
Referenced by solvedForm(), and substAndCanonize().
| Theorem TheoryArithNew::substAndCanonize | ( | const Theorem & | eq, | |
| ExprMap< Theorem > & | subst | |||
| ) | [private] |
Substitute all vars in the RHS of the equation 'eq' of the form (x = t) according to the substitution 'subst', and canonize the result.
ASSUMPTION: 't' is a fully canonized equation of the form x = t, and so is every element of subst, indexed by the LHS variable.
Definition at line 784 of file theory_arith_new.cpp.
References DebugAssert, CVC3::ExprMap< Data >::empty(), CVC3::Theorem::getRHS(), CVC3::Theory::iffMP(), CVC3::Theorem::isRewrite(), substAndCanonize(), and CVC3::Theory::substitutivityRule().
| void TheoryArithNew::collectVars | ( | const Expr & | e, | |
| std::vector< Expr > & | vars, | |||
| std::set< Expr > & | cache | |||
| ) | [private] |
Traverse 'e' and push all the i-leaves into 'vars' vector.
Definition at line 1152 of file theory_arith_new.cpp.
References CVC3::Theory::isLeaf().
| void TheoryArithNew::processFiniteInterval | ( | const Theorem & | alphaLEax, | |
| const Theorem & | bxLEbeta | |||
| ) | [private] |
Check if alpha <= ax & bx <= beta is a finite interval for integer var 'x', and assert the corresponding constraint.
Definition at line 1165 of file theory_arith_new.cpp.
References beta, canon(), canonPred(), d_rules, DebugAssert, CVC3::Theory::enqueueFact(), CVC3::ArithProofRules::finiteInterval(), CVC3::Theorem::getExpr(), CVC3::Expr::getRational(), CVC3::Theorem::getRHS(), CVC3::Theory::iffMP(), isInteger(), isIntegerThm(), CVC3::isLE(), CVC3::isMult(), CVC3::isPlus(), CVC3::Expr::isRational(), CVC3::isRational(), CVC3::ArithProofRules::multIneqn(), CVC3::TheoryArith::rat(), CVC3::Theory::substitutivityRule(), CVC3::Theory::symmetryRule(), and CVC3::Expr::toString().
Referenced by processFiniteIntervals().
| void TheoryArithNew::processFiniteIntervals | ( | const Expr & | x | ) | [private] |
For an integer var 'x', find and process all constraints A <= ax <= A+c.
Definition at line 1223 of file theory_arith_new.cpp.
References d_inequalitiesLeftDB, d_inequalitiesRightDB, isInteger(), processFiniteInterval(), and CVC3::CDList< T >::size().
| void TheoryArithNew::setupRec | ( | const Expr & | e | ) | [private] |
Recursive setup for isolated inequalities (and other new expressions).
This function recursively decends expression tree without caching until it hits a node that is already setup. Be careful on what expressions you are calling it.
Definition at line 1249 of file theory_arith_new.cpp.
References CVC3::Expr::arity(), CVC3::Expr::hasFind(), CVC3::Theory::reflexivityRule(), CVC3::Expr::setFind(), and setup().
| ArithProofRules * TheoryArithNew::createProofRules | ( | ) |
Definition at line 43 of file arith_theorem_producer.cpp.
References CVC3::Theory::theoryCore().
Referenced by TheoryArithNew().
| void TheoryArithNew::addSharedTerm | ( | const Expr & | e | ) | [virtual] |
Keep track of all finitely bounded integer variables in shared terms.
When a new shared term t is reported, all of its variables x1...xn are added to the set d_sharedVars.
For each newly added variable x, check all of its opposing inequalities, find out all the finite bounds and assert the corresponding GRAY_SHADOW constraints.
When projecting integer inequalities, the database d_sharedVars is consulted, and if the variable is in it, check the shadows for being a finite interval, and produce the additional GRAY_SHADOW constraints.
Implements CVC3::TheoryArith.
Definition at line 1278 of file theory_arith_new.cpp.
References d_sharedTerms.
| void TheoryArithNew::assertFact | ( | const Theorem & | e | ) | [virtual] |
Assert a new fact to the decision procedure.
Each fact that makes it into the core framework is assigned to exactly one theory: the theory associated with that fact. assertFact is called to inform the theory that a new fact has been assigned to the theory.
Implements CVC3::TheoryArith.
Definition at line 3010 of file theory_arith_new.cpp.
References CVC3::Expr::arity(), assertedExpr, assertedExprCount, assertEqual(), assertLower(), assertUpper(), boundsAsString(), consistent, d_rules, DebugAssert, CVC3::EQ, explanation, FatalAssert, CVC3::GE, CVC3::Theorem::getExpr(), CVC3::Expr::getKind(), getLowerBound(), CVC3::Expr::getRational(), getUpperBound(), getVariableIntroThm(), CVC3::GT, CVC3::Theory::iffMP(), intVariables, CVC3::isIneq(), isInteger(), CVC3::Theory::isLeaf(), CVC3::isMult(), CVC3::isPlus(), CVC3::isRational(), CVC3::LE, CVC3::LT, CVC3::ArithProofRules::oneElimination(), propagate, propagateTheory(), CVC3::Theory::reflexivityRule(), CVC3::Theory::setInconsistent(), CVC3::Theory::substitutivityRule(), CVC3::Theory::symmetryRule(), tableauxAsString(), CVC3::Expr::toString(), CVC3::TRACE, CVC3::UNKNOWN, unsatAsString(), CVC3::UNSATISFIABLE, and updateFreshVariables().
| void TheoryArithNew::refineCounterExample | ( | ) | [virtual] |
Process disequalities from the arrangement for model generation.
Implements CVC3::TheoryArith.
Definition at line 1294 of file theory_arith_new.cpp.
References CVC3::Theory::addSplitter(), d_inModelCreation, d_sharedTerms, DebugAssert, CVC3::Theory::findExpr(), CVC3::Theory::getBaseType(), CVC3::isReal(), CVC3::Theory::simplifyExpr(), and CVC3::TRACE.
| void TheoryArithNew::computeModelBasic | ( | const std::vector< Expr > & | v | ) | [virtual] |
Assign concrete values to basic-type variables in v.
Implements CVC3::TheoryArith.
Definition at line 1429 of file theory_arith_new.cpp.
References assignVariables(), d_inModelCreation, CVC3::Theory::findExpr(), and CVC3::TRACE.
Compute the value of a compound variable from the more primitive ones.
The more primitive variables for e are already assigned concrete values, and are available through getModelValue().
The new value for e must be assigned using assignValue() method.
| e | is the compound type expression to assign a value; | |
| vars | are the variables actually assigned. Normally, 'e' is the only element of vars. However, e.g. in the case of uninterpreted functions, assigning 'f' means assigning all relevant applications of 'f' to constant values (f(0), f(5), etc.). Such applications might not be known before the model is constructed (they may be of the form f(x), f(y+z), etc., where x,y,z are still unassigned). |
Implements CVC3::TheoryArith.
Definition at line 1452 of file theory_arith_new.cpp.
References CVC3::Theory::assignValue(), DebugAssert, CVC3::Theory::findExpr(), CVC3::isRational(), CVC3::Theory::simplify(), and CVC3::Expr::toString().
| void TheoryArithNew::checkSat | ( | bool | fullEffort | ) | [virtual] |
Check for satisfiability in the theory.
| fullEffort | when it is false, checkSat can do as much or as little work as it likes, though simple inferences and checks for consistency should be done to increase efficiency. If fullEffort is true, checkSat must check whether the set of facts given by assertFact together with the arrangement of shared terms (provided by addSharedTerm) induced by the global find database equivalence relation are satisfiable. If satisfiable, checkSat does nothing. |
Implements CVC3::TheoryArith.
Definition at line 2702 of file theory_arith_new.cpp.
References assertedExpr, assertedExprCount, checkSatSimplex(), consistent, DebugAssert, explanation, CVC3::SATISFIABLE, CVC3::Theory::setInconsistent(), CVC3::TRACE, CVC3::UNSATISFIABLE, and updateFreshVariables().
Theory-specific rewrite rules.
By default, rewrite just returns a reflexive theorem stating that the input expression is equivalent to itself. However, rewrite is allowed to return any theorem which describes how the input expression is equivalent to some new expression. rewrite should be used to perform simplifications, normalization, and any other preprocessing on theory-specific expressions that needs to be done.
Implements CVC3::TheoryArith.
Definition at line 1566 of file theory_arith_new.cpp.
References CVC3::andExpr(), canon(), CVC3::ArithProofRules::canonPlus(), canonPredEquiv(), CVC3::ArithProofRules::constPredicate(), d_rules, DebugAssert, CVC3::ArithProofRules::dummyTheorem(), CVC3::EQ, CVC3::ArithProofRules::eqToIneq(), FatalAssert, CVC3::GE, CVC3::geExpr(), CVC3::Expr::getKind(), CVC3::Theorem::getRHS(), CVC3::GT, CVC3::IS_INTEGER, CVC3::Expr::isAbsLiteral(), CVC3::Expr::isAtomic(), CVC3::isPlus(), CVC3::isRational(), CVC3::Expr::isTerm(), CVC3::LE, CVC3::leExpr(), CVC3::LT, CVC3::ArithProofRules::negatedInequality(), normalize(), NORMALIZE_UNIT, CVC3::NOT, CVC3::ArithProofRules::plusPredicate(), CVC3::TheoryArith::rat(), CVC3::Theory::reflexivityRule(), CVC3::ArithProofRules::rightMinusLeft(), CVC3::Expr::setRewriteNormal(), CVC3::Theory::simplify(), CVC3::Theory::substitutivityRule(), CVC3::Theory::theoryOf(), CVC3::Expr::toString(), CVC3::TRACE, and CVC3::Theory::transitivityRule().
Referenced by update().
| void TheoryArithNew::setup | ( | const Expr & | e | ) | [virtual] |
Set up the term e for call-backs when e or its children change.
setup is called once for each expression associated with the theory. It is typically used to setup theory-specific data for an expression and to add call-back information for use with update.
Implements CVC3::TheoryArith.
Definition at line 1730 of file theory_arith_new.cpp.
References CVC3::Expr::arity(), DebugAssert, CVC3::Expr::isEq(), CVC3::isIneq(), CVC3::isIntPred(), CVC3::Expr::isNot(), CVC3::isRational(), CVC3::Expr::isTerm(), and CVC3::TRACE.
Referenced by setupRec().
Notify a theory of a new equality.
update is a call-back used by the notify mechanism of the core theory. It works as follows. When an equation t1 = t2 makes it into the core framework, the two find equivalence classes for t1 and t2 are merged. The result is that t2 is the new equivalence class representative and t1 is no longer an equivalence class representative. When this happens, the notify list of t1 is traversed. Notify list entries consist of a theory and an expression d. For each entry (i,d), i->update(e, d) is called, where e is the theorem corresponding to the equality t1=t2.
To add the entry (i,d) to a term t1's notify list, a call must be made to t1.addNotify(i,d). This is typically done in setup.
Implements CVC3::TheoryArith.
Definition at line 1765 of file theory_arith_new.cpp.
References CVC3::Theory::assertEqualities(), CVC3::TheoryArith::canonSimp(), CVC3::Debug::counter(), DebugAssert, CVC3::debugger, CVC3::Theory::enqueueFact(), CVC3::Theory::find(), CVC3::Theory::getCommonRules(), CVC3::Theorem::getExpr(), CVC3::Theorem::getLHS(), CVC3::Theorem::getRHS(), CVC3::Expr::hasFind(), IF_DEBUG, CVC3::Theory::iffMP(), CVC3::Theory::inconsistent(), CVC3::isIneq(), CVC3::Theory::leavesAreSimp(), rewrite(), CVC3::Theory::substitutivityRule(), CVC3::Theory::symmetryRule(), CVC3::Expr::toString(), CVC3::TRACE, CVC3::Theory::transitivityRule(), and CVC3::Theory::trueExpr().
Referenced by assertLower(), and assertUpper().
An optional solver.
The solve method can be used to implement a Shostak-style solver. Since solvers do not in general combine, the following technique is used. One theory is designated as the primary solver (in our case, it is the theory of arithmetic). For each equation that enters the core framework, the primary solver is called to ensure that the equation is in solved form with respect to the primary theory.
After the primary solver, the solver for the theory associated with the equation is called. This solver can do whatever it likes, as long as the result is still in solved form with respect to the primary solver. This is a slight generalization of what is described in my (Clark)'s PhD thesis.
Implements CVC3::TheoryArith.
Definition at line 1801 of file theory_arith_new.cpp.
References DebugAssert, doSolve(), CVC3::Theorem::getLHS(), CVC3::Theorem::getRHS(), CVC3::TheoryArith::intType(), isInteger(), CVC3::Theory::isLeaf(), CVC3::Theory::isLeafIn(), CVC3::Theorem::isRewrite(), CVC3::Expr::isTerm(), and CVC3::Theory::symmetryRule().
| void TheoryArithNew::checkAssertEqInvariant | ( | const Theorem & | e | ) | [virtual] |
A debug check used by the primary solver.
Implements CVC3::TheoryArith.
Definition at line 1874 of file theory_arith_new.cpp.
| void TheoryArithNew::checkType | ( | const Expr & | e | ) | [virtual] |
Check that e is a valid Type expr.
Implements CVC3::TheoryArith.
Definition at line 1880 of file theory_arith_new.cpp.
References CVC3::Expr::arity(), DebugAssert, CVC3::Theory::getEM(), CVC3::Expr::getKind(), CVC3::Expr::getRational(), CVC3::INT, CVC3::isIntegerConst(), CVC3::REAL, CVC3::SUBRANGE, and CVC3::Expr::toString().
| void TheoryArithNew::computeType | ( | const Expr & | e | ) | [virtual] |
Compute and store the type of e.
| e | is the expression whose type is computed. |
Implements CVC3::TheoryArith.
Definition at line 1903 of file theory_arith_new.cpp.
References CVC3::Expr::arity(), CVC3::Theory::boolType(), CVC3::TheoryArith::d_intType, CVC3::TheoryArith::d_realType, CVC3::DARK_SHADOW, DebugAssert, CVC3::DIVIDE, CVC3::GE, CVC3::Theory::getBaseType(), CVC3::Theory::getEM(), CVC3::Expr::getKind(), CVC3::Expr::getRational(), CVC3::Expr::getType(), CVC3::GRAY_SHADOW, CVC3::GT, CVC3::IS_INTEGER, CVC3::isInt(), isInteger(), CVC3::Rational::isInteger(), CVC3::Expr::isRational(), CVC3::LE, CVC3::LT, CVC3::MINUS, CVC3::MULT, CVC3::PLUS, CVC3::POW, CVC3::RATIONAL_EXPR, CVC3::REAL_CONST, CVC3::Expr::setType(), CVC3::Expr::toString(), CVC3::Type::toString(), and CVC3::UMINUS.
Compute the base type of the top-level operator of an arbitrary type.
Implements CVC3::TheoryArith.
Definition at line 1985 of file theory_arith_new.cpp.
References DebugAssert, CVC3::Type::getExpr(), CVC3::Expr::getKind(), IF_DEBUG, CVC3::INT, CVC3::REAL, CVC3::TheoryArith::realType(), CVC3::SUBRANGE, and CVC3::Type::toString().
Add variables from 'e' to 'v' for constructing a concrete model.
If e is already of primitive type, do NOT add it to v.
Implements CVC3::TheoryArith.
Definition at line 1829 of file theory_arith_new.cpp.
References CVC3::Expr::begin(), CVC3::DIVIDE, CVC3::Expr::end(), CVC3::Theory::findExpr(), CVC3::Expr::getKind(), CVC3::MULT, CVC3::PLUS, CVC3::POW, CVC3::RATIONAL_EXPR, CVC3::Expr::toString(), and CVC3::TRACE.
Theory specific computation of the subtyping predicate for type t applied to the expression e.
By default returns true. Each theory needs to compute subtype predicates for the types associated with it. So, for example, the theory of records will take a record type [# f1: T1, f2: T2 #] and an expression e and will return the subtyping predicate for e, namely: computeTypePred(T1, e.f1) AND computeTypePred(T2, e.f2)
Implements CVC3::TheoryArith.
Definition at line 1856 of file theory_arith_new.cpp.
References CVC3::andExpr(), CVC3::Expr::getEM(), CVC3::Type::getExpr(), CVC3::Expr::getKind(), CVC3::INT, CVC3::IS_INTEGER, CVC3::leExpr(), CVC3::SUBRANGE, and CVC3::ExprManager::trueExpr().
Compute and cache the TCC of e.
| e | is an expression (term or formula). This function computes the TCC of e which is true iff the expression is defined. |
The default implementation is to compute TCCs recursively for all children, and return their conjunction.
Implements CVC3::TheoryArith.
Definition at line 1992 of file theory_arith_new.cpp.
References CVC3::Expr::andExpr(), CVC3::Theory::computeTCC(), DebugAssert, CVC3::DIVIDE, and CVC3::TheoryArith::rat().
| ExprStream & TheoryArithNew::print | ( | ExprStream & | os, | |
| const Expr & | e | |||
| ) | [virtual] |
Theory-specific pretty-printing.
By default, print the top node in AST, and resume pretty-printing the children. The same call e.print(os) can be used in DP-specific printers to use AST printing for the given node. In fact, it is strongly recommended to add e.print(os) as the default for all the cases/kinds that are not handled by the particular pretty-printer.
Implements CVC3::TheoryArith.
Definition at line 2117 of file theory_arith_new.cpp.
References CVC3::Expr::arity(), CVC3::DARK_SHADOW, CVC3::DIVIDE, CVC3::GE, CVC3::Expr::getKind(), CVC3::GRAY_SHADOW, CVC3::GT, CVC3::INT, CVC3::IS_INTEGER, CVC3::isInt(), CVC3::ExprStream::lang(), CVC3::LE, CVC3::LISP_LANG, CVC3::LT, CVC3::MINUS, CVC3::MULT, CVC3::NEGINF, CVC3::PLUS, CVC3::POSINF, CVC3::POW, CVC3::PRESENTATION_LANG, CVC3::Expr::print(), CVC3::TheoryArith::printRational(), CVC3::push(), CVC3::RATIONAL_EXPR, CVC3::REAL, CVC3::REAL_CONST, CVC3::SIMPLIFY_LANG, CVC3::SMTLIB_LANG, CVC3::space(), CVC3::SUBRANGE, and CVC3::UMINUS.
Theory-specific parsing implemented by the DP.
Implements CVC3::TheoryArith.
Definition at line 2007 of file theory_arith_new.cpp.
References CVC3::Expr::arity(), CVC3::Expr::begin(), DebugAssert, CVC3::DIVIDE, CVC3::divideExpr(), CVC3::Expr::end(), CVC3::GE, CVC3::geExpr(), CVC3::Expr::getEM(), CVC3::Theory::getEM(), CVC3::ExprManager::getKind(), CVC3::Expr::getKind(), CVC3::GT, CVC3::gtExpr(), CVC3::ID, CVC3::INT, CVC3::INTDIV, CVC3::IS_INTEGER, CVC3::LE, CVC3::leExpr(), CVC3::LT, CVC3::ltExpr(), CVC3::MINUS, CVC3::minusExpr(), CVC3::MOD, CVC3::MULT, CVC3::multExpr(), CVC3::NEGINF, CVC3::ExprManager::newLeafExpr(), CVC3::NULL_KIND, CVC3::Theory::parseExpr(), CVC3::PLUS, CVC3::plusExpr(), CVC3::POSINF, CVC3::POW, CVC3::powExpr(), CVC3::RAW_LIST, CVC3::REAL, CVC3::SUBRANGE, CVC3::Expr::toString(), CVC3::TRACE, CVC3::UMINUS, and CVC3::uminusExpr().
| void TheoryArithNew::registerAtom | ( | const Expr & | e | ) | [virtual] |
Registers the atom given from the core. This atoms are stored so that they can be used for theory propagation.
| e | the expression (atom) that is part of the input formula |
Reimplemented from CVC3::Theory.
Definition at line 3825 of file theory_arith_new.cpp.
References allBounds, FatalAssert, CVC3::GE, CVC3::Expr::getKind(), CVC3::Expr::getRational(), CVC3::GT, CVC3::Expr::isAbsAtomicFormula(), CVC3::LE, CVC3::LT, CVC3::Expr::toString(), and CVC3::TRACE.
Return a Gomory cut plane derivation of the variable $x_i$. Mixed integer Gomory cut can be constructed if
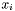 is a integer basic variable with a non-integer value
is a integer basic variable with a non-integer value 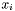 are assigned to their upper or lower bounds
are assigned to their upper or lower bounds Definition at line 3977 of file theory_arith_new.cpp.
References DebugAssert, getBeta(), CVC3::TheoryArithNew::EpsRational::getRational(), intVariables, isBasic(), and CVC3::Expr::toString().
Tries to rafine the integer constraint of the theorem. For example, x < 1 is rewritten as x <= 0, and x <(=) 1.5 is rewritten as x <= 1. The constraint should be in the normal form.
| thm | the derivation of the constraint |
Definition at line 1537 of file theory_arith_new.cpp.
References d_rules, CVC3::Expr::getKind(), CVC3::Expr::getRational(), CVC3::Theorem::getRHS(), CVC3::GT, CVC3::Rational::isInteger(), isIntegerThm(), CVC3::Theorem::isNull(), CVC3::LT, CVC3::ArithProofRules::rafineStrictInteger(), CVC3::TRACE, and CVC3::Theory::transitivityRule().
| void TheoryArithNew::propagateTheory | ( | const Expr & | assertExpr, | |
| const EpsRational & | bound, | |||
| const EpsRational & | oldBound | |||
| ) | [private] |
Propagate all that is possible from given assertion and its bound
Definition at line 3872 of file theory_arith_new.cpp.
References allBounds, d_rules, DebugAssert, CVC3::Theory::enqueueFact(), CVC3::Theory::find(), CVC3::Theory::findExpr(), CVC3::GE, CVC3::Theorem::getExpr(), CVC3::Expr::getKind(), CVC3::GT, CVC3::ArithProofRules::implyNegatedInequality(), CVC3::ArithProofRules::implyWeakerInequality(), CVC3::LE, CVC3::LT, CVC3::Theorem::toString(), CVC3::TheoryArithNew::EpsRational::toString(), CVC3::Expr::toString(), and CVC3::TRACE.
Referenced by assertFact().
Adds var to the dependencies sets of all the variables in the sum.
| var | the variable on the left side | |
| the | sum that defines the variable |
Definition at line 3745 of file theory_arith_new.cpp.
References CVC3::Expr::begin(), dependenciesMap, CVC3::Expr::end(), CVC3::Expr::toString(), and CVC3::TRACE.
Referenced by getVariableIntroThm(), and pivot().
Remove var from the dependencies sets of all the variables in the sum.
| var | the variable on the left side | |
| the | sum that defines the variable |
Definition at line 3758 of file theory_arith_new.cpp.
References CVC3::Expr::begin(), dependenciesMap, CVC3::Expr::end(), CVC3::Expr::toString(), and CVC3::TRACE.
Referenced by pivot().
| void TheoryArithNew::updateDependencies | ( | const Expr & | oldExpr, | |
| const Expr & | newExpr, | |||
| const Expr & | var, | |||
| const Expr & | skipVar | |||
| ) | [private] |
Updates the dependencies if a right side of an expression in the tableaux is changed. For example, if oldExpr is x + y and newExpr is y + z, var will be added to the dependency list of z, and removed from the dependency list of x.
| oldExpr | the old right side of the tableaux | |
| newExpr | the new right side of the tableaux | |
| var | the variable that is defined by these two expressions | |
| var | a variable to skip when going through the expressions |
Definition at line 3771 of file theory_arith_new.cpp.
References CVC3::Expr::arity(), dependenciesMap, Hash::hash_map< _Key, _Data, _HashFcn, _EqualKey >::erase(), Hash::hash_map< _Key, _Data, _HashFcn, _EqualKey >::insert(), CVC3::Theory::newVar(), CVC3::Expr::toString(), and CVC3::TRACE.
Referenced by substAndCanonizeTableaux().
| void TheoryArithNew::updateFreshVariables | ( | ) | [private] |
Update the values of variables that have appeared in the tableaux due to backtracking.
Definition at line 3731 of file theory_arith_new.cpp.
References assertedExpr, assertedExprCount, and updateValue().
Referenced by assertFact(), and checkSat().
Updates the value of variable var by computing the value of expression e.
| var | the variable to update | |
| e | the expression to compute |
Definition at line 3195 of file theory_arith_new.cpp.
References CVC3::Expr::arity(), beta, getBeta(), getLowerBound(), getUpperBound(), and unsatBasicVariables.
Referenced by getVariableIntroThm(), and updateFreshVariables().
| string TheoryArithNew::tableauxAsString | ( | ) | const [private] |
Returns a string representation of the tableaux.
Definition at line 3215 of file theory_arith_new.cpp.
References Hash::hash_map< _Key, _Data, _HashFcn, _EqualKey >::begin(), Hash::hash_map< _Key, _Data, _HashFcn, _EqualKey >::end(), and tableaux.
Referenced by assertFact(), and checkSatSimplex().
| string TheoryArithNew::unsatAsString | ( | ) | const [private] |
Returns a string representation of the unsat variables.
Definition at line 3237 of file theory_arith_new.cpp.
References unsatBasicVariables.
Referenced by assertFact(), and checkSatSimplex().
| string TheoryArithNew::boundsAsString | ( | ) | [private] |
Returns a string representation of the current bounds.
Definition at line 3260 of file theory_arith_new.cpp.
References CVC3::Expr::arity(), Hash::hash_map< _Key, _Data, _HashFcn, _EqualKey >::begin(), Hash::hash_map< _Key, _Data, _HashFcn, _EqualKey >::end(), getBeta(), getLowerBound(), getUpperBound(), lowerBound, tableaux, CVC3::Expr::toString(), CVC3::TheoryArithNew::EpsRational::toString(), and upperBound.
Referenced by assertFact(), and checkSatSimplex().
Gets the equality of the fresh variable tableaux variable corresponding to this expression. If the expression has already been asserted, the coresponding variable is returned, othervise a fresh variable is created and the theorem is returned.
| leftSide | the left side of the asserted constraint |
Definition at line 3145 of file theory_arith_new.cpp.
References assertedExpr, assertedExprCount, Hash::hash_map< _Key, _Data, _HashFcn, _EqualKey >::end(), CVC3::EQ, Hash::hash_map< _Key, _Data, _HashFcn, _EqualKey >::find(), CVC3::Theory::find(), freshVariables, CVC3::Theory::getCommonRules(), CVC3::Theorem::getExpr(), substAndCanonizeModTableaux(), CVC3::Theory::symmetryRule(), tableaux, updateDependenciesAdd(), updateValue(), and CVC3::CommonProofRules::varIntroRule().
Referenced by assertFact().
Find the coefficient standing by the variable var in the expression expr. Expresion is expected to be in canonical form, i.e either a rational constant, an arithmetic leaf (i.e. variable or term from some other theory), (MULT rat leaf) where rat is a non-zero rational constant, leaf is an arithmetic leaf or (PLUS 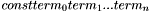 ) where each
) where each 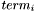 is either a leaf or (MULT
is either a leaf or (MULT 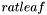 ) and each leaf in
) and each leaf in 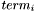 must be strictly greater than the leaf in
must be strictly greater than the leaf in 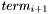 .
.
| var | the variable | |
| expr | the expression to search in |
Definition at line 2915 of file theory_arith_new.cpp.
References CVC3::Expr::arity(), CVC3::compare(), DebugAssert, CVC3::Expr::getRational(), CVC3::isMult(), CVC3::isPlus(), CVC3::isRational(), MiniSat::left(), MiniSat::right(), and CVC3::Expr::toString().
Referenced by getTableauxEntry().
| bool TheoryArithNew::isBasic | ( | const Expr & | x | ) | const [private] |
Return true iof the given variable is basic in the tableaux, i.e. it is on the left side, expressed in terms of the non-basic variables.
| x | the variable to be checked |
Definition at line 2461 of file theory_arith_new.cpp.
References Hash::hash_map< _Key, _Data, _HashFcn, _EqualKey >::end(), Hash::hash_map< _Key, _Data, _HashFcn, _EqualKey >::find(), and tableaux.
Referenced by assertLower(), assertUpper(), deriveGomoryCut(), and pivot().
Returns the coefficient at a_ij in the current tableaux, i.e. the coefficient at x_j in the row of x_i.
| x_i | a basic variable | |
| x_j | a non-basic variable |
Definition at line 2910 of file theory_arith_new.cpp.
References findCoefficient(), and tableaux.
Referenced by pivotAndUpdate(), and update().
Swaps a basic variable 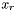 and a non-basic variable
and a non-basic variable 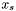 such that ars
such that ars 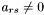 . After pivoting,
. After pivoting, 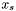 becomes basic and
becomes basic and 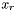 becomes non-basic. The tableau is updated by replacing equation
becomes non-basic. The tableau is updated by replacing equation
![\[x_r = \sum_{x_j \in N}{a_{rj}xj}\]](form_281.png)
with
![\[x_s = \frac{x_r}{a_{rs}} - \sum_{x_j \in N }{\frac{a_{rj}}{a_rs}x_j}\]](form_282.png)
and this equation is used to eliminate 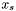 from the rest of the tableau by substitution.
from the rest of the tableau by substitution.
| x_r | a basic variable | |
| x_s | a non-basic variable |
Definition at line 2466 of file theory_arith_new.cpp.
References DebugAssert, Hash::hash_map< _Key, _Data, _HashFcn, _EqualKey >::erase(), Hash::hash_map< _Key, _Data, _HashFcn, _EqualKey >::find(), CVC3::Theorem::getExpr(), isBasic(), pivotRule(), substAndCanonizeTableaux(), tableaux, CVC3::Expr::toString(), CVC3::TRACE, updateDependenciesAdd(), and updateDependenciesRemove().
Referenced by pivotAndUpdate().
| void TheoryArithNew::update | ( | const Expr & | x_i, | |
| const EpsRational & | v | |||
| ) | [private] |
Sets the value of a non-basic variable 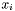 to
to 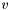 and adjusts the value of all the basic variables so that all equations remain satisfied.
and adjusts the value of all the basic variables so that all equations remain satisfied.
| x_i | a non-basic variable | |
| v | the value to set the variable 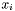 to to |
Definition at line 2500 of file theory_arith_new.cpp.
References beta, DebugAssert, dependenciesMap, Hash::hash_map< _Key, _Data, _HashFcn, _EqualKey >::end(), CVC3::Theory::find(), Hash::hash_map< _Key, _Data, _HashFcn, _EqualKey >::find(), getBeta(), getLowerBound(), getTableauxEntry(), getUpperBound(), tableaux, CVC3::TheoryArithNew::EpsRational::toString(), CVC3::Expr::toString(), CVC3::TRACE, and unsatBasicVariables.
| void TheoryArithNew::pivotAndUpdate | ( | const Expr & | x_i, | |
| const Expr & | x_j, | |||
| const EpsRational & | v | |||
| ) | [private] |
Pivots the basic variable 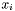 and the non-basic variable
and the non-basic variable 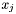 . It also sets
. It also sets 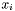 to
to 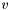 and adjusts all basic variables to keep the equations satisfied.
and adjusts all basic variables to keep the equations satisfied.
| x_i | a basic variable | |
| x_j | a non-basic variable | |
| v | the valie to assign to x_i |
Definition at line 2547 of file theory_arith_new.cpp.
References beta, DebugAssert, dependenciesMap, Hash::hash_map< _Key, _Data, _HashFcn, _EqualKey >::end(), Hash::hash_map< _Key, _Data, _HashFcn, _EqualKey >::find(), getBeta(), getLowerBound(), getTableauxEntry(), getUpperBound(), pivot(), tableaux, CVC3::TheoryArithNew::EpsRational::toString(), CVC3::Expr::toString(), CVC3::TRACE, and unsatBasicVariables.
Referenced by checkSatSimplex().
| QueryResult TheoryArithNew::assertUpper | ( | const Expr & | x_i, | |
| const EpsRational & | c, | |||
| const Theorem & | thm | |||
| ) | [private] |
Asserts a new upper bound constraint on a variable and performs a simple check for consistency (not complete).
| x_i | the variable to assert the bound on |
Definition at line 2612 of file theory_arith_new.cpp.
References CVC3::ArithProofRules::clashingBounds(), consistent, d_rules, DebugAssert, explanation, getBeta(), getLowerBound(), getLowerBoundThm(), getUpperBound(), isBasic(), CVC3::Theory::isLeaf(), propagate, CVC3::SATISFIABLE, CVC3::TheoryArithNew::EpsRational::toString(), CVC3::Expr::toString(), CVC3::TRACE, CVC3::UNKNOWN, unsatBasicVariables, CVC3::UNSATISFIABLE, update(), and upperBound.
Referenced by assertEqual(), and assertFact().
| QueryResult TheoryArithNew::assertLower | ( | const Expr & | x_i, | |
| const EpsRational & | c, | |||
| const Theorem & | thm | |||
| ) | [private] |
Asserts a new lower bound constraint on a variable and performs a simple check for consistency (not complete).
| x_i | the variable to assert the bound on |
Definition at line 2649 of file theory_arith_new.cpp.
References CVC3::ArithProofRules::clashingBounds(), consistent, d_rules, DebugAssert, explanation, getBeta(), getLowerBound(), getUpperBound(), getUpperBoundThm(), isBasic(), CVC3::Theory::isLeaf(), lowerBound, propagate, CVC3::SATISFIABLE, CVC3::TheoryArithNew::EpsRational::toString(), CVC3::Expr::toString(), CVC3::TRACE, CVC3::UNKNOWN, unsatBasicVariables, CVC3::UNSATISFIABLE, and update().
Referenced by assertEqual(), and assertFact().
| QueryResult TheoryArithNew::assertEqual | ( | const Expr & | x_i, | |
| const EpsRational & | c, | |||
| const Theorem & | thm | |||
| ) | [private] |
Asserts a new equality constraint on a variable by asserting both upper and lower bound.
| x_i | the variable to assert the bound on |
Definition at line 2686 of file theory_arith_new.cpp.
References assertLower(), assertUpper(), consistent, and CVC3::UNSATISFIABLE.
Referenced by assertFact().
| Expr TheoryArithNew::computeNormalFactor | ( | const Expr & | rhs, | |
| NormalizationType | type = NORMALIZE_GCD | |||
| ) | [private] |
Given a canonized term, compute a factor to make all coefficients integer and relatively prime
Definition at line 850 of file theory_arith_new.cpp.
References DebugAssert, CVC3::isPlus(), CVC3::isRational(), CVC3::MULT, NORMALIZE_UNIT, CVC3::TheoryArith::rat(), CVC3::RATIONAL_EXPR, and MiniSat::right().
Referenced by normalize().
| Theorem TheoryArithNew::normalize | ( | const Expr & | e, | |
| NormalizationType | type = NORMALIZE_GCD | |||
| ) | [private] |
Normalize an equation (make all coefficients rel. prime integers)
Definition at line 1464 of file theory_arith_new.cpp.
References canonPredEquiv(), computeNormalFactor(), d_rules, DebugAssert, FatalAssert, CVC3::GE, CVC3::Expr::getKind(), CVC3::GT, CVC3::isIneq(), CVC3::isMult(), CVC3::isPlus(), CVC3::isRational(), CVC3::LE, CVC3::LT, CVC3::ArithProofRules::multIneqn(), CVC3::TheoryArith::rat(), CVC3::Theory::reflexivityRule(), CVC3::Expr::toString(), and CVC3::TRACE.
Referenced by doSolve(), normalize(), and rewrite().
| Theorem TheoryArithNew::normalize | ( | const Theorem & | thm, | |
| NormalizationType | type = NORMALIZE_GCD | |||
| ) | [private] |
Normalize an equation (make all coefficients rel. prime integers) accepts a rewrite theorem over eqn|ineqn and normalizes it and returns a theorem to that effect.
Definition at line 1533 of file theory_arith_new.cpp.
References CVC3::Theorem::getRHS(), normalize(), and CVC3::Theory::transitivityRule().
Canonise the equation using the tebleaux equations, i.e. replace all the tableaux right sides with the corresponding left sides and canonise the result.
| eq | the equation to canonise |
Definition at line 3319 of file theory_arith_new.cpp.
References DebugAssert, Hash::hash_map< _Key, _Data, _HashFcn, _EqualKey >::empty(), CVC3::EQ, CVC3::Theorem::getExpr(), CVC3::Expr::getKind(), CVC3::Theorem::getRHS(), CVC3::Theory::iffMP(), CVC3::Theory::substitutivityRule(), tableaux, and CVC3::Expr::toString().
Referenced by getVariableIntroThm().
Canonise the sum using the tebleaux equations, i.e. replace all the tableaux right sides with the corresponding left sides and canonise the result.
| sum | the canonised sum to canonise | |
| the | explaining theorem |
Definition at line 3343 of file theory_arith_new.cpp.
References CVC3::Expr::arity(), CVC3::TheoryArith::canonThm(), DebugAssert, Hash::hash_map< _Key, _Data, _HashFcn, _EqualKey >::end(), Hash::hash_map< _Key, _Data, _HashFcn, _EqualKey >::find(), CVC3::Theory::find(), CVC3::Expr::getKind(), CVC3::PLUS, CVC3::Theory::reflexivityRule(), CVC3::Theory::substitutivityRule(), tableaux, CVC3::Expr::toString(), and CVC3::TRACE.
| void TheoryArithNew::substAndCanonizeTableaux | ( | const Theorem & | eq | ) | [private] |
Sustitute the given equation everywhere in the tableaux.
| eq | the equation to use for substitution |
Definition at line 3396 of file theory_arith_new.cpp.
References CVC3::Expr::arity(), CVC3::TheoryArith::canonThm(), CVC3::compare(), DebugAssert, dependenciesMap, Hash::hash_map< _Key, _Data, _HashFcn, _EqualKey >::end(), CVC3::EQ, Hash::hash_map< _Key, _Data, _HashFcn, _EqualKey >::find(), CVC3::Theory::find(), CVC3::Theorem::getExpr(), CVC3::Theorem::getRHS(), CVC3::Theory::iffMP(), MiniSat::left(), MiniSat::right(), CVC3::Theory::substitutivityRule(), tableaux, CVC3::TRACE, and updateDependencies().
Referenced by pivot().
Given an equality eq: 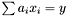 and a variable $var$ that appears in on the left hand side, pivots $y$ and $var$ so that $y$ comes to the right-hand side.
and a variable $var$ that appears in on the left hand side, pivots $y$ and $var$ so that $y$ comes to the right-hand side.
| eq | the proof of the equality | |
| var | the variable to move to the right-hand side |
Definition at line 3472 of file theory_arith_new.cpp.
References CVC3::Expr::arity(), canon(), d_rules, DebugAssert, CVC3::EQ, CVC3::Theorem::getExpr(), CVC3::Expr::getKind(), CVC3::Expr::getRational(), CVC3::Theory::iffMP(), CVC3::Theory::isLeaf(), CVC3::ArithProofRules::multEqn(), CVC3::multExpr(), CVC3::ArithProofRules::oneElimination(), CVC3::PLUS, CVC3::plusExpr(), CVC3::ArithProofRules::plusPredicate(), CVC3::TheoryArith::rat(), CVC3::Theory::symmetryRule(), CVC3::Expr::toString(), CVC3::TRACE, and CVC3::Theory::transitivityRule().
Referenced by pivot().
| Theorem TheoryArithNew::getLowerBoundExplanation | ( | const TebleauxMap::iterator & | var_it | ) | [private] |
Knowing that the tableaux row for 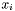 is the problematic one, generate the explanation clause. The variables in the row of
is the problematic one, generate the explanation clause. The variables in the row of 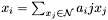 are separatied to
are separatied to
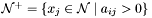
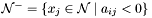
![\[\Gamma = \left\lbrace x_j \leq u_j \; | \; x_j \in \mathcal{N}^+\right\rbrace \cup \left\lbrace l_j \leq x_j \; | \; x_j \in \mathcal{N}^-\right\rbrace \cup \left\lbrace l_i \leq x_i \right\rbrace\]](form_288.png)
| var | the variable that caused the clash |
Definition at line 3534 of file theory_arith_new.cpp.
References CVC3::ArithProofRules::addInequalities(), CVC3::Expr::arity(), CVC3::ArithProofRules::canonMultConstConst(), CVC3::ArithProofRules::canonMultTermConst(), CVC3::ArithProofRules::canonPlus(), CVC3::ArithProofRules::clashingBounds(), d_rules, CVC3::Theorem::getExpr(), getLowerBoundThm(), getUpperBoundThm(), CVC3::Theory::iffMP(), CVC3::ArithProofRules::multIneqn(), CVC3::Theory::substitutivityRule(), and CVC3::Theory::symmetryRule().
Referenced by checkSatSimplex().
| Theorem TheoryArithNew::getUpperBoundExplanation | ( | const TebleauxMap::iterator & | var_it | ) | [private] |
Knowing that the tableaux row for 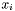 is the problematic one, generate the explanation clause. The variables in the row of
is the problematic one, generate the explanation clause. The variables in the row of 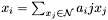 are separatied to
are separatied to
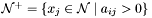
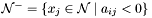
![\[\Gamma = \left\lbrace x_j \leq u_j \; | \; x_j \in \mathcal{N}^-\right\rbrace \cup \left\lbrace l_j \leq x_j \; | \; x_j \in \mathcal{N}^+\right\rbrace \cup \left\lbrace x_i \leq u_i \right\rbrace\]](form_289.png)
| var | the variable that caused the clash |
Definition at line 3621 of file theory_arith_new.cpp.
References CVC3::ArithProofRules::addInequalities(), CVC3::Expr::arity(), CVC3::ArithProofRules::canonMultConstConst(), CVC3::ArithProofRules::canonMultTermConst(), CVC3::ArithProofRules::canonPlus(), CVC3::ArithProofRules::clashingBounds(), d_rules, getBeta(), CVC3::Theorem::getExpr(), getLowerBoundThm(), getUpperBoundThm(), CVC3::Theory::iffMP(), CVC3::ArithProofRules::multIneqn(), CVC3::Theory::substitutivityRule(), CVC3::Theory::symmetryRule(), and CVC3::TRACE.
Referenced by checkSatSimplex().
| Theorem CVC3::TheoryArithNew::addInequalities | ( | const Theorem & | le_1, | |
| const Theorem & | le_2 | |||
| ) | [private] |
| QueryResult TheoryArithNew::checkSatSimplex | ( | ) | [private] |
Check the satisfiability
Definition at line 2788 of file theory_arith_new.cpp.
References CVC3::Expr::arity(), boundsAsString(), explanation, Hash::hash_map< _Key, _Data, _HashFcn, _EqualKey >::find(), getBeta(), getLowerBound(), getLowerBoundExplanation(), CVC3::Expr::getRational(), getUpperBound(), getUpperBoundExplanation(), pivotAndUpdate(), CVC3::SATISFIABLE, Hash::hash_map< _Key, _Data, _HashFcn, _EqualKey >::size(), tableaux, tableauxAsString(), CVC3::TRACE, unsatAsString(), unsatBasicVariables, and CVC3::UNSATISFIABLE.
Referenced by checkSat().
| QueryResult TheoryArithNew::checkSatInteger | ( | ) | [private] |
Check the satisfiability of integer constraints
Definition at line 2740 of file theory_arith_new.cpp.
References beta, d_rules, CVC3::Theory::enqueueFact(), getBeta(), integer_lemma, CVC3::ArithProofRules::integerSplit(), intVariables, isInteger(), CVC3::SATISFIABLE, CVC3::TRACE, and CVC3::UNKNOWN.
| TheoryArithNew::EpsRational TheoryArithNew::getLowerBound | ( | const Expr & | x | ) | const |
Gets the current lower bound on variable x.
| x | the variable |
Definition at line 2954 of file theory_arith_new.cpp.
References CVC3::Theory::find(), lowerBound, and CVC3::TheoryArithNew::EpsRational::MinusInfinity.
Referenced by assertFact(), assertLower(), assertUpper(), boundsAsString(), checkSatSimplex(), getBeta(), pivotAndUpdate(), update(), and updateValue().
| TheoryArithNew::EpsRational TheoryArithNew::getUpperBound | ( | const Expr & | x | ) | const |
Get the current upper bound on variable x.
| x | the variable |
Definition at line 2962 of file theory_arith_new.cpp.
References CVC3::Theory::find(), CVC3::TheoryArithNew::EpsRational::PlusInfinity, and upperBound.
Referenced by assertFact(), assertLower(), assertUpper(), boundsAsString(), checkSatSimplex(), getBeta(), pivotAndUpdate(), update(), and updateValue().
Gets the theorem of the current lower bound on variable x.
| x | the variable |
Definition at line 2970 of file theory_arith_new.cpp.
References DebugAssert, CVC3::Theory::find(), lowerBound, and CVC3::Expr::toString().
Referenced by assertUpper(), getLowerBoundExplanation(), and getUpperBoundExplanation().
Get the theorem of the current upper bound on variable x.
| x | the variable |
Definition at line 2979 of file theory_arith_new.cpp.
References DebugAssert, CVC3::Theory::find(), CVC3::Expr::toString(), and upperBound.
Referenced by assertLower(), getLowerBoundExplanation(), and getUpperBoundExplanation().
| TheoryArithNew::EpsRational TheoryArithNew::getBeta | ( | const Expr & | x | ) |
Gets the current valuation of variable x (beta).
| x | the variable |
Definition at line 2989 of file theory_arith_new.cpp.
References beta, CVC3::Theory::find(), getLowerBound(), getUpperBound(), unsatBasicVariables, and CVC3::TheoryArithNew::EpsRational::Zero.
Referenced by assertLower(), assertUpper(), boundsAsString(), checkSatInteger(), checkSatSimplex(), deriveGomoryCut(), getUpperBoundExplanation(), pivotAndUpdate(), update(), and updateValue().
Check the term t for integrality.
| Theorem CVC3::TheoryArithNew::isIntegerDerive | ( | const Expr & | isIntE, | |
| const Theorem & | thm | |||
| ) | [private] |
A helper method for isIntegerThm().
Check if IS_INTEGER(e) is easily derivable from the given 'thm'
| bool CVC3::TheoryArithNew::isInteger | ( | const Expr & | e | ) | [inline, private] |
Check the term t for integrality (return bool).
Definition at line 149 of file theory_arith_new.mine.h.
References isIntegerThm(), and CVC3::Theorem::isNull().
| bool CVC3::TheoryArithNew::kidsCanonical | ( | const Expr & | e | ) | [private] |
Check if the kids of e are fully simplified and canonized (for debugging).
Canonize and reduce e w.r.t. union-find database; assume all children are canonical.
Composition of canonSimplify(const Expr&) by transitivity: take e0 = e1, canonize and simplify e1 to e2, return e0 = e2.
Definition at line 161 of file theory_arith_new.mine.h.
References canonSimplify(), CVC3::Theorem::getRHS(), and CVC3::Theory::transitivityRule().
Canonize predicate (x = y, x < y, etc.).
Canonize predicate like canonPred except that the input theorem is an equivalent transformation.
Solve an equation and return an equivalent Theorem in the solved form.
takes in a conjunction equivalence Thm and canonizes it.
picks the monomial with the smallest abs(coeff) from the input
processes equalities with 1 or more vars of type REAL
processes equalities whose vars are all of type INT
One step of INT equality processing (aux. method for processIntEq()).
Take an inequality and isolate a variable.
Update the statistics counters for the variable with a coeff. c.
| void CVC3::TheoryArithNew::updateStats | ( | const Expr & | monomial | ) | [private] |
Update the statistics counters for the monomial.
| void CVC3::TheoryArithNew::addToBuffer | ( | const Theorem & | thm | ) | [private] |
Add an inequality to the input buffer. See also d_buffer.
| bool CVC3::TheoryArithNew::isStale | ( | const Expr & | e | ) | [private] |
Check if the term expression is "stale".
| bool CVC3::TheoryArithNew::isStale | ( | const Ineq & | ineq | ) | [private] |
Check if the inequality is "stale" or subsumed.
| void CVC3::TheoryArithNew::projectInequalities | ( | const Theorem & | theInequality, | |
| bool | isolatedVarOnRHS | |||
| ) | [private] |
| void CVC3::TheoryArithNew::assignVariables | ( | std::vector< Expr > & | v | ) | [private] |
| void CVC3::TheoryArithNew::findRationalBound | ( | const Expr & | varSide, | |
| const Expr & | ratSide, | |||
| const Expr & | var, | |||
| Rational & | r | |||
| ) | [private] |
| Theorem CVC3::TheoryArithNew::normalizeProjectIneqs | ( | const Theorem & | ineqThm1, | |
| const Theorem & | ineqThm2 | |||
| ) | [private] |
Take a system of equations and turn it into a solved form.
| Theorem CVC3::TheoryArithNew::substAndCanonize | ( | const Expr & | t, | |
| ExprMap< Theorem > & | subst | |||
| ) | [private] |
Substitute all vars in term 't' according to the substitution 'subst' and canonize the result.
| Theorem CVC3::TheoryArithNew::substAndCanonize | ( | const Theorem & | eq, | |
| ExprMap< Theorem > & | subst | |||
| ) | [private] |
Substitute all vars in the RHS of the equation 'eq' of the form (x = t) according to the substitution 'subst', and canonize the result.
| void CVC3::TheoryArithNew::collectVars | ( | const Expr & | e, | |
| std::vector< Expr > & | vars, | |||
| std::set< Expr > & | cache | |||
| ) | [private] |
Traverse 'e' and push all the i-leaves into 'vars' vector.
| void CVC3::TheoryArithNew::processFiniteInterval | ( | const Theorem & | alphaLEax, | |
| const Theorem & | bxLEbeta | |||
| ) | [private] |
Check if alpha <= ax & bx <= beta is a finite interval for integer var 'x', and assert the corresponding constraint.
| void CVC3::TheoryArithNew::processFiniteIntervals | ( | const Expr & | x | ) | [private] |
For an integer var 'x', find and process all constraints A <= ax <= A+c.
| void CVC3::TheoryArithNew::setupRec | ( | const Expr & | e | ) | [private] |
Recursive setup for isolated inequalities (and other new expressions).
| ArithProofRules* CVC3::TheoryArithNew::createProofRules | ( | ) |
| void CVC3::TheoryArithNew::addSharedTerm | ( | const Expr & | e | ) | [virtual] |
Notify theory of a new shared term.
When a term e associated with theory i occurs as a child of an expression associated with theory j, the framework calls i->addSharedTerm(e) and j->addSharedTerm(e)
Implements CVC3::TheoryArith.
| void CVC3::TheoryArithNew::assertFact | ( | const Theorem & | e | ) | [virtual] |
Assert a new fact to the decision procedure.
Each fact that makes it into the core framework is assigned to exactly one theory: the theory associated with that fact. assertFact is called to inform the theory that a new fact has been assigned to the theory.
Implements CVC3::TheoryArith.
| void CVC3::TheoryArithNew::refineCounterExample | ( | ) | [virtual] |
| void CVC3::TheoryArithNew::computeModelBasic | ( | const std::vector< Expr > & | v | ) | [virtual] |
Compute the value of a compound variable from the more primitive ones.
The more primitive variables for e are already assigned concrete values, and are available through getModelValue().
The new value for e must be assigned using assignValue() method.
| e | is the compound type expression to assign a value; | |
| vars | are the variables actually assigned. Normally, 'e' is the only element of vars. However, e.g. in the case of uninterpreted functions, assigning 'f' means assigning all relevant applications of 'f' to constant values (f(0), f(5), etc.). Such applications might not be known before the model is constructed (they may be of the form f(x), f(y+z), etc., where x,y,z are still unassigned). |
Implements CVC3::TheoryArith.
| void CVC3::TheoryArithNew::checkSat | ( | bool | fullEffort | ) | [virtual] |
Check for satisfiability in the theory.
| fullEffort | when it is false, checkSat can do as much or as little work as it likes, though simple inferences and checks for consistency should be done to increase efficiency. If fullEffort is true, checkSat must check whether the set of facts given by assertFact together with the arrangement of shared terms (provided by addSharedTerm) induced by the global find database equivalence relation are satisfiable. If satisfiable, checkSat does nothing. |
Implements CVC3::TheoryArith.
Theory-specific rewrite rules.
By default, rewrite just returns a reflexive theorem stating that the input expression is equivalent to itself. However, rewrite is allowed to return any theorem which describes how the input expression is equivalent to some new expression. rewrite should be used to perform simplifications, normalization, and any other preprocessing on theory-specific expressions that needs to be done.
Implements CVC3::TheoryArith.
| void CVC3::TheoryArithNew::setup | ( | const Expr & | e | ) | [virtual] |
Set up the term e for call-backs when e or its children change.
setup is called once for each expression associated with the theory. It is typically used to setup theory-specific data for an expression and to add call-back information for use with update.
Implements CVC3::TheoryArith.
Notify a theory of a new equality.
update is a call-back used by the notify mechanism of the core theory. It works as follows. When an equation t1 = t2 makes it into the core framework, the two find equivalence classes for t1 and t2 are merged. The result is that t2 is the new equivalence class representative and t1 is no longer an equivalence class representative. When this happens, the notify list of t1 is traversed. Notify list entries consist of a theory and an expression d. For each entry (i,d), i->update(e, d) is called, where e is the theorem corresponding to the equality t1=t2.
To add the entry (i,d) to a term t1's notify list, a call must be made to t1.addNotify(i,d). This is typically done in setup.
Implements CVC3::TheoryArith.
An optional solver.
The solve method can be used to implement a Shostak-style solver. Since solvers do not in general combine, the following technique is used. One theory is designated as the primary solver (in our case, it is the theory of arithmetic). For each equation that enters the core framework, the primary solver is called to ensure that the equation is in solved form with respect to the primary theory.
After the primary solver, the solver for the theory associated with the equation is called. This solver can do whatever it likes, as long as the result is still in solved form with respect to the primary solver. This is a slight generalization of what is described in my (Clark)'s PhD thesis.
Implements CVC3::TheoryArith.
| void CVC3::TheoryArithNew::checkAssertEqInvariant | ( | const Theorem & | e | ) | [virtual] |
| void CVC3::TheoryArithNew::checkType | ( | const Expr & | e | ) | [virtual] |
| void CVC3::TheoryArithNew::computeType | ( | const Expr & | e | ) | [virtual] |
Compute and store the type of e.
| e | is the expression whose type is computed. |
Implements CVC3::TheoryArith.
Add variables from 'e' to 'v' for constructing a concrete model.
If e is already of primitive type, do NOT add it to v.
Implements CVC3::TheoryArith.
Theory specific computation of the subtyping predicate for type t applied to the expression e.
By default returns true. Each theory needs to compute subtype predicates for the types associated with it. So, for example, the theory of records will take a record type [# f1: T1, f2: T2 #] and an expression e and will return the subtyping predicate for e, namely: computeTypePred(T1, e.f1) AND computeTypePred(T2, e.f2)
Implements CVC3::TheoryArith.
Compute and cache the TCC of e.
| e | is an expression (term or formula). This function computes the TCC of e which is true iff the expression is defined. |
The default implementation is to compute TCCs recursively for all children, and return their conjunction.
Implements CVC3::TheoryArith.
| ExprStream& CVC3::TheoryArithNew::print | ( | ExprStream & | os, | |
| const Expr & | e | |||
| ) | [virtual] |
Theory-specific pretty-printing.
By default, print the top node in AST, and resume pretty-printing the children. The same call e.print(os) can be used in DP-specific printers to use AST printing for the given node. In fact, it is strongly recommended to add e.print(os) as the default for all the cases/kinds that are not handled by the particular pretty-printer.
Implements CVC3::TheoryArith.
| void CVC3::TheoryArithNew::registerAtom | ( | const Expr & | e | ) | [virtual] |
Registers the atom given from the core. This atoms are stored so that they can be used for theory propagation.
| e | the expression (atom) that is part of the input formula |
Reimplemented from CVC3::Theory.
Return a Gomory cut plane derivation of the variable $x_i$. Mixed integer Gomory cut can be constructed if
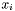 is a integer basic variable with a non-integer value
is a integer basic variable with a non-integer value 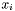 are assigned to their upper or lower bounds
are assigned to their upper or lower bounds Tries to rafine the integer constraint of the theorem. For example, x < 1 is rewritten as x <= 0, and x <(=) 1.5 is rewritten as x <= 1. The constraint should be in the normal form.
| thm | the derivation of the constraint |
| void CVC3::TheoryArithNew::propagateTheory | ( | const Expr & | assertExpr, | |
| const EpsRational & | bound, | |||
| const EpsRational & | oldBound | |||
| ) | [private] |
Propagate all that is possible from given assertion and its bound
Adds var to the dependencies sets of all the variables in the sum.
| var | the variable on the left side | |
| the | sum that defines the variable |
| void CVC3::TheoryArithNew::updateDependenciesRemove | ( | const Expr & | var, | |
| const Expr & | sum | |||
| ) | [private] |
Remove var from the dependencies sets of all the variables in the sum.
| var | the variable on the left side | |
| the | sum that defines the variable |
| void CVC3::TheoryArithNew::updateDependencies | ( | const Expr & | oldExpr, | |
| const Expr & | newExpr, | |||
| const Expr & | var, | |||
| const Expr & | skipVar | |||
| ) | [private] |
Updates the dependencies if a right side of an expression in the tableaux is changed. For example, if oldExpr is x + y and newExpr is y + z, var will be added to the dependency list of z, and removed from the dependency list of x.
| oldExpr | the old right side of the tableaux | |
| newExpr | the new right side of the tableaux | |
| var | the variable that is defined by these two expressions | |
| var | a variable to skip when going through the expressions |
| void CVC3::TheoryArithNew::updateFreshVariables | ( | ) | [private] |
Update the values of variables that have appeared in the tableaux due to backtracking.
Updates the value of variable var by computing the value of expression e.
| var | the variable to update | |
| e | the expression to compute |
| std::string CVC3::TheoryArithNew::tableauxAsString | ( | ) | const [private] |
Returns a string representation of the tableaux.
| std::string CVC3::TheoryArithNew::unsatAsString | ( | ) | const [private] |
Returns a string representation of the unsat variables.
| std::string CVC3::TheoryArithNew::boundsAsString | ( | ) | [private] |
Returns a string representation of the current bounds.
Gets the equality of the fresh variable tableaux variable corresponding to this expression. If the expression has already been asserted, the coresponding variable is returned, othervise a fresh variable is created and the theorem is returned.
| leftSide | the left side of the asserted constraint |
| const Rational& CVC3::TheoryArithNew::findCoefficient | ( | const Expr & | var, | |
| const Expr & | expr | |||
| ) | [private] |
Find the coefficient standing by the variable var in the expression expr. Expresion is expected to be in canonical form, i.e either a rational constant, an arithmetic leaf (i.e. variable or term from some other theory), (MULT rat leaf) where rat is a non-zero rational constant, leaf is an arithmetic leaf or (PLUS 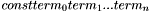 ) where each
) where each 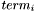 is either a leaf or (MULT
is either a leaf or (MULT 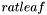 ) and each leaf in
) and each leaf in 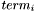 must be strictly greater than the leaf in
must be strictly greater than the leaf in 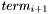 .
.
| var | the variable | |
| expr | the expression to search in |
| bool CVC3::TheoryArithNew::isBasic | ( | const Expr & | x | ) | const [private] |
Return true iof the given variable is basic in the tableaux, i.e. it is on the left side, expressed in terms of the non-basic variables.
| x | the variable to be checked |
Returns the coefficient at a_ij in the current tableaux, i.e. the coefficient at x_j in the row of x_i.
| x_i | a basic variable | |
| x_j | a non-basic variable |
Swaps a basic variable 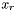 and a non-basic variable
and a non-basic variable 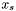 such that ars
such that ars 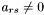 . After pivoting,
. After pivoting, 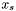 becomes basic and
becomes basic and 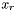 becomes non-basic. The tableau is updated by replacing equation
becomes non-basic. The tableau is updated by replacing equation
![\[x_r = \sum_{x_j \in N}{a_{rj}xj}\]](form_281.png)
with
![\[x_s = \frac{x_r}{a_{rs}} - \sum_{x_j \in N }{\frac{a_{rj}}{a_rs}x_j}\]](form_282.png)
and this equation is used to eliminate 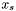 from the rest of the tableau by substitution.
from the rest of the tableau by substitution.
| x_r | a basic variable | |
| x_s | a non-basic variable |
| void CVC3::TheoryArithNew::update | ( | const Expr & | x_i, | |
| const EpsRational & | v | |||
| ) | [private] |
Sets the value of a non-basic variable 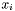 to
to 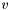 and adjusts the value of all the basic variables so that all equations remain satisfied.
and adjusts the value of all the basic variables so that all equations remain satisfied.
| x_i | a non-basic variable | |
| v | the value to set the variable 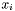 to to |
| void CVC3::TheoryArithNew::pivotAndUpdate | ( | const Expr & | x_i, | |
| const Expr & | x_j, | |||
| const EpsRational & | v | |||
| ) | [private] |
Pivots the basic variable 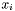 and the non-basic variable
and the non-basic variable 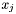 . It also sets
. It also sets 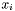 to
to 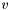 and adjusts all basic variables to keep the equations satisfied.
and adjusts all basic variables to keep the equations satisfied.
| x_i | a basic variable | |
| x_j | a non-basic variable | |
| v | the valie to assign to x_i |
| QueryResult CVC3::TheoryArithNew::assertUpper | ( | const Expr & | x_i, | |
| const EpsRational & | c, | |||
| const Theorem & | thm | |||
| ) | [private] |
Asserts a new upper bound constraint on a variable and performs a simple check for consistency (not complete).
| x_i | the variable to assert the bound on |
| QueryResult CVC3::TheoryArithNew::assertLower | ( | const Expr & | x_i, | |
| const EpsRational & | c, | |||
| const Theorem & | thm | |||
| ) | [private] |
Asserts a new lower bound constraint on a variable and performs a simple check for consistency (not complete).
| x_i | the variable to assert the bound on |
| QueryResult CVC3::TheoryArithNew::assertEqual | ( | const Expr & | x_i, | |
| const EpsRational & | c, | |||
| const Theorem & | thm | |||
| ) | [private] |
Asserts a new equality constraint on a variable by asserting both upper and lower bound.
| x_i | the variable to assert the bound on |
| Expr CVC3::TheoryArithNew::computeNormalFactor | ( | const Expr & | rhs, | |
| NormalizationType | type = NORMALIZE_GCD | |||
| ) | [private] |
Given a canonized term, compute a factor to make all coefficients integer and relatively prime
| Theorem CVC3::TheoryArithNew::normalize | ( | const Expr & | e, | |
| NormalizationType | type = NORMALIZE_GCD | |||
| ) | [private] |
Normalize an equation (make all coefficients rel. prime integers)
| Theorem CVC3::TheoryArithNew::normalize | ( | const Theorem & | thm, | |
| NormalizationType | type = NORMALIZE_GCD | |||
| ) | [private] |
Normalize an equation (make all coefficients rel. prime integers) accepts a rewrite theorem over eqn|ineqn and normalizes it and returns a theorem to that effect.
Canonise the equation using the tebleaux equations, i.e. replace all the tableaux right sides with the corresponding left sides and canonise the result.
| eq | the equation to canonise |
Canonise the sum using the tebleaux equations, i.e. replace all the tableaux right sides with the corresponding left sides and canonise the result.
| sum | the canonised sum to canonise | |
| the | explaining theorem |
| void CVC3::TheoryArithNew::substAndCanonizeTableaux | ( | const Theorem & | eq | ) | [private] |
Sustitute the given equation everywhere in the tableaux.
| eq | the equation to use for substitution |
Given an equality eq: 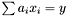 and a variable $var$ that appears in on the left hand side, pivots $y$ and $var$ so that $y$ comes to the right-hand side.
and a variable $var$ that appears in on the left hand side, pivots $y$ and $var$ so that $y$ comes to the right-hand side.
| eq | the proof of the equality | |
| var | the variable to move to the right-hand side |
| Theorem CVC3::TheoryArithNew::getLowerBoundExplanation | ( | const TebleauxMap::iterator & | var_it | ) | [private] |
Knowing that the tableaux row for 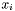 is the problematic one, generate the explanation clause. The variables in the row of
is the problematic one, generate the explanation clause. The variables in the row of 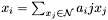 are separatied to
are separatied to
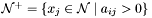
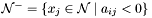
![\[\Gamma = \left\lbrace x_j \leq u_j \; | \; x_j \in \mathcal{N}^+\right\rbrace \cup \left\lbrace l_j \leq x_j \; | \; x_j \in \mathcal{N}^-\right\rbrace \cup \left\lbrace l_i \leq x_i \right\rbrace\]](form_288.png)
| var | the variable that caused the clash |
| Theorem CVC3::TheoryArithNew::getUpperBoundExplanation | ( | const TebleauxMap::iterator & | var_it | ) | [private] |
Knowing that the tableaux row for 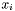 is the problematic one, generate the explanation clause. The variables in the row of
is the problematic one, generate the explanation clause. The variables in the row of 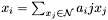 are separatied to
are separatied to
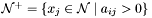
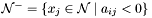
![\[\Gamma = \left\lbrace x_j \leq u_j \; | \; x_j \in \mathcal{N}^-\right\rbrace \cup \left\lbrace l_j \leq x_j \; | \; x_j \in \mathcal{N}^+\right\rbrace \cup \left\lbrace x_i \leq u_i \right\rbrace\]](form_289.png)
| var | the variable that caused the clash |
| Theorem CVC3::TheoryArithNew::addInequalities | ( | const Theorem & | le_1, | |
| const Theorem & | le_2 | |||
| ) | [private] |
| QueryResult CVC3::TheoryArithNew::checkSatSimplex | ( | ) | [private] |
Check the satisfiability
| QueryResult CVC3::TheoryArithNew::checkSatInteger | ( | ) | [private] |
Check the satisfiability of integer constraints
| EpsRational CVC3::TheoryArithNew::getLowerBound | ( | const Expr & | x | ) | const |
Gets the current lower bound on variable x.
| x | the variable |
| EpsRational CVC3::TheoryArithNew::getUpperBound | ( | const Expr & | x | ) | const |
Get the current upper bound on variable x.
| x | the variable |
Gets the theorem of the current lower bound on variable x.
| x | the variable |
Get the theorem of the current upper bound on variable x.
| x | the variable |
| EpsRational CVC3::TheoryArithNew::getBeta | ( | const Expr & | x | ) |
Gets the current valuation of variable x (beta).
| x | the variable |
| std::ostream& operator<< | ( | std::ostream & | os, | |
| const FreeConst & | fc | |||
| ) | [friend] |
| std::ostream& operator<< | ( | std::ostream & | os, | |
| const Ineq & | ineq | |||
| ) | [friend] |
| std::ostream& operator<< | ( | std::ostream & | os, | |
| const FreeConst & | fc | |||
| ) | [friend] |
| std::ostream& operator<< | ( | std::ostream & | os, | |
| const Ineq & | ineq | |||
| ) | [friend] |
CDList<Theorem> CVC3::TheoryArithNew::d_diseq [private] |
For concrete model generation
Definition at line 44 of file theory_arith_new.h.
Referenced by TheoryArithNew().
CDO<size_t> CVC3::TheoryArithNew::d_diseqIdx [private] |
Index to the next unprocessed disequality
Definition at line 46 of file theory_arith_new.h.
ArithProofRules* CVC3::TheoryArithNew::d_rules [private] |
Definition at line 47 of file theory_arith_new.h.
Referenced by addToBuffer(), assertFact(), assertLower(), assertUpper(), canon(), checkSatInteger(), doSolve(), getLowerBoundExplanation(), getUpperBoundExplanation(), normalize(), pivotRule(), processFiniteInterval(), processRealEq(), processSimpleIntEq(), propagateTheory(), rafineIntegerConstraints(), rewrite(), TheoryArithNew(), and ~TheoryArithNew().
CDO<bool> CVC3::TheoryArithNew::d_inModelCreation [private] |
Definition at line 48 of file theory_arith_new.h.
Referenced by computeModelBasic(), and refineCounterExample().
ExprMap<CDList<Ineq> *> CVC3::TheoryArithNew::d_inequalitiesRightDB [private] |
Database of inequalities with a variable isolated on the right.
Definition at line 89 of file theory_arith_new.h.
Referenced by findBounds(), processFiniteIntervals(), and ~TheoryArithNew().
ExprMap<CDList<Ineq> *> CVC3::TheoryArithNew::d_inequalitiesLeftDB [private] |
Database of inequalities with a variable isolated on the left.
Definition at line 91 of file theory_arith_new.h.
Referenced by findBounds(), processFiniteIntervals(), and ~TheoryArithNew().
CDMap<Expr, FreeConst> CVC3::TheoryArithNew::d_freeConstDB [private] |
Mapping of inequalities to the largest/smallest free constant.
The Expr is the original inequality with the free constant removed and inequality converted to non-strict (for indexing purposes). I.e. ax<c+t becomes ax<=t. This inequality is mapped to a pair<c,strict>, the smallest (largest for c+t<ax) constant among inequalities with the same 'a', 'x', and 't', and a boolean flag indicating whether the strongest inequality is strict.
Definition at line 100 of file theory_arith_new.h.
CDList<Theorem> CVC3::TheoryArithNew::d_buffer [private] |
Buffer of input inequalities.
Definition at line 102 of file theory_arith_new.h.
Referenced by addToBuffer(), and TheoryArithNew().
CDO<size_t> CVC3::TheoryArithNew::d_bufferIdx [private] |
Buffer index of the next unprocessed inequality.
Definition at line 103 of file theory_arith_new.h.
Referenced by TheoryArithNew().
const int* CVC3::TheoryArithNew::d_bufferThres [private] |
CDMap<Expr, int> CVC3::TheoryArithNew::d_countRight [private] |
Mapping of a variable to the number of inequalities where the variable would be isolated on the right.
Definition at line 108 of file theory_arith_new.h.
Referenced by updateStats().
CDMap<Expr, int> CVC3::TheoryArithNew::d_countLeft [private] |
Mapping of a variable to the number of inequalities where the variable would be isolated on the left.
Definition at line 111 of file theory_arith_new.h.
Referenced by updateStats().
CDMap<Expr, bool> CVC3::TheoryArithNew::d_sharedTerms [private] |
Set of shared terms (for counterexample generation).
Definition at line 113 of file theory_arith_new.h.
Referenced by addSharedTerm(), and refineCounterExample().
CDMap<Expr, bool> CVC3::TheoryArithNew::d_sharedVars [private] |
VarOrderGraph CVC3::TheoryArithNew::d_graph [private] |
std::set<Expr> CVC3::TheoryArithNew::intVariables [private] |
A set of all integer variables
Definition at line 500 of file theory_arith_new.h.
Referenced by assertFact(), checkSatInteger(), and deriveGomoryCut().
CDO<QueryResult> CVC3::TheoryArithNew::consistent [private] |
Are we consistent or not
Definition at line 525 of file theory_arith_new.h.
Referenced by assertEqual(), assertFact(), assertLower(), assertUpper(), checkSat(), and TheoryArithNew().
Theorem CVC3::TheoryArithNew::explanation [private] |
The theorem explaining the inconsistency
Definition at line 528 of file theory_arith_new.h.
Referenced by assertFact(), assertLower(), assertUpper(), checkSat(), and checkSatSimplex().
CDMap<Expr, BoundInfo> CVC3::TheoryArithNew::lowerBound [private] |
The map from variables to lower bounds (these must be backtrackable)
Definition at line 603 of file theory_arith_new.h.
Referenced by assertLower(), boundsAsString(), getLowerBound(), and getLowerBoundThm().
CDMap<Expr, BoundInfo> CVC3::TheoryArithNew::upperBound [private] |
The map from variables to upper bounds (these must be backtrackable)
Definition at line 605 of file theory_arith_new.h.
Referenced by assertUpper(), boundsAsString(), getUpperBound(), and getUpperBoundThm().
CDMap<Expr, EpsRational> CVC3::TheoryArithNew::beta [private] |
The current real valuation of the variables (these must be backtrackable for the last succesefull checkSAT!!!)
Definition at line 607 of file theory_arith_new.h.
Referenced by checkSatInteger(), getBeta(), pivotAndUpdate(), processFiniteInterval(), update(), and updateValue().
Maps variables to sets of variables that depend on it in the tableaux
Definition at line 617 of file theory_arith_new.h.
Referenced by pivotAndUpdate(), substAndCanonizeTableaux(), update(), updateDependencies(), updateDependenciesAdd(), and updateDependenciesRemove().
TebleauxMap CVC3::TheoryArithNew::tableaux [private] |
The tableaux, a map from basic variables to the expressions over the non-basic ones (theorems that explain them how we got there)
Definition at line 620 of file theory_arith_new.h.
Referenced by boundsAsString(), checkSatSimplex(), getTableauxEntry(), getVariableIntroThm(), isBasic(), pivot(), pivotAndUpdate(), substAndCanonizeModTableaux(), substAndCanonizeTableaux(), tableauxAsString(), and update().
Additional tableaux map from expressions asserted to the corresponding theorems explaining the introduction of the new variables
Definition at line 623 of file theory_arith_new.h.
Referenced by getVariableIntroThm().
std::set<Expr> CVC3::TheoryArithNew::unsatBasicVariables [private] |
A set containing all the unsatisfied basic variables
Definition at line 626 of file theory_arith_new.h.
Referenced by assertLower(), assertUpper(), checkSatSimplex(), getBeta(), pivotAndUpdate(), unsatAsString(), update(), and updateValue().
std::vector<Expr> CVC3::TheoryArithNew::assertedExpr [private] |
The vector to keep the assignments from fresh variables to expressions they represent
Definition at line 629 of file theory_arith_new.h.
Referenced by assertFact(), checkSat(), getVariableIntroThm(), and updateFreshVariables().
CDO<unsigned int> CVC3::TheoryArithNew::assertedExprCount [private] |
The backtrackable number of fresh variables asserted so far
Definition at line 631 of file theory_arith_new.h.
Referenced by assertFact(), checkSat(), getVariableIntroThm(), TheoryArithNew(), and updateFreshVariables().
bool CVC3::TheoryArithNew::propagate [private] |
Internal variable to see wheather to propagate or not
Definition at line 637 of file theory_arith_new.h.
Referenced by assertFact(), assertLower(), and assertUpper().
BoundInfoSet CVC3::TheoryArithNew::allBounds [private] |
Store all the atoms from the formula in this set. It is searchable by an expression and the bound. To get all the implied atoms, one just has to go up (down) and check if the atom or it's negation are implied.
Definition at line 649 of file theory_arith_new.h.
Referenced by propagateTheory(), and registerAtom().
CDO<Theorem> CVC3::TheoryArithNew::integer_lemma [private] |
The last lemma that we asserted to check the integer satisfiability. We don't do checksat until the lemma split has been asserted.
Definition at line 910 of file theory_arith_new.h.
Referenced by checkSatInteger().
CDList<Theorem> CVC3::TheoryArithNew::d_diseq [private] |
For concrete model generation
Definition at line 44 of file theory_arith_new.mine.h.
CDO<size_t> CVC3::TheoryArithNew::d_diseqIdx [private] |
Index to the next unprocessed disequality
Definition at line 46 of file theory_arith_new.mine.h.
ArithProofRules* CVC3::TheoryArithNew::d_rules [private] |
Definition at line 47 of file theory_arith_new.mine.h.
CDO<bool> CVC3::TheoryArithNew::d_inModelCreation [private] |
Definition at line 48 of file theory_arith_new.mine.h.
ExprMap<CDList<Ineq> *> CVC3::TheoryArithNew::d_inequalitiesRightDB [private] |
Database of inequalities with a variable isolated on the right.
Definition at line 89 of file theory_arith_new.mine.h.
ExprMap<CDList<Ineq> *> CVC3::TheoryArithNew::d_inequalitiesLeftDB [private] |
Database of inequalities with a variable isolated on the left.
Definition at line 91 of file theory_arith_new.mine.h.
CDMap<Expr, FreeConst> CVC3::TheoryArithNew::d_freeConstDB [private] |
Mapping of inequalities to the largest/smallest free constant.
The Expr is the original inequality with the free constant removed and inequality converted to non-strict (for indexing purposes). I.e. ax<c+t becomes ax<=t. This inequality is mapped to a pair<c,strict>, the smallest (largest for c+t<ax) constant among inequalities with the same 'a', 'x', and 't', and a boolean flag indicating whether the strongest inequality is strict.
Definition at line 100 of file theory_arith_new.mine.h.
CDList<Theorem> CVC3::TheoryArithNew::d_buffer [private] |
CDO<size_t> CVC3::TheoryArithNew::d_bufferIdx [private] |
Buffer index of the next unprocessed inequality.
Definition at line 103 of file theory_arith_new.mine.h.
const int* CVC3::TheoryArithNew::d_bufferThres [private] |
Threshold when the buffer must be processed.
Definition at line 104 of file theory_arith_new.mine.h.
CDMap<Expr, int> CVC3::TheoryArithNew::d_countRight [private] |
Mapping of a variable to the number of inequalities where the variable would be isolated on the right.
Definition at line 108 of file theory_arith_new.mine.h.
CDMap<Expr, int> CVC3::TheoryArithNew::d_countLeft [private] |
Mapping of a variable to the number of inequalities where the variable would be isolated on the left.
Definition at line 111 of file theory_arith_new.mine.h.
CDMap<Expr, Expr> CVC3::TheoryArithNew::d_sharedTerms [private] |
CDList<Expr> CVC3::TheoryArithNew::d_sharedTermsList [private] |
Backtracking database of subterms of shared terms.
Definition at line 115 of file theory_arith_new.mine.h.
CDO<unsigned> CVC3::TheoryArithNew::d_index1 [private] |
CDMap<Expr, bool> CVC3::TheoryArithNew::d_sharedVars [private] |
std::set<Expr> CVC3::TheoryArithNew::intVariables [private] |
A set of all integer variables
Definition at line 504 of file theory_arith_new.mine.h.
CDO<QueryResult> CVC3::TheoryArithNew::consistent [private] |
Are we consistent or not
Definition at line 529 of file theory_arith_new.mine.h.
CDMap<Expr, BoundInfo> CVC3::TheoryArithNew::lowerBound [private] |
The map from variables to lower bounds (these must be backtrackable)
Definition at line 607 of file theory_arith_new.mine.h.
CDMap<Expr, BoundInfo> CVC3::TheoryArithNew::upperBound [private] |
The map from variables to upper bounds (these must be backtrackable)
Definition at line 609 of file theory_arith_new.mine.h.
CDMap<Expr, EpsRational> CVC3::TheoryArithNew::beta [private] |
The current real valuation of the variables (these must be backtrackable for the last succesefull checkSAT!!!)
Definition at line 611 of file theory_arith_new.mine.h.
std::set<Expr> CVC3::TheoryArithNew::unsatBasicVariables [private] |
A set containing all the unsatisfied basic variables
Definition at line 630 of file theory_arith_new.mine.h.
std::vector<Expr> CVC3::TheoryArithNew::assertedExpr [private] |
The vector to keep the assignments from fresh variables to expressions they represent
Definition at line 633 of file theory_arith_new.mine.h.
CDO<unsigned int> CVC3::TheoryArithNew::assertedExprCount [private] |
The backtrackable number of fresh variables asserted so far
Definition at line 635 of file theory_arith_new.mine.h.
CDO<Theorem> CVC3::TheoryArithNew::integer_lemma [private] |
The last lemma that we asserted to check the integer satisfiability. We don't do checksat until the lemma split has been asserted.
Definition at line 914 of file theory_arith_new.mine.h.
 1.5.1
1.5.1