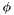 is valid in the built-in theories under a given set
is valid in the built-in theories under a given set  of assumptions. More precisely, it checks whether
of assumptions. More precisely, it checks whether
CVC3 checks whether a given formula 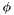 is valid in the built-in theories under a given set
is valid in the built-in theories under a given set  of assumptions. More precisely, it checks whether
of assumptions. More precisely, it checks whether
![\[\Gamma\models_T \phi\]](form_2.png)
that is, whether 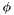 is a logical consequence of the union
is a logical consequence of the union  of the built-in theories and the set of formulas
of the built-in theories and the set of formulas  .
.
Roughly speaking, when 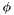 is universal and all the formulas in
is universal and all the formulas in  are existential (i.e., when
are existential (i.e., when 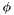 and
and  contain at most universal, respectively existential, quantifiers), CVC3 is in fact a decision procedure: it is always guaranteed (well, modulo bugs and memory limits) to return a correct "valid" or "invalid" answer. In all other cases, CVC3 is only guaranteed to be sound: it will never say that an invalid formula is valid. However, it may either never return or give up and return "unknown" even if
contain at most universal, respectively existential, quantifiers), CVC3 is in fact a decision procedure: it is always guaranteed (well, modulo bugs and memory limits) to return a correct "valid" or "invalid" answer. In all other cases, CVC3 is only guaranteed to be sound: it will never say that an invalid formula is valid. However, it may either never return or give up and return "unknown" even if 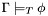 .
.
When CVC3 returns "valid" it can return a formal proof of the validity of 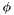 under the logical context
under the logical context  , together with the subset
, together with the subset 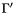 of
of  used in the proof, such that
used in the proof, such that 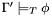 .
.
When CVC3 returns "invalid" it can return, in the current terminology, both a counter-example to 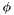 's validity under
's validity under  and a counter-model. Both a counter-example and a counter-models are a set
and a counter-model. Both a counter-example and a counter-models are a set 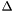 of additional formulas consistent with
of additional formulas consistent with  in
in  , but entailing the negation of
, but entailing the negation of 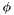 . In formulas:
. In formulas:
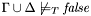 and
and 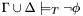 .
.
The difference is that a counter-model is given as a set of equations providing a concrete assignment of values for the free symbols in  and
and  (see QUERY for more details).
(see QUERY for more details).
CVC3 can be used in two modes: as a C/C++ library, or as a command-line executable (implemented as a command-line interface to the library). This manual mainly describes the command-line interface on a unix-type platform.
cvc3. It reads the input (a sequence of commands) from the standard input and prints the results on the standard output. Errors and some other messages (e.g. debugging traces) are printed on the standard error.
Typically, the input to cvc3 is saved in a file and redirected to the executable, or given on a command line:
# Reading from standard input: cvc3 < input-file.cvc # Reading directly from file: cvc3 input-file.cvc
Notice that, for efficiency, CVC3 uses input buffers, and the input is not always processed immediately after each command. Therefore, if you want to type the commands interactively and receive immediate feedback, use the +interactive option (can be shortened to +int):
cvc3 +int
Run cvc3 -h for more information on the available options.
The command line front-end of CVC3 supports two input languages.
We describe the input languages next, concentrating mostly on the first.
;).Any text after the first occurrence of a percent character and to the end of the current line is a comment:
%%% This is a CVC3 comment
The type system consists of value types, non-value types and subtypes of value types, all of which are interpreted as sets. For convenience, we will sometimes identify below the interpretation of a type with the type itself.
Value types consist of atomic types and structured types. The atomic types are  ,
, 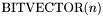 for all
for all  , as well as user-defined atomic types (also called uninterpreted types). The structured types are array, tuple, and record types, as well as ML-style user-defined (inductive) datatypes.
, as well as user-defined atomic types (also called uninterpreted types). The structured types are array, tuple, and record types, as well as ML-style user-defined (inductive) datatypes.
Non-value types consist of the type 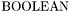 and function types. Subtypes include the built-in subtype
and function types. Subtypes include the built-in subtype 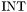 of
of 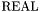 and are covered in the Subtypes section below.
and are covered in the Subtypes section below.
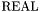 type is interpreted as the set of rational numbers. The name
type is interpreted as the set of rational numbers. The name 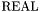 is justified by the fact that a CVC3 formula is valid in the theory of rational numbers iff it is valid in the theory of real numbers.
is justified by the fact that a CVC3 formula is valid in the theory of rational numbers iff it is valid in the theory of real numbers.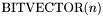 is interpreted as the set of all bit vectors of size n.
is interpreted as the set of all bit vectors of size n.
% User declarations of atomic types: MyBrandNewType: TYPE; Apples, Oranges: TYPE;
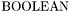 type is, perhaps confusingly, the type of CVC3 formulas, not the two-element set of Boolean values. The fact that
type is, perhaps confusingly, the type of CVC3 formulas, not the two-element set of Boolean values. The fact that 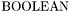 is not a value type in practice means that it is not possible for function symbols in CVC3 to have a arguments of type
is not a value type in practice means that it is not possible for function symbols in CVC3 to have a arguments of type 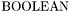 . The reason is that CVC3 follows the two-tiered structure of classical first-order logic that distinguishes between formulas and terms, and allows terms to occur in formulas but not vice versa. (An exception is the IF-THEN-ELSE construct, see later.) The only difference is that, syntactically, formulas in CVC3 are terms of type
. The reason is that CVC3 follows the two-tiered structure of classical first-order logic that distinguishes between formulas and terms, and allows terms to occur in formulas but not vice versa. (An exception is the IF-THEN-ELSE construct, see later.) The only difference is that, syntactically, formulas in CVC3 are terms of type 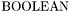 . A function symbol
. A function symbol f then can have 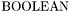 as its return type. But that is just CVC3's way, inherited from the previous systems of the CVC family, to say that
as its return type. But that is just CVC3's way, inherited from the previous systems of the CVC family, to say that f is a predicate symbol.
CVC3 does have a Boolean type proper, that is, a value type with only two elements and with the usual Boolean operations defined on it: it is BITVECTOR(1).
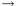 ) types are created by the mixfix type constructors
) types are created by the mixfix type constructors
![\[ \begin{array}{l} \_ \to \_ \\[1ex] (\ \_\ ,\ \_\ ) \to \_ \\[1ex] (\ \_\ ,\ \_\ ,\ \_\ ) \to \_ \\[1ex] \ldots \end{array} \]](form_16.png)
whose arguments can be instantiated by any value (sub)type, with the addition that the last argument can also be 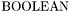 .
.
% Function type declarations UnaryFunType: TYPE = INT -> REAL; BinaryFunType: TYPE = (REAL, REAL) -> ARRAY REAL OF REAL; TernaryFunType: TYPE = (REAL, BITVECTOR(4), INT) -> BOOLEAN;
A function type of the form 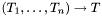 with
with 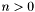 is interpreted as the set of all total functions from the Cartesian product
is interpreted as the set of all total functions from the Cartesian product 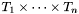 to
to  when
when  is not
is not 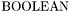 . Otherwise, it is interpreted as the set of all relations over
. Otherwise, it is interpreted as the set of all relations over 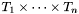
The example above also shows how to introduce type names. A name like UnaryFunType above is just an abbreviation for the type 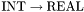 and can be used interchangeably with it.
and can be used interchangeably with it.
In general, any type defined by a type expression E can be given a name with the declaration:
name : TYPE = E;
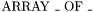 whose arguments can be instantiated by any value type.
whose arguments can be instantiated by any value type.
T1 : TYPE; % Array types: ArrayType1: TYPE = ARRAY T1 OF REAL; ArrayType2: TYPE = ARRAY INT OF (ARRAY INT OF REAL); ArrayType3: TYPE = ARRAY [INT, INT] OF INT;
An array type of the form 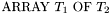 is interpreted as the set of all total maps from
is interpreted as the set of all total maps from 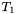 to
to 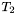 . The main conceptual difference with the type
. The main conceptual difference with the type 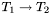 is that arrays, contrary to functions, are first-class objects of the language: they can be arguments or results of functions. Moreover, array types come equipped with an update operation.
is that arrays, contrary to functions, are first-class objects of the language: they can be arguments or results of functions. Moreover, array types come equipped with an update operation.
![\[ \begin{array}{l} [\ \_\ ] \\[1ex] [\ \_\ ,\ \_\ ] \\[1ex] [\ \_\ ,\ \_\ \ ,\ \_\ ] \\[1ex] \ldots \end{array} \]](form_25.png)
whose arguments can be instantiated by any value type.
% Tuple declaration TupleType: TYPE = [ REAL, ArrayType1, [INT, INT] ];
A tuple type of the form ![$[T_1, \ldots, T_n]$](form_26.png) is interpreted as the Cartesian product
is interpreted as the Cartesian product 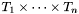 . Note that while the types
. Note that while the types 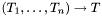 and
and ![$[T_1 \times \cdots \times T_n] \to T$](form_27.png) are semantically equivalent, they are operationally different in CVC3. The first is the type of functions that take n arguments, while the second is the type of functions of 1 argument of type n-tuple.
are semantically equivalent, they are operationally different in CVC3. The first is the type of functions that take n arguments, while the second is the type of functions of 1 argument of type n-tuple.
![\[ [\#\ l_1: \_\ ,\ \ldots\ ,\ l_n: \_\ \#] \]](form_28.png)
where 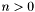 ,
, 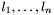 are field labels, and the arguments can be instantiated with any value types.
are field labels, and the arguments can be instantiated with any value types.
% Record declaration RecordType: TYPE = [# number: INT, value: REAL, info: TupleType #];
The order of the fields in a record type is meaningful. In other words, permuting the field names gives a different type. Note that records are (at the moment) non-recursive. For instance, it is not possible to declare a record type called Person containing a field of type Person. Recursive types are provided in CVC3 as ML-style datatypes.
![\[ \begin{array}{l} \mathrm{DATATYPE} \\ \ \ \mathit{type\_name}_1 = C_{1,1} \mid C_{1,2} \mid \cdots \mid C_{1,m_1}, \\ \ \ \mathit{type\_name}_2 = C_{2,1} \mid C_{2,2} \mid \cdots \mid C_{2,m_2}, \\ \ \ \vdots \\ \ \ \mathit{type\_name}_n = C_{n,1} \mid C_{n,2} \mid \cdots \mid C_{n,m_n} \\ \mathrm{END}; \end{array} \]](form_30.png)
Each of the 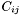 is either a constant symbol or an expression of the form
is either a constant symbol or an expression of the form
![\[ \mathit{cons}(\ \mathit{sel}_1: T_1,\ \ldots,\ \mathit{sel}_k: T_k\ ) \]](form_32.png)
where 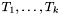 are any value types or type names for value types, including any
are any value types or type names for value types, including any 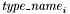 . Such declarations introduce for the datatype:
. Such declarations introduce for the datatype:
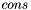 of type
of type 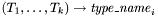 ,
,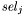 of type
of type 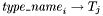 , and
, and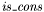 of type
of type 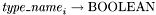 .
.Here are some examples of datatype declarations:
% simple enumeration type
% implicitly defined are the testers: is_red, is_yellow and is_blue
% (similarly for the other datatypes)
DATATYPE
PrimaryColor = red | yellow | blue
END;
% infinite set of pairwise distinct values ...v(-1), v(0), v(1), ...
DATATYPE
Id = v (id: INT)
END;
% ML-style integer lists
DATATYPE
IntList = nil | cons (head: INT, tail: IntList)
END;
% ASTs
DATATYPE
Term = var (index: INT)
| apply (arg_1: Term, arg_2: Term)
| lambda (arg: INT, body: Term)
END;
% Trees
DATATYPE
Tree = tree (value: REAL, children: TreeList),
TreeList = nil_tl
| cons_tl (first_t1: Tree, rest_t1: TreeList)
END;
Constructor, selector and tester symbols defined for a datatype have global scope. So, for instance, it is not possible for two different datatypes to use the same name for a constructor.
A datatype is interpreted as a term algebra constructed by the constructor symbols over some sets of generators. For example, the datatype IntList is interpreted as the set of all terms constructed with nil and cons over the integers.
Because of this semantics, CVC3 allows only inductive datatypes, that is, datatypes whose values are essentially (labeled, ordered) finite trees. Infinite structures such as streams or even finite but cyclic ones such as circular lists are then excluded. For instance, none of the following declarations define inductive datatypes, and are rejected by CVC3:
DATATYPE
IntStream = s (first:INT, rest: IntStream)
END;
DATATYPE
RationalTree = node1 (first_child1: RationalTree)
| node2 (first_child2: RationalTree, second_child2:RationalTree)
END;
DATATYPE
T1 = c1 (s1: T2),
T2 = c2 (s2: T1)
END;
In concrete, a declaration of 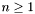 datatypes
datatypes 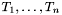 will be rejected if for any one of the types
will be rejected if for any one of the types 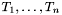 , it is impossible to build a finite term of that type using only the constructors of
, it is impossible to build a finite term of that type using only the constructors of 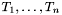 and free constants of type other than
and free constants of type other than 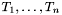 .
.
Datatypes are the only types for which the user also chooses names for the built-in operations defined on the type for:
For all the other types, CVC3 provides predefined names for the built-in operations on the type.
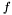 to the terms
to the terms 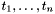 is
is  if
if 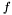 has type
has type 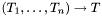 and each
and each 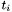 has type
has type 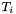 .
.Attempting to enter an ill-typed term will result in an error.
The main difference with standard many-sorted logic is that some built-in symbols are parametrically polymorphic. For instance the function symbol for extracting the element of any array has type 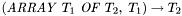 for all types
for all types 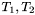 not containing function or predicate types.
not containing function or predicate types.
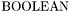 ). By and large, these are standard first-order terms built out of (typed) variables, predefined theory-specific operators, free (i.e., user-defined) function symbols, and quantifiers. Extensions include an if-then-else operator, lambda abstractions, and local symbol declarations, as illustrated below. Note that these extensions still keep CVC3's language first-order. In particular, lambda abstractions are restricted to take and return only terms of a value type. Similarly, quantifiers can only quantify variables of a value type.
). By and large, these are standard first-order terms built out of (typed) variables, predefined theory-specific operators, free (i.e., user-defined) function symbols, and quantifiers. Extensions include an if-then-else operator, lambda abstractions, and local symbol declarations, as illustrated below. Note that these extensions still keep CVC3's language first-order. In particular, lambda abstractions are restricted to take and return only terms of a value type. Similarly, quantifiers can only quantify variables of a value type.
Free function symbols include constant symbols and predicate symbols, respectively nullary function symbols and function symbols with a 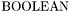 return type. Free symbols are introduced with global declarations of the form
return type. Free symbols are introduced with global declarations of the form 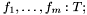 where
where 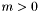 ,
, 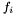 are the names of the symbols and
are the names of the symbols and  is their type:
is their type:
% integer constants a, b, c: INT; % real constants x,y,z: REAL; % unary function f1: REAL -> REAL; % binary function f2: (REAL, INT) -> REAL; % unary function with a tuple argument f3: [INT, REAL] -> BOOLEAN; % binary predicate p: (INT, REAL) -> BOOLEAN; % Propositional "variables" P,Q; BOOLEAN;
Like type declarations, such free symbol declarations have global scope and must be unique. In other words, it is not possible to globally declare a symbol more than once. This entails among other things that free symbols cannot be overloaded with different types.
As with types, a new free symbol can be defined as the name of a term of the corresponding type. With constant symbols this is done a declaration of the form 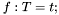 :
:
c: INT; i: INT = 5 + 3*c; j: REAL = 3/4; t: [REAL, INT] = (2/3, -4); r: [# key: INT, value: REAL #] = (# key := 4, value := (c + 1)/2 #); f: BOOLEAN = FORALL (x:INT): x <= 0 OR x > c ;
A restriction on constants of type 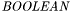 is that their value can only be a closed formula, that is, a formula with no free variables.
is that their value can only be a closed formula, that is, a formula with no free variables.
A term and its name can be used interchangeably in later expressions. Named terms are often useful for shared subterms (terms used several times in different places) since their use can make the input exponentially more concise. Named terms are processed very efficiently by CVC3. It is much more efficient to associate a complex term with a name directly rather than to declare a constant and later assert that it is equal to the same term. This point will be explained in more detail later in section Commands.
More generally, in CVC3 one can associate a term to function symbols of any arity. For non-constant function symbols this is done with a declaration of the form
![\[ f:(T_1, \ldots, T_n) \to T = \mathrm{LAMBDA}(x_1:T_1, \ldots, x:T_n): t\;; \]](form_54.png)
where 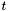 is any term of type
is any term of type  with free variables in
with free variables in 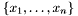 . The lambda binder has the usual semantics and conforms to the usual lexical scoping rules: within the term
. The lambda binder has the usual semantics and conforms to the usual lexical scoping rules: within the term 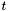 the declaration of the symbols
the declaration of the symbols 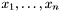 as local variables of respective type
as local variables of respective type 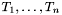 hides any previous, global declaration of those symbols.
hides any previous, global declaration of those symbols.
As a general shorthand, when 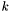 consecutive types
consecutive types 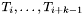 in the lambda expression
in the lambda expression 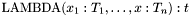 are identical, the syntax
are identical, the syntax 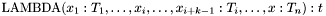 is also allowed.
is also allowed.
% Global declaration of x as a unary function symbol x: REAL -> REAL; % Local declarations of x as a constant symbol f: REAL -> REAL = LAMBDA (x: REAL): 2*x + 3; p: (INT, INT) -> BOOLEAN = LAMBDA (x,i: INT): i*x - 1 > 0; g: (REAL, INT) -> [REAL, INT] = LAMBDA (x: REAL, i:INT): (x + 1, i - 3);
Constant and function symbols can also be declared locally anywhere within a term by means of a let binder. This is done with a declaration of the form
![\[ \begin{array}{rl} \mathrm{LET} & f_1 = t_1, \\ & \vdots \\ & f_n = t_m \\ \mathrm{IN} & t ; \end{array} \]](form_62.png)
for constant symbols, and of the form
![\[ \begin{array}{rlcl} \mathrm{LET} & f_1 & = &\mathrm{LAMBDA}(x_1:T_{1,1}, \ldots, x:T_{1,n}):\; t_1, \\ & & \vdots & \\ & f_m & = & \mathrm{LAMBDA}(x_1:T_{m,1}, \ldots, x:T_{m,n}):\; t_n\ \\ \mathrm{IN} & t ; \end{array} \]](form_267.png)
for non-constant symbols. Let binders can be nested arbitrarily and follow the usual lexical scoping rules.
t: REAL =
LET g = LAMBDA(x:INT): x + 1,
x1 = 42,
x2 = 2*x1 + 7/2
IN
(LET x3 = g(x1) IN x3 + x2) / x1;
Note that the same symbol = is used, unambiguously, in the syntax of global declarations, let declarations, and as a predicate symbol.
In addition to user-defined symbols, CVC3 terms can use a number of predefined symbols: the logical symbols as well as theory symbols, function symbols belonging to one of the built-in theories. They are described next, with the theory symbols grouped by theory.
= and /=, together with the logical constants TRUE, FALSE, the connectives NOT, AND, OR, XOR, =>, <=>, and the first-order quantifiers EXISTS and FORALL, all with the standard many-sorted logic semantics.
The binary connectives have infix syntax and type 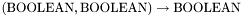 . The symbols
. The symbols = and /=, which are also infix, are instead polymorphic, having type 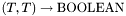 for every predefined or user-defined value type
for every predefined or user-defined value type  . They are interpreted respectively as the identity relation and its complement.
. They are interpreted respectively as the identity relation and its complement.
The syntax for quantifiers is similar to that of the lambda binder.
Here is an example of a formula built just of these logical symbols and variables:
A, B: TYPE;
quant: BOOLEAN = FORALL (x,y: A, i,j,k: B): i = j AND i /= k
=> EXISTS (z: A): x /= z OR z /= y;
Binding and scoping of quantified variables follows the same rules as in let expressions. In particular, a quantifier will shadow in its scope any constant and function symbols with the same name as one of the variables it quantifies:
A: TYPE; i,j:INT; % The first occurrence of i and of j in f are constant symbols, % the others are variables. f: BOOLEAN = i = j AND FORALL (i,j: A): i = j OR i /= j;
In addition to these standard constructs, CVC3 also has a general mixfix conditional operator of the form
![\[ \mathrm{IF}\ b\ \mathrm{THEN}\ t\ \mathrm{ELSIF}\ b_1\ \mathrm{THEN}\ t_1\ \ldots\ \mathrm{ELSIF}\ b_n\ \mathrm{THEN}\ t_n\ \mathrm{ELSE}\ t_{n+1}\ \mathrm{ENDIF} \]](form_66.png)
with 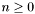 where
where 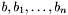 are terms of type
are terms of type 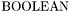 and
and 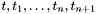 are terms of the same value type
are terms of the same value type  :
:
% Conditional term x,y,z,w:REAL; t: REAL = IF x > 0 THEN y ELSIF x >= 1 THEN z ELSIF x > 2 THEN w ELSE 2/3 ENDIF;
The theory's function symbols consist of all and only the user-defined free symbols.
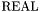 , each with the expected type: all numerals
, each with the expected type: all numerals 0, 1, ..., as well as - (both unary and binary), +, *, /, <, >, <=, >=. Non-integer constants are written in fractional form: e.g., 1/2, 3/4, etc.Since CVC3 uses infinite precision rational arithmetic, the size of natural constants expressible in the presentation language is bounded in practice only by the amount of available memory.
The operators' names are overloaded in the obvious way. For instance, the same name is used for each 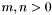 for the operator that takes a bit vector of size
for the operator that takes a bit vector of size 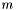 and one of size
and one of size  and returns their concatenation.
and returns their concatenation.
For each size  , there are
, there are 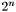 elements in the type
elements in the type 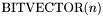 . These elements can be named using constant symbols or bit vector constants. Each element in the domain is named by two different constant symbols: once in binary and once in hexadecimal format. Binary constant symbols start with the characters
. These elements can be named using constant symbols or bit vector constants. Each element in the domain is named by two different constant symbols: once in binary and once in hexadecimal format. Binary constant symbols start with the characters 0bin and continue with the representation of the vector in the usual binary format (as an  -string over the characters 0,1). Hexadecimal constant symbols start with the characters
-string over the characters 0,1). Hexadecimal constant symbols start with the characters 0hex and continue with the representation of the vector in usual hexadecimal format (as an  -string over the characters 0,...,9,a,...,f).
-string over the characters 0,...,9,a,...,f).
Binary constant Corresponding hexadecimal constant ----------------------------------------------------------- 0bin0000111101010000 0hex0f50
In the binary representation, the rightmost bit is the least significant bit (LSB) of the vector and the leftmost bit is the most significant bit (MSB). The index of the LSB in the bit vector is 0 and the index of the MSB is n-1 for an n-bit constant. This convention extends to all bit vector expressions in the natural way.
Bit-vector operators are categorized into word-level, bitwise, arithmetic, and comparison operators.
WORD-LEVEL OPERATORS: Description Symbol Example ================================================================ Concatenation _ @ _ 0bin01@0bin0 (= 0bin010) Extraction _ [i:j] 0bin0011[3:1] (= 0bin001) Left shift _ << k 0bin0011 << 3 (= 0bin0011000) Right shift _ >> k 0bin1000 >> 3 (= 0bin0001) Sign extension SX(_,k) SX(0bin100, 5) (= 0bin11100)
For each 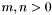 there is
there is
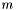 -bit vector
-bit vector 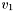 and an
and an  -bit vector
-bit vector 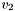 and returning the
and returning the 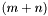 -bit concatenation of
-bit concatenation of 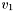 and
and 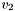 ;
;![$[i:j]$](form_77.png) for each
for each 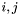 with
with 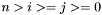 , taking an
, taking an  -bit vector
-bit vector 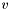 and returning the
and returning the 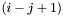 -bit subvector of
-bit subvector of 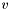 at positions
at positions 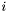 through
through 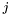 (inclusive);
(inclusive);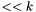 for each
for each 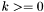 , taking an
, taking an  -bit vector
-bit vector 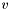 and returning the
and returning the 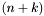 -bit concatenation of
-bit concatenation of 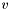 with the
with the 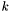 -bit zero vector;
-bit zero vector;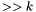 for each
for each 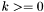 , taking an
, taking an  -bit vector
-bit vector 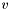 and returning the
and returning the  -bit concatenation of the
-bit concatenation of the 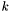 -bit zero bit vector with
-bit zero bit vector with ![$v[n-1:k]$](form_88.png) ;
;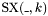 for each
for each 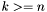 , taking an
, taking an  -bit vector
-bit vector 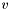 and returning the
and returning the 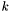 -bit concatenation of
-bit concatenation of 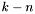 copies of the MSB of
copies of the MSB of 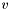 and
and 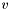 .
.
BITWISE OPERATORS: Description Symbol ============================== Bitwise AND _ & _ Bitwise OR _ | _ Bitwise NOT ~ _ Bitwise XOR BVXOR(_,_) Bitwise NAND BVNAND(_,_) Bitwise NOR BVNOR(_,_) Bitwise XNOR BVXNOR(_,_)
For each 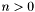 there are operators with the names and syntax above, performing the usual bitwise Boolean operations from
there are operators with the names and syntax above, performing the usual bitwise Boolean operations from  -bit arguments to an
-bit arguments to an  -bit result.
-bit result.
ARITHMETIC OPERATORS: Description Symbol ======================================== Bit vector addition BVPLUS(k,_,_,...) Bit vector multiplication BVMULT(k,_,_) Bit vector negation BVUMINUS(_) Bit vector subtraction BVSUB(k,_,_)
For each 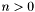 and
and 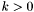 there is
there is
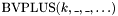 , taking two or more bit vectors of arbitrary size, and returning the
, taking two or more bit vectors of arbitrary size, and returning the 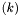 least significant bits of their sum.
least significant bits of their sum.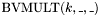 , taking two bit vectors
, taking two bit vectors 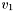 and
and 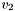 , and returning the
, and returning the 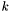 least significant bits of their product.
least significant bits of their product.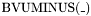 , taking an
, taking an  -bit vector
-bit vector 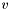 and returning the
and returning the  -bit vector
-bit vector 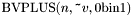 .
.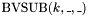 , taking two bit vectors
, taking two bit vectors 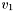 and
and 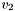 , and returning the
, and returning the 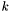 -bit vector
-bit vector 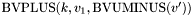 where
where 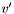 is
is 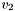 if the size of
if the size of 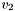 is greater than or equal to
is greater than or equal to 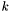 , and
, and 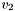 extended to size
extended to size 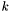 by concatenating zeroes in the most significant bits otherwise.
by concatenating zeroes in the most significant bits otherwise.CVC3 does not have dedicated operators for multiplexers. However, specific multiplexers can be easily defined with the aid of conditional terms.
% Example of 2-to-1 multiplexer
mp: (BITVECTOR(1), BITVECTOR(1), BITVECTOR(1)) -> BITVECTOR(1) =
LAMBDA (s,x,y : BITVECTOR(1)): IF s = 0bin0 THEN x ELSE y ENDIF;
In addition to equality and disequality, CVC3 provides the following comparison operators.
COMPARISON OPERATORS: Description Symbol =================================== Less than BVLT(_,_) Less than or equal to BVLE(_,_) Greater than BVGT(_,_) Greater than equal to BVGE(_,_)
For each 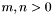 there is
there is
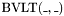 , taking an
, taking an 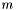 -bit vector
-bit vector 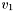 and an
and an  -bit vector
-bit vector 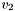 , and having the value
, and having the value 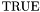 iff the zero-extension of
iff the zero-extension of  to
to 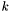 bits is less than the zero-extension of
bits is less than the zero-extension of 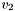 to
to 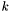 bits, where
bits, where 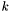 is the maximum of
is the maximum of 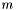 and
and  .
.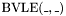 , taking an
, taking an 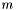 -bit vector
-bit vector 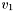 and an
and an  -bit vector
-bit vector 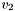 , and having the value
, and having the value 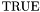 iff the zero-extension of
iff the zero-extension of 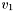 to
to 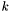 bits is less than or equal to the zero-extension of
bits is less than or equal to the zero-extension of 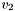 to
to 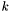 bits, where
bits, where 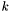 is the maximum of
is the maximum of 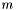 and
and  .
.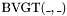 , taking an
, taking an 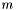 -bit vector
-bit vector 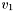 and an
and an  -bit vector
-bit vector 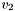 , and having the same value as
, and having the same value as 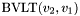 .
.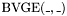 , taking an
, taking an 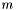 -bit vector
-bit vector 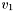 and an
and an  -bit vector
-bit vector 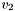 , and having the same value as
, and having the same value as 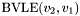 .
.Following are some example CVC3 input formulas involving bit vector expressions
Example 1 illustrates the use of arithmetic, word-level and bitwise NOT operations:
x : BITVECTOR(5); y : BITVECTOR(4); yy : BITVECTOR(3); QUERY BVPLUS(9, x@0bin0000, (0bin000@(~y)@0bin11))[8:4] = BVPLUS(5, x, ~(y[3:2])) ;
Example 2 illustrates the use of arithmetic, word-level and multiplexer terms:
bv : BITVECTOR(10); a : BOOLEAN; QUERY 0bin01100000[5:3]=(0bin1111001@bv[0:0])[4:2] AND 0bin1@(IF a THEN 0bin0 ELSE 0bin1 ENDIF) = (IF a THEN 0bin110 ELSE 0bin011 ENDIF)[1:0] ;
Example 3 illustrates the use of bitwise operations:
x, y, z, t, q : BITVECTOR(1024); ASSERT x = ~x; ASSERT x&y&t&z&q = x; ASSERT x|y = t; ASSERT BVXOR(x,~x) = t; QUERY FALSE;
Example 4 illustrates the use of predicates and all the arithmetic operations:
x, y : BITVECTOR(4); ASSERT x = 0hex5; ASSERT y = 0bin0101; QUERY BVMULT(8,x,y)=BVMULT(8,y,x) AND NOT(BVLT(x,y)) AND BVLE(BVSUB(8,x,y), BVPLUS(8, x, BVUMINUS(x))) AND x = BVSUB(4, BVUMINUS(x), BVPLUS(4, x,0hex1)) ;
Example 5 illustrates the use of shift functions
x, y : BITVECTOR(8); z, t : BITVECTOR(12); ASSERT x = 0hexff; ASSERT z = 0hexff0; QUERY z = x << 4; QUERY (z >> 4)[7:0] = x;
![$\_[\_]$](form_109.png) and
and ![$\_\ \mathrm{WITH}\ [\_]\ := \_$](form_110.png)
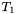 and element type
and element type 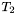 , the first operator maps an array from
, the first operator maps an array from 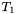 to
to 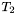 and an index into it (i.e., a value of type
and an index into it (i.e., a value of type 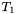 ) to the element of type
) to the element of type 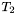 "stored" into the array at that index. The second maps an array
"stored" into the array at that index. The second maps an array 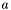 from
from 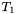 to
to 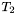 , an index
, an index 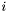 , and a
, and a 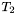 -element
-element 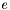 to the array that stores
to the array that stores 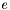 at index
at index 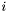 and is otherwise identical to
and is otherwise identical to 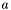 .
.Since arrays are just maps, equality between them is extensional: for two arrays of the same type to be different they have to store differ elements in at least one place.
Sequential updates can be chained with the syntax ![$\_\ \mathrm{WITH}\ [\_]\ := \_, \ldots, [\_]\ := \_$](form_113.png) .
.
A: TYPE = ARRAY INT OF REAL; a: A; i: INT = 4; % selection: elem: REAL = a[i]; % update a1: A = a WITH [10] := 1/2; % sequential update % (syntactic sugar for (a WITH [10] := 2/3) WITH [42] := 3/2) a2: A = a WITH [10] := 2/3, [42] := 3/2;
No built-in operators other than equality and disequality are provided for this family in the presentation language. Each datatype declaration, however, generates constructor, selector and tester operators as described in Section Inductive Data Types.
![$[\# l_0:T_0, \ldots, l_n:T_n \#]$](form_114.png) could be equivalently modeled as, say, the datatype
could be equivalently modeled as, say, the datatype
![\[ \begin{array}{l} \mathrm{DATATYPE} \\ \ \ \mathrm{Record} = \mathit{rec}(l_0:T_0, \ldots, l_n:T_n) \\ \mathrm{END}; \end{array} \]](form_115.png)
Tuples could be seen in turn as special cases of records where the field names are the numbers from 0 to the length of the tuple minus 1. Currently, however, tuples and records have their own syntax for constructor and selector operators.
Records of type ![$[\# l_0:T_0, \ldots, l_n:T_n \#]$](form_114.png) have the associated built-in constructor
have the associated built-in constructor 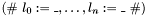 whose arguments must be terms of type
whose arguments must be terms of type 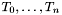 , respectively.
, respectively.
Tuples of type ![$[\ T_0, \ldots, T_n\ ]$](form_118.png) have the associated built-in constructor
have the associated built-in constructor 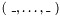 whose arguments must be terms of type
whose arguments must be terms of type 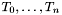 , respectively.
, respectively.
The selector operators on records and tuples follows a dot notation syntax.
% Record construction and field selection Item: TYPE = [# key: INT, weight: REAL #]; x: Item = (# key := 23, weight := 43/10 #); k: INT = x.key; v: REAL = x.weight; % Tuple construction and projection y: [REAL,INT,REAL] = ( 4/5, 9, 11/9 ); first_elem: REAL = y.0; third_elem: REAL = y.2;
Differently from datatypes, records and tuples are also provided with built-in update operators similar in syntax and semantics to the update operator for arrays. More precisely, for each record type ![$[\#\ l_0:T_0, \ldots, l_n:T_n\ \#]$](form_120.png) and each
and each 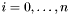 , CVC3 provides the operator
, CVC3 provides the operator
![\[ \_\ \mathrm{WITH}\ .l_i\ := \_ \]](form_122.png)
The operator maps a record 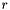 of that type and a value
of that type and a value 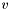 of type
of type 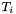 to the record that stores
to the record that stores 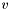 in field
in field 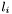 and is otherwise identical to
and is otherwise identical to 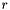 . Analogously, for each tuple type
. Analogously, for each tuple type ![$[T_0, \ldots, T_n]$](form_125.png) and each
and each 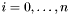 , CVC3 provides the operator
, CVC3 provides the operator
![\[ \_\ \mathrm{WITH}\ .i\ := \_ \]](form_126.png)
% Record updates Item: TYPE = [# key: INT, weight: REAL #]; x: Item = (# key := 23, weight := 43/10 #); x1: Item = x WITH .weight := 48; % Tuple updates Tup: TYPE = [REAL,INT,REAL]; y: Tup = ( 4/5, 9, 11/9 ); y1: Tup = y WITH .1 := 3;
Updates to a nested component can be combined in a single WITH operator:
Cache: TYPE = ARRAY [0..100] OF [# addr: INT, data: REAL #]; State: TYPE = [# pc: INT, cache: Cache #]; s0: State; s1: State = s0 WITH .cache[10].data := 2/3;
Note that, differently from updates on arrays, tuple and record updates are just additional syntactic sugar. For instance, the record x1 and tuple y1 defined above could have been equivalently defined as follows:
% Record updates Item: TYPE = [# key: INT, weight: REAL #]; x: Item = (# key := 23, weight := 43/10 #); x1: Item = (# key := x.key, weight := 48 #); % Tuple updates Tup: TYPE = [REAL,INT,REAL]; y: Tup = ( 4/5, 9, 11/9 ); y1: Tup = ( y.0, 3, y.1 );
ASSERT 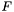 -- Add the formula
-- Add the formula 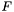 to the current logical context
to the current logical context  .
.QUERY 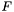 -- Check if the formula
-- Check if the formula 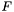 is valid in the current logical context:
is valid in the current logical context: 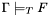 .
.CHECKSAT 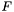 -- Check if the formula is satisfiable in the current logical context:
-- Check if the formula is satisfiable in the current logical context: 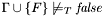 .
.WHERE -- Print all the assumptions in the current logical context  .
.COUNTEREXAMPLE -- After an invalid QUERY or satisfiable CHECKSAT, print the context that is a witness for invalidity/satisfiability.COUNTERMODEL -- After an invalid QUERY or satisfiable CHECKSAT, print a model that makes the formula invalid/satisfiable. The model is in terms of concrete values for each free symbol.CONTINUE -- Search for a counter-example different from the current one (after an invalid QUERY or satisfiable CHECKSAT).RESTART 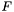 -- Restart an invalid QUERY or satisfiable CHECKSAT with the additional assumption
-- Restart an invalid QUERY or satisfiable CHECKSAT with the additional assumption 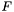 .
.
PUSH -- Save (checkpoint) the current state of the system.POP -- Restore the system to the state it was in right before the last call to PUSHPOPTO  -- Restore the system to the state it was in right before the most recent call to
-- Restore the system to the state it was in right before the most recent call to PUSH made from stack level  . Note that the current stack level is printed as part of the output of the
. Note that the current stack level is printed as part of the output of the WHERE command.
TRANSFORM 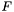 -- Simplify
-- Simplify 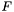 and print the result.
and print the result.PRINT 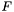 -- Parse and print back the expression
-- Parse and print back the expression 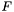 .
.OPTION option value -- Set the command-line option flag option to value. Note that option is given as a string enclosed in double-quotes and value as an integer.The remaining commands take a single argument, given as a string enclosed in double-quotes.
TRACE flag -- Turn on tracing for the debug flag flag.UNTRACE flag -- Turn off tracing for the debug flag flag.
ECHO string -- Print stringINCLUDE filename -- Read commands from the file filename.Here, we explain some of the above commands in more detail.
QUERY 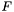 invokes the core functionality of CVC3 to check the validity of the formula
invokes the core functionality of CVC3 to check the validity of the formula 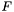 with respect to the assertions made thus far (
with respect to the assertions made thus far ( ).
). 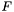 should be a formula as described in Terms and Formulas.
should be a formula as described in Terms and Formulas.There are three possible answers.
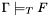 . After a valid query, the logical context
. After a valid query, the logical context  is exactly as it was before the query.
is exactly as it was before the query.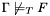 . In other words, there is a model of
. In other words, there is a model of  satisfying
satisfying 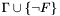 . After an invalid query, the logical context
. After an invalid query, the logical context  is augmented with new literals
is augmented with new literals 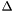 such that
such that 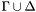 is consistent in the theory
is consistent in the theory  , but
, but 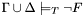 . In fact, in this case
. In fact, in this case 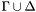 propositionally satisfies
propositionally satisfies 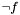 . We call the new context
. We call the new context 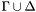 a counterexample for
a counterexample for 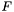 .
.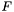 . The difference is that because CVC3 is incomplete for some theories, it cannot guarantee in this case that
. The difference is that because CVC3 is incomplete for some theories, it cannot guarantee in this case that 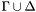 is actually consistent in
is actually consistent in  . The only sources of incompleteness in CVC3 are non-linear arithmetic and quantifiers.
. The only sources of incompleteness in CVC3 are non-linear arithmetic and quantifiers.
Counterexamples can be printed out using WHERE or COUNTEREXAMPLE commands. WHERE always prints out all of 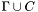 .
. COUNTEREXAMPLE may sometimes be more selective, printing a subset of those formulas from the context which are sufficient for a counterexample.
Since the QUERY command may modify the current context, if you need to check several formulas in a row in the same context, it is a good idea to surround every QUERY command by PUSH and POP in order to preserve the context:
PUSH; QUERY <formula>; POP;
CHECKSAT 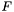 behaves identically to
behaves identically to QUERY 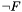 .
.RESTART 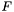 can only be invoked after an invalid query. For example:
can only be invoked after an invalid query. For example:
QUERY <formula>; Invalid. RESTART <formula2>;
The behavior of the above command will be identical to the following:
PUSH; QUERY <formula>; POP; ASSERT <formula2>; QUERY <formula>;
The advantage of using the RESTART command is that it may be much more efficient than the above command sequence. This is because when the RESTART command is used, CVC3 will re-use what it has learned rather than starting over from scratch.
A subtype 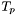 of a (sub)type
of a (sub)type  is defined as a subset of
is defined as a subset of  that satisfies an associated predicate
that satisfies an associated predicate 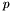 . More precisely, if
. More precisely, if 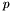 is a term of type
is a term of type 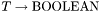 , then for every model of
, then for every model of 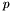 (among the models of CVC3's built-in theories),
(among the models of CVC3's built-in theories), 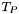 is the extension of
is the extension of 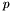 , that is, the set of all and only the elements of
, that is, the set of all and only the elements of  that satisfy the predicate
that satisfy the predicate 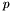 .
.
Subtypes like 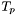 above can be defined by the user with a declaration of the form:
above can be defined by the user with a declaration of the form:
![\[ \mathit{subtype\_name}: \mathrm{TYPE} = \mathrm{SUBTYPE}(p) \]](form_142.png)
where 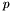 is either just a (previously declared) predicate symbol of type
is either just a (previously declared) predicate symbol of type 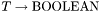 or a lambda abstraction of the form
or a lambda abstraction of the form 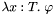 where
where 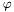 is any CVC3 formula whose set of free variables contains at most
is any CVC3 formula whose set of free variables contains at most 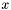 .
.
Here are some examples of subtype declarations:
Animal: TYPE; fish : Animal; is_fish: Animal -> BOOLEAN; ASSERT is_fish(fish); % Fish is a subtype of Animal: Fish: TYPE = SUBTYPE(is_fish); shark : Fish; is_shark: Fish -> BOOLEAN; ASSERT is_shark(shark); % Shark is a subtype of Fish: Shark: TYPE = SUBTYPE(is_shark); % Subtypes of REAL AllReals: TYPE = SUBTYPE(LAMBDA (x:REAL): TRUE); NonNegReal: TYPE = SUBTYPE(LAMBDA (x:REAL): x >= 0); % Subtypes of INT DivisibleBy3: TYPE = SUBTYPE(LAMBDA (x:INT): EXISTS (y:INT): x = 3 * y);
CVC3 provides integers as a built-in subtype 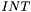 of
of 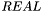 .
. 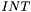 is a subtype and not a base type in order to allow mixed real/integer terms without having to use coercion functions such as
is a subtype and not a base type in order to allow mixed real/integer terms without having to use coercion functions such as 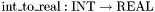
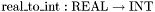 between terms of the two types. It is built-in because it is not definable by means of a first-order predicate.
between terms of the two types. It is built-in because it is not definable by means of a first-order predicate.
Note that, with the syntax introduced so far, it seems that it may be possible to define empty subtypes, that is, subtypes with no values at all. For example:
NoReals: TYPE = SUBTYPE(LAMBDA (x:REAL): FALSE);
However, any attempt to do this results in an error. This is because CVC3's logic assumes types are not empty. In fact, each time a subtype 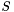 is declared CVC3 tries to prove that the subtype is non-empty; more precisely, that it is non-empty in every model of the current context. This is done simply by attempting to prove the validity of a formula of the form
is declared CVC3 tries to prove that the subtype is non-empty; more precisely, that it is non-empty in every model of the current context. This is done simply by attempting to prove the validity of a formula of the form 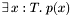 where
where  is the value type of which
is the value type of which 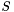 is a subtype, and
is a subtype, and 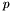 is the predicate defining
is the predicate defining 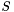 . If CVC3 succeeds, the declaration is accepted. If it fails, CVC3 will issue a type exception and reject the declaration.
. If CVC3 succeeds, the declaration is accepted. If it fails, CVC3 will issue a type exception and reject the declaration.
CVC3 might fail to prove the non-emptyness of a subtype either because the type is indeed empty in some models or because of CVC3's incompleteness over quantified formulas. Consider the following examples:
Animal: TYPE;
is_fish: Animal -> BOOLEAN;
% Fish is a subtype of Animal:
Fish: TYPE = SUBTYPE(is_fish);
Interval_0_1: TYPE = SUBTYPE(LAMBDA (x:REAL): 0 < x AND x < 1);
% Subtypes of [REAL, REAL]
StraightLine: TYPE = SUBTYPE(LAMBDA (x:[REAL,REAL]): 3*x.0 + 2*x.1 + 6 = 0);
% Constant ARRAY subtype
ConstArray: TYPE = SUBTYPE(LAMBDA (a: ARRAY INT OF REAL):
EXISTS (x:REAL): FORALL (i:INT): a[i] = x);
Each of these subtype declarations is rejected. For instance, the declaration of Fish is rejected because there are models of CVC3's background theory in which is_fish has an empty extension. To fix that it is enough to introduce a free constant of type Animal and assert that it is a Fish as we did above.
In the case of Interval_0_1 and Straightline, however, the type is indeed non-empty in every model, but CVC3 is unable to prove it. In such cases, the user can help CVC3 by explicitly providing a witness value for the subtype. This is done with this alternative syntax for subtype declarations:
![\[ \mathit{subtype\_name}: \mathrm{TYPE} = \mathrm{SUBTYPE}(p,t) \]](form_152.png)
where 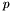 is again a unary predicate and
is again a unary predicate and 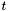 is a term (denoting an element) that satisfies
is a term (denoting an element) that satisfies 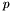 .
.
The following subtype declarations with witnesses are accepted by CVC3.
% Subtypes of REAL with witness Interval_0_1: TYPE = SUBTYPE(LAMBDA (x:REAL): 0 < x AND x < 1, 1/2); StraightLine: TYPE = SUBTYPE(LAMBDA (x:[REAL,REAL]): 3*x.0 + 2*x.1 + 6 = 0, (0, -3));
We observe that the declaration of ConstArray in the first example is rightly rejected under the empty context because the subtype can be empty in some models. However, even under contexts that exclude this possibility CVC3 is still unable to to prove the subtype's non-emptyness. Again, a declaration with witness helps in this case. Example:
zero_array: ARRAY INT OF REAL;
ASSERT FORALL (i:INT): zero_array[i] = 0;
% At this point the context includes the constant array zero_array
% and the declaration below is accepted.
ConstArray: TYPE = SUBTYPE(LAMBDA (a: ARRAY INT OF REAL):
EXISTS (x:REAL): FORALL (i:INT): a[i] = x, zero_array);
Adding witnesses to declarations to overcome CVC3's incompleteness is an adequate, practical solution in most cases.
For additional convenience (when defining array types, for example) CVC3 has a special syntax for specifying subtypes that are finite ranges of 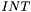 . This is however just syntactic sugar.
. This is however just syntactic sugar.
% subrange type FiniteRangeArray: TYPE = ARRAY [-10..10] OF REAL; % equivalent but less readable formulations FiniteRange: TYPE = SUBTYPE(LAMBDA (x:INT): -10 <= x AND x <= 10); FiniteRangeArray2: TYPE = ARRAY FiniteRange OF REAL; FiniteRangeArray3: TYPE = ARRAY SUBTYPE(LAMBDA (x:INT): -10 <= x AND x <= 10) OF REAL;
In essence, for every ground term of the form 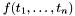 with
with 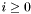 in the logical context, whenever
in the logical context, whenever 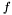 has type
has type 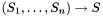 where
where 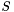 is a subtype defined by a predicate
is a subtype defined by a predicate 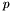 , CVC3 adds to the context the assertion
, CVC3 adds to the context the assertion 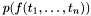 constraining
constraining 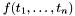 to be a value in
to be a value in 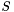 .
.
This leads to correct answers by CVC3, provided that all ground terms are well-subtyped in the logical context of the query; that is, if for all terms like 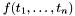 above the logical context entails that
above the logical context entails that 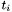 is a value of
is a value of 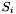 . When that is not the case, CVC3 may return spurious countermodels to a query, that is, countermodels that do not respect the subtyping constraints.
. When that is not the case, CVC3 may return spurious countermodels to a query, that is, countermodels that do not respect the subtyping constraints.
For example, after the following declarations:
Pos: TYPE = SUBTYPE(LAMBDA (x: REAL): x > 0, 1); Neg: TYPE = SUBTYPE(LAMBDA (x: REAL): x < 0, -1); a: Pos; b: REAL; f: Pos -> Neg = LAMBDA (x:Pos): -x;
CVC3 will reply "Valid", as it should, to the command:
QUERY f(a) < 0;
However it will reply "Invalid" to the command:
QUERY f(b) < 0;
or to:
QUERY f(-4) < 0;
for that matter, instead of complaining in either case that the query is not well-subtyped. (The query is ill-subtyped in the first case because there are models of the empty context in which the constant b is a non-positive rational; in the second case because in all models of the context the term -4 is non-positive.)
In contrast, the command sequence
ASSERT b > 2*a + 3; QUERY f(b) < 0;
say, produces the correct expected answer because in this case b is indeed positive in every model of the logical context.
Semantically, CVC3's behavior is justified as follows. Consider, just for simplicity (the general case is analogous), a function symbol 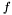 of type
of type 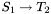 where
where 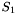 is a subtype of some value type
is a subtype of some value type 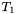 . Instead of interpreting
. Instead of interpreting 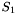 as partial function that is total over
as partial function that is total over 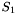 and undefined outside
and undefined outside 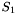 , CVC3's interprets it as a total function from
, CVC3's interprets it as a total function from 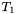 to
to 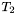 whose behavior outside
whose behavior outside 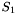 is specified in an arbitrary, but fixed, way. The specification of the behavior outside
is specified in an arbitrary, but fixed, way. The specification of the behavior outside 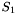 is internal to CVC3 and can, from case to case, go from being completely empty, which means that CVC3 will allow any possible way to extend
is internal to CVC3 and can, from case to case, go from being completely empty, which means that CVC3 will allow any possible way to extend 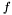 from
from 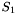 to
to 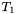 , to strong enough to allow only one way to extend
, to strong enough to allow only one way to extend 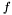 . The choice depends just on internal implementation considerations, with the understanding that the user is not really interested in
. The choice depends just on internal implementation considerations, with the understanding that the user is not really interested in 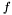 's behavior outside
's behavior outside 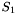 anyway.
anyway.
A simple example of this approach is given by the arithmetic division operation /. Mathematically division is a partial function from 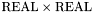 to
to 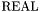 undefined over pairs in
undefined over pairs in 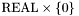 . CVC3 views
. CVC3 views / as a total function from 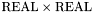 to
to 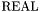 that maps pairs in
that maps pairs in 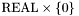 to
to 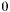 and is defined as usual otherwise. In other words, CVC3 extends the theory of rational numbers with the axiom
and is defined as usual otherwise. In other words, CVC3 extends the theory of rational numbers with the axiom 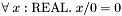 . Under this view, queries like
. Under this view, queries like
x: REAL; QUERY x/0 = 0 ; QUERY 3/x = 3/x ;
are perfectly legitimate. Indeed the first formula is valid because in each model of the empty context, x/0 is interpreted as zero and = is interpreted as the identity relation. The second formula is valid, more generally, because for each interpretation of x the two arguments of = will evaluate to the same rational number. CVC3 will answer accordingly in both cases.
While this behavior is logically correct, it may be counter-intuitive to users, especially in applications that intend to give CVC3 only well-subtyped formulas. For these applications it is more useful to the user to get a type error from CVC3 as soon as it receives an ill-subtyped assertion or query, such as for instance the two queries above. This feature is provided in CVC3 by using the command-line option +tcc. The mechanism for checking well-subtypedness is described below.
 is the union of CVC3's background theories.
is the union of CVC3's background theories.
Let us say that a (well-typed) term 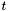 containing no proper subterms of type
containing no proper subterms of type 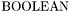 is well-subtyped in a model
is well-subtyped in a model 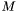 of
of  (assigning an interpretation to all the free symbols and free variables of
(assigning an interpretation to all the free symbols and free variables of 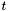 ) if
) if
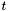 is a constant or a variable, or
is a constant or a variable, or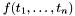 where
where 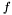 has type
has type 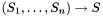 and each
and each 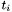 is well-subtyped in
is well-subtyped in 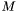 and interpreted as a value of
and interpreted as a value of 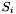 .
.
Note that this inductive definition includes the case in which the term is an atomic formula. Then we can say that an atomic formula is well-subtyped in a logical context  if it is well-subtyped in every model of
if it is well-subtyped in every model of  and
and  .
.
While this seems like a sensible definition of well-subtypedness for atomic formulas, it is not obvious how to extend it properly to non-atomic formulas. For example, defining a non-atomic formula to be well-subtyped in a model if all of its atoms are well-subtyped is too stringent. Perfectly reasonable formulas like
![\[ y > 0 \;\Rightarrow\; x/y = z \]](form_165.png)
with 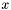 ,
, 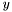 , and
, and 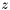 free constants (or free variables) of type
free constants (or free variables) of type 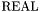 , say, would not be well-subtyped in the empty context because there are models of
, say, would not be well-subtyped in the empty context because there are models of  in which the atom
in which the atom 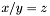 is not well-subtyped (namely, those that interpret
is not well-subtyped (namely, those that interpret 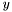 as zero).
as zero).
A better definition can be given by treating logical connectives non-strictly with respect to ill-subtypedness. More formally, but considering for simplicity only formulas built with atoms, negation and disjunction connectives, and existential quantifiers (the missing cases are analogous), we define a non-atomic formula 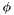 to be well-subtyped in a model
to be well-subtyped in a model 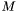 of
of  if one of the following holds:
if one of the following holds:
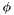 has the form
has the form 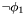 and
and 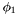 is well-subtyped in
is well-subtyped in 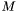 ;
;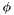 has the form
has the form 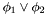 and (i) both
and (i) both 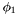 and
and 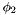 are well-subtyped in
are well-subtyped in 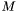 or (ii)
or (ii) 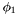 holds and is well-subtyped in
holds and is well-subtyped in 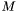 or (iii)
or (iii) 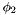 holds and is well-subtyped in
holds and is well-subtyped in 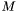 ;
;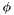 has the form
has the form 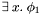 and (i)
and (i) 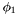 holds and is well-subtyped in some model
holds and is well-subtyped in some model 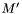 that differs from
that differs from 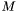 at most in the interpretation of
at most in the interpretation of 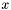 or (ii)
or (ii) 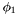 is well-subtyped in every such model
is well-subtyped in every such model 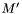 .
.
In essence, this definition is saying that for well-subtypedness in a model it is irrelevant if a formula 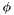 has an ill-subtyped subformula, as long as the truth value of
has an ill-subtyped subformula, as long as the truth value of 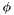 is independent from the truth value of that subformula.
is independent from the truth value of that subformula.
Now we can say in general that a CVC3 formula is well-subtyped in a context  if it is well-subtyped in every model of
if it is well-subtyped in every model of  and
and  .
.
According to this definition, the previous formula 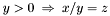 , which is equivalent to
, which is equivalent to 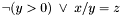 , is well-subtyped in the empty context. In fact, in all the models of
, is well-subtyped in the empty context. In fact, in all the models of  that interpret
that interpret 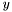 as zero, the subformula
as zero, the subformula 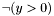 is true and well-subtyped; in all the others, both
is true and well-subtyped; in all the others, both 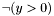 and
and 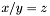 are well-subtyped.
are well-subtyped.
This notion of well-subtypedness has a number of properties that make it fairly robust. One is that it is invariant with respect to equivalence in a context: for every context  and formulas
and formulas 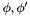 such that
such that 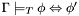 , the first formula is well-subtyped in
, the first formula is well-subtyped in  if and only if the second is.
if and only if the second is.
Perhaps the most important property, however, is that the definition can be effectively reflected into CVC3's logic itself: there is a procedure that for any CVC3 formula 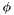 can compute a well-subtyped formula
can compute a well-subtyped formula 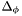 , a type correctness condition for
, a type correctness condition for 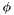 , such that
, such that 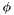 is well-subtyped in a context
is well-subtyped in a context  if and only if
if and only if 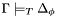 . This has the nice consequence that the very inference engine of CVC3 can be used to check the well-subtypedness of CVC3 formulas.
. This has the nice consequence that the very inference engine of CVC3 can be used to check the well-subtypedness of CVC3 formulas.
When called with the TCC option on (by using the command-line option +tcc), CVC3 behaves as follows. Whenever it receives an ASSERT or QUERY command, the system computes the TCC of the asserted formula or query and checks its validity in the current context (for ASSERTs, before the formula is added to the logical context). If it is able to prove the TCC valid, it just adds the asserted formula to the context or checks the validity of the query formula. If it is unable to prove the TCC valid, it raises an ill-subtypedness exception and aborts.
It is worth pointing out that, since CVC3 checks the validity of an asserted formula in the current logical context at the time of the assertion, the order in which formulas are asserted makes a difference. For instance, attempting to enter the following sequence of commands:
f: [0..100] -> INT; x: [5..10]; y: REAL; ASSERT f(y + 3/2) < 15; ASSERT y + 1/2 = x;
results in a TCC failure for the first assertion because the context right before it does not entail that the term y + 3/2 is in the range 0..100. In contrast, the sequence
f: [0..100] -> INT; x: [5..10]; y: REAL; ASSERT y + 1/2 = x; ASSERT f(y + 3/2) < 15;
is accepted because each of the formulas above is well-subtyped at the time of its assertion. Note that the assertion of both formulas together in the empty context with
ASSERT f(y + 3/2) < 15 AND y + 1/2 = x
or with
ASSERT y + 1/2 = x AND f(y + 3/2) < 15
is also accepted because the conjunction of the two formulas is well-subtyped in the empty context.
Specifically, when called with the option -lang smt it accepts as input an SMT-LIB benchmark belonging to one of the SMT-LIB sublogics. For a well-formed input benchmark, CVC3 returns the string "sat", "unsat" or "unknown", depending on whether it can prove the benchmark satisfiable, unsatisfiable, or neither.
At the time of this writing CVC3 supported all SMT-LIB sublogics.
We refer the reader to the SMT-LIB website for information on SMT-LIB, its formats, its logics, and its on-line library of benchmarks.
 1.5.1
1.5.1