 |
Let S be a system of constraints of the form od(a,b) << od(c,d); and let T be a cluster tree. We will say that T satisfies S (read ``T satisfies S'') if every instantiation of T satisfies S. In this section, we develop an algorithm for finding a cluster tree that satisfies a given set of constraints.
The algorithm works along the following lines: Suppose we have a solution satisfying S. Let D be the diameter of the solution. If S contains a constraint od(a,b) << od(c,d) then, since od(c,d) is certainly no more than D, it follows that od(a,b) is much smaller than D. We label ab as a ``short'' edge.
If two points u and v are connected by a path of short edges, then by the triangle inequality the edge uv is also short (i.e. much shorter than D). Thus, if we compute the connected components H of all the edges that have been labelled short, then all these edges in H can likewise be labelled short. For example, in table 1, edges vz, wx, and xy can all be labelled ``short''.
On the other hand, as we shall prove below, if an edge is not in the set H, then there is no reason to believe that it is much shorter than D. We can, in fact, safely posit that it is the same o.m. as D. We label all such edges ``long''.
We can now assume that any connected component of points connected by short edges is a cluster, and a child of the root of the cluster tree. The root of the cluster tree is then given the largest label. Its children will be given smaller labels. Each ``long'' edge now connects symbols in two different children of the root. Hence, any instantiation of the tree will make any long edge longer than any short edge.
If no edges are labelled ``long'' -- that is, if H contains the complete graph over the symbols -- then there is an inconsistency; all edges are much shorter than the longest edge. For instance, in table 2, since vw, wx, and xy are all much smaller than zy, it follows by the triangle inequality that vy is much smaller than zy. But since we also have the constraints that zy is much smaller than vz and that vz is much smaller than vy, we have an inconsistency.
The algorithm then iterates, at the next smaller scale. Since we have now taken care of all the constraints od(a,b) << od(c,d), where cd was labelled ``long'', we can drop all those from S. Let D now be the greatest length of all the edges that remain in S. If a constraint od(a,b) << od(c,d) is in the new S, then we know that od(a,b) is much shorter than D, and we label it ``short''. We continue as above. The algorithm halts when all the constraints in S have been satisfied, and S is therefore empty; or when we encounter a contradiction, as above.
We now give the formal statement of this algorithm. The algorithm uses an undirected graph over the variable symbols in S. Given such a graph G, and a constraint C of the form od(a,b) << od(c,d), we will refer to the edge ab as the ``short'' of C, and to the edge cd as the ``long'' of C. The shorts of the system S is the set of all shorts of the constraints of S and the longs of S is the set of all the longs of the constraints. An edge may be both a short and a long of S if it appears on one side in one constraint and on the other in another constraint.
procedure solve_constraints
(in S: a system of constraints of the form od(a,b) << od(c,d))
return either a cluster tree T satisfying S if S is consistent;
or false if S is inconsistent.
type: A node N of the cluster tree contains
pointers to the parent and children of N;
the field N.label, holding the integer label;
and the field N.symbols, holding the list of symbols in the leaves of N.
variables: m is an integer;
C is a constraint in S;
H,I are undirected graphs;
N,M are nodes of T;
begin if S contains any constraint of the form, ``od(a,b) << od(c,c)''
then return false;
m := the number of variables in S;
initialize T to consist of a single node N;
N.symbols:= the variables in S;
repeat H := the connected components of the shorts of S;
if H contains all the edges in S then return(false) endif;
for each leaf N of T do
if not all vertices of N are connected in H then
N.label := m;
for each connected component I of N.symbols in H do
construct node M as a new child of N in T;
M.symbols:= the vertices of I;
endfor endif endfor
S := the subset of constraints in S whose long is in H;
m := m-1;
until S is empty;
for each leaf N of T
N.label := 0;
if N.symbols has more than one symbol
then create a leaf of N for each symbol in N.symbols;
label each such leaf 0;
endif endfor end solve_constraints.
Tables 1 and 2 give two examples of the working of procedure solve_constraints. Table 1 shows how the procedure can be used to establish that the following constraints are consistent:
The Empire State Building (x) is much closer to the Washington Monument (w) than to Notre Dame Cathedral (v).
Bunker Hill (y) is much closer to the Empire State Building than to the Eiffel Tower (z).
The distance from the Eiffel Tower to Notre Dame is much less than the distance from the Washington Monument to Bunker Hill.
Table 2 shows that the following inference can be justified:
Given: The distances from the Statue of Liberty (v) to the World Trade Center (w), from the World Trade Center to the Empire State Building (x), and from the Empire State Building to the Chrysler Building (y) are all much less than the distance from the Chrysler Building to the Washington Monument (z).Infer: The Washington Monument is not much nearer to the Chrysler Building than to the Statue of Liberty.
This inference is carried out by asserting the negation of the consequent, ``The Washington Monument is much nearer to the Chrysler Building than to the Statue of Liberty,'' and showing that that collection of constraints is inconsistent. Note that if we change ``much less'' and ``much nearer'' in this example to ``less'' and ``nearer'', then the inference no longer valid.
S contains the constraints
1. od(w,x) << od(x,v).
2. od(x,y) << od(y,z).
3. od(v,z) << od(w,y).
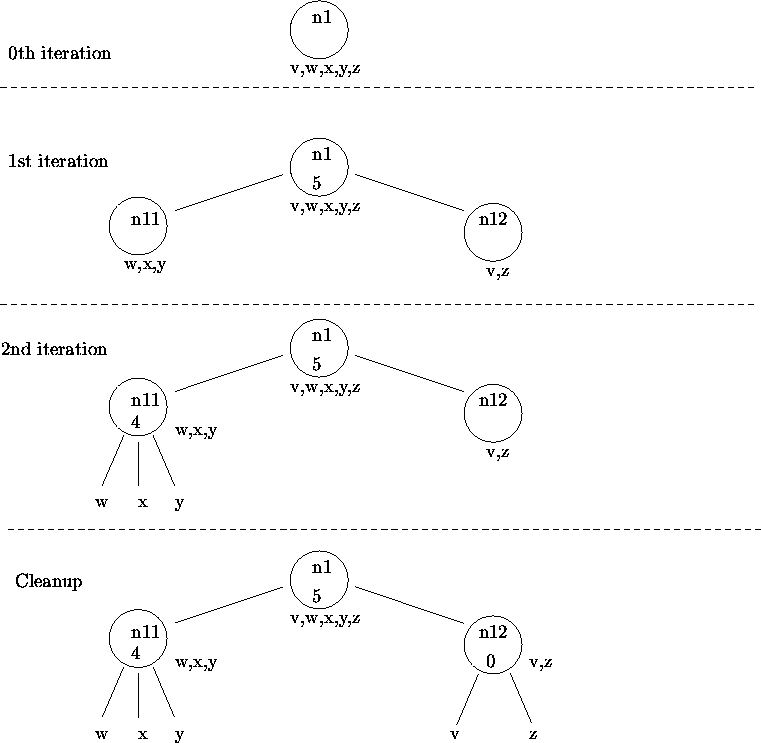
The algorithm proceeds as follows:(See Figure 2.)Initialization: The tree is initializes to a single node with n1. n1.symbols := {v,w,x,y,z}.
First iteration: The shorts of S are {wx, xy, vz}. Computing the connected components,H is set to {wx, xy, wy, vz}. n1.label := 5; Two children of n1 are created: n11.symbols := w,x,y; n12.symbols := v,z; As xv is not in H, delete constraint #1 from S. As yz is not in H, delete constraint #2 from S. S now contains just constraint #3.
Second iteration: The shorts of S are {vz }. The connected components H is just {vz}. n11.label := 4; Three children of n11 are created: n111.symbols := w; n112.symbols := x; n113.symbols := z; As wy is not in H, delete constraint #3 from S. S is now empty.
Cleanup: n12.label := 0;
Two children of n12 are created: n121.symbols := v; n122.symbols := z;
od(v,w) << od(z,y).
od(w,x) << od(z,y).
od(x,y) << od(z,y).
od(z,y) << od(v,z).
The algorithm proceeds as follows:Initialization: The tree is initializes to a single node with n1. n1.symbols := {v,w,x,y,z }.
First iteration: The shorts of S are {vw, wx, xy, zy, vz }. H is set to its connected components, which is the complete graph over v,w,x,y,z. The algorithm exits returning false
Theorem 1 states the correctness of algorithm solve_constraints. The proof is given in the appendix.
Theorem 1: The algorithm solve_constraints(S) returns a cluster tree satisfying S if S is consistent, and returns false if S is inconsistent.
There may be many cluster trees that satisfy a given set of constraints. Among these, the cluster tree returned by the algorithm solve_constraints has an important property: it has the fewest possible labels consistent with the constraints. In other words, it uses the minimum number of different orders of magnitude of any solution. Therefore, the algorithm can be used to check the satisfiability of a set of constraints in an om-space that violates axiom A.7 and has only finitely many different orders of magnitude. If the algorithm returns T and T has no more different labels than the number of different orders of magnitude in the space, then the constraints are satisfiable. If T uses more labels than the space has orders of magnitude, then the constraints are unsatisfiable.
The proof is easier to present if we rewrite algorithm solve_constraints in the following form, which returns only the number of different non-zero labels used, but does not actually construct the cluster tree.1
function num_labels(S);
if S is empty then return(0)
else return(1 + num_labels(reduce_constraints(S)))function reduce_constraints(S)
H := connected components of the shorts of S;
if H contains all the edges in S then return(false) to top-level
else return(the set of constraints in S whose long is in H)
It is easily verified that the sequence of values of S in successive recursive calls to num_labels is the same as the sequence of values of S in the main loop of solve_constraints. Therefore num_labels returns the number of different non-zero labels in the tree constructed by solve_constraints.
Theorem 2: Out of all solutions to the set of constraints S, the instantiations of solve_constraints(S) have the fewest number of different values of od(a,b), where a,b range over the symbols in S. This number is given by num_labels(S).
The proof is given in the appendix.