Algorithms
Our goal is to choose one tree from each gene, then combine those trees into
a direct acyclic graph with the fewest interbreeding events. The algorithm
can be described in two stages: tree selecting
and tree combining.
Tree Selecting
Consensus Method
Our goal is to select one tree from each gene. Therefore we would like to
select popular trees since they immediately "cover" may genes.
If there is a single tree suggested by all genes, then it suffices to select
only that tree. But usually we will see the following situation:
gene g1 suggests trees t1, t3, t5
gene g2 suggests trees t1, t2, t4
gene g3 suggests trees t1, t6, t4
gene g4 suggests trees t1, t6, t5
gene g5 suggests trees t2, t4, t7
gene g6 suggests trees t3, t5, t8
In this example we can select trees
{t1,t2,t3} to cover all genes (at
least one tree from each gene). These kind of problems are called
hitting set problems. The fewer trees we select, the easier
to combine them with a few interbreeding events (This statement is
questionable since it would be harder to combine two totally different
trees than to combine many similar trees. In practice, however, it turns
out that popular trees usually share some common structures and will be
similar after all). Therefore we would like to pick the smallest hitting
set. So in the above example, {t4,t5}
will be the right choice. Such problem is called minimum hitting set
problem. In this software, we have developed a hitting set solver to
solve it efficiently. See algorithms of the
hitting set solver for more details.
Another thing we might want to do is to ignore trees that rarely appear in the
input data since they are supported by very few evidence. Therefore we set a cutoff
frequency F in the software to discard trees that appear less
than F times in the data. If some genes are so eccentric such that every trees they
suggest are discarded, then we ignore these genes as well. The developed
algorithm is called Consensus Method:
- U <-- the set of all gene trees (duplicates removed)
- U <-- U - {t | tree t appear less than
F times in the input}
- S <-- empty set
- for each gene g do
- R <-- {t | t belongs to
U and is suggested by g}
- Append R to S
- for i in [1..MAX_ITERATION] do
- Ci <-- Hitting_Set_Solver(S, U)
- return tree collection Cx which requires the fewest
interbreeding events to be combined
The results can be found in the software
webpage.
Simulated Annealing Method
Consensus method selects trees based on their popularity. However, if all
trees appear only once (or very few times) in the data, it is much
meaningless to use this method. That is, in that case it works better to
select similar trees from each gene instead of looking for identical trees.
For this purpose we first define the similarity between trees:
Definition:
- The distance between two trees:
distance(T1, T2) = the smallest number of
interbreeding events needed to combine T1 and T2.
- Similarity: two trees are said to be similar if the distance between
them is small.
Once we define the similarity, we can easily come up with some greedy
algorithms for tree selecting:
- Similar to first heuristics:
- Pick an arbitrary tree T1 from the first gene
- for the ith gene do
- Pick the tree Ti such that
distance(T1, Ti) is minimized
- return {T1, T2, ...}
- Similar to last heuristics:
- Pick an arbitrary tree T1 from the first gene
- for the ith gene do
- Pick the tree Ti such that
distance(Ti-1, Ti) is minimized
- return {T1, T2, ...}
We develop the following algorithm by combining the above two heuristics.
We further randomize it such that it will not always run into the same
dead end. The modified algorithm:
- Randomized hybrid heuristics:
- Pick an arbitrary tree T1 from arbitrary gene
- for each other gene (in a random order) do
- Pick the tree Ti such that
distance(T1, Ti) +
distance(Ti-1, Ti) is minimized
- return {T1, T2, ...}
All these heuristics are nearly deterministic. Therefore they easily fall into
some local minima. To get out of local minima solutions, a popular method is
called simulated annealing. We first give some definitions before writing down
the whole algorithm:
Definitions:
- Evaluation of a tree collection:
Let C be a collection of gene trees (one tree from each gene).
Evaluation(C) = (The smallest number of interbreeding events
needed to combine C into a graph) *K + (Total score/rank of trees
in C)
Here K is a large enough constant such that the first term will
dominate the function (Remember the scores of trees are merely used for
tie-breaking). A tree collection is better if the evaluation score is
smaller.
- Neighbor of a tree collection:
Let C be a collection of gene trees (one tree from each gene). A neighbor
C' of C is obtained by the following random process: for each gene with
probability 1-p we include the corresponding gene tree in C to C'.
Otherwise (with probability p) randomly pick a gene tree from that
gene and add it to C'. In our software p was set to the inverse of
the number of genes. Therefore the expected number of changes from C to C'
will be 1.
Algorithm:
Simulated_Annealing(T0, T, alpha):
- Pick a starting collection C using randomized hybrid heuristics
- t <-- T0
- while t > T do
- Choose a neighbor C' of C
- d <-- Evaluation(C) - Evaluation(C')
- if d > 0 then
- C <-- C'
- else with probability ed/t :
- C <-- C'
- t <-- t * alpha
- return the best tree collection seen through the whole process
Here T0 and T stands for initial and final temperature,
respectively, while the temperature decreases exponentially with a factor
alpha every iteration. Note that even if the neighbor is worse than
the current solution, there is still some chance for the algorithm to switch
to it (especially when t is large since the probability of switching =
ed/t). That means it is possible to get out of local
minimum, which is an important feature. The spirit of this algorithm is that
the initial high temperature will make the whole system unstable. Then the
temperature cools down slowly, making it harder to switch without benefit.
See an introduction
to simulated annealing for more insight.
In this problem, a single bad tree could poison the solution seriously. So in
actual experiments the original greedy solution was rarely improved much.
Therefore instead of running a long annealing process, we also might want to
restart the algorithm several times to explore the search space as much as
we can. This is the final algorithm we developed. The experimental results
can be found in the software webpage.
Tree Combining
We use the following example (Trees are given in the
Newick tree format):
geneA: ((s1 (s2 s3) s4 s5) (s6 s7 s8))
geneB: ((s6 (s1 s2) s7 (s3 s4)) (s5 s8))
Orthologs:
s1: {geneA_11, geneB_121}
s2: {geneA_121, geneB_122}
s3: {geneA_122, geneB_141}
s4: {geneA_13, geneB_142}
s5: {geneA_14, geneB_21}
s6: {geneA_21, geneB_11}
s7: {geneA_22, geneB_13}
s8: {geneA_23, geneB_22}
All trees here are unordered, that is, the order of siblings is
unimportant. So the
Newick tree representation is not unique. For example, the following
two trees are equivalent to the above two:
geneA: ((s6 s7 s8) (s1 (s2 s3) s4 s5))
geneB: ((s6 s7 (s1 s2) (s3 s4)) (s5 s8))
Also, in
Newick tree format, a pair of parentheses corresponds to an internal
node of the tree which is the nearest common ancestor for all species
enclosed by that parentheses. For a better illustration, see our
introduction.
Definitions:
- Group:
A subset of species S forms a group if each gene tree has a
Newick tree representation such that we can insert a pair of
parentheses into that representation to enclose only species in S
without destroying the well-parenthesized structure in every tree.
- Minimal Group:
A group which contains no smaller group. Note that if A and B are both
groups, then the intersection of them will also be a group. Therefore
for any two groups A and B, one of the following relationship
holds: (1) A and B are disjoint. (2) A is a subset of B. (3) B is a
subset of A. This proposition ensures the existence of the minimal
group.
- Relationship:
- Species A and B have a closer relationship than do A and C if the
nearest common ancestor of A and B is a descendent of the nearest
common ancestor of A and C.
- In parentheses representation, A and B have a closer relationship
than do A and C if the innermost parentheses enclosing both A and B
does not enclose C.
- In subscript representation, A and B have a closer relationship than
do A and C if the longest common prefix of the subscripts of A and B
is longer than is the longest common prefix of subscripts of A and C.
Example:
- In the above example, a pair of parentheses can be inserted in the first
tree to enclose [s1 s2 s3] but not in the
second tree. So [s1 s2 s3] is not a
group. In fact, there are only three groups:
- [s1 s2 s3 s4]
- [s6 s7]
- [s1 s2 s3 s4 s5 s6 s7 s8]
The third one is the trivial group which contains all species. Group
[s1 s2 s3 s4] and
[s6 s7] are both minimal while the
trivial group is not.
- In the first tree, s3 and s5 have a closer relationship than s3 and s7.
In the second tree, however, they have a farther relationship than s3 and
s7.
Theorem:
- If s1 and s3 have a closer relationship than do s1 and s2 in some gene
tree, then any group containing both s1 and s2 must also contains s3.
- Assume G is the optimum combined graph, i.e., the one with the fewest
interbreeding events. If a subset of species S forms a group, then G has
a subtree T whose leaf set is exactly S. The root of T is the common
ancestor of species in S. In other words, the descendant set of the root
of T is S.
- Let S be the descendant set of species A. In that case, the subscripts of
orthologs in A will be the longest common prefixes of all corresponding
orthologs in species of S.
Therefore, the algorithm can be described as the following:
Main algorithm
- Grouping: Find all groups in the input data.
- Find a minimal group whose species set is denoted by S.
- For every gene tree extract the subtree containing only S. Combine these subtrees into a small graph G with the fewest interbreeding events.
- In the original trees, replace S by their common ancestor which is the
root of G.
- Insert G to our final graph.
- Repeat step 2~5 till there is only one species left. That species will
be the root of the final graph.
Example:
- Assume our program chooses [s1 s2 s3 s4]
as the first minimal group to process, the corresponding subtrees will
be:
(s1 (s2 s3) s4)
((s1 s2) (s3 s4)) -- Combining Problem 1
The next step is to combine these two trees and replace
[s1 s2 s3 s4] by a hypothetical extinct
ancestral species miss1 in original
trees:
geneA: ((s1 (s2 s3) s4 s5) (s6 s7 s8)) -->
((miss1 s5) (s6 s7 s8))
geneB: ((s6 (s1 s2) s7 (s3 s4)) (s5 s8)) -->
((s6 miss1 s7) (s5 s8))
miss1 contains orthologs
{geneA_1, geneB_1}
- The next minimal group will be [s6 s7].
The corresponding subtrees:
(s6 s7)
(s6 s7) -- Combining Problem 2
Replace [s6 s7] by a hypothetical extinct
ancestral species miss2 in original
trees:
geneA: ((miss1 s5) (s6 s7 s8)) --> ((miss1 s5) (miss2 s8))
geneB: ((s6 miss1 s7) (s5 s8)) --> ((miss2 miss1) (s5 s8))
miss2 contains orthologs
{geneA_2, geneB_1}
- Now only the trivial group [s5 s8 miss1 miss2]
is left and we get the final subtree combining problem:
((miss1 s5) (miss2 s8))
((miss2 miss1) (s5 s8)) -- Combining Problem 3
Replace [s5 s8 miss1 miss2] by a
hypothetical extinct ancestral species
miss3 in original trees:
geneA: ((miss1 s5) (miss2 s8)) --> miss3
geneB: ((miss2 miss1) (s5 s8)) --> miss3
miss3 contains orthologs
{geneA_, geneB_}
- miss3 will be the root of the combined
graph.
Next step will be solving the tree combining problems in the previous stage.
The basic strategy is to remove a minimum number of problematic species that
cause conflicts, and then combine all gene trees into one big tree (That is,
after removing those species all trees become mutually consistent). After
that, insert some intermediate missing species to complete the gene deriving
steps. Finally, pair up the removed species with proper parents and transform
the big tree into a graph.
Definitions:
- Conflict Triples: species A, B and C form a conflict triple if A
and B have a closer relationship than do A and C in gene tree
T1, but have a farther relationship than do A and C in tree
T2
Theorem:
Several trees can be combined into a big tree if and only if there is no
conflict triple.
Example:
- 2 conflict triples (s1,s2,s3) and
(s2,s3,s4) in combining problem 1:
(s1 (s2 s3) s4)
((s1 s2) (s3 s4))
- 0 conflict triples in combining problem 2:
(s6 s7)
(s6 s7)
- 4 conflict triples
(miss1,miss2,s5),
(miss1,miss2,s8),
(miss1,s5,s8) and
(miss2,s5,s8) in combining problem 3:
((miss1 s5) (miss2 s8))
((miss2 miss1) (s5 s8))
Therefore our approach can be described as the following:
- Choose a minimal set of species S and remove them such that there
is no conflict triple left
- Combine all trees into one tree
- Insert the removed species back with proper parents
Here we assume the species removed came from interbreeding events. So at the
last step we will actually associate each of them with multiple parents.
Clearly, if at the beginning we have a conflict triple (A,B,C), either A or B
or C must be in S, otherwise the removal of S will not
eliminate this triple. So again we get a hitting set problem:
Definition:
- Hitting set: Let C be a collection of sets. H is a hitting set of C if
the intersection of H and any set in C is non-empty.
- A hitting set is minimal if the removal of any element will
destroy the hitting set. A hitting set is minimum if it has the
smallest size over all hitting sets.
- Minimum hitting set problem H(C,K): C is a collection of subsets of K. Find the
minimum hitting set H of C. In this case H will always be a subset of K.
Example:
- Let K = {1,2,3,4,5,6,7}, C = {{1,4,5}, {1,2,3}, {2,6,7}, {1,3,7}}.
{3,4,6} will be a minimal hitting set (yet not minimum). In this
example, {1,2}, {1,6} and {1,7} are the only minimum hitting sets.
- In combining problem 1, the minimum hitting set of {
(s1,s2,s3),
(s2,s3,s4)}
is either {s2} or
{s3}.
- In combining problem 3, the minimum hitting set of {
(miss1,miss2,s5),
(miss1,miss2,s8),
(miss1,s5,s8),
(miss2,s5,s8)}
has size 2. In fact, any size 2 subset is a minimum hitting set.
We can model each conflict triple as a set of size 3 and K the set of all
species. Then the species removing problem in step 1 becomes a hitting set
problem. A hitting set solver was developed
to solve this NP-complete problem (The hitting set problem remains
NP-complete even under the constraint that every set has size 3).
Once we find the hitting set, we remove those species from all trees. Now we
should be able to combine the rest into a big tree (See Theorem above). In
fact this can be done by the same steps in the main
algorithm (See the following example).
Example:
- Assume we picked {s2} as the minimum
hitting set and removed it from the combining problem 1:
geneA: (s1 (s2 s3) s4) --> (s1 (s3) s4)
geneB: ((s1 s2) (s3 s4)) --> ((s1) (s3 s4))
- Now the [s3 s4] is a minimal group.
Replace it by a hypothetical species miss4
:
geneA: (s1 (s3) s4) --> (s1 miss4)
geneB: ((s1) (s3 s4)) --> ((s1) miss4)
miss4 contains orthologs
{geneA_1, geneB_14}
- Then only the trivial group [s1 miss4]
is left and we replace it by species miss5
:
geneA: (s1 miss4) --> miss5
geneB: ((s1) miss4)--> miss5
miss5 contains orthologs
{geneA_1, geneB_1}
- miss5 will be the root of the subgraph.
Note that miss1 mentioned above has
the same ortholog set with miss5, so
they are actually the same species. Let's use
miss1 to represent the root.
The combined subgraph:
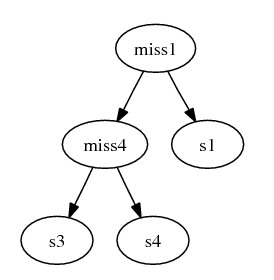
After combining the subtrees, we complete gene deriving steps by inserting
intermediate hypothetical species.
Example:
- From above we inferred that miss4
{geneA_1, geneB_14} is an ancestor of s3
{geneA_122, geneB_141}. But there are 3 gene mutation steps
happening in between:
geneA_1 --> geneA_12,
geneA_12 --> geneA_122 and
geneB_14 --> geneB_141.
Therefore there are 3 possible evolutionary path:
- {geneA_1, geneB_14} --> {geneA_12, geneB_14} --> {geneA_122,
geneB_14} --> {geneA_122, geneB_141}
- {geneA_1, geneB_14} --> {geneA_12, geneB_14} --> {geneA_12,
geneB_141} --> {geneA_122, geneB_141}
- {geneA_1, geneB_14} --> {geneA_1, geneB_141} --> {geneA_12,
geneB_141} --> {geneA_122, geneB_141}
- Deciding which path yields fewer interbreeding events in the final graph
is an NP-hard problem. Therefore our software will randomly choose one
path. Say we take the first one, the intermediate species inserted will
be miss6 {geneA_12, geneB_14} and
miss7 {geneA_122, geneB_14}. Similarly,
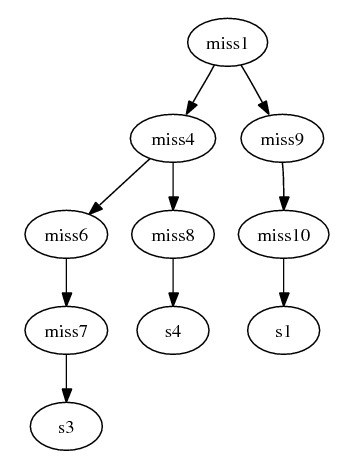
assume we insert the following paths (edges) to this graph:
- miss4 {geneA_1, geneB_14} --> miss6 {geneA_12, geneB_14} -->
miss7 {geneA_122, geneB_14} --> s3 {geneA_122, geneB_141}
- miss4 {geneA_1, geneB_14} --> miss8 {geneA_13, geneB_14} -->
s4 {geneA_13, geneB_142}
- miss1 {geneA_1, geneB_1} --> miss9 {geneA_11, geneB_14} -->
miss10 {geneA_11, geneB_12} --> s1 {geneA_11, geneB_121}
- miss1 {geneA_1, geneB_1} --> miss4 {geneA_1, geneB_14}
- The combined graph becomes:
Finally, we infer the parents of removed species by their orthologs.
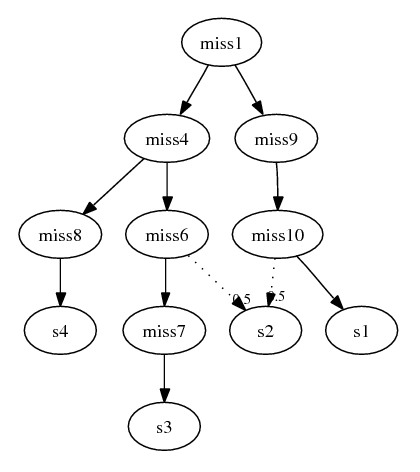
Example:
- Here is only one removed species: s2
{geneA_121, geneB_122}. Recall that
geneA_121 must be derived from geneA_12
and miss6 is the only species
containing that ortholog in this subgraph. Therefore
miss6 must be a parent of
s2. Similarly, since
miss10 is the only species containing
ortholog geneB_12 for deriving
geneB_122, it must also be a parent of
s2. The final subgraph:
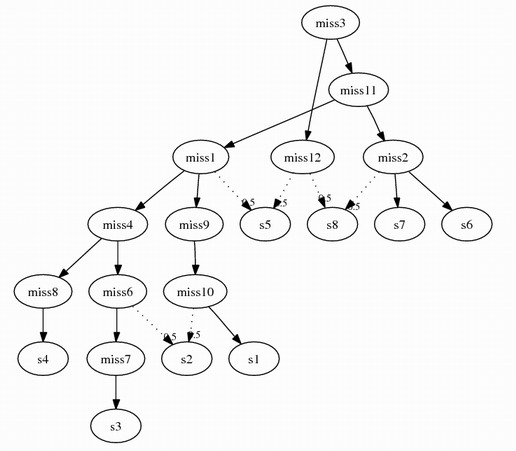
Following this algorithm, assume we remove s5 and s8 from combining problem 3,
2 more intermediate species will be inserted:
miss11 {geneA_, geneB_1}
miss12 {geneA_, geneB_2}
The complete combined graph:
Grouping
We start with a set of two species and recursively bring in species which are
close to some species in the set. The algorithm can be described as the
following:
- Arbitrarily pick species s1 and s2
- s+ <-- {s1, s2}
- Until s+ does not change do
- Consider a species t outside s+ :
- for each gene g and any two species x, y in
s+ :
- if x and t have a
closer relationship than do y and t then
-
Add t into s+
-
break
- return s+
Repeat this procedure with all possible combinations of s1 and s2 such that
we can obtain all possible groups (There are some minor things to be worried
about. For more details, see the paper).
Hitting Set Solver
Here we introduce three approximation/heuristic algorithms solving the
general hitting set problem.
Algorithm 1 - Three approximation algorithm:
- H <-- empty set
- while H not yet hit all set in C do
- Pick a set not yet hit, add every element in
that set to H
- return H
Note in our case that every set in C has size 3, this algorithm has a
theoretical guarantee: if the minimum hitting set has size k, then the
size of the returned hitting set will not exceed 3k. In computer
science jargon, we say this algorithm yields an approximation factor
of 3. However, practically it doesn't work very will. This algorithm might
not even report a minimal hitting set! For the above example, the output
would be {1,4,5,2,6,7} whose size is exactly 3 times the optimum size. In our
program, redundant elements in the solution are removed such that the final
output will be minimal. However, the performance is still not that great in
general. We kept this implementation merely because it reaches the best known
approximation ratio.
Algorithm 2 - Frequency heuristic (greedy) algorithm:
- H <-- empty set
- while H not yet hit all set in C do
- Choose the element hitting the most un-hit sets and add
it to H
- return H
This algorithm also has a theoretical guarantee: an approximation factor of O (lnN), where N is the total number of sets. However, this algorithm is
popular not because of the theoretical aspect, but because this seems like the
most natural thing to do. For above example, the algorithm will pick 1 first.
After that {2,6,7} becomes the only un-hit set and any one element of it will
be picked in the second iteration. The final output will be the minimum
solution. Unfortunately, this algorithm is almost deterministic therefore it
easily falls into some local minima, which prevents further improvements of
the solution.
Algorithm 3 - Random hitting algorithm:
- H <-- K
- P <-- a random permutation of K
- for e in P do
- if H-e is still a hitting set then
- H <-- H-e
- return H
This strategy is quite different. Instead of starting with an empty set,
we initially takes all elements in K, which is guaranteed to be a hitting set.
Then the algorithm tries to discard elements in a random order. The good news
is it always has the opportunity to achieve the optimum solution. If we repeat
the algorithm enough times, the probability that it returns a nearly optimum
solution will be high. However, if the problem size is huge, we will need to
repeat the algorithm many times for a good solution, which makes the software
too inefficient.
Our hitting set solver combines all three strategies since each of them
has its pros and cons. The final solver runs the first two deterministic
algorithm once and the third randomized algorithm MAX_ITERATION times. Then
it reports the best solution seen.
back to software homepage
Chien-I Liao



