Elastic Burst detection

Yunyue Zhu
Courant Institute of Mathematical Sciences
Department of Computer Science
New York University
yunyue@cs.nyu.edu
http://cs.nyu.edu/yunyue/index.html

Dennis Shasha
Courant Institute of Mathematical Sciences
Department of Computer Science
New York University
shasha@cs.nyu.edu
http://cs.nyu.edu/cs/faculty/shasha/index.html

Motivation

In many applications, people are interested in discovering intervals with unusually large numbers of events.

In astrophysics, the sky is constantly observed for high-energy particles. When a particular astrophysical event happens, a shower of high-energy particles arrives in addition to the background noise. This yields an unusually high number of detectable events over a time period.
In telecommunication, if the number of packages lost within a certain time period exceeds some threshold, it might indicate some network anomaly.
In finance, stocks with unusual high trading volumes should attract the notice of traders (or perhaps regulators).

Formally, the problem of interest is to discover a subsequence of the time series that have a particular aggregate significantly different from that aggregate in most time periods of the same size. In the case of burst detection, the aggregate is sum. (In fact, we can be more general than this. The aggregate function must be monotonic with window inclusion, i.e. if window1 is included in window2, then agg(window1) is less than agg(window2). Also, the test for interestingness of the aggregate is magnitude, where larger is most interesting. Sum is one example, but so is, for example, spread i.e., the max value in a window less the min value in the window.) If we know the duration of the time interval, we can maintain the sum over sliding windows of the known window size and raise an alarm when the moving sum is above a threshold. Unfortunately, in many cases, we cannot predict the duration of the burst period. For example, in astrophysics, a burst of high-energy particles associated with a special event might last for a few milliseconds or a few hours or even a few days. Similarly, in finance, a burst may result from insider trading, the attempt to buy or sell a large bunch of stocks, or from price collapse of a significant stock as happened for example on January 18, 2002 to Imclone stock after news of the Martha Stuart scandal. The formal definition of the problem of burst detection is as follows.

Given a time series of positive numbers x_1,x_2,...,x_n, and a threshold function f(w), w=1,2,...,n, find the subsequences of any size such that their sums are above the thresholds, i.e.,

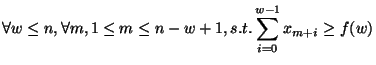
A brute force search has to examine all the sliding window sizes and starting positions. Because there are O(n^2) windows for a sequence of size n, the lower bound of the time complexity is O(n^2). This is very slow for many applications. However, in most applications, we are interested only in those few windows that experience bursts. We present here a burst searching program whose time complexity is approximately proportional to the size of the output, i.e. the number of windows with bursts, and that requires one pass over the input. Here is a pictorial description of the algorithm. Here is a paper.

Installation

The burst detector runs in a high performance interpreted environment called K.

To begin with, therefore, please download trial K from kx.com . The license is good for a limited duration, but is renewable an unlimited number of times. K and our program run equally well on linux and windows.
Send email to shasha@cs.nyu.edu. If you care to describe your application, we'd be glad to hear about it. In any case, we will send you instructions for downloading the program:
- burst.k -- the software
- burstin -- a sample time series
- threshin -- a sample list of thresholds
- You can then run the program by typing
  k burst

Semantics of the Input

The input time series is of the following format:
x1
x2
x3
...
The input threshold is of the following format:
w1,f(w1)
w2,f(w2)
w3,f(w3)
...
If the sum of the subsequence in a window with size w_i is larger than f(w_i), we say that the window experiences burst.

Semantics of the Result

The output of the program is list of tuples as follows.
Window Size, Starting Position, Ending Position
Each tuple means that in the time series, between positions Starting Position and Ending Position, all the sliding windows with size Window Size experience bursts.

Options

The program has a few command line options: k burst [+f filename1 filename2]

With no options, the input time series comes from the file burstin and thresholds come from the file threshin .
+f foo bar -- specifies that the input file of time series and threshold are foo and bar instead of burstin and threshin .

Support

This material is based upon work partly supported by the United States National Science Foundation under grants IIS-9988636 and N2010-0115586. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation. This support is greatly appreciated.