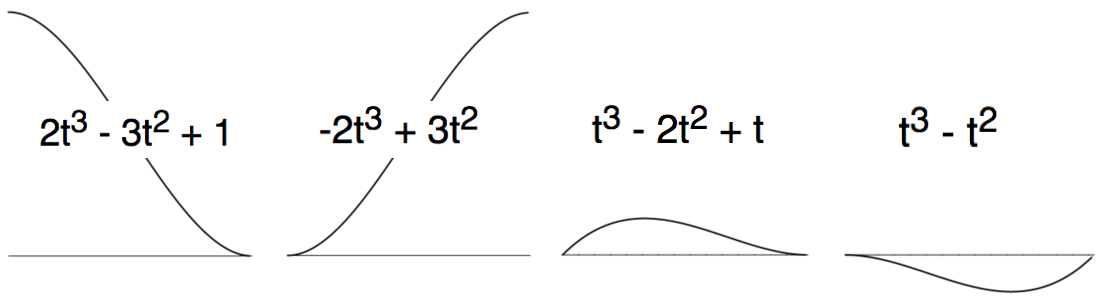Notes for Monday October 21:
Cubic Splines and Bicubic Patches

 

SPLINES

The word "spline" had its origin in ship building. To create smooth hull shapes, ancient ship builders would drive pegs into the ground, and then lay down a very large thin flexible strip of wood (the "spline") that would be forced into a curve by the position of the pegs.

They would then use the resulting smooth curve as a guide for cutting the lumber that they would use to create the hulls of their ships.

In more recent times, beginning in the 1960s, designers in the automotive and aerospace industries started using computer software to generate smooth curves when designing their vehicles. Their key innovation was to use parametric cubic curves and parametric bicubic surfaces, and that is the topic we are covering this week.

 

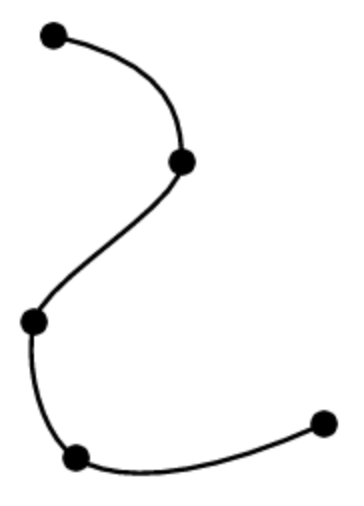
PARAMETRIC CUBIC CURVES

The underlying math for creating smooth splines is generally to create a set of parametric cubic curves that fit together seamlessly, so that they appear to form a single smooth curve. The general recipe is as follows:

  • Divide the curve into simple curved segments.

  • The position and orientation at the end of each segment is the same as the position and orientation at the beginning of the next segment.

  • The points that begin and end segments are called "key points".

  • Each segment is a parametric curve x(t), y(t), (and optionally z(t)), where t varies between 0.0 and 1.0.

  • In particular, the position along each dimension of every segment is a cubic function:

    x(t) = ax * t3 + bx * t2 + cx * t + dx
    y(t) = ay * t3 + by * t2 + cy * t + dy

After defining the above functions x(t) and y(t), it's easy to draw the resulting spline segment. For example: 

   function drawSpline(x, y, dt) {
      let a = [x(0), y(0)];
      for (let t = dt ; t <= 1 ; t += dt) {
         let b = [x(t), y(t)];
         drawLine(a, b); // we are assuming some drawLine() function has been defined.
         a = b;
      }
   }
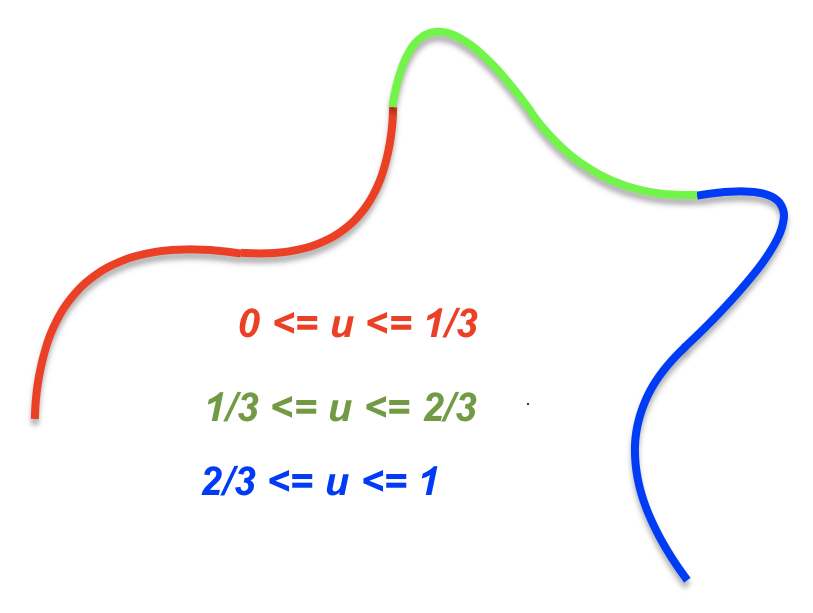
Creating more complex curves

You can also string together multiple cubic spline curves together to create a more complex curve, as you can see in the figure to the right. Suppose you want to define a parametric curve with many twists and turns, that varies along some parameter 0.0 ≤ u ≤ 1.0.

You can define that curve as a succession of N parametric cubic curves: 

   [ [ax,bx,cx,dx] , [ay,by,cy,dy] ]0,
   [ [ax,bx,cx,dx] , [ay,by,cy,dy] ]1,
   [ [ax,bx,cx,dx] , [ay,by,cy,dy] ]2,
   ...
To evaluate this curve at some value of u, first compute which cubic curve is to be evaluated: 
   i = floor(N * u)
Then compute the parametric position within that cubic curve: 
   t = N * u - i
In the above discussion, the curve can be three dimensional, rather than two dimensional. In that case, each cubic curve segment would be described by: 

   [ [ax,bx,cx,dx] , [ay,by,cy,dy] , [az,bz,cz,dz] ]i

 

TRANSLATING FROM THE HUMAN DESIGNER TO THE COMPUTER

For most human beings, it would be extremely difficult to design such curves by directly typing the coefficients of cubic polynomials. For this reason, we create other ways of defining those coefficients, which are more human-friendly.

All such methods work by transforming some easier to understand set of values into the underlying cubic coefficients (a,b,c,d). In class we went over two of the more important such methods, Hermite splines and Bezier splines.

 

HERMITE SPLINES

If our human user wants to define things in terms of the position and orientation at the beginning and end of each cubic spline segment, then we use the Hermite spline.

We do all the math independently for each coordinate (eg: x and y, or x,y and z).

P0 = value at start of the segment (where t = 0).
P1 = value at end of the segment (where t = 1).
R0 = slope at start of the segment (where t = 0).
R1 = slope at end of the segment (where t = 1).

We create four "basis functions", each of which varies only one thing:

only P0: 2t3 - 3t2 + 1
only P1:-2t3 + 3t2
only R0:  t3 - 2t2 + t
only R1:  t3 - t2

So to get from (P0,P1,R0,R1) to the coefficients (a,b,c,d) that define cubic polynomial a * t^3 + b * t^2 + c * t + d, we apply the Hermite Basis Matrix, which is just a way of describing these four basis functions. Each of the four functions is described in a single column of the Hermite Matrix:

a
b
c
d		  ⇐  2
-3
0
1		 -2
3
0
0		 1
-2
1
0		 1
-1
0
0		  ×  P0
P1
R0
R1

 

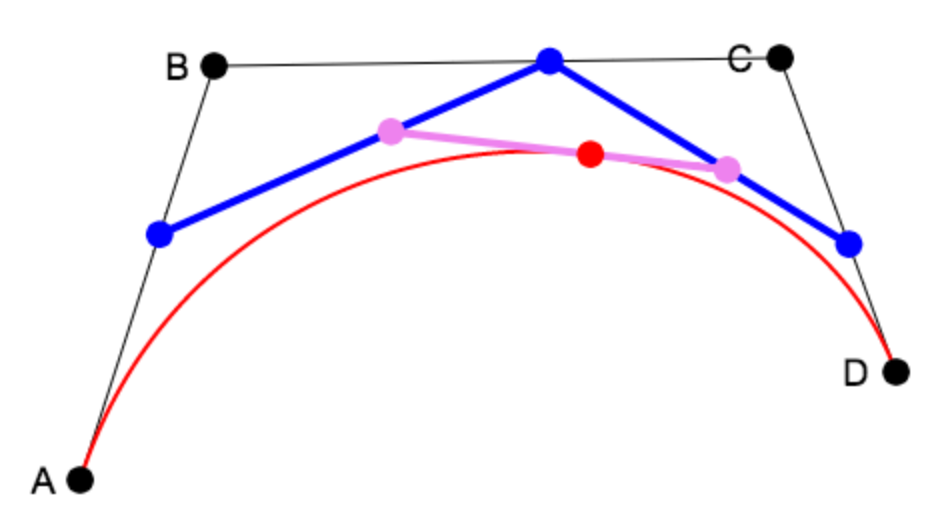
BEZIER SPLINES

If our human user wants to define things by moving points around on a screen, then the Bezier spline is a good choice.

Again, we do the math independently for each coordinate.

A = value at start of the segment (where t = 0).
B = value at a first "guide point".
C = value at a second "guide point".
D = value at end of the segment (where t = 1).

The math is basically successive linear interpolations: 

   mix (
      mix ( mix(A,B,t) , mix(B,C,t) , t ),
      mix ( mix(B,C,t) , mix(C,D,t) , t ),
      t
   )

where we define mix(a,b,t) as linear interpolation:

(a,b,t) ⇒ (1 - t) * a + t * b

In other words: 

   (1-t) * ( (1-t) * ((1-t)*A + t*B)  +  t * ((1-t)*B + t*C) )
     +
     t   * ( (1-t) * ((1-t)*B + t*C)  +  t * ((1-t)*C + t*D) )

When you multiply everything out, this turns into: 

       (1-t) * (1-t) * (1-t) * A +
   3 * (1-t) * (1-t) *   t   * B +
   3 * (1-t) *   t   *   t   * C +
         t   *   t   *   t   * D

This gives us what we need to go from key values (A,B,C,D) to cubic coefficients (a,b,c,d). Each line of the above equation can be turned into a column of the characteristic Bezier Basis Matrix:

a
b
c
d		  ⇐  -1
3
-3
1		 3
-6
3
0		 -3
3
0
0		  1
0
0
0		  ×  A
B
C
D

 

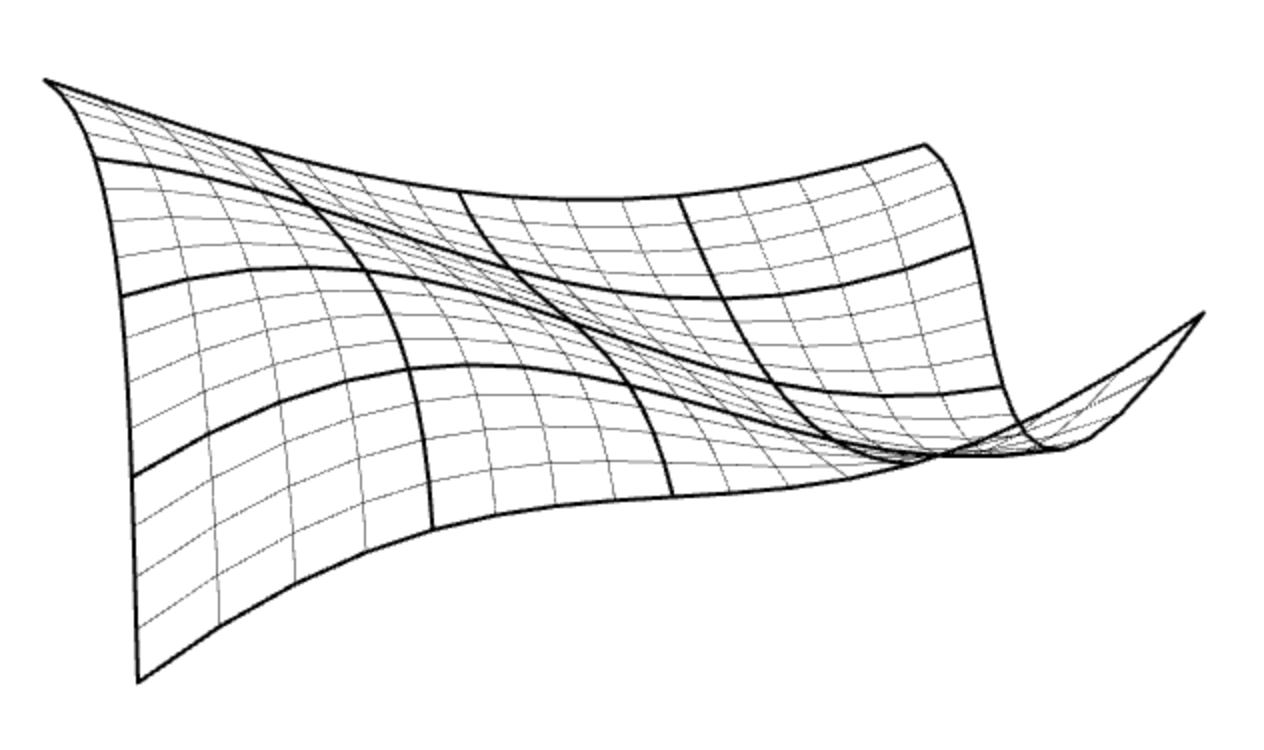
BEZIER BICUBIC SURFACE PATCHES

We can extend the idea of parametric cubic curves to bicubic patches. Instead of mapping a single parameter t to a curve, we map two parameters u and v to a patch of curved surface. As with cubic curves, we generally find it useful to transform our representation of such surface patches into something easier to understand, perhaps using a Bezier or Hermite transformation.

For example, each point in the above patch was determined by applying a Bezier transformation to a 4x4 matrix P of 16 key points:

[u3 u2 u 1]   •   Bz   •   P   •   BzT   •   [v3 v2 v 1]T

 

A NOTE ON COMPUTING SURFACE NORMALS TO MAKE SHAPES LOOK ROUNDED

As we discussed in class, here is a general purpose way to compute surface normals to create the appearance of a smooth rounded surface.

  1. For each polygonal face of the surface, compute an unnormalized face normal.

  2. For each vertex, sum up the unnormalized face normals of faces that adjoin that vertex, and then normalize the result.
To compute the unnormalized face normal of a polygonal face for step 1 above: 
   V = [0,0,0]
   For every three successive vertices A,B,C of the face, going around counterclockwise:
      V += cross(B - A, C - B)
Recall that cross product of two vectors [ax,ay,az] and [bx,by,bz] is: 
      [ ay*bz - az*by , az*bx - ax*bz , ax*by - ay*bx ]
Note that you will need to do some bookkeeping to know which faces adjoin which vertices. This is actually quite easy in the special case where you have a rectangular mesh.

In that special case, you just need to compute the face normal for every quad (that is, rectangular face) lower bounded on the grid by (col,row)

Then for every vertex at (col,row), you can sum up the face normals for the four quads that are lower bounded on the grid by, respectively: 

   (col-1,row-1) , (col,row-1) , (col-1,row) , (col,row)
 

HOMEWORK

In the last part of class I showed you my implementation of cubic splines and bicubic patches as a 3D scene.

hw7.zip contains a variation on that scene, with key parts of the implementation missing.

Your first job is to fill in those missing parts. There are lots of implementation notes in the code comments to help you along.

When the scene is fully implemented, it will look like the image to the right.

I have already implemented for you the definition of both the Hermite and Bezier basis matrices, a function to convert from any such basis to cubic curve coefficients, and another function to convert from any such basis to bicubic patch coefficients.

Rather than just use the shapes I've created, I would like you to create your own shapes. As usual, be creative, have fun, animate things in an interesting way.

In the included code, I've also implemented texture mapping. Feel free to add cool and interesting textures to the scene you create.

 

Some additional notes on the code in the homework:

  • The mesh creation function createMeshVertices() is responsible for calling the function that creates vertices at various values of u and v. In the case of creating a ribbon shape, uvToCubicCurvesRibbon() is that function. It gets called by the mesh creation function each time a vertex needs to be added.

    uvToCubicCurvesRibbon() will be called by createMeshVertices() with different values of u and v passed in. As u varies, we get points along the length of the ribbon. As v varies, we get points along the width of the ribbon.

  • To figure out the direction along the ribbon at any given value of u, we take close spaced samples along the center line of the ribbon. For example, we can take the difference between the point P0 at (u,0) and the point P1 at (u+.001,0), which gives the direction (dx,dy) along the ribbon. More precisely, (dx,dy) = normalize(P1 - P0).

    Once we have point P0 along u along the center line of the ribbon, as well as direction vector (dx,dy) along the direction of the ribbon, then we use the perpendicular direction (-dy,dx) across the width of the ribbon, which varies in v. One edge of the ribbon (where v = 0.0) is at P0 - width*(-dy,dx) and the other edge of the ribbon (where v = 1.0) is at P0 + width*(-dy,dx).