Parametric surfaces and texture mapping
PARAMETRIC SURFACES
A parametric surface is defined by two parameters: u and v. As u and v each vary between 0.0 and 1.0, you can use them to define a sort of rubber sheet, by defining some function that maps
(u,v) → [x,y,z]
In practice, it is useful to also return a surface normal:
(u,v) → [x,y,z, nx,ny,nz]In the following section we will go over how to create a triangle mesh that implements an approximation to a parametric surface.
To do this efficiently, we will make use of triangle strips.
APPROXIMATING A PARAMETRIC SURFACE WITH A RECTANGULAR MESH
As we discussed in class, we can approximate a parametric surface with a rectangular mesh with M columns and N rows of vertices, containing a regular spacing of discrete values of u and v.
For example, the mesh below has 5 columns and 4 rows of vertices, where each vertex is represented by an "X":
X---X---X---X---X v = 1
| | | | |
X---X---X---X---X v = 2/3
| | | | |
X---X---X---X---X v = 1/3
| | | | |
X---X---X---X---X v = 0
0 1/4 2/4 3/4 1 ⟵ values of u
For example, the row which is second from the top and
second from the left (shown in red) represents a vertex
at u = 1/4 and v = 2/3.
REPRESENTING AN ENTIRE MESH AS A SINGLE TRIANGLE STRIP
Note:
I had a bug in my previous version of the below,
which ended up flipping the resulting shapes inside out.
An astute student kindly pointed out the error,
and it has now been corrected.
Very sorry about that.
-KP
We can represent an entire such mesh as a single triangle strip, consisting of rows that zigzag back and forth first right to left, then left to right, and so on.
The bottom row goes from right to left, and consists of the first 2M vertices, representing the first 2 * (M-1) triangles, as follows:
⟵ ⟵ ⟵ ⟵
2M-1 2M-3 2M-5 3 1
| / | / | / | / |
| / | / | ... | / |
| / | / | / | / |
2M-2 2M-4 2M-6 2 0
⟵ ⟵ ⟵ ⟵
The second row defines 2M-1 more vertices (without repeating the last one),
and doubles back from left to right,
representing the next 2 * (M-1) triangles, as follows:
⟶ ⟶ ⟶ ⟶
2M 2M+2 2M+4 4M-4 4M-2
| \ | \ | \ | \ |
| \ | \ | ... | \ |
| \ | \ | \ | \ |
| 2M+1 2M+3 4M-5 4M-3
⟶ ⟶ ⟶ ⟶
After that we keep zigzagging back and forth,
right to left for even numbered rows,
then left to right for odd numbered rows.
Here, for example, is what the first three rows look like:
6M-3 6M-5 6M-7 4M+1 4M-1
| / | / | / | / |
| / | / | ... | / |
| / | / | / | / |
6M-4 6M-6 6M-8 4M |
2M 2M+2 2M+4 4M-4 4M-2
| \ | \ | \ | \ |
| \ | \ | ... | \ |
| \ | \ | \ | \ |
| 2M+1 2M+3 4M-5 4M-3
2M-1 2M-3 2M-5 3 1
| / | / | / | / |
| / | / | ... | / |
| / | / | / | / |
2M-2 2M-4 2M-6 2 0
Note that most vertices in the mesh are represented twice, because the vertices on the bottom edge of any row are repetitions of the same vertex on the top edge of the row directly below it.
For example, vertex 2M+1 has the same values as vertex 2M-3, since both of these vertices are at the parametric location u = 1/(N-1), v = 1/(M-1). Both of these vertices are shown in red.
Since each rectangle in the mesh represents two triangles, there will be a total of 2 * (M-1) * (N-1) triangles.
DEFINING A SHAPE AS A TRIANGLE MESH
In order to build the triangle mesh that represents a particular parametric shape, you need to implement the function:
createMesh(M, N, callback)where M is the number of columns, N is the number of rows, and
callback
is a function that converts
(u,v) to
[x,y,z, nx,ny,nz].
To create this function, you need to implement
the zigzag algorithm described above.
If you implement it correctly, then
your createMesh() function
will return a flat array of:
(1 + (2*M - 1) * (N - 1)) * VERTEX_SIZEfloating point values, where
VERTEX_SIZE is the number of floating point values
in a single vertex.
For example, if M = 5, N = 4 and VERTEX_SIZE = 6,
your function would return an array containing (1 + 9 * 3) * 6 = 168
floating point values.
SPHERE
Given u and v, we can define the callback function
uvToSphere(u,v)
that will create a unit sized sphere as follows:
θ = 2πu
φ = πv - π/2
x = cos(θ) cos(φ)
y = sin(θ) cos(φ)
z = sin(φ)
return [x,y,z, x,y,z] // note that the surface normal is also x,y,z
Just to check whether you are on the right track,
if you make the following call:
createMeshVertices(5, 3, uvToSphere);you should get something like the following result (after removing small round-off errors):
[ 0, 0, -1, 0, 0, -1, 1, 0, 0, 1, 0, 0, 0, 0, -1, 0, 0, -1, 0, -1, 0, 0, -1, 0, 0, 0, -1, 0, 0, -1, -1, 0, 0, -1, 0, 0, 0, 0, -1, 0, 0, -1, 0, 1, 0, 0, 1, 0, 0, 0, -1, 0, 0, -1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, -1, 0, 0, -1, 0, 0, 0, 0, 1, 0, 0, 1, 0, -1, 0, 0, -1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1 ]
TORUS
Given u and v, we can define the callback function
uvToTorus(u,v)
that will create a unit sized torus with inner tube radius r as follows:
θ = 2πu
φ = 2πv
x = cos(θ) (1 + r cos(φ))
y = sin(θ) (1 + r cos(φ))
z = r sin(φ)
nx = cos(θ) cos(φ)
ny = sin(θ) cos(φ)
nz = sin(φ)
return [x,y,z, nx,ny,nz]
OPEN TUBE
Given u and v, we can define the callback function
uvToTube(u,v)
that will create a unit sized open cylindrical tube as follows:
θ = 2πu
x = cos(θ)
y = sin(θ)
z = 2v - 1
return [x,y,z, x,y,0]
CAPPED CYLINDER
To create a capped cylinder, we can
vary v from 0.0 to 1.0 in six steps.
To do this, we can call createMesh(M, N, uvToCylinder)
with N = 6.
Steps 0 and 1 represent a cap at the back where z = -1. Steps 2 and 3 represent the sides of the cylindrical tube. Steps 4 and 5 represent a cap at the front where z = 1.
The algorithm
uvToCylinder(u,v)
can use to generate a cylindrical mesh
is then as follows:
c = cos(2πu)
s = sin(2πu)
z = max(-1, min(1, 10*v - 5))
switch (floor(5.001 * v)) {
case 0: case 5: return [ 0,0,z, 0,0,z ] // center of back/front end cap
case 1: case 4: return [ c,s,z, 0,0,z ] // perimeter of back/front end cap
case 2: case 3: return [ c,s,z, c,s,0 ] // back/front of cylindrical tube
}
TEXTURE MAPPING
We went over texture mapping in class, and learned about the MIPMapping antialiasing algorithm, created by Lance Williams in 1981, and still a mainstay of real-time computer graphics after all these years (it's built into every GPU).
Then we looked at an example of actual code that does texture mapping.
I don't want to give you too much homework for next week, since this will be a short week, so I'm not going to ask you to do anything for texture mapping for this week's homework. I think we will be able to roll that into the homework for a week later.
COOL VIDEOS WE WATCHED
At the end of class we watched the following two videos:
- The Academy Award winning 2003 short film Ryan by Chris Landreth
- The iconic kitchen scene from Jurassic Park
HOMEWORK
For your homework, which is due by class time on Monday October 21, I would like you to create a scene with multiple different shapes, including cubes, ellipsoids, tori and cylinders.
Once again, have fun with it. Be imaginative and creative. Make something really cool and interesting and animated.
Note:
To draw different shapes within the same
animation frame, you can load a different
vertexArray
into
the buffer before calling drawArrays(),
using either
gl.TRIANGLES
or
gl.TRIANGLE_STRIP
as appropriate.
As a reference,
I used the onDraw() code
below
to produce the scene to the right:
function onDraw(t, projMat, viewMat, state, eyeIdx) {
gl.uniformMatrix4fv(state.uViewLoc, false, new Float32Array(viewMat));
gl.uniformMatrix4fv(state.uProjLoc, false, new Float32Array(projMat));
let drawShape = (color, type, vertices) => {
gl.uniform3fv(state.uColorLoc, color);
gl.uniformMatrix4fv(state.uModelLoc, false, m.value());
gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(vertices), gl.STATIC_DRAW);
gl.drawArrays(type, 0, vertices.length / VERTEX_SIZE);
}
m.identity();
m.translate(-.6,.5,-4);
m.scale(.4,.4,.4);
drawShape([1,1,0], gl.TRIANGLE_STRIP, sphereVertices);
m.identity();
m.translate(-.6,-.5,-4);
m.rotateY(-1);
m.rotateX(-1);
m.scale(.29,.29,.29);
drawShape([1,0,1], gl.TRIANGLES, cubeVertices);
m.identity();
m.translate(.6,.5,-4);
m.rotateY(-1);
m.rotateX(.5);
m.scale(.33,.33,.33);
drawShape([0,1,1], gl.TRIANGLE_STRIP, torusVertices);
m.identity();
m.translate(.6,-.5,-4);
m.rotateY(-.5);
m.rotateX(-.5);
m.scale(.33,.33,.4);
drawShape([1,.5,.5], gl.TRIANGLE_STRIP, cylinderVertices);
}
|
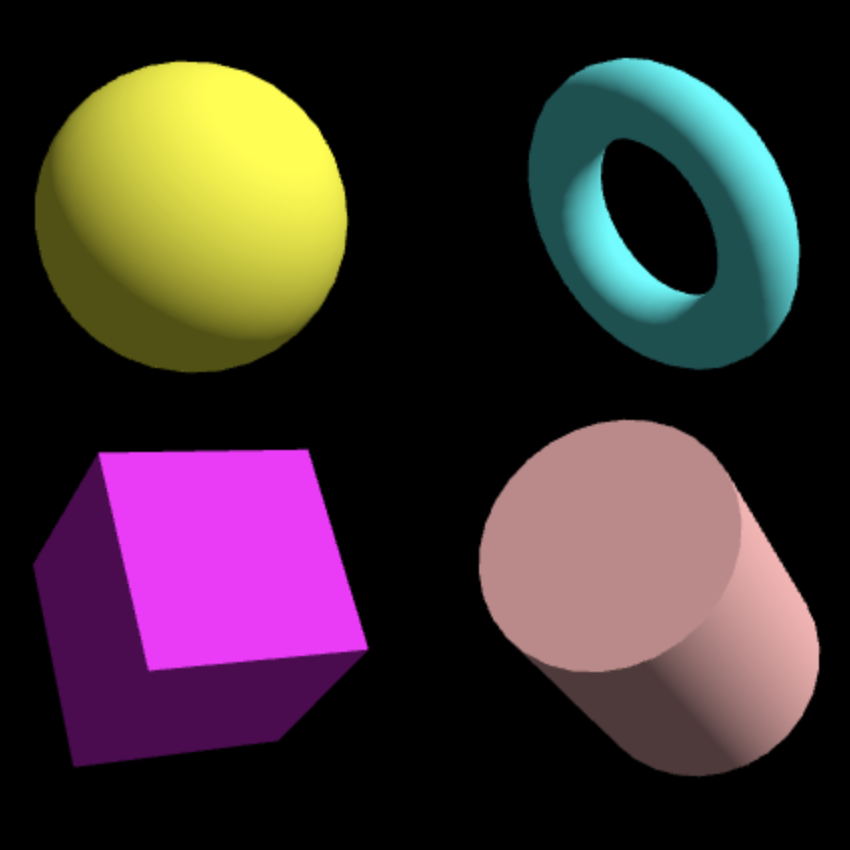
|
For this assignment you can just copy the same code base
that you used for the previous week's assignment.
To change "week5" to "week6", you just need to do the following:
- Copy the entire
hw5directory to a directory calledhw6. Then make all the following changes within directoryhw6. - In
index.html, change every instance of "week5" to "week6". - Rename
worlds/week5toworlds/week6. - Rename
worlds/week6/week5.jstoworlds/week6/week6.js. - In
worlds/week6/week6.js, change every instance of "week5" to "week6".