Your homework will be to implement the rendering pipeline through z-fufffering and shading. This will be a two-week assignment, due before class on Tuesday November 6. You will learn how to do shading per pixel at next week's guest lecture. Everything else you need was covered in this week's' class and is described in the notes below.

REVIEW: VERTICES AND FACES:

To review what we discussed in class earlier in the semester, a general way to store polyhedral meshes is to use a vertex array and a face array. Each element of the vertex array contains point/normal values for a single vertex:

vertices = { { x,y,z, nx,ny,nz }₀, { x,y,z, nx,ny,nz }₁, ... }

COMPUTING NORMALS, TRANSFORMING NORMALS:

If you want to create the illusion of smooth interpolated normals when you're approximating rounded shapes (like spheres and cylinders) you can do so either by using the normalized derivative of the associated implicit surface - which in the special case of the unit sphere is just the same as x,y,z itself - or else you can use the following brute force method:

1. For each face, approximate both gradient direction and surface area of that face by summng the cross products between v₁-v₀ and v₂-v₁, where v₀, v₁ and v₂ are successive vertices around the face, taken three at a time.

2. For each vertex, sum up the gradients for all faces that contain that vertex. Normalizing this sum gives a good approximation to the normal vector at this vertex.

To transform a normal vector, you need to transform it by the transpose of M^-1, where M is the matrix that you are using to transform the associate vertex location. Here is a MatrixInverter class that you can use to compute the matrix inverse.

SHADING:

Next Tuesday, while I'm off climbing the Great Wall of China, Elif Tosun (not Denis Zorin) will be giving a guest lecture on how to shade a vertex. That is, on how to convert a point/normal vertex from (x,y,z,nx,ny,nz) to a point/color vertex (x,y,z,r,g,b).

For now, you can just test things out by using some very simple mapping from normals to shading such as:

r = g = b = 255 * (1 + nx + ny + nz) / 2.75;

SCAN CONVERSION AND Z-BUFFERING:

The Z-buffer algorithm is a way to get from triangles to shaded pixels.

You use the Z buffer algorithm to figure out which thing is in front at every pixel when you are creating fully shaded versions of your mesh objects.

The algorithm starts with an empty zBuffer, indexed by pixels [X,Y], and initially set to zero for each pixel (ie: 1 / &inf;). You also need an image FrameBuffer filled with background color. You already have an image FrameBuffer within your MISApplet.

The general flow of things is:

• Loop through all your polygons, where each polygon has a list of vertices, where you've already run a Vertex Shader to convert normal (nx,ny,nz) to color (r,g,b).

• Split the polygon into triangles, where each triangle vertex has:
  • An (x,y,z) location
  • A (nx,ny,nz) surface normal

• Transform the vertices of the triangle according to your animation.

• Do the view transformation on the x,y,z location of each vertex

• Clip the polygon by the z = -ε plane, keeping just the part for which z ≤ -ε.

  You may end up with a four sided shape, which you need to split into two triangles, and then do all the steps that follow independently for each of these two triangles.

• Each triangle vertex has:
  • An (x,y,z) location
  • An (r,g,b) color

• Do the perspective transformation on the x,y,z location of each vertex to (px,py,pz) = (f*x/z,f*y/z,f/z), where f is focal length.

• Do the viewport transformation on px an py, to convert them to integer pixel values (X,Y).

• Split the triangle into a top and bottom scan-line-aligned trapezoid. To do this you'll need to split one of the triangle's edges, and you'll need to interpolate the location and color at that edge. Each of these trapezoids has four vertex locations on the image:
  (X_TL, Y_TOP)   (X_TR, Y_TOP)

  (X_BL, Y_BOTTOM)   (X_BR, Y_BOTTOM)

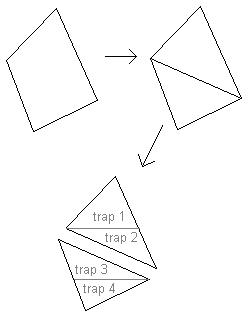
  You can see the process repesented here: First a polygon is split into triangles, and the each triangle is split into scan-line aligned trapezoids:

         

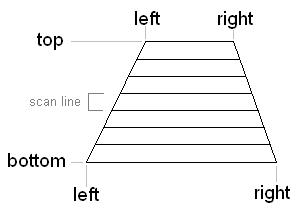
  Each vertex of one of these scan-line aligned trapezoids will have both color and perspective z, or (r,g,b,pz).

• Scan convert the trapezoid by linear interpolation to get a single span with a leftmost pixel X_LEFT and a rightmost pixel X_RIGHT. You will have an (r,g,b,pz) at each of these ends.

• Scan convert the single span by linear interpolation to get an (r,g,b,pz) value at each pixel.

  If pz < zBuffer[X,Y] then replace the values at that pixel:

  zBuffer[X,Y] ← pz
  frameBuffer[X,Y] ← (r,g,b)
  

• Display the frameBuffer

A note about linear interpolation:

In order to interpolate values from the triangle to the trapezoid, then from the trapezoid to the horizontal span for each scan-line, then from the span down individual pixels, you do linear interpolation.

Generally speaking, linear interpolation involves the following two steps:

• Compute some linear interpolant t, where t is between zero and one.

• Use t to do linear interpolation between two values a and b:

  value = a + t * (b - a)

In order to compute t, you just need your extreme values and the intermediate value where you want the results. For example, to compute the value of t to interpolate from scan-line Y_TOP and Y_BOTTOM to a single scan-line Y:

t = (double)(Y - Y_TOP) / (Y_BOTTOM - Y_TOP)

t = (double)(X - X_LEFT) / (X_RIGHT - X_LEFT)

I suggest you get your algorithm working on a single example triangle before trying to apply the algorithm working on your actual scene data.

You might want to do the straightforward linear interpolation described above for your first implementation, and then switch over to the incremental methods that we discussed in class after you have gotten a visible result.

If you recall from class, the fast incremental method involves first computing an increment for each numeric value at each stage of of interpolation, first for incrementing the change in value per scan-line for the outer-loop vertical interpolation, and then for incrementing the change in value per horizontal pixel along a single scan-line.

And, as we said in class, to make incremental methods run blazingly fast, you would do these incremental calculations not in floating point but in fixed point integer, shifting up temporarily by some reasonable number of bits such as 12.