HW1

Zbuffers

Now that we've visited ray tracing, we're going back mesh objects. We'll continue to use the PixApplet method for setting the color at each pixel that you have been using for ray tracing.

VERTICES AND FACES:

To review what we discussed in class earlier in the semester, a general way to store polyhedral meshes is to use a vertex array and a face array. Each element of the vertex array contains point/normal values for a single vertex:

vertices = { { x,y,z, nx,ny,nz }₀, { x,y,z, nx,ny,nz }₁, ... }

Each element of the face array contains an ordered list of the vertices in that face:

faces = { { v₀,v₁,v₂,... }₀, { v₀,v₁,v₂,... }₁, ... }

A vertex is specified by both its location and its normal vector direction. As I said in class, if vertex normals are different, then we'll adopt the convention that two vertices are not the same - even if x,y,z are the same.

COMPUTING NORMALS, TRANSFORMING NORMALS:

If you want to create the illusion of smooth interpolated normals when you're approximating rounded shapes (like spheres and cylinders) you can do so either by using special purpose methods for that particular shape (like using the direction from the center of a sphere to each vertex - as we discussed in class), or else you can use the following more general purpose method:

For each face, approximate the gradient for that face by taking the cross product between v₁-v₀ and v₂-v₁, where v₀, v₁ and v₂ are the first three vertices in that face.

For each vertex, sum up the gradients for all faces that contain that vertex. Normalizing this sum gives a good approximation to the normal vector at this vertex.

To transform a normal vector, you need to transform it by the transpose of M^-1, where M is the matrix that you are using to transform the associate vertex location. Here is a MatrixInverter class that you can use to compute the matrix inverse.

As usual, try to make fun, cool and interesting content. See if you can make various shapes that are built up from things like tubes and cylinders or tori, as in the applet I showed in class. We haven't done all the math yet that we would need to do spline surfaces like teapots.

MATERIALS AND LIGHTS:

When rendering a phong-shaded scene you will want to have a list of Materials, where each Material object gives the data that you need to simulate a particular kind of surface using the Phong algorithm (eg: DiffuseColor, SpecularColor, etc.).

You will also want to have a list of Light sources, where each light source L_i has a direction (x,y,z) and a illuminance color (r,g,b):

L_i = { x , y , z , r , g , b }

Z-BUFFERING:

The Z-buffer algorithm is a way to get from triangles to shaded pixels.

You use the Z buffer algorithm to figure out which thing is in front at every pixel when you are creating fully shaded versions of your mesh objects, such as when you use the Phong surface shading algorithm.

The algorithm starts with an empty zBuffer, indexed by pixels [X,Y], and initially set to zero for each pixel. You also need an image FrameBuffer filled with background color. This frameBuffer can be the pix[] array you currently use for ray tracing.

The general flow of things is:

Loop through all your polygons, where each polygon has a list of vertices and a Material object identifier.
Split the polygon into triangles, where each triangle vertex has:
- An (x,y,z) location
- A (nx,ny,nz) surface normal
Transform the vertices of the triangle according to your animation.
Do the view transformation on the x,y,z location of each vertex
Clip the polygon by the z = -ε plane, keeping just the part for which z ≤ -ε.
You may end up with a four sided shape, which you need to split into two triangles, and then do all the steps that follow independently for each of these triangles.
Do shading/lighting on each vertex, using the (x,y,z) and (nx,ny,nz) and the Material properties. After you do this, each triangle vertex has:
- An (x,y,z) location
- An (r,g,b) color
Do the perspective transformation on the x,y,z location of each vertex to (px,py,pz) = (f*x/z,f*y/z,f/z), where f is focal length.
Do the viewport transformation on px an py, to convert them to integer pixel values (X,Y).
Split the triangle into a top and bottom scan-line-aligned trapezoid. To do this you'll need to split one of the triangle's edges, and you'll need to interpolate the location and color at that edge. Each of these trapezoids has four vertex locations on the image:

(X_TL, Y_TOP) (X_TR, Y_TOP)
(X_BL, Y_BOTTOM) (X_BR, Y_BOTTOM)

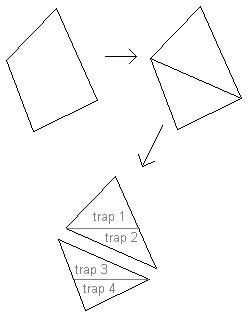
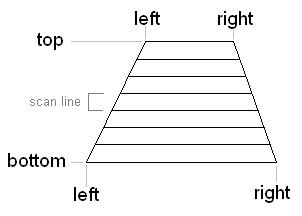
You can see the process repesented here: First a polygon is split into triangles, and the each triangle is split into scan-line aligned trapezoids:

Each vertex of one of these scan-line aligned trapezoids will have both color and perspective z, or (r,g,b,pz).
Scan convert the trapezoid by linear interpolation to get a single span with a leftmost pixel X_LEFT and a rightmost pixel X_RIGHT. You will have an (r,g,b,pz) at each of these ends.
Scan convert the single span by linear interpolation to get an (r,g,b,pz) value at each pixel.
If pz < zBuffer[X,Y] then replace the values at that pixel:
zBuffer[X,Y] ← pz
frameBuffer[X,Y] ← (r,g,b)
Display the frameBuffer

A note about linear interpolation:

In order to interpolate values from the triangle to the trapezoid, then from the trapezoid to the horizontal span for each scan-line, then from the span down individual pixels, you'll need to use linear interpolation.

Generally speaking, linear interpolation involves the following two steps:

Compute some linear interpolant t, where t is between zero and one.
Use t to do linear interpolation between two values a and b:

value = a + t * (b - a)

In order to compute t, you just need your extreme values and the intermediate value where you want the results. For example, to compute the value of t to interpolate from scan-line Y_TOP and Y_BOTTOM to a single scan-line Y:

t = (double)(Y - Y_TOP) / (Y_BOTTOM - Y_TOP)

t = (double)(X - X_LEFT) / (X_RIGHT - X_LEFT)