|
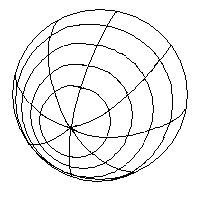
θ = 2 π u
φ = π v - π/2
x(u,v) = cos(θ) cos(φ)
|
|
This assignment is going to focus on two things:
θ = 2 π u
φ = π v - π/2x(u,v) = cos(θ) cos(φ)
y(u,v) = sin(θ) cos(φ)
z(u,v) = sin(φ)
Note that the range of values for θ and φ are, respectively:
0 ≤ θ ≤ 2π Longitude: circle around the "equator" (where z = 0) -π/2 ≤ φ ≤ π/2 Latitude: "south pole" (where z = -1) to "north pole" (where z = +1)
Your job is to do several things. First, use the above information to fill a mesh
double sphereMesh[][][] = new double[M][N][3];where M and N are the number of columns and rows of the sphereMesh, and each entry
sphereMesh[i][j] is a vertex of the mesh.
You should choose values of M and N that produce a
sphereMesh that you think looks good.
As we discussed in class, you'll want to generate i and j in a loop:
for (int i = 0 ; i < M ; i++)
for (int j = 0 ; j < N ; j++) {
double u = i / (M - 1.0);
double v = j / (N - 1.0);
// COMPUTE x,y,z HERE AND PUT THE RESULTS INTO sphereMesh[i][j]
}
Once you have this sphereMesh, then you can use it to create and display spheres and ellipsoids. To create a particular sphere or ellipsoid, you need, in addition to a sphereMesh, a matrix T.
You can render your sphereMesh as follows:
loop through your source sphereMesh and
copy transformed points to a temporary mesh array tempMesh[M][N][3]:
for (int i = 0 ; i < M ; i++)
for (int j = 0 ; j < N ; j++)
T.copy(sphereMesh[i][j], tempMesh[i][j]);
Then you can loop through all the little squares of your temporary mesh,
and display each one as a triangle:
for (int i = 0 ; i < M-1 ; i++)
for (int j = 0 ; j < N-1 ; j++) {
drawQuad(tempMesh[i][j], tempMesh[i+1][j], tempMesh[i+1][j+1], tempMesh[i][j+1]);
}
As we said in class, for now you can draw each quadrilateral
simply by drawing its four edges.
What about persepective?
You can take perpective into account simply by adding a perspective transformation at the very end of your transform routine:
void transform(double src[], double dst[]) {
...
dst[0] = focalLength * dst[0] / dst[2];
dst[1] = focalLength * dst[1] / dst[2];
}
The above models a camera pinhole positioned at the origin
(after all transformations have been done).
Because this camera is looking toward negative z,
all your objects should have negative z coordinates,
and you should use a negative value for focalLength.
A reasonable value for focalLength is something like -3.0.
What you should make:
I would like you to make some sort of cool scene out of a collection of spheres and ellipsoids. You make the different ellipsoids by creating the appropriate matrices.
As we went over in class, here is the general flow of things:
- Initialize:
- Create all the object meshes
- Do each frame of the animation:
- Compute all object transformation matrices for this frame;
- Loop through all objects:
- Apply transformation matrix to mesh;
put the result into an internal copy of the mesh;- Loop through the transformed mesh copy, rendering each quadrangle.
As I said in class,
you'll be able to build and animate far more interesting things
if you can use a stack matrix with push() and pop()
methods, as we showed in class
in that little
swinging arm example.
Here is one implementation of a Matrix stack class that you can use if you like:
public class MatrixStack {
int top = 0, stackSize = 20;
Matrix3D stack[] = new Matrix3D[stackSize];
public MatrixStack() {
for (int i = 0 ; i < stackSize ; i++)
stack[i] = new Matrix3D();
}
public void push() {
if (top < stackSize) {
stack[top+1].copy(stack[top]);
top++;
}
}
public void pop() {
if (top > 0)
--top;
}
public Matrix3D get() { return stack[top]; }
}
A note about focal length and depth of field
In my haste at the end of the class I spoke carelessly about focal length and depth of field. Actually, this is a really interesting subject, which deserves to be understood properly.
For those of you who are interested, focal length refers to how far away the lens in a camera is behind the film, when the camera is focused at infinity. For example, most consumer cameras have a really short focal length, because they need to be compact from back to front.
At any given setting, a camera is focused (creates the sharpest image on the film) of a subject at some particular distance away. Depth of field refers to how much the distance of an object can vary from this optimum distance, before that object goes out of focus.
As we mentioned in class, closing down the aperture (which effectively makes the lens diameter smaller) produces a greater depth of field, because this narrows the cone of light reaching the film, thereby shrinking the circle of confusion of the out-of-focus light.
But how does focal length effect depth of field?
Properly speaking, it actually has no effect, even though it seems to have an effect. It certainly appears that those consumer cameras with their really short focal lengths have a greater depth of field than do cameras with longer focal length lenses. But they actually don't.
Here's what's going on: Suppose you try to take a picture of some object A with two cameras. Let's call the cameras S and L, where camera S has a short focal length, and camera L has a long focal length. Further, suppose there is another object B in the frame, which is farther away, so it appears smaller and out of focus.
For example, in the two images below, the image on the left shows what we'd see from camera S, and the image on the right shows what we'd see from camera L.
| 
| |
|---|---|---|
| With short FL camera S | With long FL camera L |
It certainly seems that object B is more in focus in the left-most image. But that is just an illusion. If you look carefully, you can see that there is no more detail in object B when seen through camera S than when seen through camera L. It just seems like there is, because the same blurry information is shrunk into a smaller portion of the image.