HW4

Homework 5, due Monday, Oct 20.

Yes, it's time for ray tracing!

How do I trace a ray to a sphere?

As we discussed in class, a ray can be defined as v + tw, where v is the ray origin, w is the ray direction vector, and t >= 0.

So to ray trace to a sphere, you need to plug in the point:

( v_x + t w_x , v_y + t w_y , v_z + t w_z )

as the x,y,z values in the equation of a sphere:

( x - c_x)² + ( y - c_y)² + ( z - c_z)² - r² = 0

to obtain:

( v_x + t w_x - c_x)² + ( v_y + t w_y - c_y)² + ( v_z + t w_z - c_z)² - r² = 0

When you multiply out the above polynomial, you'll find that it is a quadratic equation in t, with the constant terms v_x, v_y, v_z, w_x, w_y, w_z, c_x, c_y, c_z and r appearing in various places.

You'll need to find t by solving this quadratic equation. The quadratic equation will have real roots if and only if the ray intersects the sphere.

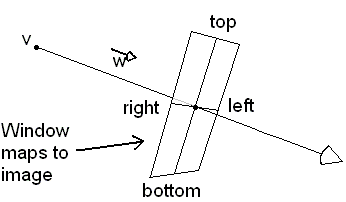
How do I ray trace an image?

To ray trace an image, you need to set up a Window that floats in front of your eye point v. Ray tracing through various points in this window will give you the value at different pixels in your image.

For now, you can use a fixed eye point at the origin, so that v = (0,0,0), and a fixed unit-square Window that sits at some focal length f from the origin in negative z. The coordinates of the four corners of this Window will be: (-.5,-.5,-f), (.5,-.5,-f), (-.5,.5,-f) and (.5,.5,-f).

To ray trace through any pixel in your image, you'll need to construct the proper direction vector w that corresponds to that pixel. For example, if your image is a square with N×N pixels, with pixel (0,0) at the upper right corner, then pixel (i,j) will be in the direction (i/N-.5,.5-j/N,-f). You can normalize this direction vector (ie: rescale it to unit length) to obtain the w for pixel (i,j).

If my ray hits two or more spheres, what should I see?

If the ray hits various spheres, different values of t will be returned by each. The visible sphere along the ray is the one that returns the lowest positive t value.

How do I shade a sphere?

Every point on a smooth surface has a surface normal vector n, which is the vector direction that points perpendicularly outward from the surface at that point. Given a point (s_x,s_y,s_z) on a sphere centered at (c_x,c_y,c_z) of radius r, it is particularly easy to get the normal vector n at that point:

n = ( s_x-c_x , s_y-c_y , s_z-c_z ) / r

One very simple model of a light source is a unit length direction vector L = (L_x,L_y,L_z). You an think of this as a source of light that is so far away, like the Sun, that all the rays of light which come from it are parallel.

Remember that the inner product (sometimes called the "dot product") of two vectors a and b is given by a • b = a_xb_x+ a_yb_y+ a_zb_z. Once you have a surface normal, you can find a brightness by doing a simple shading calculation, using the inner product between surface normal n and the light direction L:

0.2 + 0.8 * max( 0, n • L )

This will give you a gray level for the sphere, like the simple three-spheres example I showed in class. In the above equation, the "0.2" is an ambient lighting factor, so that the sphere never completely goes black. The "0.8" controls how responsive the sphere is to the light source from direction L. You can vary each of these parameters to taste. If you want, you can also tint the result by some (red,green,blue) color constant, in order to make different spheres of different colors.

So what's the assignment?

I want you to create a scene consisting entirely of spheres of various sizes, positions, and possibly colors. Try to think of some sort of interesting scene. You can certainly have spheres intersect with each other. The first thing I think of is a snowman, but I'm sure you can think of other things as well.

What about extra credit?

It is straightforward to do shadows. Once you have determined which is the visible surface point s for a pixel, all you need to do is trace a ray from s in the direction L. If your "shadow ray" hits anything, then you should use only ambient lighting at that pixel (that's the "0.2" in the equation above).

Also, once a ray hits a sphere, and you have determined the surface point s and the surface normal n, then you can treat the sphere as a mirror, and reflect the ray off the sphere. In this way, you can create really cool scenes with multiple reflection bounces, adding a little bit of color at each bounce. This produces really spectacular images, for relatively little work. To do this, you need to be able to compute the mirror direction of the ray. This reflection direction is given by:

w - 2 (n • w) n