



Next: Setting the options
Up: The Script sql.m and
Previous: The Script sql.m and
The problem is defined by the following data:
-
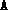
- a structure
 with three fields:
with three fields:
-
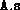
-
a matrix with m rows and
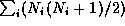 columns. The kth row holds the symmetric block
diagonal matrix
columns. The kth row holds the symmetric block
diagonal matrix 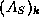 stored as a vector
stored as a vector
-
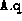
-
a matrix with m rows and
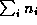 columns.
The kth row holds the block vector
columns.
The kth row holds the block vector 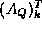
-
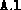
-
a matrix with m rows and
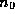 columns. The kth
row holds the vector
columns. The kth
row holds the vector 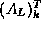
-
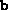
- the vector b defining the dual objective function.
Its length m is equal to the number of primal constraints
-
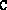
- a structure with three fields,
defining the primal objective function:
-
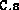
-
the block diagonal matrix
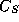
-
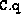
-
the block vector
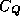
-
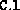
-
the vector
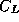
-
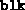
- a structure with three fields defining the block sizes:
-
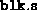
-
a vector whose length is the number of blocks in the block diagonal
matrix
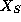 and with entries set to the matrix block sizes
and with entries set to the matrix block sizes 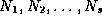 .
Note that these numbers must be all greater or equal to two, as any blocks
with size one should be incorporated in the vector
.
Note that these numbers must be all greater or equal to two, as any blocks
with size one should be incorporated in the vector 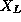
-
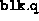
-
a vector whose length is the number of blocks in the block vector
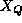 and with entries set to the vector block sizes
and with entries set to the vector block sizes 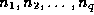 .
Note that these numbers must be all greater or equal to two, as each vector
block has a special first component and at least one other component
.
Note that these numbers must be all greater or equal to two, as each vector
block has a special first component and at least one other component
-
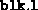
-
the scalar
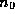 (the length of
(the length of 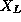 )
)
Important: If one or more of the three parts of the SQLP
is not present, the corresponding field of 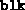 may be set
to 0, or to the Matlab empty matrix
may be set
to 0, or to the Matlab empty matrix [ ], or left
unspecified. In any of these cases,
the corresponding fields of 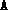 and
and 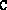 ,
if set, will be ignored.
,
if set, will be ignored.
Important: In order to be able to use the mex files,
all block diagonal matrices must be stored in Matlab's
sparse format, unless they contain only one block.
format, unless they contain only one block.
In particular, 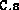 must be stored in sparse format, unless it
has only one block. If it has only one block, it may be stored
in either sparse or full format. The vectors
must be stored in sparse format, unless it
has only one block. If it has only one block, it may be stored
in either sparse or full format. The vectors
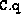 ,
, 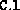 and
and 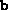 are stored in full format.
The matrices
are stored in full format.
The matrices 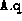 and
and 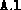 may be stored in either sparse or
full format. There are four different ways to set up the
matrix
may be stored in either sparse or
full format. There are four different ways to set up the
matrix 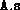 , whose rows represent
, whose rows represent 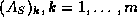 :
:
-
Constructing
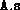 directly using the function svec.m,
which converts block diagonal matrices to vector representation.
The function smat.m restores the symmetric matrix from such
a vector. These routines are invoked by
directly using the function svec.m,
which converts block diagonal matrices to vector representation.
The function smat.m restores the symmetric matrix from such
a vector. These routines are invoked by
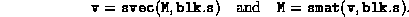
The block diagonal matrix M passed to svec.m
must be stored in sparse format if it has more than one block.
By default, the blocks are assumed to be dense. If the user wishes to
take advantage of the sparsity in the blocks of the matrix M,
then a third, optional parameter
sparseblks can be passed to svec.m. When
 , svec.m treats the blocks as sparse,
and returns a sparse vector.
, svec.m treats the blocks as sparse,
and returns a sparse vector.
These routines preserve the inner
product, i.e. if 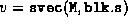 and
and 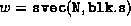 for block diagonal matrices M, N, then
for block diagonal matrices M, N, then

-
Using the routine makeA.m, which calls svec.m, to
construct
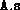 from given predefined matrices. This is invoked by
from given predefined matrices. This is invoked by
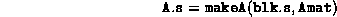
where blk.s is as above and Amat is a one-dimensional
cell array. The
kth component of the cell array Amat is the matrix 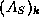 .
Cell arrays are indexed using braces
.
Cell arrays are indexed using braces 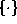 . For example,
to set
. For example,
to set 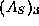 assign a matrix value to
Amat{3}; this must be in sparse format if it has more
than one block. The individual blocks of the block diagonal data
matrices are treated by default as being dense.
If they are sparse, and the user wishes to take
advantage of this sparsity, a third optional parameter spblocks
may be passed to makeA.m, and this parameter
should be set to the value 1.
In this case the matrix
assign a matrix value to
Amat{3}; this must be in sparse format if it has more
than one block. The individual blocks of the block diagonal data
matrices are treated by default as being dense.
If they are sparse, and the user wishes to take
advantage of this sparsity, a third optional parameter spblocks
may be passed to makeA.m, and this parameter
should be set to the value 1.
In this case the matrix 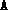 will be stored using the sparse matrix
storage option.
will be stored using the sparse matrix
storage option.
-
Using the routine import.m to load all the data (
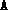 ,
, 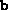 ,
,
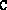 and
and 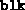 ) from a plain ASCII file. This is invoked by
) from a plain ASCII file. This is invoked by
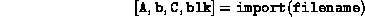
The ASCII data in the file must be stored in a special compact format
that is described in Appendix A. The file name must have a
period and an extension (anything other than the standard Matlab
extensions mat, mex etc.) following the period.
The user-specified extension is important as Matlab treats
file names without an extension as mat files.
The routine export.m implements the reverse operation, saving
a problem's data in an ASCII file, in a format recognized by
import.m.
-
Loading a mat file defining the data
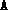 ,
, 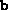 ,
, 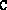 ,
, 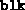 ,
saved previously by Matlab's save command, using Matlab's
load command. This option may be used to load all the
examples (from control theory and truss topology design) benchmarked
in Appendix C, for which mat
files are available from the SDPpack home page.
,
saved previously by Matlab's save command, using Matlab's
load command. This option may be used to load all the
examples (from control theory and truss topology design) benchmarked
in Appendix C, for which mat
files are available from the SDPpack home page.




Next: Setting the options
Up: The Script sql.m and
Previous: The Script sql.m and
Madhu Nayakkankuppam
Wed Jun 25 18:01:54 EDT 1997
 with three fields:
with three fields:
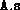
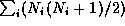 columns. The kth row holds the symmetric block
diagonal matrix
columns. The kth row holds the symmetric block
diagonal matrix 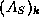 stored as a vector
stored as a vector
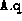
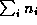 columns.
The kth row holds the block vector
columns.
The kth row holds the block vector 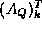
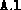
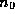 columns. The kth
row holds the vector
columns. The kth
row holds the vector 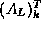
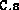
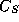
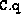
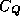
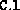
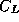
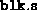
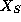 and with entries set to the matrix block sizes
and with entries set to the matrix block sizes 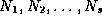 .
Note that these numbers must be all greater or equal to two, as any blocks
with size one should be incorporated in the vector
.
Note that these numbers must be all greater or equal to two, as any blocks
with size one should be incorporated in the vector 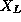
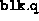
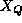 and with entries set to the vector block sizes
and with entries set to the vector block sizes 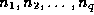 .
Note that these numbers must be all greater or equal to two, as each vector
block has a special first component and at least one other component
.
Note that these numbers must be all greater or equal to two, as each vector
block has a special first component and at least one other component
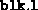
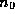 (the length of
(the length of 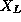 )
)