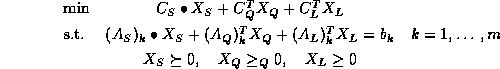
We treat the primal mixed semidefinite-quadratic-linear program (SQLP):
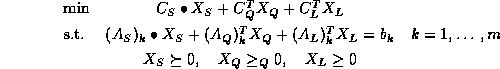
where ![]() is a block diagonal symmetric matrix variable,
with block sizes
is a block diagonal symmetric matrix variable,
with block sizes ![]() ,
, ![]() ,
, ![]() ,
, ![]() respectively,
each greater or equal to two;
respectively,
each greater or equal to two;
![]() is a block vector variable,
with block sizes
is a block vector variable,
with block sizes ![]() respectively,
each greater or equal to two;
and
respectively,
each greater or equal to two;
and ![]() is a vector of length
is a vector of length ![]() .
The quantities
.
The quantities ![]() and
and ![]() ,
, ![]() ,
are block diagonal matrices.
The quantities
,
are block diagonal matrices.
The quantities ![]() and
and ![]() ,
, ![]() are block vectors, and
are block vectors, and
![]() and
and ![]() ,
, ![]() , are vectors.
All vectors are column vectors.
The quantity
, are vectors.
All vectors are column vectors.
The quantity ![]() is the trace inner product (
is the trace inner product ( ![]() ),
i.e.
),
i.e. ![]() .
.
Each of the three inequalities in this primal program has a different meaning, each corresponding to a different kind of cone:
 constraints. Writing
constraints. Writing where
![]()
the constraint ![]() , i.e.
, i.e. ![]() means that,
for each block i,
means that,
for each block i,
Any convex quadratic constraint can be converted to this form.
The standard form given here is a very convenient one. The dual SQLP is
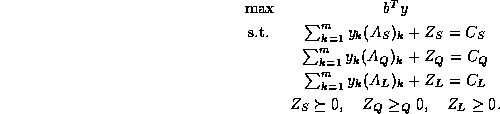
Note again the three different kinds of inequalities on the
three dual slack variables. In control applications, the first
of the three is usually called a linear matrix inequality (LMI),
since it can also be written ![]() .
.
We shall use the following notation. Let
where ![]() denotes the Frobenius matrix norm.
Assuming the existence of a strictly feasible primal or dual point,
it is well known that the optimality conditions may be
expressed by the primal feasibility equation
denotes the Frobenius matrix norm.
Assuming the existence of a strictly feasible primal or dual point,
it is well known that the optimality conditions may be
expressed by the primal feasibility equation ![]() ,
the dual feasibility equation
,
the dual feasibility equation ![]() , and the complementarity
condition
, and the complementarity
condition ![]() (together with the inequality constraints).
We will also wish to refer to the quantities
(together with the inequality constraints).
We will also wish to refer to the quantities