Often, problems arise in nonstandard form, but in many cases they
are easily converted to the SQLP form. For example, if one
wishes to place nonnegativity bound constraints on some or all of
the components of 
, one introduces a primal constraint and
a new component of 
for each such bound, e.g. constraining
. The disadvantage of this approach
is the increase in dimension size, but the advantage is its
convenience. As another example, if one has upper and lower
bounds on a variable, one uses two inequality constraints: again,
this approach has disadvantages, but has the virtue of simplicity.
A less obvious example is how to handle
mixed inequalities and equalities. For example, suppose one has
the two constraints
where { 
} and { 
} are symmetric matrices.
The first constraint is called an LME (linear matrix equality)
and the second an LMI. One introduces one dual slack matrix for
the LMI and two for the LME, giving
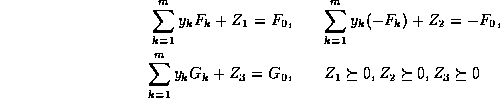
which is then in the required dual block semidefinite form. The disadvantage of this approach is that the corresponding primal solution set is not bounded; this sometimes leads to numerical difficulties, but is worth trying.