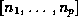 ,
with
,
with 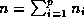 ,
let
,
let 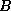 denote the space of all real,
symmetric,
denote the space of all real,
symmetric, 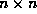 block diagonal matrices whose
block diagonal matrices whose  diagonal block is of size
diagonal block is of size 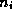 .
The inner product on this space is
.
The inner product on this space is
Given a positive integer vector 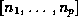 ,
with
,
with 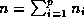 ,
let
,
let 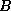 denote the space of all real,
symmetric,
denote the space of all real,
symmetric, 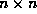 block diagonal matrices whose
block diagonal matrices whose  diagonal block is of size
diagonal block is of size 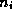 .
The inner product on this space is
.
The inner product on this space is
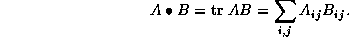
By 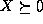 , where
, where 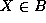 , we mean that X is positive
semidefinite, i.e. all its diagonal blocks are positive semidefinite.
Consider the semidefinite program (SDP)
, we mean that X is positive
semidefinite, i.e. all its diagonal blocks are positive semidefinite.
Consider the semidefinite program (SDP)
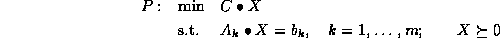
where C and 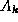 ,
,  are all fixed matrices in
are all fixed matrices in 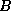 ,
and the unknown variable X also lies in
,
and the unknown variable X also lies in 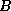 . The dual program is
. The dual program is
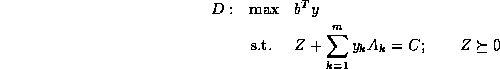
where the dual slack matrix Z also lies in 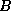 .
In the special case
.
In the special case 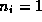 ,
, 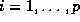 , the SDP reduces to a linear program.
It is assumed that the matrices
, the SDP reduces to a linear program.
It is assumed that the matrices 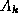 ,
,  , are linearly
independent.
, are linearly
independent.
We shall use the notation

where 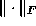 denotes the Frobenius matrix norm.
Assuming a Slater condition,
i.e. the existence of a strictly feasible primal or dual point of SDP,
it is well known that the optimality conditions of SDP may be
expressed by the equations
denotes the Frobenius matrix norm.
Assuming a Slater condition,
i.e. the existence of a strictly feasible primal or dual point of SDP,
it is well known that the optimality conditions of SDP may be
expressed by the equations 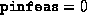 ,
,
 , and
, and  (together with the
semidefinite conditions
(together with the
semidefinite conditions 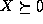 and
and 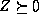 ).
).