Lecture #14 Programming Languages MISHRA 95

G22.2210

Programming Languages: PL

B. Mishra
New York University.


Lecture # 14

---Slide 1---
MATHEMATICA: History

• Designed by Stephen Wolfram, a physicist by training. Current system is implemented and marketed by Wolfram Research, Inc. Runs on many platforms: IBM PCs, Apple machines, Sun and Sparc Workstations, Silicon Graphics, various other mainframes...

• Closely related to its intellectual ancestor SMP, a symbolic manipulation language designed by Wolfram in Caltech, while he was a graduate student.

• Other languages sharing many of its features: AXIOM, Macsyma, Maple, MatLab, MathCad, Scratchpad...

---Slide 2---
Features

• Interactive

• A Prototyping Language. Very high-level language

• Interfaces with C via MathLink

• Multi-media environment: Computations involving Numerics, Symbolics, Graphics, Animation and Sounds

• Spectrum of styles: Rule-based styles, functional programming styles in one end to traditional Pascalish imperative style

• Mix-and-match styles---
  criteria for choice of a style:
  Readability, Efficiency, Modifiability & Simplicity

---Slide 3---
Numerical Programming

• Numerical Types:
  Integers, Rationals, Real & Complex Numbers
  

  Examples: 1, 1/2, 0.5, 1+2I, E^( 2 I Pi)

• (Obvious) Arithmetic and logical operations:
  

  +, -, * (x*y x y), /, ^, <, <=, >, >=

• Singularities:
  

  1/Infinity 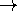0
Infinity/Infinity 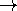Indeterminate
1/0 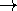ComplexInfinity
FulForm[Infinity] 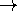DirectedInfinity[1]
  

• Precision & Accuracy

  • Precision = Total Number of Significant Digits
  • Accuracy = Position of the Decimal Point

  Command N (e.g., N[sin[5]] or N[sin[5],20]) computes the numerical value of an expression to the required precision

---Slide 4---
Example

• A program that takes a complex number a + i b as input and outputs its complex conjugate a - i b

• Program conj

        conj[z_?NumberQ] := Re[z] - I Im[z];
        conj[DirectedInfinity[z_]] :=
              DirectedInfinity[Re[z] - I Im[z]];
        conj[DirectedInfinity[]] := DirectedInfinity[];
        conj[Indeterminate]  := Indeterminate;
  

• NSum, NProd, NIntegrate
  

  • NSum[expr[i], {i, L, U}]
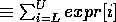
  • NProd[expr[i], {i, L, U}]
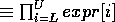
  • NIntegrate[expr[x], {x, L, U}]

---Slide 5---
Symbolic Programming

• Basic Objects:
  

  Polynomials, Rational Functions, Partial Fraction (Representation of Rational Functions), Trigonometric Expressions, Power Series, Limits, Derivatives and Integrals, Differential Forms

• Example: Chebycheff Polynomials
  

  

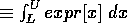
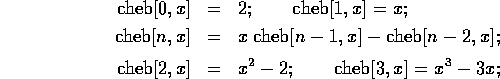
       cheb1[0,x_] := 2;
       cheb1[1,x_] := x;
       cheb1[n_,x_] := (x cheb1[n-1,x] - cheb1[n-2,x])//
                          Expand;
  

---Slide 6---
Symbolic Programming (Contd)

• A different (and faster) implementation:

       cheb2[n_,x_] := TrigReduce[2 Cos[n th]]/.
                                Cos[th] -> x/2 //
                                Expand;
  

  Why does it work?

  

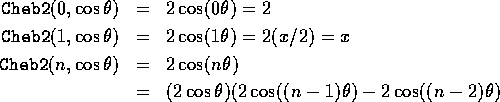
  Why is it faster?

---Slide 7---
Data Structure: LIST

• Elementary data structure is a list:
  

  List of numbers, list of symbols, list of symbolic expressions, etc.

• Any ``listable'' function can act on a list.
  (Like MAPCAR)

      A = Table[n!, {n,1,5}]
  =>  {1, 2, 6, 24, 120}
      Log[A]
  =>  {0, Log[2], Log[6], Log[24], Log[120]}
  

• High-dimensional lists:

      Table[{i + j x}, {i, 2}, {j, 5, 7}]
  =>  {{{1 + 5 x}, {1 + 6 x}, {1 + 7 x}},
       {{2 + 5 x}, {2 + 6 x}, {2 + 7 x}}}
  

• General Forms:

       Table[expression, iterator]
  

---Slide 8---
List Operations

• List access and Some list operations:

       listA = Table[Random[Integer, {0, 15}], {10}]
  =>   {12, 7, 4, 12, 2, 5, 2, 5, 10, 3}
       listA[[3]]
  =>   4
       Take[listA, 4]
  =>   {12, 7, 4, 12}
       First[listA]
  =>   12
       Rest[listA]
  =>   {7, 4, 12, 2, 5, 2, 5, 10, 3}
       Prepend[listA, 5]
  =>   {5,12, 7, 4, 12, 2, 5, 2, 5, 10, 3}
  

• A sampling of other operations:

  >> Sort, Reverse, RotateLeft, RotateRight
  >> Drop, Take, Insert, Append, Prepend,'
           First, Last, Rest
  >> Length, Dimension
  >> Partition, Flatten
  

---Slide 9---
List Operations

• Combining Lists:

       A = {1, 2, 3, 4}; B = {3, 4, 5, 6};
       Intersection[A, B]
  =>   {3, 4}
       Union[A, B]
  =>   {1, 2, 3, 4, 5, 6}
       Join[A, B]
  =>   {1, 2, 3, 4, 3, 4, 5, 6}
  

• Predicate-Based Selection: Select

        Select[{-3, 2, 4.5, 7, a, 5, -5}, Positive]
  =>    {2, 4.5, 7, 5}
  

• Apply and Map:

        Apply[f, {a, b, c}]
  =>    f[a, b, c]
        Map[f, {a, b, c}]
  =>    {f[a], f[b], f[c]}
        Apply[Plus, {1, 2, 3, 4}]
  =>    10
        Map[#^2&, {a, b, c, d}]
  =>    {a^2, b^2, c^2, d^2}
  

---Slide 10---
Assignments: Immediate

• Immediate Assignment ``=''
  

  A name can be bound to a numerical and symbolic value:

      a = 3            =>    3
      a + 7            =>    10
                               2
      a = x^2 + y      =>    x   + y
  
                               1
      1/a              =>    ------
                               2
                             x   + y
  

  A value can be unassigned as follows:

      a = .
      a                =>    a
  

---Slide 11---
Assignments: Delayed

• Delayed Assignment ``:=''
  

  If we write L-val := R-val, then L-val's value is an ``unevaluated expression.'' Whenever MATHEMATICA needs to evaluate L-val subsequently, only then the evaluation of the R-val is made.

       a = 3
  
       f  = a                  =>     3
       g := a
  
       a = 5
       f                       =>     3
       g                       =>     5
  

---Slide 12---
Delayed Assignment

• Another Example:

       random1 = Random[]      =>     0.495874
       random2 := Random[]
  
       Table[random1, {5}]
  =>   {0.495874, 0.495874, 0.495874, 0.495874, 0.495874}
       Table[random2, {5}]
  =>   {0.02327, 0.71788, 0.430938, 0.862341, 0.128564}
  

• Figure out what happens in the
  following MATHEMATICA program:

    factorial[1] := 1;
    factorial[n_] := factorial[n] = n factorial[n-1]
  

• Multiple Assignments are allowed.

           a = b = c = d = e
  =>       e
  

---Slide 13---
Procedural Programming: Conditionals

• Simplest Form

     lhs := rhs /; test
  

  The definition is Valid if the test is true.

    g[x_] := 1/; x > 0
    g[x_] := -1/; x <= 0
  

• Variations: If-Then-Else

    h[x_] := If[ x > 0, 1, -1, 0]
  

  Which and Switch

   j[x_] := Which[ x > 0, 1,   x < 0, -1,  True, 0]
   foo[x_] := Switch[Mod[x,3]
                 0, a,   1, b,   2, c,   -, error]
  

• Boolean Relations

     == (EQUAL), != (UNEQUAL), === (SAME), =!= (UNSAME)
     TrueQ, && (AND), || (OR)
  

---Slide 14---
Procedural Programming: Loops

• Do, While and For

     Do[ Print[i^2], {i, 1, 5}]
  
     Do[ Print[i], {i, 2a, 6a, a} ]
  

  Iterator = 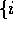, start, stop, incr+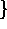

     Do[ Print[{i, j}], {i, 3}, {j, i} ]
  => {1, 1}
     {2, 1}
     {2, 2}
     {3, 1}
     {3, 2}
     {3, 3}
  
     While[test, body]
  
     For[start, test, step, body]
  

---Slide 15---
Examples

• Big Examples

   Fib[k_Integer?Positive] :=
    Module[{fn1 = 1, fn2 = 0},
     While[ fn1 < k, 
      {fn1, fn2} = {fn1 + fn2, fn1}
     ]; fn2
    ]
  
   SameTest[l_List] :=
    Module[{i},
     For[i=1,
      (i<Length[l]) && (l[[1]] === l[[i]]),
      i++,
      ];
     l[[1]] === l[[i]]
    ]
  

• Break[] and Continue[]
  

  Break exits the innermost enclosing loop.

  Continue skips the remaining portion of the loop body for the current iteration

---Slide 16---
Defining Your Own Iterator: Until

• Until[body, test]

     Begin["`Private`"]
  
     Attributes[Until] = {HoldAll}
  
     Until[body_, test_] :=
       Module[{t},
         For[t=False, !t, t=test, body]
       ]
  
     End[]
  

  Note: In this case, the attribute HoldAll prevents evaluation of the arguments body & test

• Application of Until

     i = 1; Until[ Print[i++], i== 5]
  

• Until in the infix notation

     i = 1;
     (Print[i++]) ~Until~ (i==5)
  

---Slide 17---
Functional Programming

• Pure (or Anonymous) Function

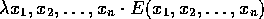  translates to E[#1, #2, ..., #n] &

• Examples

     Map[#^2 &, a + b + c]
      2    2    2
  => a  + b  + c
     Map[Take[#,2]&, {{2,1,7}, {4,1,5}, {3,1,2}}]
  => {{2, 1}, {4, 1}, {3, 1}}
  

• Iterated Applications

      r = 2;
      Nest[(# + r/#)/2&, N[1,40], 7]
   => 1.41421356237309504880168872420969807857
  

  Nest[f, expr, n] applies the function f to expr n times.

• Other Related Operators:
  FixedPoint, Fold, FoldList

---Slide 18---
Example: PowerSet

    CopyPut[l_List, x_] :=
      Join[l, Table[
              Append[l[[i]], x], {i, Length[l]}
      ]]

    PowerSet[l_List] := Fold[CopyPut, {{}}, l]

    PowerSet[{a, b, c}]
=>  {{}, {a}, {b}, {a, b},
     {c}, {a, c}, {b, c}, {a, b, c}}

---Slide 19---
Procedural vs. Functional Programming

• Define a function SS2L that takes three numbers as arguments and returns the sum of the squares of the two larger numbers.

• Procedural Style

   SS2L1[x_, y_, z_] :=
     If[x > y,
       If[y > z, x^2 + y^2, x^2 + z^2],
       If[x > z, x^2 + y^2, y^2 + z^2]
     ]
  

• Functional Style

   SS2L2[x_, y_, z_] :=
     Apply[Plus, Take[
            Sort[{x, y, z}], -2
     ]^2 ]
  

---Slide 20---
Pattern Matching

• Patterns are used to recognize types of expressions and their order. This information is used to reorganize the structure. This feature provides a powerful transformational paradigm.

• Pattern is represented as ``_'' and can be added ``name'' (e.g., name_), ``type'' and ``?test'' (e.g., arg_type?test)

     lg[n1_ n2_] := lg[n1] + lg[n2]
     lg[n1_^n2_] := n2 lg[n1]
   
     lg[x y z]
  => lg[x] + lg[y] + lg[z]
     lg[x y x y x y]
  => 3 lg[x] + 3 lg[y]
  

---Slide 21---
Stylistic Remarks

• Example

     g[l_List] := First[l]^Last[l]
  
     g[{2, 2}]          => 4
     g[{2, 3, 3, 2}]    => 4
  

• Preferred Style:
  

  g[{first_,last_}] := first^last
  or g[list:{_, _}] := First[list]^last[list]

• Some More Examples

     myMap[f_,{}] := {}
     myMap[f_,{a_,b___}] := Prepend[myMap[f,{b}],f[a]]
  
     myMap[g, {1, 2, 3}]
  => {g[1], g[2], g[3]}
  
     find9[{_,".",a___,"9","9","9","9","9","9",___}]
           := Langth[{a}]
     find9[Characters[ToString[N[Pi,800]]]]  =>  761
  

---Last Slide---
Final Remarks

• Omitted Topics 1: Rule-based programming, Simplification. Lazy and Eager Evaluation.
• Omitted Topics 2: Scopes and Contexts. Functions: Block, Module and With.
  Packages.
• Omitted Topics 3: Graphics, Sound and Animation.

[End of Lecture #14]