 MISHRA
MISHRA
Lecture #2
Programming Languages  MISHRA
MISHRA
 Full Programming
Language. E.g., Job Control Language,
Database Language.
Full Programming
Language. E.g., Job Control Language,
Database Language.
 a Programming Language
a Programming Language
---Slide 2---
Church-Turing Thesis
Any function that can be described finitely and computed in finite time is Turing-computable.Every computable function is Turing-computable.
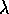 -calculus
-calculus
---Slide 3---
Unsolvable Problems!
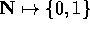 .
.
There are functions that are not Turing-computable.
---Slide 4---
Turing Machine
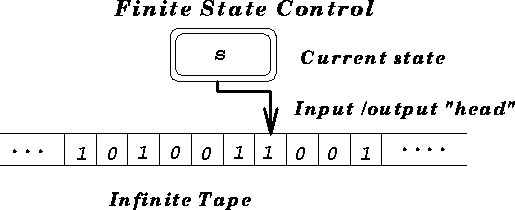
---Slide 5---
Turing Machine
Given any Turing machineand some input
, a universal Turing machine
will mimic (i.e., simulate) the behavior of
on
.
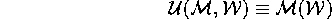
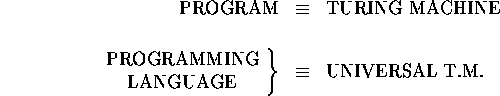
---Slide 6---
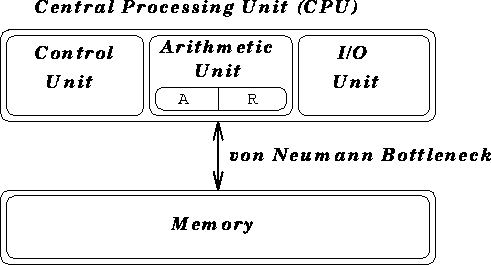
von Neumann Architecture
 John von Neumann
John von Neumann
---Slide 7---
Instruction Set Architecture
A := A + M[i]; A := A - M[i];
A := A + |M[i]|; A := A - |M[i]|;
A := - M[i]; A := |M[i]|; A := -|M[i]|;
A := A * 2; A := A div 2;
{A, R} := { (M[i]*R) div 2^39, (M[i]*R) mod 2^39 };
{A, R} := { A mod M[i], A div M[i] };
A := M[i]; M[i] := A; R := M[i]; A := R;
goto M[i].left; goto M[i].right;
if A >= 0 if A >= 0
goto M[i].left; goto M[i].right;
---Slide 8---
Modifiable Statements
M[i].left from A
M[i].right from A
9.left) A := <address>; 9.right) Modify M[10].left from A; 10.left) goto M[3].leftQuestion: Where does the control transfer?
---Slide 9---
Machine Language
---Slide 10---
Assembly Language
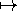 Codes
Codes
---Slide 11---
Translators
The target code takes input data and produces output data at run time
Takes instructions and input data and produces output data.
K := I + J; LOAD I; 1001 0000;
ADD J; 0001 0001;
STORE K; 1010 0010;
(High-Level) (Assembly) (Machine)
---Slide 12---
Description of a Programming Language
---Slide 13---
Syntax
<sentence> ::= <noun> <verb> <noun> ::= bud | sam | tom <verb> ::= hacks | builds | proves
---Slide 14---
Syntax (contd)
"Illegal variable name" "Missing semicolon"
---Slide 15---
Semantics
Allows precise interpretation of a program.
---Slide 16---
Semantics Analysis
function F(x, y: integer) returns integer is
if x = y
then y + 1
else F(x, F(x - 1, y + 1));
if x = y then y + 1 else x + 1
if x >= y then x + 1 else y - 1
---Slide 17---
Types of Semantics
C on UNIX
---Slide 18---
Principle of Orthogonality
---Slide 19---
Control Structures
begin S0; S1 end;
if B0 then S0 case E of
else if B1 then S1 L0: S0;
... ...
else Sn; Ln: Sn
end;
while B do S; for I := I0 to In
do S;
goto L; break; return; continue; exit; raise Exception abort;
---Slide 20---
Data Structures
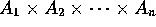 . (Cartesian Product)
. (Cartesian Product)
Projection or Field Selection operation
selects a component. Examples: Pascal and Ada
record, C struct.
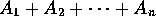 . (Disjoint Union or Co-product)
. (Disjoint Union or Co-product)
Injection operation constructs elements from the sum
by means of a ``tag''. Examples: Pascal and Ada
variant record, C union.
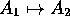 (Injective Map, Array)
(Injective Map, Array)
Application or Subscription operation maps a
value in the domain (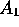 ) to a unique value in the range
(
) to a unique value in the range
(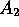 ). Examples: Pascal, Ada &
). Examples: Pascal, Ada & C array
C and Pascal.
---Slide 21---
Examples of Domain Constructions
record
i: integer;
c: char
end;
record case tag: Boolean of
true: (i: integer);
false: (c: char)
end;
array[char] of integer;
---Slide 22---
Principle of Abstraction
---Slide 23---
Examples of Abstractions
var F, G: real; function Convert(F: real):real;
G := (F-32.0)*5.0/9.0; begin
Convert := (F-32.0)*5.0/9.0
end;
begin procedure Swap(var U: real;
var U, V, Temp: real; var V: real);
var Temp: real;
Temp := U; begin
U := V; Temp := U;
V := Temp U := V;
end; V := Temp
end;
const n: integer; type function
type String = String(const n: integer);
array[1..n] of char; begin
String = array[1..n] of char
end;
---Slide 24---
Principle of Correspondence
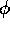 and a compatible actual
parameter, A
and a compatible actual
parameter, A
the effect on a block body of the qualifying declarationshould be identical to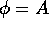
the effect on an abstraction body withas its formal parameter and A the corresponding actual argument.
var i: integer; procedure p(i: integer);
begin begin
i := -j; write(i)
write(i) end;
end; begin
p(-j)
end;
---Last Slide---
Principle of Qualification
C in procedure
procedure p(I: I');
begin
C
end;
corresponds to command C in block
var I: I';
begin
C
end;
[End of Lecture #2]