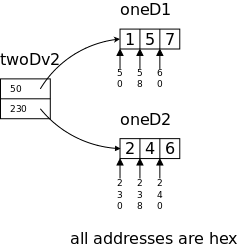
long oneD1[3] = {1, 5, 7},
oneD2[3] = {2, 4, 6};
*twoDv2[2] = {oneD1, oneD2};
// = {&oneD1[0], oneD2[0]
Start Lecture #01
I start at 0 so that when we get to chapter 1, the numbering will agree with the text.
There is a web site for the course. You can find it from my home page, which is listed above, or from the department's home page.
Start Lecture #01marker above can be thought of as
End Lecture #00.
The course has several texts.
https://diveintosystems.cs.swarthmore.edu/x86_64/antora/diveintosystems/betaThe material on C is standard, but the order of presentation is not. A difference between this book and K&R is that the latter starts with low-level I/O (read and print one character) whereas this book starts with a higher level approach.
Computer Organizationportion of the course. It is required.
Grades are based on the labs and exams; the weighting will be
approximately
20%*LabAverage + 35%*MidtermExam + 45%*FinalExam (but see homeworks
below).
I make a distinction between homeworks and labs.
Labs are
Homeworks are
Homeworks are numbered by the class in which they are assigned. So any homework given today becomes part of homework #1. Even if I do not give homework today, any homework assigned next class would become homework #2. In general the homework present in the notes for lecture #n is homework #n.
You may develop (i.e., write and test) lab assignments on any system you wish, e.g., your laptop. However, ...
NYU Brightspace.
This will be covered in the recitations.
I feel it is important for CS students to be familiar with basic
client-server computing (related to cloud computing
) in which
one develops software on a client machine (for us, most likely one's
personal laptop), but runs it on a remote server (for us,
linserv1.cims.nyu.edu).
This requires three steps.
I have supposedly given you each an account on linserv1 (and access), which takes care of step 1. Accessing linserv1 and access is different for different client (laptop) operating systems.
seelinserv1, but can
seeaccess. So from outside (you play the Duo/MFA game and) log into access; then you are inside.
If you receive a message from linserv1 about an authentication failure, please follow the advice below from the systems group.
The first line of defense in all cases of authentication failure is to attempt a password reset. Please visit https://cims.nyu.edu/webapps/password/reset to do so. Within 15 minutes of a password reset submission, instructions to retrieve the new password will be sent to xyz123@nyu.edu. Please e-mail helpdesk@cims.nyu.edu in the event that the password reset either fails, or that the new password does not work (be sure to preface your ssh command with your username, e.g. ssh xyz123@access.cims.nyu.edu).
Good methods for obtaining help include
This course uses (and teaches) the C programming language. You must write your labs in C (or C++, but we will not teach the latter). Moreover C, but not C++, will appear on exams.
The rules for incompletes and grade changes are set by the school and not the department or individual faculty member.
The rules set by CAS can be found in <http://cas.nyu.edu/object/bulletin0608.ug.academicpolicies.html>, which states:
The grade of I (Incomplete) is a temporary grade that indicates that the student has, for good reason, not completed all of the course work but that there is the possibility that the student will eventually pass the course when all of the requirements have been completed. A student must ask the instructor for a grade of I, present documented evidence of illness or the equivalent, and clarify the remaining course requirements with the instructor.
The incomplete grade is not awarded automatically. It is not used when there is no possibility that the student will eventually pass the course. If the course work is not completed after the statutory time for making up incompletes has elapsed, the temporary grade of I shall become an F and will be computed in the student's grade point average.
All work missed in the fall term must be made up by the end of the following spring term. All work missed in the spring term or in a summer session must be made up by the end of the following fall term. Students who are out of attendance in the semester following the one in which the course was taken have one year to complete the work. Students should contact the College Advising Center for an Extension of Incomplete Form, which must be approved by the instructor. Extensions of these time limits are rarely granted.
Once a final (i.e., non-incomplete) grade has been submitted by the instructor and recorded on the transcript, the final grade cannot be changed by turning in additional course work.
This email from the assistant director, describes the policy.
Dear faculty, The vast majority of our students comply with the department's academic integrity policies; see www.cs.nyu.edu/web/Academic/Undergrad/academic_integrity.html www.cs.nyu.edu/web/Academic/Graduate/academic_integrity.html Unfortunately, every semester we discover incidents in which students copy programming assignments from those of other students, making minor modifications so that the submitted programs are extremely similar but not identical. To help in identifying inappropriate similarities, we suggest that you and your TAs consider using Moss, a system that automatically determines similarities between programs in several languages, including C, C++, and Java. For more information about Moss, see: http://theory.stanford.edu/~aiken/moss/ Feel free to tell your students in advance that you will be using this software or any other system. And please emphasize, preferably in class, the importance of academic integrity. Rosemary Amico Assistant Director, Computer Science Courant Institute of Mathematical Sciences
Yifeng Ko <yk1962@nyu.edu> is the official tutor for this course. He will announce his schedule.
The tutoring will be via zoom. I will give more details about the tutoring zoom when I get them.
Remark: The chapter/section numbers for the material on C, agree with Kernighan and Plauger. However, the material is quite standard so, as mentioned before, if you already own a C book that you like, it should be fine.
Since Java includes much of C, my treatment can be very brief for the parts in common (e.g., control structures).
You should be reading the first few chapters of K&R or Dive into Systems for the next few lectures.
C programs consist of functions, which contain statements, and variables, the latter store values.
Hello WorldFunction
#include <stdio.h>
main() {
printf("Hello, world\n");
}
Although this program works, the second line should really be
int main(int argc, char *argv[]) {
I know this looks weird for now but remember how long it took you to
really understand
public static void main (String[] args)
Like Java.
Like Java
The program on the right is trivial. However, I wish to use it to introduce lvalues and rvalues. Each variable (in this program x and y) has two values associated with it: its address and the contents of that address. The latter is often called the value of the variable.
main() {
int x=5, y=8;
y = x+2;
}
Consider the program's assignment statement y = x+2;. To evaluate the right hand side (RHS) we need to know that the value of x is 5; we are not interested in knowing the address in which this 5 is stored. This value, 5, is called the rvalue of x because it is what is needed when x occurs on the RHS. In contrast the fact that 8 is the rvalue of y is not relevant since y does not occur on the RHS.
The LHS contains just y. But the fact that y has the value (specifically the rvalue) 8, is not relevant. What is relevant is the address of y since that is where the system must store the 7 that results from the addition. The address of y is called its lvalue since it is what is needed when y occurs on the LHS.
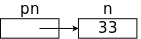
#include <stdio.h>
main() {
int n = 0, *pn;
pn = &n;
*pn = 33;
printf("n = %d\n", n);
}
This idea of addresses is a central theme of CSO because it is one key in understanding how Computer Systems are Organized.
The program on the far right is actually correct and prints "n = 33".
The beginnings of an explanation is the diagram on the near right:
pn is a pointer to n, the (r)value of
pn is the lvalue (aka the address) of n.
#include <stdio.h>
main() {
int F, C;
int lo=0, hi=300, incr=20;
for (F=lo; F<=hi; F+=incr) {
C = 5 * (F-32) / 9;
printf("%d\t%d\n", F, C);
}
}
right amountof space to print the corresponding argument.
#include <stdio.h>
#define LO 0
#define HI 300
#define INCR 20
main() {
int F;
for (F=LO; F<=HI; F+=INCR)
printf("%3d\t%5.1f\n", F,
(F-32)*(5.0/9.0));
}
The simplest (i.e., most primitive) form of character I/O is getchar() and putchar(), which read and print a single character.
Both getchar() and putchar() are declared in stdio.h.
#include <stdio.h>
main() {
int c;
while ((c = getchar()) != EOF)
putchar(c);
}
File copy is conceptually trivial: getchar() a char and then putchar() this char until eof. The code is on the right and does require some comment despite is brevity.
extraparens, which are definitely not extra.
Homework: (1-7) Write a (C-language) program to print the value of EOF. (This is 1-7 in the book but I realize not everyone will have the book so I will type the problems into the notes.)
Homework: Write a program to copy its input to its output, replacing each string of one or more blanks by a single blank.
while (getchar() != EOF) ++numChars; for (numChars = 0; getchar() != EOF; ++numChars);
This is essentially a one-liner, which I have written in two different ways: once with a while loop and once with a for loop.
Now we need two tests: end-of-line and end-of-input. Perhaps the following is really a two-liner, but it does have only one semicolon.
while ((c = getchar()) != EOF) if (c == '\n') ++numLines;
So if a file has no newlines, it has no lines. Demo this with echo -n >noEOF "hello"
The Unix wc program prints the number of characters, words, and lines in the input. It is clear what the number of characters means. The number of lines is the number of newlines (so if the last line doesn't end in a newline, it doesn't count). The number of words is less clear. In particular, what should be the word separators?
#include <stdio.h>
#define WITHIN 1
#define OUTSIDE 0
main() {
int c, num_lines, num_words, num_chars;
int within_or_outside = OUTSIDE;
num_lines = num_words = num_chars = 0;
while ((c = getchar()) != EOF) {
++num_chars;
if (c == '\n')
++num_lines;
if (c == ' ' || c == '\n' || c == '\t')
within_or_outside = OUTSIDE;
else if (within_or_outside == OUTSIDE) {
// starting a word
++num_words;
within_or_outside = WITHIN;
}
}
printf("%d %d %d\n", num_lines, num_words, num_chars);
}
Homework: (1-12) Write a program that prints its input one word per line.
Remark: Class accounts on linserv1.
First round of your class accounts for 201-003 and 202-002 were
created tonight, and students will receive a welcome message if they
are getting a new account. Any student who previously had a CIMS
account in the past (whether or not it is active) will not get an
email but their account will be adjusted as necessary for use for
your class. The password reset link may be useful especially to
those students:
https://cims.nyu.edu/webapps/password/reset
We will re-run the class account creation scripts daily until the
drop deadline.
Thanks,
Shirley
Remark: The tutor has revised the hours. The hours listed in section 0.10 of these notes have been updated.
We are hindered in our examples because we don't yet know how to input anything other than characters and haven't yet written the program to convert a string of characters into an integer (easy) or (significantly harder) a floating point number.
#include <stdio.h>
#define N 10 // imagine you read in N
main() {
int i;
float x, sum=0, mu;
for (i=0; i<N; i++) {
x = i; // imagine you read in x
sum += x;
}
mu = sum / N;
printf("The mean is %f\n", mu);
}
#include <stdio.h>
#define N 10 // imagine you read in N
#define MAXN 1000
main() {
int i;
float x[MAXN], sum=0, mu;
for (i=0; i<N; i++) {
x[i] = i; // imagine you read in x[i]
}
for (i=0; i<N; i++) {
sum += x[i];
}
mu = sum / N;
printf("The mean is %f\n", mu);
}
#include <stdio.h>
#include <math.h>
#define N 5 // imagine you read in N
#define MAXN 1000
main() {
int i;
double x[MAXN], sum=0, mu, sigma;
for (i=0; i<N; i++) {
x[i] = i; // imagine you read in x[i]
sum += x[i];
}
mu = sum / N;
printf("The mean is %f\n", mu);
sum = 0;
for (i=0; i<N; i++) {
sum += pow(x[i]-mu,2);
}
sigma = sqrt(sum/N);
printf("The std dev is %f\n", sigma);
}
I am sure you know the formula for the mean (average) of N numbers: Add the numbers and divide by N. The mean is normally written μ. The standard deviation is the RMS (root mean square) of the deviations-from-the-mean, it is normally written σ. Symbolically, we write μ = ΣXi/N and σ = √(Σ((Xi-μ)2)/N). (When computing σ we sometimes divide by N-1 not N. Ignore the previous sentence.)
The first program on the right naturally reads N, then reads N numbers, and finally computes the mean of the latter. There is a problem; we don't know how to read numbers.
So I faked it by having N a symbolic constant and making x[i]=i.
I do not like the second version with its gratuitous array. It is (a little) longer, slower, and more complicated. Much worse it takes space (i.e., requires memory) proportional to N, for no reason. Hence it might not run at all for large N and small machines. However, I have seen students write such programs. Apparently, there is an instinct to use a three step procedure for all programming assignments:
But that is silly if, as in this example, you no longer need each value after you have read the next one.
The last example is a good use of arrays for computing the standard deviation using the RMS formula above. We do need to keep the values around after computing the mean so that we can compute all the deviations from the mean and, using these deviations, compute the standard deviation.
Note that, unlike Java, no use of new (or the
C analogue
malloc()) appears.
Arrays declared as in this program have a lifetime of the routine in which they are declared. Specifically sum and x are both allocated when main is called and are both freed when main is finished.
Note the declaration int x[MAXN] in the third version. In C, to declare a complicated variable (i.e., one that is not a primitive type like int or char), you write what has to be done to the variable to get one of the primitive types.
In C if we have int X[10]; then writing X in your
program is the same as writing &X[0].
& is the address of
operator.
More on this later when we discuss pointers.
There is of course no limit to the useful functions one can write. Indeed, the main() programs we have written above are all functions.
#include <stdio.h>
// Determine letter grade from score
// Demonstration of functions
char letter_grade (int score) {
if (score >= 90) return 'A';
else if (score >= 80) return 'B';
else if (score >= 70) return 'C';
else if (score >= 60) return 'D';
else return 'F';
} // end function letter_grade
main() {
short quiz;
char grade;
quiz = 75; // should read in quiz
grade = letter_grade(quiz);
printf("For a score of %3d the grade is %c\n",
quiz, grade);
} // end main
cc -o grades grades.c; ./grades
For a score of 75 the grade is C
A C program is a collection of functions (and global variables). Exactly one of these functions must be called main and that is the function at which execution begins.
One important issue is type matching. If a function f takes one int argument and f is called with a short, then the short must be converted to an int. Since this conversion is widening, the compiler will automatically coerce the short into an int, providing it knows that an int is required.
It is fairly easy for the compiler to know all this providing f() is defined before it is used, as in the code on the right.
We see on the right a function letter_grade defined. It has one int argument and returns a char.
Finally, we see the main program that calls the function.
The main program uses a short to hold the numerical grade and then calls the function with this short as the argument. The C compiler generates code to coerce this short value to the int required by the function.
// Average and sort array of random numbers
#define NUMELEMENTS 50
void sort(int A[], int n) {
int temp;
for (int x=0; x<n-1; x++)
for (int y=x+1; y<n; y++)
if (A[x] < A[y]) {
temp = A[y];
A[y] = A[x];
A[x] = temp;
}
}
double avg(int A[], int num) {
int sum = 0;
for (int x=0; x<n; x++)
sum = sum + A[x];
return (sum / n);
}
main() {
int table[NUMELEMENTS];
double average;
for (int x=0; x<NUMELEMENTS; x++) {
table[x] = rand(); /* assume defined */
printf("The elt in pos %d is %d\n",
x, table[x]);
}
average = avg(table, NUMELEMENTS );
printf("The average is %5.1f ", average);
sort(table, NUMELEMENTS );
for (x-=; x<NUMELEMENTS; x++)
printf("The element in position %3d is %3d \n",
x, table[x]);
}
The next example illustrates a function that has an array argument.
Remember that in a C declaration you decorate
the item being
declared with enough stuff (e.g., [], *) so that the result is a
primitive type such as int, double, or
char.
The function sort has two parameters, the second one n is simply an int. The parameter A, however, is more complicated. It is the kind of thing that when you take an element of it, you get an int.
That is, A is an array of ints.Unlike the array example in section 1.6, A does not have an explicit upper bound on its index. This is because the function can be called with arrays of different sizes. Since the function needs to know the size of the array (look at the for loops), a second parameter n is used for this purpose.
This example has two function calls: main calls both avg and sort. Looking at the call from main to sort we see that table is assigned to A and NUMELEMENTS is assigned to n. Looking at the code in main itself, we see that indeed NUMELEMENTS is the size of the array table and thus in sort, n is the size of A.
All seems well provided the called function appears before the function that calls it. Our examples have followed this convention.
So far so good; but if f calls g and (recursively) g calls f, we are in trouble. How can we have f before g, and also have g before f?
This will be answered very soon.
#include <stdio.h>
int f(int a, int b) {
a = a+b;
return a;
}
main() {
int x = 10;
int y = 20;
int ans;
ans = f(x, y);
}
Arguments in C are passed by value (the same as Java does for arguments that are not objects).
The simple example on the right illustrates a few points. First, some terminology. The variables a and b in f() are called parameters of f() whereas, x and y are called arguments of the call f(x, y).
When main() calls f() the values in the arguments are copied into the corresponding parameters. However, when f() returns, the values now in the parameters are NOT copied back to the arguments. This explains why the value in ans differs from the final value in x.
Try to avoid the fairly common error of assuming Copy-in AND Copy-out semantics.
Start Lecture #02
Remark: Homework #1 was entered on Brightspace 3 September; it is due 10 September.
Remark: The tutor sent a msg giving hours.
Unlike Java, C does not have a string datatype. A string in C is an array of chars. String operations like concatenate and copy (assignment) become functions in C. Indeed there are a number of standard library routines that act on strings.
Strings in C are null terminated
.
That is, a string of length 5 actually contains 6 characters, the 5
characters of the string itself and a sixth character = '\0' (called
null) indicating the end of the string.
This is a big deal.
Our goal is a program that reads lines from the terminal, converts them to C strings by appending '\0', and prints the longest line found. Pseudo code would be
while (more lines)
read line
if (line longer than previous longest)
save line and its length
print the saved line
Thus we need the ability to read in a line and the ability to save a line. We write two functions getLine() and copy() for these tasks (the book uses getline (all lower case), but that doesn't compile for me since there is a library routine in stdio.h with the same name and different signature).
#include <stdio.h> #define MAXLINE 1000 int getLine(char line[], int maxline); void copy(char to[], char from[]);
int main() { int len, max; char line[MAXLINE], longest[MAXLINE]; max = 0; while ((len=getLine(line,MAXLINE))>0) if (len > max) { max = len; copy(longest,line); } if (max>0) printf("%s", longest); return 0; }
int getLine(char s[], int lim) { int c, i; for (i=0; i<lim-1 && (c=getchar())!=EOF && c!='\n'; ++i) s[i] = c; if (c=='\n') { s[i]= c; ++i; } s[i] = '\0'; return i; }
void copy(char to[], char from[]) { int i; i=0; while ((to[i] = from[i]) != '\0') ++i; }
Given the two supporting routines, main is fairly simple, needing only a few small comments.
declare (or define) before useso either main would have to come last or the declarations are needed. Since only main uses the routines, the declarations could have been in main but it is common practice to put them outside as shown. Although these routines are not recursive (and hence we could have placed the called routine before the caller), declarations like the one shown are needed for recursive routines.
This function is discussed further in recitation.
The line is returned in the parameter s[], the function
itself returns the length.
The for continuation condition
in getLine
is rather complex.
(Note that the for loop has an empty body; the entire
action occurs in the for statement itself.)
The condition part of the for tests for 3 situations.
Perhaps it would be clearer if the test was simply i<lim-1 and the rest was done with if-break statments inside the loop.
In C, if you write f(x)+g(y)+h(z) you have
no guarantee of the order the functions will be invoked.
(Thus the program would be non-deterministic if g() modified
something used by f().)
However, the && and || operators do
guarantee left-to-right ordering to enforce short-circuit
condition evaluation.
This ordering is important here since the test for '\n'
must be performed after the getchar() has
assigned its value to c.
The copy() function is declared and defined to return void.
Homework: Simplify the for condition in getline() as just indicated.
#include <stdio.h>
#include <math.h>
#define A +1.0 // should read
#define B -3.0 // A,B,C
#define C +2.0 // using scanf()
void solve (float a, float b, float c);
int main() {
solve(A,B,C);
return 0;
}
void solve (float a, float b, float c) {
float d;
d = b*b - 4*a*c;
if (d < 0)
printf("No real roots\n");
else if (d == 0)
printf("Double root is %f\n", -b/(2*a));
else
printf("Roots are %f and %f\n",
((-b)+sqrt(d))/(2*a),
((-b)-sqrt(d))/(2*a));
}
#include <stdio.h>
#include <math.h>
#define A +1.0 // main() should
#define B -3.0 // read A,B,C
#define C +2.0 // using scanf()
void solve(void); // declaration of solve()
float a, b, c; // definitions
int main() { // definition of main()
extern float a, b, c; // declarations
a=A;
b=B;
c=C;
solve();
return 0;
}
void solve () { // definition of solve()
extern float a, b, c; // declarations
float d;
d = b*b - 4*a*c;
if (d < 0)
printf("No real roots\n");
else if (d == 0)
printf("Double root is %f\n", -b/(2*a));
else
printf("Roots are %f and %f\n",
((-b)+sqrt(d))/(2*a),
((-b)-sqrt(d))/(2*a));
}
The two programs on the right find the real roots (no imaginary numbers) of the quadratic equation
ax2+bx+c
They proceed by using the standard technique of first calculating the discriminant
d = b2-4ac
Since these programs deal only with real roots, they punt when d<0.
The programs themselves are not of much interest.
Indeed a Java version would be too easy
to be a midterm exam
question in 101.
Our interest is confined to the way in which the
coefficients a, b, and c are passed from
the main() function to the helper
routine solve().
The main() function calls a function solve() passing it as arguments the three coefficients, A,B,C.
There is little to say. Method 1 is a simple program and uses nothing new.
The second main() program communicates with solve() using external variables rather than arguments/parameters.
declare (or define) before use. If you define before using, you don't need to also declare. But if you have recursion (f() calls g() and g() calls f()), you can't have both definitions before the corresponding uses so you
Similar to Java: A variable name must begin with a letter and then can use letters and numbers. An underscore is a letter, but you shouldn't begin a variable name with one since that is conventionally reserved for library routines. Keywords such as if, while, etc are reserved and cannot be used as variable names.
C has very few primitive types.
naturalsize of an integer on the host machine.
There are qualifiers that can be added. One pair is long/short, which are used with int. Typically short int is abbreviated short and long int is abbreviated long.
long is guaranteed be at least as big as int, which is guaranteed to be as least as big as short.
There is no short float, short double, or long float. The type long double specifies extended precision.
The qualifiers signed or unsigned can be applied to char or any integer type. They basically determined how the sign bit is interpreted. An unsigned char uses all 8 bits for the integer value and thus has a range of 0–255; whereas, a signed char has an integer range of -128–127.
Note: We will have much more to say about data types, e.g., signed and unsigned, next month after we finish our treatment of C.
A normal integer constant such as 123 is an int, unless it is too big in which case it is a long. But there are other possibilities.
There are no string variables in C. Although there are no string variables, there are string constants, written as zero or more characters surrounded by double quotes. A null character '\0' is automatically appended.
Alternative method of assigning integer values to symbolic names.
enum Boolean {false, true}; // false is zero, true is 1
enum Month {Jan=1, Feb, Mar, Apr, May, Jun, Jul, Aug, Sep, Oct, Nov, Dec};
Simple examples.
int x, y; char c; double q1, q2;
(Stack allocated, i.e., local) arrays are simple since the entire array is allocated not just a reference (no new/malloc required).
int x[10];
Initializations may be given.
int x=5, y[2]={44,6}; z[]={1,2,3};
char str[]="hello, world\n";
The qualifier const makes the variable read only so it must be initialized in the declaration.
Mostly the same as java.
Please do not call % the mod (or modulo) operator, unless you know that the operands are positive. The correct name for % is the remainder operator.
Again very little difference from Java.
Please remember that && and || are required to be short-circuit operators. That is, they evaluate the right operand only if needed.
There are two kinds of conversions: automatic conversions, called coercions, and explicit conversions, called casts.
C coerces narrow
arithmetic types to wide ones.
{char, short} → int → long
float → double → long double
long → float // precision can be lost
int atoi(char s[]) {
int i, n=0;
for (i=0; s[i]>='0' && s[i]<='9'; i++)
n = 10*n + (s[i]-'0'); // assumes ascii
return n;
}
The program on the right (ascii to integer) converts a character string representing an integer to the integral value.
Unsigned coercions are more complicated; you can read about them in the book or wait a few weeks when we will cover them.
The syntax
(type-name) expression
converts the value to the type specified. Note that e.g., (double) x converts the value of x; it does not change x itself.
Homework: (2.3) Write the function htoi(s), which converts a string of hexadecimal digits (including an optional 0x or 0X) into its equivalent integer value. The allowable digits are 0 through 9, a through f, and A through F.
The same as Java.
Remember that neither x++ nor ++x are the same as x=x+1 because, with the operators, x is evaluated only once, which becomes important when x is itself an expression with side effects.
x[i++]++ // increments some (which?) element of an array x[i++] = x[i++]+1 // puts incremented value in ANOTHER slot
In fact the last line is illegal (what order do you do the two increments of i?)
Homework: (2-4). Write an alternate version of squeeze(s1,s2) (defined in the text) that deletes each character in the string s1 that matches any character is the string s2.
#include <stdio.h>
int main(void) {
int x = 4, y = 1;
printf("x&y=%i x&&y=%i\n", x&y, x&&y);
return 0;
}
x%y=0 x&&y=1
The same as Java
Note that x&&y is different from x&y.
int bitcount (unsigned x) {
int b;
for (b=0; x!=0; x>>= 1)
if (x&01) // octal (not needed)
b++;
return b;
}
The same as Java: += -= *= /= %= <<= >>= &= ^= |=
The program on the right counts how many bits of its argument are 1. Right shifting the unisigned x causes it to be zero-filled. Anding with a 1, gives the LOB (low order bit). Writing 01 indicates an octal constant (any integer beginning with 0; similarly starting with 0x indicates hexadecimal). Both are convenient for specifying specific bits (because both 8 and 16 are powers of 2). Since the constant in this case has value 1, the 0 has no effect.
printf("You enrolled in %d course%s.\n", n, (n==1) ? "" : "s");
The same as Java:
Homework: (2-10). Rewrite the function lower(), which converts upper case letters to lower case with a conditional expression instead of if-else.
| Operators | Associativity |
|---|---|
| () [] -> . | left to right |
| ! ~ ++ -- + - * & (type) sizeof | right to left |
| * / % | left to right |
| + - | left to right |
| << >> | left to right |
| < <= > >= | left to right |
| == != | left to right |
| & | left to right |
| ^ | left to right |
| | | left to right |
| && | left to right |
| || | left to right |
| ?: | right to left |
| = += -= *= /= %= &= ^= |= <<= >>= | right to left |
| , | left to right |
The table on the right is copied (hopefully correctly) from the book. It includes all operators, even those we haven't learned yet. I certainly don't expect you to memorize the table. Indeed one of the reasons I typed it in was to have an online reference I could refer to since I do not know all the precedences.
Homework: Check the table above for typos and report any you find.
Not everything is specified. For example if a function takes two arguments, the order in which the arguments are evaluated is not specified. Consider f(x++,x++);
Also the order in which operands of a binary operator like + are evaluated is not specified. So f() could be evaluated before or after g() in the expression f()+g(). This becomes important if, for example, f() alters a global variable that g() reads.
#include <stdio.h>
void main (void) {
int x=3, y;
y = + + + + + x;
y = - + - + + - x;
y = - ++x;
y = ++ -x;
y = ++ x ++;
y = ++ ++ x;
}
Question: Which of the expressions on the right are
illegal?
Answer: The last three.
They apply ++ to values not variables (i.e, to rvalues not
lvalues).
I mention this because at this point in a previous semester there was some discussion about ++ ++. The distinction between lvalues and rvalues will become very relevant when we discuss pointers.
Since pointers have presented difficulties for students in the past, I use every opportunity that arises to give ways of looking at the problem.
Since ++ does an assignment (as well as an addition) it needs a place to put the result, i.e., an lvalue.
Start Lecture #03
int t[]={1,2};
int main() {
22;
return 0;
}
C is an expression language; so the constant 22
and
the assignment x=33
have values (i.e., rvalues).
One simple statement is an expression followed by a semicolon;
For example, the program on the right is legal.
As in Java, a group of statements can be enclosed in braces to form a compound statement or block. We will have more to say about blocks later in the course.
Same as Java.
Same as Java.
Same as Java.
Same as Java.
#include <ctype.h>
int atoi(char s[]) {
int i, n, sign;
for (i=0; isspace(s[i]); i++) ;
sign = (s[i]=='-') ? -1 : 1;
if (s[i]=='+' || s[i]=='-')
i++;
for (n=0; isdigit(s[i]); i++)
n = 10*n + (s[i]-'0');
return sign * n;
}
Same as Java. As we shall see, the loops in the book show the hand of a master.
The program on the right (ascii to integer) illustrates several points, as well as being extremely useful in its own right.
workis done in the termination test.
for (i=0, j=0; i+j<n; i++,j+=3)
printf ("i=%d and j=%d\n", i, j);
If two expressions are separated by a comma, they are evaluated left to right and the final value is the value of the one on the right. This operator often proves convenient in for statements when two variables are to be incremented.
Same as Java.
Same as Java.
The syntax is
goto label;
for (...) {
for (...) {
while (...) {
if (...) goto out;
}
}
}
out: printf("Left 3 loops\n");
The label has the form of a variable name. A label followed by a colon can be attached to any statement in the same function as the goto. The goto transfers control to that statement.
Note that a break in C (or Java) only leaves one level of looping so would not suffice for the example on the right.
The goto statement was deliberately omitted from Java. Poor use of goto can result in code that is hard to understand and hence goto is rarely used in modern practice.
The goto statement was much more commonly used in the past.
Homework: Write a C function escape(char s[], char t[]) that converts the characters newline and tab into two character sequences \n and \t as it copies the string t to the string s. Use the C switch statement. Also write the reverse function unescape(char s[], char t[]).
#include <stdio.h>
#define MAXLINE 100
int getline(char line[], int max);
int strindex(char source[], char searchfor[]);
char pattern[]="x y"; // "should" be input
int main() {
char line[MAXLINE];
int found=0;
while (getline(line,MAXLINE) > 0)
if (strindex(line, pattern) >= 0) {
printf("%s", line);
found++;
}
return found;
}
int getline(char s[], int lim) {
int c, i;
i = 0;
while (--lim>0 && (c=getchar())!=EOF
&& c!='\n')
s[i++] = c;
if (c == '\n')
s[i++] = c;
s[i] = '\0';
return i;
}
int strindex(char s[], char t[]) {
int i, j, k;
for(i=0; s[i]!='\0'; i++) {
for (j=i,k=0; t[k]!='\0' && s[j]==t[k];
j++,k++) ;
if (k>0 && t[k]=='\0')
return i;
}
return -1;
}
The Unix utility grep (Global Regular Expression Print) prints all occurrences of a given string (or more generally a regular expression) from standard input. A very simplified version is on the right.
The basic program is
while there is another line
if the line contains the string
print the line
Getting a line and seeing if there are more is getline(); a slightly revised version is on the right. Note that a length of 0 means EOF was reached; an "empty" line still has a newline char '\n' and hence has length 1.
Printing the line is printf().
Checking to see if the string is present in the line is the new code. The choice made was to define a function strindex() that is given two strings s and t and returns the position in s (i.e., the index in the array) where t occurs. strindex() returns -1 if t does not occur in s.
The program is on the right; further comments follow.
C-style, i.e., the declarations specify what you do to each parameter in order to get a char or int. These are not definitions of getline() and strindex(), which are given later. The declarations include only the header information and not the body; they describe only how to use the functions, not what the functions do.
Note that a function definition is of the form
return-type function-name(parameters) {
declarations and statements
}
The default return type is int, but I recommend not utilizing this fact and instead always declaring the return type.
The return statement is like Java.
The book correctly gives all the defaults and explains why they are what they are (compatibility with previous versions of C). I find it much simpler to always
A C program consists of external objects, which are either variables or functions.
Variables and functions defined outside any function are called external.
Variables defined inside a function are called internal.
Functions defined inside another function would also be
called internal; however standard C does not have internal
functions.
That is, you cannot in C define a function inside another function.
In this sense C is not a fully block-structured language
(see block structure
below).
As stated, a variable defined outside functions is external. All subsequent functions in that file will see the definition (unless it is overridden by an internal definition).
External variables can be used, instead of parameters/arguments to pass information between functions. It is sometimes convenient not to repeat a long list of arguments common to several functions. However, using external variables also has problems: It makes the exact information flow harder to deduce when reading the program.
When we solved quadratic equations in section 1.10 our second method used external variables.
Scope rules determine the visibility of names in a program. In C the scope rules are fairly simple.
Since C does not have internal functions, all internal names are variables. Internal variables can be automatic or static. We have seen only automatic internal variables, and this section will discuss only them. Static internal variables are discussed in section 4.6 below.
An automatic variable defined in a function is visible from the
definition until the end of the function (but see
If the same variable name is defined internal to two functions, the variables are unrelated.
Parameters of a function are the same as local variables in these respects.
int main(...) {...}
int value;
float joe(...) {...}
float sam;
int bob(...) {...}
An external name (function or variable) is visible from the point of its definition (or declaration as we shall see below) until the end of that file. In the example on the right
There can be only one definition of a given external name in the entire program (even if the program includes many files). However, there can be multiple declarations of the same name.
A declaration describes a variable (gives its type) but does not allocate space for it. A definition both describes the variable and allocates space for it.
extern int X; extern double z[]; extern float f(double y);
Thus we can put declarations of a variable X, an array z[], and a function f() at the top of every file and then X and z are visible in every function in the entire program. Declarations of z[] do not give its size since space is not allocated; the size is specified in the definition.
If declarations of joe() and bob() were added at the top of the previous example, then main() would be able to call them.
If an external variable is to be initialized, the initialization must be put with the definition, not with a declaration.
How to tell apart declarations or definitions
#include <stdio.h>
double f(double x);
int main() {
float y;
int x = 10;
printf("x in main is %i\n", x);
printf("f(x) is %f\n", f(x));
return 0;
}
double f(double x) {
printf("x in f is %f\n", x);
return x;
}
x in main is 10
x in f is 10.000000
f(x) is 10.000000
The code on the right shows how valuable having the types declared can be. The function f() is the identity function. However, main() knows that f() takes a double so the system automatically converts x to a double when calling f().
It would be awkward to have to change every file in a big programming project when a new function was added or had a change of signature (types of arguments and return value). What is done instead is that all the declarations are included in a single header file. The definitions remain scattered over many files. (Each function is naturally defined only once).
For now assume the entire program is in one directory. Create a file with a name like functions.h containing the declarations of all the functions. Then early in every .c file write the line
#include "functions.h"
Note the quotes not angle brackets, which indicates that
functions.h is located in the current directory, rather
than in the standard placethat is used for <>.
We need to distinguish the lifetime of the value in a variable from the visibility of the variable.
Consider the variable x in the trivial example
void f(void) { int x = 5; printf(%d\n", x++); }
No matter how many times f() is called, the value printed will always be 5. This is because each call re-initializes x to 5. We say that the lifetime of x's value is one execution of the function. In contrast an external variable maintains values assigned to it; its lifetime is permanent.
In addition, x, a local variable, is not visible in any other function. That is, the visibility of x is local to the function in which it is defined.
The adjective static has very different meanings when applied to internal and external variables.
int main(...){...}
static int b16;
void sam(...){...}
double beth(...){...}
If an external variable is defined with the static attribute, its visibility is limited to the current file. In the example on the right b16 is naturally visible in sam() and beth(), but not main(). The addition of static means that if another file has a definition or declaration of b16, with or without static, the two b16 variables are not related.
If an internal variable is declared static, its lifetime is the entire execution of the program. This means that if the function containing the variable is called twice, the value of the variable at the start of the second call is the final value of that variable at the end of the first call.
As we know, there are no internal functions in standard C. If an (external) function is defined to be static, its visibility is limited to the current file (as for static external variables).
Ignore this section. Register variables were useful when compilers were primitive. Today, compilers can generally decide, better than programmers, which variables should be put in register.
Standard C does not have internal functions, that is you cannot in C define a function inside another function. In this sense C is not a fully block-structured language.
Of course C does have internal variables; we have used them in almost every example. That is, most functions we have written (and will write) have variables defined inside them.
#include <stdio.h>
int main(void) {
int x = 5;
printf ("The value of outer x is %d\n", x);
{
int x = 10;
printf ("The value of inner x is %d\n", x);
}
printf ("The value of the outer x is %d\n", x);
return 0;
}
The value of outer x is 5.
The value of inner x is 10.
The value of outer x is 5.
Also C does have block structure with respect to variables.
This means that inside a block (remember that a block is a bunch of
statements surrounded by {}) you can define a new variable
with the same name as the old one.
These two variables are
For example, the program on the right produces the output shown.
Remark: The gcc compiler for C does permit one to define a function inside another function. These are called nested functions. Some consider this gcc extension to be evil; we will not use it.
Note that we have used nested blocks many times without calling them out. Specifically, when you use {} to group the body of a for loop or the then portion of an if-then-else these also are blocks since they are enclosed by {}.
Homework: Write a C function int odd (int x) that returns 1 if x is odd and returns 0 if x is even. Can you do it without an if statement?
Static and external variables are, by default, initialized to zero. Automatic i.e., non-static, internal variables (the only kind left) are not initialized by default.
As in Java, you can write int X=5-2;. For external or static scalars, that is all you can do.
int x=4; int y=x-1;
For automatic, internal scalars the initialization expression can involve previously defined values as shown on the right (even function calls are permitted).
int BB[8] = {4,9,2}
int AA[] = {3,5,12,7};
char str[] = "hello";
char str[] = {'h','e','l','l','o','\0'}
You can initialize an array by giving a list of initializers as shown on the right.
The same as Java.
Normally, before the compiler proper sees your program, a utility called the C preprocessor is invoked to include files and perform macro substitutions.
#include <filename> #include "filename"
We have already discuss both forms of file inclusion.
In both cases the file mentioned is textually inserted at the point
of inclusion.
The difference between the two is that the first form looks for
filename in a system-defined standard place
;
whereas, the second form first looks in the current directory.
#define MAXLINE 20 #define MULT(A, B) ((A) * (B)) #define MAX(X, Y) ((X) > (Y)) ? (X) : (Y) #undef getchar
We have already used examples of macro substitution similar to the first line on the right. The second line, which illustrates a macro with arguments is more interesting.
Without all the parentheses on the RHS, the MULT macro
would still be legal, but would (sometimes) give the wrong answers.
Question: Why?
Answer: Consider MULT(x+4, y+3)
Note that macro substitution is not the same as a function call (with standard call-by-value or call-by-reference semantics). Even with all the parentheses in the third example you can get into trouble since MAX(a++,5) can increment a twice. If you know call-by-name from algol 60 fame, this will seem familiar.
We probably will not use the fourth form. It is used to un-define a macro from a library so that you can write another version.
There is some fancy stuff involving # in the RHS of the macro definition. See the book for details; I do not intend to use it.
#if integer-expr ... #elif integer-expr ... #else ... #endif
The C-preprocessor has a very limited set of control flow items. On the right we see how the C
if (cond1) ... else if (cond2) ... else .. end if
construct is written. The individual conditions are simple integer expressions consisting of integers, some basic operators and little else. Perhaps the most useful additions are the preprocessor function defined(name), which evaluates to 1 (true) if name has been #define'd, and the ! operator, which converts true to false and vice versa.
#if !defined(HEADER22) #define HEADER22 // The contents of header22.h // goes here #endif
We can use defined(name) as shown on the right to ensure that a header file, in this case header22.h, is included only once.
Question: How could a header file be included
twice unless a programmer foolishly wrote the same #include
twice?
Answer: One possibility is that a user might
include two systems headers h1.h and h2.h each of
which includes h3.h.
Two other directives #ifdef and #ifndef test whether a name has been defined. Thus the first line of the previous example could have been written ifndef HEADER22.
#if SYSTEM == MACOS
#define HDR "macos.h"
#elsif SYSTEM == WINDOWS
#define HDR "windows.h"
#elsif SYSTEM == LINUX
#define HDR "linux.h"
#else
#define HDR "empty.h"
#endif
#include HDR
On the right we see a slightly longer example of the use of preprocessor directives. Assume that the name SYSTEM has been set to the name of the system on which the current program is to be run (not compiled). Assume also that individual header files have been written for macos, windows, and linux systems. Then the code shown will include the appropriate header file.
Note: The quotes used in the various #defines for HDR are not required by #define, but instead are needed by the final #include.
public class X {
int a;
public static void main(String args[]) {
int i1;
int i2;
i1 = 1;
i2 = i1;
i1 = 3;
System.out.println("i2 is " + i2);
X x1 = new X();
X x2 = new X();
x1.a = 1;
x2 = x1; // NOT x2.a = x1.a
x1.a = 3;
System.out.println("x2.a is " + x2.a);
}
}
Pointers are a big difference between Java and C. You can read chapter 2 of Dive into Systems for another account of C pointers.
Much of the material on pointers has no explicit analogue in Java; it is there kept under the covers. If in Java you have an Object obj, then obj is actually what C would call a pointer. The technical term is that Java has reference semantics for all objects. In C this will all be quite explicit
To give a Java example, look at the snippet on the right. The first part works with integers. We define 2 integer variables; initialize the first; set the second to the first; change the first; and print the second. Naturally, the second has the initial value of the first, namely 1.
The second part deals with X, a trivial class, whose objects have just one data component, an integer called a. We mimic the above algorithm. We define two X's and work with their integer field (a). We then proceed as above: initialize the first integer field; set the second to the first; change the first; and print the second. The result is different from the above! In this case the second has the altered value of the first, namely 3.
The key difference between the two parts is that (in Java) simple scalars like i1 have value semantics; whereas objects like x1 have reference semantics. But enough Java, we are interested in C.
You will learn later this semester and again in 202, that the OS finagles memory in ways that would make Bernie Madoff smile. But, in large part thanks to those shenanigans, user programs can have a simple view of memory. For us C programmers, memory is just a large array of consecutively numbered locations.
The machine model we will use in this course is that the fundamental unit of addressing is a byte and a character (a char) exactly fits in a byte. Other types like short, int, double, float, long normally take more than one byte, but always a consecutive range of bytes.
One consequence of our memory model is that associated with int z=5; are two numbers. The first number is the address of the location in which z is stored. The second number is the value stored in that location; in this case that value is 5. The first number, the address, is often called the lvalue; the second number, the contents, is often called the rvalue. Why l and r? I know we did this already; I think it is worth repeating.
Consider
z = z + 1;
To evaluate the right hand side (RHS) we need to add 5 to 1.
In particular, we need the value contained in the memory location
assigned to z, i.e., we need 5.
Since this value is what is needed to evaluate the RHS of an
assignment statement it is called an rvalue.
Then we compute 6=5+1. Where should we put the 6? We look at the LHS and see that we put the 6 into z; that is, into the memory location assigned to z. Since it is the location that is needed when evaluating a LHS, the address is called an lvalue.
Start Lecture #04
As we have just seen, when a variable appears on the LHS, its lvalue or address is used. What if we want the address of a variable that appears on the RHS; how do we get it?
In a language like Java the answer is simple; we don't.
In C we use the unary operator & and write p=&x; to assign the address of x to p. After executing this statement we say that p points to x or p is a pointer to x. That is, after execution, the rvalue of p is the lvalue of x. In other words the value of p is the address of x.
int x=13;
Look at the declarations on the right. x is familiar; it is an integer variable initially containing 13. Specifically, the rvalue of x is (initially) 13. What about the lvalue of x, i.e., the location in which the 13 is stored? It is not an int; it is an address into which an int can be stored. Alternately said it is pointer to an int.
The unary prefix operator & produces the address of a variable, i.e., &x gives the lvalue of x, i.e. it gives a pointer to x.
The unary operator * does the reverse action. When * is applied to a pointer, it gives the object (object is used in the English not OO sense) pointed to. The * operator is called the dereferencing or indirection operator.
int x=13; int *p = &x;
Now look at the declaration of p on the right. It says that p is the kind of thing, that when you apply * to it you get an int, i.e., p is a pointer to an int. That is why we can initialize p to &x.
Note: Try to avoid the common error of thinking the second line on the right initializes *p to &x. It doesn't. It declares and initializes p not *p.
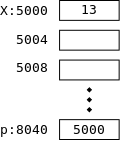
On the right we show how p and x might be stored in memory. After we finish with C we will study the memory model in more detail. Here I just give enough to understand that pointers like p are also variables that are stored just like ints, floats, and chars.
The basic storage unit on modern computers is a byte. We shall assume that a char fits perfectly in a byte. However, ints, floats, and pointers are bigger. Each requires several bytes. For today assume each is 4 bytes.
In the diagram on the right x happens to be stored in locations 5000-5003 (i.e., each box is 4 bytes). x has value 13; more precisely its rvalue is 13. Since the address of x is 5000, the lvalue of x is 5000.
The integer pointer p happens to be stored in 8040-8043; i.e., its address or lvalue happens to be 8040. Since p points to x, the rvalue of p equals the lvalue of x, which is 5000.
// part one of three int x=1; int y=2; int z[10]; int *ip; int *jp; ip = &x;
Consider the code sequence on the right (part one). The first 3 lines we have seen many times before; the next three are new. Recall that in a C declaration, all the doodads around a variable name tell you what you must do to the variable to get the base type at the beginning of the line. Thus the fourth line says that if you dereference ip (i.e., if you look at the contents of the address in ip, not of ip), you get an integer. Common parlance is to call ip an integer pointer (which is why I named it ip). Similarly, jp is another integer pointer.
At this point both ip and jp are uninitialized. The last line sets ip to the address, of x. Note that the types match, both ip and &x are pointers to an int.
// part two of three y = *ip; // L1 *ip = 0; // L2 ip = &z[0]; // L3 *ip = 0; // L4 jp = ip; // L5 *jp = 1; // L6
In part two, L1 sets y=1 as follows: ip now points to x, * does the dereference so *ip is x. Since we are evaluating the RHS, we take the contents not the address of x and get 1.
L2 sets x=0;. The RHS is clearly 0. Where do we put this zero? Look at the LHS: ip currently points to x, * does a dereference so *ip is x. Since we are on the LHS, we take the address and not the contents of x and hence we put 0 into x.
L3 changes ip; it now points to z[0]. So L4 sets z[0]=0;
Pointers can be used without the deferencing operator. L5 sets jp to ip. Since ip currently points to z[0], jp now does as well. Hence L6 sets z[0]=1;
// part three of three ip = &x; // L1 *ip = *ip + 10; // L2 y = *ip + 1; // L3 *ip += 1; // L4 ++*ip; // L5 (*ip)++; // L6 *ip++; // L7
Part three begins by re-establishing ip as a pointer to x so L2 increments x by 10 and L3 sets y=x+1;.
L4 increments x by 1 as does L5 (because the unary operators ++ and * are right associative).
L6 also increments x, but L7 does not.
By right associativity we see that the increment precedes the
dereference, so the pointer is incremented (not the pointee
).
The full story awaits section 5.4
below.
void bad_swap(int x, int y) {
int temp;
temp = x;
x = y;
y = temp;
}
The program on the right is what a novice programer just learning C (or Java) would write. It is supposed to swap the two arguments it is called with. However, it fails due to call by value semantics for function calls in C.
When another function calls swap(a,b) the values of the arguments a and b are transmitted to the parameters x and y and then swap() interchanges the values in x and y. But when swap() returns, the final values in x and y are NOT transmitted back to the arguments: a and b are unchanged.
But functions that change the values of their arguments are useful! We won't give them up without a fight.
Actually, what is needed is to be able to change the value of
variables used in the caller (even if some related
variables
become the arguments) and that distinction is the key.
Just because we want to swap the values of a
and b, doesn't mean the arguments have to be literally
a and b.
void swap(int *px, int *py) {
int temp;
temp = *px;
*px = *py;
*py = temp;
}
The program on the right has two parameters px and py each of which is a pointer to an integer (*px and *py are the integers). Since C is a call-by-value language, changes to the parameters, which are the pointers px and py would not result in changes to the corresponding arguments. But the program on the right doesn't change the pointers at all, instead it changes the values they point to.
Since the parameters are pointers to integers, so must be the
arguments.
A typical call to this function would be
int A=10,B=20; swap(&A,&B);
It is crucial to understand, how this call results in A becoming 20, the value previously in B, and B becoming 10, the value previously in A.
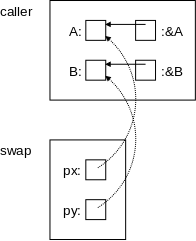
On the right is a pictorial explanation.
A has a certain address.
&A equals
that address (more precisely the
rvalue of &A = the lvalue of A).
Similarly for py, &B, and B.
These are shown by the solid arrows in the diagram.
The call swap(&A,&B) copies (the rvalue of) &A into (the rvalue of) the first parameter, which is px. Similarly for &B and the second parameter, py. These are shown by the dotted arrows. Thus the value of px is the address of A, which is indicated by the arrow. Again, to be pedantic, the rvalue of px equals the rvalue of &A, which equals the lvalue of A. Similarly for py, &B, and B.
Swapping px with py would change the dotted arrows, but would not change anything in the caller. However, we don't swap px with py; instead we swap *px with *py. That is, we dereference the pointers and swap the things pointed to! This subtlety is the key to understanding the effect of many C functions. It is crucial.
Homework: Write rotate3(A,B,C) that sets A to the old value of B, sets B to old C, and C to old A.
Homework: Write plusminus(x,y) that sets x to old x + old y and sets y to old x - old y.
Start Lecture #05
#include <stdio.h> #define BUFSIZE 100 char buf[BUFSIZE]; int bufp = 0; int getch(void); void ungetch(int); int getint(int *pn);
int getch(void) { return (bufp>0) ? buf[--bufp] : getchar(); }
void ungetch(int c) { if (bufp >= BUFSIZE) printf("ungetch: too many chars\n"); else buf[bufp++] = c; }
#include <stdio.h> #include <ctype.h> int getint(int *pn) { int c, sign; while (isspace(c=getch())) ; if (!isdigit(c) && c!=EOF && c!='+' && c!='-') { ungetch(c); return 0; } sign = (c=='-') ? -1 : 1; if (c=='+' || c=='-') c = getch(); for (*pn = 0; isdigit(c); c=getch()) *pn = 10 * *pn + (c-'0'); *pn *= sign; if (c != EOF) ungetch(c); return c; }
The program pair getch() and ungetch() generalize getchar() by supporting the notion of unreading a character, i.e., having the effect of pushing back several already read characters.
Note that ungetch() is careful not to exceed the size of the buffer used to stored the pushed back characters. Remember that the C compiler does not generate run-time checks that prevent you from accessing an array beyond its bound. As mentioned previously, a number of break ins had been enabled by the lack of such checks in library programs.
Also shown is getint(), which reads an integer from standard input (stdin) using getch() and ungetch().
getint() returns the integer read via a parameter. As we have seen the new value of a parameter is not passed back to the caller. Hence, getint() uses the pointer/address business we just saw with swap().
Specifically any change made to pn by getint() would be invisible to the caller. However, getint() changes *pn; a change the caller does see.
The value returned by the function itself is the status: zero means the next characters do not form an integer, EOF (which is negative) means we are at the end of file, positive means an integer has been found.
Briefly the program works as follows.
Skip blanks
Check for legality
Determine sign
Evaluate number
one digit at a time
Although short, the program is not trivial. Indeed, there are some details to note.
123(no newline at the end), it will set *pn=123 as desired but will return EOF. I suspect that most programs using getint() will, in this case, ignore *pn and just treat it as EOF.
If you were asked to produce a getint() function you would have three tasks.
The third is clearly the easiest task. I suspect that the first is the hardest.
Homework: 5-1. As written, getint() treats a + or - not followed by a digit as a valid representation of zero. Fix it to push such a character back on the input.
> Hi, > > Many students have submitted CIMS acount requests because they are > enrolled in UA.0201-005. This is just a heads up that I am rejecting > all of these in the request system since the class accounts should be > made directly by the systems staff with use of the class roster. This > is Allan Gottlieb's class so I am copying in case he hasn't yet formally > requested class accounts for all his students. > > Best, > Stephanie Hi Stephanie, Thanks for the heads up. Indeed, Allan has requested class accounts for his students in this course, and they have been created by us based on the roster. Allan, in case you don't have it, you may point any student who is unsure of their account status to this link, where they may view their current status and reset their password if desired: https://cims.nyu.edu/webapps/password/reset Thanks, Aric
In C pointers and arrays are closely related. As the book says
Any operation that can be achieved by array subscripting can also be done with pointers.
The authors go on to say
The pointer version will in general be faster but, at least to the uninitiated, somewhat harder to understand.
The second clause is doubtless correct; but perhaps not the first. Remember that the 2e was written in 1988 (1e in 1978). Compilers have improved considerably in the past 30+ years and, I suspect, would turn out nearly as fast code for many of the array versions.
The next few sections present some simple examples using pointers.
int a[5], *pa; pa = &a[0];
int x = *pa; x = *(pa+1);
x = a[0]; x = *a;
int i; x = a[i]; x = *(a+i);
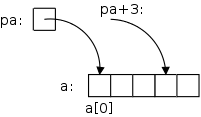
On the far right we see some code involving pointers and arrays. After the first two lines are executed we get the diagram shown on the near right. pa is a pointer to the first element of the array a. Remember that, as in Java, the first element of a C array a is a[0]. Similarly, pa+3 is a pointer to the fourth element of the array.
But note that pa+3 is just an expression and not a container (no lvalue): you can't put another pointer into pa+3 just like you can't put another integer into i+3.
The next line sets x (which is a container) equal to (the rvalue of) a[0]; the line after that sets x=a[1].
Then we explicitly set x=a[0].
The line after that has the same effect! That is because in C the value of array name equals the address of its first element. (The rvalue of a = the rvalue of &a[0] = the address of a[0] = the lvalue of a[0].) Again note that a (i.e., &a[0]) is an expression, not a variable, and hence is not a container.
Said yet another way a and pa have the same value
(rvalue) but are not the same thing
!
Similarly, the last two lines each have the same effect, this time for a general element of the array a[i].
int a[5], *pa; pa = &a[0]; pa = a; a = pa; // illegal &a[0] = pa; // illegal
Both pa and a are pointers to ints. In particular a is defined to be &a[0]. Although pa and a have much in common, there is an important difference: pa is a variable, its value can be changed; whereas &a[0] (and hence a) is an expression and not a variable. In particular the last two lines on the right are illegal.
Another way to say this is that &a[0] is not an lvalue.
This is similar to the legality of x=y+5;
versus the
illegality of y+5=x;
int mystrlen(char *s) {
int n;
for (n=0; *s!='\0'; s++,n++) ;
return n;
}
The code on the right illustrates how well C pointers, arrays, and strings work together. What a tiny program to find the length of an arbitrary string!
Note that the body of the for loop is null; all the work is done in the for statement itself.
char str[50], *pc;
// calculate str and pc
mystrlen(pc);
mystrlen(str);
mystrlen("Hello, world.");
Note the various ways in which mystrlen() can be called.
decoratea variable with enough stuff to obtain one of the primitive types.
#include <stdio.h>
int x, *p;
int main () {
p = &x;
x = 12;
printf("p = %p\n", p);
printf("*p = %d\n", *p);
p++;
printf("p = %p\n", p);
printf("*p = %d\n", *p);
}
The example on the right below illustrates well the difference between a variable, in this case x, and its address &x. The first value printed is the address of x. This is not 12. Instead, it is some (probably large) number that happens to be the address of x.
In fact when run on my laptop the program produced the following output.
p = 0x7fc41fc78040 *p = 12 p = 0x7fc41fc78044 *p = 0
Let's go over this 7-line main() function line by line.
next integer after xis printed. But there is no integer after x. Hence the program is erroneous! Its output in unpredictable!
Note: Incrementing p does not increment x. Instead, the result is that p points to the next integer after x. In this program there is no further integer after x, so the result is unpredictable and the program is erroneous. Specifically, the value of *p is now unpredictable. On my system the value of *p was 0, but that can NOT be counted on. If, instead of pointing to x, we had p point to A[7] for some large int array A, then the last line would have printed the value of A[8] and the penultimate line would have printed the address of A[8].
Remarks:
#include <stdio.h>
int mystrlen (char *s);
int main () {
char stg[] = "hello";
printf ("The string %s has %d characters\n",
stg, mystrlen(stg));
}
int mystrlen (char s[]) {
int i;
for (i = 0; s[i] != '\0'; i++) ;
return i;
}
int mystrlen (char *s) {
int i = 0;
while (*s++ != '\0')
i++;
return i;
}
On the right we show two versions of a string length function. The first version uses array notation for the string; the second uses pointer notation. The main() program is identical for the two versions so is shown only once.
Note how very close the two string length functions are. This is another illustration of the similarity of arrays and pointers in C.
Note the two declarations
int mystrlen (char *s); int mystrlen (char s[]);
They are used 3 times in the code on the right. In C these two declarations are equivalent. Changing any or all of them to the other form does not change the meaning of the program.
I realize an array does not at first seem the same as a pointer. Remember that the array name itself is equal to a pointer to the first element of the array. Hence declaring
float a[5], *b;
results in a and b having the same type (pointer to float). But the array a has additionally been defined; that is, space for 5 floats has been allocated. Hence a[3] = 5; is legal. b[3] = 5 is syntactically legal, but may be semantically invalid and abort at runtime, unless b has previously be set to point to sufficient space.
In the pointer version of mystrlen() we encounter a common C idiom *s++. First note that the precedence of the operators is such that *s++ means *(s++). That is, we are moving (incrementing) the pointer and examining what it used to point at. We are not incrementing a part of the string. Specifically, we are not executing (*s)++;
void changeltox (char *s) {
while (*s != '\0') {
if (*s == 'l')
*s = 'x';
s++;
}
}
The program on the right loops through the input string and replaces each occurence of l with x.
The while loop and increment of s could have been combined into a for loop.
This version is written in pointer style.
Homework: Rewrite changeltox() to use array style and a for loop.
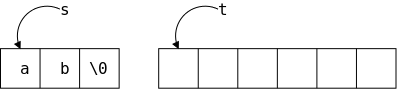
void mystrcpy (char *t, char *s) {
while ((*t++ = *s++) != '\0') ;
}
Check out the ONE-liner on the right. Note especially the use of standard idioms for marching through strings and for finding the end of the string.
Slick, very slick!
Even slicker is to note that '\0' has value 0 and testing != 0 is
just testing so the while statement is equivalent to
while (*t++ = *s++);
But the program is scary, very scary!
Question: Why is it scary?
Answer: Because there is no length check.
If the character array t (or equivalently the block of characters t points to) is smaller than the character array s, then the copy will overwrite whatever happens to be located right after the array t.
The lack of such length checks has permitted a number of security breaches.
double f(int *a); double f(int a[]);
The two lines on the right are equivalent when used as a function declaration (or, with the semicolon replaced by a {, as the head line of a function definition). The authors say they prefer the first. For me it is not so clear cut. In mystrlen() above I would indeed prefer char *s as written since I think of a string as a block of chars with a pointer to the beginning.
double dotprod(double A[], double B[]);
However, if I were writing an inner product routine (a.k.a. dot product), I would prefer the array form as on the right since I think of dot product as operating on vectors.
But of course, more important than which one I prefer or the authors prefer, is the fact that they are equivalent in C.
Note: The definition
int a[10];
reserves space for 10 ints and no
pointers; whereas the definition
int *a;
reserves space for no ints and
1 pointer.
#include <stdio.h> void f(int *p);
int main() { int A[20]; // initialize all of A f(A+6); return 0; }
void f(int *p) { printf("legal? %d\n", p[-2]); printf("legal? %d\n", *(p-2)); }
In the code on the right, main() first declares an integer array A[] of size 20 and initializes all its members (how the initialization is done is not important). Then main(), in a effort to protect the beginning of A[], passes only part of the array to f(). Remembering that A+6 means (&A[0])+6, which is &A[6], we see that f() receives a pointer to the 7th element of the array A.
The author of main() mistakenly believed that A[0],..,A[5] are hidden from f(). Let's hope this author is not on the security team for the board of elections.
Since C uses call by value, we know that f() cannot change the value of the pointer A+6 in main(). But f() can use its copy of this pointer to reference or change all the values of A, including those before A[6]. On the right, f() successfully references A[4].
It naturally would be illegal for f() to reference (or worse change) p[-9].
Start Lecture #06
A important point is that, given the declaration int *pa; the increment pa+=3 does not simply add three to the address stored in pa. Instead, it increments pa so that it points 3 integers further forward (since pa is a pointer to an integer). If pc is a pointer to a double, then pc+3 increments pc so that it points 3 doubles forward.
#include <stdio.h>
void main (void) {
int q[] = {11, 13, 15, 19};
int *p = q; // initializes p NOT *p
printf("*p = %d\n", *p);
printf("*p++ = %d\n", *p++);
printf("*p = %d\n", *p);
printf("*++p = %d\n", *++p);
printf("*p = %d\n", *p);
printf("++*p = %d\n", ++*p);
}
To better understand pointers, arrays, ++, and *, let's go over the code on the right line by line. For reference the precedence table is here. The output produced is
*p = 11 *p++ = 11 *p = 13 *++p = 15 *p = 15 ++*p = 16
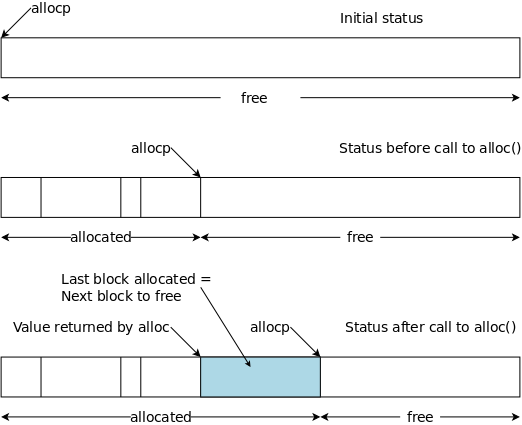
#define ALLOCSIZE 15000 static char allocbuf[ALLOCSIZE]; static char *allocp = allocbuf;
char *alloc(int n) { if (allocp+n ≤ allocbuf+ALLOCSIZE) { allocp += n; return allocp-n; // previous value } else // not enough space return 0; }
void afree (char *p) { if (p>=allocbuf && p<allocbuf+ALLOCSIZE) allocp = p; }
On the right is a primitive storage allocator and freer, alloc() and afree(). This pair of routines distributes and reclaims memory from a buffer allocbuf. The internal pointer allocp points to the boundary between already allocated memory (on the left of allocp in the diagrams) and memory still available for allocation (on the right).
The top picture shows the initial state: nothing is allocated; everything is free.
Looking at the middle (before) diagram we see four blocks that have been allocated and a large free region on the right. The routines alloc() and afree control the internal pointer allocp.
When alloc(n) is called, with a non-negative integer argument, it returns a pointer to a block of n characters and then moves allocp to the right, indicating that these n characters are no longer available.
When afree(p) is called with the pointer returned by alloc(), it resets the state of alloc()/afree() to what it was before the call to alloc().
A very strong assumption is being made that calls
to alloc()/afree() are executed in a stack-like manner, i.e.,
the routines assume that a block being freed is
the
These routines would be useful for managing storage for C automatic, local variables. They are far from general. The standard library routines malloc()/free() do not make this assumption and as a result are considerably more complicated.
Since pointers, not array positions are communicated to users of alloc()/afree(), these users do not need to know the name of the array, which is kept under the covers via static.
Notes:
no object. Although a literal 0 is permitted; most programmers use NULL.
Homework: What is wrong with the following calls to alloc() and afree()? Assume that ALLOCSIZE is big enough.
char *p1, *p2, *p3; p1 = alloc(10); p2 = alloc(20); p3 = alloc(15); afree(p3); afree(p1); afree(p2);
If pointers p and q point to elements of the same array (or string), then comparisons between the pointers using <, <=, ==, !=, >, and >= all work as expected.
If pointers p and q do not point to members of the same array, the value returned by comparisons is undefined, with one exception: p pointing to an element of an array and q pointing to the first element past the array.
Any pointer can be compared to 0 via == and !=.
Normally,
Again we need p and q pointing to elements of the same array. In that case, if p<=q, then q-p+1 equals the number of elements from p to q (including the elements pointed to by p and q).
#include <stdio.h> void changeltox(char *z); void mystrcpy char *s, char *t); char *alloc(int n);
int main() { char string[] = "hello"; char *string2 = alloc(6); mystrcpy(string2, string); changeltox(string); printf ("String is now %s\n", string); printf ("String2 is now %s\n", string2); }
These examples are interesting in their own right, beyond showing how to use the allocator.
We have already written a program changeltox() that changes one character to another in a given string.
After initializing the string to "hello", the code on the right first copies it (using mystrcpy(), a one liner presented above) and then makes changes in the original. Thus, at the end, we have two versions of the string: the before and the after.
As expected the output is
String is now hexxo String2 is now hello
So far, so good. Let's try something fancier.
Recall the danger warning given with the code for mystrcpy(char *x, char *y): The code copies all the characters in y (i.e., up to and including '\0') to x ignoring the current length of x. Thus, if y is longer than the space allocated for x, the copy will overwrite whatever happens to be stored right after x.
#include <stdio.h>
void changeltox (char*);
void mystrcpy (char *s, char *t);
char *alloc(int n);
int main () {
char string[] = "hello";
char *string2 = alloc(2);
char *string3 = alloc(6);
mystrcpy (string2, string);
printf ("String2 is now %s\n", string2);
printf ("String3 is now %s\n", string3);
mystrcpy (string3, string);
changeltox (string);
printf ("The string is now %s\n", string);
printf ("String2 is now %s\n", string2);
printf ("String3 is now %s\n", string3);
}
The example on the right illustrates the danger. When the code on the right is compiled with the code for changeltox(), mystrcpy(), and alloc(), the following output occurs.
String2 is now hello String3 is now llo The string is now hexxo String2 is now hehello String3 is now hello
What happened?
The string in string contains the 5 characters in the word
hello
plus the ascii null '\0' to end the string.
(The array string has 6 elements so the string fits
perfectly.)
The major problem occurs with the first execution of
mystrcpy() because we are copying 6 characters into a
string that has room for only 2 characters (including the ascii
null).
This executes flawlessly
copying the 6 characters to an area
of size 6 starting where string2 points.
These 6 locations include the 2 slots allocated to string2
and then the next four locations.
Normally it is very hard to tell what has been overwritten, and the
resulting bugs can be very difficult to find.
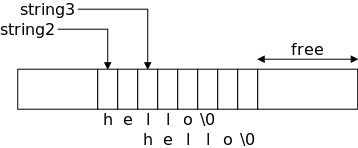
In this situation it is not hard to see what was overwritten since
we know how alloc() works.
The excess
6-2=4 characters are written into the first 4
slots of string3.
When we print string2 the first time we see no problem!
A string pointer just tells where the string starts, it continues up
to the ascii null.
So string2 does have all of hello
(and the
terminating null).
Since string3 points 2 characters after string2,
the string string3 is just the substring
of string2 starting at the third character.
The second mystrcpy copies the six(!) characters in the
string hello
to the 6 bytes starting at the location pointed
to by string3.
Since the string string2 includes the location pointed to by
string3, both string2 and string3 are
changed.
The changeltox() execution works as expected.
As we know, C does not have string variables, but does have string constants. This arrangement sometimes requires care to avoid errors.
char amsg[] = "hello";
char *msgp = "hello";
int main () {...}
Let's see if we can understand the following rules, which can appear strange at first glance.
Perhaps the following will help.
void mystrcpy (char *s, char *t) {
while (*s++ = *t++) ;
}
Our first version of this program tested if the assignment did not return the character '\0', which has the value 0 (a fact about ascii null). However checking if something is not 0 is the same (in C) as asking if it is true. Finally, testing if something is true is the same as just testing the something. The C rules can seem cryptic, but they are consistent.
If you have been trembling with fright over this scary function, rest assured and see the following homework problem.
Homework: 5-5 (first part). Write a version of the library functions
char *strncpy(char *s, char *t, int n)
This copies at most n characters
from t to s.
This code is not scary like other copies since a user of the
routine can simply declare s to have space
for n characters.
int mystrlen(char *s) {
char *p = s;
while (*p)
p++;
return p-s;
}
The code on the right applies the technique used to get the slick string copy to the related function string length. In addition it uses pointer subtraction. Note that when the return is executed, p points just after the string (i.e., to the terminating null) and s points to its beginning. Thus the difference gives the length.
Normally, pointer subtraction is defined only when both pointers point to the same array or string (or some other objects we haven't studied yet). The point is that you cannot meaningfully subtract two pointers pointing to different objects (say both point to different integer variables). One exception is that subtraction is guaranteed to work if one points to an element of an array and the other points one element past that same array. The function mystrlen() does not utilize this exception since the terminating null is part of the string.
int mystrcmp(char *s, char *t) {
for (; *s == *t; s++,t++)
if (*s == '\0')
return 0;
return *s - *t;
}
We next produce a string comparison routine that returns a negative integer if the string s is lexicographically before t, zero if they are equal, and a positive integer if s is lexicographically after t.
The loop takes care of equal characters. The function returns 0 if we reached the end of the equal strings.
If the loop concludes early, we have found the first difference.
A key is that if exactly one string has ended, its character ('\0')
is smaller
then the other string's character.
This is another ascii fact (ascii null is zero. the rest are
positive).
I tried to produce a version using while(*s++ == *t++), but I failed since the loop body and the post loop code was dealing with the subsequent character. I suppose it could have been forced to work if I used a bunch of constructions like *(s-1), but that would have been ugly.
For the moment forget that C treats pointers and arrays almost the same. For now just think of a character pointer as another data type.
So we can have an array of 9 character pointers, e.g., char *A[9]. (Note that it is not a pointer to an array of 9 characters.) We shall see fairly soon that this is exactly how some systems (e.g. Unix) transmit command-line arguments to the main() function.
#include <stdio.h>
int main() {
char *STG[3] = { "Goodbye", "cruel", "world" };
printf ("%s %s %s.\n", STG[0], STG[1], STG[2]);
STG[1] = STG[2] = STG[0];
printf ("%s %s %s.", STG[0], STG[1], STG[2]);
return 0;
}
Goodbye cruel world.
Goodbye Goodbye Goodbye.
The code on the right defines an array of 3 character pointers, each of which is initialized to (point to) a string. The first printf() has no surprises. But the assignment statement should fail since we allocated space for three strings of sizes 8, 6, and 6 and now want to wind up with three strings each of size 8 and we didn't allocate any additional space.
However, it works perfectly and the resulting output is shown as well.
Question: What happened?
How can space for 8+6+6 characters be enough for 8+8+8?
Answer: We do not have three strings
of size 8.
Instead, we have one string of size 8, with three character pointers
pointing to it.
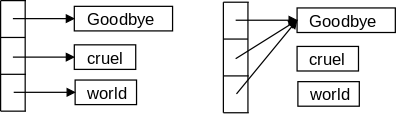
The picture on the right shows a before and after view of the array and the strings.
This suggests and interesting possibility. Imagine we wanted to sort long strings alphabetically (really lexicographically). Let's not get bogged down in the sort itself and assume it is a simple interchange sort that loops and, if a pair is out of order, executes a swap, which is something like
temp = x; x = y; y = temp;
If x, y, and temp are (long but varying size) strings then we have some issues to deal with.
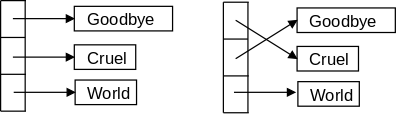
Both of these issues go away if we maintain an array of pointers to the strings. If the string pointed to by A[i] is out of order with respect to the string pointed to by A[j], we swap the (fixed size, short) pointers not the strings that they point to.
This idea is illustrated on the right.
The code on the right below, plus the mystrcmp() function above, produces the output on the left.
#include <stdio.h>
void sort(int n, char *C[]) {
int i,j;
char *temp;
for (i=0; i<n-1; i++)
for (j=i+1; j<n; j++)
if (mystrcmp(C[i],C[j]) > 0) {
temp = C[i];
C[i] = C[j];
C[j] = temp;
}
}
int main() {
char *STG[] = {"Hello","99","3","zz","best"};
int i,j;
for (i=0; i<5; i++)
printf ("STG[%i] = \"%s\"\n", i, STG[i]);
sort(5,STG);
for (i=0; i<5; i++)
printf ("STG[%i] = \"%s\"\n", i, STG[i]);
return 0;
}
STG[0] = "Hello" STG[1] = "99" STG[2] = "3" STG[3] = "zz" STG[4] = "best" STG[0] = "3" STG[1] = "99" STG[2] = "Hello" STG[3] = "best" STG[4] = "zz"
You might feel that the sort fails due to call-by-value the same way bad_swap failed previously. Since call-by-value initially copies the arguments into the parameters, but does not, at the end, copy the parameters back to the arguments, swapping C[I] with C[j] has no effect since the parameters C[i] and C[j] are not copied back. But no, C[i] is not a parameter, the array C is the parameter and C[i] is pointed to by C. Yes, this is subtle; but it is also crucial!
You might question if the output is indeed sorted. For example, we remember that ascii '3' is less than ascii '9', and we know that in ascii 'b'<'h'<'z', but why is '9'<'b' and why is 'H'<'b'?
Well, I don't know why they are, but they are. That is, in ascii the digits come before the capital letters, which in turn come before the lower-case letters.
#include <stdio.h>
int main(int argc, char *argv[]) {
char c1 = '1', c2 = '2';
char ac[10] = "wxyXYZ"; // ac = Array of Chars
ac[1] = c1;
ac[2] = c2;
printf("ac[1]=%c ac[2]=%c\n", ac[1], ac[2]);
char *pc1, *pc2; // pc = Pointer to Char
pc1 = &ac[3];
pc2 = pc1+1;
printf("*pc1=%c *pc2=%c\n", *pc1, *pc2);
char *apc[10]; // Array of Pointers to Char
apc[3] = pc1; // Points at ac[3]
apc[4] = pc2-2; // Points at ac[2]
printf("*apc[3]=%c *apc[4]=%c\n", *apc[3], *apc[4]);
return 0;
}
The program on the right includes several types of variables. In particular we find chars, an array of chars, pointers to chars, and an array of pointers to chars.
The program, when run, produces the following output.
ac[1]=1 ac[2]=2 *pc1=X *pc2=Y *apc[3]=X *apc[4]=2
You should first confirm that the types are correct. For example, is * always applied to a pointer? Since all the prints use %c for the values printed, all those values must be chars. Are they?
Then confirm that you agree with the values produced.
At one point the program adds 1 to the char pointer pc1. At another point it subtracts 2 from another char pointer. This is valid only if the final value of the pointer is pointing inside the same array as the initial value (or to one location past the end of the array). Is this the case?
Start Lecture #07
void matmul(int n, int k, int m, double A[n][k],
double B[k][m], double C[n][m]) {
int i,j,l;
for (i=0; i<n; i++)
for (j=0; j<m; j++) {
C[i][j] = 0.0;
for (l=0; l< k; l++)
C[i][j] += A[i][l]*B[l][j];
}
}
C does have normal multidimensional arrays. For example, the code on the right multiplies two matrices. Matrices (the simple 2-dimensional type in linear algebra) are rectangular: all rows have the same number of columns.
In some sense C, like Java, has only one-dimensional arrays. However, a one-dimensional array of one-dimensional arrays of doubles is close to a two-dimensional array of doubles. One difference is the notation: C/Java uses A[][], indicating a 1D array of 1D arrays, rather than A[,] of algebra. Another difference is that, in the example on the right, A[j] is a legal (one-dimensional) array (of size k) if 0≤j<n.
The biggest difference is that a C/Java 2D array need not be rectangular, that is the rows need not be the same length. This will become clear in the next few sections.
int A[2][3] = { {5,4,3}, {4,4,4} };
int B[2][3][2] = { { {1,2}, {2,2}, {4,1} },
{ {5,5}, {2,3}, {3,1} } };
Multidimensional arrays can be initialized. Once you remember that a two-dimensional array is a one-dimensional array of one-dimensional arrays, the syntax for initialization exemplified on the right is not surprising.
(C, like most modern languages uses row-major ordering so the last subscript varies the most rapidly.)
#include <stdio.h>
int main(int argc, char *argv[]) {
int A[3][3] = { {1,2,3}, {4,5,6}, {7,8,9} };
printf("*(A[1]+1)=%d\n", *(A[1]+1) );
return 0;
}
Looking at the code on the right we see that A[1] can be thought of as a 1D array so, when written without the second subscript.
char amsg[] = "hello";
int main(int argc, char *argv[]) {
printf("%c\n", amsg[100]);
}
Note: Note that an array of size 1 is similar to an array of size 10 and that a pointer to X is very similar to array of X. For example the code on the right compiles and runs (it is illegal but not caught by the compiler) in part because the types match.
A related comment is that a pointer to a character is the same as a pointer to 10 characters as far as the C compiler is concerned.
char *monthName(int n) {
static char *name[] = {"Illegal",
"Jan", "Feb", "Mar", "Apr",
"May", "Jun", "Jul", "Aug",
"Sep", "Oct", "Nov", "Dec"};
return (n<1 || n>12) ? name[0] : name[n];
}
The initialization syntax for an array of pointers follows the general rule for initializing an array: Enclose the initial values inside braces.
Looking at the code on the right we see this principle in action. I believe the most common usage of pointer arrays is for an array of character pointers as in this example.
Question: How are those initializers pointers;
they look like constant strings?
Answer: A string is a pointer to the first
character.
int A[3][4]; int *B[3];
Consider the two definitions on the right. They look different, but both A[2][3] and B[2][3] are legal (at least syntactically). The real story is that the two definitions most definitely are different. (In fact Java arrays have a great deal in common with the 2nd form in C.)
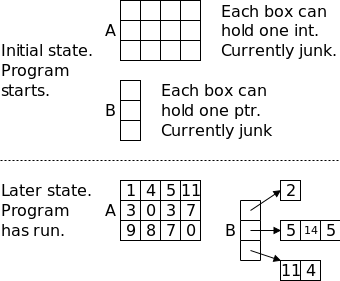
The declaration int A[3][4]; allocates space for 12 integers (really 12 containers each of which can hold an integer), which are stored consecutively so that A[i][j] is (a container holding) the (4*i+j)th integer stored (counting from zero). With the simple declaration written, none of the integers is initialized, but we have seen how to initialized them.
The declaration int *B[3]; allocates space for
NO integers.
It does allocate space for 3 pointers (to
integers).
The pointers are not initialized so they currently point to junk.
The program must somehow arrange for each of them to point to a
group of integers (and must figure out when the group ends).
An important point is that the groups may have different lengths.
The technical jargon is that we can have a ragged array
as
shown in the bottom of the picture.
#include <stdio.h>
int main(int argc, char *argv[]) {
int A[3][3] = { {1,2,3}, {4,5,6}, {7,8,9} };
int B0[1] = {2}, B1[3]={5,14,5}, B2[2] = {11,4};
int *B[3] = {B0, B1, B2};
printf("*(A[1]+1)=%d\n", *(A[1]+1) );
printf("A[1,1]=%d\n", A[1][1] );
printf("*(B[1]+1)=%d\n", *(B[1]+1) );
printf("B[1][1]=%d\n", B[1][1]);
return 0;
}
The code sequence on the right shows the comparison between
initializing a 2-D array of integers and initializing a 1-D array of
pointers to integers.
Note how B is initialized to a 1D array of integer pointers.
The example also illustrates that C supports ragged arrays.
When the program is run the output produced is
*(A[1]+1)=5 A[1][1]=5 *(B[1]+1)=14 B[1][1]=14
Although ragged arrays of Integers (and Floats) are used in C, you are more likely to see a ragged array of chars, that is a 1-D array of pointers to (varying length) strings.
We have already seen two examples of this: The monthName program just above and the Goodbye Cruel World diagrams in section 5.6. We next illustrate that every C main() program on Unix (e.g., on Linux) also uses a (ragged) array of strings, i.e. an array of character pointers.
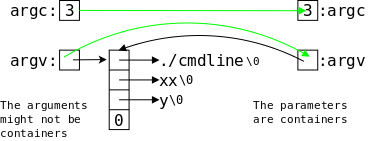
On the right is a picture of how arguments are passed to a (Unix) command. It this case the command executed was
./cmdline xx y;
The arguments generated by the system are shown on the left The green arrows show those arguments being copied into the parameters of the main program. (The black arrows are simply pointers, as before.) Each main() program has two parameters: an integer, normally called argc for argument count, and an array of character pointers, normally called argv for argument vector.
As always, a naked array name is a pointer to the first element. argv in the main() program is best thought of as a pointer that has been initialized to point to the first element of the array of pointers. The diagram makes clear that both arguments, argc and argv, are containers In particular they have lvalues, i.e., they can appear on the LHS of an assignment statement. (Of course, with call-by-value any changes to the parameters are not passed back to the arguments.)
Since the same program can have multiple names (more on that later), argv[0], the first element of the argument vector, is a pointer to a character string containing the name by which the command was invoked. Subsequent elements of argv point to character strings containing the arguments given to the command. Finally, there is a NULL pointer to indicate the end of the pointer array.
The integer argc gives the total number of pointers, including the pointer to the name of the command. Thus, the smallest possible value for argc is 1 and argc=3 for the picture above.
#include <stdio.h>
int main(int argc, char *argv[argc]) {
int i;
printf("My name is %s; ", argv[0]);
printf("I was called with %d argument%s.\n",
argc-1, (argc==2) ? "" : "s");
for (i=1; i<argc; i++)
printf("Argument #%d is %s.\n", i, argv[i]);
}
sh-4.0$ cc -o cmdline cmdline.c
sh-4.0$ ./cmdline
My name is ./cmdline; I was called with 0 arguments.
sh-4.0$ ./cmdline x
My name is ./cmdline; I was called with 1 argument.
Argument #1 is x.
sh-4.0$ ./cmdline xx y
My name is ./cmdline; I was called with 2 arguments.
Argument #1 is xx.
Argument #2 is y.
sh-4.0$ ./cmdline -o cmdline cmdline.c
My name is ./cmdline; I was called with 3 arguments.
Argument #1 is -o.
Argument #2 is cmdline.
Argument #3 is cmdline.c.
sh-4.0$ cp cmdline mary-joe
sh-4.0$ ./mary-joe -o cmdline cmdline.c
My name is ./mary-joe; I was called with 3 arguments.
Argument #1 is -o.
Argument #2 is cmdline.
Argument #3 is cmdline.c.
The code on the right shows how a program can access its name and any arguments it was called with.
Having both a count (argc) and a trailing NULL pointer (argv[argc]==NULL) is redundant, but convenient. The code on the right treats argv as an array. It loops through the array using the count argc as an upper bound, but does not make use of the trailing NULL. Another style (using NULL but not argc) would look something like
while (*argv)
printf("%s\n", *argv++);
which treats argv as a pointer and terminates when argv points to NULL.
The second frame on the right shows a session using the code directly above. We assume the first frame is stored in the file cmdline.c
Now we can get rid of some symbolic constants that should have been specified at run time.
Here are two before and after examples. The code on the left uses symbolic constants; on the right we use command-line arguments.
#include <stdlib.h>
#include <stdio.h> #include <stdio.h>
#define LO 0
#define HI 300
#define INCR 20
main() { int main (int argc, char *argv[argc]) {
int F; int F;
for (F=LO; F<=HI; F+=INCR) for (F=atoi(argv[1]); F<=atoi(argv[2]);
F+=atoi(argv[3]))
printf("%3d\t%5.1f\n", F, printf("%3d\t%5.1f\n", F,
(F-32)*(5.0/9.0)); (F-32)*(5.0/9.0));
return 0;
} }
Notes.
abnormally(it doesn't return 0).
#include <stdlib.h>
#include <stdio.h> #include <stdio.h>
#include <math.h> #include <math.h>
#define A +1.0 // should read
#define B -3.0 // A,B,C
#define C +2.0 // using scanf()
void solve (float a, float b, float c); void solve (float a, float b, float c);
int main() { int main(int argc, char *argv[argc]) {
solve(A,B,C); solve(atof(argv[1]), atof(argv[2]),
atof(argv[3]));
return 0; return 0;
} }
void solve (float a, float b, float c){ void solve (float a, float b, float c){
float d; float d;
d = b*b - 4*a*c; d = b*b - 4*a*c;
if (d < 0) if (d < 0)
printf("No real roots\n"); printf("No real roots\n");
else if (d == 0) else if (d == 0)
printf("Double root is %f\n", printf("Double root is %f\n",
-b/(2*a)); -b/(2*a));
else else
printf("Roots are %f and %f\n", printf("Roots are %f and %f\n",
((-b)+sqrt(d))/(2*a), ((-b)+sqrt(d))/(2*a),
((-b)-sqrt(d))/(2*a)); ((-b)-sqrt(d))/(2*a));
} }
Notes.
don't check the arguments. Now we specify them correctly.
include <string.h>
include <stdio.h>
include <ctype.h>
int main (int argc, char *argv[argc]) {
int c, makeUpper=0;
if (argc > 2)
return -argc; // error return
if (argc == 2)
if (strcmp(argv[1], "-toupper")) {
printf("Arg %s illegal.\n", argv[1]);
return -1;
}
else // -toupper was arg
makeUpper=1;
while ((c = getchar()) != EOF)
if (!isdigit(c)) {
if (isalpha(c) && makeUpper)
c = toupper(c);
putchar(c);
}
return 0;
}
Often a leading minus sign (-) is used for command-line arguments that are optional.
The program on the right removes all digits from the input.
If it is given the optional argument -toupper
it also
converts all letters to upper case using the toupper()
library routine.
Notes
BooleanmakeUpper.
Demo this function on my laptop. It is the file c-progs/rem-digit.c.
Homework: At the very end of chapter 3 you wrote escape() that converted a tab character into the two characters \t (it also converted newlines but ignore that). Call this function detab() and call the reverse function entab(). Combine the entab() and detab functions by writing a function tab that has one command-line argument.
tab -en # performs like entab() tab -de # performs like detab()
#include <stdio.h>
#include <string.h>
#define MAXLINE 1000
int getline(char *line, int max);
// find: print lines matching argv[1]
int main(int argc, char *argv[]) {
char line[MAXLINE];
int found = 0;
if (argc != 2)
printf("Usage: find pattern\n");
else
while (getline(line, MAXLINE) > 0)
if (strstr(line, argv[1]) != NULL) {
printf("%s", line);
found++;
}
return found;
}
Each of the programs in this section accepts a command-line argument (call it pattern) and when executed the program echos all input lines that contain the pattern. These programs are useful in their own right. However, our main interest is the pointer/character/string/array manipulations that occur.
This first version, which is shown on the right, simply echos those input lines that contain the command-line argument. This version is fairly simple thanks to the library routine strstr(s1, s2), which checks whether string s2 occurs in s1. The declaration of strstr(s1,s2) is found in string.h.
In fact strstr(s1,s2) indicates the location in s1 where s2 occurs, but we do not use this information as we want to know only if the pattern occurs in the line, not where.
The pattern we are looking for is the first command-line argument so the routine checks each input line to see if argv[1] occurs. If it does occur, the line is printed.
Now we permit two optional command-line arguments.
except, indicates that we are to reverse the sense of the comparison and print those lines that do not contain the pattern.
number, specifies that the line number is printed for all matching lines.
A common convention, which is followed for this example, is to use
a single letter (preceded by -
) for optional command-line
arguments.
In this case we use -x for except
and -n
for number
.
We also follow the convention of allowing these single letter
options to be combined.
Hence the single argument -nx
(or -xn
) can be used
instead of -n -x
(or -x -n
).
In all four cases, we print lines not matching the
string given in the the required argument and for each such line we
also print its line number.
In summary we want to process all arguments that start
with -
and for each one check every character after
the -
.
#include <stdio.h>
#include <string.h>
#define MAXLINE 1000
int getline(char *line, int max);
// find: print lines matching pattern
int main(int argc, char *argv[]) {
char line[MAXLINE];
long lineno = 0;
int c, except = 0, number = 0, found = 0;
while (--argc > 0 && (*++argv)[0] == '-')
while (c = *++argv[0])
switch (c) {
case 'x':
except = 1;
break;
case 'n'
number = 1;
break;
default:
printf("find: illegal option %c\n", c);
argc = 0;
found = -1;
break;
}
if (argc != 1)
printf("Usage: find -x -n pattern\n");
else
while (getline(line, MAXLINE) > 0) {
lineno++;
if ((strstr(line, *argv) != NULL) != except) {
if (number)
printf("%ld:", lineno);
printf("%s", line);
}
}
return found;
}
The entire program is quite clever and well done, especially the part that handles the variable number of optional arguments. I strongly suggest you give it careful study. In class we will concentrate on how the program processes the variable number of arguments. In particular we will study the distinction between the pink *(++argv)[0] and the yellow *++argv[0].
In class I want to discuss the pink and yellow highlighted regions, both of which contain *, ++, argv, and [0] in that order when read left to right. The difference between them is a pair of parentheses, that determine the order the operations are applied. Let's start with the pink.
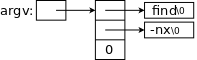
Recall that, when execution begins, argv points to an array of char pointers. Specifically, it initially points at the first entry of the array, argv[0], which itself points at the name of the executable. Hence ++argv initially points at a pointer to the first command-line argument, which is a string (during subsequent iterations it points at subsequent arguments). Hence, *++argv initially points to the first argument and (*++argv)[0] (which can also be written as **++argv) is the first character of the first argument. This character is what would be a '-', if we have an optional argument. Subsequent iterations of this while loop increment argv to point to subsequent arguments.
The () are needed since [] has higher precedence than *. Indeed, it is these () that distinguish the pink from the yellow, which we look at next.
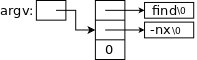
When the yellow is executed, argv points at an argument that begin with a '-'. More precisely argv points at the pointer to a character string that begins with a '-'. Hence argv[0] is the character pointer, and ++argv[0] (initially) points at the character after the '-', and *++argv[0] is (initially) the character after the '-'.
Since we can have multiple options, each specified by a single character (in this example the max is 2, but the code is more general), the (inner) while loop moves character by character across the argument.
The outer while moves from argument to argument executing the inner loop for each one until it reaches an argument not beginning with a '-' (or runs out of arguments, which is an error).
Start Lecture #08
Remark: Lab1 is assigned. It is on Brightspace and is due 12 October (two weeks from today). Lateness penalty is 2pts/day for the first 5 days then 5 pts/day. Good luck!
#include <ctype.h>
#include <string.h>
#include <stdio.h>
// Program to illustrate function pointers
int digitToStar(int c); // Cvt digit to *
int letterToStar(int c); // Cvt letter to *
int main (int argc, char *argv[argc]) {
int c;
int (*funptr)(int c);
if (argc != 2)
return argc;
if (strcmp(argv[1],"digits") == 0)
funptr = &digitToStar;
else if (strcmp(argv[1],"letters") == 0)
funptr = &letterToStar;
else
return -1;
while ((c=getchar()) != EOF)
putchar((*funptr)(c));
return 0;
}
int digitToStar(int c) {
if (isdigit(c))
return '*';
return c;
}
int letterToStar(int c) {
if (isalpha(c))
return '*';
return c;
}
In C you can do very little with functions, mostly define them and call them (and take their address, see what follows).
However, pointers to functions (called function pointers) are real values. You can do a lot with function pointers.
One reason the system can do more with function pointers than with functions is that all function pointers (indeed all pointers) are the same length.
The program on the right is a simple demonstration of function pointers. Two very simple functions are defined.
The first function, digitToStar() accepts an integer (representing a character) and return an integer. If the argument is a digit, the value returned is (the integer version of) '*'. Otherwise the value returned is just the unchanged value of the argument.
Similarly letterToStar() converts a letter to '*' and leaves all other characters unchanged.
The star of the show is funptr. Read its declaration carefully: The variable funptr is the kind of thing that, once de-referenced, is the kind of thing that, given an integer, produces an integer.
So it is a pointer to something. That something is a function from integers to integers.
The main program checks the (mandatory) argument. If the argument is "digits", funptr is set to the address of digitToStar(). If the argument is "letters", funptr is set to the address of letterToStar(). So funptr is a pointer to one of two functions.
Then we have a standard getchar()/putchar() loop with a slight twist. The character (I know it is an integer) sent to putchar() is not the naked input character, but is instead the input character processed by whatever function funptr points to. Note the "*" in the call to putchar().
Note: C permits abbreviating &function-name to function-name. So in the program above we could write
funptr = digitToStar; funptr = letterToStar;
instead of
funptr = &digitToStar; funptr = &letterToStar;
I don't like that abbreviation so I don't use it. Others do like it and you may use it if you wish.
#include <stdio.h>
#include <stdlib.h>
int funA(int x) {printf("A x=%d\n", x); return x+10; }
int funB(int x) {printf("B x=%d\n", x); return x+20; }
int funC(int x) {printf("C x=%d\n", x); return x+30; }
int (*funPtrArr[])(int x) = {&funA, &funB, &funC};
int main(int argc, char *argv[]) {
int x = atoi(argv[1]);
int y = atoi(argv[2]);
printf("x=%d\n", x);
int z;
z = (*funPtrArr[0])(x);
printf ("z=%d\n", z);
z = (*funPtrArr[1])(y);
printf ("z=%d\n", z);
z = (*funPtrArr[2])(100);
printf ("z=%d\n", z);
}
Function pointers are especially useful when there are many functions involved and you have a function pointer array.
On the right is a simple, but rather silly example.
When run with input 4 5
, it produces the following
output.
x=4 A x=4 z=14 B x=5 z=25 C x=100 z=130
We are basically skipping this section.
It gives some examples of more complicated declarations than we have
seen (but are just more of the same
—one example is
below).
The main part of the section presents a program that converts C
definition to/from more-or-less English equivalents.
Here is one example of a complicated declaration. It is basically the last one in the book with function arguments added.
char (*(*f[3])(int x))[5]
Remembering that *f[3] (like *argv[argc]) is an array of 3 pointers to something not a pointer to an array of 3 somethings, we can unwind the above to.
The variable f is an array of size three of pointers.
Remembering that *(g)(int x) = *g(int x) is a function returning a pointer and not a pointer to a function, we can further unwind the monster to.
The variable f is an array of size three of pointers to functions taking an integer and returning a pointer to an array of size five of characters.
One more (the penultimate from the book).
char (*(f(int x))[5])(float y)
The function f takes an integer and returns a pointer to an array of five pointers to functions, each taking a float and returning a character.
For a start, a Java programmer can think of structures as basically classes and objects without methods.
On the right we see some simple structure declarations for use in a geometry application. They should be familiar from your experience with Java classes in CS101 and CS102.
#include <math.h>
struct point {
double x;
double y;
};
struct rectangle {
struct point ll;
struct point ur;
} rect1;
double f(struct point pt);
struct point mkPoint(double x, double y);
struct point midPoint(struct point pt1,
struct point pt2);
int main(int argv, *char argv[]) {
struct point pt1={40.,20.}, pt2;
struct rectangle rect1;
pt2 = pt1;
rect1.ll = pt2;
pt1.x += 1.0;
pt1.y += 1.0;
rect1.ur = pt1;
rect1.ur.x += 2.;
return 0;
}
The top declaration defines the struct point type. This is similar to defining a class without methods.
As with Java classes, structures in C help organize data by permitting you to treat related data as a unit. In the case of a geometric point, the x and y coordinates are closely related mathematically and, as components of the struct point type, they become closely related in the program's data organization.
The next definition defines both a new type struct rectangle and a variable rect1 of this type. Note that we can use struct point, a previously defined struct, in the declaration of struct rectangle.
Recall from plane geometry that a rectangle (we assume its sides are parallel to the axes) is determined by its lower left ll and upper right ur corners.
The next group declares a function f() having a structure parameter, then a function mkPoint() with a structure result, and finally declares midPoint() having both structure parameters and a structure result.
The definition in main() of pt1 illustrates an initialization. C does not support structure constants. Hence you could not in main() have the assignment statement
pt1 = {40., 20.};
We see in the executable statements of main() that one can assign a point to a point as well as assigning to each component.
Since the rectangle rect1 is composed of points, which are in turn composed of doubles, we can assign a point to a point component of a rectangle and can assign a double to a double component of a point component of a rectangle.
If you wrote Java programs for geometry (we did when I last taught 201/202), they probably had classes like rectangle and point and had objects like pt1, pt2, and rect1. Given these classes, the assignment statements in our C-language main() function would have been more or less legal Java statements as well.
The only legal operations on a structure are copying it, assigning
to it as a unit, taking its address with &, and assessing its
members.
Note that copying a structure
includes passing one as a
parameter to a function or returning the value of a function.
double dist (struct point pt) {
return sqrt(pt.x*pt.x + pt.y*pt.y);
}
struct point mkPoint(double x, double y) {
// return {x, y}; invalid in C
struct point pt;
pt.x = x;
pt.y = y;
return pt;
}
struct point midpoint(struct point pt1,
struct point pt2){
// return (pt1 + pt2) / 2; not C
struct point pt;
pt.x = (pt1.x+pt2.x) / 2;
pt.y = (pt1.y+pt2.y) / 2;
return pt;
}
void mvToOrigin(struct rectangle *r){
(*r).ur.x = (*r).ur.x - (*r).ll.x;
r->ur.y = r->ur.y - r->ll.y;
r->ll.y = 0;
r->ll.x = 0;
}
On the right we see four geometry functions. Although all four deal with structs, they do so differently. A function can receive and return structures, but you may prefer to specify the constituent native types instead. A third alternative is to utilize a pointer to a struct.
As we have seen, functions can take structures as parameters, but is that a good idea? Should we instead use the components as parameters or perhaps pass a pointer to the structure? For example, if main() wishes to pass pt1 (of type struct point) to a function f(), should we write.
Naturally, the declaration of f() will be different in the three cases. When would each case be appropriate?
Java constructor likefunction that produces a structure from its constituents, for example mkPoint(pt1.x, pt2.y) above would produce a new point having coordinates a
mixtureof pt1 and pt2.
*followed by the standard component selection operator
.. Due to precedence, the parentheses are needed.
->.
Note: The ->
abbreviation is
employed almost universally.
Constructs like ptr1->elt5 are very common; the
long form
(*ptr1).elt5 is much less common.
Homework: Write two versions of mkRectangle, one that accepts two points, and one that accepts 4 real numbers.
int f(int x) {
if (x&1)
return 3*x+1;
return x >> 1;
}
#define MAXVAL 10000
#define ARRAYBOUND (MAXVAL+1)
int G[ARRAYBOUND];
int P[ARRAYBOUND];
struct gameValType {
int G[ARRAYBOUND];
int P[ARRAYBOUND];
} gameVal;
struct gameValType {
int G;
int P;
} gameVal[ARRAYBOUND];
#define NUMEMPLOYEES 2
struct employeeType {
int id;
char gender;
double salary;
} employee[NUMEMPLOYEES] = {
{ 32, 'M', 1234. },
{ 18, 'F', 1500. }
};
Consider the following game. (The code is on the right does one step.)
So, starting with N=5, you get 16 8 4 2 1.
starting with N=7, you get
7 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1.
and starting with N=27, you get
27 82 41 ... 9232 ... 160 80 40 20 10 5 16 8 4 2 1.
It is an deep open problem in number theory if every positive integer eventually get to 1. This has been checked for MANY numbers. Let G[i] be the number of rounds of the game needed to get from i to 1. G[1]=0, G[2]=1, G[7]=16, G[27]=111. (Define G[0]=-1)
Factoring into primes is fun too. So let P[N] be the number of distinct prime factors of N. P[2]=1, P[16]=1, P[12]=2 (define P[0]=P[1]=0).
This leads to two arrays as shown on the right in the second frame.
We might want to group the two arrays into a structure as in the third frame. This version of gameVal is a structure of arrays. In this frame the number of distinct prime factors of 763 would be stored in gameVal.P[763]
In the fourth frame we grouped together the values of G[n] and P[n]. This version of gameVal is an array of structures. In this frame the number of distinct prime factors of 763 would be stored in gameVal[763].P
If we had a database with employeeID, gender, and salary, we might use the array of structures in the fifth frame. Note the initialization. The inner {} are not needed, but I believe they make the code clearer.
How big is the employee array of structures? How big is employeeType?
C provides two versions of the sizeof unary operator to answer these questions.
These functions are not trivial and indeed the answers are system dependent ... for two reasons.
Example: Assume char requires 1 byte, int requires 4, and double requires 8. Let us also assume that each type must be aligned on an address that is a multiple of its size and that a struct must be aligned on an address that is a multiple of 8.
So the data in struct employeeType requires 4+1+8=13 bytes. But three bytes of padding are needed between gender and salary so the size of the type is 16.
Homework: How big is each version of sizeof(struct gameValType)? How big is sizeof employee?
#include <stdio.h>
int main (int argc, char *argv[argc]) {
struct howBig {
int n;
double y;
} howBigAmI[] = { {26, 18.}, {33, 99.} };
printf ("howBigAmI has %ld entries.\n",
sizeof howBigAmI / sizeof(struct howBig));
}
In the example above it is easy to look at the initialization and count the array bound for employee. An annoyance is that you need to change the #define for NUMEMPLOYEES if you add or remove an employee from the initialization list.
A more serious problem occurs if the list is long in which case manually counting the number of entries is tedious and, much worse, error prone.
Instead we can use sizeof and sizeof() to have the compiler compute the number of entries in the array. The code is shown on the right. The output produced is
howBigAmI has 2 entries.
int getword(char *word, int lim) {
int c, getch(void);
void ungetch(int);
char *w = word;
while (isspace(c = getch())) ;
if (c != EOF)
*w++ = c;
if (!isalpha(c)) {
*w = '\0';
return c;
}
for ( ; --lim > 0; w++)
if (!isalnum(*w = getch())) {
ungetch(*w);
break;
}
*w = '\0';
return word[0];
}
As its name suggests the purpose of getword() is to get (i.e., read) the next word from the input. It's first parameter is a buffer into which getword() will place the word found. Although declared as a char *, the parameter is viewed as pointing to many characters, not just one. The second parameter throttles getword(), restricting the number of characters it will read. Thus getword() is not scary; the caller need only ensure that the first parameter points to a buffer at least as big as the second parameter specifies.
The definition of a word is technical. (It is chosen to enable programs like the keyword counting example in the next section.) A word is either a string of letters and digits beginning with a letter, or a single non-whitespace character. The return value of the function itself is the first character of the word, or EOF for end of file, or the character itself if it is not alphabetic.
The program has a number of points to note.
man isalnum.
Note that getword() above (which is from the text) requires the use of getch() and ungetch() from the text (and notes). The versions of these two routings in the standard library are slightly different and getword() fails if you use them.
#include <stdio.h>
#include <ctype.h>
#include <string.h>
#define MAXWORDLENGTH 50
struct keytblType {
char *keyword;
int count;
} keytbl[] = {
{ "break", 0 },
{ "case", 0 },
{ "char", 0 },
{ "continue", 0 },
// others
{ "while", 0 }
};
#define NUMKEYS (sizeof keytbl / sizeof keytbl[0])
int getword(char *, int); // no var names given
struct keytblType *binsearch(char *);
int main (int argc, char *argv[argc]) {
char word[MAXWORDLENGTH];
struct keytblType *p;
while (getword(word,MAXWORDLENGTH) != EOF)
if (isalpha(word[0]) &&
((p=binsearch(word)) != NULL))
p->count++;
for (p=keytbl; p<keytbl+NUMKEYS; p++)
if (p->count > 0)
printf("%4d %s\n", p->count, p->keyword);
return 0;
}
struct keytblType *binsearch(char *word) {
int cond;
struct keytblType *low = &keytbl[0];
struct keytblType *high = &keytbl[NUMKEYS];
struct keytblType *mid;
while (low < high) {
mid = low + (high-low) / 2;
if ((cond = strcmp(word, mid->keyword)) < 0)
high = mid;
else if (cond > 0)
low = mid+1;
else
return mid;
}
return NULL;
}
The program on the right illustrates well the use of pointers to structures and also serves as a good review of many C concepts. The overall goal is to read text from the console and count the occurrence of C keywords (such as break, if, int, and others.). After reading the input, the program prints a list of all the keywords that were present and how many times each occurred.
Lets examine the code on the right.
enoughso that it points to the next entry.
midpointbetween high and low. But, other than that oddity, I find it striking how array-like the code looks. That is, the manipulations of the pointers could just as well be manipulating indices.
Note/Suggestion: The code just above won't compile and run by itself. It needs getword(), which needs getch() and ungetch(), which are further back. Some of these are in standard libraries, but the library versions are slightly different and will not work with program above.
I believe it would be instructive for you to put the pieces all together into a single .c file which you then compile and run. As data you can type in (or cut and past in) any C program and it should work. At least it worked for me.
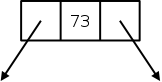
Consider a basic binary tree. A small example is shown on the near right; one cell is detailed on the far right. Looking at the diagram on the far right suggests a structure with three components: left, right, and value. The first two refer to other tree nodes and the third is an integer.
I am fairly sure you did trees in 101-102 but I will describe the C version as though it is completely new. I will say that in both Java and C the key is the use of pointers. In C this will be made very explicit by the use of *. In Java it was somewhat under the covers.
struct bad {
struct bad left;
int value;
struct bad right;
};
struct treenode_t {
struct treenode_t *left;
int value;
struct treenode_t *right;
};
Since trees are recursive data structures you might expect some sort of recursive structure in the C or Java declaration. Consider struct bad defined on the right. (You might be fancier and have a struct tree, which contains a struct root, which has in turn an int value and two struct tree's).
But struct bad and its fancy friends are infinite
data structures: The left and right components are the same type as
the entire structure.
So the size of a struct bad is the size of
an int plus the size of two struct bad's.
Since the size of an int exceeds zero, the total size must
be infinite.
Some languages permit infinite structures providing you never try to
materialize
more than a finite piece.
But C is not one of those languages.
So for us, struct bad is bad!
Instead, we use struct treenode_t as shown on the right (names like treenode_t are a shorter and very commonly used alternative to names like treenodeType).
The key is that a struct treenode_t does not contain an internal struct treenode_t. Instead it contains pointers to two internal struct treenodes t.
Be sure you understand why struct treenode_t is finite and corresponds exactly to the tree picture above.
struct s {
int val;
struct t *pt;
};
struct t {
double weight;
struct s *ps;
};
What if you have two structure types that need to reference each other. You cannot have a struct s contain a struct t if struct t contains a struct s. If you did try that, then each struct s would contain a struct t, which would in turn contain a struct s, which would contain ... .
Once again pointers come to the rescue as illustrated on the right. Neither structure is infinite. A struct s contains one integer and one pointer. A struct t contains one double and one pointer. Neither is a subset of the other, instead each references (points at) the other
Start Lecture #09
Remark: getword() from last time is quite a clever program. Imagine if it was run with itself as data. The first time called it returns int. The next time it is called yields getword, then (, then char, then * ... .
struct llnode_t {
long data;
struct llnode_t *next;
}

Probably the most familiar 1D unbounded data structure (beyond the 1D array) is the linked list, which is well studied in 101-102. On the near right we have a diagram of a small linked list and on the far right we show the C declaration of a structure corresponding to one node in the diagram. Again we note that a struct llnode_t does not contain a struct llnode_t. Instead, it contains a pointer to such a node.
With one pointer in each node the structure has a natural 1D geometric layout. Trees, in contrast, have two pointers per node and have a natural 2D geometric layout.
Instead of trees, we will investigate a different 2-dimensional structure, a linked list of linked lists. This structure (or something similar) will likely become the subject of the future lab 2.
Although all the actual data are strings (i.e., char *), there are two different types of structures present, the vertical list of struct node2d's (2D nodes) and the many horizontal lists of struct node1d's (1D nodes).
Actually it is a little more complicated.
Each horizontal list has a list head that is a node2d and
there must be somewhere (not shown in the diagram) a pointer to
the first
node2d (i.e., the node with
data joe).
The three decreasing length horizontal lines indicate that the
pointer in question is null.
(I borrow that symbol from electrical engineering, where it is used
to represent ground
.)
struct node1d {
struct node1d *next;
char *name;
};
struct node2d {
struct node1d *first;
char *name;
struct node2d *down;
};
The structure declarations are on the right. Perhaps I should have called them struct node1d_t and struct node2d_t.
Be sure you understand why the picture above agrees with the C declarations on the right.
The diagram (and the code) suggests a hierarchy: the nodes in the
left hand column are higher level
than the others.
You can think of the struct node1d's on a single row
belonging to a list headed by the struct node2d on the left
of that same row.
Note that every struct node1d is the same (rather small)
size independent of the length of the name.
Similarly, all the struct node2d's are the same size (but
bigger that the struct node1d's).
In that sense the figure is misleading since is suggests that
alice
is larger that joe
. The confusion is that the
node does not contain the actual 6 characters in alice
('a', 'l', 'i', 'c', 'e',
'\0') but rather a (fixed size) pointer to the
name.
Said using C terminology the name component is a fixed size pointer. The possibly large string is the object pointed to by name, i.e., it is *name. But *name is a char, which is even smaller than a pointer. It would be more precise to say that name points to the first character of the string; you must look at the string itself to see where it ends.
2d node name=joe
1d node name=xy2
1d node name=sally
1d node name=e342
2d node name=alice
2d node name=R2D2
1d node name=cso
1d node name=c3pO
How should we print the above structure.
I suggest, and probably lab2 will require, that you use the style
shown on the right.
(You might put quotes around the strings.)
The idea behind this style is the following.
From this printout one can see immediately, for example, that the 2D list has three entries and that the middle 2D node has an empty sublist of 1D nodes.
One question remains.
The string itself can be big.
If the length is a constant, then the compiler can be asked to leave
space
for it.
Question: What if the string is generated at
runtime?
Answer: malloc().
As you know, in Java, objects (including arrays) have to be created via the new operator. We have seen that in C this is not always needed: you can declare a struct rectangle and then declare several rectangles.
However, this doesn't work if you want to generate the rectangles during run time. When you are writing a program to process 2D lists, you won't know how many 2d nodes or 1d nodes will be needed. That number will be determined by the data read when the program is run.
In addition the size of the strings that name each node will also not be known until runtime.
So we need a way to create an object during run time. In C this uses the library function malloc(), which takes one argument, the amount of space to be allocated. The function malloc() allocates the requested space and returns a pointer to it. The companion function free() takes as argument a pointer that was obtained from malloc and makes the corresponding space available for future malloc()s.
These two new functions should remind you of the similar pair we studied a few lectures ago. The new functions are considerably more sophisticated than the old ones.
storage allocatersin some detail.
Since malloc() is not part of C, but is instead just a library routine, the compiler does not treat it specially (unlike the situation with new, which is part of Java). Since malloc() is just an ordinary function, and we want it to work for dynamically created objects of any type (e.g., an int, a char *, a struct treenode, etc), and there is no way to pass the name of a type to a function, two questions arise.
The alignment question is easy and can be essentially ignored at this time. This is fortunate since we haven't studied (or even defined) alignment yet, but will do so soon after we finish with C.
The answer to the alignment question (which will become clear when we study alignment) is that we simply have malloc() return space aligned on the most stringent requirement. So, on a system where long doubles and all structures require 16-byte alignment and all other data types require 8-byte, 4-byte, 2-byte, or 1-byte alignment, then malloc() always returns space aligned on a 16-byte boundary (i.e., the address is a multiple of 16).
Ensuring type correctness is not automatic, but not hard. Specifically, malloc() returns a void *, which means that the value returned is a pointer that must be explicitly coerced to the correct type. For example, lab 2 might contain code like
struct node2d *p2d; p2d = (struct node2d *) malloc(sizeof(struct node2d));
An application calls the library routine free(void *p) to return memory obtained by malloc(). Indeed p must be a pointer returned by a previous call to malloc(). Note, as mentioned above, that the order in which chunks of memory are freed need not match the order in which they were obtained.
It is clearly an error to continue using memory you already freed. Such errors often lead to crashes with very little useful diagnostic information available.
Advice: Try very hard not to make that error.
Note: See, in addition, section 7.8.5 below.
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv) {
int n;
char *As;
scanf("%d", &n);
As = (char *) malloc((1+n) * sizeof(char));
for (int i = 0; i<n; i++)
As[i] = 'A';
As[n] = '\0';
printf("As is: %s\n", As);
return 0;
}
The program on the right reads an integer n and then produces a string containing n As (plus, of course, the trailing NULL to mark the end of the string). Note that n is unbounded and the only limit is the (virtual and physical) memory on your system. malloc() is used to obtain the memory needed for all n As.
Note that malloc() is declared in the system library stdlib.h, which explains the second #include.
Also note that As, which is a character pointer, is quite
comfortable in its dual role as a character array.
Of course the declaration char *A
does not allocate
any space for the characters.
That job is handled by malloc().
At various points in lab2, you may need to
create a node
, either a struct node2d or a
struct node1d.
These individual nodes cannot be simply declared since we don't know
until runtime how many there will be of each type and what will be
the individual names.
The situation will be that a user
of your lab has entered a
command such as:
append2d name2
A first call to getword() yields append2d
so you
know you are creating a new struct node2d and placing it at
the end of the existing vertical
list.
A second call to getword() yields name2
which is
the string you are to place in the newly-created
struct node2d.
Note that the lab provides an upper bound on the length
of name2
.
Since the node and the string must be created, TWO calls to malloc() are used. My code has the following comments.
// create a 2D node with the given name and null 1D sublist // first malloc space for the node // now malloc() space for the name (i.e., the real string)
Skipped
Instead of declaring pointers to trees via
struct treenode *ptree;
we can write
typedef struct treenode *Treeptr;
Treeptr ptree;
Thus treeptr is a new name for the type
struct treenode *.
As another example, instead of
char *str1, *str2;
We could write
typedef char *String;
String str1, str2;
Note that this does not give you a new type; it just gives you a new name for an existing type. In particular str1 and str2 are still pointers to characters even if declared as a String above.
A common convention is to capitalize the a typedef'ed name.
struct something {
int x;
union {
double y;
int z;
}
}
Traditionally union was used to save space when memory was expensive. Perhaps with the recent emphasize on very low power devices, this usage will again become popular. Looking at the example on the right, y and z would be assigned to the same memory locations. Since the size allocated is the larger of what is needed the union takes space max(sizeof(double),sizeof(int)) rather than sizeof(double)+sizeof(int) if a union was not done.
It is up to the programmer to know what is the actual variable stored. The union shown cannot be used if y and z are both needed at the same time.
It is risky since there is no checking done by the language.
A union is aligned on the most severe alignment of its constituents. This can be used in a rather clever way to meet a requirement of malloc().
As we mentioned above when discussing malloc(), it is sometimes necessary to force an object to meet the most severe alignment constraint of any type in the system. How can we do this so that if we move to another system where a different type has the most severe constraint, we only have to change one line?
struct something {
int x;
struct something *p;
// others
} obj;
// assume long most severely aligned
typedef long Align
union something {
struct dummyname {
int x;
union something *p;
// others
} s;
Align dummy;
}
typedef union something Something;
Say struct something, as shown in the top frame on the right, is the type we want to make most severely aligned.
Assume that on this system the type long has the most severe alignment requirement and look at the bottom frame on the right.
The first typedef captures the assumption that long has the most severe alignment requirement on the system. If we move to a system where double has the most severe alignment requirement, we need change only this one line. The name Align was chosen to remind us of the purpose of this type. It is capitalized since one common convention is to capitalize all typedefs.
The variable dummy is not to be used in the program. Its purpose is just to force the union, and hence s to be most severely aligned.
In the program we declare an object say obj to be of type Something (with a capital S) and use obj.s.x instead of obj.x as in the top frame. The result is that we know the structure containing x is most severely aligned.
See section 8.7 if you are interested.
Skipped
This pair form the simplest I/O routines.
#include <stdio.h>
int main (int argc, char *argv[argc]) {
int c;
while ((c = getchar()) != EOF)
if (putchar(c) == EOF)
return EOF;
return 0;
}
The function getchar() takes no parameters and returns an integer. This integer is the integer value of the character read from stdin or is the value of the symbolic parameter EOF (normally -1), which is guaranteed not the be the integer value of any character.
The function putchar() takes one integer parameter, the integer value of a character. The character is sent to stdout and is returned as the function value (unless there is an error in which case EOF is returned).
The code on the right copies the standard input (stdin), which is usually the keyboard, to the standard output (stdout), which is usually the screen.
We built getch() / ungetch() from getchar().
Homework: 7.1. Write a program that converts upper case to lower or lower case to upper, depending on the name it is invoked with, as found in argv[0]
We have already seen printf(). A surprising characteristic of this function is that it has a variable number of arguments. The first argument, called the format string, is required. The number of remaining arguments depends on the value of the first argument. The function returns the number of characters printed, but the return value is rarely used. Technically the declaration of printf() is
int printf(char *format, ...);
The format string contains regular characters, which are just sent
to stdout unchanged and conversion specifications
,
each of which determines how the value of the next argument is to be
printed.
Each conversion specification begins with a %
, which is
optionally followed by some modifiers, and ends with a conversion
character.
We have not yet seen any modifiers but have seen a few conversion characters, specifically d for an integer (i is also permitted), c for a single character, s for a string, and f for a real number.
There are other conversion characters that can be used, for example, to get real numbers printed using scientific notation. The book gives a full table.
There are a number of modifiers to make the output line up and look
better.
For example, %12.3f means that the real number will be
printed using 12 columns (or more if the number is too big to fit in
12 columns) with 3 digits after the decimal point.
So, if the number was 36.3 it would be printed as
||||||36.300
where I used |
to represent a blank.
Similarly -1000. would be printed as |||-1000.000
.
These two would line up nicely if printed via
printf("%12.3f\n%12.3f\n\n", 36.3, -1000.);
The function
int sprintf(char *string, char *format, ...);
is very similar to printf(). The only difference is that, instead of sending the output to stout (normally the screen), sprintf() assigns it to the first argument specified.
char outString[50]; int d = 14; sprintf(outString, "The value of d is %d\n", d);
For example, the code snippet on the right sets the first 23 characters of outString to The value of d is 14 \n\0 while the remaining 27 characters of outString continue to be uninitialized.
Since the system cannot in general check that the first argument is big enough, care is needed by the programmer, for example checking that the returned value is no bigger than the size of the first argument. In summary, sprintf() is scary. A good defense is to use instead snprintf(), which like strncpy(), guarantees than no more than n bytes will be assigned (n is an additional parameter to snprintf).
As we mentioned, printf() takes a variable number of arguments. But remember that printf() is not special, it is just a library function, not an object defined by the language or known specially to the compiler. That is, anyone can write a C program with declaration
int myfunction(int x, float y, char *z, ...)
and it will have three named arguments and zero or more unnamed arguments.
There is some magic needed to get the unnamed arguments. However, the magic is needed only by the author of the function; not by a user of the function.
Related to the Java Scanner class is the C function scanf().
The function scanf() is to printf() as getchar() is to putchar(). As with printf(), scanf() accepts one required argument (a format string) and a variable number of additional arguments. Since this is an input function, the additional arguments give the variables into which input data is to be placed.
Consider the code fragment shown on the top frame to the right and assume that the user enters on the console the lines shown on the bottom frame.
int n;
double x;
char str[50];
scanf("%d %f %s", &n, &x, str);
22 37.5
no-blanks-here
The function
int sscanf(char *string, char *fmt, ...);
is very similar to scanf(). The only difference is that, instead of getting the input from stdin (normally the keyboard), sscanf() gets it from the first argument specified.
Start Lecture #10
Remarks:
So far all our input has been from stdin and all our output has been to stdout (or from/to a string for sscanf()/sprintf).
What if we want to read or write a file?
In Unix you can use the redirection operators of the command
interpreter (the shell), namely < and
>, to have stdin and/or stdout refer
to a file.
But what if you want input from 2 or more files?
Before we can specify files in our C programs, we need to learn a (very) little about the file pointer.
Before a file can be read or written, it must be opened.
The library function fopen() is given two arguments, the
name of the file and the mode
; it returns a file pointer.
Consider the code snippet on the right. The type FILE is defined in <stdio.h>. We need not worry about how it is defined.
FILE *fp1, *fp2, *fp3, *fp4;
FILE *fopen(char *name, char *mode);
fp1 = fopen("cat.c", "r");
fp2 = fopen("../x", "a");
fp3 = fopen("/tmp/z", "w");
fp4 = fopen("/tmp/q", "r+");
After the file is opened, the file name is no longer used; subsequent commands (reading, writing, closing) use the file pointer.
The function fclose(FILE *fp) breaks the connection established by fopen().
Just as getchar()/putchar() are the basic one-character-at-a-time functions for reading and writing stdin/stdout, getc()/putc() perform the analogous operations for files (really for file pointers). These new functions naturally require an extra argument, a pointer to the file to read from or write to.
Since stdin/stdout are actually file pointers (they are constants not variables) we have the definitions
#define getchar() getc(stdin) #define putchar(c) putc((c), stdout)
I think this will be clearer when we do an example, which is our next task.
#include <stdio.h>
main (int argc, char *argv[argc]) {
FILE *fp;
void filecopy(FILE *, FILE *);
if (argc == 1) // NO files specified
filecopy(stdin, stdout);
else
while(--argc > 0) // argc-1 files
if((fp=fopen(*++argv, "r")) == NULL) {
printf ("cat: can't open %s\n", *argv);
return 1;
} else {
filecopy(fp, stdout);
fclose(fp);
}
return 0;
}
void filecopy (FILE *ifp, FILE *ofp) {
int c;
while ((c = getc(ifp)) != EOF)
putc(c, ofp);
}
The name cat is short for catenate, which is a synonym of concatenate.
If cat is given no command-line arguments (i.e., if argc=1), then it just copies stdin to stdout. This is not useless: for one thing remember < and >.
If there are command-line arguments, they must all be the names of existing files. In this case, cat concatenates the files and writes the result to stdout. The method used is simply to copy each file to stdout one after the other.
The copyfile() function uses the standard getc()/putc() loop to copy the file specified by its first argument ifp (input file pointer) to the file specified by its second argument. In this application, the second argument is always stdout so copyfile() could have been simplified to take only one argument and to use putchar().
Note the check that the call to fopen() succeeded; a very good idea.
Note also that cat uses very little memory, even if concatenating 100GB files. It would be an unimaginably awful design for cat to read all the files into some ENORMOUS character array and then write the result to stdout.
A problem with cat is that error messages are written to the same place as the normal output. If stdout is the screen, the situation would not be too bad since the error message would occur at the end. But if stdout were redirected to a file via >, we might not notice the message.
Since this situation is common, there are actually three standard file pointers defined: In addition to stdin and stdout, the system defines stderr.
Although the name suggests that it is for errors (and that is indeed its primary application), stderr is really just another file pointer, which (like stdout) defaults to the screen).Even if stdout is redirected by the standard > redirection operator, stderr will still appear on the screen.
There is also syntax to redirect stderr, which can be used if desired.
As mentioned previously a command should return zero if successful and non-zero if not. This is quite easy to do if the error is detected in the main() routine itself.
What should we do if main() has called joe(), which has called f(), which has called g(), and g() detects an error (say fopen() returned NULL)?
It is easy to print an error message (sent to stderr, now that we know about file pointers). But it is a pain to communicate this failure all the way back to main() so that main() can return a non-zero status.
Exit() to the rescue. If the library routine exit(n) is called, the effect is the same as if the main() function executed return n. So executing exit(0) terminates the command normally and executing exit(n) with n>0 terminates the command and gives a status value indicating an error.
The library function
int ferror(FILE *fp);
returns non-zero if an error occurred on the stream fp. For example, if you opened a file for writing and sometime during execution the file system became full and a write was unsuccessful, the corresponding call to ferror() would return non-zero.
The standard library routine
char *fgets(char *line, int maxchars, FILE *fp)
reads characters from the file fp and stores them plus a trailing '\0' in the string line. Reading stops when a newline is encountered (it is read and stored) or when maxchars-1 characters have been read (hence, counting the trailing '\0', at most maxchars will be stored).
The value returned by fgets is normally line. If an end of file or error occurs, NULL is returned instead.
The standard library routine
int fputs(char *line, FILE *fp)
writes the string line to the file fp. The trailing '\0' is not written and line need not contain a newline. The return value is zero unless an error occurs in which case EOF is returned.
A laundry list. I typed them all in to act as convenient reference. Let me know if you find any errors.
This subsection represents a technical point; for this class you can replace size_t by int.
Consider the return type of strlen(), which the length of the string parameter. It is surely some kind of integral type but should it be short int, int, long int or one of the unsigned flavors of those three?
Since lengths cannot be negative, the unsigned versions are better since the maximum possible value is twice as large. (On the machines we are using int is at least 32-bits long so even the signed version permits values exceeding two billion, which is good enough for us).
The two main contenders for the type of the return value from strlen() are unsigned int and unsigned long int. Note that long int can be, and usually is, abbreviated as long.
If you make the type too small, there are strings whose length you cannot represent. If you make the type bigger than ever needed, some space is wasted and, in some cases, the code runs slower.
Hence the introduction of size_t, which is defined in
stdlib.h.
Each system specifies whether size_t is
unsigned int or unsigned long (or something
else).
For the same reason that the system-dependent type size_t is used for the return value of strlen, size_t is also used as the return type of the sizeof operator and is used several places below.
These are from string.h, which must be #include'd. The versions with n added to the name limit the operation to n characters. In the following table n is of type size_t and c is an int containing a character; src and dest are strings (i.e., character pointers, char *); and cs and ct are constant strings (const char *).
I indicated which inputs may be modified by writing the string name in red. Remember that a string in C is represented by a character pointer.
| Call | Meaning |
|---|---|
| strcat(dest,src) | Concatenate src on to the end of dest (changing dest) and return dest. |
| strncat(dest,src,n) | The same but concatenates no more than n characters. |
| strcmp(cs,ct) | Compare s and t lexicographically. Returns a negative, zero, or positive int if s is respectively <, =, or > t |
| strncmp(cs,ct,n) | The same but compares no more than n characters. |
| strcpy(dest,ct) | Copy ct to s and return dest. |
| strncpy(dest,ct,n) | Similar but copies no more than n characters and pads with '\0' if ct has fewer than n characters. The result might NOT be '\0' terminated. |
| strlen(cs) | Returns the length of cs (not including the terminating '\0') as a size_t value. |
| strchr(cs,c) | Returns a pointer to the first c in cs or NULL if c is not in cs. |
| strrchr(cs,c) | Returns a pointer to the last c in cs or NULL if c is not in cs. |
| strstr(cs,ct) | Returns a pointer to the first occurrence of ct in cs or NULL if c is not in cs. |
These functions are from ctype.h, which must be #include'd. Each of them takes an integer argument (representing a character or the value EOF) and return an integer.
| Call | Meaning |
|---|---|
| isalpha(c) | Returns true (non-zero) if (and only if)
c is alphabetic. In our locale this means a letter. |
| isupper(c) | Returns true if c is upper case. |
| islower(c) | Returns true if c is lower case. |
| isdigit(c) | Returns true if c is a digit. |
| isalnum(c) | Returns true if isalpha(c) or isdigit(c). |
| toupper(c) | Returns c converted to upper case if c is a letter; otherwise returns c. |
| tolower(c) | Returns c converted to lower case if c is a letter; otherwise returns c. |
int ungetc(int c, FILE *fp) pushes back
to the
input stream the character c.
It returns c or EOF if an error was
encountered.
This function is from stdio.h, which must be #include'd.
Only one character can be pushed back, i.e., it is not safe to call ungetc() twice without an call in between that consumes the first pushed back character. The function ungetch() found in the book and these notes does not have this restriction.
#include <stdio.h>
#include <stdlib.h>
int main (int argc, char *argv[argc]) {
int status;
printf("Hello.\n");
status = system("dir; date");
printf("Goodbye: status %d\n", status);
return 0;
}
The function system(char *s) runs the command contained in the string s and returns an integer status.
The contents of s and the value of the status is system dependent.
On my system, the program on the right when run in a directory containing only two files x and y produced the following output.
Hello. x y Sun Mar 7 16:05:03 EST 2010 Goodbye: status 0
This function is in stdlib.h, which must be #include'd.
We have already seen
void *malloc(size_t n)
which returns pointer to n bytes of uninitialized storage. If the request cannot be satisfied, malloc() returns NULL.
The related function
void *calloc(size_t n, size_t size)
returns a pointer to a block of storage adequate to hold an array
of n objects each of size size.
The storage is initialized to all zeros.
The function
void free (void *p)
is used to return storage obtained from malloc() or calloc().
for (p = head; p != NULL; p = p->next)
free(p);
for (p = head; p != NULL; p = q) {
q = p-> next;
free (p);
}
| Call | Meaning |
|---|---|
| sin(x) | sine |
| cos(x) | cosine |
| atan(x) | arctangent |
| exp(x) | exponential ex |
| log(x) | natural logarithm loge(x) |
| log10(x) | common logarithm log10(x) |
| pow(x,y) | xy |
| sqrt(x) | square root, x≥0 |
| fabs(x) | absolute value |
These functions are from math.h, which must be #include'd. In addition (at least on on my system and linserv1.nyu.edu) you must specify a linker option to have the math library linked. If your mathematical program consists of A.c and B.c and the executable is to be named prog1, you would write
cc -o prog1 -l m A.c B.c
All the functions in this section have double's as arguments and as result type. The trigonometric functions express their arguments in radians and the inverse trigonometric functions express their results in radians.
Random number generation (actually pseudo-random number generation) is a complex subject. The function rand() given in the book is an early and not wonderful generator; it dates from when integers were 16 bits. I recommend instead (at least on linux and linserv.nyu.edu)
long int random(void) void srandom(unsigned int seed)
The random() function returns an integer between 0 and RAND_MAX. You can get different pseudo-random sequences by starting with a call to srandom() using a different seed. Both functions are in stdlib.h, which must be #include'd.
On my linux system RAND_MAX (also in stdlib.h) is defined as 231-1, which is also INT_MAX, the largest value of an int. It looks like linserv.nyu.edu doesn't define RAND_MAX, but does use the same psuedo-random number generator.
Remark: Let's write some programs/functions.

At the lowest level of abstraction each of these forms of code are just sequences of bits.
Modern electronics can quickly distinguish 2 states of an electric signal: low voltage and high voltage. Low has always been around 0 volts; high was 5 volts for a long while now is below 3.5 volts.
Since this is not a EE course we will abstract the situation and say that a signal is in one of two states, low (a.k.a. 0) and high (a.k.a. 1).
On the right we see plots of voltage (vertical) vs time (horizontal).
in the middle.
It is fine if you ignore the middle and bottom pictures.
| decimal base 10 |
binary base 2 |
base 4 |
octal base 8 |
hex base 16 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 | 2 |
| 3 | 11 | 3 | 3 | 3 |
| 4 | 100 | 10 | 4 | 4 |
| 5 | 101 | 11 | 5 | 5 |
| 6 | 110 | 12 | 6 | 6 |
| 7 | 111 | 13 | 7 | 7 |
| 8 | 1000 | 20 | 10 | 8 |
| 9 | 1001 | 21 | 11 | 9 |
| 10 | 1010 | 22 | 12 | A |
| 11 | 1011 | 23 | 13 | B |
| 12 | 1100 | 30 | 14 | C |
| 13 | 1101 | 31 | 15 | D |
| 14 | 1110 | 32 | 16 | E |
| 15 | 1111 | 33 | 17 | F |
| 16 | 10000 | 100 | 20 | 10 |
Since (for us) a signal can be in one of two states, it is convenient to use binary (a.k.a. base 2) notation. That way if we have three signals with the first and third high and the middle one low, we can represent the situation using 3 binary digits, specifically 101.
Recall that to calculate the numeric value of a ordinary (base 10, i.e., decimal) number the right most digit is multiplied by 100=1 the next digit to the left by 101=10, the next digit by 102=100, etc.
For example 6205 = 6*103 + 2*102 + 0*101 + 5*100 = 6*1000 + 2*100 + 0*10 +5*1.
Similarly binary numbers work the same way so, for example the
binary number 11001 has value (written in decimal)
1*24 + 1*23 + 0*22 +
0*21 + 1*22 = 1*16 + 1*8 + 0*4 + 0*2 +1*1
= 16+8+1 = 25.
We normally use decimal (i.e., base 10) notation where each digit is conceptually multiplied by a power of 10. The use of 10 digits is strongly related to our having 10 fingers (aka digits).
We all know about the ten's place
, hundred's place
,
etc.
The feature that the same digit is valued 1/10 as much if it is one
place further to the right continues to hold to the right of the
decimal point.
Computer hardware uses binary (i.e., base 2) arithmetic so to understand hardware features we could write our numbers in binary. The only problem with this is that binary numbers are long. For example, the number of US senators would be written 1100100 and the number of miles to the sun would need 25 bits (binary digits).
This suggests that decimal notation is more convenient. The problem with relying on decimal notation is that we need binary notation to express multiple electrical signals and it is difficult to convert between decimal and binary because ten is not an integral power of 2.
The table on the right (for now only look at the first two columns) shows how we write the numbers from 0 to 16 in both base 10 and base 2.
Start Lecture #11
Remarks:
Base 10 is familiar to us, which is certainly an enormous advantage, but it is hard to convert base 10 numbers to/from base 2 and we need base 2 to express hardware operation. Base 2 corresponds well to the hardware but is verbose for large numbers.
Let's try a compromise, base 4.
To convert between base four and base two is easy since the four
base 4 digits
(I hate that expression, for me digit means
base 10) correspond exactly to the four possible pairs of bits.
base 4 bits
0 00
1 01
2 10
3 11
Look again at the table above but now concentrate on columns two and three.
We see that it is easy to convert back and forth between base 2 and base 4. But base 4 numbers are still a little long for comfort: a number needing n bits would use ⌈n/2⌉ base four digits.
A base 8 number would need ⌈n/3⌉ digits for an n-bit base 2 number because 8=23 and a base 16 number would need ⌈n/4⌉. Base 8 (called octal) would be good, and was used when I learned about computers. The C language dates from this time and C has support for octal. Base 16 (called hexadecimal) is used now and C supports it.
Question: Why the switch from base 8 to base
16?
Answer: Words in a 1960s computer had 36 bits and
36 is divisible by 3 so a word consisted of exactly 12 octal digits.
Words in modern computers have 32 bits and 32 is divisible by 4 (but
not by 3) so a 32-bit word consists of exactly 8 base-16 digits.
(Recently the word size has increased to 64 bits, but 64 is also
divisible by 4 and a 64-bit word consists of exactly 16 base-16
digits.)
Question: Why were there 36-bit words?
Answer: Characters then were 6 bits so a 36-bit
word held six characters.
Base 16 is called hexadecimal.
We need 16 symbols for the 16 possible digits; the first 10 are obvious 0,1,...,9. We need 6 more to represent ten, eleven, ..., fifteen.
We use A, B, C, D, E, F to represent the extra 6 digits. When we write a hexadecimal number we precede it with 0x.
So 0x1234 = 1*(16)3 + 2*(16)2 + 3*(16)1 + 4*(16)0 is quite a bit bigger than 1234 = 1*(10)3 + 2*(10)2 + 3*(10)1 + 4*(10)0
You convert a base-16 to/from binary one hexadecimal digit (4 bits) at a time. For example
1011000100101111 = 1011 0001 0010 1111 = B 1 2 F = 0xB12F
Look again at the table above right and notice that groups of four bits do match one hex digit.
You need to learn (or figure out) that 0xA3 + 0x3B = 0xDE and worse 0xFF + 0xBB = 0x1BA and much worse 0xFA * 0xAF = 0xAAE6.
Although fundamentally hardware is based on bits, we will normally think of computers as byte oriented. A byte (aka octet) consists of 8 bits (or two hex characters). As we learned, the primitive types in C (char, int, double, etc) are each a multiple of bytes in size. In fact, the multiples are powers of 2 so individual data items are 1, 2, 4, 8, or 16-bytes long.
#include <string.h>
#include <stdio.h>
void showBytes (unsigned char *start, int len) {
int i;
for (i=0; i<len; i++)
printf("%p %5x %c\n", start+i, *(start+i), start[i]);
}
int main(int argc, char *argv[]) {
showBytes(argv[1], strlen(argv[1]));
}
The simple program on the right prints its first argument in hex. Actually it does a little more, it prints the address of each character of the first argument, and then prints the character twice, first as a hex number and then as a character. Remember that in C, a character is an integer type.
./a.out jB4k 0x7ffd3892789d 6a j 0x7ffd3892789e 42 B 0x7ffd3892789f 34 4 0x7ffd389278a0 6b k
Several points to note.
#include <stdio.h>
int main(int argc, char *argv[]) {
int idx;
char c[3];
short s[3];
int i[3];
long l[3];
float f[3];
double d[3];
for (idx=0; idx<3; idx++) {
printf("%p %p %p %p\n", &c[idx],
&s[idx], &i[idx], &l[idx]);
}
printf("\n");
for (idx=0; idx<3; idx++) {
printf("%p %p\n", &f[idx], &d[idx]);
}
}
The program on the right produces the following output.
0x7fff73546565 0x7fff73546502 0x7fff73546508 0x7fff73546520 0x7fff73546566 0x7fff73546504 0x7fff7354650c 0x7fff73546528 0x7fff73546567 0x7fff73546506 0x7fff73546510 0x7fff73546530 0x7fff73546514 0x7fff73546540 0x7fff73546518 0x7fff73546548 0x7fff7354651c 0x7fff73546550
Note that the chars are one byte apart, shorts are two bytes apart, ints and floats, are four bytes apart, and longs and doubles are eight bytes apart.
Also note that chars (which are of size 1) can start on any byte, shorts (which are of size 2) can start only on even numbered byte, ints and floats (which are of size 4) can start only on addresses that are a multiple of 4, and longs and doubles (which are of size 8) can start only on addresses that are a multiple of 8.
In general data items of size n must be aligned on addresses that are a multiple of n.
This answers a question we posed concerning malloc(), namely malloc() returns addresses that are a multiple of the most severe alignment restriction on the system. Normally this is 16.
We think of memory as composed of 8-bit bytes and the bytes in memory are numbered. So if you could find a memory as small as 1KB (kilobyte) you could address the individual bytes as byte 0, byte 1, ... byte 1023. If you numbered them in hexadecimal it would be byte 0 ... byte 3FF.
As we learned a C-language char takes one byte of storage so its address would be one number.
A 32-bit integer requires 4 bytes. I guess one could imagine storing the 4 bytes spread out in memory, but that isn't done. Instead the integer is stored in 4 consecutive bytes, the lowest of the four byte addresses is the address of the integer.
Normally, integers are aligned i.e, the lowest address is a multiple of 4. On many systems a C-language double occupies 8 consecutive bytes the lowest numbered of which is a multiple of 8.
Let's consider a 4-byte (i.e., 32-bit) integer N that is stored in the four bytes having address 0x100-0x103. The address of N is therefore 0x100, which is a multiple of 4 and hence N is considered aligned.
Let's say the value of N in binary is
0010|1111|1010|0101|0000|1110|0001|1010
which in hex
(short for hexadecimal) is 0x2FA50E1A.
So the four bytes numbered 100, 101, 102, and 103 will contain 2F A5
0E 1A.
However, a question still remains: Which byte contains which pair of
hex digits?
Unfortunately two different schemes are used. In little endian order the least significant byte is put in the lowest address; whereas in big endian order the most significant byte is put in the lowest address.
Consider storing in address 0x1120 our 32-bit (aligned) integer, which contains the value 0x2FA50E1A. A little endian machine would store it this way.
byte address 0x1120 0x1121 0x1122 0x1123
contents 0x1A 0x0E 0xA5 0x2F
In contrast a big endian machine would store it this way.
byte address 0x1120 0x1121 0x1122 0x1123
contents 0x2F 0xA5 0x0E 0x1A
int main(int argc, char *argv[]) {
int a = 54321;
showBytes((char *)&a, sizeof(int));
}
On the right is an example using the showBytes() routine defined just above that gives (in hex) the four bytes in the integer 54321. The output produced is (ignoring the third column)
0x7ffd0a0ed8f4 31 0x7ffd0a0ed8f5 d4 0x7ffd0a0ed8f6 0 0x7ffd0a0ed8f7 0
So the four bytes are 0x31, 0xD4, 0x0, and 0x0. If the number in hex is 31 D4 00 00 it would be much bigger than 54321 decimal. Instead the number is 00 00 D4 31 hex which does equal 54321 decimal.
So the processor in my laptop is little endian (as are all x86 processors).
Homework: 2.58.
Remark: Now imagine connecting a little endian machine to a big-ending machine and sending an int from one to the other one byte at a time.
As we know a string is a null terminated array of chars; each char occupies one byte. Given the string "tom", the char 't' will occupy one byte, 'o' will occupy the next (higher) byte, 'm' will occupy the next byte and '\0' the next (last) byte.
There is no issue of byte ordering (endian) since each character is stored in one byte and consecutive characters are stored in consecutive bytes.
Compiled code is stored in the same memory as data. However, unlike data, the format of code is not standardized. That is, the same C program when compiled on different systems will result in different bit patterns.
We will see many examples later.
Start Lecture #12
MIDTERM EXAM
Start Lecture #13
Now we know how to represent integers and characters in terms of bits and how to write each using hexadecimal notation. But what about operations like add, subtract, multiply, and divide.
We will approach this slowly and start with operations on individual bits, operations like AND and OR.
To define addition for integers you need to give a procedure for adding 2 numbers, You can't simply list all the possible addition problems since there are an infinite number of integers. However, there are only 2 possible bits and hence for a binary (i.e., two operand) operation on bits there are only four possible examples and we simply list all four possible questions and the corresponding answers. This list is often called a truth table.
The following diagram does this for six basic bit-level operations.
Just below each truth tables is the symbol used for that operation
when drawing a diagram of an electronic circuit
(a circuit diagram
).
| A | ~A |
| 0 | 1 |
| 1 | 0 |
| A | B | A&B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| A | B | A|B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
| A | B | ^ |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| A | B | NAND |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| A | B | NOR |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |

Once you know to compute A|B for A and B each a single bit, you can define A|B for A and B equal length bit vectors. You just apply the operator to corresponding bits.
The same applies to &, ~, and ^.
For example 0101 | 0010 = 0111 and 1100 ^ 1010 = 0110.
It turns out that if you have enough chips that compute only NAND, you are able to wire them together to support any Boolean function. We call NAND universal for this reason. This is also true of NOR but it is not true of any other two input primitive.
| ~A | NOT A |
| A&B | A AND B |
| A|B | A OR B |
| A^B | A XOR B |
C directly supports NOT, AND, OR, and XOR as shown on the table to the left and mentioned previously in section 2.9. Note that these operations are bit-wise. That is, bit zero of the result depends only on bit zero of the operand(s), bit one of the result depends only on bit one of the operands, etc.
C does not have explicit support for NAND or for NOR.
Done previously. Be careful not to confuse bit-level AND (&) with logical AND (&&). The logical operators (&&, ||, and ! treat any nonzero value as TRUE, and zero as FALSE. Also the value returned is always 0 or 1.
Note, for example that !0x00 = 0x01; whereas ~0x00=0xFF.
Also remember that C guarantees short-circuit
evaluation of
&& and ||.
In particular ptr&&*ptr cannot generate a null
pointer exception since, when ptr is null, *ptr is
not evaluated.
This was introduced in C99 so is not in the text. You may use it, but it is not required for the course.
In C, the expression x<<b shifts x b bits to the left. The b most left bits of x are lost and the b right most bits of x become 0.
There is a corresponding right shift >> but there is a question on what to do with the high order (sign) bit.
In a logical right shift all the bits move right and the new HOB becomes a zero. The >> operator is always a logical right shift for unsigned values.
In an arithmetic right shift, again all the bits shift right, but the new HOB becomes a copy of the old high order bit.
Most (perhaps all) systems perform arithmetic right shifts when the values are signed.Homework: 2.61, 2.64.
Start Lecture #14
Integers in C come in several sizes and two flavors
.
A char is a 1-byte integer; a short is a 2-byte
integer; and an int is a 4-byte integer.
The size of a long is system dependent.
It is 4 bytes (32 bits) on a 32-bit system and 8 bytes (64 bits) on
a 64-bit system.
What about the two flavors
?
That comes next.
The first flavor of C integers is unsignted.
We illustrate only unsigned short; the other sizes are
essentially the same (but with a different number of bits).
So we have 16 bits in each short integer, representing from right to
left 20 to 215.
If all these 16 bits are 1s, the value is
215+214+213+212+
211+210+29+28+
27+26+25+24+
23+22+21+20
= 216-1 = 65,535.
Question: Why?
Answer: If the number were one bigger, it would
be a 1 followed by 16 zero bits so its value would be 216.
In a sense these encodings are the most natural. They are used and they are well supported in the C language. Naturally the sum of two very big 16-bit unsigned numbers would need 17 bits; this is called overflow. Nonetheless, the situation is good for unsigned addition:
But there is a problem. Unsigned encodings have no negative numbers. That is why I didn't mention subtracting the bigger from the smaller.
To include negative numbers there must be a way to indicate the sign of the number. Also, since some shorts will be negative and we have the same number of shorts as unsigned shorts (because we sill have 16 bits), there will be fewer positive shorts than we had for unsigned shorts.
Before specifying how to represent negative numbers, let's do the easy case of non-negative numbers (i.e., positive and zero). For non-negative numbers set the leftmost bit (called the sign bit) to zero and use the remaining bits as above. Since the left bit (the high order bit or HOB) is for the sign we have one fewer for the number itself so the largest short has a zero HOB and 15 one bits, which equals 215-1 = 32,767.
We could do the analogous technique for negative
numbers: set the HOB to 1 and use the remaining 15 bits for the
magnitude (the absolute value in mathematics).
This technique is called the sign-magnitude
representation
and was used in the past, but is not common now.
One annoyance is that you have two representations of zero
0000000000000000 and 1000000000000000.
We will not use this encoding.
Instead of just flipping the leftmost (or sign) bit as above we form the so-called 2s-complement. For simplicity I will do 4-bit two's complement and just talk about the 16-bit analogue (and 32- and 64-bit analogues), which are essentially the same.
With 4 bits, there are 16 possible numbers. Since twos complement notation has one only representation for each number (including 0), there are 15 nonzero values. Since there are an odd number of nonzero values, there cannot be the same number of positive and negative values. In fact 4-bit two's complement notation has 8 negative values (-8..-1), and 7 positive values (1..7). (In sign magnitude notation there are the same number of positive and negative values, which is convenient; but there are two representations for zero, which is inconvenient.)
The high order bit (hob) i.e., the leftmost bit is called the sign bit. The sign bit is zero for positive numbers and for the number zero; the sign bit is one for negative numbers.
Zero is written simply 0000.
1-7 are written 0001, 0010, 0011, 0100, 0101, 0110, 0111. That is, you set the sign bit to zero and write 1-7 using the remaining three lob's (low order bits). This last statement is also true for zero.
-1, -2, ..., -7 are written by taking the two's complement of the corresponding positive number. The two's complement of a (binary) number is computed in two steps.
If you take the two's complement of -1, -2, ..., -7, you get back the corresponding positive number. Try it.
If you take the two's complement of zero you get zero. Try it.
What about the 8th negative number?
-8 is written 1000.
But if you take its (4-bit) two's complement, you
must get the wrong number because the correct
number (+8) cannot be expressed in 4-bit two's complement
notation.
Remarks:
Recall that the two's complement of x is ~x + 1. We want the two's complement to be the additive inverse. Let's see if it is. Remember that ~x is x complement and -x is the twos complement which equals ~x+1.
Two'sComp(x) = ~x + 1
x + Two'sComp(x) = x + (~x + 1)
= (x + ~x) + 1
= (111...111) + 1
= (-1) + 1
= 0
Success!
Amazingly easy (if you ignore overflows).
You could reasonably ask what does this funny notation have to do with negative numbers. Let me make a few comments.
Question: What does -1 mean mathematically?
Answer: It is the unique number that, when added
to 1, gives zero.
Our representation of -1 does do this (using regular binary addition and discarding the final carry-out) so we do have -1 correct.
Question: What does negative n
mean, for n>0?
Answer: It is the unique number that, when
added to n, gives zero.
The 1s complement of n when added to n gives
all 1s, which is -1.
Thus the 2s complement, which is one larger, will give zero, as
desired.
| Decimal | Hex | Binary | |
|---|---|---|---|
| Unsigned Max | 65535 | FF FF | 11111111 11111111 |
| Unsigned Min | 0 | 00 00 | 00000000 00000000 |
| Signed Max | 32767 | 7F FF | 01111111 11111111 |
| Signed Min | -32768 | 80 00 | 10000000 00000000 |
| -1 | -1 | FF FF | 11111111 11111111 |
The table on the right shows the extreme values for both unsigned and signed 16-bit integers. It the signed case we also show the representation of -1 (there is no unsigned -1).
Note that the signed values all use the twos-complement representation. In fact I doubt we will use sign/magnitude (or ones'-complement) for integers any further.
| Width (bits) | ||||
|---|---|---|---|---|
| 8 | 16 | 32 | 64 | |
| Unsigned Max | 255 | 65,535 | 4,294,967,295 | 18,446,744,073,709,551,615 |
| Signed Max | 127 | 32,767 | 2,147,483,647 | 9,223,372,036,854,775,807 |
| Signed Min | -128 | -32,768 | 2,147,483,647 | -9,223,372,036,854,775,808 |
The second table on the right shows the max and min values for various sizes of integers (1, 2, 4, and 8 bytes).
General rule: Be Careful!
.
#include <stdio.h>
int main(int argc, char *argv[]) {
int i1=-1, i2=-2;
unsigned int u1, u2=2;
u1 = i1; // implicit cast (unsigned)
printf("u1=%u\n", u1);
printf( "%s\n", (i2>u2) ? "yes" : "no");
return 0;
}
The code in the right illustrates why we must be careful when mixing unsigned and signed values. The fundamental rule that is applied in C when doing such conversions (actually called casts) is that the bit pattern remains the same even though this sometimes means that the value changes.
When I ran the code on the right, the output was
u1=4294967295 yes
When the code executes u1=i1, the bits in i1 are all ones and this bit pattern remains the same when the value is cast to unsigned and placed in u1. So u1 becomes all 1s which is a huge number, as we see in the output.
When we compare i2>u2, either the -2 in i2 must be converted to unsigned or the 2 in u2 must be converted to signed. The rule in C is that the conversion goes from signed to unsigned so the -2 bit pattern in i2 is reinterpreted as an unsigned value. With that interpretation i2 is indeed much bigger that the 2 in u2.
We have just seen signed/unsigned conversions.
How about short to int or int to long?
How about unsigned int to unsigned long?
I.e., converting when the sizes are different but
the signedness
is the same.
In summary C converts in the following order. That is, types on the left are converted to types on the right.
int → unsigned int → long → unsigned long → float → double → long double.
What if you want to put an int into a short or put a long into an int?
Bits are simply dropped from the left, which can alter both the value and the sign.
Advice: Don't do it.
Be careful!!
Binary addition (i.e., addition of binary numbers) is performed the same as decimal addition. You can add a column of numbers in binary as with decimal, but we will be content to just add two binary numbers.
You proceed right to left and may have to carry a "1".
The only problem is overflow, i.e., where the sum requires more bits than are available. That means there is a carry out of the HOB. For example if you were using 3-digit decimals, the sum 834+645 does not fit in 3 digits (there is a carry out of the hundreds place into what would be the thousands place). Similarly using 4-bit binary numbers, the sum 0111+1001 does not fit in 4 bits.
When there is no overflow, (computer, i.e., binary) addition is conceptually done right to left one bit at a time with carries just like we do for base 10.
In reality very clever tricks are used to enable
multiple bits to be added at once.
You could google ripple carry
and carry lookahead
or
see my lecture notes for computer architecture.
The news is very good—you just add as though it were unsigned addition and throw away any carry-out from the HOB (high order bit).
Only overflow is a problem (as it was for unsigned). However, detecting overflow is not the same as for unsigned. Consider 4-bit 2s complement addition; specifically (-1) + (-1). 1111 + 1111 = 11110 becomes 1110 after dropping the carry-out. But overflow did not occur 1110 is the correct sum of 1111 + 1111!
The correct rule is that overflow occurs when and only when the carry into the HOB does not equal the carry out of the HOB.
Recall that with two's complement there is one more negative number than positive number. In particular, the most-negative number has no positive counterpart. Specifically, for n-bit twos complement numbers, the range of values is
most neg = -2n-1 ... 2n-1-1 = most pos
For every value except the most neg, the negation is obtain by simply taking the two's complement, independent of whether the original number was positive, negative, or zero.
Multiply the two n-bit numbers, which gives up to 2n-bits and discard the n HOBs. Again, the only problem is overflow.
3 * (-4) = 11100
11
-----
11100
11100
------
1010100
A surprise occurs. You just mulitply, the twos complement numbers and truncate the HOBs and ... it works—except for overflow.
On the board do 3 * (-4) using 5 bits.
3 = 00011; 4 = 00100; (~4) = 11011; (-4) = 11100
The multiplication is on the right.
Now truncate 1010100 to 5 bits.
You get y = 10100.
Is this y = -12?
~y = 01011. -y = 01100 = 8+4 = 12
It works!
You can multiply x*2k (k≥0) by just shifting x<<k. This is reasonably clear for x≥0, but works for 2s complement as well.
Note that compilers are clever and utilize identities like
x * 24 = x * (32-8) = x*32 - x*8 = x<<5 - x<<3
The reason for doing this is that shift/add/sub are faster than multiplication.
Division is even slower than multiplication; so we note that right shifting by k gives the same result as dividing by 2k. Actually it gives the floor of the division.
If the value 2k is unsigned, use logical right shift; if it is signed use arithmetic right shift.
Addition and multiplication work unless there is an overflow.
Adding two n-bit unsigned numbers gives (up to) an (n+1)-bit result, which we fit into n bits by dropping the HOB. So you get an overflow if the HOB of the result is 1
Multiplying two n-bit unsigned numbers gives (up to) a 2n-bit result, which we fit into n bits by dropping the n HOBs. So you get an overflow if any of the n HOBs of the result are 1.
Same idea but detecting overflow is more complicated. For addition of n-bit numbers, which includes subtraction, the non-obvious rule is that an overflow occurs if the carry into the HOB (bit n-1) != the carry-out from that bit.
Homework:
Recitation topic.
Exactly analogous to decimal numbers with a decimal point. Just as 0.01 in decimal is one-hundredth, 0.01 in binary is one-quarter and 0x0.01 is one-twohundredfiftysixth.
If instead of powers of 2, we used powers of 10, the above would be how we write numbers with decimal points.
Fractional binary notation requires considerable space for numbers that are very large in magnitude or very near zero.
5 * 2100 = 101000000...0
| 100 0s |
2-100 = 0.00000000001
| 100 0s |
(The second example above uses sign-magnitude.
But numbers like these comes up in science all the time and the solution
used is often called scientific notation
.
Avagadro's number ~ 6.02 * 1023
Light year ~ 5.88 * 1012 miles
The coefficient is called the mantissa or significand.
In computing we use IEEE floating point, which is basically the same solution but with an exponent base of 2 not 10. As we shall see there are some technical differences.
Represent a floating number as
(-1)s × M × 2E
Where
Naturally, s is stored in one bit.
For single precision (float in C) E is stored 8 bits and M is stored in 23. Thus, a float in C requires 1+8+23 = 32 bits.
For double precision (double in C) E is stored in 11 bits and M in 52. Thus, a double in C requires 1+11+52 = 64 bits.
Now it gets a little complicated; the values stored are not simply E and M and there are 3 classes of values.
Lets just do single precision, double precision is the same idea just with more bits. The number of bits used for the exponent is 8
Although the exponent E itself can be positive, negative, or zero the value stored exp is unsigned. This is accomplished by biasing the E (i.e., adding a constant so the result is never negative).
With 8 bits of exponent, there are 256 possible unsigned values for exp, namely 0...255. We let E = exp-127 so the possible values for E are -127...128.
Stated the other way around, the value stored for the exponent is the true exponent +127.
With scientific notation we write numbers as, for example. 9.4534×1012. An analogous base 2 example would be 1.1100111×210.
Note that in 9.4535 the four digits after the decimal point each
distinguish between 10 possibilities whereas the digit before the
decimal point only distinguishes between 9 possibilities, so is not
fully used
.
Note also that in 1.1100111 the 1 to the left distinguishes between one possibility, i.e. is useless.
IEEE floating point does not store the bit to the left of the
binary point because is always 1 (actually see below for the other
two classes of values
).
Let F = 15213.010
= 111011011011012
= 1.11011011011012×213
fract stored = 110110110110100000000002
exp stored = 13+127 = 140 = 100011002
sign stored = 0
value stored = 0 10001100 11011011011010000000000
Used when the stored exponent is all zeros, i.e., when the exponent is as negative as possible, i.e., when the number is very close to 0.0.
The value of the significant and exponent in terms of the stored value is slightly different.
Note there are two zeros since ieee floating point is basically sign magnitude.
Used when the stored exponent is all ones, i.e., when the exponent is a large as possible.
If the significand stored is all zeros, the value represents
infinity (positive or negative
), for example overflow when
doing 1.0/0.0.
If the significand is not all zero, the value is called NaN for not-a-number. It is used in cases like sqrt(-1.0), infinity - infinity, infinity × 0.
IEEE floating point represents numbers as (-1)s × M × 2 E. There are extra complications to store the most information in a fixed number of bits.
The book covers the Intel architecture, which dominates laptops, desktops, and data centers. Some of the fastest supercomputers also have (many) intel CPUs.
It is not used in cell phones and tablets.
The Intel architecture has been remarkably successful from commercial and longevity standpoints.
Modern systems are backwards compatible with the 8086 version introduced in 1978 (more than 40! years ago). In addition to the commercial advantages of backwards compatibility, its implementation is a technological tour-de-force, which has won awards for its engineering.
It has a horrendously complicated instruction set. It is called a CISC (Complex Instruction Set Computer) design. Architectures designed in the last few decades tend to have RISC (Reduced Instruction Set Computer) designs and current implementations of the Intel architecture actually (during execution!) translate many of the complex instructions to a simpler core set.
The book (wisely) only covers a small subset of the possible instructions. For example, we limit arithmetic to operations on 64-bit data, ignoring the 32- 16- and 8-bit arithmetic supplied for backwards compatibility. If you use gcc (or cc) on your laptop (or access, or linserv1) you will see these instructions
We have normally compiled C program with a simple cc command. Different C compilers can produce different assembly for the same C program. Also normally the goal of the compile is to generate high performance output. We instead are interested in simple assembler output. As a result, to compile the program joe.c we will use the command
gcc -Og -S joe.c
On many computers, in particular on linserv1, gcc
and cc are the same, but the -Og is needed to
generated simple (vs. high performance) assembly code.
The -S tells the compiler to make available the generated
assembly language code.
The machine state of any processor has details that are under the covers in C or Java or Python or ... . The state for the Intel architecture includes.
Memory is simply a huge array of bytes. Compiled instructions as well as data reside here. A portion of memory is used as a stack to support procedure calls and returns.
Since the data and the program instructions are stored in memory, the CPU needs to fetch both during execution. The CPU sends an address to memory which responds with the contents of that address.
When the CPU needs to store a computed result into memory, it again sends the address in addition to sending the new value.
In summary
Remarks: Mostly repeated from last class.
Read. We will soon learn what many of these instructions do.
On access.cims.nyu.edu I have written mstore.c from the book.
long mult2(long, long);
void multstore(long x, long y, long *dest) {
long t = mult2(x,y);
*dest = t;
}
| Register Name | Conventional Use |
Register Name | Conventional Use |
|
|---|---|---|---|---|
| %rax | Return Value | %r8 | 5th argument | |
| %rbx | callee saved | %r9 | 6th argument | |
| %rcx | 4th argument | %r10 | caller saved | |
| %rdx | 3rd argument | %r11 | caller saved | |
| %rsi | 2nd argument | %r12 | callee saved | |
| %rdi | 1st argument | %r13 | callee saved | |
| %rbp | callee saved | %r14 | callee saved | |
| %rsp | stack pointer | %r15 | callee saved |
I compiled mstore.c on crackle2 with gcc -Og -S , which generates mstore.s. I then removed the lines in mstore.s beginning with a dot. This gives the same code as the book. Here it is with line numbers and comments added (as in the book).
// void multstore(long x, long y, long *dest) // x in %rdi, y in %rsi, dest in %rdx 1 multstore: 2 pushq %rbx // save %rbx on stack 3 movq %rdx, %rbx // copy dest to %rbx 4 call mult2 // call mult2(x, y) 5 movq %rax, (%rbx) // store result at *dest 6 popq %rbx // restore %rbx 7 ret // return
| C declaration | Intel data type | Suffix | Size in bytes |
|---|---|---|---|
| char | Byte | b | 1 |
| short | Word | w | 2 |
| int | Double word | l | 4 |
| long | Quad word | q | 8 |
| char * | Quad word | q | 8 |
| float | Single precision | s | 4 |
| double | Double precision | d | 8 |
integers(which includes pointers, i.e., addresses) can be (on a 64-bit machine) either 1, 2, 4, or 8 bytes in length.
Most operations are performed on the 16 registers (the fastest memory in the system). But memory can be accessed directly as well. Typically, data is moved from memory to registers, then operated on (add, sub, etc) and then put back in memory.
For historical reasons concerning backward compatibility the registers have funny names.
We will look at 3 types of assembly instructions.
As we shall see, most operations have one or two operands. There are three types of operands.
The register names above are for the full 64-bit registers. For each of these registers there are other names for the low-order 32-bit subset, the low-order 16-bit subset, and the low-order 8-bit subset. We will use only the names for the full 64-bit operands.
| Type | Example | Value if Source (r-value) | Value if Destination (l-value) |
|---|---|---|---|
| Immediate | $-3.2 | -3.2 | Not possible |
| Immediate | $0x10F | 271 | Not possible |
| Register | %rax | Contents of register rax | The register itself |
| Memory | 12345 | Contents of memory location 12345 | The location itself |
| Memory | (%rax) | Contents of memory at location specified in register rax | The memory location specified in register rax |
| Memory | 0xF(%rax) | Contents of mem loc(15 + contents rax) | The mem location (15 + contents rax) |
| Memory | (%rax,%rbx) | Contents of loc (contents rax + contents rbx | The location (contents rax + contents rbx) |
| Memory | 8(%rax,%rbx) | Contents of loc (8 + contents rax + contents rbx | The location (8 + contents rax + contents rbx) |
| Memory | (,%rbx,4) | Contents of loc 4*(contents rbx) | The location 4*(contents rbx) |
| Memory | 15(,%rbx,8) | Contents of loc (15 + 8*contents rbx) | The location (15 + 8*contents rbx) |
| Memory | (%rax,%rbx,2) | Contents of loc (contents rax + 2*contents rbx) | The location (contents rax + 2*contents rbx) |
| Memory | 23(%rax,rbx,4) | Contents of loc (23 + contents rax + 4*contents rbx) | The location (23 + contents rax + 1*contents rbx) |
The basic data movement instruction is called move and is written mov with a suffix to indicate the size of the data item moved. It is somewhat misnamed; it is really a copy not a move.
The src is given first then the destination (the reverse of C). For example the C statement *dest = t; might become movq %rax, (%rbx)
A move instruction cannot have both operands in memory, at least one must be a register (or the source an immediate).
long plus(long x, long y);
void sumstore (long x, long y,
long *dest) {
long t = plus(x, y);
*dest = t;
}
sumstore:
pushq %rbx
movq %rdx, %rbx
call plus
movq %rax, (%rbx)
popq %rbx
ret
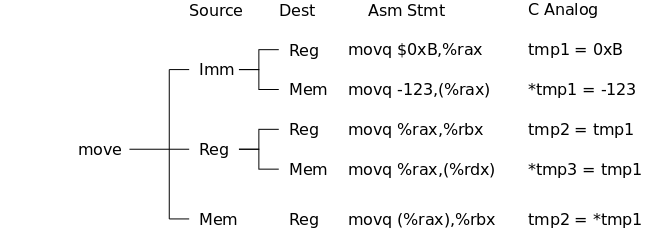
The size of a specified register must match the size of the move itself.
There are variants of move that sign extend or zero extend. These are used when you move a value to a longer format.
For example, movzbl moves from a byte to a doubleword (32-bits) by zero extending (on the left).
Similarly, movsbw moves from a byte to a word (16-bits) by sign extending (replicating the sign bit).
There are other special cases as well, see the book for details. One oddity is that, when the target is a register movzbl acts the same as movzbq: it moves the byte and then zeros the high-order 7 bytes of the quadword even though it name suggest it would only zero the 3 high-order bytes of the double word.
void swap(int *xp, int *yp) {
int t0, t1;
t0 = *xp;
t1 = *yp;
*xp = t1;
*yp = t0;
}
Note: This swap uses two temporaries. The one we did a month ago used only one. However, that algorithm uses memory to memory moves so needs to be modified for the intel machine language.
The most general form is Disp(Rb,Ri,S)
Explain why this (complicated) address is useful for stepping through a C array.
Special Cases
| Expression | Address Computation | Address |
|---|---|---|
| 0x8(%rdx) | 0xf000 + 0x8 | 0xf008 |
| (%rdx,%rcx) | 0xf000 + 0x100 | 0xf100 |
| (%rdx,%rcx,4) | 0xf000 + 4*0x100 | 0xf400 |
| 0x80(,%rdx,2) | 2*f000 + 0x80 | 0x1e080 |
Assume these two registers have been set in advance.
Then the table on the right shows various address that can be composed using these two registers and some subsets of the general addressing mode above.
The intel architecture has support for a stack maintained in
memory.
The three key components are the two instructions
pushq Src and
popq Dest
and the dedicated register %rsp
Although the Src operand of pushq can be fairly
general we will use only the case where Src is simply a
register, for example %rbp.
Then the instruction
pushq %rbp
has the same effect as the two instruction sequence.
subq $8,%rsp
movq %rbp,(%rsp)
Analogously,
popq %rax
has the same effect as the two instruction sequence.
movq (%rsp),%rax
addq $8,%rsp
Show how this corresponds to an (upside down) stack.
Recall that a memory address can be complicated, it can involve two registers, a scale factor, and an additive constant. Sometimes you want that arithmetic on some registers but don't want to reference memory at all. There is an instruction to do just that. It is called load effective address: leaq.
leaq Src, Dest
Typical uses
leaq (%rdi,%rdi,2), %rax # t <-- x+x*2 = 3x
salq $2, %rax # t <-- t<<2 = 4t = 12x
Start Lecture #16
For now we shall ignore possible overflows.
So by the miracle of 2s complement
signed and unsigned are
the same!
Instruction Effect C Equivalent incq Dest Dest = Dest + 1 Dest++ decq Dest Dest = Dest - 1 Dest-- negq Dest Dest = -Dest Dest = -Dest; notq Dest Dest = ~Dest Dest = ~Dest;
Instruction Effect C Equivalent addq Src,Dest Dest = Dest + Src Dest += Src; subq Src,Dest Dest = Dest - Src Dest -= Src; imulq Src,Dest Dest = Dest * Src Dest *= Src; xorq Src,Dest Dest = Dest ^ Src Dest ^= Src; orq Src,Dest Dest = Dest | Src Dest |= Src; andq Src,Dest Dest = Dest & Src Dest &= Src;
There are of course left and right shifts, but remember that there are two kinds of right shift: arithmetic right shift, which sign extends, and logical, which just adds zeros on the left.
For consistency
the assembler also has logical and
arithmetic left shift commands but they are just synonyms for the
same operation, which adds zeros on the right.
Instruction Effect C Equivalent salq k,Dest Dest = Dest << k Dest <<= Src; shlq k,Dest Dest = Dest << k Dest <<= Src; sarq k,Dest Dest = Dest >> k Dest >>= Src; shrq k,Dest Dest = Dest >> k Dest >>= Src;
Although I wrote the two right shifts as having the same C equivalent; they are different. The book writes >>A and <<L to distinguish them. In C they are written the same, but most, if not all, C compilers use arithmetic right shift for signed values and logical right shift for unsigned.
A cheat sheet is on Brightspace/contents
void swap3(long *xp, long *yp, long *zp) {
long t = *xp;
*xp = *yp;
*yp = *zp;
*zp = t;
}
Homework: Write an assembly language version of swap3().
Notes:
A = B + Cas a binary operation. However, it does not fit the examples of binary operators above because, counting the destination, there are three operands.
Below left is a C program (written to look a little like assembler).
On the right is the assembler version, which assumes that initially x is in %rdi, y is in %rsi, and z is in rdx.
The register usage is in the middle.
arith:
leaq (%rdi,%rsi), %rax // t1
addq %rdx, %rax // t2
leaq (%rsi,%rsi,2), %rdx
salq $4, %rdx // t4
leaq 4(%rdi,%rdx), %rcx // t5
imulq %rcx, %rax // ans
ret
| Register | Use |
| %rdi | x |
| %rsi | y |
| %rdx | z,t4 |
| %rax | t1,t2,ans |
| %rcs | t5 |
long arith (long x, long y,
long z) {
long t1 = x+y;
long t2 = z+t1;
long t3 = x+4;
long t4 = y*48;
long t5 = t3 + t4;
long ans = t2 * t5;
return ans;
}
Note that
The normal (integer) multiply imulq Src,Dest is the analogue of addq. That is the 64-bit (quadword) src is multiplied by the 64-bit Dest and the (low-order 64 bits of the) product becomes the new contents of Dest.
Thanks to the miracle of 2s complement, this one instructions works for both unsigned and signed operands.
As with addq and subq, overflow is possible. Indeed, the true product can require 128 bits. There is a special operation (indeed two operations) that preserve all 128 bits of the product.
The 128-bit multiplies (one for signed and one for unsigned) do not fall into the pattern of the previous operations. Instead only one of the operands is specified in the instruction; the other operand must be %rax.
In addition, the location of the 128-bit result is not given in the instruction. Instead, the high-order 64-bits always go into %rdx and the low order 64-bits go inot %rax.
There is no normal
divide or modulus
instruction.
Instead you first place the 128-bit dividend in %rdx
(high order) and %rax (low order) and then issue
divq src (for unsigned division) or idivq src (for
signed division).
In either case the quotient is put into %rax and the
remainder into %rdx
If the dividend is only 64-bits, it naturally is placed in the low-order register %rax and %rdx should be either all zeros or all one to act as the sign extension of %rdx. The cqto (copy quad to octal) does exactly this.
So far we can do assignment statements and arithmetic. What about if/then/else or while?
The idea is that some arithmetic (or other) operation (e.g., an
add) generates a condition (e.g., a negative value) and some
subsequent operation (e.g., a conditional jump) needs to know the
condition from the add.
The solution employed is to have every add (and other operations)
set certain 1-bit condition codes
that can be used by a
subsequent jump instruction to decide whether to actually jump.
We will consider four condition codes; each 1-bit in size.
In fact we will mostly ignore overflow and will emphasize only ZF and SF.
Remember that the arithmetic instructions (like add and sub) can not tell if the operands are signed or unsigned so they might set either (or both) the CF and OF flags.
The condition for setting OF for an addition t=a+b is
(a>0 && b>0 && t<0) || (a<0 && b<0 && t>0)
The lea instruction does not affect the condition codes.
Logical operations set carry and overflow to zero.
Shifts set carry to the last bit shifted out and set overflow to zero.
Inc and Dec set OF and ZF but leave CF unchanged.
cmpq S1,S2 sets the condition codes the same as sub S2-S1 would set them (note S2-S1), but does not store the arithmetic result anywhere.
Similarly testq S1,S2 sets the condition codes the same as andq but does not store the result. So testq %rdx,%rdx sets ZF if %rdx is zero.
You can set a single byte to 0 or 1 based on certain combination of condition codes. This enables you to save the value of the flags, which change frequently during execution This uses the so-called setX operation, where X is replaced by am abbreviated name of the comparison desired (e.g., Less-or-Equal). For example.
In all cases the low order byte is set to zero or one and the remaining bytes are unchanged (see below for movzbq that addresses this issue).
| Instruction | Synonym | D Becomes | Set Condition |
|---|---|---|---|
| sete D | setz D | ZF | Equal / Zero |
| setne D | setnz D | ~ZF | Not Equal / Not Zero |
| sets D | SF | Negative | |
| setns D | ~SF | Nonnegative | |
| setg D | setnle D | ~SF & ~ZF | (signed) Greater |
| setge D | setnl D | ~SF | (signed) Greater or Equal |
| setl D | setnge D | SF | (signed) Less |
| setle D | setng D | SF | ZF | (signed) Less or Equal |
| seta D | snbe D | ~CF & ~ZF | Above (unsigned Greater) |
| setae D | setnb D | ~CF | Above or Equal (unsigned Greater or Equal) |
| setb D | setnae D | CF | Below (unsigned Less) |
| setbe D | setna D | CF | ZF | Below or Equal (unsigned Less or Equal) |
Recall that the set instruction sets a byte. We will normally want values in C longs (which are 8 bytes). The solution is to use the 1 byte register that is contained inside the desired 8 byte register. There are names for the low byte of each of the 16 registers. In particular, %al is the low byte of %rax. We then must zero out the other 7 bytes. The movzbq does this and (as mentioned previously) so does (oddly) movzbl. I mention this oddity twice since, in the following example, the compiler on access uses movzbl (not movzbq) which, were it true to its name, would not zero the high-order 4 bytes.
Below left is a C program. On the right is the assembler version and the register usage is in the middle.
cmpq %rsi, %rdi # compare x and y setg %a1 # set low byte %rax movzbq %a1, %rax # zero out the rest
| Register | Use |
| %rdi | Argument x |
| %rsi | Argument y |
| %rax | Return value |
long GT(long x, long y) {
return x > y;
}
The operation specifies the condition that decides whether you jump, the operand specifies the target to jump to. Elsewhere in the program you have a statement label with that target.
.always
...
je .goHere // jumps if ZF is set
...
jge .goThere // jumps if ~(SF^OF) evaluates true (for us, just ~SF)
...
jmp .always // unconditional jump
.goHere
...
.gothere
...
In general jmp *operand evaluates the operand and jumps to that location. This usage of * is similar to C's For example:
| Instruction | Synonym | Condition | Description |
|---|---|---|---|
| jmp Label | 1 | Direct Jump | |
| jmp *Operand | 1 | Indirect Jump | |
| je Label | jz | ZF | Equal / zero |
| jne Label | jnz | ~ZF | Not equal / not zero |
| js Label | SF | Negative | |
| jns Label | ~SF | Nonnegative | |
| jg | jnle | ~SF&~ZF | Greater (signed) |
| jge | jnl | ~SF | Greater or Equal (signed) |
| jl | jnge | SF | Less (signed) |
| jle | jng | SF|ZF | Less or Equal (signed) |
| ja Label | jnbe | ~CF&~ZF | Above (unsigned) |
| jae Label | jnb | ~CF | Above or equal (unsigned) |
| jb Label | jnae | CF | Below (unsigned) |
| jbe Label | jna | CF|ZF | Below or equal (unsigned) |
Skipped.
Below left is a C program (written to look a little like
assembler).
On the right is the assembler version.
The register usage is in the middle.
absdiff:
cmpq %rsi, %rdi // compare x, y
jle .L4
movq %rdi, %rax // x > y
subq %rsi, %rax
ret
.L4: // x <= y
movq %rsi, %rax
subq %rdi, %rax
ret
| Register | Use |
| %rdi | x |
| %rsi | y |
| %rax | ans |
long absdiff (long x, long y) {
long ans;
if (x > y)
ans = x - y;
else
ans = y - x;
return ans;
}
Instead of jumping to the correct case, it is sometimes faster to
evaluate both possibilities and them move the right one to the
answer.
This is because, in modern machines, pipelining is very important
and conditional branches break the pipeline
.
Below left is the C program (written to look a little like assembler). On the right is the assembler version. The register usage is in the middle.
absdiff:
movq %rdi, %rax
subq %rsi, %rax // ans = x-y
movq %rsi, %rdx
subq %rdi, %rdx // tmp = y-x
cmpq %rsi, %rdi // cmp x : y
cmovle %rdx, %rax // if <=,
ret // overwrite
| Register | Use |
| %rdi | x |
| %rsi | y |
| %rax | ans |
| %rdx | tmp |
long absdiff (long x, long y) {
long ans;
if (x > y)
ans = x - y;
else
ans = y - x;
return ans;
}
The assembly language does not include a do-while construct. Hence we re-write the C using an if and a goto.
long count (unsigned long x) {
long ans = 0;
loop:
ans += x & 0x1;
x >>= 1;
if (x)
goto loop;
return ans;
}
===>>>
long count (unsigned long x) {
long ans = 0;
do {
ans += x & 0x1;
x >>= 1;
} while (x);
return ans;
}
For this problem we are given a C long and wish to determine how many of its 64 bits are one. The algorithm is clear; check each bit and, if it is 1, increment ans.
First we show the easy conversion from normal
C to
goto C
.
We simply replace the do-while by an if plus a
goto.
count:
movq $0, %rax // ans = 0
.Loop:
movq %rdi, %rdx
andq $1, %rdx // tmp = x & 1
addq %rdx, %rax // ans += tmp
shrq %rdi // x >>= 1
jne .Loop // if (x)
ret // goto loop
| Register | Use |
| %rdi | x |
| %rax | ans |
| %rdx | tmp |
Next we generate the assembler from the "goto C". For this simple program, that is an easy task and is shown on the right. Also shown is the usual register assignment table.
Note, however, that even in this easy program, one can stumble. Specifically, it is easy to mistakenly use sarq, instead of shrq, thereby introducing a infinite loop.
The idea is to convert a while loop into a do-while loop. All that is needed is to deal with testing the loop condition on entry to the loop.
We will consider two (fairly similar) methods and apply them to the same simple example as above.
Note that for our simple example, the same Body can be used with while and with do-while.
goto test;
loop:
Body
test:
if (Test)
goto loop;
done:
===>>>
while (Test)
Body
The idea is to keep the Body before the test as in do-while, but jump over Body when you first enter the loop.
On the right we show the C version of a generic while and then its conversion to do-while.
long count (unsigned long x) {
long ans = 0;
goto test;
loop:
ans += x & 0x1;
x >>= 1;
test:
if (x)
goto loop;
return ans;
}
===>>>
long count (unsigned long x) {
long ans = 0;
while (x) {
ans += x & 0x1;
x >>= 1;
}
return ans;
}
On the right we show the conversion for the specific program used to count 1 bits. You can see how close the while and do-while are.
long count (unsigned long x) {
long ans = 0;
if (!x) goto done:
loop:
ans += x & 0x1;
x >>== 1;
if (x)
goto loop;
done:
return ans;
}
===>>>
long count (unsigned long x) {
long ans = 0;
while (x) {
ans += x & 0x1;
x >>= 1;
}
return ans;
}
The second conversion method is to introduce an initial test and goto to the do-while version to reproduce the while behavior.
In the example shown on the right the transformation is applied blindly, which results in an obvious inefficiency: Specifically, the first goto jumps to a return.
Any decent compiler would replace this goto with a return. It is normally silly to jump to a jump.
Covered in recitation. Slides on home page.
Slides on home page.
I will start by showing the basic idea. Then I will give an example with actual assembly code.
if (x==13)
// do thing13;
else if (x==22)
// do thing22;
else if (x==5)
// do thing5
...
else
// do default;
if (x==1)
// do thing1;
else if (x==2)
// do thing2;
else if (x==3)
// do thing3
...
else
// do default;
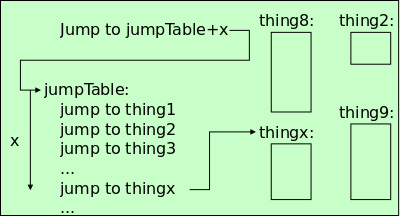
You can always treat switch(x) as a big if-then-else, something like what is shown on the far right above. A disadvantage is that if you have n different cases you will execute on average about n/2 tests before you are successful.
The time when a switch statement is particularly efficient is when the various cases are selected by a (nearly) contiguous range of integers.
Highlighted in yellow we show the simplest case where the possible values for x are 1,2,3,... .
In this case we construct a jump table, i.e., a table of jumps. The first jump in the table jumps to thing1, the second to thing2, etc. See the diagram above in light green. You use the value in x to jump to the correct jump in the table and from there you jump to the correct thing.
Note that even if there are hundreds of things, you execute only two jumps: one into the table and then one to the correct thing.
// the jump table
.align 8
.JmpTbl
jmp .L10
jmp .L11
jmp .L12
jmp .Ldefault
jmp .L1415
jmp .L1415
// The switch code
// preamble, assuming
// s is stored in %rdi
// ans stored in %rax
.switch_eg:
movq $1, %rax // ans = 1
subq 10, %rdi
cmpq $5, %rdi
ja .Ldefault
jmp .JmpTbl(,%rdi,8)
// the "things" go here
Note the possibilities.
long sw_eg
(long s, long y,
long z) {
long ans=1;
switch (s) {
case 10:
ans = y+z;
break;
case 11:
ans = y-z;
case 12:
ans += 7
case 14:
case 15:
ans =z-y
default:
ans = 2;
}
return ans;
}
Above we first see a simple C case statement. Next to it we note that this simple example covers many possibilities.
Then we show the begining of the switch code. We first initialize ans = 1; and then handle the out-of-bounds cases. Note that the ja (jump above) uses an UNsigned comparison so catches both %rdi>5 and %rdi<0. The jmp instruction jumps to a location 8*%rdi bytes past the .JmpTbl, making the assumption that each jmp instruction in the table is 8 bytes long.
Finally, we see the jump table. In this simple implementation the jump table is just a table of jumps to labels corresponding to the cases in the switch statement. So the switch statement translates to a jump into the table and then a jump to the specific case. We will soon see a better implementation that reduces these two jumps to just one (indirect) jump. This new implementation will also drop the (perhaps incorrect) assumption that jmp instructions are 8 bytes long.
Later we will show the assembly code for the various cases, which I
referred to as things
above.
.align 8 .JmpTbl .quad .L10 // s = 10 .quad .L11 // s = 11 .quad .L12 // s = 12 .quad .Ldefault // s = 13 .quad .L1415 // s = 14 .quad .L1415 // s = 15 // replace jmp .JmpTbl(,%rdi,8) // with jmp* .JmpTbl(,%rdi,8)
Instead of jumping to the correct jump, we can use a single
jmp*, a so-called indirect jump.
The idea is that instead of a table of jumps with
the ith jump targeting the ith
thing, we have, as shown on the right, a table of address,
where the ith address is the address
of ith thing.
We still have to write the things
.
When we do, the thing
for s==10 will have statement
label .L10, etc.
As mentioned above, the indirect jump is quite a powerful instruction. When executed it first does the address calculation specified in the instruction (for us multiplying %rdi by 8 and adding the address specified by the label .LJmpTbl). It then accesses the resulting address and reads its contents. Finally, it jumps to the address just read. Phew.
Another advantage is that we can specify (via .quad) that each address will be 8 bytes in length (as needed by the jmp*).
We will show each case separately. The C code is on the right; the assembler code is in the middle with a yellow background; and the registers assigned are a table on the left
ans = 1;
switch(s) {
case 10: // .L10
ans = y+z;
break;
...
}
.L10:
movq %rsi, %rax # y
addq %rdx, %rax # y + z
ret # return
| Register | Use |
| %rdi | s |
| %rsi | y |
| %rdx | z |
| %rax | ans |
We will see very soon that the specific registers chosen were not arbitrary. There are definite conventions that we must follow.
switch(s) {
...
case 11: // .L11
ans = y-z
// fall through
case 12: // .L12
ans += 7;
break;
.L11:
movq %rsi, %rax # y
subq %rdx, %rax # y - z
jmp .Merge1112
.L12:
movq $1, %rax # ans = 1
.Merge1112:
addq $7, %rax
ret # return
| Register | Use |
| %rdi | s |
| %rsi | y |
| %rdx | z |
| %rax | ans |
Note that when case 12 is selected we don't want the effect of case 11. Hence we re-initialize ans.
There is no case 13 so we use the default.
switch(s) {
...
// multiple cases
case 14: // .L1415
case 15:
ans = z-y;
break;
.L14:
.L15:
movq %rdx, %rax # z
subq %rsi, %rax # z - y
ret # return
| Register | Use |
| %rdi | s |
| %rsi | y |
| %rdx | z |
| %rax | ans |
Since these cases are identical we just use two labels for the same section.
switch(s) {
...
default: // .Ldefault
ans = 2;
break;
}
.Ldefault:
movq $2, %rax # ans = 2
ret
| Register | Use |
| %rdi | s |
| %rsi | y |
| %rdx | z |
| %rax | ans |
The default case: ans = 2;
Slides on home page.
right afterthe call point in f().
We treat these three issues in turn
Memory allocation/de-allocation for variables local to a procedure follows a stack-like discipline. That is
oldvalues they had are not restored). So the call of g() by f() necessitates space be set aside for g()'s local variables.
give backthe space used for them and reuse this space later for other purposes.
The basics from 101/102 will be enough.
When I think of a (non-linked) stack, I visualize a column that gets
taller on pushes and shorter on pops.
That is, I view the stack a being grounded
at a low place and
growing and shrinking at its highest address.
The x86-64 run-time stack has the opposite properties: As indicated
in the diagram on the upper right, the stack's fixed bottom
is at
a very high address.
It is sort of fixed in the sky; it grows and shrinks by having
its other end, its top
, get lower and higher.
When implementing a stack, the designer must also decide whether top points to the location containing the last element inserted, or the space where the next element will go.
The x86-64 run-time stack uses the first technique. Hence a pop() first retrieves the value and then increments top; whereas a push() first decrements top.
Another choice made for the Intel stack is to dedicate a register (a precious commodity) to holding the top-of-stack pointer. Specifically, %rsp (register-stack-pointer) is used for this purpose.
So to push onto the stack the value currently in %rdx one could write.
subq $8, %rsp movq %rdx, (%rsp) // assume %rdx contains 0x12FA
This results in the picture on the bottom right showing a bigger stack and a smaller value in the stack pointer %rsp. Register %rdx itself unchanged, but its value is now at the top of the stack. A pop would retrieve that value.
In fact there is a single instruction pushq SRC that
both decrements %rsp and inserts SRC on the top of
the stack
In our case
pushq %rdx
accomplishes the desired stack push.
Naturally there is also a popq. Both pushq and popq require that %rsp be used as the stack pointer. This last comment leads to the following table.
Start Lecture #17
| Register Name | Conventional Use |
Register Name | Conventional Use |
|
|---|---|---|---|---|
| %rax | Return Value | %r8 | 5th argument | |
| %rbx | callee saved | %r9 | 6th argument | |
| %rcx | 4th argument | %r10 | caller saved | |
| %rdx | 3rd argument | %r11 | caller saved | |
| %rsi | 2nd argument | %r12 | callee saved | |
| %rdi | 1st argument | %r13 | callee saved | |
| %rbp | callee saved | %r14 | callee saved | |
| %rsp | stack pointer | %r15 | callee saved |
The table on the right gives the conventional use of the 16 registers in the I86-64 architecture. With a very few exceptions, these are not enforced (or used) by the hardware but more by compilers.
In most cases it would not matter which registers were assigned to which purpose, providing it was done consistently. It would not work if, for example, compilers put the first argument in %r11 but looked for the first parameter to be in %r13.
Two examples where it does matter to the hardware are (the 128-bit multiply and divide) and (the pushq/popq pair) where specific registers have specific hardware functions.
Assume we are studying the assembler code of g(), which was called by f(). If a register is labeled callee saved, and it is altered by g() (the callee), g() must save the register and restore it before returning since f() (the caller) is permitted to assume this behavior.
In contrast, if the register is labeled caller saved, g() can alter it and not restore the original value since that was the responsibility of f(), the caller.
Note that caller-saves implies callee-(might)-destroy.
In addition to the registers explicitly listed as caller saved, all 6 registers used for arguments and the one register used for the return value may be altered by the callee, g() in our example. Hence these seven should also be considered caller save.
Consider writing the function g() in the situation where f() calls g() and g() calls h(). In this (common) case g() may need to save every register that it modifies, both caller saved and callee saved. Explain why.
long sum2(long x, long y) {
return x+y;
}
long sum3(long x, long y,
long z) {
return x+y+z;
}
sum2:
leaq (%rdi,%rsi), %rax
ret
sum3:
addq %rsi, %rdi
leaq (%rdi,%rdx), %rax
ret
| Register | Use |
| %rdi | x |
| %rsi | y |
| %rdx | z |
| %rax | retVal |
The assembler was obtained via
cc -Og -S simple.c
Without the -Og the assembly language produced would have been much more complicated.
Notes:
long add2(long, long);
void addStore(long x, long y,
long *dest) {
long t = add2(x,y);
*dest = t;
}
addstore:
pushq %rbx
movq %rdx, %rbx
call add2
movq %rax, (%rbx)
popq %rbx
ret
| Register | Use |
| %rdi | x |
| %rsi | y |
| %rdx | dest |
Assume add2() is compiled separately and like sum2() calculates the sum of 2 integers. The trick in addstore() is that it needs to put that sum in the memory location given in dest. This seems easy, dest is given in register %rdx.
The trouble is that, since %rdx is caller-saved, add2() might change its value, hence addstore() must save %rdx before calling add2() and must restore it after that call. The simplest way would be to use the stack. The compiler chose instead to save %rdx in %rbx (a callee-saved register) and save/restore %rbx on the stack.
The third argument (in %rdx, naturally) is a address. Notice how it is enclosed in () to access memory. (Actually, as just mentioned, %rdx is copied into %rbx, which is then placed in parentheses).
addstore() is an example of a middle
function g
in the triple
f()->g()->h().
See how it treats the caller-saved %rdx and the callee-saved
%rbx.
Start Lecture #18
// return sum; set diff
long sumDiff(long a, long b,
long *diff) {
*diff = a - b;
return a + b;
}
sumDiff:
movq %rdi, %rax
subq %rsi, %rax
movq %rax, (%rdx)
leaq (%rdi,%rsi), %rax
ret
| Register | Use |
| %rdi | a |
| %rsi | b |
| %rdx | dest |
| %rax | tmp ret |
We know SumDiff will need to set %rax (which is caller-saved) to the returned value. But before calculating the returned value, it can use that register as a temporary.
Note that it requires two instructions to set %rax=%rdi-%rsi
long mult2 (long, long);
void multStore(long x, long y,
long *dest) {
long t = mult2(x, y);
*dest = t;
}
long mult2 (long a, long b) {
long ans = a * b;
return ans;
}
<multStore>:
pushq %rdx # caller save
callq mult2 # multq(x,y)
popq %rdx # restore reg
movq %rax,(%rdx) # store at dest
ret # return
<mult2>:
movq %rdi,%rax # a
imulq %rsi,%rax # a * b
ret # return
| Register | Use |
| %rdi | x a |
| %rsi | y b |
| %rdx | dest |
| %rax | ans |
The C program on the far right is simple and so is the assembly.
One point to note is the first two parameters multStore() receives are the same (and in the same order) as the first two arguments multStore() passes to mult2(). Were they in the reverse order, some movq's would be needed.
Another point is that, since %rdx is caller-saved, mult2() can destroy it and hence multstore() must save and restore it.
A third point is that, since %rdx contains dest (an address), the assembly syntax (%rdx) corresponds to *dest.
Homework:
Assume the C call mult2(x,y) was
instead mult2(y,x).
What would the assembly language for multStore() look like?
Do not make use of the mathematical identity
x * y = y * x
The diagram on the far right shows the run-time stack just before f() calls g(). The diagram on the near right shows the stack after g() has begun execution.
The green region is the portion of the stack associated with the current invocation of f(). (If f is recursive there can be several stack frames for f(), but ignore that for now).
The blue region is for functions that are higher in the call chain leading to f().
When f() actually calls g(), the first thing that happens is that the return address (the address in f() where g() is to return when finished) is pushed on the stack and is momentarily the top-of-stack. The return address is considered part of f()'s stack frame.
The stack frame for g() (or any other function) typically contains three groups of items.
callee saved, which means f() can depend on them containing the same values when g() returns as they contained when f() called g(). So, if g() needs to modify any of those registers (perhaps to perform some computation), it needs to save them someplace and restore them when g() returns to f().
The stack does not normally contain instructions to be executed. The instructions are stored in a different part of the memory and do not change during execution.
Note: It is possible for some parts of the stack frame for g() to be empty. Indeed, some functions g() don't need a stack frame at all. For example if g() doesn't call another function, there is no argument build area. If, furthermore, g() is simple, its local variables and computation may fit in the registers designated for its use (we shall discuss these caller-save registers, and their callee-save counterparts soon).
Transfer of control from f() to g() is
accomplished by the procedure call
callq target
which
Eventually, the called program mult2() returns by executing a retq, which
Note:
In the examples we have seen, the target has been a label.
This is the common situation and is the one we will emphasize.
Also possible, however, is an indirect call
callq *operand
where operand is one of
the address forms we have seen above (the most complicated
being Disp(Rb,Ri,S)).
In the callq *operand, case the jump is to the address
that is the contents of operand.
Show the animation on slides 11-14, which corresponds to the multstore()/mult2() example just given.
| Register Name | Conventional Use |
Register Name | Conventional Use |
|
|---|---|---|---|---|
| %rax | Return Value | %r8 | 5th argument | |
| %rbx | callee saved | %r9 | 6th argument | |
| %rcx | 4th argument | %r10 | caller saved | |
| %rdx | 3rd argument | %r11 | caller saved | |
| %rsi | 2nd argument | %r12 | callee saved | |
| %rdi | 1st argument | %r13 | callee saved | |
| %rbp | callee saved | %r14 | callee saved | |
| %rsp | stack pointer | %r15 | callee saved |
In the x86-64 architecture, the primary method of data transfer between the calling procedure (f() above) and the called procedure (g() above) is via machine registers used to transmit arguments in the caller to the corresponding parameters in the callee. In the other direction the return value in the callee is transmitted to the function value in the caller, again using a register. As mentioned above and repeated to the right, specific registers are designated for these purposes.
Thanks to these conventions if f(), containing a call
g(x,y), is compiled on monday in LA using a California C
compiler, the values of x and y will be stored
in %rdi and %rsi respectively.
Then, if on Wednesday
g(long a, long b)
is compiled in Newark using a NJ compiler, g() will
retrieve the values for a and b from %rdi
and %rsi respectively.
The first choice for local variables (in g() say) is to use some of the leftover registers (since registers can be accessed much faster than stack elements). However, if g() is complex, it probably has more local variables than would fit in the available registers.
A second reason for storing local variables in memory rather than a register is that the & operator (in C) may have been used. Remember, that when &var is used in C, the compiler is required to provide the address of var.
A third reason for stack usage is for large
objects like
arrays and structures.
long incr(long *p,
long val) {
long x = *p;
long y = x + val;
*p = y;
return x;
}
incr:
movq (%rdi), %rax
addq %rax, %rsi
movq %rsi, (%rdi)
ret
| Register | Use |
|---|---|
| %rdi | p |
| %rsi | val, y |
| %rax | x, ret |
The incr() function is like x++ in that it increases *p and returns the old (pre-incremented) value.
Note that the C code is not what you would normally write; rather it is there to help understand the assembler. In particular, C programmers would not have the variable y. Instead, they would write simply *p = x+val;
long call_incr() {
long v1 = 15213;
long v2 = incr(&v1, 3000);
return vi + v2;
}
call_incr:
subq $8, %rsp
movq %15213, (%rsp)
movq $3000, %rsi
leaq (%rsp), %rdi
call incr
addq (%rsp), %rax
addq $8, %rsp
ret
| Register | Use |
|---|---|
| %rdi | &v1 |
| %rsi | 3000 |
| %rax | v2, ret |
See slides 20-24 for diagrams illustrating the execution of call_incr. In those slides the lines in red have just been executed.
manually, i.e, we decrement the stack pointer in one instruction and store the constant in the second.
As mentioned a common method of transferring values from the calling program (say f()) to the called program (say g()) is for f() to put a value in an agreed upon register and for g() to access that register. For constants this works without issues.
But what if we want to share a variable x that both f() and g() use? If f() puts x into a register and calls g(), is g() permitted to say increment the register?
The answer is yes
and no
.
Consider the situation where f() calls g(x) which in turn calls h(x). g() must answer two questions.
Some registers e.g. %r12 are designated as callee-save. This means that, answering question 1 above, g() (the callee) must restore the restore the register to the value it had when f() called g(). It also means that, answering question 2, g() can assume that h() restores the register to the value it had when g() called h().
Other registers are designated as caller-save. For these registers, answering question 1 above, g() need not restore the register before returning to f(). It also means that in answering question 2 g() cannot assume that h() restores the register when h() returns to g().
Our table of registers lists 6 registers as callee-save and only 2 as caller-save, but this is misleading. The 6 registers designated for arguments and the one register designated for the return value are also caller-save, for a total of 2+6+1=9 caller-save registers.
long call_incr2(long x) {
long v1 = 15213;
long v2 = incr(&v1, 3000);
return x+v2;
}
call_incr2:
pushq %rbx
subq 8, %rsp
movq %rdi, %rbx
movq $15213, (%rsp)
movl $3000, %rsi
leaq (%rsp), %rdi
call incr
addq %rbx, %rax
addq $8, %rsp
popq %rbx
ret
| Register | Use |
| %rdi | x |
| %rax | ret |
| %rbx | tmp |
| %rsp | stk |
Look at the recursive routine pcount() below. It counts the total number of 1 bits in x. I realize that pcount() can be easily written without recursion.
When pcount calls pcount, we have two different x's. In particular the x in the child is a right-shifted version of the x in the parent. We need both and cannot overwrite one with the other.
If all the bits of x are 1, the recursion will go on for 64 levels and we must keep all that information around using only 16 registers.
/* Recursive popcount */
long pcount
(unsigned long x) {
if (x == 0)
return 0;
else
return (x & 1) +
pcount(x >> 1);
}
pcount:
movq $0, %rax
testq %rdi, %rdi
je .L6
pushq %rbx
movq %rdi, %rbx
andq $1, %rbx
shrq %rdi
call pcount
addq %rbx, %rax
popq %rbx
.L6:
ret
| Register | Use |
| %rdi | x |
| %rax | ret |
| %rbx | tmp |
The assembly code is only about a dozen instructions and uses only 3 registers.
The stack.
Do the computation on the board with x=00...00101 binary (= 0x000000000000005).
Imagine redoing it with x=0xFFFFFFFFFFFFFFFF.
There would still be only about a dozen instructions in the program (several executed many times) and still only 3 registers would be used. However, many different values of %rbx would be pushed on to the stack and subsequently popped off and used. At one point (when all the calls are done, but none of the returns) there would be about 64 values on the stack.
The register saving conventions (caller/callee) prevent one invocation of the function from altering registers that another invocation still is using.
long A[5]; // 8B each char *B[5]; // 8B each double C[5]; // 8B each int D[5]; // 4B each float E[5]; // 4B each short F[5]; // 2B each char G[5]; // 1B each
Consider the declarations
long A[10], *p, i;
If we reference A[i] and increment i, we reference
the next element of A, which is 8 bytes further in memory.
In C, the same thing occurs with pointers.
If we write
p = &A[2]; p++;
again p advances not by
one, but by eight, the space (in bytes) used for
one long.
// Array access
long arrElt(long z[], long idx) {
return z[idx];
}
movq (%rdi,%rsi,8), %rax ret
| Register | Use |
| %rdi | &z[0] |
| %rsi | idx |
| %rax | ret |
Notes:
// Array addition
void arrAdd(long A[],
long B[],
long C[]) {
long i;
for (i=0; i<10; i++)
A[i] = B[i] + C[i];
}
arrAdd: xorl %rax, %rax .L2: movq (%rdx,%rax,8), %r8 addq (%rsi,%rax,8), %r8 movq %r8, (%rdi,%rax,8) incq %rax cmpq $10, %rax jne .L2 ret
| Register | Use |
| %rdi | &A[0] |
| %rsi | &B[0] |
| %rdx | &C[0] |
| %rax | i |
| %r8 | tmp |
Notes:
Start Lecture #19

Consider the declaration of twoD on the right. It is a two dimensional array of longs. As we saw earlier in the course, it can be viewed as a matrix with 2 rows and three columns. It is stored contiguously as shown in the bottom of the diagram.
In C as in most, if not all, modern languages a 2D array is stored
in row major
order; each row is stored contiguously.
When viewed as a matrix it is stored the way a book is read in
English.
Let's do the general case where twoD
has R rows and C columns, and each element of the
array requires K bytes.
Let A be the address of twoD[0,0].
Then the address of twoD[i,j] is
A + i * (C * K) + j * K = A + (i*C + j) * K
A key to understanding the somewhat cryptic-looking formula is that C * K is the space required to store one complete row of the matrix.
long oneD1[3] = {1, 5, 7},
oneD2[3] = {2, 4, 6};
*twoDv2[2] = {oneD1, oneD2};
// = {&oneD1[0], oneD2[0]

We did this when learning C. See section K&R-5.9. C hides much of the details; now they will all come out.
The idea is that, instead of using a 2D matrix of elements, we can implement a 2D array as a 1D array of pointers to 1D arrays of elements.
To access the entry with value 7 in the nested array we would write twoD[0][2]
To access the entry with value 7 in the multi-level array we would write twoDv2[0][2], i.e., we write the same thing.
But they are implemented quite differently in assembler. The first version first does some arithmetic (see above) to calculate the needed address and then accesses that address. The second version access one element of twoDv2 to find (a pointer to) the correct oneD array and then accesses the appropriate entry in that array. The summary is that the first requires more arithmetic; the second an extra memory access.
See slide set machine-level-5.pptx
slides number 11-13 for
a larger example and more details
Skipped
Skipped
struct st {
long a;
long b[10];
long c[10];
};
void f(struct st *s) {
long i;
for (i=0; i<10; i++)
s->b[i] = s->c[i];
}
f: movq $0, %rax jmp .L2 .L3: movq 88(%rdi,%rax,8), %rdx movq %rdx, 8(%rdi,%rax,8) addq $1, %rax .L2: cmpq $9, %rax jle .L3 ret
| Register | Use |
| %rdi | s |
| %rax | i |
| %rdx | tmp;tmp |
The C code on the right is a simple loop copying one array to another, each of which happens to be part of the same structure. A pointer to this structure is the sole parameter of f().
Note that the address IN s (not of s) is the address of s->a. Also s->b[0] is located 8 bytes after the address in s and s->c[0] is 80 bytes after that.
Admire the last two movq's in the assembly code, which contain the most complicated memory address form.
Notes:
struct rec {
long a[3];
long i;
struct rec *next;
};
void set_val
(struct rec *r, long val) {
while (r) {
long i = r->i;
r->a[i] = val;
r = r->next;
}
}
.L3: # loop:
movq 24(%rdi), %rax # i = Mem[r+18]
movq %rsi, (%rdi,%rax,8) # Mem[r+8*i] = val
movq 32(%rdi), %rdi # r = Mem[r+32]
testq %rdi, %rdi # test r
jne .L3 # loop if r != 0
ret
| Register | Use |
| %rdi | r |
| %rsi | val |
| %rax | i |
On the right we see a small program involving a strange data
structure.
We have a C struct, containing an array a[] of three longs
and another long i, indicating which of the 3 elements
of the array is the active element
.
These structs are linked together via a next pointer.
The set_val() function is given a pointer to one of these
structures (presumably the head of a list) and another
long val.
The goal is to set all the active elements
in the list to
val.
Try not to be confused by the pink diagram using hex addresses; whereas, the assembler uses decimal. I used hex for the diagrams since all entries are multiples of 8, which is most readily expressed in hex.
The assembly program is simple but studying the addressing is worthwhile. The first line grabs i (remember decimal 24 is hex 18); the second line updates the ith entry of a; finally we loop if next is not NULL.
Remark: The program assumes that the list has at least one entry, i.e., it assumes r≠NULL.
Skipped.
struct stt {
char c1;
long l1;
char c2;
long l2;
} ss, *pstt
How do we align ss, which is a struct stt? First we look at the components: c1 and c2 are each 1 byte and can be aligned on any byte. However, l1 and l2 are each 8 bytes and hence must be aligned on an 8-byte boundary. That is the address of each one must be a multiple of 8.
The four components of the structure have 2 different alignment requirements. The rule employed is that the structure itself must be aligned to conform to the strictest alignment of its components, which in this case says that every variable of type struct stt must be aligned on an 8-byte boundary.
So ss begins on an 8-byte boundary. c1 can begin anywhere; so far so good. But l1 must be aligned on a 8-byte boundary and that means we need 7 bytes of (wasted) padding. This repeats for c2 and l2

Look how much better it lays out if we put first the bigger components (with the more stringent alignment requirements). The compiler is not permitted to change the order of components; the programmer must do it.
skipped
skipped
Most programming is done in high level languages. In this chapter we looked under the covers at the level of instructions that the computer actually executes.
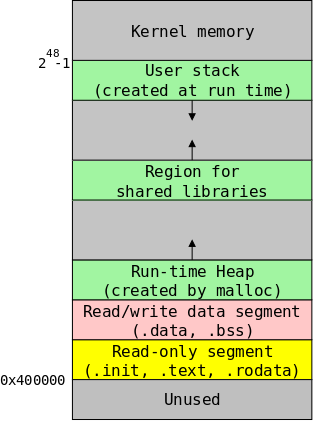
The diagram on the right gives an overview of the memory regions in a running program under Linux. We will study this in more detail next chapter. For now we just want to mention examples of each region type.
These regions can grow during during execution, which requires extra attention by the system so that one such region does not overwrite another. They contain read/write data. The heap grows when malloc() is called; the stack grows when register %rsp is decremented, which occurs on most procedure invocations. We will see shared libraries soon.
These regions, which contain executable/non-writable instructions,
do not grow and do not change their contents during execution.
This text
region contains the compiled assembler
instructions we have studied.
Shared libraries are a memory-saving idea that permits many running
programs to share, for example, the library routine
printf().
Statically allocated data including global variables, static variables, and string constants. Unlike local variables inside C functions that come and go when procedures are called and return, these variables remain for the lifetime fof the execution.
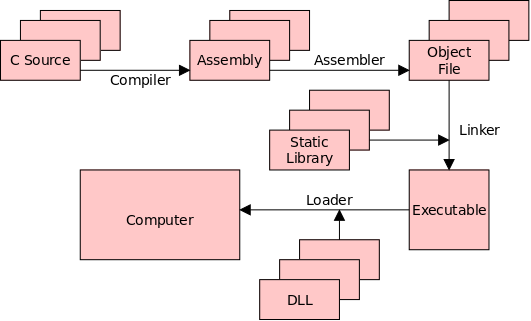
The program cc (or gcc) is technically more than
a compiler.
It invokes a series of programs that step by step transform
your C source program into an form executable by the
computer hardware.
Since cc controls
or drives
the compilation
process it is sometimes called a compiler driver
.
We have already seen that cc includes a compiler translating C code to assembly language and an assembler translating assembly to actual computer instructions. Those are the first two arrows in the diagram on the right.
Now we want to go further in the diagram.
Remark: Although we normally use cc to compile C programs, it can also be used to translate assembly language into native machine instructions. Indeed you can enter the pipeline any point and can leave an any point downstream from the entry. The entry point is determined by the name of the input file: cc x.c starts at the first arrow, cc x.s starts at the second, etc. The exit point is determined by flags to the cc command: cc -s x.c stops after the first arrow; cc -o x.c stops after the second.
We first study static linking, which is the vertical line at the
right of the diagram.
Static linking is performed by a program normally called the linker,
which is invoked automatically by the compiler driver cc.
In linux/unix the linker program is (unfortunately) called load file
, which can be executed.
Note: The linker was originally called a linkage editor by IBM.
Historical note: The linker on Unix was mistakenly called ld (for loader), which is unfortunate since it links but does not load.
Unix was originally developed at Bell Labs; the seventh edition of Unix was made publicly available (perhaps earlier ones were somewhat available). The 7th ed man page for ld begins (see https://cm.bell-labs.com/7thEdMan).
.TH LD 1
.SH NAME
ld \- loader
.SH SYNOPSIS
.B ld
[ option ] file ...
.SH DESCRIPTION
.I Ld
combines several
object programs into one, resolves external
references, and searches libraries.
By the mid 80s the Berkeley version (4.3BSD) man
page referred to ld as link editor
and this more accurate
name is now standard in Unix/Linux distributions.
During the 2004-05 fall semester a student wrote to me:
BTW - I have meant to tell you that I know the lady who wrote ld. She told me that they called it loader, because they just really didn't have a good idea of what it was going to be at the time.
Linking is the process of collecting and combining various pieces of code and data into a single file that can be loaded into memory and executed.
Remarks on Midterm Grades
file main.c
#include <stdio.h> int x = 10; void f(void); int main(int argc, char *argv[]) { printf("main says x is %d\n", x); f(); }
file f.c
#include <stdio.h> extern int x; void f(void) { int y = 20; printf("f says x is %d\n", x); printf("f says y is %d\n", y); }
For a simple example of what the linker needs to do, consider the small example on the right consisting of two files main.c and f.c, which are compiled separately.
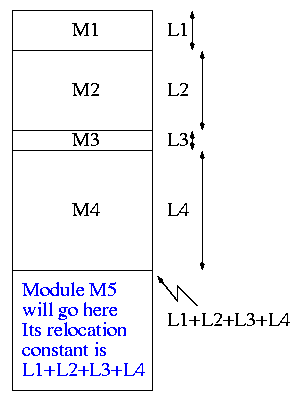
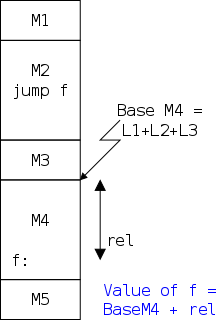
The diagram on the far fight illustrates relocating relative addresses. Specifically, it shows that the relocation constant is calculated as the sum of the lengths of the preceding modules. Once the relocation constant C is known, each absolute address in the modulated is calculated simply as the corresponding relative address + C.
The diagram on the near right illustrates resolving external references. In this case the reference is to f(). Note that the Base of M4 is the same as its relocation constant, i.e., the sum of the lengths of the preceding modules.
Note from the diagram on the near right, that the linker
encounters the required address jump f
before it knows the
necessary relocation constant.
The simplest solution (but not the fastest) is for the linker to make two passes over the modules. During pass 1 the relocation constants for each module are determined and a symbol table is produced giving the absolute address for each global symbol. During pass 2, references to external addresses are resolved using the symbol table constructed during pass 1.
The table on the right tabulates the information contained in an ELF binary. The various fields contain the following information.
| Elf header |
|---|
| Segment header table |
| .text section |
| .rodata section |
| .data section |
| .bss section |
| .symtab section |
| .rel.text section |
| .rel.data section |
| .debug section |
| Section header table |
The linker symbols (which are stored in the linker symbol table) come in three flavors.
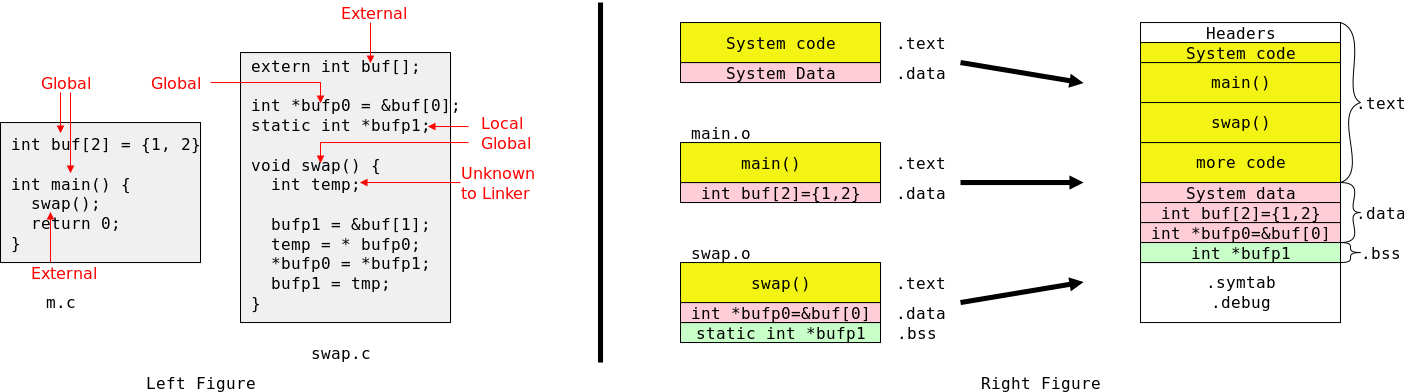
The left figure above shows a very simple C program that nonetheless exercises many of the linker's abilities.
Note the distinction between global references, which define symbols, and external references that need to be resolved by the linker to equate to the corresponding global.
Also note that bufp1, although known only to swap.c, must be given a slot by the linker. Since it is static, bufp1 must maintain its value across multiple calls to swap() and hence, unlike tmp, cannot be stored on the stack.
As an optimization the executable file does not contain space for bufp1, just a count of how much space to reserve when the executable is loaded.
We see in the right figure that the linker combines corresponding segments from each object file when producing the executable that is the linker's output.
Recall that declarations give just the type of an identifier. This tells the compiler how to interpret the identifier, but does not necessarily reserve space for the identifier. Declarations that reserve storage are called definitions.
file f1.c:
int svar1=5;
int sfun1(int x) {
code
}
file f2.c:
int wvar1;
int wfun1(int z);
int sfun2(void) {
int igsym1=3;
}
Looking at the code on the right
The linker obeys the following rules.
multiply defined symbolerror.
int x; int x=7; Both x's are the same; the second is strong.
f1() {...} f2() {...} The second x is chosen.
int x; Two strong symbols have the same name, f1.
f1() {...} f1() {...} Link time error.
int x; int x; Both x's are the same; each is weak.
f1() {...} f2() {...} *Either* could become the location for x.
int x=7; double x; The first x is strong and is chosen.
int y=5; f2() {...} Writes to x in f2() WILL overwrite y!
f1() {...} Scary!
int x; double x; Both x's weak; either might be chosen
int y; f2() {...} Writes to x in f2() MIGHT overwrite y!
f1() {...} Maximum terror!!
Start Lecture #20
Remark: The final for this class will be on zoom, just like the midterm. I mistakenly copied something for 202 into our class notes for 201. The erroneous comment has been removed.
The figure in 7.1 contains two kinds of libraries: statically-linked libraries that are processed by the linker and dynamically-linked libraries (DLLs) processed by the loader. How do they differ?
You know well that when your programs run, some functions are executed that you did not write (e.g. printf()). Many common routines are placed in libraries that the linker searches by default.
Too coarse and too fine
One (or a few) big file(s), but (each) with an index stating which functions are contained and where in the file they are located, a so-called static library. A static library has a .a suffix because it is an archive of several .o files.
When linking a program the linker (ld) automatically searches (the index in) the standard C archive libc.a. If a function referenced by the user program is found in the index, the corresponding .o file is extracted from the archive and linked with the program.
So 1500+ functions are available in just one archive file, but only the dozen or so actually referenced are linked in.
Since cc knows
to search libc.a, no
further user action is needed.
Actually cc knows
to search a number of standard
archives.
For other library routines, the user must tell the linker to search
the corresponding archive by giving the appropriate option to
the cc command.
Assume you (as system administrator) have compiled all the .c files you want to put in the standard library libc.a. Then you would execute one very long archive (ar) command, which concatenates the files and constructs the index. Specifically, you would write.
ar rs libc.a atoi.o printf.o strcpy.o random.o ... (1500+ entries)
The linker makes one pass over the .a and .o files in the order that the names were given on the command line. During this process, the linker maintains a list of currently unresolved references.
When a .a file is encountered in the list, the linker searches the archive's index and links in any file containing a definition for a currently unresolved reference.
If any references remain after the linker has completed its scan of the files mentioned on the command line, the linker prints an error message and the command fails.
For this reason the compiler drivers cc and gcc search the standard libraries after processing the files you mentioned explicitly on the command line.
// f.c
void f(void) {
return;
}
// callf.c
void f(void);
int main (int argc, char *argv[]) {
f();
}
$ cc -c f.c
$ ar rs libf.a f.o
$ cc -c callf.c
$ cc libf.a callf.o
callf.o: In function `main':
callf.c:(.text+0x10): undefined reference to `f'
collect2: error: ld returned 1 exit status
$ cc callf.o libf.a
$ ./a.out
So far so good, we compiled a main program and a utility program and have placed the latter in an archive. You might want to think of f() as printf(), and the archive as libc.a.
Now look at the fourth command, which attempts to link the two functions f() and callf().
This command fails asserting that it cannot resolve the reference to f().
But why? We just put f() in libf.a and included the latter in our link command (remember that the compiler driver cc invokes the linker, ld).
The trouble is that the linker looks at libf.a before it looks at callf() and thus sees no need to link in f().
When the compiler driver is given the archive at the end of the command (as in the last line), the linker detects the need for f() before processing the archive and hence extracts f.o and all is well.
Now that we have shown how the linker resolves external references, we turn to its other main function, relocation. Recall that the linker receives as input a number of independently produced object files. Each of these object files likely contains a .text section (containing the executable code), a .data section (containing the read/write initialized data, and several other sections.
The linker combines all the .text sections into one, and
similarly for the other sections.
We gave an overview of this action when we discussed
relocating relative addresses
in section O'H-7.2.A.
We are skipping the detailed explanation given in O'H-7.7.1 and
O'H-7.7.2.
Skipped.
Skipped.
As indicated in section 7.6 the linker combines the .text (compiled code) sections from all the .o files into one such section for the executable file. Similarly all the .rodata sections are combined. The linker also generates a .init section containing system code run to start the program.
The diagram on the right shows all three in yellow.
They are often referred to as read-only code
, even though they
contain data.
The unifying property is that, when the program executes, the yellow
section is read-only.
Similarly, the pink region is produced containing all the .data (initialized data) sections as well as all the .bss (uninitialized data) sections. These two sections are in pink and represent data that may be rewritten during execution.
Note: The .bss data are actually initialized to zero by the loader. They are called uninitialized since the initial value itself is not in the elf file (since it is known to be zero).
The yellow and pink segments remain their original size during execution. This makes their run-time placement in RAM easy; just put one after the other. But we know programs grow (and shrink) in size during execution: We can call malloc()/free() and we have seen stack pushs and pops during function invocation and exits. Loading regions that grow comes next.

Unlike the previous diagrams, the figure on the right, does not show the contents of a file, but rather the contents of memory during execution of the user program.
As mentioned the yellow and pink sections are easy to load since they don't change size and don't need to move. We use green to indicate regions that can grow.
We have already met two of the green regions (the stack and heap), and have seen them grow during execution. We will discuss shared libraries next section.
If you ignore the middle green region, we have a great situation: one region is at high addresses, the other is at low addresses, and they grow toward each other. If they grow into each other the program aborts, but for a good reason: it needs more memory than we have.
But with three growing regions, no matter where we place them, a situation can arise where two of them collide, but there is still space available; the free space is in the wrong place.
The previous comment about three region is correct, but seems of no
practical importance since the amount of initially free memory is
enormous.
After all, 248 = 281,474,976,710,656 is almost 300
terabytes, which vastly exceeds the total RAM on all our laptops
combined.
Who can afford this much memory?
The answer comes in chapter 9.
If two jobs are running at the same time how can both of their yellow sections start at 0x400000? Why don't their stacks collide?
The answers come in chapter 9.
Again referring to the figure in section 7.1, we have just discussed static libraries (.a files) used by the linker and now wish to go one step further and discuss shared libraries used by the loader.
#include <dlfcn.h>
int x[2] = {1,2}, y[2] = {3,4}, z[2];
int main(int argc; char *argv[]) {
void *handle;
void (*addvec)(int *, int *, int *, int);
// dynamically load the shared lib containing addvec()
handle = dlopen("./libvector.so", RTLD_LAZY);
if (!handle) {
fprintf(stderr, ...);
exit(1);
}
// get ptr to addvec()
addvec = dlsym(handle, "addvec");
if ((error = dlerror()) != NULL) {
fprintf(stderr, ...);
exit(1);
}
// now *addvec is a "normal" function
*addvec(x, y, z, 2);
}
The book gives two real world uses of run-time dynamic linking and loading, specifically software distribution and high performance web servers.
On the right is a skeleton program that dynamically links during run time.
The function addvec() adds two 1D-arrays producing a third array (the 4th argument is the dimensionality of the arrays). We assume addvec() has been previously compiled and placed in the shared library ./libvector.so.
Multiple steps are involved in executing the addvec() function contained in the libvector library.
lazylinking).
We have seen that an advantage of dynamic shared libraries is that, when many processes are all using the same library (e.g., most C programs use printf() from the standard C library, libc.a), we need only one version of the code in memory.
A difficulty arises with jump instructions. If the jump instruction includes the target address explicitly, all programs linking that shared function would need to put it in the same place so that the given address will jump to the same instruction in all copies. This is not practical; it would essentially require a fixed starting memory address for every program in all the shared libraries.
Instead PIC is employed, i.e., every instructions can be in any location. Here is a simple example (making the simplifying assumptions that every instruction is 4 bytes in length and that the argument of the jump instruction is the address to jump to
0x100000 addl %rsi, %rdi 0x100004 subl $5, %rsi 0x100008 cmpl %rsi, %rdi 0x10000C jg $0x100000
This program assumes that the addl instruction is loaded into location 0x100000 and would not work if all the instructions were loaded starting in 0x200000. We say the code sequence is not position independent.
Now consider consider a fictitious instruction picj that jumps to the current location plus the argument. Then the following code
0x100000 addl %rsi, %rdi
0x100004 subl $5, %rsi
0x100008 cmpl %rsi, %rdi
0x10000C picjg $-0xC
works the same as the above but also works if loaded in 0x200000 or
any place else.
It is called position independent code and is just what we needed at
the end of section 7.10.
There is more to PIC then this, but the idea remains the same: have the compiler generate code that works correctly no matter where the code is loaded. See the book for more complicated examples.

Skipped
List of useful utilities.
Now we understand all the boxes and arrows in the diagram that began our study of linkers and that is repeated on the right.
However, we will get a better understanding of the advantages of dynamic linking when we study virtual memory in chapter 9.
What do we want from an ideal memory?
leakdata)
We will emphasize the first two, skip the third, and mention the last two.
Laws of Hardware: The Basic Memory Trade-off
We can get/buy/build small and fast
and
big and slow
.
Our goal is to mix the two and get a good approximation to the impossible big and fast.
| Name | Trans per bit | Access time |
Needs refresh | Volatile | Cost | Where used |
|---|---|---|---|---|---|---|
| SRAM | 4 or 6 | 1x | No | Yes | 100x | Cache Memory |
| DRAM | 1 | 10x | Yes | Yes | 1x | Main Memory |
Two varieties: Static RAM (SRAM) and Dynamic RAM (DRAM).
RAM constitutes the memory in most computer systems. Unlike tapes or CDs they are not limited to sequential access. The table on the right compares the two varieties.
SRAM is much faster but (for the same cost) has much lower capacity. Specifically, trans per bit gives the number of transistors needed to implement one bit of each memory type. The 4-transistor SRAM is harder to manufacture than the 6-transistor version.
Both SRAM and DRAM are volatile, which means that, if the power is turned off, the memory contents are lost. Due to the volatility of both RAM varieties, when a computer is powered on, its first accesses are to some other memory type (normally a ROM—read-only memory).
DRAM, in addition to needing power, needs to be refreshed. That is, even if power remains steady, DRAM will lose its contents if it is not accessed. Hence there is circuitry to periodically generate dummy accesses to the DRAM, even if the system is otherwise idle.
I have in my office some disks from the 1980s and 90s. Unlike modern disks, these relics are big enough to see the active components. In normal years, I drag some of these monsters to class and show their internals. For today, we will have to settle for some pictures (one picture is from Henry Muhlpfordt).

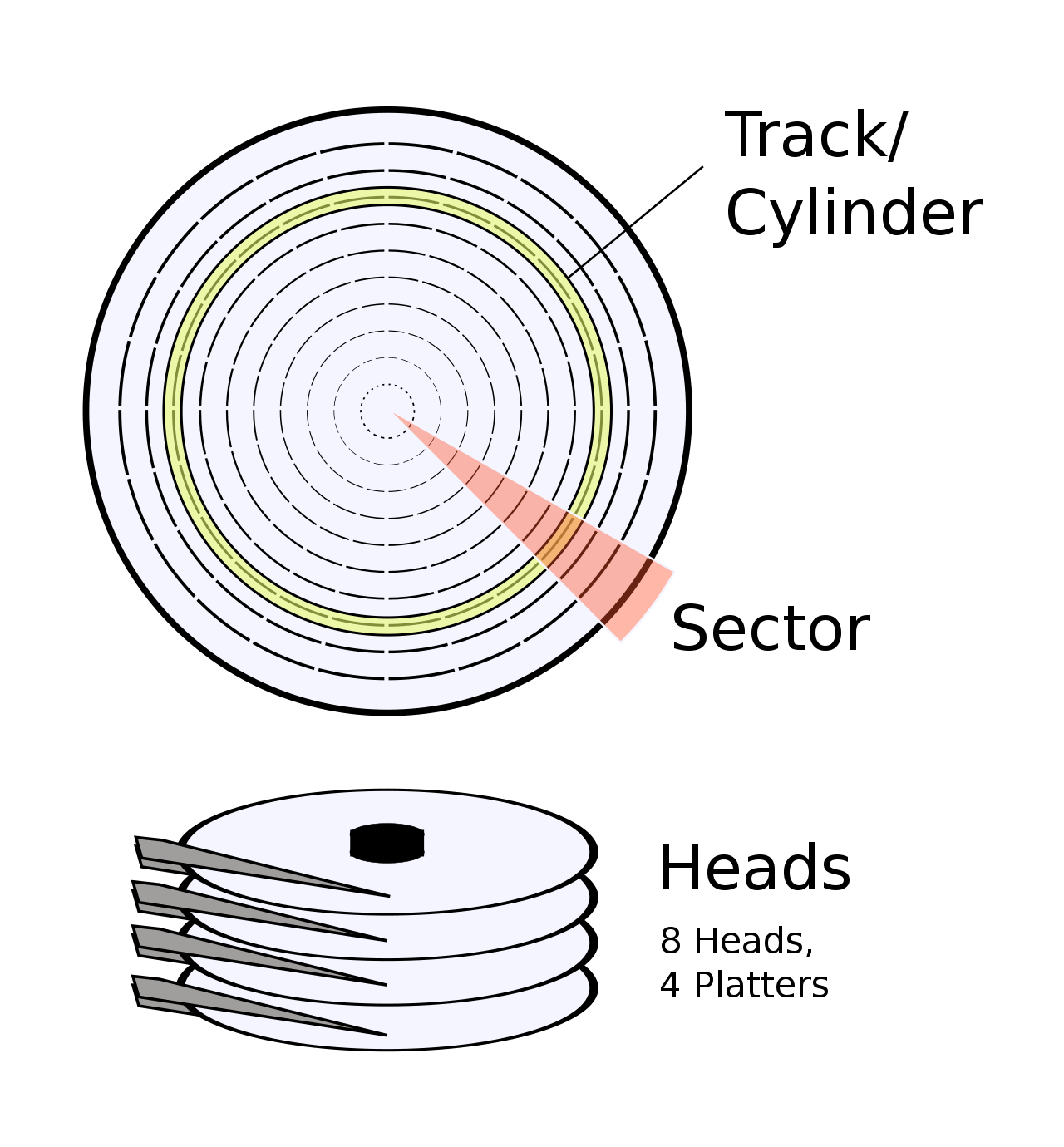
Disks are huge (~1TB).
and slow (10ms).
Unlike RAM, disks have moving parts.
Unlike tape, disks support random access.
Consider the following characteristics of a disk.
settling time.)
It is important to realize that a disk always transfers (reads or writes) a fixed-size sector.
Current commodity disks have (roughly) the following performance.
The above performance figures are quite extraordinary. For a large sequential transfer, in the first 10ms, no bytes are transmitted; in the next 10ms, 1,000,000 bytes are transmitted.
The OS actually reads blocks, each of which is 2k sectors. The OS sets the number of sectors per block when it creates a filesystem.
This analysis suggests using large disk blocks, 100KB or more. But much space would be wasted since many files are small. Moreover, transferring small files would take longer with a 100KB block size.
In practice typical block sizes are 4KB-8KB.
Multiple block sizes have been tried (e.g., blocks
are 8KB but a file can also have fragments
that are a
fraction of a block, say 1KB).
This is flash RAM (the same stuff that is in thumb drives
)
organized in sector-like blocks as is a disk.
hard diskan SSD has no moving parts (and hence is much faster).
The blocks in an SSD can be written a large number
of times
(thousands or tens of thousands).
However, this large number
is not large enough to be
ignored.
Instead frequently accessed data is moved to previously unused
portions of the device.
Summary: Everything is getting better but the rates of improvement are quite different for different technologies..
SRAM: factor of 100 DRAM: factor of 50,000 DISK: factor of 3,000,000
SRAM: factor of 100 DRAM: factor of 10 DISK: factor of 25 CPU: factor of 2,000 (includes multiprocessor effect)
The hierarchy is needed to close the processor-memory performance gap, i.e., the gap between processor speed improvement and DRAM speed improvement.
Alternately said it is the gap between the processors need for data and the (DRAM) memory's ability to supply data.
Remember we want to cleverly mix some small/fast memory with a large pile of big/slow memory and get a result that approximates well the performance of the impossible big/fast memory.
The idea will be to put the important stuff
is the
small/fast and the rest in big/slow.
But what stuff is important?
The answer is that we want to put into small/fast the data and instructions that are likely to be accessed in the near future and leave the rest in big/slow. Unfortunately this involves knowing the future, which is impossible.
We need heuristics for predicting what memory addresses will likely be accessed in the near future. The heuristic used is the principle of locality: programs will likely access in the near future addresses close to those they accessed in the near past.
The principle of locality is not a law of nature: One can write programs that violate the principle, but normally the principle works very well. Unless you want your programs to run slower, there is no reason to deliberately violate the principle. Indeed, programmers seeking high performance, try hard to increase the locality of their programs.
We often use the term temporal locality for the tendency that referenced locations are likely to be re-referenced soon and use the term spacial locality for the tendency that locations near referenced locations are themselves likely to be referenced soon.
We will have more to say about locality when we study caches.
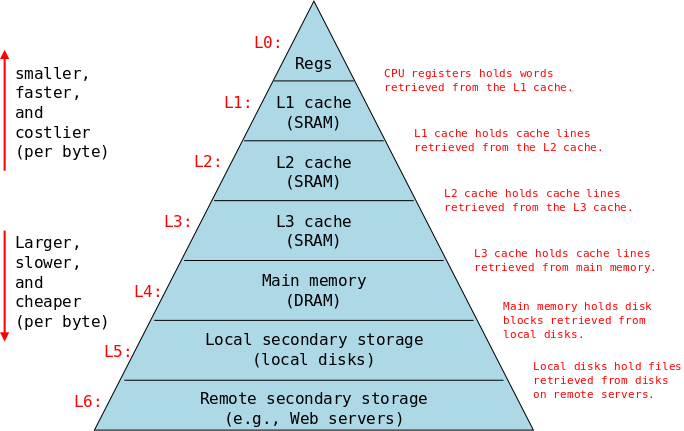
In fact there is more than just small/fast vs big/slow. We have minuscule/blitz-speed, tiny/super-fast, ..., enormous/tortoise-like. Starting from the fastest/smallest, a modern system will have.
Today a register is typically 8 bytes in size and a computer will have a few dozen of them, all located in the CPU. A register can be accessed in well under a nanosecond and modern processors access at least one register for most operations.
In modern microprocessor designs (think phones, not laptops), arithmetic and many other operations are performed on values currently in registers. Values not in registers must be moved there prior to operating on them.
Registers are a very precious resource and the decision which data to place in registers and when to do so (which normally entails evicting some other data currently in that register) is a difficult and well studied problem. The effective utilization of registers is an important component of compiler design—we will not study it in this course.
For the moment ignore the various levels of caches and think of a single cache as an intermediary between the main memory, which (conceptually, but not in practice) contains the entire program, and the registers, which contains only the currently most important few dozen values.
In this course we will study the high-level design of caches and the performance impact of successful caching.
A memory reference that is satisfied by the cache requires much less time (say one tenth to one hundredth the time) than a reference satisfied by main memory.
Our primary study of the memory hierarchy will be at the
cache/main-memory boundary.
(In 202, we emphasize the main-memory/local-disk boundary.)
In 201 we will see the performance effects of various
hit ratios
, i.e., the percentage of memory references
satisfied in the cache vs satisfied by the main memory.
When first introduced, a cache was the small and fast storage class and main memory was the big and slow. Later the performance gap widened between main memory and caches so intermediate memories were introduced to bridge the gap. The original cache became the L1 cache, and the gap bridgers became the L2 and L3.
The fundamental ideas remained the same: if we make it smaller it can be faster; it we let it be slower, it can be bigger.
For now, we shall pretend that the entire program including its
data resides in main memory.
Later in this course and again in 202, operating systems, we will
study the effect of demand paging
, in which the main memory
acts as a cache for the disk system that actually contains the
program.
We know that the disk subsystem holds all our files and thus is much larger than main memory, which holds only the currently executing programs. It is also much slower: a disk access requires several MILLIseconds; whereas a main memory access is a fraction of a MICROsecond. The time ratio is about 100,000.
One possibility is robot controlled storage, where the robot automatically fetches the requested media and mounts it. Tertiary Storage is sometimes called nearline storage because it is nearly online.
Other possibilities are web servers and local-area-network-accessible disks. We shall not discuss these possibilities.
Requires some human action to mount the device (e.g., inserting a cd). Hence the data is not always available.
In the hierarchy diagram above, we see three levels of caches. But in a sense every level, except the bottom, is a cache of the level below it. The main memory in your laptop is a cache of your disk. Compared to disk, the main memory is small and fast. We will see in chapter 9 another sense in which main memory is a cache of the disk.
If a program chose to reference random locations, the hierarchy would not work since we would have no clue what portion of the big/slow memory we should place in the small/fast memory. But in practice programs do not reference random locations; rather references exhibit locality.
In this chapter, we will concentrate on the cache-to-main-memory interface. That is, for us the cache will be the small/fast memory and the main (DRAM) memory will be big/slow.
A cache is a small fast memory between the processor and the main memory. It contains a subset of the contents of the main memory.
A Cache is organized in units of blocks or lines. Common block sizes are 16, 32, and 64 bytes.
A block is the smallest unit we can move between a cache and main
memory
Start Lecture #21
Remark: The final for this class will be on zoom, just like the midterm. I mistakenly copied something for 202 into our class notes for 201. The erroneous comment has been removed.
Definitions
Let m be the cache hit time. Let M be the miss penalty, i.e., the additional time for a cache miss. Let p be the probability that a memory access is a cache hit.
Then the average time is
Avg access time = p*m + (1-p)(m+M)
= m + (1-p) M
The goal is to run fast, i.e. to have the average access time small. So we want to
Assume the following (somewhat reasonable) data.
What is the average access time?
First note that 0.1μs = 100ns.
Then the above equation tells us that the average access time
is
1ns + (1-0.9) * 100ns = 1ns + 0.1(100ns) = 11ns
Lets spend more and get double speed SRAM (i.e., m=0.5ns), but save
money and get half speed DRAM (i.e., M=200ns.).
Then the average access time is
0.5ns + (1-0.9) * 200ns = 0.5ns + 0.1(200ns) =
20.5ns
Bad idea.
Let's try again.
Forget the double speed SRAM.
Instead, spend the money saved on half speed DRAM and get a cache
with one quarter the miss rate.
Then the average access time is
1ns + (1-0.975) * 200ns = 1ns + 0.025(200ns) =
6ns.
Good.
But how do we lower the miss rate?
Stay tuned.
Consider the following address (in binary).
10101010_11110000_00001111_11001010.
This is a 32-bit address.
I used underscores to separated it into four 8-bit pieces just to
make it easy to read; the underscores have no significance.
Machine addresses are non-negative (unsigned) so the address above is a large positive number (greater than 2 billion).
All the computers we shall discuss in this section are byte addressed. Thus the 32-bit number references a byte. So far, so good.
We will assume in our study of caches that each word is four bytes. That is, we assume the computer has 32-bit words. This is not always true (many old machines had 16-bit, or smaller, words; and many new machines have 64-bit words), but to repeat, in our study of caches, we will always assume 32-bit words.
Since 32 bits is 4 bytes, each word contains 4 bytes. We assume aligned accesses, which means that a word (a 4-byte quantity) must begin on a byte address that is a multiple of the word size, i.e., a multiple of 4. So word 0 includes bytes 0-3; word 1 includes bytes 4-7; word n includes bytes 4n, 4n+1, 4n+2 and 4n+3. The four consecutive bytes 6-9 do NOT form a word.
Question: What word includes the byte address given above,
10101010_11110000_00001111_11001010?
Answer:
10101010_11110000_00001111_110010, i.e, the address divided
by 4.
Question: What are the other bytes in this word?
Answer:
10101010_11110000_00001111_11001000,
10101010_11110000_00001111_11001001,
and
10101010_11110000_00001111_11001011
Question: What is the byte offset of the original
byte in its word?
Answer: 10 (i.e., two), the address mod 4..
Question: What are the byte-offsets of the other
three bytes in that same word?
Answer: 00, 01, and 11 (i.e, zero, one, and
three).
Blocks vary in size. We will not make any assumption about the block size, other than that it is a power of two number of bytes. For the examples in this subsection, assume that each block is 32 bytes.
Since we assume aligned accesses, each 32-byte block has a byte address that is a multiple of 32. So block 0 is bytes 0-31, which is words 0-7. Block n is bytes 32n, 32n+1, ..., 32n+31.
Question: What block includes our byte address
10101010_11110000_00001111_11001010?
Answer: 10101010_11110000_00001111_110,
i.e., the byte address divide by 32 (the number of bytes in the
block) or the word address divided by 8 (the number of words in the
block).
We start with a tiny cache having a very simple cache organization, one that was used on the Decstation 3100, a 1980s workstation. In this design, cache lines (and hence memory blocks) are one word long.
Also in this Decstation 3100 design each memory block can only go in one specific cache line.
cache block number) is the memory block number modulo the number of blocks in the cache.
set associative cacheswe will also study.
We shall assume that each memory reference issued by the processor is for a single, complete word.
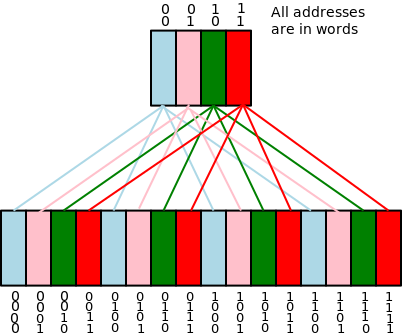
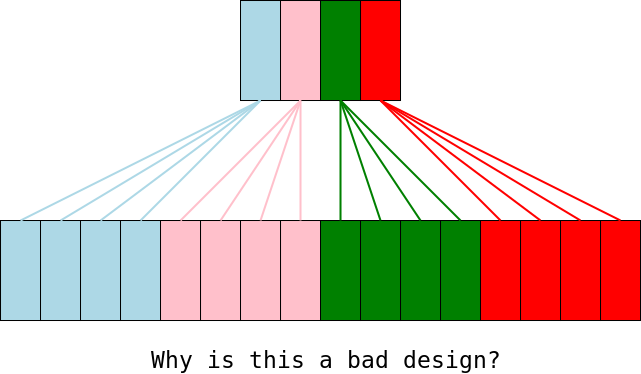
On the right is a diagram representing a direct mapped cache with C=4 blocks and a memory with M=16 blocks.
Let's assume each cache block and each memory block is one word long and to keep it simple we assume that each reference is to a single aligned word.
How can we find a memory block in such a cache? This is actually two questions in one.
The second question is the easier. Let C be the number of blocks in the cache. Then memory block number N can be found only in cache line number N mod C (it might not be present at all).
Referring to the diagram we have 16 memory blocks and 4 cache blocks so we will have to assign N/C=16/4 memory blocks to each cache block. (In this example N=C2, but that is a coincidence.)
In fact we assign memory block N to cache block N mod C
For example, in the upper diagram to the right all the green blocks in memory are assigned to the one green block in the cache.
Contrast this diagram with bad design immediately below it.
The good design has the important property that consecutive memory blocks are assigned to different cache blocks. Consider an important array. Its elements will be spread out in the cache and will not fight with each other for the same cache slot. For example in the picture any 4 consecutive memory slots will be assigned to 4 different cache slots.
So the first question reduces to:
Is memory block N present in cache block
N mod C?
Start Lecture #22
Remark: The final for this class will be on zoom, just like the midterm. I mistakenly copied something for 202 into our class notes for 201. The erroneous comment has been removed.
Referring to the diagram we note that, since only a green memory
block can appear in the green cache block, we know that the
rightmost two bits of the number of any memory block in the green
cache block are 10 (the number of the green cache block).
So to determine if a specific green memory block is in the green
cache block we need the rest
of the memory block number.
Specifically is the memory block in the green cache
block 0010,
0110, 1010,
or 1110?
It is also possible that the green cache block is empty
(called invalid), i.e, it is possible that no memory block is in
this cache block.
restof the address (i.e., red digits lost when we reduced the block number modulo the size of the cache) to see if the block in the cache is the memory block of interest. That number is N/C, using the terminology above. (Again, don't be confused by the coincidence that in this example N/C = N mod C. The coincidence occurs because N=C2).
| Addr(10) | Addr(2) | hit/miss | block# |
|---|---|---|---|
| 22 | 10110 | miss | 110 |
| 26 | 11010 | miss | 010 |
| 22 | 10110 | hit | 110 |
| 26 | 11010 | hit | 010 |
| 16 | 10000 | miss | 000 |
| 3 | 00011 | miss | 011 |
| 16 | 10000 | hit | 000 |
| 18 | 10010 | miss | 010 |
When the system is first powered on, all the cache blocks are invalid so all the valid bits are off.
On the right is a table giving a larger example, with C=8 (rather than 4, as above) and M=32 (rather than 16).
We still have M/C=4 memory blocks eligible to be stored in each cache block. Thus there are two tag bits for each cache block.
Remarks:

Shown on the right is a eight entry, direct-mapped cache with block size one word. As usual all references are for a single word (blksize=refsize=1). In order to make the diagram and arithmetic smaller, the machine has only 10-bit addressing (i.e., the memory has only 210=1024 bytes), instead of more realistic 32- or 64-bit addressing.
Above the cache we see a 10-bit address issued by the processor.
There are several points to note.
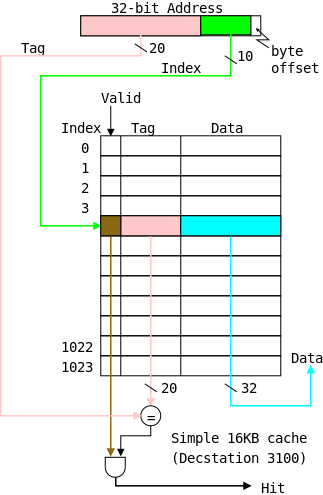
The circuitry needed for a simple cache (direct mapped, blksize=refsize=1) is shown on the right. The only difference between this cache and the example above is size. This cache holds 1024 blocks (not just 8) and the memory holds 230 = 210*3 = (210)3 ∼1,000,000,000 blocks (not just 256). That is, the cache size is 4KB and the memory size is 4GB.
To determine if we have a hit or a miss, and to return the data in case of a hit is quite easy, as the circuitry indicates.
Make sure you understand the division of the 32 bit address into 20, 10, and 2 bits.
Calculate on the board the total number of bits in this cache and the number used to hold data.
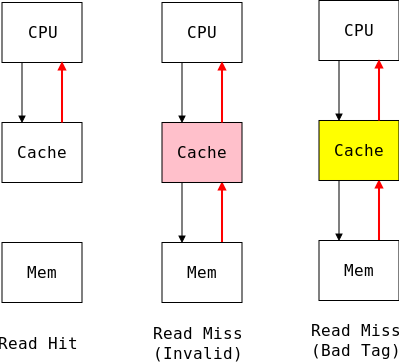
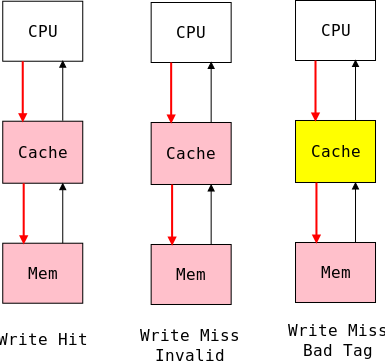
The action required for a read hit is clear, namely return to the processor the data found in the cache.
For a read miss, the best action is fairly clear, but requires some thought.
The simplest write policy is write-through, write-allocate (see below for definitions). The decstation 3100 discussed above adopted these policies and performed the following actions for any write, hit OR miss. (The 3100 was a personal workstation not a fancy supercomputer costing millions of dollars, so simplicity of the design was important. This desire for simplicity also explains why, for the 3100, block size = reference size = 1 word and the cache is direct mapped.)
Although the above policy has the advantage of simplicity (it performs the same actions for all writes, hits or misses; and simplifies the handling of read misses), it is out of favor due to its poor performance (other designs make few requests to main memory).
Divide the memory block number by the number of cache blocks. The quotient is the tag and the remainder is the cache block number.
MBN --- = tag MBN % NCB = CBN NCB
Analogy: If you have N numerical address but only n<N mailboxes available, one possibility (the one we use in caches) is to put mail for address M in mailbox M%n. Then to distinguish addresses assigned to the same mailbox you need the quotient M/n. In caches we call the mailbox assigned the cache index (or cache line or cache block number) and we call the quotient needed for disambiguation the tag.
The key principle is the
Fundamental Theorem of Fifth Grade
Dividend = Quotient * Divisor + Remainder
We divide the dividend (the memory block number) by the divisor (the number of cache blocks) and look in the cache slot whose number is the Remainder (the cache index or line number). We check whether the Quotient (the tag) matches the stored value.
Homework: Consider a cache with the following properties, which are essentially the ones we have been using to date:
| movl | $0x11ff, | 0x0 |
| movl | 0x0, | %r8 |
| movl | $0x22FF, | 0x80 |
| movl | 0x0, | %r9 |
| movl | $0x33FF, | 0x8 |
| movl | $0x44FF, | 0x8 |
| movl | $0x55FF, | 0x38 |
| movl | $0x66FF, | 0x28 |
| movl | 0x38, | %r10 |
The cache is initially empty
, i.e. all the valid bits are 0.
Then the references on the right are issued in the order given.
Remind me to do this one in class next time.
The setup we have described does not take much advantage of spatial locality. The idea of having a multiword blocks is to bring into the cache words near the referenced word since, by spatial locality, they are likely to be referenced in the near future.
We continue to assume that all references are for one word and that all memory address are 32-bits and reference a byte. For a while, we will continue to assume that the cache is direct mapped.
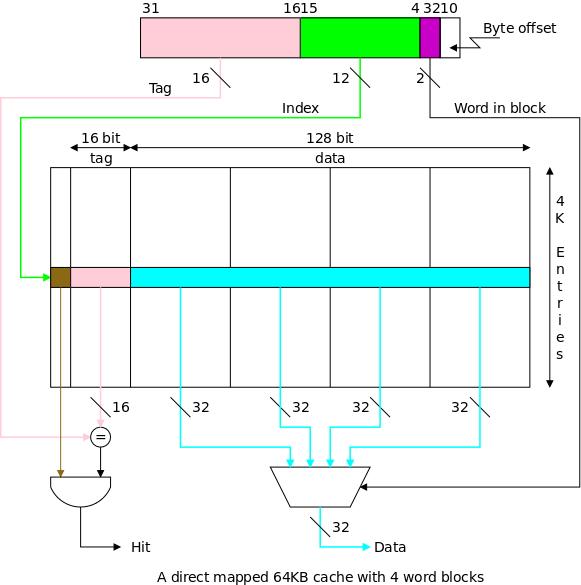
The figure on the right shows a 64KB direct mapped cache with
4-word (16-byte) blocks.
Questions: For this cache, when the memory word
referenced is in a given block, where in the cache does the block
go, and how do we find that block in the cache?
Answers:
Show from the diagram how this gives the pink portion for the tag and the green portion for the index or cache block number.
Consider the cache shown in the diagram above and a reference to word 17003.
Summary: Memory word 17003 resides in word 3 of cache block 154 with tag 154 set to 1 and with valid 154 true.
The cache size or cache capacity is the size of the data portion of the cache (normally measured in bytes).
For the caches we have seen so far this is the block size times the number of entries. For the diagram above this is 16B * 4K = 64KB. For the simpler direct mapped caches block size = word size. So the cache size is the word size times the number of entries. Specifically the cache in the previous diagram has size 4B * 4K = 16KB.
You should not be surprised to hear that a bigger cache has a higher hit rate. The interesting comparison is between the last cache and an enlarged version of the previous cache with 16K entries i.e. comparing two caches of size 64KB. Experiments have shown that spacial locality does occur and real programs have higher hit rates on caches with 4-word blocks than they do on caches with 1-word blocks.
For a simple example imagine a program that sweeps once through an array of one million entries, each one word in size. For our simple cache, the hit rate is zero! For the last cache, the hit rate is .75.
Note that the total size of the cache includes all
the bits.
Everything except for the data portion is considered overhead since
it is not part of the running program.
For the caches we have seen so far the total size is
(block size + tag size + 1) * the number of
entries
We shall not emphasize total size in this class, but we do in 436,
computer architecture.
write allocate): Fetch the needed line from memory, return the referenced word to the processor.
write allocateand
store through): Read the new line from memory replacing the old line in the cache and return the referenced word to the processor.
store through).
write-backpolicy is harder but has the advantage that if we update the variable z 100 times before evicting its cache block, we only send the last value of z to memory. Is this reduction of memory accesses worth the extra complexity?
Homework: Consider two 256KB direct-mapped caches (i.e., each cache contains 256KB of data). As always, a memory (byte) address is 32 bits and all references are for a 4-byte word. The first cache has a block size of one word, the second has a block size of 32 words.
Consider the following sad story. Jane's computer has a cache that holds 1000 blocks and Jane has a program that only references 4 (memory) blocks, namely blocks 13, 1013, 113013, and 7013. In fact the references occur in order: 13, 1013, 113013, 7013, 13, 1013, 113013, 7013, 13, 1013, 113013, 7013, 13, 1013, 113013, 7013, etc. Referencing only 4 memory blocks and having room for 1000 blocks in her cache, Jane expected an extremely high hit rate for her program. In fact, the hit rate was zero. She was so sad, she gave up her job as a web-mistress, went to medical school, and is now a brain surgeon at the mayo clinic in Rochester MN.
So far we have studied only direct mapped caches, i.e., those for which the block number in the cache is determined by the memory block number, i.e., there is only one possible location in the cache for any block. In Jane's sad story I picked four memory blocks so that they were all assigned to the same cache block and hence kept evicting each other. The rest of the cache was unused and essentially wasted.
Although this direct-mapped organization is no longer used because it gives poor performance, it does have one performance advantage: To check for a hit we need compare only one tag with the high-order bits of the addr.
The direct-mapped organization, in which a given memory block can be placed in only one possible cache block, is one extreme. The other extreme is called a fully associative cache in which a memory block can be placed in any cache block. Since any memory block can be in any cache block, the cache index tells us nothing about which memory block is stored there. Hence the tag must be the entire memory block number. Moreover, we don't know which cache block to check so we must check all cache blocks to see if we have a hit.
Most common for caches is an intermediate configuration called set associative or n-way associative (e.g., 4-way associative). The value of n is typically a small power of 2.
If the cache has B blocks, we group them into B/n sets each of size n. Since an n-way associative cache has sets of size n blocks, it is often called a set size n cache. For example, you often hear of set size 4 caches.
In a set size n cache, memory block number K is stored in set number K mod (the number of sets), which equals K mod (B/n).
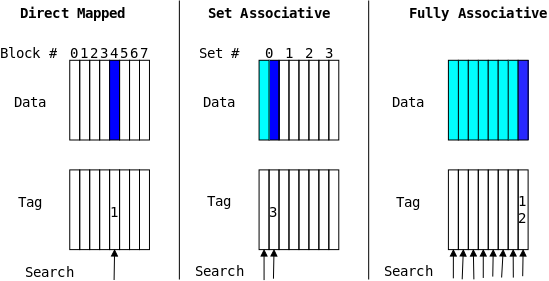
The picture on the right shows a system storing memory block 12 in three cache, each cache having 8 blocks. The left cache is direct mapped; the middle one is 2-way set associative; and the right one is fully associative.
We have already done direct mapped caches but to repeat:
The middle picture shows a 2-way set associative cache also called a set size 2 cache. A set is a group of consecutive cache blocks.
The right picture shows a fully associative cache, i.e. a cache where there is only one set and it is the entire cache.
For a cache holding n blocks, a set-size n cache is fully associative. Any set-size 1 cache is direct mapped.
When the cache was organized by blocks and we wanted to find a given memory word we first converted the word address to the MemoryBlockNumber (by dividing by the #words/block) and then formed the division
MemoryBlockNumber / NumberOfCacheBlocks
The remainder gave the index in the cache and the quotient gave the tag. We then referenced the cache using the index just calculated. If this entry is valid and its tag matches the tag in the memory reference, that means the value in the cache has the right quotient and the right remainder. Hence the cache entry has the right dividend, i.e., the correct memory block.
Recall that for the a direct-mapped cache, the cache index is the cache block number (i.e., the cache is indexed by cache block number). For a set-associative cache, the cache index is the set number.
Just as the cache block number for a direct-mapped cache is the memory block number mod the number of blocks in the cache, the set number for a set-associative cache is the (memory) block number mod the number of sets.
Just as the tag for a direct mapped cache is the memory block number divided by the number of blocks in the cache, the tag for a set-associative cache is the memory block number divided by the number of sets in the cache.
Summary: Divide the memory block number by the number of sets in the cache. The quotient is the tag and the remainder is the set number. (The remainder is normally referred to as the memory block number mod the number of sets.)
Do NOT make the mistake of thinking that a set size 2 cache has 2 sets, it has NCB/2 sets each set containing 2 blocks.
Ask in class.
Question: Why is set associativity good?
For example, why is 2-way set associativity better than direct
mapped?
Answer: Consider referencing two arrays of size
50KB that start at location 1MB and 2MB.
Question: What is the advantage of
associativity?
Answer: The advantage of increased associativity is
normally an increased hit ratio.
Question: What are the disadvantages?
Answer: It is slower, bigger, and uses more energy
due to the extra logic.
Remark: Go over the homework from last time. -- Note that an absolute memory address say location 0x0 does not have ().
Start Lecture #23
We know that a cache is smaller than a central memory and realize that at any one time only a subset of the central memory can be cache resident. Given a central memory address A we want to know
Actually we answered them in reverse order. We first determined where A must be in the cache if it's there at all, and then we look to see if it is there.
We started with a simple cache (direct mapped, blocksize one word). This cache contained only 4 words (2-bit addresses) and the central memory had only 16 words (4-bit addresses). Given a word in memory, we divided its MBN (its memory word) address by the NCB (# words in the cache) and examined the quotient and remainder (div and mod). By coincidence 16 = 42 so both the div and mod are 2-bit numbers; in general they are not the same size. We used the remainder (mod) to specify the index, i.e., the cache location for this word (in the diagram the index is the color) and used the quotient (called the tag) to determine, for example, if the green cache entry is the particular green memory block we desire.
The basic idea is to first number the units in the big and small memories, second divide the number given to a unit in the big memory by the number of units in the small. In the simplest example above, the number of a memory unit was its word address and the number of cache units was the number of words in the cache.
In reality, memory is composed of blocks (each several words) and caches are composed of sets (each several blocks). Specifically, given the cache parameters and memory byte address (32-bits) we proceed as follows.

To divide 134782993 by 100, you reach for a pencil not a calculator! You draw a vertical line with the pencil; the left part is the div (aka quotient) and the right part is the mod (aka remainder). You use the same vertical line technique to divide a binary number by 8=23 (or by 4K=212).
Question: How do we find a memory block in a 4KB
4-way set associative cache with block size 1 word?
Answer: This is more complicated than for the
simple direct mapped caches we started with.
The three macro steps are:
We proceeds as follows. (Do on the board an example: address 0x000A0A08 = 00000000_00001010_00001010_00001000)
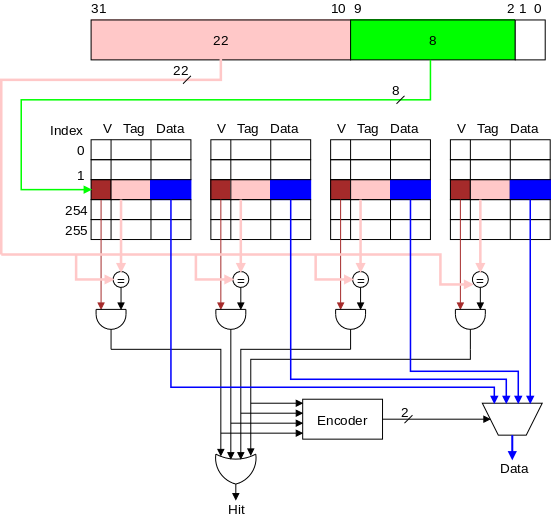
Done on The Board
In 2020-21, the class is taught remotely and the zoom whiteboard crashes. So we fake it. The example has address hex 0x000A0A08 = 00000000_00001010_00001010_00001000 in binary. The cache remains 256KB 4-way set associative, with blocksize one word.
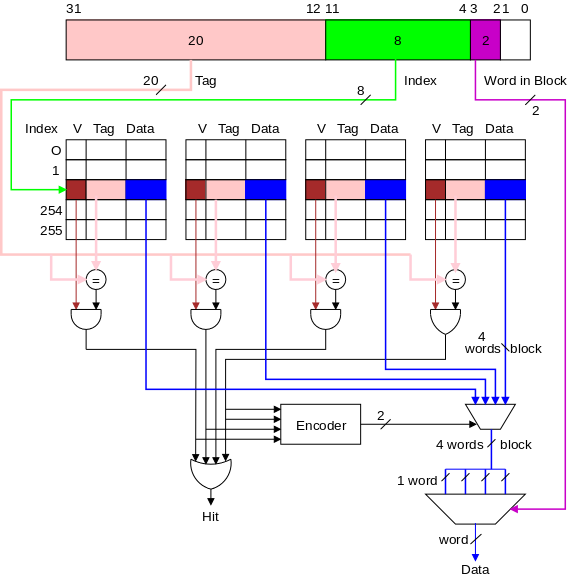
This is a fairly simple combination of the two ideas and is illustrated by the diagram on the right.
datacoming out of the multiplexor at the bottom right of the previous diagram is now a block. In the diagram on the right, the block is 4 words.
Our description and picture of multi-word block, direct-mapped caches is here, and our description and picture of single-word block, set-associative caches is just above. It is useful to compare those two picture with the one on the right to see how the concepts are combined.
Below we give a more detailed discussion of which bits of the memory address are used for which purpose in all the various caches.
When an existing block must be replaced, which victim should we choose? The victim must be in the same set (i.e., have the same index) as the new block. With direct mapped (a.k.a 1-way associative) caches, this determines the victim so the question doesn't arise.
With a fully associative cache all resident blocks are candidate victims. For an n-way associative cache there are n candidates. Victim selection in the fully-associative case is covered extensively in 202. We will only mention some possible algorithms.
When you write a C language assignment statement
y = x+1;
the processor must first read the value
of x from the memory.
This is called a load
instruction.
The processor also must write the new value of y into memory.
This is called a "store" instruction.
For a direct mapped cache with 1-word blocks we know how to do everything (we assume Store-Allocate and Write-Through).
If a block contains multiple words the only difference for us is that on a miss the rest of the block must be obtained from memory and stored in the cache.
An extra complication arises on a cache miss (either a load or a store). If the set is full (i.e., all blocks are valid) we must replace one of the existing blocks in the set and we are not learning which one to replace. As mentioned previously, in 202 you will learn how operating systems deal with a similar problem. However, caches are all hardware and hence must be fast so cannot adopt the complicated OS solutions.
We will not deal with this replacement question seriously in 201.
BigIs a Cache?
There are two notions of size.
Definition: The cache size is the capacity of the cache.
Another size of interest is the total number of bits in the cache, which includes tags and valid bits. For the 4-way associative, 1-word per block cache shown above, this size is computed as follows.
Question: For this cache, what fraction of the
bits are user data?
Answer: 4KB / 55Kb = 32Kb / 55Kb = 32/55.
Calculate in class the equivalent fraction for the last diagrammed cache, having 4-word blocks (and still 4-way set associative).
As always we assume a byte addressed machines with all references to a 4-byte word.
The 2 LOBs are not used (they specify the byte within the word, but all our references are for a complete word). We show these two bits in white. We continue to assume 32-bit addresses so there are 230 words in the address space.
Let us review various possible cache organizations and determine for each the tag size and how the various address bits are used. We will consider four configurations each a 16KB cache. That is the size of the data portion of the cache is 16KB = 214 bytes = 212 words.
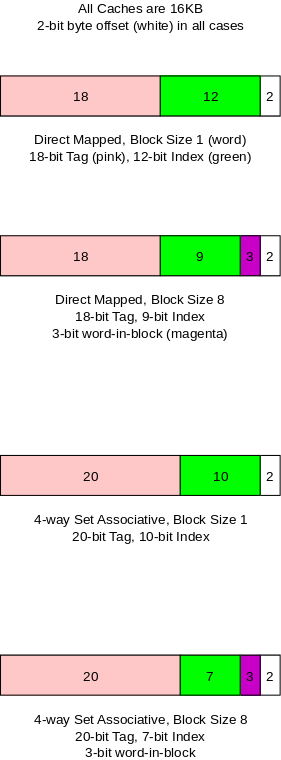
This is the simplest cache.
Modestly increasing the block size is an easy way to take advantage of spacial locality.
Increasing associativity improves the hit rate but only a modest associativity is practical.
The two previous improvements are often combined.
On the board calculate, for each of the four caches, the memory overhead percentage. For all four, the cache size is 16KB.
Homework: Redo the four caches above with the size of the cache increased from 16KB to 64KB determining the number of bits in each portion of the address as well as the overhead percentages.
Given the cache parameters and memory byte address (32-bits).
The memory blksize is 1 word. The cache is 64KB direct mapped. To which set is each of the following 32-bit memory addresses (given in hex) assigned and what are the associated tags?
Answer. Let's follow the three step procedure above for each address.
The block size 64B. The cache is 64KB, 2-way set associative. To which set is each of the following 32-bit memory addresses (given in hex) assigned and what are the associated tags?
Answer. Same 3-step procedure.
Homework: Redo the second example just above for a 2MB set size 16 cache with a block size of 64B (these are the sizes of one of the caches on at intel i7 processors). What is the total size of this cache.
We have already (briefly) discussed both these choices.
The issue of unified vs split I and D caches is covered in 436, Computer Architecture. We are not covering it in 201.
Similarly we are leaving the analysis of multilevel-caches to 436.
Trade-offs, Trade-offs, and more Trade-offs
For compute-intensive programs with significant run times, the programmer can often speed up execution by making the program cache-friendly, i.e., by increasing locality.
This is a much-studied problem, especially by programmers of numerical algorithms on supercomputers. Often one can reorder operations to improve spacial locality. Specifically (in say C) one can try to reference a 2D matrix by rows (i.e., the second subscript varies faster) rather than by columns
double A[100][200], sum
// by rows
for (int i=0; i<1024; i++)
for int j=0; j<2048; j++)
sum += A[i][j];
double A[100][200], sum
// by columns
for (int j=0; j<1024; j++)
for int i=0; ij<2048; i++)
sum += A[i][j];
For example consider the trivial example on the far right and
assume a cache block is the size of 8 C doubles and the cache holds
128 blocks.
The elements of matrix A are referenced in the order
A[0,0], A[0,1], A[0,2], ... A[0,2047], A[1,0],
..., A[1023,2047]
A[0,0] will be a fault, but (since the elements are stored
consecutively), the next 7 references will be to the same block and
hence will be hits.
This pattern repeats and the hit rate is 7/8.
In contrast the similar example on the near right references the
same elements but in the order
A[0,0], A[1,0], ...
Consecutive references are to far apart memory locations and hence
target distinct cache blocks so we do not get any hits at all.
Please don't let the above trivial example give you the
misimpression that improving cache performance just involves
interchanging the order of nested loops.
Just do a google search for
high performance matrix multiply
to get an idea of the
serious effort that is involved.
Skipped
The desire for memory to be big and fast (and other properties)
meets the reality that memory is ether big and slow
or
small and fast
.
Real systems contain a multilevel memory hierarchy where higher
levels are smaller and faster than lower levels.
Successful designs put the important data in higher levels. Choosing which data to put in higher levels is guided by the locality principles.
In this chapter we emphasized the cache (sram) / main memory (dram) boundary. Chapter 9 will look at the lower boundary between main memory (now considered small and fast) and local disk (big and slow).
We have been a little casual about memory addresses. When you write a program you view the memory addresses as starting at a fixed location, probably 0. But there are often several programs running at once. They can't all start at 0! In OS we study this topic extensively.
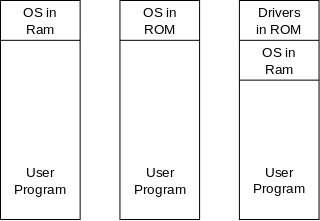
Way back when (say 1950s), the picture on the right was representative of computer memory. Each tall box is the memory of the system. Three variants of the OS location are shown, but we can just use the one on the left.
Note that there is only one user program in the system so, we can imagine that it starts at a fixed location (we use zero for convenience).
Using the appropriate technical terms we note that the virtual address, i.e., the addresses in the program, are equal to the physical addresses, i.e., the address in the actual memory (i.e., the RAM). The virtual address is also called the logical address and the physical address is also called the real address.
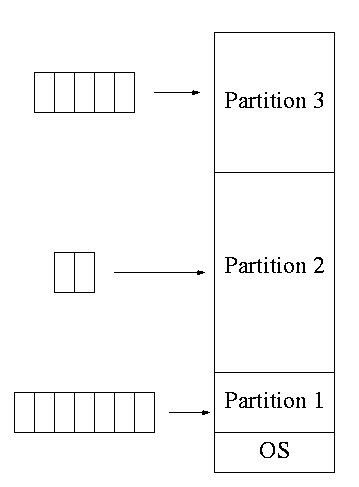
The diagram on the right illustrates the memory layout for multiple jobs running on a very early IBM multiprogramming system entitled MFT (multiprogramming with a fixed number of tasks).
When the system was booted (which took a number of minutes) the division of the memory into a few partitions was established. One job at a time was run in each partition, so the diagrammed configuration would permit 3 jobs to be running at once. That is it supported a multiprogramming level of 3.
If we ignore the OS or move it to the top of memory instead of the bottom, we can say that the job in partition 1 has its memory starting in location 0 of the RAM, i.e., it logical addresses (the addresses in the program) are equal to its physical addresses (the addresses in the RAM).
However, for the other partitions, this situation does not hold. For example assume two copies of job J are running, one copy in partition 1 and another copy in partition 2. Since the jobs are the same, all the logical addresses are the same. However, every physical address in partition 2 is greater than every physical address in partition 1.
Specifically, equal logical addresses in the two copies have physical addresses that differ by exactly the size of partition 1.
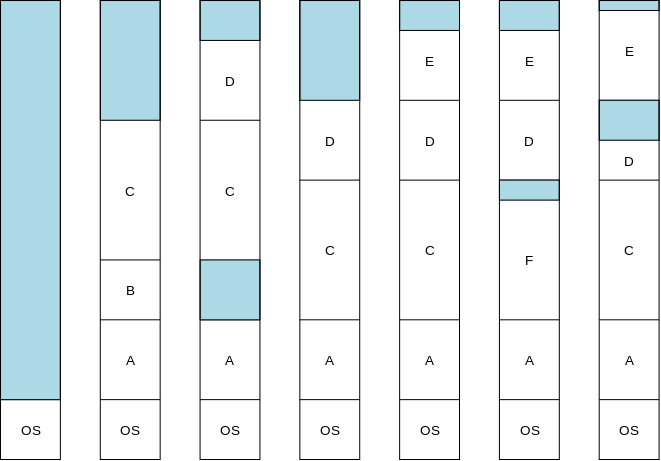
The picture on the right shows a swapping system. Each tall box represents the entire memory at a given point in time. The leftmost box represents boot time when only the OS is resident (blue shading represent free memory). Subsequent boxes represent successively later points in time.
The first snapshot after boot time shows three processes A, B, and
C running.
Then B finishes and D starts.
Note the blue hole
where B used to be.
The system needs to run E but each of the two holes is too small.
In response the system moves C and D so that E can fit.
Then F temporarily preempts C (C is swapped out
then swapped
back in).
Finally D shrinks and E expands.
In summary, not only does each process have its own set of physical addresses, but, even for a given unchanging process, the physical addresses change over time.
However, each process stays consistent, i.e., the physical address space remains contiguous for each process. The processes are not interleaved with each other. When you are seated in a plane that is climbing, your waist stays the same distance below your shoulders.
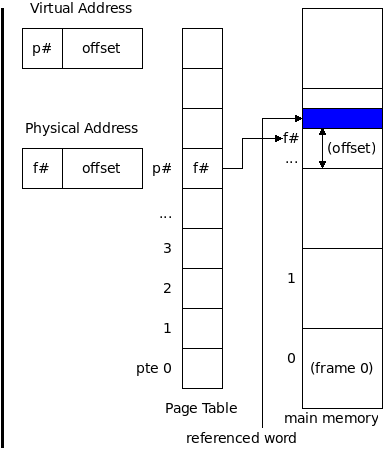
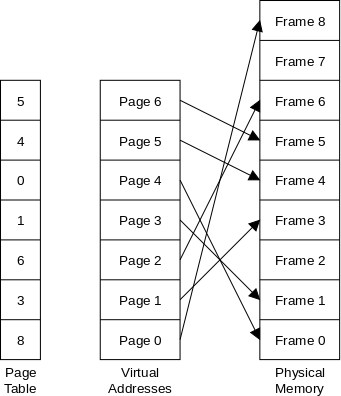
Now it gets crazy.
Moving a processes is an expensive operation. Part of the cause for this movement is that, in a swapping system, the process must be contiguous in physical memory.
As a remedy the (virtual) memory of the process is divided into fixed size regions called virtual pages and the physical memory is divided into fixed sized regions called physical pages. Virtual pages are often called pages and physical pages are often called frames
All pages are the same size; all frames are the same size; and the page size equals the frame size. So every page fits perfectly in any frame.
The pages are indiscriminately placed in frames without trying to keep consecutive pages in consecutive frames. The mapping from pages to frames is indicated in the diagram by the arrows.
But this can't work! Programs are written under the assumption that, in the absent of branches, consecutive instructions are executed consecutively. In particular, after executing the last instruction in page 4, we should execute the first instruction in page 5. But page 4 is in frame 0 and the last instruction in frame 0 is followed immediately by the first instruction in frame 1, which is the first instruction in page 3.
In summary the program needs to be executed in the order given by its pages, not by its frames.
This is where the page table is used. Before fetching the next instruction or data item, its virtual address is converted into the corresponding physical address as follows. Similar to the procedure with caches, we divide the virtual address by the page size and look at the quotient and remainder. (The former is the page number and the latter the offset in the page.) We look up the page number p# in the page table to find the corresponding entry, called the page table entry or PTE. The PTE contains the associated frame number f#. The offset in the frame is the same as the offset in the page. (Since the page size is always a power of 2, the division is done using a pencil).
Start Lecture #24
Remark: The cheet sheets for the final are on Brightspace.
We see in the paging example directly above that there are two kinds of address: virtual addresses and physical addresses. The set of virtual address in the program is called its virtual address space. We also call it the virtual memory of the process. Similarly we have the physical address space (or physical memory), which is composed of all the physical addresses. These two address spaces will help answer some previously raised questions.
The program contains virtual address. The real memory is accessed via physical addresses. Hence we must convert (on the fly) each virtual address to a physical address. This requires separating the page# from the offset, which is easy and fast, and reading the page table, which is easy but slow. We are essentially saying that each memory access in the program requires two access, first the page table and then the memory itself.
We must eliminate this two-to-one slowdown, or the whole idea is doomed.
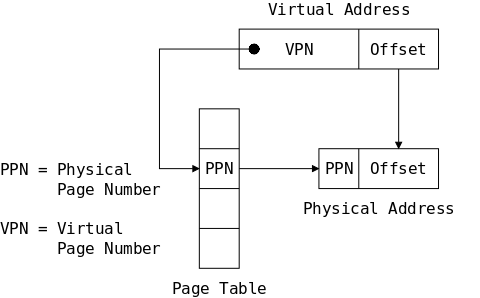
Translating each virtual address into the corresponding physical address is the job of the Memory Management Unit or MMU. So far this looks to be a simple task.
As noted this simplicity belies the performance penalty of converting each memory reference into two references. We will fix this with a caching-like approach, specifically we shall cache the page table in a structure called a TLB (translation lookaside buffer).
In addition we shall make the scheme more complicated in order to permit modern computers to concurrently execute programs whose total memory requirement exceed the memory present on the system.
In section 9.1 we have seen a series of historical advances enabling computer systems to fit more and more jobs in memory simultaneously.
Modern systems have gone a step beyond the simple paging scheme previously described and use instead demand paging in which it is no longer true that the entire program is in memory all the time it runs. Instead all the program's virtual pages are on disk. Only some pages are, in addition, in physical pages as in the figures above. For other pages the page table simply lists that the physical page is not resident in memory, i.e. there is no physical page containing this virtual page.
A program reference to a non-resident virtual page is called a page fault and triggers much activity. Specifically, an unused physical page must be found (often by evicting the virtual page currently residing in this physical page) and the referenced virtual page must be read from the disk into this newly available physical page.
If the above sounds similar to caching, you are right!
For caching, the SRAM acts as a small/fast
cache of the big/slow DRAM.
For the demand paging scheme just described the DRAM acts as a
small/fast cache
of the big/slow disk.
This question comes up in caching as well (how big should a cache block be?).
Because of the differing speed characteristics of disks and RAM, the typical page size is a few thousand bytes (4K and 8K are common) instead of the tens of bytes common for cache blocks.
Skipped.
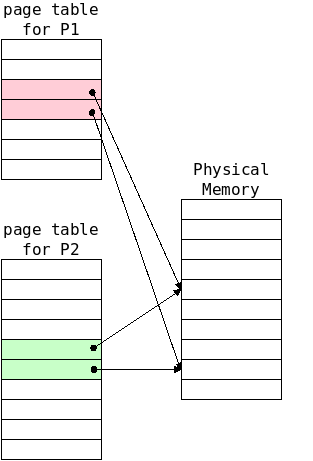
The separation of Virtual Memory from Physical Memory offers several advantages.
Our treatment emphasizes one process running on one CPU.
Today, even simple systems have multiple processors
running
many processes.
We will ignore multiple processors in this course,
but must acknowledge multiple processes.
In 202 Operating Systems we consider multiple processes and
multiple processors in more detail.
One change needed is that my pictures indicate one page table, which maps virtual page numbers to physical page numbers. In reality there is a separate page table for each process. For 201, we simply note that when the OS switches from running one process to running another it must determine the location of the new process's page table. Our diagrams ignore this detail.
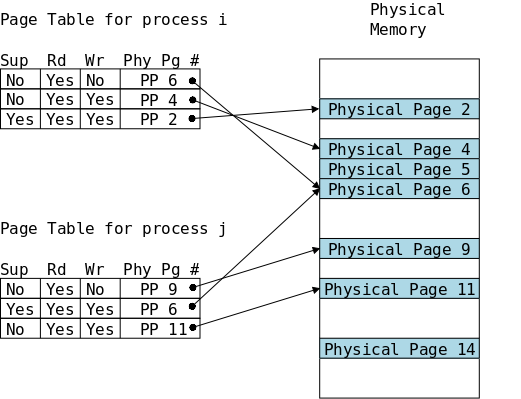
Since the page table is read for each memory reference, we can use it to hold protection information. (A similar technique is used to have some files belonging to one user not writable by other users.)
The diagram on the right shows the first three entries in the page tables for two processes i and j with three permission bits per virtual page.
supervisor mode required. Must the process be in supervisor mode to access this page. We will not emphasize the Sup protection bit in 201; supervisor mode will be discussed in 202 Operating Systems.
We see that each process can read each of it's first three virtual pages.
Process j cannot write physical page 9, perhaps its virtual page 0 contains text or read-only data.
Most interesting is physical page 6, which is shared between the two processes. Each process can read the physical page, but using different virtual addresses in the two processes: Physical page 6 is virtual page 0 in process i, but it is virtual page 1 in process j. Process j can write the shared page, but process i cannot. Perhaps this page contains data produced by process j and consumed by process i, the so called producer-consumer problem, which you will study in 202.
Note that the diagram is definitely not drawn to scale. Each blue box is a physical page, which is a few thousand bytes in size. The protection flags are a single bit each. The physical page number boxes are pointers to physical memory, these pointers need log(N) bits where N is the maximum possible number of physical pages. Since log(N) will probably not exceed 64 in our lifetime, 8 bytes is a good estimate for the size of these boxes.
Recall that in section 9.2 when describing demand paging we wrote
all the program's virtual pages are on disk.
Only some pages are, in addition, in physical
pages
.
To distinguish those virtual pages that have corresponding physical pages from those that do not, we define another bit stored in each PTE, the valid bit. When the valid bit is true (the good case) there is a copy of the virtual page in memory and the PTE contains the number of that physical page, as in the example just above in section 9.5. Copying the terminology from caches, we call this case a page hit.
If there is no physical page for a given virtual page, we have the bad case, commonly called a page fault (or a page miss). In this case the physical page number field contains junk
The diagram on the right illustrates the steps performed in the good case. Although the terminology used is most appropriate for a load, the steps are very similar for a store as well.
When a process runs, the MMU references that process's page table, which we treat as a simple 1-dimensional array of PTEs.
Then to load a data item in the good case involves the 5 steps shown on the right
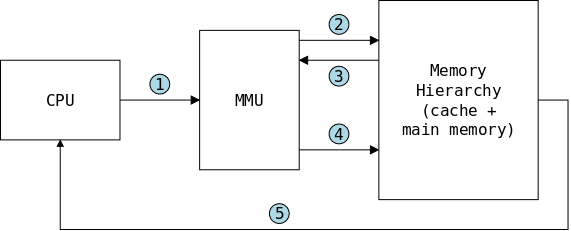
The full story for the bad case involves the operating system and we cover it in more detail in 202. The first three steps from the previous diagram remain intact. Steps 4 and 5 differ.
If the virtual address in invalid (for example outside the range of virtual addresses for this process), the OS kills the process.
If the virtual address is valid, but there is no physical address (the valid bit is off), a page fault has occurred and again the OS (and 202) are involved. Very briefly (and grossly over-simplified) an existing virtual page is evicted from its physical page and this now-empty physical is used to hold the requested virtual address.
Now that we understand the difference between virtual and physical address, we can discuss the trade-off between caching based on each.
An address from the program itself is the virtual address, the system then translates it to the physical address using the page table, as described above. Thus, with a virtual address based cache, the cache lookup can begin right away; whereas, with a physical address based cache, the cache lookup must be delayed until the translation to physical address has completed.
Many concurrently running processes will have the same virtual addresses (for example, all processes have their stacks starting at the same virtual address). However, all these virtual addresses are different physical address and represent parts of different programs. Hence they must be cached separately. But with a straightforward virtual address cache, all the virtual address for the base of the stack would be assigned to the same cache slot. Instead, the virtual address caching scheme adds complexity to the cache hardware to distinguish identical virtual address issued by different processes.
We have two remaining problems to solve.
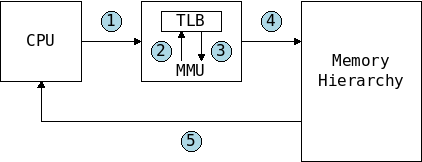
Modern systems dedicate a small virtually addressed cache to hold a small number of PTEs. This cache is very fast because it is small and located within the MMU (hence on the CPU chip itself). Thus, when the PTE is found in the TLB (a TLB hit), transmissions numbered 2 and 3 in the above diagram are avoided.
TLB misses (fortunately a rare occurrence) proceed as above: all 5 steps are performed
Often the TLB has a high degree of associativity, which improves its hit rate.
Start Lecture #25
Remark: A practice final is on Brightspace (resources tab). IMPORTANT: The practice final only covers the material since the midterm. Don't be mislead. The real final will be cumulative, i.e. will cover all the material in the course.
Remark: Two cheat sheets are in the resources tab of Brightspace: one has some C library names the other is for assembler. Both may be used on the final.
At first glance the size of a page table does not seem significant: For each physical page, we need 1 PTE. Since each physical page is several KB and each PTE is just several bytes, the later is merely about 0.1% overhead.
The problem is that, as described so far, the entire page table must be stored in physical memory, even though the vast majority of the entries indicate that the corresponding virtual page is invalid (and hence there is no corresponding physical page).
For the Intel architecture we have used, the virtual address space (see this previous diagram) starts at 0x400000 and ends at 248-1. Since the machine is byte addressable, the virtual size of the process includes nearly 248 bytes.
If the page table were just 0.1% of this number, it would require physical memory (the kind you must buy) of about 248-10 Bytes or 256GB for each process!
Recall that most of the virtual space in the process diagram is in gray, i.e., is unused.
I hope the diagram on the right is helpful.
Everything in the diagram is in physical memory.
For example, the label virt page 96
abbreviates
the physical page containing virtual page 96
.
Consider a process with exactly 100=102 virtual pages. Instead of defining a single page table with 100 entries, we partition those 100 entries into 10 groups of 10.
For the moment imagine all 10 of these tables exist: The first table points to the first 10 pages (0-9). The second table points to pages 10-19, etc. These are called level 2 tables. We then need a level 1 table pointing to the level 2 tables. The level 1 table has a blue border in the diagram.
Now look for the physical page corresponding to virtual page 11. Yesterday we would have referenced the single page table, selected its 11th (or 12th) entry, and followed the pointer to the physical page containing virtual page 11.
Today it is harder. We first go to the blue (i.e. level 1) table and follow entry number 1 (because 11 starts with 1), which takes us to the correct level 2 table. From there we follow entry number 1 (because 11 ends with 1) and arrive finally at the physical page corresponding to virtual page 11.
I suggest you try try to find the physical page containing virtual page 57.
Pages are commonly 4KB or 8KB as are level 2 tables; let's say each is 8KB to be definite. Each PTE is typically 8B so each level 2 table contains 1K=1024 PTEs. These 1K PTEs, refer to 1K pages or 8MB of the process's virtual address space.
The big advantage occurs because most virtual pages are not in physical memory. For example, none of the virtual pages 20-29 have physical pages. Hence slot 2 in the blue table is null and there is no corresponding level 2 table.
Even including the overhead of the blue table, the diagram shows an improvement: There are only 40 total table entries; whereas yesterday's simple page table would have had 100 entries.
The advantage is greater for bigger examples and especially when you consider 3- and 4-level tables.
Additionally, note that only the level 1 table needs to be permanently memory resident. The level 2 tables can be created as needed and can be paged in and out as needed.
The book does a lengthy example including caches and a TLB. We will concentrate on just the paging aspect.
| VPN | PPN | Valid |
|---|---|---|
| 00 | 28 | 1 |
| 01 | - | 0 |
| 02 | 33 | 1 |
| 03 | 02 | 1 |
| 04 | - | 0 |
| 05 | 16 | 1 |
| 06 | - | 0 |
| 07 | - | 0 |
| 08 | 13 | 1 |
| 09 | 17 | 1 |
| 0A | 9 | 1 |
| 0B | - | 0 |
| 0C | - | 0 |
| 0D | 2D | 1 |
| 0E | 11 | 1 |
| 0F | 0D | 1 |
The page table contains one PTE for each virtual page. A PTE contains several components; for simplicity we consider only the valid bit and the PPN.
For simplicity we assume a 1-level page table. Since there are 256 virtual pages, the table has 256 rows. On the right, we show only the first 16 (0-15) decimal. Speaking in hex we show the first 1016 (016-0F16).
Question: What are the physical address, the PPN,
and the PPO for the virtual address 023416?
Answer: 023416 =
00_0010_0011_01002.
The low order 6 bits of the address are the VPO and the high order 8
bits are the VPN.
(Throughout this example binary page numbers are red and binary page
offsets are green).
So VPO =
11_01002 =
3416 = 52.
Similarly, VPN =
0000_10002 =
0816 = 8.
As always PPO = VPO =
11_01002 =
3416 = 52.
The page table tells us that virtual page number 0816 is
valid and can be found in physical page 1316 =
01_00112.
Hence the physical address is
01_0011_11_01002 =
0100_1111_01002
= 4F416.
Skipped
Skipped
For many programs, the (maximum) size of each data structure is known to the programmer at the time the program is written. That is the easy case. Sometimes (in C) we use #define to make explicit these maximums and thereby ease the burden of changing the maximums when needed.
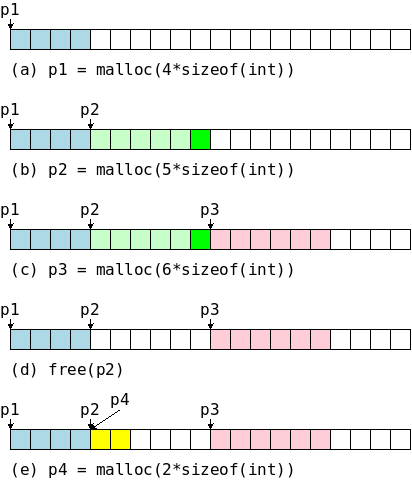
Other times we want to let the running program itself determine the amount of memory used. For example we have malloc() and its variants in C and new in java.
Moreover, sometimes we want to return no-longer-needed memory prior to program termination. This is free() in C. What about Java?
The malloc()/free() team deals with allocating virtual memory from (and returning virtual memory to) a region that grows and shrinks dynamically called the heap (see this previous diagram).
In the diagram on the right (which is from the book) we see malloc()/free in action. Each small square represents 4B (the size of an int) and we will insure alignment on an 8B boundary. Initially, malloc's internal pointer P points to the beginning of the heap, which we assume is properly aligned. You should imagine the diagram extending to the right with many, many, many more white boxes.
waists4B in darker green and gives the user p2, which points to 24 available bytes.
Note that achieving the above semantics is not trivial. That is, malloc() and free() are not trivial programs like the alloc()/afree() pair we did earlier in the semester. In particular, the alloc()/afree() pair required that the user could afree() only the most recent block obtained from alloc(). The ,alloc()/afree() scheme for obtaining and returning blocks required a stack-like LIFO ordering.
When the size of a data structure depend on parameter known only at
run time, the best
/ most natural response is to
first read (or compute) the parameter and pass it
to malloc() to obtain the right size data structure.
Also you may wish to return some of the memory before termination.
overhead, i.e., memory used but not specifically requested.
This is wasted space within an allocated region. One example was the padding used to maintain alignment. Some allocators only dispense blocks of certain sizes (e.g. buddy system and powers of 2).

p1 = malloc(100); p2 = malloc(100); p3 = malloc(100); free(p1); free(p3); p4 = malloc(200);
This is wasted space outside any allocated region. It occurs when there is enough free memory but not in one piece.
For example, consider the code on the right and assume that after the third malloc(), no space remained. Then the two end blocks are freed giving a total of 200B free, but split in two 100B pieces. Hence the fourth malloc() fails.
This is difficult problem whose occurrence is impossible to predict since it depends on knowing the future. Common heuristics employed are to keep free memory in a few large pieces rather than a large number of small pieces.
The format of a block on an implicit free list is shown on the right. It consists of a header followed by the payload and any padding needed to ensure proper alignment. The header contains the size of the block (including the header and any padding) as well as a flag indicating whether the block is free or has been allocated The block size can be thought of as a pointer to the next block and that is how we show it it in the diagrams below.
The name implicit free list is a little funny. It is really a list of all blocks, both free and allocated. All blocks have a header, which contains the block length and status (free or allocated).
In the diagram that follow, we have four (green) free blocks and one (red) allocated block.
The block given to the user includes the payload and any possible padding. It does not include the size and allocated bit. Indeed, the user must not alter that word.
Note that with an implicit list we must also keep a color
bit
with each block stating if the block is free.
Recall that the green portion includes any padding needed for alignment (or other) purpose.
Finding a Free Block)
Three methods have been considered.
best fittingblock (i.e., the smallest one that is big enough).
Often the free block chosen by the given algorithm is bigger than the user requested. There are two possible continuations.


What happens if malloc() cannot satisfy the current request for a free block of size 5? If the state is as in the first diagram, the only free blocks are of size 4,2,4,2 and we cannot satisfy the request. In this case, the next section will show us how to coalesce the first two free blocks into one of size 7. But if the request was for a size 20 free block, we would fail: there simply isn't enough space available.
On the right is a familiar diagram showing the (virtual) memory allocated for a running process. Note that the green heap section has an arrow indicating that it can grow.
What happens is that malloc() executes an sbrk() system call and poof the black line moves up and the heap gets bigger. (You will learn more about system calls in 202).
The simplest implementation is to just change the color of the returned block from red to green. But there is a problem. The previous free list diagram ends with two adjacent green blocks of size 4 and 2, but we cannot satisfy a request for a size 5 block. This is called false fragmentation. Fortunately, a simple coalescing of the last two blocks gives a size 7 free block.

So a linear traversal of the free blocks would enable us to coalesce adjacent free blocks. In an implicit free list we would have to traverse the entire (i.e., free plus allocated) list.
Instead of scanning the list to find blocks to coalesce, we might want to coalesce when we free a block. Since the block header in not given to the user, it still points to the next block. If the latter is free, we can easily coalesce. Therefore, if blocks are freed in reverse order, then checking the successor will accomplish all possible coalescing.
As just noted, when a block is freed, free() can check if the successor is free and and, if so, coalesce. The boundary tag method of Knuth extends this to the predecessor as well. The difficulty was that although the block's header points to the successor, there is no pointer to the predecessor. The boundary tag method adds a footer at the end of the block that contains a reverse pointer (making the list doubly linked).
Assume that the first red block is freed by the user and is merged
with the first green block to give a free (i.e., green) block
containing four boxes.
If we were using boundary tags (i.e. double link the list) the
implicit free list would becomes:
 Remember that the allocated/free bit, which I color-code red/green
is actually stored in both the header and footer.
Remember that the allocated/free bit, which I color-code red/green
is actually stored in both the header and footer.
The block being freed has two neighbors and, assuming an implicit free list, each can be allocated or free. this gives the four cases shown on the upper right.
In all four cases the middle (white) block becomes green and is then is merged with any adjacent green block, which can be located above, below or both.
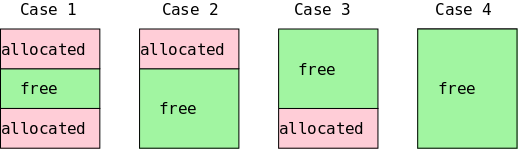
The four possible results are shown in the lower diagram. The lengths in the header and footer, must be updated to reflect any merges that occur,
Largely skipped; just a few comments about an implicit list allocator.
Have multiple free lists each holding free blocks of roughly the same size.
buddysystem uses blocksizes that are powers of 2. It is very fast but can have significant internal fragmentation.
As mentioned previously, Java has analogue of malloc() namely new, but has no analogue of free(). What is going on?
Java systems (and some others) automatically determine when
dynamically allocated memory can no longer be referenced by the
user's program (such memory is called garbage
).
The system then automatically frees such memory.
This procedure is called garbage collection and is a serious subject that we will not treat in depth.
Skipped.
Skipped.
Start Lecture #26
The normal (and simplest) instruction ordering is one after the other in order of their address. Now we consider more complex changes to the basic sequential control flow. Much of this involves the OS and you will see more in 202.
Some alterations of control flow are familiar and do not involve the OS, e.g., jump, call, return.
"Exceptional control flow" occurs in reaction to changes in system state: e.g., keyboard Ctrl-C, divide-by-zero.
interruptedor
preemptedby the OS so that the latter can switch to another user program.
Exceptions are a form of exceptional control flow that are implemented partly in hardware and partly in software (typically in the OS).
Well prior to the exception occurring, the OS sets up a jump table. This is similar to the jump table we saw when implementing a switch statement. Each exception type has a number and the system branches into the jump table indexed by that number and from there branches to the handler for that exception. Again this is similar to our implementation of the switch statement in the assembler section of the course.
The entries are sometimes called interrupt vectors. The table is established during OS boot time.
The memory used for the table is is not accessible to user programs, which is important since the jump table is executed in supervisor (privileged) mode
segmentation fault.
Note: We are drifting into OS from CSO. I cover this material in much more detail when teaching 202.
A process is a program in execution.
Note: Process
is a software concept.
Do not confuse it with the hardware concept processor
.
The OS works hard to provide the following illusions to each running process.
Skipped.
zombiestate until its parent reaps it.
To show how the four stars enable much of process management, consider the following highly simplified shell (the Unix command interpreter).
while (true)
display_prompt()
read_command(command)
if (fork() != 0)
waitpid(...) <--Omit this line; get a background job
else
execve(command)
endif
endwhile
The fork() system call duplicates the process. That is, we now have a second process, which is a child of the process that actually executed the fork(). The parent and child are very, VERY nearly identical. For example they have the same instructions, they have the same data, and they are both currently executing the fork() system call.
But there is a difference!
The fork() system call returns a zero in the child process and returns a positive integer in the parent. In fact the value returned to the parent is the PID (process ID) of the child.
Thus, the parent and child execute different branches of the if-then-else in the code above.
Removing the waitpid(...) lets the child run in the background
while the parent (the shell
) can start another job.
Remark: Next class I shall go over the practice final. I suggest you work on it before then. The last class will be devoted to answering any questions you have.
Start Lecture #27
RemarksReview of practice final
Start Lecture #28
General question answer session
Redo 8.4.A with ipad to draw diagram dynamically.
Remark: End of material eligible for the CSO final exam.
A clock on a computer is an electronic signal. If you plot a clock with the horizontal axis time and the vertical axis voltage, the result is a square wave as shown on the right.
A cycle is the period of the square wave generated by the clock.
You can think of the computer doing one instruction during one cycle. That is not correct: The truth is that instructions take several cycles but they are pipelines so in the ideal one instruction finishes each clock cycle.
We shall assume the clock is a perfect square wave with all periods equal.
Note: I added interludes because I realize that CS students have little experience in these performance calculations.
Modern processors have several caches. We shall study just two, the instruction cache and the data cache, normally called the I-Cache and D-Cache.
Every instruction that the computer executes has to be fetched from memory and the I-Cache is used for such references. So the I-cache is accessed once for every instruction.
In contrast only some instructions access the memory for data.
The most common instructions making such accesses are
the load and store instructions.
For example the C assignment statement
y = x + 1;
generates a load to fetch the value of x and a store to
update the value of y.
There is also an add that does not reference memory.
The diagram on the right shows all the possibilities
If both caches have a miss, the misses are processed one at a
time because there is only one central memory.
We assume separate instruction and data caches.
Do the following performance example on the board. It would be an appropriate final exam question.
double speedmachine? It would be double speed if there was a 0% miss rate.
A lower base (i.e. miss-free) CPI makes misses appear more expensive since waiting a fixed amount of cycles for the memory corresponds to losing more instructions if the CPI is lower.
A faster CPU (i.e., a faster clock) makes misses appear more expensive since waiting a fixed amount of time for the memory corresponds to more cycles if the clock is faster (and hence more instructions since the base CPI is the same).
Homework: Consider a system that has a miss-free CPI of 2, a D-cache miss rate of 5%, an I-cache miss rate of 2%, has 1/3 of the instructions referencing memory, and has a memory that gives a miss penalty of 20 cycles.
Note: Larger caches typically have higher hit rates but longer hit times.
Reviewed caches again and answer students' questions.
As requested I wrote out another example. Here it is.
At the end of the last class I was asked to do another problem with
sizes
.
In particular finding which address bits are the tag and which are
the cache index.
In this class we will always make the following assumptions with regard to caches.
One conclusion is that the low-order (i.e., the rightmost) two bits of the 32 bit address specifies the byte in the word and hence are not used by the cache (which always supplies the entire word).
We will use the following cache.
I use a three step procedure.
Memory Block Number.
For the cache just described
We will use the three step procedure mentioned in Extra.2.
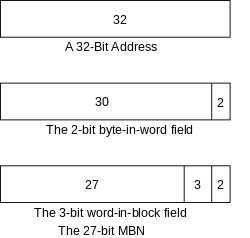
The top picture shows the 32-bit address.
The rightmost 2 bits give the byte in word, which we don't use since we are interested only in the entire word not a specific byte in the word. That is shown in the second picture. Note that there are 4 = 22 bytes in the word. The exponent 2 is why we need 2 address bits.
The next 3 bits from the right give the word-in-block. There are 8 words in the block (see Extra.2) and 8=23 so we need 3 bits.
The remaining 27 bits are the MBN.So NCS = 212, which answers question 3 of Extra.4
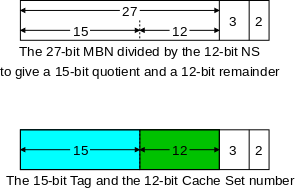
The MBN is 27 bits and NCS is 212.
Dividing a 27-bit number by a 12-bit number gives a (27-12)-bit quotient and a 12-bit remainder.
(This last statement is analogous to the more familiar statement that dividing a 5-digit number by 100=102 gives a (5-2)-digit quotient and a 2-digit remainder. To divide a 5 digit number by 100, you don't use a calculator, you just chop off the rightmost 2 digits as the remainder and remaining (5-2) digits form the quotient. Example 54321/100 equals 543 with a remainder of 21.)
The remainder is the cache set (the row in a diagram of the cache). It is shown in green. In blue we see the quotient, which is the tag.
So to answer questions 1 and 2. The high-order 15 (blue) bits form the 15-bit tag.
In the cache each 8-word block comes with a 15-bit tag and a 1-bit
valid flag.
Each of these cells
(I don't know if they have a name) thus
contains 8 32-bit words + 16 bits.
(I realize 16 bits is 2 bytes but often the number of bits is not
always a
multiple of 8.)
So each cell is 8*32+16 bits.
There are 2 cells in each set and 212 sets in the cache
so the total size of the cache is.
212 × 2 × (8×32 + 16) bits