V22.0201 Computer Systems Organization
2018-19 Fall—Allan Gottlieb
Tuesdays and Thursdays 3:30-4:45 Room 102 Ciww

Start Lecture #1

Chapter 0 Administrivia

I start at 0 so that when we get to chapter 1, the numbering will agree with the text.

0.1 Contact Information

0.2 Course Web Page

There is a web site for the course. You can find it from my home page, which is listed above, or from the department's home page.

0.3 Textbook

The course has two texts.

0.4 Email, and the Class Mailing List

0.5 Grades

Grades are based on the labs and exams; the weighting will be approximately
30%*LabAverage + 30%*MidtermExam + 40%*FinalExam (but see homeworks below).

0.6 The Upper Left Board

I use the upper left board for lab/homework assignments and announcements. I should never erase that board. Viewed as a file it is group readable (the group is those in the room), appendable by just me, and (re-)writable by no one. If you see me start to erase an announcement, please let me know.

I try very hard to remember to write all announcements on the upper left board and I am normally successful. If, during class, you see that I have forgotten to record something, please let me know. HOWEVER, even if I forgot and no one reminds me, the assignment has still been given.

0.7 Homeworks and Labs

I make a distinction between homeworks and labs.

Labs are

Homeworks are

0.7.1 Homework Numbering

Homeworks are numbered by the class in which they are assigned. So any homework given today is homework #1. Even if I do not give homework today, any homework assigned next class would be homework #2. So the homework present in the notes for lecture #n is homework #n (even if I inadvertently forgot to write it to the upper left board).

0.7.2 Doing Labs on non-NYU Systems

You may develop (i.e., write and test) lab assignments on any system you wish, e.g., your laptop. However, ...

0.7.3 Obtaining Help with the Labs

Good methods for obtaining help include

  1. Asking me during office hours (see my home page for my hours).
  2. Asking the mailing list.
  3. Asking another student.
  4. But ...
    Your lab must be your own.
    That is, each student must submit a unique lab. Naturally, simply changing comments, variable names, etc. does not produce a unique lab.

0.7.4 Computer Language Used for Labs

This course uses the C computer language.

0.8 A Grade of Incomplete

The rules for incompletes and grade changes are set by the school> and not the department or individual faculty member. The rules set by CAS can be found in <http://cas.nyu.edu/object/bulletin0608.ug.academicpolicies.html>, which states:

The grade of I (Incomplete) is a temporary grade that indicates that the student has, for good reason, not completed all of the course work but that there is the possibility that the student will eventually pass the course when all of the requirements have been completed. A student must ask the instructor for a grade of I, present documented evidence of illness or the equivalent, and clarify the remaining course requirements with the instructor.

The incomplete grade is not awarded automatically. It is not used when there is no possibility that the student will eventually pass the course. If the course work is not completed after the statutory time for making up incompletes has elapsed, the temporary grade of I shall become an F and will be computed in the student's grade point average.

All work missed in the fall term must be made up by the end of the following spring term. All work missed in the spring term or in a summer session must be made up by the end of the following fall term. Students who are out of attendance in the semester following the one in which the course was taken have one year to complete the work. Students should contact the College Advising Center for an Extension of Incomplete Form, which must be approved by the instructor. Extensions of these time limits are rarely granted.

Once a final (i.e., non-incomplete) grade has been submitted by the instructor and recorded on the transcript, the final grade cannot be changed by turning in additional course work.

0.9Academic Integrity Policy

This email from the assistant director, describes the policy.

  Dear faculty,

  The vast majority of our students comply with the
  department's academic integrity policies; see

  www.cs.nyu.edu/web/Academic/Undergrad/academic_integrity.html
  www.cs.nyu.edu/web/Academic/Graduate/academic_integrity.html

  Unfortunately, every semester we discover incidents in
  which students copy programming assignments from those of
  other students, making minor modifications so that the
  submitted programs are extremely similar but not identical.

  To help in identifying inappropriate similarities, we
  suggest that you and your TAs consider using Moss, a
  system that automatically determines similarities between
  programs in several languages, including C, C++, and Java.
  For more information about Moss, see:

  http://theory.stanford.edu/~aiken/moss/

  Feel free to tell your students in advance that you will be
  using this software or any other system.  And please emphasize,
  preferably in class, the importance of academic integrity.

  Rosemary Amico
  Assistant Director, Computer Science
  Courant Institute of Mathematical Sciences

Remark: The chapter/section numbers for the material on C, agree with Kernighan and Plauger. However, the material is quite standard so, as mentioned before, if you already own a C book that you like, it should be fine.

Chapter 1 A Tutorial Introduction

Since Java includes much of C, my treatment can be very brief for the parts in common (e.g., control structures).

1.1 Getting Started

C programs consist of functions, which contain statements, and variables, the latter store values.

The Hello World Function

  #include <stdio.h>
  main()
  {
    printf("Hello, world\n");
  }

Although the this program works, the second line should be int main(int argc, char *argv[])
Remember how long it took you to really understand public static void main (String[] args)

1.2 Variables and Arithmetic Expressions

1.3 The For Statement

1.4 Symbolic Constants

Fahrenheight-Celsius

  #include <stdio.h>
  main() {
    int F, C;
    int lo=0, hi=300, incr=20;

    for (F=lo; F<=hi; F+=incr) {
      C = 5 * (F-32) / 9;
      printf("%d\t%d\n", F, C);
    }
  }

Floating Point Fahrenheight-Celcius

  #include <stdio.h>
  #define LO 0
  #define HI 300
  #define INCR 20
  main() {
    int F;
    for (F=LO; F<=HI; F+=INCR)
      printf("%3d\t%5.1f\n", F, (F-32)*(5.0/9.0));
  }

1.5 Character Input and Output

getchar() / putchar()

The simplest (i.e., most primitive) form of character I/O is getchar() and putchar(), which read and print a single character.

Both getchar() and putchar() are defined in stdio.h.

1.5.1 File Copying

  #include <stdio.h>
  main() {
    int c;
    while ((c = getchar()) != EOF)
      putchar(c);
  }

File copy is conceptually trivial: getchar() a char and then putchar() this char until eof. The code is on the right and does require some comment despite is brevity.

Homework: Write a (C-language) program to print the value of EOF. (This is 1-7 in the book but I realize not everyone will have the book so I will type them in.)

Homework: (1-9) Write a program to copy its input to its output, replacing each string of one or more blanks by a single blank.

1.5.2 Character Counting

This is essentially a one-liner (in two ways).

    while (getchar() != EOF)  ++numChars;
  
    for (nc = 0; getchar() != EOF; ++nc);

1.5.3 Line Counting

Now we need two tests. Perhaps the following is really a two-liner, but it does have only one semicolon.

  while ((c = getchar()) != EOF)  if (c == '\n')  ++numLines;

So if a file has no newlines, it has no lines. Demo this with echo -n >noEOF "hello"

1.5.4 Word Counting

The Unix wc Program

The Unix wc program prints the number of characters, words, and lines in the input. It is clear what the number of characters means. The number of lines is the number of newlines (so if the last line doesn't end in a newline, it doesn't count). The number of words is less clear. In particular, what should be the word separators?

  #include <stdio.h>
  #define WITHIN   1
  #define OUTSIDE  0
  main() {
    int c, num_lines, num_words, num_chars, within_or_outside;
    within_or_outside = OUTSIDE; // C doesn't have Boolean type
    num_lines = num_words = num_chars = 0;
    while ((c = getchar()) != EOF) {
      ++num_chars;
      if (c == '\n')
        ++num_lines;
      if (c == ' ' || c == '\n' || c == '\t')
        within_or_outside = OUTSIDE;
      else if (within_or_outside == OUTSIDE) { // starting a word
        ++num_words;
        within_or_outside = WITHIN;
      }
    }
    printf("%d %d %d\n", num_lines, num_words, num_chars);
  }

Homework: (1-12) Write a program that prints its input one word per line.

1.6 Arrays

We are hindered in our examples because we don't yet know how to input anything other than characters and don't want to write the program to convert a string of characters into an integer or (worse) a floating point number.

Mean and Standard Deviation

  #include <stdio.h>
  #define N  10   // imagine you read in N
  main() {
    int i;
    float x, sum=0, mu;
    for (i=0; i<N; i++) {
      x = i;  // imagine you read in X[i]
      sum += x;
    }
    mu = sum / N;
    printf("The mean is %f\n", mu);
  }

  #include <stdio.h>
  #define N  10   // imagine you read in N
  #define MAXN  1000
  main() {
    int i;
    float x[MAXN], sum=0, mu;
    for (i=0; i<N; i++) {
      x[i] = i;  // imagine you read in X[i]
    }
    for (i=0; i<N; i++) {
      sum += x[i];
    }
    mu = sum / N;
    printf("The mean is %f\n", mu);
  }

  #include <stdio.h>
  #include <math.h>
  #define N  5   // imagine you read in N
  #define MAXN  1000
  main() {
    int i;
    double x[MAXN], sum=0, mu, sigma;
    for (i=0; i<N; i++) {
      x[i] = i;  // imagine you read in x[i]
      sum += x[i];
    }
    mu = sum / N;
    printf("The mean is %f\n", mu);
    sum = 0;
    for (i=0; i<N; i++) {
        sum += pow(x[i]-mu,2);
    }
    sigma = sqrt(sum/N);
    printf("The std dev is %f\n", sigma);
  }

I am sure you know the formula for the mean (average) of N numbers: Add the numbers and divide by N. The mean is normally written μ. The standard deviation is the RMS (root mean squared) of the deviations-from-the-mean, it is normally written σ. Symbolically, we write μ = ΣXi/N and σ = √(Σ((Xi-μ)2)/N). (When computing σ we sometimes divide by N-1 not N. Ignore the previous sentence.)

The First Version (Just the Mean; No Array Used)

The first program on the right naturally reads N, then reads N numbers, and the computes the mean of the latter. There is a problem; we don't know how to read numbers.

So I faked it by having N a symbolic constant and making x[i]=i.

The Second Version (Just the Mean: Array Used)

I do not like the second version with its gratuitous array. It is (a little) longer, slower, and more complicated. Much worse it takes space proportional to N, for no reason. Hence it might not run at all for large N. However, I have seen students write such programs. Apparently, there is an instinct to use a three step procedure for all assignments:

  1. Read everything in.
  2. Do all the computation.
  3. Print all the answers.

But that is silly if, as in this example, you no longer need each value after you have read the next one.

The Third Version Mean and Standard Deviation)


The last example is a good use of arrays for
  computing the standard deviation using the RMS formula above.
  We do need to keep the values around after computing the mean so
  that we can compute all the deviations from the mean and, using
  these deviations, compute the standard deviation.


Note that, unlike Java, no use of new (or the C analogue
  malloc()) appears.


Arrays declared as in this program have a lifetime of the routine in
  which they are declared.
  Specifically sum and x are both allocated when
  main is called and are both freed when main is finished.


Arrays in Java are references.
  So, when you write in a Java function f()


  int[] A = new int[3];



The lifetime of the array is not tied to the lifetime
  of f().
  We will battle with lifetimes in C later in the course when we look
  carefully at pointers and malloc().



Non-primitive Declarations


Note the declaration int x[MAXN] in the third version.
  In C, to declare a complicated variable (i.e., one that is not a
  primitive type like int or char), you write what
  has to be done to the variable to get one of the primitive
  types.



In C if we have int X[10]; then writing X in your
  program is the same as writing &X[0].
  & is the address of operator.
  More on this later when we discuss pointers.



1.7 Functions


There is of course no limit to the useful functions one can write.
  Indeed, the main() programs we have written above are all
  functions.


A C program is a collection of functions (and global variables).
  Exactly one of these functions must be called main and that
  is the function at which execution begins.


  #include <stdio.h>
  // Determine letter grade from score
  // Demonstration of functions
  char letter_grade (int score) {
    if      (score >= 90) return 'A';
    else if (score >= 80) return 'B';
    else if (score >= 70) return 'C';
    else if (score >= 60) return 'D';
    else                  return 'F';
  }  // end function letter_grade

  main() {
    short quiz;
    char grade;
    quiz = 75;   // should read in quiz
    grade = letter_grade(quiz);
    printf("For a score of %3d the grade is %c\n",
           quiz, grade);
  } // end main
  cc -o grades grades.c; ./grades
  For a score of  75 the grade is C



One important issue is type matching.
  If a function f takes one int argument and
  f is called with a short, then the
  short must be converted to an int.
  Since this conversion is widening, the compiler will automatically
  coerce the short into an int, providing it knows
  that an int is required.


It is fairly easy for the compiler to know all this
  providing f() is defined before it is used, as in
  the code on the right.



Computing Letter Grades


We see on the right a function letter_grade defined.
  It has one int argument and returns a char.


Finally, we see the main program that calls the
  function.


The main program uses a short to hold the
  numerical grade and then calls the function with this short
  as the argument.
  The C compiler generates code to coerce this short value to
  the int required by the function.



Averages and Sorting


  // Average and sort array of random numbers
  #define NUMELEMENTS 50
  void sort(int A[], int n) {
    int temp;
    for (int x=0; x<n-1; x++)
      for (int y=x+1; y<n; y++)
        if (A[x] < A[y]) {
          temp   = A[y];
          A[y]   = A[y+1];
          A[y+1] = temp;
        }
  }
  
  double avg(int A[], int num) {
    int sum = 0;
    for (int x=0; x<n; x++)
      sum = sum + A[x];
    return (sum / n);
  }
  
  main() {
    int table[NUMELEMENTS];
    double average;
    for (int x=0; x<NUMELEMENTS; x++) {
      table[x] = rand(); /* assume defined */
      printf("The elt in pos %d is %d\n",
             x, table[x]);
    }
    average = avg(table, NUMELEMENTS );
    printf("The average is %5.1f ", average);
    sort(table, NUMELEMENTS );
    for (x-=; x<NUMELEMENTS; x++)
      printf("The element in position %3d is %3d \n",
             x, table[x]);
  }



The next example illustrates a function that has an array
  argument.


Remember that in a C declaration you decorate the item being
  declared with enough stuff (e.g., [], *) so that the result is a
  primitive type such as int, double, or
  char.


The function sort has two parameters, the second one
  n is simply an int.
  The parameter A, however, is more complicated.
  It is the kind of thing that when you take an element of it, you get
  an int.

  That is, A is an array of ints.

Unlike the array example in section 1.6, A does not
  have an explicit upper bound on its index.
  This is because the function can be called with arrays of different
  sizes.
  Since the function needs to know the size of the array (look at the
  for loops), a second parameter n is used for
  this purpose.


This example has two function calls:
  main calls both avg and sort.
  Looking at the call from main to sort we see that
  table is assigned to A and
  NUMELEMENTS is assigned to n.
  Looking at the code in main itself, we see that indeed
  NUMELEMENTS is the size of the array table and
  thus in sort, n is the size of A.


All seems well provided the called function appears
  before the function that calls it.
  Our examples have followed this convention.


So far so good; but if f calls g and (recursively)
  g calls f, we are in trouble.
  How can we have f before g, and g before
  f?


This will be answered in our next example.



Start Lecture #2
 


1.8 Arguments—Call by Value


Arguments in C are passed by value (the same as Java does
  for arguments that are not objects).



1.9 Character Arrays


Unlike Java, C does not have a string datatype.
  A string in C is an array of chars.
  String operations like concatenate and copy (assignment) become
  functions in C.
  Indeed there are a number of standard library routines for
  strings.


The most common implementation of strings in C is
  null terminated.
  That is, a string of length 5 actually contains 6 characters, the 5
  characters of the string itself and a sixth character = '\0' (called
  null) indicating the end of the string.



Print Longest Line


This program reads lines from the terminal, converts them to C strings
  by appending '\0', and prints the longest one found.
  Pseudo code would be


  while (more lines)
    read line
    if (longer than previous longest)
      save line and its length



Thus we need the ability to read in a line and the ability to save
  a line.
  We write two functions getLine and copy for these
  tasks (the book uses getline (all lower case), but that doesn't
  compile for me since there is a library routine in stdio.h with the
  same name and different signature).


  #include <stdio.h>
  #define MAXLINE 1000
  int getLine(char line[], int maxline);
  void copy(char to[], char from[]);

  int main() {
    int len, max;
    char line[MAXLINE], longest[MAXLINE];
    max = 0;
    while ((len=getLine(line,MAXLINE))>0)
      if (len > max) {
        max = len;
        copy(longest,line);
      }
    if (max>0)
      printf("%s", longest);
    return 0;
  }

  int getLine(char s[], int lim) {
    int c, i;
    for (i=0; i<lim-1 &&
              (c=getchar())!=EOF &&
              c!='\n';
         ++i)
      s[i] = c;
    if (c=='\n') {
      s[i]= c;
      ++i;
    }
    s[i] = '\0';
    return i;
  }

  void copy(char to[], char from[]) {
    int i;
    i=0;
    while ((to[i] = from[i]) != '\0')
      ++i;
  }




The main() Function


Given the two supporting routines, main is
  fairly simple, needing only a few small comments.


    
  
  1. Note that getLine and copy are declared
    before main.
    They are defined later in the file but C requires
    declare (or define) before use so either main would have to
    come last or the declarations are needed.
    Since only main uses the routines, the declarations could
    have been in main but it is common practice to put them
    outside as shown.
    2. 
  
  2. Note %s inside printf.
    This is used for (null-terminated) strings.
    3. 
  
  3. Note that main is declared to return an integer and
    it does return 0.
    In unix at least, this is the indication of a successful
    run.
    4. 
  
  4. Note the while loop structure.
    Having a parenthesized assignment as part of the condition being
    tested is a fairly common idiom.
    5. 




The getline() Helper


The for continuation condition
  in getLine is rather complex. 
  (Note that the for loop has an empty body; the entire
  action occurs in the for statement itself.)


The condition part of the for tests for 3 situations.


    
  
  1. We have filled up s[].
    2. 
  
  2. We get to the end of the input.
    3. 
  
  3. We find an end-of-line
    4. 



Perhaps it would be clearer if the test was simply
  i<lim-1 and the rest was done with if-break
  statments inside the loop.



A Subtlety in The Three Tests


In C, if you write f(x)+g(y)+h(z) you have
  no guarantee of the order the functions will be invoked.
  However, the && and || operators do
  guarantee left-to-right ordering to enforce short-circuit
  condition evaluation.




The copy() Helper


The copy() function is declared and defined
  to return void.



Homework: Simplify the for condition
  in getline() as just indicated.



1.10 External Variables and Scope



Solving Quadratic Equations


  #include <stdio.h>
  #include <math.h>
  #define A +1.0   // should read
  #define B -3.0   // A,B,C
  #define C +2.0   // using scanf()
  void solve (float a, float b, float c);
  int main() {
    solve(A,B,C);
    return 0;
  }
  void solve (float a, float b, float c) {
    float d;
    d = b*b - 4*a*c;
    if (d < 0)
      printf("No real roots\n");
    else if (d == 0)
      printf("Double root is %f\n", -b/(2*a));
    else
      printf("Roots are %f and %f\n",
             ((-b)+sqrt(d))/(2*a),
             ((-b)-sqrt(d))/(2*a));
  }

  #include <stdio.h>
  #include <math.h>
  #define A +1.0   // main() should read
  #define B -3.0   // A,B,C
  #define C +2.0   // using scanf()
  void solve(void);
  float a, b, c;   // definition
  int main() {
    extern float a, b, c; // declaration
    a=A;
    b=B;
    c=C;
    solve();
    return 0;
  }
  void solve () {
    extern float a, b, c; // declaration
    float d;
    d = b*b - 4*a*c;
    if (d < 0)
      printf("No real roots\n");
    else if (d == 0)
      printf("Double root is %f\n", -b/(2*a));
    else
      printf("Roots are %f and %f\n",
             ((-b)+sqrt(d))/(2*a),
             ((-b)-sqrt(d))/(2*a));
  }



The two programs on the right find the real roots (no complex
  numbers) of the quadratic equation


  ax2+bx+c



They proceed by using the standard technique of first calculating
  the discriminant
  
    d = b2-4ac
  

  These programs deal only with real roots, i.e., when
  d≥0.


The programs themselves are not of much interest.
  Indeed a Java version would be too easy to be a midterm exam
  question in 101.
  Our interest is confined to the method in which the
  coefficients a, b, and c are passed from
  the main() function to the helper
  routine solve().



Method 1 Arguments and Parameters


The first program calls a function solve()
  passing it as arguments the three coeficients A,B,C.


There is little to say.
  Method 1 is a simple program and uses nothing new.



Method 2 External (a.k.a. Global) Variables


The second program communicates with solve
  using external variables rather than arguments/parameters.










Chapter 2 Types, Operators, and Expressions



2.1 Variable Names


Similar to Java: A variable name must begin with a letter and then
  can use letters and numbers.
  An underscore is a letter, but you shouldn't begin a variable name
  with one since that is conventionally reserved for library routines.
  Keywords such as if, while, etc are reserved and
  cannot be used as variable names.



2.2 Data Types and Sizes


C has very few primitive types.



There are qualifiers that can be added.
  One pair is long/short, which are used with int.
  Typically short int is abbreviated short and
  long int is abbreviated long.


long must be at least as big as int, which must
  be as least as big as short.


There is no short float,  short double,
    or  long float.
  The type long double specifies extended precision.


The qualifiers signed or unsigned can be applied to
  char or any integer type.
  They basically determined how the sign bit is interpreted.
  An unsigned char uses all 8 bits for the integer value and
  thus has a range of 0–255; whereas, a signed char has
  an integer range of -128–127.



2.3 Constants



Integer Constants


A normal integer constant such as 123 is an int, unless it
  is too big in which cast it is a long.
  But there are other possibilities.




String Constants


Although there are no string variables, there are string constants,
  written as zero or more characters surrounded by double quotes.
  A null character '\0' is automatically appended.




Enum Constants


Alternative method of assigning integer values to symbolic names.


  enum Boolean {false, true}; // false is zero, true is 1
  enum Month {Jan=1, Feb, Mar, Apr, May, Jun, Jul, Aug, Sep, Oct, Nov, Dec};




2.4 Declarations


Perhaps they should be called definitions since space is allocated.


Similar to Java for scalars.


  int x, y;
  char c;
  double q1, q2;



(Stack allocated) arrays are simple since the entire array is
  allocated not just a reference (no new/malloc required).


  int x[10];



Initializations may be given.


  int x=5, y[2]={44,6}; z[]={1,2,3};
  char str[]="hello, world\n";



The qualifier const makes the variable read only so it
  must be initialized in the declaration.



2.5 Arithmetic Operators


Mostly the same as java.


Please do not call % the mod operator, unless you
  know that the operands are positive.



2.6 Relational and Logical Operators


Again very little difference from Java.


Please remember that && and || are required to be
  short-circuit operators.
  That is, they evaluate the right operand only if needed.



2.7 Type Conversion


There are two kinds of conversions: automatic conversion,
  called coercion, and explicit conversions.



Automatic Conversions


C coerces narrow arithmetic types to wide ones.


  {char, short} → int → long
  float → double → long double
  long → float   // precision can be lost



  int atoi(char s[]) {
    int i, n=0;
    for (i=0; s[i]>='0' && s[i]<='9'; i++)
      n = 10*n + (s[i]-'0');  // assumes ascii
    return n;
  }



The  program on the right (ascii to integer) converts a character
  string representing an integer to the integral value.



Unsigned coercions are more complicated; you can read about them in
  the book.



Explicit Casts


The syntax


  (type-name) expression



converts the value to the type specified.
  Note that e.g., (double) x converts the value
  of x; it does not change x
  itself.


Homework: 2-3.
  Write the function htoi(s), which converts a string of
  hexadecimal digits (including an option 0x or 0X) into its
  equivalent integer value.
  The allowable digits are 0 through 9, a through f, and A through
  F.



2.8 Increment and Decrement Operators


The same as Java.


Remember that x++ or ++x are not the same as
  x=x+1 because, with the operators, x is evaluated
  only once, which becomes important when x is itself an
  expression with side effects.


  x[i++]++ // increments some (which?) element of an array
  x[i++] = x[i++]+1 // puts incremented value in ANOTHER slot



Homework: 2-4.
  Write an alternate version of squeeze(s1,s2) that deltets
  ecah character that mataches any character is the string
  s2.



2.9 Bitwise Operators


The same as Java




2.10 Assignment Operators and Expressions


  int bitcount (unsigned x) {
    int b;
    for (b=0; x!=0; x>>= 1)
      if (x&01) // octal (not needed)
        b++;
    return b;
  }



The same as Java:
  += -= *= /= %= <<= >>= &= ^= |=


The program on the right counts how many bits of its argument are 1.
  Right shifting the unisigned x causes it to be
  zero-filled.
  Anding with a 1, gives the LOB (low order bit).
  Writing 01 indicates an octal constant (any integer beginning with
  0; similarly starting with 0x indicates hexadecimal).
  Both are convenient for specifying specific bits (because both 8 and
  16 are powers of 2).
  Since the constant in this case has value 1, the 0 has no
  effect.



Homework: 2-10.
  Rewrite the function lower(), which converts upper case
  letters to lower case with a conditional expression instead
  of if-else.



2.11 Conditional Expressions


  printf("You enrolled in %d course\s.\n", n, (n==1) ? "" : "s");



The same as Java:




  Precedence and Associativity of C Operators
  
OperatorsAssociativity

  

  
() [] -> .left to right

  
! ~ ++ -- + - * & (type) sizeof
    right to left

  
* / %left to right

  
+ -left to right

  
<< >>left to right

  
< <= > >=left to right

  
== !=left to right

  
&left to right

  
^left to right

  
|left to right

  
&&left to right

  
||left to right

  
?:right to left

  
= += -= *= /= %= &= ^= |= <<= >>=
    right to left

  
,left to right




2.12 Precedence and Order of Evaluation


The table on the right is copied (hopefully correctly) from the
  book.
  It includes all operators, even those we haven't learned yet.
  I certainly don't expect you to memorize the table.
  Indeed one of the reasons I typed it in was to have an online
  reference I could refer to since I do not know all the
  precedences.


Homework: Check the table above for typos and
  report any on the mailing list.


Not everything is specified.
  For example if a function takes two arguments, the order in which
  the arguments are evaluated is not specified.


Also the order in which operands of a binary operator like + are
  evaluated is not specified.
  So f() could be evaluated before or after g() in
  the expression f()+g().
  This becomes important if, for example, f() alters a global
  variable that g() reads.



Start Lecture #3
 


  #include <stdio.h>
  void main (void) {
    int x=3, y;
    y = + + + + + x;
    y = - + - + + - x;
    y = - ++x;
    y = ++ -x;
    y = ++ x ++;
    y = ++ ++ x;
  }



Question: Which of the expressions on the right are
  illegal?

  Answer: The last three.
  They apply ++ to values not variables (i.e, to r-values not
  l-values).


I mention this because at the end of last time there was some
  discussion about ++ ++ and ++++.
  The distinction between l-values and r-values will become very
  relevant when we discuss pointers.


Since pointers have presented difficulties for students in the
  past, I use every opportunity to give ways of looking at the
  problem.


Since ++ does an assignment (as well as an addition) it
  needs a place to put the result, i.e., an l-value.



Chapter 3: Control Flow



3.1 Statements and Blocks


  int t[]={1,2};
  int main() {
    22;
    return 0;
  }



C is an expression language; so 22 and
  x=33 have values.
  One simple statement is an expression followed by a semicolon;
  For example, the program on the right is legal.


As in Java, a group of statements can be enclosed in braces to form
  a compound statement or block.
  We will have more to say about blocks later in the course.



3.2 If-Else


Same as Java.



3.3 Else-IF


Same as Java.



3.4 Switch


Same as Java.



3.5 Loops—While and For


  #include <ctype.h>
  int atoi(char s[]) {
    int i, n, sign;
    for (i=0; isspace(s[i]); i++) ;
    sign = (s[i]=='-') ? -1 : 1;
    if (s[i]=='+' || s[i]=='-')
      i++;
    for (n=0; isdigit(s[i]); i++)
      n = 10*n + (s[i]-'0');
    return sign * n;
  }



Same as Java.
  As we shall see, the loops in the book show the hand of a
  master.


The program on the right (ascii to integer) illustrates several
  points.




The Comma Operator


  for (i=0, j=0; i+j<n; i++,j+=3)
    printf ("i=%d and j=%d\n", i, j);



If two expressions are separated by a comma, they are evaluated
  left to right and the final value is the value of the one on the
  right.
  This operator often proves convenient in for statements
  when two variables are to be incremented.





3.6 Loops—Do-While


Same as Java.



3.7 Break and Continue


Same as Java.



3.8 Goto and Labels


The syntax is


  goto label;



  for (...) {
    for (...) {
      while (...) {
        if (...) goto out;
      }
    }
  }
  out: printf("Left 3 loops\n");



The label has the form of a variable name.
  A label followed by a colon can be attached to any statement in the
  same function as the goto.
  The goto transfers control to that statement.


Note that a break in C (or Java) only leaves one level of
  looping so would not suffice for the example on the right.


The goto statement was deliberately omitted from Java.
  Poor use of goto can result in code that is hard to
  understand and hence goto is rarely used in modern
  practice.


The goto statement was much more commonly used in the
  past.


Homework: Write a C
  function escape(char s[], char t[]) that converts the
  characters newline and tab into two character sequences \n
  and \t as it copies the string t to the
  string s.
  Use the C switch statement.
  Also write the reverse function unescape(char s[], char
  t[]).



Chapter 4 Functions and Program Structure



4.1 Basics of Functions



Very Simplified Unix grep


The Unix utility grep (Global Regular Expression Print) prints all
  occurrences of a given string (or more generally a regular
  expression) from standard input.
  A very simplified version is on the right.


The basic program is


  while there is another line
    if the line contains the string
      print the line



Getting a line and seeing if there is more is getline();
  a slightly revised version is on the right.
  Note that a length of 0 means EOF was reached; an "empty" line still
  has a newline char '\n' and hence has length 1.


Printing the line is printf().


  #include <stdio.h>
  #define MAXLINE 100
  int getline(char line[], int max);
  int strindex(char source[], char searchfor[]);
  char pattern[]="x y"; // "should" be input
  main() {
    char line[MAXLINE];
    int found=0;
    while (getline(line,MAXLINE) > 0)
      if (strindex(line, pattern) >= 0) {
        printf("%s", line);
        found++;
      }
    return found;
  }

  int getline(char s[], int lim) {
    int c, i;
    i = 0;
    while (--lim>0 && (c=getchar())!=EOF && c!='\n')
      s[i++] = c;
    if (c == '\n')
      s[i++] = c;
    s[i] = '\0';
    return i;
  }

  int strindex(char s[], char t[]) {
    int i, j, k;
    for(i=0; s[i]!='\0'; i++) {
      for (j=i,k=0; t[k]!='\0' && s[j]==t[k]; j++,k++) ;
      if (k>0 && t[k]=='\0')
        return i;
    }
    return -1;
  }



Checking to see if the string is present is the new code.
  The choice made was to define a function strindex() that is
  given two strings s and t and returns the position
  (the index in the array) in s where t occurs.
  strindex() returns -1 if t does not occur
  in s.


The program is on the right; some comments follow.




Form of a Function Definition


Note that a function definition is of the form


  return-type function-name(parameters)
  {
    declaratons and statements
  }



The default return type is int, but I recommend not
  utilizing this fact and instead always declaring the return
  type.



 


The return statement is like Java.



4.2 Functions Returning Non-integers


The book correctly gives all the defaults and explains why they are
  what they are (compatibility with previous versions of C).
  I find it much simpler to always


    
  
  1. Use no defaults when defining a function.
    
  
    2. 
  
  2. Declare all functions that are used in a file.
    Have these declarations early, before any function
    definitions.
    3. 




4.3 External Variables


A C program consists of external objects, which are either
  variables or functions.



External vs. Internal


Variables and functions defined outside any function are called
  external.


Variables defined inside a function are
  called internal.


Functions defined inside another function would also be
  called internal; however standard C does not have internal
  functions.
  That is, you cannot in C define a function inside another function.
  In this sense C is not a fully block-structured language
  (see block structure below).



Defining External Variables


As stated, a variable defined outside functions is external.
  All subsequent functions in that file will see the definition
  (unless it is overridden by an internal definition).


These can be used, instead of parameters/arguments to pass
  information between functions.
  It is sometimes convenient to not have to repeat a long list of
  arguments common to several functions, but using external variables
  has problems as well:
  It makes the exact information flow harder to deduce when reading
  the program.


When we solved quadratic equations in section 1.10 our second
  method used external variables.



4.4 Scope Rules


The scope rules give the visibility of names in a program.
  In C the scope rules are fairly simple.



Internal Names (Variables)


Since C does not have internal functions, all internal names are
  variables.
  Internal variables can be automatic or static.
  We have seen only automatic internal variables, and this section
  will discuss only them.
  Static internal variables are discussed in section 4.6
  below.


An automatic variable defined in a function is visible from the
  definition until the end of the function (but see
  block structure, below).


If the same variable name is defined internal to two functions, the
  variables are unrelated.


Parameters of a function are the same as local variables in this
  respect.



External Names


  int main(...) {...}
  int value;
  float joe(...) {...}
  float sam;
  int bob(...) {...}



An external name (function or variable) is visible from the point
  of its definition (or declaration as we shall see below) until the
  end of that file.
  In the example on the right main() cannot call
  joe() or bob(), and cannot use either
  value or sam.
  bob() can call joe(), but not vice versa.



Definitions and Declarations


There can be only one definition of an external name in
  the entire program (even if the program includes many files).
  However, there can be multiple declarations of the same
  name.


A declaration describes a variable (gives its type) but does not
  allocate space for it.
  A definition both describes the variable and allocates space for
  it.


  extern int X;
  extern double z[];
  extern float f(double y);



Thus we can put declarations of a variable X, an array
  z[], and a function f() at the top of every file
  and then X and z are visible in every function in
  the entire program.
  Declarations of z[] do not give its size since space is not
  allocated; the size is specified in the definition.


If declarations of joe() and bob() were added
  at the top of the previous example, then main() would be
  able to call them.


If an external variable is to be initialized, the initialization
  must be put with the definition, not with a declaration.



4.5 Header Files


  #include <stdio.h>
  double f(double x);
  int main() {
    float y;
    int x = 10;
    printf("x is %f\n", (double)x);
    printf("f(x) is %f\n", f(x));
    return 0;
  }
  double f(double x) {
    return x;
  }
  x is 0.000000
  f(x) is 10.000000



The code on the right shows how valuable having the types declared
  can be.
  The function f() is the identity function.
  However, main() knows that f() takes a
  double so the system automatically converts x to a
  double.


Without the explicit cast (double) in the
  first printf(), the compiler would give a warning about a
  type mismatch, but the program would still work.
  I prefer to put in the casts and not have to worry about the
  warnings.


It would be awkward to have to change every file in a big
  programming project when a new function was added or had a change of
  signature (types of arguments and return value).
  What is done instead is that all the declarations are included in a
  header file.


For now assume the entire program is in one directory.
  Create a file with a name like functions.h containing the
  declarations of all the functions.
  Then early in every .c file write the line
  
    #include  "functions.h"
  

  Note the quotes not angle brackets, which indicates that functions.h
  is located in the current directory, rather than in the standard
  place that is used for <>.



4.6: Static Variables


The adjective static has very different meanings when
  applied to internal and external variables.



  int main(...){...}
  static int b16;
  void sam(...){...}
  double beth(...){...}



If an external variable is defined with the static
  attribute, its visibility is limited to the current file.
  In the example on the right b16 is naturally visible in
  sam() and beth(), but not main().
  The addition of static means that if another file
  has a definition or declaration of b16, with or without
  static, the two b16 variables are not related.


If an internal variable is declared static, its
  lifetime is the entire execution of the program.
  This means that if the function containing the variable is called
  twice, the value of the variable at the start of the second call is
  the final value of that variable at the end of the first call.



Static Functions


As we know there are no internal functions in standard C.
  If an (external) function is defined to be static, its
  visibility is limited to the current file (as for static external
  variables).



4.7 Register Variables


Ignore this section.
  Register variables were useful when compilers were primitive.
  Today, compilers can generally decide, better than
  programmers, which variables should be put in register.



Start Lecture #4
 


4.8: Block Structure


Standard C does not have internal functions, that is you cannot in
  C define a function inside another function.
  In this sense C is not a fully block-structured language.


Of course C does have internal variables; we have used them in
  almost every example.
  That is, most functions we have written (and will write) have
  variables defined inside them.


  #include <stdio.h>
  int main(void) {
    int x = 5;
    printf ("The value of outer x is %d\n", x);
    {
      int x = 10;
      printf ("The value of inner x is %d\n", x);
    }
    printf ("The value of the outer x is %d\n", x);
    return 0;
  }
  The value of outer x is 5.
  The value of inner x is 10.
  The value of outer x is 5.



Also C does have block structure with respect to variables.
  This means that inside a block (remember that a block is a bunch of
  statements surrounded by {}) you can define a new variable
  with the same name as the old one.
  These two variables are unrelated.
  The lifetime of the new variable is just the lifetime of the
  execution of the block in which it is defined.


For example, the program on the right produces the output shown.


Remark: The gcc compiler for C does permit one to
  define a function inside another function.
  These are called nested functions.
  Some consider this gcc extension to be evil.





Homework: Write a C funcion
  int odd (int x) that returns 1 if x is odd
  and returns 0 if x is even.
  Can you do it without an if statement?



4.9 Initialization



Default Initialization


Static and external variables are, by default, initialized to zero.
  Automatic, internal variables (the only kind left) are
  not initialized by default.



Initializing Scalar Variables


As in Java, you can write int X=5-2;.
  For external or static scalars, that is all you can do.


  int x=4;
  int y=x-1;



For automatic, internal scalars the initialization expression can
  involve previously defined values as shown on the right (even
  function calls are permitted).



Initializing Arrays


  int BB[8] = {4,9,2}
  int AA[] = {3,5,12,7};
  char str[] = "hello";
  char str[] = {'h','e','l','l','o','\0'}



You can initialize an array by giving a list of initializers as
  shown on the right.




4.10 Recursion


The same as Java.



4.11 The C Preprocessor


Normally, before the compiler proper sees your program, a utility
  called the C preprocessor is invoked to include files and perform
  macro substitutions.



4.11.1 File Inclusion


  #include <filename>
  #include "filename"



We have already discuss both forms of file inclusion.
  In both cases the file mentioned is textually inserted at the point
  of inclusion.
  The difference between the two is that the first form looks for
  filename in a system-defined standard place;
  whereas, the second form first looks in the current directory.



4.11.2 Macro Substitution


  #define MAXLINE 20
  #define MULT(A, B) ((A) * (B))
  #define MAX(X, Y)  ((X) > (Y)) ? (X) : (Y)
  #undef getchar



We have already used examples of macro substitution similar to the
  first line on the right.
  The second line, which illustrates a macro with arguments is more
  interesting.


Without all the parentheses on the RHS, the macro would be legal,
  but would (sometimes) give the wrong answers.

  Question: Why?

  Answer: Consider MULT(x+4, y+3)


Note that macro substitution is not the same as a
  function call (with standard call-by-value or call-by-reference
  semantics).
  Even with all the parentheses in the third example you can get into
  trouble since MAX(x++,5) can increment x twice.
  If you know call-by-name from algol 60 fame, this will seem
  familiar.


We probably will not use the fourth form.
  It is used to un-define a macro from a library so that you can write
  another version.


There is some fancy stuff involving # in the RHS of the macro
  definition.
  See the book for details; I do not intend to use it.



  #if integer-expr
  ...
  #elif integer-expr
  ...
  #else
  ...
  #endif



4.11.3 Conditional Inclusion


The C-preprocessor has a very limited set of control flow items.
  On the right we see how the C


  if (cond1)
  ...
  else if (cond2)
  ...
  else
  ..
  end if



construct is written.
  The individual conditions are simple integer expressions consisting
  of integers, some basic operators and little else.
  Perhaps the most useful additions are the preprocessor
  function defined(name), which evaluates to 1 (true)
  if name has been #define'd, and the ! operator,
  which converts true to false and vice versa.


  #if !defined(HEADER22)
  #define HEADER22
  // The contents of header22.h
  // goes here
  #endif



We can use defined(name) as shown on the right to ensure
  that a header file, in this case header22.h, is included
  only once.


Question: How could a header file be included
  twice unless a programmer foolishly wrote the same #include
  twice?

  Answer: One possibility is that a user might
  include two systems headers h1.h and h2.h each of
  which includes h3.h.


Two other directives #ifdef and #ifndef test
  whether a name has been defined.
  Thus the first line of the previous example could have been written
  ifndef HEADER22.


  #if SYSTEM == MACOS
    #define HDR "macos.h"
  #elsif SYSTEM == WINDOWS
    #define HDR "windows.h"
  #elsif SYSTEM == LINUX
    #define HDR "linux.h"
  #else
    #define HDR "empty.h"
    #define MSG No header found for System
  #endif
  #include HDR



On the right we see a slightly longer example of the use of
  preprocessor directives.
  Assume that the name SYSTEM has been set to the name of the system
  on which the current program is to be run (not
  compiled).
  Assume also that individual header files have been written for
  macos, windows, and linux systems.
  Then the code shown will include the appropriate header file.


In addition, if the SYSTEM is not one of the three on which the
  program is designed to be run, the code to the right will define
  MSG, a diagnostic that could be printed.


Note: The quotes used in the
  various #defines for HDR are not required
  by #define, but instead are needed by the final
  #include.



Chapter 5 Pointers and Arrays


  public class X {
    int a;
    public static void main(String args[]) {
      int i1;
      int i2;
      i1 = 1;
      i2 = i1;
      i1 = 3;
      System.out.println("i2 is " + i2);
      X x1 = new X();
      X x2 = new X();
      x1.a = 1;
      x2 = x1;     // NOT x2.a = x1.a
      x1.a = 3;
      System.out.println("x2.a is " + x2.a);
    }
  }



Much of the material on pointers has no explicit analogue in Java;
  it is there kept under the covers.
  If in Java you have an Object obj, then obj is
  actually what C would call a pointer.
  The technical term is that Java has reference semantics for all
  objects.
  In C this will all be quite explicit


To give a Java example, look at the snippet on the right.
  The first part works with integers.
  We define 2 integer variables; initialize the first; set the second
  to the first; change the first; and print the second.
  Naturally, the second has the initial value of the first, namely
  1.


The second part deals with X, a trivial class, whose
  objects have just one data component, an integer.
  We mimic the above algorithm.
  We define two X's and work with their integer field
  (a).
  We then proceed as above: initialize the first integer field; set
  the second to the first; change the first; and print the second.
  The result is different from the above!
  In this case the second has the altered value of the first, namely
  3.


The key difference between the two parts is that (in Java) simple
  scalars like i1 have value semantics; whereas objects
  like x1 have reference semantics.
  But enough Java, we are interested in C.



5.1 Pointers and Addresses


You will learn in 202, that the OS finagles memory in ways that
  would make Bernie Madoff smile.
  But, in large part thanks to those shenanigans, user programs can
  have a simple view of memory.
  For us C programmers, memory is just a large array of consecutively
  numbered addresses.


The machine model we will use in this course is that the
  fundamental unit of addressing is a byte and a character
  (a char) exactly fits in a byte.
  Other types like short, int, double,
  float, long normally take more than one byte, but
  always a consecutive range of bytes.



l-values and r-values


One consequence of our memory model is that associated with
  int z=5; are two numbers.
  The first number is the address of the location in which z
  is stored.
  The second number is the value stored in that location; in this case
  that value is 5.
  The first number, the address, is often called the l-value; the
  second number, the contents, is often called the r-value.
  Why l and r?


Consider z = z + 1;
 To evaluate the right hand side
  (RHS) we need to add 5 to 1.
  In particular, we need the value contained in the memory location
  assigned to z, i.e., we need 5.
  Since this value is what is needed to evaluate the RHS of an
  assignment statement it is called an r-value.


Then we compute 6=5+1.
  Where should we put the 6?
  We look at the LHS and see that we put the 6 into z; that
  is, into the memory location assigned to z.
  Since it is the location that is needed when evaluating a LHS, the
  address is called an l-value.



The Unary Operators & and *


As we have just seen, when a variable appears on the LHS, its
  l-value or address is used.
  What if we want the address of a variable that appears on the RHS;
  how do we get it?


In a language like Java the answer is simple; we don't.


In C we use the unary operator & and
  write p=&x; to assign the address of x
  to p.
  After executing this statement we say that p points to
  x or p is a pointer to x.
  That is, after execution, the r-value of p is the l-value
  of x.


  int x=3;
  int *p = &x;



Look at the declarations on the right.
  x is familiar; it is an integer variable initially
  containing 3.
  Specifically, the r-value of x is 3.
  What about the l-value of x, i.e., the location in which
  the 3 is stored?
  It is not an int; it is an address into which
  an int can be stored.
  Alternately said it is pointer to an int.


The unary prefix operator & produces the address of a
  variable, i.e., &x gives the l-value of x, i.e. it
  gives a pointer to x.


The unary operator * does the reverse action.
  When * is applied to a pointer, it gives the value of the
  object (object is used in the English not OO sense) pointed to.
  The * operator is called the dereferencing or
  indirection operator.


Now look at the declaration of p, which says
  that p is the kind of thing that when you apply *
  to it you get an int, i.e., p is a pointer to an
  int.
  That is why we can initialize p to &x.


  // part one of three
  int x=1;
  int y=2;
  int z[10];
  int *ip;
  int *jp;
  ip = &x;



Consider the code sequence on the right (part one).
  The first 3 lines we have seen many times before; the next three are
  new.
  Recall that in a C declaration, all the doodads around a variable
  name tell you what you must do the variable to get the base type at
  the beginning of the line.
  Thus the fourth line says that if you dereference ip you
  get an integer.
  Common parlance is to call ip an integer pointer (which is
  why we named it ip).
  Similarly, jp is another integer pointer.


At this point both ip and jp are uninitialized.
  The last line sets ip to the address, of x.
  Note that the types match, both ip and &x are
  pointers to an int.


  // part two of three
  y = *ip;     // L1
  *ip = 0;     // L2
  ip = &z[0];  // L3
  *ip = 0;     // L4
  jp = ip;     // L5
  *jp = 1;     // L6



In part two, L1 sets y=1 as follows: ip now points
  to x, * does the dereference so *ip is x.
  Since we are evaluating the RHS, we take the contents not the
  address of x and get 1.


L2 sets x=0;.
  The RHS is clearly 0.
  Where do we put this zero?
  Look at the LHS:
  ip currently points to x, * does a dereference
  so *ip is x.
  Since we are on the LHS, we take the address and not the contents of
  x and hence we put 0 into x.


L3 changes ip; it now points to z[0].
  So L4 sets z[0]=0;


Pointers can be used without the deferencing operator.
  L5 sets jp to ip.
  Since ip currently points to z[0], jp
  does as well.
  Hence L6 sets z[0]=1;





  // part three of three
  ip = &x;         // L1
  *ip = *ip + 10;  // L2
  y = *ip + 1;     // L3
  *ip += 1;        // L4
  ++*ip;           // L5
  (*ip)++;         // L6
  *ip++;           // L7



Part three begins by re-establishing ip as a pointer
  to x so L2 increments x by 10 and the L3
  sets y=x+1;.


L4 increments x by 1 as does L5
  (because the unary operators ++ and * are right
  associative).


L6 also increments x, but L7 does not.
  By right associativity we see that the increment precedes the
  dereference, but the full story awaits section 5.4
  below.



5.2 Pointers and Function Arguments


  void bad_swap(int x, int y) {
    int temp;
    temp = x;
    x = y;
    y = temp;
  }



The program on the right is what a novice programer just learning C
  (or Java) would write.
  It is supposed to swap the two arguments it is called with, but
  fails due to call by value semantics for function calls in C.


What happens is, when another function calls swap(a,b)
  the values of the arguments a
  and b are transmitted to the parameters x
  and y and then swap() interchanges the values
  in x and y.
  But when swap() returns, the final values
  in x and y are NOT transmitted
  back to the arguments: a and b are unchanged.


But programs that change their arguments are useful!


Actually, what is useful is to be able to change the value of
  variables used in the caller (even if some other variables
  become the arguments) and that distinction is the key.
  Just because we want to swap the values of a
  and b, doesn't mean the arguments have to be literally
  a and b.


  void swap(int *px, int *py) {
    int temp;
    temp = *px;
    *px = *py;
    *py = temp;
  }



The program on the right has two parameters px and
  py each of which is a pointer to an integer (*px
  and *py are the integers).
  Since C is a call-by-value language, changes to the parameters,
  which are the pointers px and py
  would not result in changes to the corresponding arguments.
  But the program on the right doesn't change the pointers at all,
  instead it changes the values they point to.


Since the parameters are pointers to integers, so must be the
  arguments.
  A typical call to this function would
  be swap(&A,&B).


Understanding how this call results in A receiving the
  value previously in B and B receiving the value
  previously in A is crucial.

swap

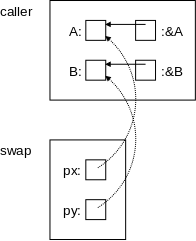
On the right is a pictorial explanation.
  A has a certain address.
  &A equals that address (more precisely the
  r-value of &A = the l-value of A).
  Similarly for B and &B.
  These are shown by the solid arrows in the diagram.


The call swap(&A,&B) copies (the r-value
  of) &A into (the r-value of) the first parameter, which
  is px.
  Similarly for &B and the second parameter, py.
  These are shown by the dotted arrows.
  Thus the value of px is the address of A, which is
  indicated by the arrow.
  Again, to be pedantic, the r-value of px equals the r-value
  of &A, which equals the l-value of A.
  Similarly for B and py.


Swapping px with py would change the dotted
  arrows, but would not change anything in the caller.
  However, we don't swap px with py, instead we
  swap *px with *py.
  That is we dereference the pointers and swap the things pointed to!
  This subtlety is the key to understanding the effect of many C
  functions.
  It is crucial.


Homework: Write rotate3(A,B,C) that sets
  A to the old value of B, sets B to old
  C, and C to old A.


Homework: Write plusminus(x,y) that sets
  x to old x + old y and sets y
  to old x - old y.



Start Lecture #5
 


A Larger Example—getch(), ungetch(), and getint()


The program pair getch() and ungetch() generalize
  getchar() by supporting the notion of unreading a
  character, i.e., having the effect of pushing back several already
  read characters.


Note that ungetch() is careful not to exceed the size of
  the buffer used to stored the pushed back characters.
  Remember that C does not generate run-time checks that you are not
  accessing an array beyond its bound.
  Recall I mentioned that in the past an number of break ins were
  caused by the lack of such checks in library programs like this.


  #include <stdio.h>
  #define BUFSIZE 100
  char buf[BUFSIZE];
  int  bufp = 0;
  int  getch(void);
  void ungetch(int);
  int getint(int *pn);

  int getch(void) {
    return (bufp>0) ? buf[--bufp] : getchar();
  }

  void ungetch(int c) {
    if (bufp >= BUFSIZE)
      printf("ungetch: too many chars\n");
    else
      buf[bufp++] = c;
  }

  #include <stdio.h>
  #include <ctype.h>
  int getint(int *pn) {
    int c, sign;
    while (isspace(c=getch())) ;
    if (!isdigit(c) && c!=EOF && c!='+' && c!='-') {
      ungetch(c);
      return 0;
    }
    sign = (c=='-') ? -1 : 1;
    if (c=='+' || c=='-')
      c = getch();
    for (*pn = 0; isdigit(c); c=getch())
      *pn = 10 * *pn + (c-'0');
    *pn *= sign;
    if (c != EOF)
      ungetch(c);
    return c;
  }



Also shown is getint(), which reads an integer from
  standard input (stdin) using getch()
  and ungetch().


getint() returns the integer read via a parameter.
  As we have seen the new value of a parameter is not passed back to
  the caller.
  Hence, getint() uses the pointer/address business we just
  saw with swap().


Specifically any change made to pn by getint()
  would be invisible to the caller.
  However, getint() changes only *pn; a change the
  caller does see.


The value returned by the function itself gives the status, zero
  means the next characters do not form an integer, EOF (which is
  negative) means we are at the end of file, positive means an integer
  has been found.


Briefly the program works as follows.


  Skip blanks
  Check for legality
  Determine sign
  Evaluate number
    one digit at a time



Although short, the program is not trivial.
  Indeed, there some details to note.



If, in real life, you were asked to produce a getint()
  function you would have three tasks.


    
  
  1. Write, in precise English, a detailed specification of what is
    to happen in all cases.
    2. 
  
  2. Write a C program implementing this specification.
    3. 
  
  3. Get the C syntax right.
    4. 



The third is clearly the easiest task.
  I suspect that the first is the hardest.


Homework: 5-1.
  As written, getint() treats a + or - not
  followed by a digit as a valid representation of zero.
  Fix it to push such a character back on the input.



5.3 Pointers and Arrays


In C pointers and arrays are closely related.
  As the book says



  Any operation that can be achieved by array subscripting can also be
  done with pointers.
  


The authors go on to say



  The pointer version will in general be faster but, at least to the
  uninitiated, somewhat harder to understand.



The second clause is doubtless correct; but perhaps not the first.
  Remember that the 2e was written in 1988 (1e in 1978).
  Compilers have improved considerably in the past 20+ years and, I
  suspect, would turn out nearly as fast code for many of the array
  versions.


The next few sections present some simple examples using
  pointers.



A Tiny Example


  int a[5], *pa;
  pa = &a[0];

  int x = *pa;
  x = *(pa+1);

  x = a[0];
  x = *a;

  int i;
  x = a[i];
  x = *(a+i);


array-ptr

On the far right we see some code involving pointers and arrays.
  After the first two lines are executed we get the diagram shown on
  the near right.
  pa is a pointer to the first element of the array
  a.
  pa+3 would be a pointer to the fourth element of the
  array.


But note that pa+3 is not a container; you can't put
  another pointer into pa+3 just like you can't put
  another int into i+3.


The next line sets x (which is a container) equal to (the
  r-value of) a[0]; the line after that
  sets x=a[1].


Then we explicitly set x=a[0].


The line after that has the same effect!
  That is because in C the value of array name equals the address of
  its first element.
  (The r-value of a = the r-value of &a[0] = the address
  of a[0].)
  Again note that a (i.e., &a[0]) is an expression, not a
  variable, and hence is not a container.


Said yet another way a and pa have the same value
  (r-value) but are not the same thing!


Similarly, the next three lines each have the same effect, this
  time for a general element of the array a[i].



An Subtle Difference Between Array Names and Pointers (one more time)


  int a[5], *pa;
  pa = &a[0];
  pa = a;
  a = pa;        // illegal
  &a[0] = pa;    // illegal



Both pa and a are pointers to ints.
  In particular a is defined to be &a[0].
  Although pa and a have much in common,
  there is an important difference:
  pa is a variable, its value can be changed;
  whereas &a[0] (and hence a) is not a variable.
  In particular the last two lines on the right are illegal.


Another way to say this is that &a[0] is not an l-value.
  This is similar to the legality of x=5; versus the
  illegality of 5=x;



Calculating the Length of a String: mystrlen()



The Program Itself


  int mystrlen(char *s) {
    int n;
    for (n=0; *s!='\0'; s++,n++) ;
    return n;
  }



The code on the right illustrates how well the C
  pointers, arrays, and strings mesh.
  What a tiny program to find the length of an arbitrary string!


Note that the body of the for loop is null; all the work
  is done in the for statement itself.



Calling mystrlen()


  char str[50], *pc;
  // calculate str and pc
  mystrlen(pc);
  mystrlen(str);
  mystrlen("Hello, world.");




  Note the various ways in which mystrlen() can be
  called.


    
  
  1. The first call shown exactly matches the function declaration.
    That is, both the argument (in the function call) and the
    parameter (in the function definition) have the same type, a
    pointer to a char.
    Don't forget in a C declaration you decorate a variable
    with enough stuff to obtain one of the primitive types.
    2. 
  
  2. The second call matches as well, once we remember that an array
    name has the same value as a pointer to the first value.
    3. 
  
  3. Finally, the third is like the second since a string constant
    is a character array.
    4. 


  




One More Time: Value Versus Address (or r-value Versus l-value)


  #include <stdio.h>
  int x, *p;
  int main () {
    p = &x;
    x = 12;
    printf("p = %p\n", p);
    printf("*p = %d\n", *p);
    p++;
    printf("p = %p\n", p);
    printf("*p = %d\n", *p);
  }



The example on the right illustrates well the difference between a
  variable, in this case x, and its address &x.
  The first value printed is the address of x.
  This is not 12.
  Instead, it is some (probably large) number that happens to be the
  address of x.


Just as %d is used to print integers, %p is used
  for pointers.
  On my system the line printed was

      p = 0x7fbcb9319040


Incrementing p does not
  increment x.
  Instead, the result is that p points to the next integer
  after x.
  In this program there is no further integer after x, so the
  result is unpredictable.
  I consider the program to be erroneous.
  Specifically, the value of *p is now unpredictable.
  On my system the value of p was 0x7fbcb9319040.
  The value of *p was 0, but that can NOT be counted on.
  If, instead of x, we had p point to A[7]
  for some large double array A, then the last line
  would have printed the value of A[8] and
  the penultimate line would have printed the address
  of A[8].



String Length with Arrays and Pointers


#include <stdio.h>
int mystrlen (char *s);
int main () {
  char stg[] = "hello";
  printf ("The string %s has %d characters\n",
          stg, mystrlen(stg));
}

int mystrlen (char *s) {
  int i = 0;
  while (*s++ != '\0')
    i++;
  return i;
}

int mystrlen (char s[]) {
  int i;
  for (i = 0; s[i] != '\0'; i++) ;
  return i;
}



On the right we show two versions of a string length function.
  The first version uses array notation for the string; the second
  uses pointer notation.
  The main() program is identical in the two versions so is
  shown only once.


Note how very close the two string length functions are.
  This is another illustration of the similarity of arrays and
  pointers in C.


Note the two declarations


  int mystrlen (char *s);
  int mystrlen (char s[]);



They are used 3 times in the code on the right.
  In C these two declarations are equivalent.
  Changing any or all of them to the other form does not change the
  meaning of the program.


I realize an array does not at first seem the same as a pointer.
  Remember that the array name itself is equal to a pointer to the
  first element of the array.
  Hence declaring


  float a[5], *b;



results in a and b having the same type (pointer
  to float).
  But a has additionally been defined; that
  is, space for 5 floats has been allocated.
  Hence a[3] = 5; is legal.
  b[3] = 5 is syntactically legal, but may abort at runtime,
  unless b has previously be set to point to sufficient
  space.


In the first version of mystrlen() we encounter a common C
  idiom *s++.
  First note that the precedence of the operators is such that
  *s++ is the same as *(s++).
  That is, we are moving (incrementing) the pointer and examining what
  it used to point at.
  We are not incrementing a part of the string.
  Specifically, we are not executing (*s)++;



Simple Substitution


  void changeltox (char *s) {
    while (*s != '\0') {
      if (*s == 'l')
        *s = 'x';
      s++;
    }
  }



The program on the right simply loops through the input string and
  replaces each occurence of l with x.


The while loop and increment of s could have been
  combined into a for loop.


This version is written in pointer style.


Homework:
  Rewrite changeltox() to use array style and a for
  loop.





String Copy


  void mystrcpy (char *s, char *t) {
    while ((*s++ = *t++) != '\0') ;
  }



Check out the ONE-liner on the right.
  Note especially the use of standard idioms for marching through
  strings and for finding the end of the string.


Slick!


But scary, very scary!


Question: Why is it scary?

  Answer: Because there is no length check.


If the character array s (or equivalently
  the block of characters s points to) is smaller than the
  character array t, then the copy will overwrite whatever
  happens to be located right after the array s.


The lack of such length checks has permitted a number of security
  breaches.



Using int *A vs int A[] as a Parameter


  double f(int *a);
  double f(int a[]);



The two lines on the right are equivalent, when used as a function
  declaration (or, without the semicolon) as the head line of a
  function definition).
  The authors say they prefer the first.
  For me it is not so clear cut.
  In mystrlen() above I would indeed
  prefer char *s as written since I think of a string as
  a block with a pointer to the beginning.


  double dotprod(double A[], double B[]);



However, if I were writing an inner product routine (a.k.a. dot
  product), I would prefer the array form as on the right
  since I think of dot product as operating on vectors.


But of course, more important that what I prefer or the authors
  prefer, is the fact that they are equivalent in C.



Passing Part of an Array


  #include <stdio.h>
  void f(int *p);

  int main() {
    int A[20];
    // initialize all of A
    f(A+6);
    return 0;
  }

  void f(int *p) {
    printf("legal? %d\n", p[-2]);
    printf("legal? %d\n", *(p-2));
  }



In the code on the right, main() first declares an integer
  array A[] of size 20 and initializes all its members (how
  the initialization is done is not important).
  Then main(), in a effort to protect the beginning
  of A[], passes only part of the array to f().
  Remembering that A+6 means (&A[0])+6, which is
  &A[6], we see that f() receives a pointer to the
  7th element of the array A.


The author of main() mistakenly believes
  that A[0],..,A[5] are hidden from f().
  Let's hope this author is not on the security team for the board of
  elections.


Since C uses call by value, we know that f() cannot change
  the value of the pointer A+6 in main().
  But f() can use its copy of this pointer to reference or
  change all the values of A, including those
  before A[6].
  On the right, f() successfully
  references A[4].


It naturally would be illegal for f() to reference (or
  worse change) p[-9].



5.4: Address Arithmetic


  #include <stdio.h>
  void main (void) {
    int q[] = {11, 13, 15, 19};
    int *p = q;
    printf("*p = %d\n", *p);
    printf("*p++ = %d\n", *p++);
    printf("*p = %d\n", *p);
    printf("*++p = %d\n", *++p);
    printf("*p = %d\n", *p);
    printf("++*p = %d\n", ++*p);
 }



A crucially important point is that, given the declaration
  int *p; the increment pa+=3 does not simply
  add three to the address stored in pa.
  Instead, it increments pa so that it points 3
  integers further forward (since pa is a
  pointer to an integer).
  If pc is a pointer to a double, then
  pc+3 increments pc so that it points 3
  doubles forward.


To better understand pointers, arrays, ++, and *, let's go over the
  code on the right line by line.
  For reference the precedence table
  is here.
  The output produced is


  *p = 11
  *p++ = 11
  *p = 13
  *++p = 15
  *p = 15
  ++*p = 16


  

A Simple Storage Allocator


  #define ALLOCSIZE 15000
  static char allocbuf[ALLOCSIZE];
  static char *allocp = allocbuf;

  char *alloc(int n) {
    if (allocp+n ≤ allocbuf+ALLOCSIZE) {
      allocp += n;
      return allocp-n;   // previous value
    } else               // not enough space
      return 0;
  }

  void afree (char *p) {
    if (p>=allocbuf && p<allocbuf+ALLOCSIZE)
      allocp = p;
  }



On the right is a primitive storage allocator and freer.
  When alloc(n) is called, with an non-negative integer
  argument n, it returns a pointer to a block of
  n characters.


When afree(p) is called with the pointer returned
  by alloc(), it resets the state of alloc()/afree()
  to what it was before the call to alloc().


A very strong assumption is made that calls
  to alloc()/afree() are made in a stack-like manner.
  These routines would be useful for managing storage for C automatic,
  local variables.
  They are far from general.
  The standard library routines malloc()/free() do not make
  this assumption and as a result are
  considerably more complicated.


Since pointers, not array positions are communicated to users
  of alloc()/afree(), these users do not need to know
  anything about the array, which is kept under the covers via
  static.


Notes.


    
  
  1. The initialization of allocp is the same as setting
    it to &allocbuf[0].
    2. 
  
  2. Normally, the only reasonable initial values for a pointer are
    zero or some expression involving the addresses of previously
    declared objects.
    3. 
  
  3. C guarantees that no valid pointer has value zero.
    That is, &x is never zero.
    Thus setting a pointer to zero is a way of saying it points to
    no object.
    Although a literal 0 is permitted; most programmers
    use NULL.
    4. 
  
  4. Question: What happens if n<0?
    
    Answer: The new allocation gets memory that is
    part of a previous allocation.
    Even worse if *very* negative; scary!
    5. 




Start Lecture #6
 


Pointer Comparison


If pointers p and q point to elements of the same
  array, then comparisons between the pointers
  using <, <=, ==, !=, >,
  and >= all work as expected.


If pointers p and q do not point to members of
  the same array, the value returned by comparisons is undefined, with
  one exception: p pointing to an element of an array and
  q pointing to the first element past the array.


Any pointer can be compared to 0 via == and !=.
  Normally, NULL is used, but an actual literal 0 is
  permitted.



Pointer Subtraction


Again we need p and q pointing to elements of the
  same array.
  In that case, if p<=q, then p-q+1 equals the
  number of elements from p to q (including the
  elements pointed to by p and q).



Using the Allocator


These examples are interesting in their own right, beyond showing
  how to use the allocator.



  #include <stdio.h>
  void changeltox(char *z);
  void mystrcpy char *s, char *t);
  char *alloc(int n);

  int main() {
    char stg[] = "hello";
    char *stg2 = alloc(6);
    mystrcpy(stg2, stg);
    changeltox(stg);
    printf ("String is now %s\n", stg);
    printf ("String2 is now %s\n", stg2);
  }



Making Changes in a New String


We have already written a
  program changeltox() that changes one character to another
  in a given string.


After initializing the string to "hello", the code on the right
  first copies it (using mystrcpy(), a one liner presented
  above) and then makes changes in the original.
  Thus, at the end, we have two versions of the string: the before and
  the after.


As expected the output is


  String is now hexxo
  String2 is now hello



So far, so good.
  Let's try something fancier.



Mismatched Sizes and the Resulting Mess


Recall the danger warning given with the code for
  mystrcpy(char *x, char *y): The code copies
  all the characters in y (i.e., up to and including
  '\0') to x ignoring the current length
  of x.
  Thus, if y is longer than the space allocated
  for x, the copy will overwrite whatever happens to be
  stored right after x.


  #include <stdio.h>
  void changeltox (char*);
  void mystrcpy (char *s, char *t);
  char *alloc(int n);
  int main () {
    char stg[] = "hello";
    char *stg2 = alloc(2);
    char *stg3 = alloc(6);
    mystrcpy (stg2, stg);
    printf ("String2 is now %s\n", stg2);
    printf ("String3 is now %s\n", stg3);
    mystrcpy (stg3, stg);
    changeltox (stg);
    printf ("The string is now %s\n", stg);
    printf ("String2 is now %s\n", stg2);
    printf ("String3 is now %s\n", stg3);
  }



The example on the right illustrates the danger.
  When the code on the right is compiled with the code for
  changeltox(), mystrcpy(), and alloc(),
  the following output occurs.


  String2 is now hello
  String3 is now llo
  The string is now hexxo
  String2 is now hehello
  String3 is now hello



What happened?


The string in stg contains the 5 characters in the word
  hello plus the ascii null '\0' to end the string.
  (The array stg has 6 elements so the string fits
  perfectly.)


The major problem occurs with the first execution of
  mystrcpy() because we are copying 6 characters into a
  string that has room for only 2 characters (including the ascii
  null).
  This executes flawlessly copying the 6 characters to an area
  of size 6 starting where stg2 points.
  These 6 locations include the 2 slots allocated to stg2 and
  then the next four locations.
  Normally it is very hard to tell what has been overwritten, and the
  resulting bugs can be very difficult to find and fix.


In this situation it is not hard to see what was overwritten since
  we know how alloc() works.
  The excess 6-2=4 characters are written into the first 4
  slots of stg3.

mess

When we print stg2 the first time we see no problem!
  A string pointer just tells where the string starts, it continues up
  to the ascii null.
  So stg2 does have all of hello (and the terminating
  null).
  Since stg3 points 2 characters after stg2, the
  string stg3 is just the substring of stg2 starting
  at the third character.


The second mystrcpy copies the six(!) characters in the
  string hello to the 6 bytes starting at the location pointed
  to by stg3.
  Since the string stg2 includes the location pointed to by
  stg3, both stg2 and stg3 are changed.


The changeltox() execution works as expected.



5.5: Character Pointers and Functions


As we know C does not have string variables, but does have string
  constants.
  This arrangement sometimes requires care to avoid errors.



char amsg[]="hello"; vs char *msgp="hello";


  char amsg[] = "hello";
  char *msgp = "hello";
  int main () {...}



Let's see if we can understand the following rules, which can
  appear strange at first glance.


    
  
  1. amsg (a character pointer) cannot be changed
    (amsg is an r-value not an l-value).
    However, both amsg[1] (an 'e')
    and *(amsg+1) (the same 'e') can be changed.
    2. 
  
  2. msgp (a character pointer) can be changed, but both
    *(msgp+2) (an 'l') and msgp[2] (the
    same 'l') cannot be changed.
    3. 



Perhaps the following will help.


    
  
  1. amsg is defined to be &amsg[0], which is
    an expression not a variable; it is not a container.
    So it is only an r-value, not an l-value.
    But amsg does point to a block of 6 containers.
    Hence de-referencing amsg (or amsg+1) does yield
    a container.
    Remember that *(amsg+1) is just amsg[1].
    2. 
  
  2. msgp is a variable.
    Hence msgp is an l-value (a container) and can be
    changed.
    However it points to a bunch of character constants none of which
    are variables and hence none cannot be changed.
    3. 




The C Idiom for String Copy


  void mystrcpy (char *s, char *t) {
    while (*s++ = *t++) ;
  }



The previous version of this program tested if the assignment did
  not return the character '\0', which has the value 0 (a fact about
  ascii null).
  However checking if something is not 0 is the same (in C) as asking
  if it is true.
  Finally, testing if something is true is the same as just testing
  the something.
  The C rules can seem cryptic, but they are consistent.


If you are trembling with fright over this scary
  function, rest assured and see the following homework problem.


Homework: 5-5 (first
  part).
  Write a version of the library functions
  
    char *strncpy(char *s, char *t, int n)
  

  This copies at most n characters
  from t to s.
  This code is not scary like other copies since the user of the
  routine can simply declare s to have space
  for n characters.





Slick String Length Using Pointer Substraction


  int mystrlen(char *s) {
    char *p = s;
    while (*p)
      p++;
    return p-s;
  }



The code on the right applies the technique used to get the slick
  string copy to the related function string length.
  In addition it use pointer subtraction.
  Note that when the return is executed, p points
  just after the string (i.e., the character array) and s
  points to its beginning.
  Thus the difference gives the length.


Recall that this is the one case where subtraction of pointers is
  well defined.



String Comparison


  int mystrcmp(char *s, char *t) {
    for (; *s == *t; s++,t++)
      if (*s == '\0')
        return 0;
    return *s - *t;
  }



We next produce a string comparison routine that is returns a
  negative integer if the string s is lexicographically
  before t, zero if they are equal, and a positive integer if
  s is lexicographically after t.


The loop takes care of equal characters.
  The function returns 0 if we reached the end of the equal
  strings.


If the loop concludes, we have found the first difference.


A key is that if exactly one string has ended, its character ('\0')
  is smaller then the other string's character.
  This is another ascii fact (ascii null is zero the rest are
  positive).


I tried to produce a version using while(*s++ == *t++),
  but that failed since the loop body and the post loop code was
  dealing with the subsequent character.
  I suppose it could have been forced to work if I used a bunch of
  constructions like *(s-1), but that would have been
  ugly.



5.6: Pointer Arrays; Pointers to Pointers


For the moment forget that C treats pointers and arrays almost the
  same.
  For now just think of a character pointer as another data type.


So we can have an array of 9 character pointers, e.g.,
  char *A[9].
  We shall see fairly soon that this is exactly how some systems
  (e.g. Unix) store command line arguments.


  #include <stdio.h>
  int main() {
    char *STG[3] = { "Goodbye", "cruel", "world" };
    printf ("%s %s %s.\n", STG[0], STG[1], STG[2]);
    STG[1] = STG[2] = STG[0];
    printf ("%s %s %s.", STG[0], STG[1], STG[2]);
    return 0;
  }

  Goodbye cruel world.
  Goodbye Goodbye Goodbye.



The code on the right defines an array of 3 character pointers,
  each of which is initialized to a string.
  The first printf() has no surprises.
  But the assignment statement should fail since we allocated space
  for three strings of sizes 8, 6, and 6 and now want to wind up with
  three strings each of size 8 and we didn't allocate any additional
  space.


However, it works perfectly and the resulting output is shown as
  well.


Question: What happened?
  How can space for 8+6+6 characters be enough for 8+8+8?

  Answer: The reason it works is that we
  do not have three strings of size 8.
  Instead we have one string of size 8, with three character pointers
  pointing to it.

goodbye

The picture on the right shows a before and after view of the array
  and the strings.


This suggests and interesting possibility.
  Imagine we wanted to sort long strings alphabetically (really
  lexicographically).
  Not to get bogged down in the sort itself assume it is a simple
  interchange sort that loops and, if a pair is out of order, it
  executes a swap, which is something like


  temp = x;
  x = y;
  y = temp;



If x, y, and temp are (varying size,
  long) strings then we have some issues to deal with.


    
  
  1. It is expensive to do the three assignments if the strings are
    very long.
    2. 
  
  2. If one of the strings is longer than the space allocated for
    another, we either overwrite something else (and potentially end
    the world) or refuse the copy and hence not complete the
    sort.
    3. 


sortstrings

Both of these issues go away if we maintain an array of pointers to
  the strings.
  If the string pointed to by A[i] is out of order with
  respect to the string pointed to by A[j], we swap the
  (fixed size, short) pointers not the strings that they point to.


This idea is illustrated on the right.


  #include <stdio.h>
  void sort(int n, char *C[n]) {
    int i,j;
    char *temp;
    for (i=0; i<n-1; i++)
      for (j=i+1; j<n; j++)
        if (mystrcmp(C[i],C[j]) > 0) {
          temp = C[i];
          C[i] = C[j];
          C[j] = temp;
        }
  }
  int main() {
    char *STG[] = {"hello","99","3","zz","best"};
    int i,j;
    for (i=0; i<5; i++)
      printf ("STG[%i] = \"%s\"\n", i, STG[i]);
    sort(5,STG);
    for (i=0; i<5; i++)
      printf ("STG[%i] = \"%s\"\n", i, STG[i]);
    return 0;
  }



Putting all the pieces together, the code on the right,
  plus the mystrcmp() function above, produces the following
  output.


  STG[0] = "hello"
  STG[1] = "99"
  STG[2] = "3"
  STG[3] = "zz"
  STG[4] = "best"
  STG[0] = "3"
  STG[1] = "99"
  STG[2] = "best"
  STG[3] = "hello"
  STG[4] = "zz"



Note the first line of the sort function, in particular
  the n in char C[n].
  This is an addition made to C in 1999 (the language is called
  sometimes called C-99 to distinguish it from C-89 or ansii-C as
  described in our text, and K&R-C as described in the first
  edition of our text).
  Our text would write C[] instead of C[n].


You might question if the output is indeed sorted.
  For example, we remember that ascii '3' is less than ascii
  '9', and we know that in ascii 'b'<'h'<'z',
  but why is '9'<'b'?


Well, I don't know why it is, but it is.
  That is, in ascii the digits do in fact come before the letters.



Another Example


  #include <stdio.h>
  int main(int argc, char *argv[]) {
    char c1 = '1', c2 = '2';

    char ac[10] = "wxyXYZ";   // ac = Array of Chars
    ac[1] = c1;
    ac[2] = c2;
    printf("ac[1]=%c ac[2]=%c\n", ac[1], ac[2]);

    char *pc1, *pc2;          // pc = Pointer to Char
    pc1 = &ac[3];
    pc2 = pc1+1;
    printf("*pc1=%c *pc2=%c\n", *pc1, *pc2);

    char *(apc[10]);          // Array of Pointers to Char
    apc[3] = pc1;             // Points at ac[3]
    apc[4] = pc2-2;           // Points at ac[2]
    printf("*apc[3]=%c *apc[4]=%c\n", *apc[3], *apc[4]);
    return 0;
  }



The program on the right includes several types of variables.
  In particular we find chars, an arrays of chars,
  pointers to chars, and an array of pointers
  to chars.


The program, when run, produces the following output.


  ac[1]=1 ac[2]=2
  *pc1=X *pc2=Y
  *apc[3]=X *apc[4]=2



You should first confirm that the types are correct.
  For example, is * always applied to a pointer?
  Since all the prints use %c for the values printed, all
  those values must be chars.
  Are they?


Then confirm that you agree with the values produced.


At one point the program adds 1 to the char
  pointer pc1.
  At another point it subtracts 2 from another char pointer.
  This is valid only if the final value of the pointer is pointing
  inside the same array as the initial value.
  Is this the case?



5.7: Multi-dimensional Arrays


  void matmul(int n, int k, int m, double A[n][k],
       double B[k][m], double C[n][m]) {
    int i,j,l;
    for (i=0; i<n; i++)
      for (j=0; j<m; j++) {
        C[i][j] = 0.0;
        for (l=0; l< k; l++)
          C[i][j] += A[i][l]*B[l][j];
      }
  }



C does have normal multidimensional arrays.
  For example, the code on the right multiplies two matrices.


In some sense C, like Java, has only one-dimensional arrays.
  However, a one-dimensional array of one-dimensional arrays of
  doubles is close to a two-dimensional array of doubles.
  One difference is the notation: C/Java uses A[][] rather
  than A[,].
  Another is that, in the example on the right, A[n] is a
  legal (one-dimensional) array.


The biggest difference is that the array need not be
  rectangular, that is the rows need not be the same length.


The declaration in the function was not legal in the version of C
  described in our text.


  int A[2][3] = { {5,4,3}, {4,4,4} };
  int B[2][3][2] = { { {1,2}, {2,2}, {4,1} },
                     { {5,5}, {2,3}, {3,1} } };



Multidimensional arrays can be initialized.
  Once you remember that a two-dimensional array is a one-dimensional
  array the syntax for initialization is not surprising.



  (C, like most modern languages uses row-major ordering so the last
  subscript varies the most rapidly.)




Start Lecture #7
 


  char amsg[] = "hello";
  int main(int argc; char *argv[]) {
    printf("%c\n", amsg[100]);
  }



Note: Last time I ended with remarks relating an
  array of size 1 to an array of size 10 and that a pointer to X is very
  similar to array of X.
  The point was that code on the right compiles and runs (it is
  illegal but not caught) in part because the types match.




5.8: Initialization of Pointer Arrays


  char *monthName(int n) {
    static char *name[] = {"Illegal",
      "Jan", "Feb", "Mar", "Apr",
      "May", "Jun", "Jul", "Aug",
      "Sep", "Oct", "Nov", "Dec"};
    return (n<1 || n>12) ? name[0] : name[n];
  }



The initialization syntax for an array of pointers follows the
  general rule for initializing an array:
  Enclose the initial values inside braces.


Question: How do we write an initial value for a
  pointer?

  Answer: We remember that an array is just a pointer
  to the first element.


Looking at the code on the right we see this principle in action.
  I believe the most common usage is for an array of character
  pointers as in the example.



5.9: Pointers vs. Multi-dimensional Arrays


  int  A[3][4];
  int *B[3];



Consider the two declarations on the right.
  They look different, but both A[2][3] and
  B[2][3] are legal (at least syntactically).
  The real story is that they most definitely are different.
  (In fact Java arrays have a great deal in common with the 2nd form
  in C.)

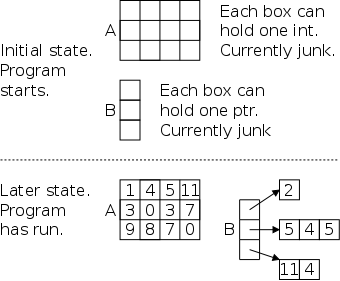
pointer array

The declaration int A[3][4]; allocates space for 12
  integers, which are stored consecutively so that A[i][j]
  is the (4*i+j)th integer stored (counting from
  zero).
  With the simple declaration written, none of the integers is
  initialized, but we have seen how to initialized
  them.


The declaration int *B[3]; allocates space for
  NO integers.
  It does allocate space for 3 pointers (to
  integers).
  The pointers are not initialized so they currently point to junk.
  The program must somehow arrange for each of them to point to a
  group of integers (and must figure out when the group ends).
  An important point is that the groups may have different lengths.
  The technical jargon is that we can have a ragged array as
  shown in the bottom of the picture.



Arrays of Strings


The last diagram on the right show the relationship between a 2-D
  array of integers and a 1-D array of pointers to integers noting
  that the latter supports ragged arrays.
  In C probably more common than a ragged array of integers, is a
  ragged array of chars, that is a 1-D array of pointers to (varying
  length) strings.


We have already seen two examples of this.
  The monthName program just above and the
  Goodbye Cruel World diagrams in section 5.6.
  We next illustrate that every C main() program on Unix
  (e.g., on Linux) also uses a ragged array of chars, i.e., an array
  of strings.





5.10: Command-line Arguments

cmdline

On the right is a picture of how arguments are passed to a (Unix)
  command.
  Each main() program receives two arguments an integer,
  normally called argc for argument count, and an array of
  character pointers, normally called argv for argument
  vector.


The diagram shows argv as an array and the code below
  treats it that way as well.
  As always, an array name is also a pointer to the first element.
  If you view argv as a pointer, then you would draw a box
  for it with an arrow pointing to the array.
  The book pictures it that way.


  #include <stdio.h>
  int main(int argc, char *argv[argc]) {
    int i;
    printf("My name is %s.\n", argv[0]);
    printf("I was called with %d argument%s\n",
           argc-1, (argc==2) ? "" : "s");
    for (i=1; i<argc; i++)
      printf("Argument #%d is %s.\n", i, argv[i]);
   }

  sh-4.0$ cc -o cmdline cmdline.c
  sh-4.0$ ./cmdline
  My name is ./cmdline.
  I was called with 0 arguments.
  sh-4.0$ ./cmdline x
  My name is ./cmdline.
  I was called with 1 argument.
  Argument #1 is x.
  sh-4.0$ ./cmdline xx y
  My name is ./cmdline.
  I was called with 2 arguments.
  Argument #1 is xx.
  Argument #2 is y.
  sh-4.0$ ./cmdline -o cmdline cmdline.c
  My name is ./cmdline.
  I was called with 3 arguments.
  Argument #1 is -o.
  Argument #2 is cmdline.
  Argument #3 is cmdline.c.
  sh-4.0$ cp cmdline mary-joe
  sh-4.0$ ./mary-joe -o cmdline cmdline.c
  My name is ./mary-joe.
  I was called with 3 arguments.
  Argument #1 is -o.
  Argument #2 is cmdline.
  Argument #3 is cmdline.c.



Since the same program can have multiple names (more on that
  later), argv[0], the first element of the argument vector,
  is a pointer to a character string containing the name by which the
  command was invoked.
  Subsequent elements of argv point to character strings
  containing the arguments given to the command.
  Finally, there is a NULL pointer to indicate the end of the pointer
  array.

  
The integer argc gives the total number of
  pointers, including the pointer to the name of the command.
  Thus, the smallest possible value for argc is 1 and
    argc is 3 for the picture drawn above.


The code on the right shows how a program can access its name and
  any arguments it was called with.


Having both a count (argc) and a trailing NULL pointer
  (argv[argc]==NULL) is redundant, but convenient.
  The code I wrote treats argv as an array.
  It loops through the array using the count as an upper bound.
  Another style would use something like


  while (*argv)
    printf("%s\n", *argv++);



which treats argv as a pointer and terminates when
  argv points to NULL.


The second frame on the right shows a session using the code
  directly above it.


    
  
  1. First, we show how to compile a C program and not have the
    result called a.out.
    2. 
  
  2. Next we run the resulting program with differing numbers of
    arguments.
    Note the use of the conditional expression to get singular and
    plural correct.
    3. 
  
  3. Finally, we show one way (via copying the executable) that the
    same program can have more than one name.
    We could have renamed/moved the executable as well.
    Another way would have been to recompile the program giving a
    different file name after -o (or not using -o
    and getting a.out).
    In 202 you will learn two other ways (hard and soft links).
    4. 




Simple Application of Command Line Arguments


Now we can get rid of some symbolic constants that should be
  specified at run time.


Here are two before and after examples.
  The code on the left uses symbolic constants; on the right we use
  command line arguments.



Fahrenheight to Celcius


                                  #include <stdlib.h>
  #include <stdio.h>              #include <stdio.h>
  #define LO 0
  #define HI 300                  
  #define INCR 20                 
  main() {                        int main (int argc, char *argv[argc]) {
    int F;                          int F;
    for (F=LO; F<=HI; F+=INCR)      for (F=atoi(argv[1]); F<=atoi(argv[2]);
                                         F+=atoi(argv[3]))
      printf("%3d\t%5.1f\n", F,       printf("%3d\t%5.1f\n", F,
             (F-32)*(5.0/9.0));              (F-32)*(5.0/9.0));
                                    return 0;
  }                               }



Notes.


    
  
  1. Now main() is specified correctly; it returns an
    integer and has the complicated argument structure we just
    described.
    As written on the left the program terminates abnormally
    (it doesn't return 0).
    2. 
  
  2. We use of atoi() to convert the ascii (character) form
    of the numerical inputs into integers.
    3. 




Solving Quadratic Equations


                                            #include <stdlib.h>
#include <stdio.h>                          #include <stdio.h>
#include <math.h>                           #include <math.h>
#define A +1.0   // should read                  
#define B -3.0   // A,B,C                        
#define C +2.0   // using scanf()           
void solve (float a, float b, float c);     void solve (float a, float b, float c);
int main() {                                int main(int argc, char *argv[argc]) {
  solve(A,B,C);                               solve(atof(argv[1]), atof(argv[2]),
                                                    atof(argv[3]));
  return 0;                                   return 0;
}                                           }
void solve (float a, float b, float c){     void solve (float a, float b, float c){
  float d;                                    float d;
  d = b*b - 4*a*c;                            d = b*b - 4*a*c;
  if (d < 0)                                  if (d < 0)
    printf("No real roots\n");                  printf("No real roots\n");
  else if (d == 0)                            else if (d == 0)
    printf("Double root is %f\n",               printf("Double root is %f\n",
           -b/(2*a));                                  -b/(2*a)); 
  else                                        else
    printf("Roots are %f and %f\n",             printf("Roots are %f and %f\n",
           ((-b)+sqrt(d))/(2*a),                       ((-b)+sqrt(d))/(2*a),
           ((-b)-sqrt(d))/(2*a));                      ((-b)-sqrt(d))/(2*a));
}                                           }



Notes.


    
  
  1. Again main() is now specified correctly.
    When we had main() we said don't check the
    arguments.
    Now we specify them correctly.
    2. 
  
  2. This time we need atof() since the arguments are
    floating point.
    3. 




  include <string.h>
  include <stdio.h>
  include <ctype.h>
  int main (int argc, char *argv[argc]) {
    int c, makeUpper=0;
    if (argc > 2)
      return argc;   // error return
    if (argc == 2)
      if (strcmp(argv[1], "-toupper")) {
        printf("Arg %s illegal.\n", argv[1]);
        return -1;
      }
      else   // -toupper was arg
        makeUpper=1;
    while ((c = getchar()) != EOF)
      if (!isdigit(c)) {
        if (isalpha(c) && makeUpper)
          c = toupper(c);
        putchar(c);
      }
     return 0;
  }



Specifying Options


Often a leading minus sign (-) is used for optional command line
  arguments.


The program on the right removes all digits from the input.
  If it is given the argument -toupper it also converts all
  letters to upper case using the toupper() library routine.


Notes



Demo this function on my laptop.


Homework:
  At the very end of chapter 3 you wrote escape() that
  converted a tab character into the two characters \t
  (it also converted newlines but ignore that).
  Call this function detab() and call the reverse function
  entab().
  Combine the entab() and detab functions by writing
  a function tab that has one command line argument.


  tab -en   # performs like entab()
  tab -de   # performs like detab()




5.11: Pointers to Functions


  #include <ctype.h>
  #include <string.h>
  #include <stdio.h>
  // Program to illustrate function pointers
  int digitToStar(int c);   // Cvt digits to *
  int letterToStar(int c);  // Cvt letters to *
  int main (int argc, char *argv[argc]) {
    int c;
    int (*funptr)(int c);
    if (argc != 2)
      return argc;
    if (strcmp(argv[1],"digits")==0)
      funptr = &digitToStar;
    else if (strcmp(argv[1],"letters")==0)
      funptr = &letterToStar;
    else
      return -1;
    while ((c=getchar())!=EOF)
      putchar((*funptr)(c));
    return 0;
  }

  int digitToStar(int c) {
    if (isdigit(c))
      return '*';
    return c;
  }

  int letterToStar(int c) {
    if (isalpha(c))
      return '*';
    return c;
  }



In C you can do very little with functions, mostly define them
  and call them (and take their address, see what follows).


However, pointers to functions (called function pointers) are real
  values.
  You can do a lot with function pointers.


    
  
  1. A function can return a function pointer.
    2. 
  
  2. You can declare variables that hold function pointers.
    3. 
  
  3. You can have an array of function pointers.
    4. 
  
  4. You can have a structure with function pointer components.
    5. 
  
  5. A function can take a function pointer argument.
    6. 
  
  6. etc.
    7. 



The program on the right is a simple demonstration of function
  pointers.
  Two very simple functions are defined.


The first function, digitToStar() accepts an integer
  (representing a character) and return an integer.
  If the argument is a digit, the value returned is (the integer
  version of) '*'.
  Otherwise the value returned is just the unchanged value of the
  argument.


Similarly letterToStar() convert a letter to '*' and
  leaves all other characters unchanged.


The star of the show is funptr.
  Read its declaration carefully:
  The variable funptr is the kind of thing that, once
  de-referenced, is the kind of thing that, once given an integer, is
  an integer.


So it is a pointer to something.
  That something is a function from integers to integers.


The main program checks the (mandatory) argument.
  If the argument is "digits", funptr is set to the address of
  digitToStar().
  If the argument is "letters", funptr is set to the address
  of letterToStar().


Then we have a standard getchar()/putchar() loop with a
  slight twist.
  The character (I know it is an integer) sent to putchar()
  is not the naked input character, but instead is the input character
  processed by whatever function funptr points to.
  Note the "*" in the call to putchar().


Note: C permits abbreviating &function-name to
  function-name.
  So in the program above we could say


  funptr = digitToStar;
  funptr = letterToStar;



instead of


  funptr = &digitToStar;
  funptr = &letterToStar;



I don't like that abbreviation so I don't use it.
  Others do like it and you may use it if you wish.


One difference between a function pointer and a
  function is their size.
  A big function is big, a small function is small, and an enormous
  function is enormous.
  However all function pointers are the same size.
  Indeed, all pointers in C are the same size.
  This makes them easier for the system to deal with.



5.12: Complicated Declarations


We are basically skipping this section.
  It shows some examples more complicated than we have seen (but are
  just more of the same—one example is below).
  The main part of the section presents a program that converts C
  definition to/from more-or-less English equivalents.


Here is one example of a complicated declaration.
  It is basically the last one in the book with function arguments
  added.


  char (*(*f[3])(int x))[5]



Remembering that *f[3] (like *argv[argc] is an
  array of 3 pointers to something not a pointer to an array of 3
  somethings, we can unwind the above to.


The variable f is an array of size three of pointers.


Remembering that *(g)(int x) = *g(int x) is a
  function returning a pointer and not a pointer to a function, we can
  further unwind the monster to.


The variable f is an array of size three of pointers to
  functions taking an integer and returning a pointer to an array of
  size five of characters.


One more (the penultimate from the book).


  char (*(f(int x))[5])(float y)



The function f takes and integer and returns a pointer to
  an array five pointers to functions taking a real and returning a
  character.





Chapter 6: Structures


For a start, a Java programmer can think of structures as basically
  classes and objects without methods.



Section 6.1: Structure Basics


  #include <math.h>
  struct point {
    double x;
    double y;
  };
  struct rectangle {
    struct point ll;
    struct point ur;
  } rect1;

  double f(struct point pt);
  struct point mkPoint(double x, double y);
  struct point midPoint(struct point pt1,
                        struct point pt2);

  int main(int argv, *char argv[]) {
    struct point pt1={40.,20.}, pt2;
    pt2 = pt1;
    rect1.ll = pt2;
    pt1.x += 1.0;
    pt1.y += 1.0;
    rect1.ur = pt1;
    rect1.ur.x += 2.;
    return 0;
  }

  

On the right we see some simple structure declarations for use in a
  geometry application.
  They should be familiar from your experience with Java classes in
  CS101 and CS102.


The top declaration defines the struct point type.
  This is similar to defining a class without methods.


As with Java classes, structures in C help organize data by
  permitting you to treat related data as a unit.
  In the case of a geometric point, the x and y
  coordinates are closely related mathematically and, as components of
  the struct point type, they become closely related in
  the program's data organization.


The next definition defines both a new type
  struct rectangle and a variable rect1 of this
  type.
  Note that we can use struct point, a previously
  defined struct, in the declaration of struct
  rectangle.


Recall from plane geometry in high school that a rectangle is
  determined by its lower left ll and upper right ur
  corners.


The definition in main() of pt1 illustrates an
  initialization.
  C does not support structure constants.
  Hence you could not in main() have the assignment
  statement


  pt1 = {40., 20.};



as an executable statement within main().


We see in the executable statements of main() that one can
  assign a point to a point as well as assigning to each
  component.


Since the rectangle rect1 is composed of points,
  which are in turn composed of doubles, we can assign
  a point to a point component of
  a rectangle and can assign a double to a
  double component of a point component of
  a rectangle.


If you wrote a Java program for geometry (we did when I last taught
  201/202), it probably had classes like rectangle
  and point and had objects like pt1, pt2,
  and rect1.
  Given these classes, the assignment statements in our
  C-language main() function would have been more or less
  legal Java statements as well.



Start Lecture #8
 


Remark: Lab#1 assigned



6.2: Structures and Functions


  double dist (struct point pt) {
    return sqrt(pt.x*pt.x+pt.y*pt.y);
  }

  struct point mkPoint(double x, double y) {
    // return {x, y};   not C
    struct point pt;
    pt.x = x;
    pt.y = y;
    return pt;
  }

  struct point midpoint(struct point pt1,
                        struct point pt2){
    // return (pt1 + pt2) / 2;  not C
    struct point pt;
    pt.x = (pt1.x+pt2.x) / 2;
    pt.y = (pt1.y+pt2.y) / 2;
    return pt;
  }

  void mvToOrigin(struct rectangle *r){
    (*r).ur.x = (*r).ur.x - (*r).ll.x;
    r->ur.y = r->ur.y - r->ll.y;
    r->ll.y = 0;
    r->ll.x = 0;
  }



The only legal operations on a structure are copying it, assigning
  to it as a unit, taking its address with &, and assessing its
  members.


On the right we see four geometry functions.
  Although all four deal with structs, they do so
  differently.
  A function can receive and return structures, but you may prefer to
  specify the constituent native types instead.
  A third alternative is to utilize a pointer to
  a struct.


    
  
  1. The first function dist() takes a struct point
    as an argument and returns a double.
    This seems appropriate since geometrically we think of the distance
    between 2 points not between 4 numbers.

    2. 
  
  2. The second function mkpoint() in contrast
    has double arguments and returns a struct point.
    It would have been illegal for mkpoint to have included
    a
         return {x, y}
     statement since C
    does not support this.

    3. 
  
  3. Next we have midpoint(), which has
    struct point parameters and return type.
    We think of a midpoint of two points not of four numbers.
    It would be nice for midpoint to be basically a 1-liner
    
        return {(pt1 + pt2) / 2}
    
    but again that is not C.

    4. 
  
  4. The last function mvToOrigin(), which moves a rectangle
    so that its lower left corner is at the origin, takes one
    parameter, a pointer to a
    struct rectangle.
    I will say more about this function just below.
    5. 



As we have seen, functions can take structures as parameters, but
  is that a good idea?
  Should we instead use the components as parameters or perhaps pass a
  pointer to the structure?
  For example, if main() wishes to pass pt1 to a
  function f(), should we write.


    
  
  1. f(pt1)
    2. 
  
  2. f(pt1.x, pt1.y)
    3. 
  
  3. f(&pt1)
    4. 



Naturally, the declaration of f() will be different in
  the three cases.
  When would each case be appropriate?


    
  
  1. f(pt1) This form is the most natural
    where the parameter is viewed as a point, not as two real numbers.
    Our example was distance from the
    origin int dist(pt).
    2. 
  
  2. f(pt1.x, pt1.y)  A common example is a
    Java constructor like function that produces a structure
    from its constituents, for example mkPoint(pt1.x, pt2.y)
    above would produce a new point having coordinates
    a mixture of pt1 and pt2.
    
    Another possibility is viewing midpoint() above as a
    function on rectangles, in which case the arguments
    to midpoint() rect1.pt1 and rect1.pt2
    are the components of the rect1.
    3. 
  
  3. f(&pt1) A simple reason for using
    the address is that it might be significantly shorter than the
    structure itself and thus it would be faster and take less memory
    to pass the address.
    
    A perhaps more interesting reason to pass the address is so that
    the receiving function can modify the argument.
    This is shown in mvToOrigin().
    
    The first assignment statement in mvToOrigin() uses the
    standard dereferencing operator * followed by the standard
    component selection operator ..
    Due to precedence, the parentheses are needed.
    
    The remaining three lines use the abbreviation ->.
    4. 



Note: The -> abbreviation is
  employed almost universally.
  Constructs like ptr1->elt5 are very common; the
  long form (*ptr1).elt5 is much less common.



Homework: Write two
  versions of mkRectangle, one that accepts two points, and
  one that accepts 4 real numbers.



6.3: Arrays of Structures (and Structures of Arrays)


  #define MAXVAL 10000
  #define ARRAYBOUND (MAXVAL+1)
  int G[ARRAYBOUND];
  int P[ARRAYBOUND];

  struct gameValType {
    int G[ARRAYBOUND];
    int P[ARRAYBOUND];
  } gameVal;

  struct gameValType {
    int G;
    int P;
  } gameVal[ARRAYBOUND];

  #define NUMEMPLOYEES 2
  struct employeeType {
    int id;
    char gender;
    double salary;
  } employee[NUMEMPLOYEES] = {
    { 32, 'M', 1234. },
    { 18, 'F', 1500. }
  };



Consider the following game.


    
  
  1. Start with a positive integer N
    2. 
  
  2. If N is 1, stop.
    3. 
  
  3. If N is even, divide by 2.
    4. 
  
  4. If N is odd, set N = 3N+1.
    5. 



So, starting with N=7, you get

  7 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1.

  and starting with N=27, you get

  27 82 41 ... 9232 ... 160 80 40 20 10 5 16 8 4 2 1.


It is an open problem if all positive integer eventually get to 1.
  This has been checked for MANY numbers.
  Let G[i] be the number of rounds of the game needed to get 1.
  G[1]=0, G[2]=1, G[7]=16.


Factoring into primes is fun too.
  So let P[N] be the number of distinct prime factors of N.
  P[2]=1, P[16]=1, P[12]=2 (define P[1]=0).


This leads to two arrays as shown on the right in the top
  frame.


We might want to group the two arrays into a structure as in the
  second frame.
  This version of gameVal is a structure of arrays.
  In this frame the number of distinct prime factors of 763 would be
  stored in gameVal.P[763].


In the third frame we grouped together the values of G[n]
  and P[n].
  This version of gameVal is an array of structures.
  In this frame the number of distinct prime factors of 763 would be
  stored in gameVal[763].P.


If we had a database with employeeID, gender, and salary, we might
  use the array of structures in the fourth frame.
  Note the initialization.
  The inner {} are not needed, but I believe they make the code
  clearer.



The sizeof and sizeof() Operators


How big is the employee array of structures?
  How big is employeeType?


C provides two versions of the sizeof unary operator to
  answer these questions.



These functions are not trivial and indeed the answers are system
  dependent ... for two reasons.


    
  
  1. Certain primitive types (e.g., int) may have different
    sizes in different systems.
    2. 
  
  2. The alignment requirements may be different.
    3. 



Example:  Assume char requires 1 byte, int
  requires 4, and double requires 8.
  Let us also assume that each type must be aligned on an address that
  is a multiple of its size and that a struct must be aligned
  on an address that is a multiple of 8.


So the data in struct employeeType requires
  4+1+8=13 bytes.
  But three bytes of padding are needed between gender and
  salary so the size of the type is 16.


Homework: How big is
  each version of sizeof(struct gameValType)?
  How big is sizeof employee?



Calculating the Number of Elements in an Array


  #include <stdio.h>
  int main (int argc, char *argv[argc]) {
    struct howBig {
      int n;
      double y;
    } howBigAmI[] = { {26, 18.}, {33, 99.} };
    printf ("howBigAmI has %ld entries.\n",
      sizeof howBigAmI / sizeof(struct howBig));
  }



In the example above it is easy to look at the initialization and
  count the array bound for employee.
  An annoyance is that you need to change the #define for
  NUMEMPLOYEES if you add or remove an employee from the
  initialization list.


A more serious problem occurs if the list is long in which case
  manually counting the number of entries is tedious and, much worse,
  error prone.


Instead we can use sizeof and sizeof() to have
  the compiler compute the number of entries in the array.
  The code is shown on the right.



Start Lecture #9
 


getword(char *word, int limit)


  int getword(char *word, int lim) {
    int c, getch(void);
    void ungetch(int);
    char *w = word;

    while (isspace(c = getch())) ;
    if (c != EOF)
      *w++ = c;
    if (!isalpha(c)) {
      *w = '\0';
      return c;
    }
    for ( ; --lim > 0; w++)
      if (!isalnum(*w = getch())) {
        ungetch(*w);
        break;
      }
    *w = '\0';
    return word[0];
  }  



As its name suggests the purpose of getword() is to get
  (i.e., read) the next word from the input.
  It's first parameter is a buffer into which getword() will
  place the word found.
  Although declared as a char *, the parameter is viewed as
  pointing to many characters, not just one.
  The second parameter throttles getword(), restricting the
  number of characters it will read.
  Thus getword() is not scary; the caller need only ensure
  that the first parameter points to a buffer at least as big as the
  second parameter specifies.


The definition of a word is technical.
  A word is either a string of letters and digits beginning with a
  letter, or a single non-white space character.
  The return value of the function itself is the first character of
  the word, or EOF for end of file, or the character itself if it is
  not alphabetic.


The program has a number of points to note.


    
  
  1. The declaration of w initializes w,
    not *w.

    2. 
  
  2. Question: Changing word
    in getword() would not affect the caller, so why do we
    need w?
    
    Answer: w is created and used so that
    the original value of word is available
    for word[0] at the end.

    3. 
  
  3. The expression *w++ is a common C idiom; make sure you
    understand what it does.
    In particular, the assignment 2 lines below *w++
    does not overwrite the value stored.

    4. 
  
  4. The library routine isaphanum() returns true for a
    letter or digit.
    You can find this information on any unix machiine (e.g.,
    access.cims.nyu.edu) by typing man alphanum.
    5. 




6.4: Pointers to Structures


  #include <stdio.h>
  #include <ctype.h>
  #include <string.h>
  #define MAXWORDLENGTH 50
  struct keytblType {
    char *keyword;
    int  count;
  } keytbl[] = {
    { "break", 0 },
    { "case", 0 },
    { "char", 0 },
    { "continue", 0 },
    // others
    { "while", 0 }
  };
  #define NUMKEYS (sizeof keytbl / sizeof keytbl[0])
  int getword(char *, int); // no var names given
  struct keytblType *binsearch(char *);

  int main (int argc, char *argv[argc]) {
    char word[MAXWORDLENGTH];
    struct keytblType *p;
    while (getword(word,MAXWORDLENGTH) != EOF)
      if (isalpha(word[0]) &&
          ((p=binsearch(word)) != NULL))
        p->count++;
    for (p=keytbl; p<keytbl+NUMKEYS; p++)
      if (p->count > 0)
        printf("%4d %s\n", p->count, p->keyword);
    return 0;
  }

  struct keytblType *binsearch(char *word) {
  int cond;
    struct keytblType *low = &keytbl[0];
    struct keytblType *high =  &keytbl[NUMKEYS];
    struct keytblType *mid;
    while (low < high) {
      mid = low + (high-low) / 2;
      if ((cond = strcmp(word, mid->keyword)) < 0)
        high = mid;
      else if (cond > 0)
        low = mid+1;
      else
        return mid;
    }
    return NULL;
  }



The program on the right illustrates well the use of pointers to
  structures and also serves as a good review of many C concepts.
  The overall goal is to read text from the console and count the
  occurrence of C keywords (such as break, if,
  etc.).
  At the end print out a list of all the keywords that were present
  and how many times each occurred.


Now lets examine the code on the right.


    
  
  1. The first interesting item is keytbl, the table of
    keywords.
    It is an array of struct keytblType; each entry of the
    array contains string and an integer.

    2. 
  
  2. The initialization of keytbl serves two purposes.
    Each string is set to a C keyword and each count is initialized to
    zero.
    The size of the array is determined by the initialization and the
    next line cleverly determines that size.
    The entries are initialized in alphabetical order, which permits
    the use of a binary search to find an entry.

    3. 
  
  3. The main program contains two loops: The first computes the
    counts and the second outputs the results.
    
      
      
    1. The first loop calls getword() and terminates on
        receiving EOF.
        The word is looked up in the keytbl using
        binsearch.
        The value returned by binsearch is either a pointer
        to the table entry found or NULL if the word is not a
        keyword (i.e., is not in the table).
        If the word is found, the corresponding count is
        incremented.
      
        I don't believe the isalpha() test is needed since,
        if the character is not a letter, binsearch will
        return NULL; it is presumably there to save a useless
        search.
      2. 
      
    2. The second loop traverses the table and prints out all
        entries with non-zero counts.
        Note the test used in the for statement and
        remember that the increment p++
        increments p by enough so that it points to
        the next entry.
      3. 
    
    
  

    4. 
  
  4. As I suspect you know, a binary search is quite efficient (its
    running time is logarithmic in the size of the table) and very
    easy to get wrong (< vs. <=, mid vs. mid-1
    vs. mid+1, etc.).
    The only real difference between this one and the one I hope you
    saw in 102, is that the code on the right is pointer based not
    array based.
    This explains the mysterious code to set mid to the
    midpoint between high and low.
    But, other than that oddity, I find it striking how array-like
    the code looks.
    That is, the manipulations of the pointers could just as well be
    manipulating indices.

    5. 
  
  5. If you have the text as well as your 101-102 material, I believe
    it would be useful for you to compare the following three versions
    of binary search.
    
      
      
    1. The java, array-based version from 101-102.
      2. 
      
    2. The C, array-based version from section 6.3 of our
        text (not covered in these notes).
      3. 
      
    3. The C, pointer-based version on the right.
      4. 
    
    
  
    6. 






6.5: Self-referential Structures

tree node
binary tree

Consider a basic binary tree.
  A small example is shown on the near right; one cell is detailed on
  the far right.
  Looking at the diagram on the far right suggests a structure with
  three components: left, right, and value.
  The first two refer to other tree nodes and the third is an
  integer.


I am fairly sure you did trees in 101-102 but I will still describe
  the C version.
  I will say that in both Java and C the key is the use of pointers.
  In C this is made very explicit by the use of *.
  In Java it is somewhat under the covers.


  struct bad {
    struct bad left;
    int value;
    struct bad right;
  };



  struct treenode_t {
    struct treenode_t *left;
    int value;
    struct treenode_t *right;
  };



Since trees are recursive data structures you might expect some
  sort of recursive structure.
  Consider struct bad defined on the right.
  (You might be fancier and have a struct tree, which
  contains a struct root, which has an integer value and two
  struct tree's).


But struct bad and its fancy friends are infinite
  data structures: The left and right components are the same type as
  the entire structure.
  So the size of a struct bad is the size of
  an int plus the size of two struct bad's.
  Since the size of an int exceeds zero, the total size must
  be infinite.
  Some languages permit infinite structures providing you never try to
  materialize more than a finite piece.
  But C is not one of those languages so for us struct bad is
  bad!


Instead, we use struct treenode_t as shown on
  the right (names like treenode_t are a shorter and very commonly
  used alternative to names like treenodeType).


The key is that a struct treenode does not
  contain an internal struct treenode.
  Instead it contains pointers to two internal
  struct treenodes.


Be sure you understand why struct treenode_t is finite and
  corresponds exactly to the picture above it.



Mutually Referential/Recursive Structures


  struct s {
    int val;
    struct t *pt;
  };
  struct t {
    double weight;
    struct s *PS;
  };



What if you have two structure types that need to reference each
  other.
  You cannot have a struct s contain a struct t if
  the struct t contains a struct s.
  If you did the size of s would exceed the size
  of t and the size of t would exceed the size
  of s.


Once again pointers come to the rescue as illustrated on the right.
  Neither structure is infinite.
  A struct s contains one integer and one pointer.
  A struct t contains one double and one pointer.
  Neither is a subset of the other, instead each references (points at)
  the other



Linked Lists: An Unbounded 1D Data Structure


  struct llnode_t {
    long data;
    struct llnode_t *next;
  }  


linked-list

Probably the most familiar 1D unbounded data structure is the
  linked list, well studied in 101-102.
  On the near right we have a diagram of a small linked list and
  further to the right we show the C declaration of a structure
  corresponding to one node in the diagram.
  Again we note that a struct llnode_t does not
  contain an struct llnode_t.
  Instead it contains a pointer to such a node.


With one pointer in each node the structure has a natural 1D
  geometric layout.
  Trees, in contrast, have two pointers per node and have a natural 2D
  geometric layout.



Nested Linked Links: Another 2D Data Structure

2d-structures

Instead of trees, we will investigate a different 2-dimensional
  structure, a linked list of linked lists.
  Eventually, this will become the subject of lab 2, but not until
  after lab1 is due.


Although all the actual data are strings (i.e., char *),
  there are two different types of structures present, the vertical
  list of node2d's and the many horizontal lists of
  node1d's.


Actually it is a little more complicated.
  Each horizontal list has a list head that is a node2d and
  there must be somewhere (not shown in the diagram) a pointer to
  the first node2d (i.e., the node with
  data joe).


The three decreasing length horizontal lines indicated that the
  pointer in question is null.
  (I borrow that symbol from electrical engineering, where it is used
  to represent ground.



The form of the individual nodes


  struct node2d {
    struct node1d *first;
    char *name;
    struct node2d *down;
  };
  struct node1d {
    struct node1d *next;
    char *name;
  };



The structure definitions are on the right.


Be sure you understand why the picture above agrees with the C
  code on the right.


The diagram (and the code) suggests a hierarchy: the nodes in the
  left hand column are higher level than the others.
  You can think of the struct node1d's on a single row
  belonging to a list headed by the struct node2d on the left
  of that same row.


Note that every struct node1d is the same (rather small)
  size independent of the length of the name.
  In that sense the figure is misleading since is suggests that
  alice is larger that joe.
  The confusion is that the node does not contain the
  name alice but rather a (fixed size) pointer to the
  name.


Said using C terminology name the component of the
  structure is a fixed size pointer.
  The possibly large string is the object pointed to by name,
  i.e., it is *name.
  But *name is a char, which is even smaller than a
  pointer.
  Better said is that name points to the first character of
  the string; you must look at the string itself to see where it
  ends.


One question remains.
  The string itself can be big.
  If it is a constant, then the compiler leaves space for it.
  
Question: What if the string is generated at
  runtime?

  Answer: malloc().




6.5.A More on 2D Linked Lists


This was presented in lecture 11, but belongs here A problem during
  the original presentation of 2D linked lists was it was hard to see
  the structures and diagrams at the same time.
  I have a handout that has the diagram illustrating the Example
  Configuration on one side of the page and the other side of the page
  shows the output from printConfig() applied to the
  example.


Let's go through mkExConfig to see how to generate the Example
  Configuration.



Diagram From Class



mkExampleConfig.c



Output




Start Lecture #10
 


Remark: A practice midterm is available.
  See the course home page.
  It is probably too long.



malloc()


As you know, in Java objects (including arrays) have to be created
  via the new operator.
  We have seen that in C this is not always needed: you can declare
  a struct rectangle and then declare several
  rectangles.


However, this doesn't work if you want to generate the rectangles
  during run time.
  When you are writing lab 2, you won't know how many 2d nodes or 1d
  nodes will be needed.


So we need a way to create an object during run time.
  In C this uses the library function malloc(), which takes
  one argument, the amount of space to be allocated.
  The function malloc() returns a pointer to this space.


Since malloc() is not part of C, but is instead just a
  library routine, the compiler does not treat it specially (unlike
  the situation with new, which is part of
  Java).
  Since malloc() is just an ordinary function, and we want it
  to work for dynamic objects of any type (e.g., an int, a
  char *, a struct treenode, etc), and
  there is no way to pass the name a type to a function, two questions
  arise.


    
  
  1. How do we arrange that the space returned by malloc()
    meets the alignment requirements of the object we desire?
    2. 
  
  2. How do we arrange that the pointer returned by
    malloc() is a pointer to the correct type.
    3. 



The alignment question is easy and can be essentially ignored.
  We just have malloc() return space aligned on the most
  stringent requirement.
  So, if double requires 8-byte alignment, and all structures
  require 16-byte alignment, and all other data types require 4-byte
  alignment, then malloc() always returns space aligned on a
  16-byte boundary (i.e., the address is a multiple of 16).


Ensuring type correctness is not automatic, but not hard.
  Specifically, malloc() returns a void *,
  which means it is a pointer that must be explicitly coerced to the
  correct type.
  For example, lab 2 might contain code like


  struct node2d *p2d;
  p2d = (struct node2d *) malloc(sizeof(struct node2d));




free()


The library routine free(void *p) returns to the system
  memory obtained by malloc().
  Indeed p must be a pointer returned by a previous call to
  malloc().
  Note that the order in which items are freed need not match the
  order in which they were obtained.


It is clearly an error to continue using memory you already freed.
  It will very likely lead to a crash with very little useful
  diagnostic information available.


Advice: Try very hard not to make this error.



Note


See in addition section 7.8.5 below.







  
6.6: Table Lookup

  
Skipped


  
6.7: Typedef

  
Instead of declaring pointers to trees via

  
    struct treenode *ptree;
  

  we can write
  
    typedef struct treenode *Treeptr;
    Treeptr ptree;
  

  Thus treeptr is a new name for the type
  struct treenode *.
  As another example, instead of
  
    char *str1, *str2;
  

  We could write
  
    typedef char *String;
    String str1, str2;
  

  
Note that this does not give you a new type; it
    just gives you a new name for an existing type.
    In particular str1 and str2 are still pointers to
    characters even if declared as a String above.

  
A common convention is to capitalize the a typedef'ed
    name.


  
6.8: Unions


  
Saving Space by Sharing Memory between 2 or More Variables

  
    struct something {
    int x;
    union {
    double y;
    int z;
    }
    }
  

  
Traditionally union was used to save space when memory was
    expensive.
    Perhaps with the recent emphasize on very low power devices, this
    usage will again become popular.
    Looking at the example on the right, y and z would
    be assigned to the same memory locations.
    Since the size allocated is the larger of what is needed the union
    takes space max(sizeof(double),sizeof(int)) rather than
    sizeof(double)+sizeof(int) if a union was not done.

  
It is up to the programmer to know what is the actual variable
    stored.
    The union shown cannot be used if y and z are both
    needed at the same time.

  
It is risky since there is no checking done by the language.


  
Meeting Alignment Constraints

  
A union is aligned on the most severe alignment of its
    constituents.
    This can be used in a rather clever way to meet a requirement of
    malloc().

  
As we mentioned above when discussing malloc(), it is
    sometimes necessary to force an object to meet the most severe
    alignment constraint of any type in the system.
    How can we do this so that if we move to another system where a
    different type has the most severe constraint, we only have to
    change one line?

  
    struct something {
    int x;
    struct something *p;
    // others
    } obj;
    
// assume long most severely aligned
      typedef long Align
      union something {
      struct dummyname {
      int x;
      union something *p;
      // others
      } s;
      Align dummy;
      }
      typedef union something Something;
  

  
Say struct something, as shown in the top frame on the
    right, is the type we want to make most severely aligned.

  
Assume that on this system the type long has the most
    severe alignment requirement and look at the bottom frame on the
    right.

  
The first typedef captures the assumption that
    long has the most severe alignment requirement on the
    system.
    If we move to a system where double has the most severe
    alignment requirement, we need change only this one line.
    The name Align was chosen to remind us of the purpose of
    this type.
    It is capitalized since one common convention is to capitalize all
    typedefs.

  
The variable dummy is not to be used in the program.
    Its purpose is just to force the union, and
    hence s to be most severely aligned.

  
In the program we declare an object say obj to be
    of type Something (with a capital S) and use
    obj.s.x instead of obj.x as in the top frame.
    The result is that we know the structure containing
    x is most severely aligned.

  
See section 8.7 if you are interested.


  
6.9: Bit Fields

  
Skipped







Start Lecture #11
 


Chapter 7: Input and Output



7.1: Standard Input and Output



getchar() and putchar()


This pair form the simplest I/O routines.


  #include <stdio.h>
  int main (int argc, char *argv[argc]) {
    int c;
    while ((c = getchar()) != EOF)
      if (putchar(c) == EOF)
        return EOF;
    return 0;
  }



The function getchar() takes no parameters and returns an
  integer.
  This integer is the integer value of the character read from
  stdin or is the value of the symbolic parameter EOF
  (normally -1), which is guaranteed not the be the integer value of
  any character.


The function putchar() takes one integer parameter, the
  integer value of a character.
  The character is sent to stdout and is returned as the
  function value (unless there is an error in which case EOF is
  returned.


The code on the right copies the standard input (stdin), which is
  usually the keyboard, to the standard output (stdout), which is
  usually the screen.


We built the getch() / ungetch()
  from getchar().


Homework: 7.1.
  Write a program that converts upper case to lower or lower case to
  upper, depending on the name it is invoked with, as found in
  argv[0]



Formatted Output—printf


We have already seen printf().
  A surprising characteristic of this function is that it has a
  variable number of arguments.
  The first argument, called the format string, is required.
  The number of remaining arguments depends on the value of the first
  argument.
  The function returns the number of characters printed, but that is
  not so often used.
  Technically its declaration is


  int printf(char *format, ...);



The format string contains regular characters, which are just sent
  to stdout unchanged and conversion specifications,
  each of which determines how the value of the next argument is to be
  printed.


The conversion specification begins with a %, which is
  optionally followed by some modifiers, and ends with a conversion
  character.


We have not yet seen any modifiers but have seen a few conversion
  characters, specifically d for an integer (i is
  also permitted), c for a single character, s for a
  string, and f for a real number.


There are other conversion characters that can be used, for
  example, to get real numbers printed using scientific notation.
  The book gives a full table.


There are a number of modifiers to make the output line up and look
  better.
  For example, %12.3f means that the real number will be
  printed using 12 columns (or more if the number is too big to fit in
  12 columns) with 3 digits after the decimal point.
  So, if the number was 36.3 it would be printed as
  ||||||36.300 where I used | to represent a blank.
  Similarly -1000. would be printed as |||-1000.000.
  These two would line up nicely if printed via


  printf("%12.3f\n%12.3f\n\n", 36.3, -1000.);






  


A Relative of printf(): sprintf()


The function


  int sprintf(char *string, char *format, ...);



is very similar to printf().
  The only difference is that, instead of sending the output to
  stout (normally the screen), sprintf() assigns it
  to the first argument specified.


  char outString[50];
  int d = 14;
  sprintf(outString, "The value of d is %d\n", d);



For example, the code snippet on the right results in the first 23
  characters (assuming I counted correctly) of outString
  containing The value of d is 14 \n\0 while the remaining 27
  characters of outString continue to be uninitialized.


Since the system cannot in general check that the first argument is
  big enough, care is needed by the programmer, for example checking
  that the returned value is no bigger than the size of the first
  argument.
  That is, sprintf() is scary.
  A good defense is to use instead snprintf(), which
  like strncpy(), guarantees than no more than n
  bytes will be assigned (n is an additional parameter
  to strncpy).



7.3 Variable-length Argument Lists


As we mentioned, printf() takes a variable number of
  arguments.
  But remember that printf() is not special, it is just a
  library function, not an object defined by the language or known to
  the compiler.
  That is, anyone can write a C program with declaration


  int myfunction(int x, float y, char *z, ...)



and it will have three named arguments and zero or more unnamed
  arguments.


There is some magic needed to get the unnamed arguments.
  However, the magic is needed only by the author of the
  function; not by a user of the
  function.



7.4 Formatted Input—scanf


Related to the Java Scanner class is the C function
  scanf().


The function scanf() is to printf()
  as getchar() is to putchar().
  As with printf(), scanf() accepts one required
  argument (a format string) and a variable number of additional
  arguments.
  Since this is an input function, the additional arguments give the
  variables into which input data is to be placed.


Consider the code fragment shown on the top frame to the right and
  assume that the user enters on the console the lines shown on the
  bottom frame.


  int n;
  double x;
  char str[50];
  scanf("%d  %lf  %s %20s", &n, &x, str);

  22 37.5
  no-blanks-here





A Relative of scanf(): sscanf()


The function


  int sscanf(char *string, char *fmt, ...);



is very similar to scanf().
The only difference is that, instead of getting the input
from stdin (normally the keyboard), sscanf() gets it
from the first argument specified.



7.5 File Access


So far all our input has been from stdin and all our
  output has been to stdout (or from/to a string for
  scanf()/sprintf).


What if we want to read and write a file?

  As I mentioned in class you can use the redirection operators of
  the command interpreter (the shell), namely < and
  >, to have stdin and/or stdout refer
  to a file.


But what if you want input from 2 or more files?



Opening and Closing Files; File Pointers


Before we can specify files in our C programs, we need to learn a
  (very) little about the file pointer.


Before a file can be read or written, it must be opened.
  The library function fopen() is given two arguments, the
  name of the file and the mode; it returns a file pointer.


Consider the code snippet on the right.
  The type FILE is defined in <stdio.h>.
  We need not worry about how it is defined.


  FILE *fp1, *fp2, *fp3, *fp4;
  FILE *fopen(char *name, char *mode);
  fp1 = fopen("cat.c", "r");
  fp2 = fopen("../x", "a");
  fp3 = fopen("/tmp/z", "w");
  fp4 = fopen("/tmp/q", "r+");



    
  
  1. The file cat.c in the current directory is opened for
    reading and some information about this file is recorded
    in *fp1.
    2. 
  
  2. The file x in the parent directory is opened for
    appending; x is created if it doesn't exist.
    3. 
  
  3. The file z in /tmp is opened for writing.
    Previous contents of z are lost.
    4. 
  
  4. The file q in /tmp is opened for reading and/or
    writing.
    (When mixing reads and writes, care is needed.)
    5. 



After the file is opened, the file name is no longer used;
  subsequent commands (reading, writing, closing) use the file
  pointer.


The function fclose(FILE *fp) breaks the connection
  established by fopen().




  getc()/putc(): The File Versions of getchar()/putchar()



Just as getchar()/putchar() are the basic
  one-character-at-a-time functions for reading and writing
  stdin/stdout, getc()/putc() perform the analogous
  operations for files (really for file pointers).
  These new functions naturally require an extra argument, a pointer
  to the file to read from or write to.


Since stdin/stdout are actually file pointers (they are
  constants not variables) we have the definitions


  #define getchar()    getc(stdin)
  #define putchar(c)   putc((c), stdout)



I think this will be clearer when we do an example, which is our
  next task.



An Example cat.c


  #include <stdio.h>
  main (int argc, char *argv[argc]) {
    FILE *fp;
    void filecopy(FILE *, FILE *);
    if (argc == 1) // NO files specified
      filecopy(stdin, stdout);
    else
      while(--argc > 0)  // argc-1 files
        if((fp=fopen(*++argv, "r")) == NULL) {
          printf ("cat: can't open %s\n", *argv);
          return 1;
        } else {
          filecopy(fp, stdout);
          fclose(fp);
        }
    return 0;
  }

  void filecopy (FILE *ifp, FILE *ofp) {
    int c;
    while ((c = getc(ifp)) != EOF)
      putc(c, ofp);
  }



The name cat is short for catenate, which is short for
  concatenate :-).


If cat is given no command line arguments (i.e., if
  argc=1), then it just copies stdin to
  stdout.
  This is not useless: for one thing remember < and
  >.


If there are command line arguments, they must all be the names of
  existing files.
  In this case, cat concatenates the files and writes the
  result to stdout.
  The method used is simply to copy each file to stdout one
  after the other.


The copyfile() function uses the standard
  getc()/putc() loop to copy the file specified by its first
  argument ifp (input file pointer) to the file specified by
  its second argument.
  In this application, the second argument is always
  stdout so copyfile() could have been simplified to
  take only one argument and to use putchar().


Note the check that the call to fopen() succeeded; a very
  good idea.


Note also that cat uses very little memory, even if
  concatenating 100GB files.
  It would be an unimaginably awful design for cat to read
  all the files into some ENORMOUS character array
  and then write the result to stdout.




  7.6: Error Handling—Stderr and Exit
  (and Ferror())




Stderr


A problem with cat is that error messages are written to
  the same place as the normal output.
  If stdout is the screen, the situation would not be too bad
  since the error message would occur at the end.
  But if stdout were redirected to a file via >,
  we might not notice the message.


Since this situation is common there are actually three standard
  file pointers defined: In addition to stdin and
  stdout, the system defines stderr.

  Although the name suggests that it is for errors and that is indeed
  its primary application, stderr is really just another file
  pointer, which (like stdout) defaults to the screen).

Even if stdout is redirected by the standard >
  redirection operator, stderr will still appear on the
  screen.


There is also syntax to redirect stderr, which can be used
  if desired.



Exit()


As mentioned previously a command should return zero if successful
  and non-zero if not.
  This is quite easy to do if the error is detected in the
  main() routine itself.


What should we do if main() has called joe(),
  which has called f(), which has called g(), and
  g() detects an error (say fopen() returned
  NULL)?


It is easy to print an error message (sent to stderr, now
  that we know about file pointers).
  But it is a pain to communicate this failure all the way back
  to main() so that main() can return a
  non-zero status.


Exit() to the rescue.
  If the library routine exit(n); is called, the effect is the
  same as if the main() function
  executed return n.
  So executing exit(0) terminates the command normally and
  executing exit(n) with n>0 terminates the
  command and gives a status value indicating an error.



Ferror()


The library function


  int ferror(FILE *fp);



returns non-zero if an error occurred on the stream fp.
  For example, if you opened a file for writing and sometime during
  execution the file system became full and a write was unsuccessful,
  the corresponding call to ferror() would return
  non-zero.




  7.7 Line Input and Output (fgets() and fputs())



The standard library routine


  char *fgets(char *line, int maxchars, FILE *fp)



reads characters from the file fp and stores them plus a
  trailing '\0' in the string line.
  Reading stops when a newline is encountered (it is read and stored)
  or when maxchars-1 characters have been read (hence,
  counting the trailing '\0', at most maxchars will be
  stored).


The value returned by fgets is line; on end of
  file or error, NULL is returned instead.


The standard library routine


  int fputs(char *line, FILE *fp)



writes the string line to the file fp.
  The trailing '\0' is not written and line need not contain
  a newline.
  The return value is zero unless an error occurs in which case EOF
  is returned.





Start Lecture #12
 


Remark: Midterm is 25 October.



7.8 Miscellaneous Functions


A laundry list.
  I typed them all in to act as convenient reference.
  Let me know if you find any errors.



The integer type size_t


This subsection represents a technical point; for this class you
  can replace size_t by int.


Consider the return type of strlen(), which the length of
  the string parameter.
  It is surely some kind of integral type but should it be
  short int, int, long int or one of
  the unsigned flavors of those three?


Since lengths cannot be negative, the unsigned versions
  are better since the maximum possible value is twice as large.
  (On the machines we are using int is at least 32-bits long
  so even the signed version permits values exceeding two billion,
  which is good enough for us).


The two main contenders for the type of the return value from
  strlen() are unsigned int and
  unsigned long int.
  Note that long int can be, and usually is, abbreviated
  as long.


If you make the type too small, there are strings whose length you
  cannot represent.
  If you make the type bigger than ever needed, some space is wasted
  and, in some cases, the code runs slower.


Hence the introduction of size_t, which is defined in
  stdlib.h.

  Each system specifies whether size_t is
  unsigned int or unsigned long (or something
  else).


For the same reason that the system-dependent type size_t is
  used for the return value of strlen, size_t is
  also used as the return type of the sizeof operator and is
  used several places below.



7.8.1 String Operations


These are from string.h, which must be #include'd.
  The versions with n added to the name limit the operation to
  n characters.
  In the following table n is of type size_t and
  c is an int containing a character;
  s and t are strings (i.e., character pointers,
  char *); and cs and ct are
  constant strings (const char *).


In addition to the naming distinction s vs cs, I
  further indicated which inputs may be modified by writing the string
  name in red.




  
CallMeaning

  

    strcat(s,ct)
    Concatenate ct on to the end of c
      (changing s) and return s.
  

  

    strncat(s,n,ct)
    The same but concatenates no more than n characters.
  

  

    strcmp(cs,ct)
    Compare s and t lexicographically.
      Returns a negative, zero, or  positive int if
      s is respectively <, =, or
      > t
  

  

    strncmp(cs,ct,n)
    The same but compares no more than n characters.
  

  

    strcpy(s,ct)
    Copy ct to s and return s.
  

  

    strncpy(s,ct,n)
    Similar but copies no more than n characters and
      pads with '\0' if ct has fewer than n
      characters.
      The result might NOT be '\0'
      terminated.
  

  

    strlen(cs)
    Returns the length of cs (not including the
      terminating '\0') as a size_t value.
  

  

    strchr(cs,c)
    Returns a pointer to the first
      c in s or NULL if c is not
      in cs.
  

  

    strrchr(cs,c)
    Returns a pointer to the last
      c in cs or NULL if c is not
      in cs.
  





7.8.2 Character Testing and Conversion


These are from ctype.h, which must be
  #include'd.
  All these functions take an integer argument (representing a
  character or the value EOF) and return an integer.




  

    Call
    Meaning
  

  

    isalpha(c)
    Returns true (non-zero) if (and only if)
      c is alphabetic.
      In our locale this means a letter.
  

  

    isupper(c)
    Returns true if c is upper case.
  

  

    islower(c)
    Returns true if c is lower case.
  

  

    isdigit(c)
    Returns true if c is a digit.
  

  

    isalnum(c)
    Returns true if isalpha(c)
      or isdigit(c).
  

  

    toupper(c)
    Returns c converted to upper case if c is a
      letter; otherwise returns c.
  

  

    tolower(c)
    Returns c converted to lower case if c is a
      letter; otherwise returns c.
  





7.8.3 Ungetc


int ungetc(int c, FILE *fp) pushes back to the
  input stream the character c.
  It returns c or EOF if an error was
  encountered.


Only one character can be pushed back, i.e., it is not safe to call
  ungetc() twice without an call in between that consumes the
  first pushed back character.


This function is from stdio.h, which must be
  #include'd.





7.8.4 Command Execution


  #include <stdio.h>
  #include <stdlib.h>
  int main (int argc, char *argv[argc]) {
    int status;
    printf("Hello.\n");
    status = system("dir; date");
    printf("Goodbye: status %d\n", status);
    return 0;
  }



The function system(char *s) runs the command contained in
  the string s and returns an integer status.


The contents of s and the value of the status is system
  dependent.


On my system, the program on the right when run in a directory
  containing only two files x and y produced the
  following output.


Hello.
x  y
Sun Mar  7 16:05:03 EST 2010
Goodbye: status 0



This function is in stdlib.h, which must be
  #include'd.





7.8.5 Storage Management



Malloc()


We have already seen


  void *malloc(size_t n)



which returns pointer to n bytes of uninitialized storage.
  If the request cannot be satisfied, malloc() returns
  NULL.



Calloc()


The related function
  
    void *calloc(size_t n, size_t size)
  

  returns a pointer to a block of storage adequate to hold an array
  of n objects each of size size.
  The storage is initialized to all zeros.



Free()


The function


  void free (void *p)



is used to return storage obtained from malloc()
  or calloc().



Remarks


  for (p = head; p != NULL; p = p->next)
    free(p);

  for (p = head; p != NULL; p = q) {
    q = p-> next;
    free (p);
  }



    
  
  1. It is crucial that the pointer argument to free() was
    obtained by a call to malloc() or calloc()
    (or realloc(), which we shall not use).
    2. 
  
  2. Equally bad is to reference space after free'ing it.
    For example the code on the top right is buggy since
    p->next uses the p that has just been
    free'd.
    Instead the bottom loop should be used.
    3. 
  
  3. The two arguments to calloc() are not silly.
    You cannot simply multiply them to determine the amount of storage
    needed due to padding requirements.
    Indeed, the space needed is system dependent.
    4. 
  
  4. The pointers returned by malloc() and calloc
    are properly aligned, but must be cast to the appropriate
    type.
    5. 




7.8.6 Mathematical Functions


These functions are from math.h, which must be
  #include'd.
  In addition (at least on on my system and i5.nyu.edu) you must
  specify a linker option to have the math library linked.
  If your mathematical program consists of A.c and B.c and the
  executable is to be named prog1, you would write


  cc -o prog1 -l m A.c B.c



All the functions in this section have double's as
  arguments and as result type.
  The trigonometric functions express their arguments in radians and
  the inverse trigonometric functions express their results in
  radians.



  
Call
    Meaning

  
sin(x)
    sine

  
cos(x)
    cosine

  
atan(x)
    arctangent

  
exp(x)
    exponentialex

  
log(x)
    natural logarithm loge(x)

  
log10(x)
    common logarithm log10(x)

  
pow(x,y)
    xy

  
sqrt(x)
    square root, x≥0

  
fabs(x)
    absolute value





7.8.7 Random Number Generation


Random number generation (actually pseudo-random number generation)
  is a complex subject.
  The function rand() given in the book is an early and not
  wonderful generator; it dates from when integers were 16 bits.
  I recommend instead (at least on linux and i5.nyu.edu)


  long int random(void)
  void srandom(unsigned int seed)



The random() function returns an integer between 0 and
  RAND_MAX.
  You can get different pseudo-random sequences by starting with a
  call to srandom() using a different seed.
  Both functions are in stdlib.h, which must be
  #include'd.


On my linux system RAND_MAX (also in stdlib.h) is defined
  as 231-1, which is also INT_MAX, the largest
  value of an int.
  It looks like i5.nyu.edu doesn't define RAND_MAX, but does use the
  same psuedo-random number generator.



Remark: Let's write some programs/functions.


    
  
  1. Write a program (most-vowels) that reads lines and prints the
    one with the most vowels together with a count of how many
    vowels it contains.
    2. 
  
  2. Write a function (repstr) that accepts a count and a string
    and returns a newly allocated string containing the
    concatenation of the original string the specified number of
    times.
    3. 
  
  3. Write a function (mergeint) that merges two sorted arrays of
    integers A and B into C.
    The signature is
    
    mergeInt(int n, int m, int A[n], int B[m], int C[n+m]);
  
    4. 
  
  4. Think about how to do this for arrays of (varying length)
    strings.
    5. 
  
  5. The 5 -> 16 -> 8 -> 4 -> 2 -> 1 game.
    
      
      
    1. Write a function f giving the next number:
        f(5)=16; f(1)=4.
        What should the signature be?
      2. 
      
    2. Write a program that repeatedly reads an integer and
        prints out the generated sequence upto 1.
      3. 
      
    3. Modify the previous program to instead accept three
        arguments, which act like the three parts of a for.
        The program plays the game for all integers starting at the
        first argument, incrementing by the third, up to the
        second.
      4. 
      
    4. Modify the previous to accept an optional -b or
        --brief argument.
        If present, don't print the sequence, instead just print its
        length.
      5. 
      
    5. Modify the previous to accept an optional -s or
        --summary argument that prints only the number
        having the longest sequence and the sequence (OK to
        re-calculate).
        If the -b is also present, just print the number
        and the length of the sequence (not OK to recalculate).
      6. 
    
    
  
    6. 




Remark: End of material to be covered on the
  midterm exam.





Review of solutions to practice midterm.










Chapter O'H-2 Representing and Manipulating Information



O'H-2.1 Information Storage



Computers are Inherently Binary Machines


Modern electronics can quickly distinguish 2 states of an
  electric signal: low voltage and high voltage.
  Low has always been around 0 volts; high was 5 volts for a long
  while now is below 3.5 volts.


Since this is not a EE course we will abstract the situation and
  say that a signal is in one of two states, low (a.k.a. 0) and high
  (a.k.a. 1).



Binary Notation



  

    decimal
base 10		
       binary
base 2		
    
   base 4		
     octal
   base 8		
    hex   
  base 16		
  

  
00000

  
11111

  
210222

  
311333

  
41001044

  
51011155

  
61101266

  
71111377

  
8100020108

  
9100121119

  
1010102212A

  
1110112313B

  
1211003014C

  
1311013115D

  
1411103216E

  
1511113317F

  
16100001002010




Since for us a signal can be in one of two states, it is convenient
  to use binary (a.k.a. base 2) notation.
  That way if we have three signals with the first and third high and
  the middle one low, we can represent the situation using 3 binary
  digits, specifically 101.


Recall that to calculate the numeric value of a ordinary (base 10,
  i.e., decimal) number the right most digit is multiplied by
  100=1 the next digit to the left by 101=10,
  the next digit by 102=100, etc.


For example 6205 = 6*103 + 2*102 +
  0*101 + 5*100 = 6*1000 + 2*100 + 0*10 +5*1.


Similarly binary numbers work the same way so, for example the
  binary number 11001 has value (written in decimal)

  1*24 + 1*23 + 0*22 +
  0*21 + 1*22 = 1*16 + 1*8 + 0*4 + 0*2 +1*1
  = 16+8+1 = 25.


We normally use decimal (i.e., base 10) notation where each digit
  is conceptually multiplied by a power of 10.
  We all know about the ten's place, hundred's place,
  etc.
  The feature that the same digit is valued 1/10 as much if it is one
  place further to the right continues to hold to the right of the
  decimal point.


Computer hardware uses binary (i.e., base 2) arithmetic so to
  understand hardware features we could write our numbers in binary.
  The only problem with this is that binary numbers are long.
  For example, the number of US senators would be written 1100100 and
  the number of miles to the sun would need 25 bits (binary
  digits).


This suggests that decimal notation is more convenient.
  The problem with relying on decimal notation is that we need binary
  notation to express multiple electrical signals and it is difficult
  to convert between decimal and binary because ten is not an integral
  power of 2.


The table on the right (for now only look at the first two columns)
  shows how we write the numbers from 0 to 16 in both base 10 and
  base 2.



O'H-2.1.1 Hexadecimal Notation



A Base 4 Compromise?


Base 10 is familiar to us, which is certainly an enormous
  advantage, but it is hard to convert base 10 numbers to/from base 2
  and we need base 2 to express hardware circuits.
  Base 2 corresponds well to the hardware but is verbose for large
  numbers.


Let's try a compromise, base 4.


To convert between base four and base two is easy since the four
  base 4 digits (I hate that expression, for me digit means
  base 10) correspond exactly to the four possible pairs of bits.


  base 4   bits
    0       00
    1       01
    2       10
    3       11



Look again at the table above but now concentrate on columns two
  and three.


We see that it is easy to convert back and forth between base 2 and
  base 4.
  But base 4 numbers are still a little long for comfort: a number
  needing n bits would use ⌈n/2⌉ base four digits.


A base 8 number would need ⌈n/3⌉ digits for an n-bit
  base 2 number because 8=23 and a base 16 number would
  need ⌈n/4⌉.
  Base 8 (called octal) would be good, and was used when I learned
  about computers; base 16 is used now.


Question: Why the switch from 8 to 16?

  Answer: Words in a 1960s computer had 36 bits and
  36 is divisible by 3.
  Words in modern computers have 32 bits and 32 is divisible by 4.
  (Recently the word size has increased to 64 bits, but 64 is also
  divisible by 4.)


Question: Why 36-bit words?

    Answer: six 6-bit characters per word.


Base 16 is called hexadecimal.


We need 16 symbols for the 16 possible digits; the first 10 are
  obvious 0,1,...,9.
  We need 6 more to represent ten, eleven, ..., fifteen.


We use A, B, C, D, E, F to represent the extra 6 digits
  and when we write a hexadecimal number we precede it with 0x.



The Big Advantage of Base 16 Over Base 10


You convert base 16 to/from binary one hexadecimal digit (4 bits)
  at a time.
  For example


  1011000100101111 = 1011 0001 0010 1111 = B 1 2 F = 0xB12F  



Look again at the table above right and notice that groups of four
  bits do match one hex digit.



The Downside


You need to learn that A3 + 3B = DE and
  FF + BB = 1BA.



O'H-2.1.2 Data Sizes


Although fundamentally hardware is based on bits, we will normally
  think of it as byte oriented.
  A byte (or octet) consists of 8 bits or two hex characters.
  As we learned, the primitive types in C (char, int, double, etc) are
  a multiple of bytes in size.
  In fact, the multiple is a power of 2 so variables (and hence data
  items) are 1, 2, 4, 8, or 16-bytes long.



An Example


  #include <string.h>
  #include <stdio.h>
  void showBytes (unsigned char *start, int len) {
    int i;
    for (i=0; i<len; i++)
	printf("%p %5x%5x\n", start+i, *(start+i), start[i]);
   }
  int main(int argc, char *argv[]) {
    showBytes(argv[1], strlen(argv[1]));
  }



The simple program on the right prints its first argument in
  hex.
  Actually it does a little more, it prints the address of each
  character of the first argument and then the hex value of the
  character twice once in pointer style and once in array style.


A sample run follows.


  sh-4.4$ ./a.out iB4e
  0x7ffe3f4af516    69   69
  0x7ffe3f4af517    42   42
  0x7ffe3f4af518    34   34
  0x7ffe3f4af519    65   65
  sh-4.4$



Note that capital letters come before lower case and digits come
  before either.
  Those are properties of ASCII and (I believe) unicode.



O-H'2.1.3 Addressing and Byte Ordering


We think of memory as composed of 8-bit bytes and the bytes in
  memory are numbered.
  So if you could find a 1KB (kilobyte) memory you could address the
  individual bytes as byte 0, byte 1, ... byte 1023.
  If you numbered them in hexadecimal it would be byte 0 ... byte
  3FF.


As we learned a C-language char takes one byte of storage
  so its address would be one number.


A 32-bit integer requires 4 bytes.
  I guess one could imagine storing the 4 bytes spread out in memory,
  but that isn't done.
  Instead the integer is stored in 4 consecutive bytes, the
  lowest of the four byte addresses is the address of the integer.


Normally, integers are aligned i.e, the lowest address is
  a multiple of 4.
  On many systems a C-language double occupies 8 consecutive
  bytes the lowest numbered of which is a multiple of 8.



Start Lecture #13
 


Little Endian vs. Big Endian


Let's consider a 4-byte (i.e., 32-bit) integer N that is
  stored in the four bytes having address 0x100-0x103.
  The address of N is therefore 0x100, which is a multiple of
  4 and hence N is considered aligned.


Let's say the value of N in binary is

  0010|1111|1010|0101|0000|1110|0001|1010
 which in hex
  (short for hexadecimal) is 0x2FA50E1A.
  So the four bytes numbered 100, 101, 102, and 103 will contain 2F A5
  0E 1A.
  However, a question still remains: Which byte contains which pair of
  hex digits?


Unfortunately two different schemes are used.
  In little endian order the least significant byte is put in
  the lowest address; whereas in big endian order the most
  significant byte is put in the lowest address.


Consider storing in address 0x1120 our 32-bit (aligned) integer,
  which contains the value 0x2FA50E1A.
  A little endian machine would store it this way.


  byte address  0x1120 0x1121 0x1122 0x1123
      contents   0x1A   0x0E   0xA5   0x2F



In contrast a big endian machine would store it this way.


  byte address  0x1120 0x1121 0x1122 0x1123
      contents   0x2F   0xA5   0x0E   0x1A 



  int main(int argc, char *argv[]) {
    int a = 54321;
    showBytes((char *)&a, sizeof(int));
  }



An Example Using showBytes()


On the right is an example using
  the showBytes() routine defined just above that gives (in
  hex) the four bytes in the integer 54321.
  The output produced is


  0x7ffd0a0ed8f4    31   31
  0x7ffd0a0ed8f5    d4   d4
  0x7ffd0a0ed8f6     0    0
  0x7ffd0a0ed8f7     0    0



So the four bytes are 0x31, 0xD4, 0x0, and 0x0.
  If the number in hex is 31 D4 00 00 it would
  be much bigger than 54321 decimal.
  Instead the number is 00 00 D4 31 hex which does equal 54321
  decimal.


So my laptop is little endian (as are all x86 processors).



O'H-2.1.4 Representing Strings


As we know a string is a null terminated array of chars; each char
  occupies one byte.
  Given the string "tom", the char 't' will occupy one byte, 'o' will
  occupy the next (higher) byte, 'm' will occupy the next byte and
  '\0' the next (last) byte.


There is no issue of byte ordering (endian) since each character
  is stored in one byte and consecutive characters are stored in
  consecutive bytes.



O-H'2.1.5 Representing Code



O'H-2.1.6 Introduction to Boolean Algebra


Now we know how to represent integers and characters in terms of
  bits and how to write each using hexadecimal notation.
  But what about operations like add, subtract, multiply, and
  divide.


We will approach this slowly and start with operations on
  individual bits, operations like AND and OR.


To define addition for integers you need to give a procedure or
  adding 2 numbers, you can't simply list all the possible addition
  problems since there are an infinite number of integers.
  However there are only 2 possible bits and hence for a binary (i.e.,
  two operand) operation on bits there are only four possible examples
  and we simply list all four possible questions and the corresponding
  answers.
  This list is normally called a truth table.


The following diagram does this for six basic operations.
  Just below the truth tables are the symbols used for each operation
  when drawing a diagram of an electronic circuit
  (a circuit diagram).



  NOT
  
AX

  
01

  
10





  NAND
  
ABX

  
001

  
011

  
101

  
110





  NOR
  
ABX

  
001

  
010

  
100

  
110





  AND
  
ABX

  
000

  
010

  
100

  
111





  OR
  
ABX

  
000

  
011

  
101

  
111





  XOR
  
ABX

  
000

  
011

  
101

  
110



gates



O'H-2.1.7 Bit-Level Operations in C



  
~ANOT A

  
A&BA AND B

  
A|BA OR B

  
A^BA XOR B




C directly supports NOT, AND, OR, and XOR as shown on the table to
  the left and mentioned previously in section 2.9.
  Note that these operations are bit-wise.
  That is, bit zero of the result depends only on bit zero of the
  operand(s), bit one of the result depends only on bit one of the
  operands, etc.


C does not have explicit support for NAND or for NOR.


It turns out that if you have enough chips that compute only NAND,
  you are able to wire them together to support any
  Boolean function.
  We call NAND universal for this reason.
  This is also true of NOR but it is not true of any other two input
  primitive.



O'H'2.1.8 Logical Operations in C


Done previously.
  Be careful not to confuse bit-level AND (&) with logical AND
  (&&).
  The latter treat any nonzero value as TRUE, and zero as FALSE.
  Similarly for bit-level OR (|) and logical OR (||).


Note, for example that !0x00 = 0x01; whereas ~0x00=0x11.


Also remember that C guarantees short-circuit evaluation of
  && and ||.
  In particular ptr&&*ptr cannot generate a null
  pointer exception since, when ptr is null, *ptr is
  not evaluated.



Boolean in C


This was introduced in C99 so is not in the text.
  You may use it, but it is not required for the course.



O'H-2.1.9 Shift Operations in C


In C, the expression x<<b
  shifts x b bits to the left.
  The b most left bits of x are lost and
  the b right most bits of x become 0.


There is a corresponding right shift >> but there is a
  question on what to do with the sign bit.
  More on this later.



O'H-2.2 Integer Representations



O'H-2.2.1 Integral Data Types


Computer integers come in several sizes and two flavors.
  A char is a 1-byte integer; a short is a 2-byte
  integer; and an int is a 4-byte integer.
  The size of a long is system dependent.
  It is 4 bytes (32 bits) on a 32-bit system and 8 bytes (64 bits) on
  a 64-bit system.


What about the two flavors?
  That comes next.



O'H-2.2.2 Unsigned Encodings


Let's talk only about short; the others are essentially
  the same only bigger.
  So we have 16 bits in each integer representing from right to left
  20 to 215.
  If all these 16 bits are 1s, the value is 216-1 = 65,535.
  
Question: Why?

  Answer: Draw it on the board.


In a sense these encodings are the most natural.
  They are used and they well supported in the C language.
  Naturally the sum of the two very big 16-bit unsigned numbers would
  need 17 bits; this is called overflow.
  Nonetheless, the situation is good for unsigned addition:



But there is a problem.
  Unsigned encodings have no negative numbers.



O'H-2.2.3 Two's-Complement Encoding


To include negative numbers there must be a way to indicate the
  sign of the number.
  Also since some numbers will be negative and we have the same number
  of numbers (because we sill have 16 bits), there will be
  fewer positive numbers for short than we had for
  unsigned short.


Before specifying how to represent negative numbers, let's do the
  easy case of non-negative numbers (i.e., positive and zero).
  For non-negative numbers set the leftmost bit to zero and use the
  remaining bits as above.
  Since the left bit (the high order bit or HOB) is for the sign we
  have one fewer for the number itself so the largest short is zero
  with 15 ones, which is 215-1 = 32,767.


We could do the analogous technique for negative
  numbers: set the HOB to 1 and use the remaining 15 bits for the
  magnitude (the absolute value in mathematics).
  This technique is called the sign-magnitude representation
  and was used, but is not common now.
  One annoyance is that you have two representations of zero
  0000000000000000 and 1000000000000000.
  We will not use this encoding.


Instead of just flipping the leftmost (or sign) bit as above we
  form the so-called 2s-complement.
  For simplicity I will do 4-bit two's complement and just talk about
  the 16-bit analogue (and 32- and 64-bit analogues), which is
  essentially the same.



4-bit Twos's Complement Numbers


With 4 bits, there are 16 possible numbers.
  Since twos complement notation has one representation for each
  number, there are 15 nonzero values.
  Since there are an odd number of nonzero values, there
  cannot be the same number of positive and negative
  values.
  In fact 4-bit two's complement notation has 8 negative values
  (-8..-1), and 7 positive values (1..7).
  (In sign magnitude notation there are the same number of positive
  and negative values, but there are two representations for zero,
  which is inconvenient.)


The high order bit (hob) on the left is the sign bit.
  The sign bit is zero for positive numbers and for the number zero;
  the sign bit is one for negative numbers.


Zero is written simply 0000.


1-7 are written 0001, 0010, 0011, 0100, 0101, 0110, 0111.
  That is, you set the sign bit to zero and write 1-7 using the
  remaining three lob's (low order bits).
  This last statement is also true for zero.


-1, -2, ..., -7 are written by taking the two's complement
  of the corresponding positive number.
  The two's complement is computed in two steps.


    
  
  1. Take the (ordinary) complement, i.e. change ones to zeros and
    zeros to ones.
    This is sometimes called the one's complement.
    
    For example, the (4-bit) one's complement of 3 is 1100.
    2. 
  
  2. Add 1.
    
    For example, the (4-bit) two's complement of 3 is 1101.
    3. 



If you take the two's complement of -1, -2, ..., -7, you get back
  the corresponding positive number.
  Try it.


If you take the two's complement of zero you get zero.
  Try it.


What about the 8th negative number?

  -8 is written 1000.

  But if you take its (4-bit) two's complement, you
  must get the wrong number because the correct
  number (+8) cannot be expressed in 4-bit two's complement
  notation.



Two's Complement Addition and Subtraction


Amazingly easy (if you ignore overflows).




Comments on Two's Complement


You could reasonably ask what does this funny notation have to do
  with negative numbers.
  Let me make a few comments.


Question: What does -1 mean mathematically?

  Answer: It is the unique number that, when added
  to 1, gives zero.


Our representation of -1 does do this (using regular binary
  addition and discarding the final carry-out) so we do have -1
  correct.


Question: What does negative n
  mean, for n>0?

  Answer: It is the unique number that, when
  added to n, gives zero.


The 1s complement of n when added to n gives
  all 1s, which is -1.

  Thus the 2s complement, which is one larger, will give zero, as
  desired.



Size Ranges for 16-bit Numbers




  
Width (bits)

  
8163264

  
Unsig
Max		25565,535
    4,294,967,29518,446,744,073,709,551,615
  
Signed
Max		12732,767
    2,147,483,6479,223,372,036,854,775,807
  

  
Signed
Min		-128-32,768
    2,147,483,647-9,223,372,036,854,775,808
  

  






  

    DecimalHexBinary
  

  

    Unsigned
Max		65535FF FF
    11111111 11111111
  

  

    Unsigned
Min		000 0000000000 00000000
  

  

    Signed
Max		327677F FF
    01111111 11111111
  

  

    Signed
Min		-3276880 00
    10000000 00000000
  

  

    -1-1FF FF11111111 11111111
  




The table on the near right shows the extreme values for both
  unsigned and signed 16-bit integers.
  It the signed case we also show the representation of -1
  (there is no unsigned -1).


Note that the signed values all use the twos-complement
  representation.
  In fact I doubt we will use sign/magnitude (or ones'-complement) for
  integers any further.


The table on the far right shows the max and min values for
  various sizes of integers (1, 2, 4, and 8 bytes).



Start Lecture #14
 


O'H-2.2.4 Conversions between Signed and Unsigned


General rule: Be Careful!.



O'H-2.2.5 Signed versus Unsigned in C


  #include <stdio.h>
  int main(int argc, char *argv[]) {
    int i1=-1, i2=-2;
    unsigned int u1, u2=2;
    u1 = i1; // implicit (unsigned)
    printf("u1=%u\n", u1);
    printf( "%s\n", (i2>u2) ? "yes" : "no");
    return 0;
  }



The code in the right illustrates why we must be careful when
  mixing unsigned and signed values.
  The fundamental rule that is applied in C when doing such
  conversions (actually called casts) is that the bit pattern
  remains the same even though this sometimes means
  that the value changes.


When the code on the right is executed, the output is


  u1=4294967295
  yes



When the code executes u1=i1, the bits in i1 are
  all ones and this bit pattern remains the same when the value is
  cast to unsigned and placed in u1.
  So u1 becomes all 1s which is a huge number as we see in
  the output.


When we compare i2>u2, either the -2 in i2
  must be converted to unsigned or the 2 in u2 must be
  converted to signed.
  The rule in C is that the conversion goes to unsigned so the -2 bit
  pattern in i2 is reinterpreted as an unsigned value.
  With that interpretation i2 is indeed much bigger that the
  2 in u2.



O'H-2.2.6 Expanding the Bit Representation of a Number


We have just seen signed/unsigned conversions.
  How about short to int or int to long?

  How about unsigned int to unsigned long?
  I.e., converting when the sizes are different but
  the signedness is the same.




Summary of Conversion Ordering


In summary C converts in the following order.
  That is, types on the left are converted to types on the right.



  
          int →
    unsigned int →
    long →
    unsigned long →
    float →
    double →
    long double.
  




O'H-2.2.7 Truncating Numbers


What if you want to put an int into a short or
  put a long into an int?


Bits are simply dropped from the left, which can alter both the
  value and the sign.


Advice: Don't do it.



O'H-2.2.8 Advice on Signed versus Unsigned


Be careful!!



O'H-2.3 Integer Arithmetic



O'H-2.3.1 Unsigned Addition


The only problem is overflow, i.e., where the addends use all the
  bits and hence the sum requires one more.


When there is no overflow, addition is conceptually done right to
  left one bit at a time with carries just like we do for base 10.


In reality very clever tricks are used to enable
  multiple bits to be added at once.
  You could google ripple carry and carry lookahead or
  my lecture notes for computer architecture.



O'H-2.3.2 Two's-Complement Addition


The news is very good—you just add as though it were
  unsigned addition and throw out any carry-out from the HOB (high
  order bit).


Only overflow is a problem (as it was for unsigned).



O-H-2.3.3 Two's Complement Negation


Recall that with two's complement there is one more negative number
  than positive number.
  In particular, the most-negative number has no positive counterpart.
  Specifically, for n-bit twos complement numbers, the range of values
  is


  most neg = -2n-1 ... 2n-1-1 = most pos



For every value except the most neg, the negation is obtain by
  simply taking the two's complement, independent of whether the
  original number was positive, negative, or zero.



O;H-2.3.4 Unsigned Multiplication


Multiply the two n-bit numbers, which gives 2n-bits and discard the
  n HOBs.
  Again, the only problem is overflow.



O'H-2.3.5 Two's Complement Multiplication


A surprise occurs.
  You just mulitply, the twos complement numbers and truncate the
  HOBs and ... it works—except for overflow.



Start Lecture #15
 


Midterm Exam



Start Lecture #16
 


Remark: Reviewed midterm answers.



O'H-2.3.6 Multiplying by Constants


You can multiply x*2k by just forming x<<k.
  This is reasonably clear for x≥0, but works for 2s complement as
  well.


Note that compilers are clever and utilize identities like


  x * 24  =  x * (32-8)  =  x*32 - x*8  =  x<<5 - x<<3




O'H-2-3-7 Dividing by Powers of 2


Right shift by k does divide by 2k.
  Actually it gives the floor of the division.


If the value is unsigned, use logical right shift;  if it is
  signed use arithmetic right shift.



O'H-2.3.8 Final Thoughts on Integer Arithmetic



Unsigned


Addition and multiplication work unless there is an overflow.


Adding two n-bit unsigned numbers gives (up to) an (n+1)-bit
  result, which we fit into n bits by dropping the HOB.
  So you get an overflow if the HOB of the result is 1


Multiplying two n-bit unsigned numbers gives (up to) a 2n-bit
  result, which we fit into n bits by dropping the n HOBs.
  So you get an overflow if any of the n HOBs of the result are 1.



Two's Complement.


Same idea but detecting overflow is more complicated.
  For addition of n-bit numbers, which includes subtraction, the
  non-obvious rule is that an overflow occurs if the carry into the
  HOB (bit n-1) != the carry-out from that bit.



Start Lecture #17
 


O'H-2.4 Floating Point



2.4.1 Fractional Binary Numbers


Exactly analogous to decimal numbers with a decimal point.
  Just as 0.01 in decimal is one-hundredth, 0.01 in binary is
  one-quarter and 0x0.01 is one-twohundredfiftysixth.



Why Not Used


Fractional binary notation requires considerable space for numbers
  that are very large in magnitude or very near zero.


  5 * 2100 = 1010000000...0
             | 100 0s |
  -2-100 = -0.00000000001
             | 100 0s |



(The second example above uses sign-magnitude.


But this problem comes up in science all the time and the solution
  used is often called scientific notation.

  Avagadro's number ~ 6.02 * 1023

  Light year ~ 5.88 * 1012 miles


The coefficient is called the mantissa or significand.


In computing we use IEEE floating point, which is basically the
  same solution but with an exponent base of 2 not 10.
  As we shall see there are some technical differences.



2.4.2 IEEE Floating-Point Representation


Represent a floating number as


  (-1)s × M × 2E



Where



Naturally, s is stored in one bit.


For single precision (float in C) E is stored 8 bits and M is
  stored in 23.
  Thus, a float in C requires 1+8+23 = 32 bits.


For double precision (double in C) E is stored in 11 bits and M in
  52.
  Thus, a double in C requires 1+11+52 = 64 bits.


Now it gets a little complicated; the values stored are not simply
  E and M and there are 3 classes of values.



The Exponent as Stored


Lets just do single precision, double precision is the same idea
  just with more bits.
  The number of bits used for the exponent is 8



Although the exponent E itself can be positive, negative, or zero
  the value stored exp is unsigned.
  This is accomplished by biasing the E (i.e., adding a constant so
  the result is never negative).


With 8 bits of exponent, there are 256 possible unsigned values for
  exp, namely 0...255.
  We let E = exp-127 so the possible values for E are -127...128.


Stated the other way around, the value stored for the exponent is
  the true exponent +127.



The Significand as Stored


With scientific notation we write numbers as, for example.
  9.4534×1012.
  An analogous base 2 example would be
  1.1100111×210.


Note that in 9.4535 the four digits after the decimal point each
  distinguish between 10 possibilities whereas the digit before the
  decimal point only distinguishes between 9 possibilities, so is not
  fully used.


Note also that in 1.1100111 the 1 to the left distinguishes
  between one possibility, i.e. is useless.


IEEE floating point does not store the bit to the right of the
  binary point because is always 1 (actually see below for the other
  two classes of values).



An Example (Single Precision, 32 Bits)


  Let F        = 15213.010
               = 111011011011012
               = 1.11011011011012×213
  fract stored = 110110110110100000000002
  exp stored   = 13+127 = 140 = 100011002
  sign stored  = 0
  value stored = 0 10001100 11011011011010000000000




Denormalized (Subnormal) Encoding


Used when the stored exponent is all zeros, i.e., when the exponent
  is as negative as possible, i.e., when the number is very close to
  0.0.


The value of the significant and exponent in terms of the stored
  value is slightly different.


Note there are two zeros since ieee floating point is basically
  sign magnitude.



Special Values Encoding


Used when the stored exponent is all ones, i.e., when the exponent
  is a large as possible.


If the significand stored is all zeros, the value represents
  infinity (positive or negative), for example overflow when
  doing 1.0/0.0.


If the significand is not all zero, the value is called NaN for
  not-a-number.
  It is used in cases like sqrt(-1.0), infinity - infinity, infinity
  × 0.



Summary


IEEE floating point represents numbers as (-1)s ×
  M × 2 E.
  There are extra complications to store the most information in a
  fixed number of bits.



Start Lecture #18
 


Chapter 7 Linking


The linking material below does not follow the book.



7.A The Big Picture: What is the Problem?


            file main.c

  #include <stdio.h>
  int x = 10;
  void f(void);

  int main(int argc, char *argv[]) {
    printf("main says x is %d\n", x);
    f();
  }

            file f.c

  #include <stdio.h>
  extern int x;

  void f(void) {
    int y = 20;
    printf("f says x is %d\n", x);
    printf("f says y is %d\n", y);
  }



For a simple example of what the linker needs to do, consider the
  small example on the right consisting of two files main.c
  and f.c.


    
  
  1. When compiling main.c, the compiler does not know the
    contents of f.c.
    In particular it does not know how big the resulting compiled code
    for f() will be.
    Since it doesn't know how much room to leave for f(), it
    leaves no room and assumes that main() starts at the
    beginning of the compiled code.
    2. 
  
  2. Similarly, when compiling f.c the size
    of main.c is not known so the compiler assumes
    that f() is at the beginning of the compiled code.
    3. 
  
  3. At least one of these assumptions must be wrong!
    One of the functions will have to come after the other one.
    4. 
  
  4. Put another way the local addresses generated by the compiler
    when compiling each file are based on the starting address for
    that compilation.
    In each case this base address is assumed to be zero (or some
    other constant) which can't be right for both compilations.
    5. 
  
  5. The terminology used is that these address
    are relative to the base address for the given
    compilation.
    6. 
  
  6. The linker sees the (compiled version of) both files and
    decides which goes first, second, etc.
    7. 
  
  7. Assuming the module to be placed first starts at the beginning
    of memory, the absolute address for each local
    address in that module is equal to its relative address.
    8. 
  
  8. For the module to be placed second, the size of the first module
    must be added to each relative address to obtain the corresponding
    absolute address.
    9. 
  
  9. So one task for the linker is to
    relocate relative addresses into the
    corresponding absolute addresses.
    10. 
  
  10. The second problem to be solved is that when
    compiling main.c the compiler does not know where the
    function f() will be loaded and when
    compiling f.c the compiler does not know where x
    will be loaded.
    11. 
  
  11. In both cases the symbol in question
    is external to the module being loaded and the
    loader is required to
    resolve external addresses.
    12. 


relocate
resolve

The diagram on the far fight illustrates relocating relative
  addresses.
  Specifically it shows how to calculate the relocation constant as
  the sum of the lengths of the  preceding modules.
  Once the relocation constant C is known, each absolute address is
  calculated simply as the corresponding relative address + C.


The diagram on the near right illustrates resolving external
  references.
  In this case the reference is to f().
  Note that the Base of M4 is the same as its relocation constant,
  i.e., the sum of the lengths of the preceding modules.



7.A.1 Two Passes Help


Note from the diagram on the near right, that the linker
  encounters the required address jump f before it knows the
  necessary relocation constant.


The simplest solution (but not the fastest) is for the linker to
  make two passes over the modules.
  During pass 1 the relocation constants for each module are
  determined.
  During pass 2, the external address are resolved using the
  relocation constants determined during pass 2.



7.A.2 Why Not Have the Compiler Do All This?


It could and by some definitions of the compiler it
  does.


For the example at the beginning of this section, we could type
  simply


  cc main.c f.c;   ./a.out



and everything works.
  This is because cc includes running the linker.


More significantly, the linker could be built into the compiler if
  you wanted to always compile the entire program at once, which you
  don't.
  Remember that the entire program includes printf().



7.A.3 The Compilation Process

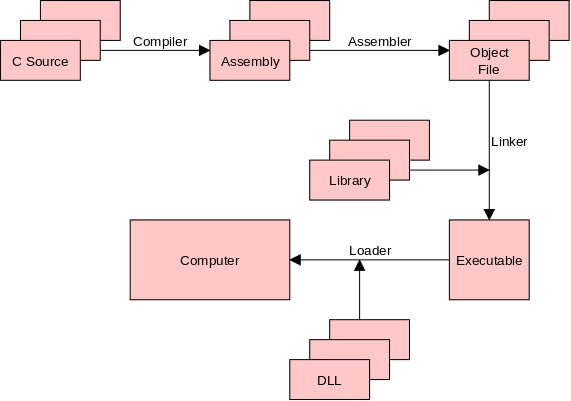
compilation

One could think of the assembler as part of the compiler in which
  case the diagram would lack the boxes and arrow labeled
  assembly/assembler.


Alternatively one could notice that some compilers have two stages:
  first C is compiled to an intermediate language, which in the second
  stage is converted to assembler.
  The diagram would then include an extra set of boxes for the first
  stage output and there would be two compiler arrows (stage1 and
  stage2).


In the original diagram as well as in these two alternatives the
  compiler only does one module at a time and the linker is needed to
  combine the results.



7.A.4 Some Rules


Recall that declarations give the type of an identifier; they tell
  the compiler how to interpret the identifier; they do not
  necessarily reserve space for the identifier.
  Declarations that reserve storage are called definitions.


      file f1.c

  int svar=5;
  int sfun1(int x) {
    code
  }



     file f2.c

  int wvar1;
  int wfun1(int z);
  int sfun2(void) {
    int igsym1=3;
  }



    
  
  1. External definitions are considered strong symbols
    by the linker
    2. 
  
  2. External declarations are considered weak symbols
    by the linker
    3. 
  
  3. Internal declarations or definitions are not considered at all
    by the linker.
    4. 



Looking at the code on the right, functions sfun1()
  and sfun2() and variable svar1 are each strong
  symbols.
  In contrast wsym1 and wfun1() are weak symbols.
  Finally, igsym1 is ignored (actually not seen) by the
  linker.


The linker obeys the following rules.


    
  
  1. There can be only one strong symbol with a given name.
    If more than one strong symbol has the same name, the linker
    reports a multiply defined symbol error.
    2. 
  
  2. If there are one of more weak symbols with the same name as a
    strong symbol, the linker resolves all references to the symbol
    name to the strong symbol.
    3. 
  
  3. If there are one or more weak symbols with the same name, but
    no strong symbol with that name, the linker picks one of the weak
    symbols and resolves all references to that one.
    4. 




7.A.5 A Few C Language Examples


  int x;                          Two strong symbols have the same name.
  f1() {}         f1() {}         Link time error.

  int x;          int x;          Both x's are the same.
  f1() {}         f2() {}         Either might be chosen as location for x.

  int x=7;        int x;          Both x's are the same.
  f1() {}         f2() {}         The first x will be chosen.

  int x=7;        double x;       Writes to x in f2() WILL overwrite y!
  int y=5;        f2() {}         Scary!
  f1() {}

  int x;          double x;       Writes to x in f2() MIGHT overwrite y!
  int y;          f2() {}         Even scarier than the previous!
  f1() {}




Static vs. Dynamic Linking


The figure in 7.A.3 contains two kinds of libraries:
  statically-linked libraries that are processed by the linker and
  dynamically linked libraries (DLLs) processed by the loader.
  How do they differ?



Static Linking


You know well that when your programs run, functions are executed
  that you did not write (e.g. printf()).
  Many common routines are placed in libraries that the linker
  searched by default.
  For example the cc (or gcc) command on crackle2 automatically
  searches libc.a, which contains compiled versions of many
  common C programs like strcpy.
  This one library contains hundreds of functions, but it is indexed
  so the linker only includes the ones you used.
  (It is called a .a file because it is an archive of many
  routines.)


These libraries are called static libraries and
  the linking just discuss is called static linking.
  After this static linking is performed, an executable file results,
  which just needs be loaded into memory and executed.


Conceptually, we are done: we have an executable file.


However, a large computing system might have thousands (or more)
  user programs stored on disk all containing strcpy() and
  the RAM on a large busy machine might have dozens of programs running
  each of which contains strcpy().


Perhaps more dramatic would be the space used by multiple copies
  of huge graphics libraries contained in many graphical programs.



Dynamic Linking, DLLs and Shared Libraries


To minimize the duplication just discussed many systems employ
  dynamic linking.
  Instead of (statically) linking in a copy of e.g., strcpy()
  only a stub routine is linked and when the program is loaded into
  RAM the stub is replaced by the real code.
  The savings occurs in two ways.




Chapter 6 Memory Hierarchy



6.1 Storage Technology


What do we want from an ideal memory?



We will emphasize the first two.



Unfortunate Laws of Hardware


    
  
  1. Big and Fast are essentially contradictory, they are traded-off
    against each other.
    2. 
  
  2. Big, Fast, and Cheap is basically hopeless.
    3. 




The Basic Trade-off Becomes the Basic Goal


We can get/buy/build either
  small and fast or
  big and slow.


Our goal is to mix the two and get a good approximation to the
  impossible big and fast.




6.1.1 Random Access Memory (RAM)


Two varieties: Static RAM (SRAM) and Dynamic RAM (DRAM).



  

    NameTrans
per bit		Access
time		
    Needs
refresh		Volatile
    CostWhere used
  

  

    SRAM4 or 61x
    NoYes
    100xCache
  

  

    DRAM110x
    YesYes
    1xMain Memory
  




RAM constitutes the memory in most computing devices.
  Unlike tapes or CDs they are not limited to sequential access.
  The table on the right compares them.


SRAM is much faster and (for the same cost) much lower capacity.
  Trans per bit gives the number of transistors needed to implement
  one bit of each memory type.
  (The 4-transistor version is denser but harder to manufacture.)


Both SRAM and DRAM are volatile, meaning that, if the power is
  turned off, the memory contents are lost.
  Due to the volatility of both RAM varieties, when a computer is
  started its first accesses are to some other memory type (normally a
  ROM or read-only memory).


DRAM, in addition to needing power, needs to be refreshed.
  That is even if power remains steady, DRAM will lose its contents if
  it is not accessed.
  Hence there is circuitry to periodically generate dummy accesses to
  the DRAM, even if the system is otherwise idle.



6.1.2 Disk Storage.


Disks are huge and slow.
  Unlike RAM disks have moving parts.
  At the end of a semester I will bring some old ones to class for us
  to look at.
  Unlike modern disks, these relics are big enough to see the active
  components.


For today we will have to settle for some pictures and words
  (z*/h*/me*).



Magnetic Disks (Hard Drives)


Show a real disk opened up and illustrate the components.



Consider the following characteristics of a disk.




Disk Performance‐Choice of Block Size




It is important to realize that disks always transfers (read or
  write) a fixed-size block.





Current commodity disks have (roughly) the following
  performance.



This is quite extraordinary.
  For a large sequential transfer, in the first 10ms,
  no bytes are transmitted; in the next
  10ms, 1,000,000 bytes are transmitted.
  This analysis suggests using large disk blocks, 100KB or more.


But the internal fragmentation would be severe since many files
  are small.
  Moreover, transferring small files would take longer with a 100KB
  block size.


In practice typical block sizes are 4KB-8KB.


Multiple block sizes have been tried (e.g., blocks
  are 8KB but a file can also have fragments that are a
  fraction of a block, say 1KB).



Start Lecture #19
 


6.1.3 Solid State Disks (SSDs)


This is flash RAM (the same stuff that is in thumb drives)
  organized in sector-like blocks as is a disk.
  Unlike RAM, SSD is non volatile; unlike a disk it has no moving
  parts (and hence is much faster then a hard disk).
  It is also more expensive per byte than a hard disk.


The blocks in an SSD can be written a large number of times.
  However, the large number is not large enough to be
  completely ignored.



6.1.4 Storage Technology Trends


Summary: Everything is getting better but the rates of improvement
  are quite different.



Cost per Byte Decrease from 1985 to 2015


  SRAM:  factor of 100
  DRAM:  factor of 50,000
  DISK:  factor of 3,000,000




Speed Increase from 1985 to 2015


  SRAM:  factor of 100
  DRAM:  factor of 10
  DISK:  factor of 25
  CPU:   factor of 2,000 (includes multiprocessor effect)




6.2 Locality


Remember we want to cleverly mix some small/fast memory with a
  large pile of big/slow memory and get a result that approximates
  the performance of the impossible big/fast memory.


The idea will be to put the important stuff is the
  small/fast and the rest in big/slow.
  But what stuff is important?


The answer is that we want to put into small/fast the data and
  instructions that will be accessed in the near future and leave the
  rest in big/slow.
  Unfortunately this involves knowing the future, which is
  impossible.


We need a heuristic for predicting what memory addresses will be
  accessed in the near future.
  The heuristic used is the principle of locality: programs
  will access in the near future addresses near those they accessed in
  the near past.


The principle of locality is not a law of nature, one can write
  programs that violate the principle, but on average it works very
  well.
  Unless you want your programs to run slower, there is no reason to
  deliberately violate the principle.
  Indeed, programmers needing high performance, try hard to increase
  the locality of their programs.


We often use the term temporal locality for the tendency
  that referenced locations are likely to be re-referenced soon and
  use the term spacial locality for the tendency that
  locations near referenced locations are themselves referenced
  soon.



6.3 The Memory Hierarchy


In fact there is more than just small/fast vs big/slow.
  We have minuscule/light-speed, tiny/super-fast, ...,
  enormous/tortoise-like.
  Starting from the fastest/smallest a modern system will have.


    
  
  1. Registers
    2. 
  
  2. Level 1 (L1) Cache
    3. 
  
  3. L2 Cache
    4. 
  
  4. L3 Cache
    5. 
  
  5. Main Memory
    6. 
  
  6. Secondary Storage (Local Disks)
    7. 
  
  7. Tertiary Storage (Robotic Disks)
    8. 
  
  8. Offline Storage
    9. 




Registers


Today a register is typically 8 bytes in size and a computer will
  have a few dozen of them, all located in the CPU.
  A register can be accessed in well under a nanosecond and modern
  processors access at least one register most operations.


In modern microprocessor designs, arithmetic and many other
  operations are performed on values currently in registers.
  Values not in registers must be moved there prior to operating on
  them.


Registers are a very precious resource and the decision which data
  to place in registers and when to do so (which normally entails
  evicting some other data) is a difficult and well studied
  problem.


The effective utilization of registers is an important component
  of compiler design—we will not study it in this course.



Caches


For the moment ignore the various levels of caches and think of a
  cache as an intermediary between the main memory, which
  (conceptually, but not in practice) contains the entire program, and
  the registers, which contains only the currently most important few
  dozen values.


In this course we will study the high-level design of caches and
  the performance impact of successful caching.


A memory reference that is satisfied by the cache requires much
  less time (say one tenth to one hundredth the time) than a reference
  satisfied by main memory.


Our main study of the memory hierarchy will be at the
  cache/main-memory boundary.
  We will see the performance effects of various hit ratios,
  i.e., the percentage of memory references satisfied in the cache vs
  satisfied by the main memory.



Multilevel Caches


When first introduced, a cache was the small and
  fast storage class and main memory was the big and slow.
  Later the performance gap widened between main memory and caches so
  intermediate memories were introduced to bridge the gap.
  The original cache became the L1 cache, and the gap bridgers became
  the L2 and L3.
  The fundamental idea remained the same: if we make it smaller it can
  be faster.



Main Memory


We will pretend that the entire program including its data resides
  in main memory.
  In the next course, 202 operating systems, we will study the effect
  of demand paging, in which the main memory acts as a cache
  for the disk system that actually contains the program.



Secondary Storage (Local Disks)


We know that the disk subsystem holds all our files and thus is
  much larger than main memory, which holds only the currently
  executing programs.
  It is also much slower: a disk access requires a
  few MILLIseconds; whereas a main memory access is a fraction of a
  MICROsecond.
  The time ratio is about 100,000.



Tertiary Storage


This is some robot controlled storage, where the robot
  automatically fetches the requested media and mounts it.
  Tertiary Storage is sometimes called nearline storage because it is
  nearly online.



Offline (Removable) Storage


Requires some human action to mount the device (e.g., inserting a
  cd).
  Hence the data is not always available.



6.4 Cache Memories



6.4.1 Generic Cache Memory Organization


A cache is a small fast memory between the
  processor and the main memory.
  It contains a subset of the contents of the main memory.


A Cache is organized in units of blocks
  or lines.
  Common block sizes are 16, 32, and 64 bytes.


A block is the smallest unit we can move between a cache and main
  memory (some designs move subblocks, but we
    will not discuss such designs).



A hit occurs when a memory reference is found in the upper level
  (small, fast) of the memory hierarchy.


Definitions
  




Addressing Bytes, (4-byte) Words, and Blocks


Consider the following address (in binary).
  10101010_11110000_00001111_11001010.

  This is a 32-bit address.
  I used underscores to separated it into four 8-bit pieces just to
  make it easy to read; the underscores have no significance.


Machine addresses are non-negative (unsigned) so the address above
  is a large positive number (greater than 2 billion).


All the computers we shall discuss are byte addressed.
  Thus the 32-bit number references a byte.
  So far, so good.



The (4-Byte) Word Addressed and the Byte Offset


We will assume in our study of caches that each word
  is four bytes.
  That is, we assume the computer has 32-bit words.
  This is not always true (many old machines had 16-bit, or smaller,
  words; and many new machines have 64-bit words), but to repeat, we
  will always assume 32-bit words.


Since 32 bits is 4 bytes, each word contains 4 bytes.
  Recall that we assume aligned accesses, which means that a word (a
  4-byte quantity) must begin on a byte address that is a multiple of
  the word size, i.e., a multiple of 4.
  So word 0 includes bytes 0-3; word 1 includes bytes 4-7; word n
  includes bytes 4n, 4n+1, 4n+2 and 4n+3; and the four consecutive
  bytes 6-9 do NOT form a word.


Question: What word includes the byte address given above,
  10101010_11110000_00001111_11001010?

  Answer: 
  10101010_11110000_00001111_110010, i.e, the address divided
  by 4.

  Question: What are the other bytes in this word?

  Answer: 
  10101010_11110000_00001111_11001000,  
  10101010_11110000_00001111_11001001,  
  and
  10101010_11110000_00001111_11001011


Question: What is the byte offset of the original
  byte in its word?
 
  Answer: 10 (i.e., two), the address mod 4..

  Question: What are the byte-offsets of the other
  three bytes in that same word?

  Answer: 00, 01, and 11 (i.e, zero, one, and
  three).



The 32-Byte Block Addressed and the Word and Byte Offset


Blocks vary in size.
  We will not make any assumption about the block size, other than
  that it is a power of two number of bytes.
  For the examples in this subsection, assume that each block is 32
  bytes.


Since we assume aligned accesses, each 32-byte block has a byte
  address that is a multiple of 32.
  So block 0 is bytes 0-31, which is words 0-7.
  Block n is bytes 32n, 32n+1, ..., 32n+31.


Question: What block includes our byte address
  10101010_11110000_00001111_11001010?

  Answer: 10101010_11110000_00001111_110,
  i.e., the byte address divide by 32 (the number of bytes in the
  block) or the word address divided by 8 (the number of words in the
  block).



6.4.2 Direct-Mapped Caches


We start with a very simple cache organization, one that was used
  on the Decstation 3100, a 1980s workstation.
  In this design cache lines (and hence memory blocks) are one word
  long.



Also in this design each memory block can only go in one specific
  cache line.



We shall assume that each memory reference issued by the processor
  is for a single, complete word.



Accessing a Direct-Mapped Cache


On the right is a diagram representing a direct mapped cache with
  C=4 blocks and a memory with M=16 blocks.


How can we find a memory block in such a cache?
  This is actually two questions in one.


    
  
  1. Is the memory block present in the cache?
    2. 
  
  2. Where in the cache is the memory block, assuming it is
    present?
    3. 


cache-addressing

The second question is the easier.
  Let C be the number of blocks in the cache.
  Then memory block number N can be found only in cache line
  number N mod C (it might not be present at
  all).


But many memory blocks are assigned to that same cache line.
  For example, in the diagram to the right all the
  green blocks in memory are assigned to the one green block in the
  cache.


So the first question reduces to:
  
    Is memory block N present in cache block N/C?
  



Referring to the diagram we note that, since only a green memory
  block can appear in the green cache block, we know that the
  rightmost two digits of the memory block in the green cache block
  are 10 (the number of the green cache block).
  So to determine if a specific green memory block is in the green
  cache block we need the rest of the memory block number.
  Specifically is the memory block in the green cache
  block 0010,
  0110, 1010,
  or 1110?
  It is also possible that the green cache block is empty (called
  invalid), i.e, it is possible that no memory block is in this cache
  block.
 


When the system is powered on, all the cache blocks are invalid so
  all the valid bits are off.



  
Addr(10)Addr(2)hit/missblock#

  
2210110miss110

  
2611010miss010

  
2210110hit110

  
2611010hit010

  
1610000miss000

  
300011miss011

  
1610000hit000

  
1810010miss010




On the right is a table giving a larger example, with C=8
  (rather than 4, as above) and M=32 (rather than 16).


We still have M/C=4 memory blocks eligible to be stored in
  each cache block.
  Thus there are two tag bits for each cache block.




Cache Contents, Hits, and Misses


Shown on the right is a eight entry, direct-mapped cache with block
  size one word.
  As usual all references are for a single word (blksize=refsize=1).
  In order to make the diagram and arithmetic smaller the machine has
  only 10-bit addressing (i.e., the memory has only
  210=1024 bytes), instead of more realistic 32- or 64-bit
  addressing.

cache-contents

Above the cache we see a 10-bit address issued by the processor.


There are several points to note.


    
  
  1. The valid bit.
    If this bit is not set, then the entire line is invalid.
    When the system is first powered on all the lines are invalid.
    2. 
  
  2. This machine, like all the ones we will study is byte addressed
    and has 4-byte words.
    Since the cache only handles references to a word, the rightmost
    two bits of the address from the processor, which specify the byte
    offset within the word, are ignored for cache access.
    3. 
  
  3. The (byte) address given is 1101010011.
    4. 
  
  4. Once we drop the byte-offset bits, the word address of the
    reference is 11010100.
    Since the block size is one word, the block number is also
    11010100.
    Since the cache has eight entries, the cache line number is
    11010100 mod 8 = 11010100 mod 23 = 100 (the low order
    three bits).
    5. 
  
  5. We see that the valid bit is on for entry 100 (i.e., entry 4)
    so the line is valid.
    6. 
  
  6. However, the tags do not match.
    Hence the reference is a cache miss.
    7. 
  
  7. Question: Would a memory reference 1000001001
    be a hit or miss?
    
    Answer: A hit since the tags match (100000).
    8. 
  
  8. Question: Would a memory reference 0000001001
    be a hit or miss?
    
    Answer: A miss since the tags do not match
    (100000 vs 000000)).
    9. 
  
  9. Explain in class how we know that the data field in entry 2
    contains the contents of word 130.
    10. 
  
  10. Make sure you understand why the other data fields contain the
    contents indicated.
    11. 




Start Lecture #20
 



Circuitry Needed to Detect Hits and Misses


The circuitry needed for a simple cache (direct mapped,
  blksize=refsize=1) is shown on the right.
  The only difference from the example above is size.
  This cache holds 1024 blocks (not just 8) and the memory holds
  230∼1,000,000,000 blocks (not just 256).
  That is, the cache size is 4KB and the memory size is 4GB.


To determine if we have a hit or a miss, and to return the data in
  case of a hit is quite easy, as the circuitry indicates.


Make sure you understand the division of the 32 bit address into
  20, 10, and 2 bits.


Calculate on the board the total number of bits in this cache and
  the number used to hold data.


Ignore the Write-through and write allocate comments,
  as we are not studying cache designs in that much detail.



Processing a Read for this Simple Cache


The action required for a hit is clear, namely return to the
  processor the data found in the cache.


For a miss, the best action is fairly clear, but requires some
  thought.




The Decstation 3100 Write Policy


The simplest write policy is write-through, write-allocate.
  The decstation 3100 discussed above adopted this policy and
  performed the following actions for any write, hit or miss, (recall
  that, for the 3100, block size = reference size = 1 word and the
  cache is direct mapped).


    
  
  1. Index the cache using the correct LOBs (i.e., not the very
    lowest order bits as these give the byte offset).
    2. 
  
  2. Write the data and the tag into the cache.
    
  
    3. 
  
  3. Set Valid to true (it may already be true).
    4. 
  
  4. Send the request to main memory.
    5. 



Although the above policy has the advantage of simplicity,
  it is out of favor due to its poor performance.




  
Improvement:  Use a Write Buffer


  
Unified vs Split I and D (Instruction and Data) Caches





Improvement: Multiword Blocks


The setup we have described does not take any advantage of spatial
  locality.
  The idea of having a multiword block size is to bring into the cache
  words near the referenced word since, by spatial locality, they are
  likely to be referenced in the near future.


We continue to assume that all references are for one word
  and (for a while) that the cache is direct mapped.

cache-bigblock

The figure on the right shows a 64KB direct mapped cache with
  4-word (16-byte) blocks.

  Questions: For this cache, when the memory word
  referenced is in a given block, where in the cache does the block
  go, and how do we find that block in the cache?

  Answers:



Show from the diagram how this gives the pink portion for the tag
  and the green portion for the index or cache block number.


Consider the cache shown in the diagram above and a reference to
  word 17003.



Summary: Memory word 17003 resides in word 3 of
  cache block 154 with tag 154 set to 1 and with valid 154 true.


The cache size or cache capacity is
  the size of the data portion of the cache (normally measured in
  bytes).


For the caches we have see so far this is the block size times the
  number of entries.
  For the diagram above this is 64KB.
  For the simpler direct mapped caches block size = word size so the
  cache size is the word size times the number of entries.


Note that the total size of the cache includes all the bits.
  Everything except for the data portion is considered overhead since
  it is not part of the running program.


For the caches we have see so far the total size is

       (block size + tag size + 1) * the number of entries


Let's compare the pictured cache with another one containing 64KB
  of data, but with one word blocks.


    
  
  1. Calculate on the board the total number of bits in each cache;
    this is not simply 8 times the cache size in
    bytes.
    2. 
  
  2. If the references are strictly sequential the pictured cache
    has 75% hits; the simpler cache with one word blocks
    has no hits.
    3. 



How do we process read/write hits/misses for a cache with multiword
  blocks?



Why not make block size enormous?
  For example, why not have the cache
  be one huge block.




Start Lecture #21
 


Review Cache Material



6.4.3 Set Associative Caches



Improvement: Associative Caches


Consider the following sad story.
  Jane's computer has a cache that holds 1000 blocks and Jane has a
  program that only references 4 (memory) blocks, namely blocks 23,
  1023, 123023, and 7023.
  In fact the references occur in order: 23, 1023, 123023, 7023, 23,
  1023, 123023, 7023, 23, 1023, 123023, 7023, 23, 1023, 123023, 7023,
  etc.
  Referencing only 4 blocks and having room for 1000 in her cache,
  Jane expected an extremely high hit rate for her program.
  In fact, the hit rate was zero.
  She was so sad, she gave up her job as web-mistress, went to medical
  school, and is now a brain surgeon at the mayo clinic in Rochester
  MN.



The Easy Way Out: Direct Mapped


So far we have studied only  direct
  mapped caches, i.e., those for which the location in the
  cache is determined by the address, i.e., there is
  only one possible location in the cache for any
  block.
  In Jane's sad story four memory blocks were assigned to the same
  cache block so they kept evicting each other and the rest of the
  cache was unused.


Although this organization does not give good performance it does
  have one advantage: to check for a hit we need compare
  only one tag with the HOBs of the addr.



Going All the Way: Fully Associative


The other extreme is a fully associative
 cache in which a memory block can be placed in any cache block.




The Middle Ground: Set Associative


Most common for caches is an intermediate
  configuration called set associative or n-way associative
  (e.g., 4-way associative).
  The value of n is typically a small power of 2.


If the cache has B blocks, we group them into B/n
  sets each of size n.
  Since an n-way associative cache has sets of size n blocks,
  it is often called a set size n cache.
  For example, you often hear of set size 4 caches.


In a set size n cache, memory block number K is stored in set
  number (K mod the number of sets), which equals K mod (B/n).


The picture below shows a system storing memory block 12 in three
  cache, each having 8 blocks.
  The left cache is direct mapped; the middle one is 2-way set
  associative; and the right one is fully associative.





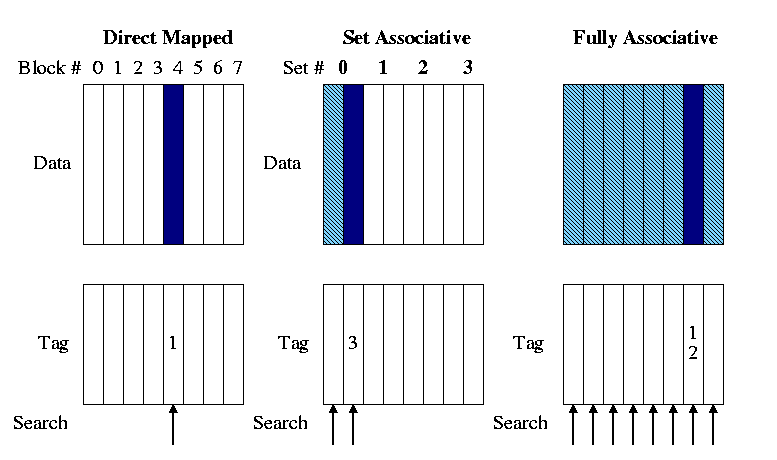
The Left-Hand Diagram: Direct Mapped


We have already done direct mapped caches but to repeat:




The Middle Diagram: Set Associative


The middle picture shows a 2-way set associative
  cache also called a set size 2 cache.
  A set is a group of consecutive cache blocks.




The Right-Hand Diagram: Fully Associative


The right picture shows a fully associative cache, i.e. a cache
  where there is only one set and it is the entire cache.



For a cache holding n blocks, a set-size n cache is
  fully associative and a set-size 1 cache is direct
  mapped.



Start Lecture #22
 


Note: If you have N numerical address but
  only n<N mailboxes available, one possibility (the one
  we use in caches) is to put mail for address M in
  mailbox M%n.
  Then to distinguish address assigned to the same mailbox you need
  the quotient M/n.
  In caches we call the mailbox assigned the cache index and the
  quotient needed to disambiguate is called the tag.


The key principle is


  Dividend = Quotient * Divisor + Remainder



We look in the Remainder (the cache index) store the Quotient (the
  tag) and know the Divisor (the number of cache slots).
  Hence we can determine the Dividend (the memory block number).



Remark: In class extend the example from last
  lecture by doing a 4-way set associative cache.



Remark: A preview of the first part of lab3 is
  here.



When the cache was organized by blocks and we wanted to find a
  given memory word we first converted the word address to the
  MemoryBlockNumber (by dividing by the #words/block and then formed
  the division


  MemoryBlockNumber / NumberOfCacheBlocks



The remainder gave the index in the cache and the quotient gave the
  tag.
  We then referenced the cache using the index just calculated.
  If this entry is valid and its tag matches the tag in the memory
  reference, that means the value in the cache has the right quotient
  and the right remainder.
  Hence the cache entry has the right dividend, i.e., the correct memory
  block.



Determining the Set Number and the Tag


Recall that for the a direct-mapped cache, the cache
  index is the cache block number (i.e., the cache is indexed by cache
  block number).
  For a set-associative cache, the cache index is the set
  number.


Just as the cache block number for a direct-mapped cache is the
  memory block number mod the number of blocks in the cache, the set
  number for a set-associative cache is the (memory) block number mod
  the number of sets.


Just as the tag for a direct mapped cache is the memory block
  number divided by the number of blocks in the cache, the tag for a
  set-associative cache is the memory block number divided by the
  number of sets in the cache.


Summary: Divide the memory block number by the
  number of sets in the cache.
  The quotient is the tag and the remainder is the set number.
  (The remainder is normally referred to as the memory block number mod
  the number of sets.)


Do NOT make the mistake of thinking that a set
  size 2 cache has 2 sets, it has NCB/2 sets each of size 2.


Ask in class.



Question: Why is set associativity good?
  For example, why is 2-way set associativity better than direct
  mapped?

  Answer: Consider referencing two arrays of size 50K
  that start at location 1MB and 2MB.




Locating a Block in the Cache


Question: How do we find a memory block in a 4KB
  4-way set associative cache with block size 1 word?

  Answer: This is more complicated than for a
  comparable direct mapped cache.
  We proceeds as follows.

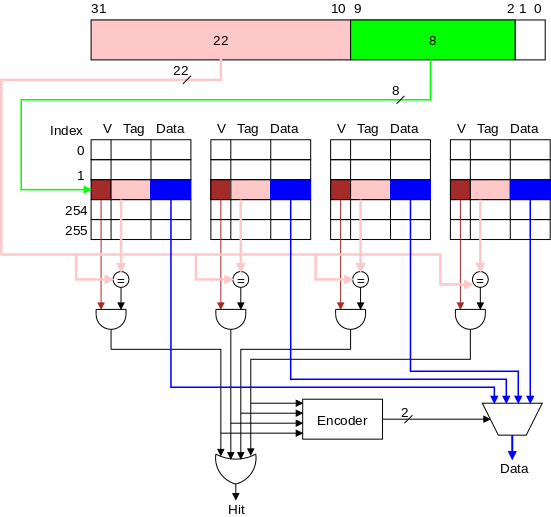
cache-4-way

    
  
  1. First drop the low 2 bits (byte in word) of the memory address,
    leaving 30 bits for the memory word number (MWN).
    2. 
  
  2. The MBN = the MWN since, in this example, the block size is 1
    word.
    3. 
  
  3. Each set contains 4 blocks = 4 words = 16B.
    4. 
  
  4. Hence the cache has 4KB/16B=256 sets
    5. 
  
  5. Divide the memory block number by the number of sets.
    The quotient is the tag.
    That is, tag = MBN / NS = MBN / 256.
    Since 256=28, dividing by 256 is simply simply
    separating the dividend into two pieces: the right 8 bits are the
    remainder and the rest is the quotient.
    6. 
  
  6. The quotient, i.e, the tag, is shown in pink in the
    diagram.
    7. 
  
  7. The remainder (i.e., the memory block number mod the number of
    sets) is the set number (i.e., the index of the entry).
    This portion of the address is shown in green.
    Again note that, since the divisor is a power of 2 (specifically,
    256), calculating the quotient and divisor does not require a
    division).

    8. 
  
  8. Compare all the tags and valid bits in the set
    with the tag of the memory block.
    9. 
  
  9. If any valid tag matches, a hit has occurred
    and the corresponding data entry contains the memory block.
    10. 
  
  10. If more than one valid tag matches, an error has occurred: the
    same memory block is stored in two or more sets.
    11. 
  
  11. If no valid tag matches, a miss has
    occurred.
    12. 



The advantage of increased associativity is normally an increased
  hit ratio.


Question: What are the disadvantages?

  Answer: It is slower, bigger, and uses more energy
  due to the extra logic.



Combining Set-Associativity and Multiword Blocks

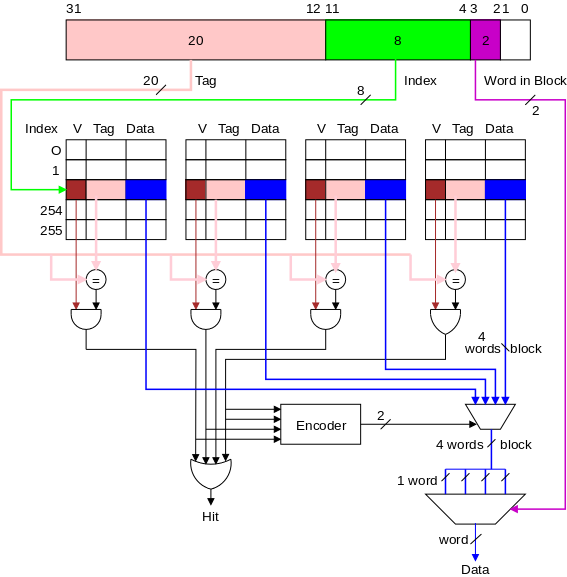
cache-4-way-big-block

This is a fairly simple combination of the two ideas and is
  illustrated by the diagram on the right.


    
  
  1. Start with the picture just above for a set-associative cache
    with blocksize = 1 word.
    2. 
  
  2. Each blue portion of the cache is now a 4-word block, not
    just a single word.
    3. 
  
  3. Hence the data coming out of the multiplexor at
    the bottom right of the previous diagram is now a block.
    In the diagram on the right, the block is 4 words.
    4. 
  
  4. As with direct-mapped caches having multi-word blocks, we again
    use the word-within-block bits to choose the proper word.
    In the diagram this is performed by the very bottom multiplexor,
    using the magenta word-within-block bits as the selector
    line.
    5. 
  
  5. Note that this cache is bigger than the one above.
    Each has 256 sets.
    Each has 256*4=1024 blocks.
    But the bottom has bigger blocks.
    6. 



Our description and picture of multi-word block, direct-mapped
  caches is here, and our description
  and picture of single-word block, set-associative caches is just
  above.
  It is useful to compare those two picture with the one on the right
  to see how the concepts are combined.


Below we give a more detailed
  discussion of which bits of the memory address are used for which
  purpose in all the various caches.



Choosing Which Block to Replace


When an existing block must be replaced, which victim should we
  choose?
  The victim must be in the same set (i.e., have the same index) as
  the new block.
  With direct mapped (a.k.a 1-way associative) caches, this determines
  the victim so the question doesn't arise.


With a fully associative cache all resident blocks are candidate
  victims.
  For an n-way associative cache there are n candidates.
  We will not consider these question.
  Victim selection in the fully-associative case is covered
  extensively in 202.



Summary of What We Officially Know How to Do For Loads and Stores


When you write y = x+1; in C the processor must read the
  value of x from memory.
  This is called a load instruction.
  The processor also must write the new value of y
  to memory.
  This is called a "store" instruction.



Direct Mapped Caches


For a direct mapped cache with 1-word blocks we know
  how to do everything.



If a block contains multiple words the only difference for us is
  that on a store miss the rest of the block must be obtained from
  memory and stored in the cache.



Set Associative Caches


An extra complication arises on a cache miss (either
  a load or a store).
  If the set is full (i.e., all blocks are valid) we must replace one
  of the existing blocks in the set and we are not learning which one
  to replace.
  As mentioned previously, in 202 you will learn how operating systems
  deal with a similar problem.
  However, caches are all hardware and hence must be fast so cannot
  adopt the complicated OS solutions.



Start Lecture #23
 


How Big Is a Cache?


There are two notions of size.


Definition: The cache size
  is the capacity of the cache.



Another size of interest is the total number of
  bits in the cache, which includes tags and valid bits.
  For the 4-way associative, 1-word per block cache shown above, this
  size is computed as follows.



Question: For this cache, what fraction of the
  bits are user data?

  Answer: 4KB / 55Kb = 32Kb / 55Kb = 32/55.


Calculate in class the equivalent fraction for the last diagrammed
  cache, having 4-word blocks (and still 4-way set associative).



Tag Size and Division of the Address Bits


We continue to assume a byte addressed machines with all references
  to a 4-byte word.


The 2 LOBs are not used (they specify the byte within the word, but
  all our references are for a complete word).
  We show these two bits in white.
  We continue to assume 32-bit addresses so there are 230
  words in the address space.


Let us review various possible cache organizations and determine
  for each the tag size and how the various address bits are used.
  We will consider four configurations each a 16KB cache.
  That is the size of the data portion of the cache
  is 16KB = 4 kilowords = 212 words.




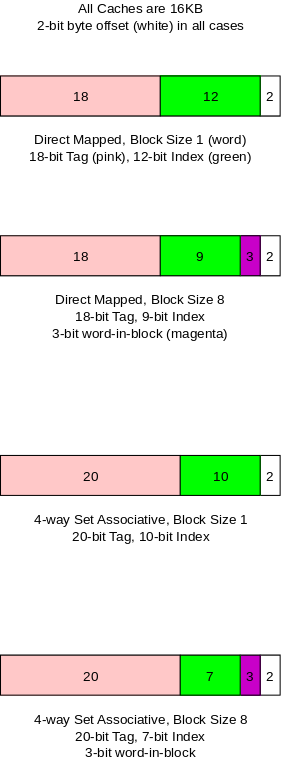
Direct Mapped, Block Size 1 (Word)


This is the simplest cache.




Direct Mapped, Block Size 8


Modestly increasing the block size is an easy way to
  take advantage of spacial locality.




4-Way Set Associative, Block Size 1


Increasing associativity improves the hit rate but
  only a modest associativity is practical.




4-Way Set Associative, Block Size 8


The two previous improvements are often combined.



On the board calculate, for each of the four caches, the memory
  overhead percentage.


Homework: Redo the four
  caches above with the size of the cache increased from 16KB to 64KB
  determining the number of bits in each portion of the address as
  well as the overhead percentages.



Start Lecture #24
 


Summary of Bit Division


Given the cache parameters and memory byte address (32-bits).


    
  
  1. Calculate MBN, the memory block number.
    
      
      
    1. Divide the byte address by 4 (drop low order 2 white bits)
        to get the memory word address.
      2. 
      
    2. Divide by #words/block (drop magenta bits used for word in
        block).
      3. 
    
    
  
    2. 
  
  2. Calculate NCS, the number of cache sets (the number of rows in
    the cache diagrams).
    
      
      
    1. NCB (num cache blks) = Cache size / blksize
      2. 
      
    2. NCS = NCB / (num blks per set, i.e., the set size)
      3. 
    
    
  
    3. 
  
  3. Divide MBN / NCS.
    The remainder is the set number, which is the index, i.e., the
    row, in the cache).
    These are low order (green) bits.
    The quotient is the tag; these are high order (pink) bits.
    4. 




First Example


The memory blksize is 1 word.
  The cache is 64KB direct mapped.
  To which set is each of the following 32-bit memory addresses
  (given in hex) assigned and what are the associated tags?


    
  
  1. 1000000016
    2. 
  
  2. 0101F00F16
    3. 
  
  3. 1234567816
    4. 



Answer.
  Let's follow the three step procedure above for each address.


    
  
  1. 1000000016 = 228.
    
      
      
    1. The first step is to find MBN.
        The memory word number for this address is 226
        (there are 4 bytes in a word).
        For this example the memory block number MBN is also
        226, since the blocksize is one word.
      2. 
      
    2. The second step is to find NCS.
        We are given that the cache has size 64KB so it has
        216 bytes or 214 words.
        Since the blocksize is one word, the cache has
        214 blocks and, since the set size is 1 (direct
        mapped), NCS = 214/1 = 214.
      3. 
      
    3. Divide MBN / NCS.
        226 / 214 has quotient 212
        and remainder 0.
        So the set assigned to 1000000016 is set 0 and the
        tag is 212.
      4. 
      
    
  
    2. 
  
  2. 0101F00F16
    
      
      
    1. Let's write the address in base 2 with a - between each
        group of 4 bits.
        So the address is 0000-0001-0000-0001-1111-0000-0000-1111.
        That is the byte number, there are again 4 bytes in a block
        so, to get the MBN, we need to divide the above number by 4,
        which means drop the low order two bits.
        This gives MBN=00-0000-0100-0000-0111-1100-0000-0011.
      2. 
      
    2. The cache is the same as above so NCS=214.
      3. 
      
    3. Divide MBN / NCS.
        Since the divisor is again 214, the set assigned is
        again the low order 14 bits of the MBN and the TAG is the
        remaining high order bits.
        Specifically the assigned set is 11-1100-0000-0011 =
        1C0316 and the tag is
        0000-0001-0000-0001 = 10116.
      4. 
    
    
  
    3. 
  
  3. 1234567816: This would be too error prone to do in
    binary so is ruled out of contention.
    4. 




Second Example


The memory blksize 64B.
  The cache is 64KB, 2-way set associative.
  To which set is each of the following 32-bit memory addresses
  (given in hex) assigned and what are the associated tags?


    
  
  1. 1000000016
    2. 
  
  2. 0101F00F16
    3. 
  
  3. 1234567816: Ruled out of contention.
    4. 



Answer.  Same 3-step procedure.


    
  
  1. 1000000016 = 228.
    
      
      
    1. Now the blksize is 64=26 Bytes so the MBN =
        228/26 = 222.
      2. 
      
    2. NCB = 64KB / (26Bytes/Blk) = 210.
        Set size is 2 so NCS = NCB / 2 = 29.
      3. 
      
    3. Divide MBN / NCS.
        222 / 29 = 213 remainder 0.
        So the set assigned is set 0 and the tag is
        213.
      4. 
    
    
  
    2. 
  
  2. 0101F00F16
    
      
      
    1. MBN = 0101F00F16 / 26 =
        0000-0001-0000-0001-1111-0000-0000-1111 / 26 =
               0100-0000-0111-1100-0000.
      
      2. 
      
    2. NCS is still 29.
      3. 
      
    3. Divide MBN / NCS.
        The set number is the remainder (the low order 9 bits) and the
        tag is the quotient (the remaining high order bits).
        Specifically the set number is 1-1100-0000 = 1C016
        and the tag is 10-0000-0011 = 20316.
      4. 
    
    
  
    3. 



Note: Should have last time calculated the memory
  overhead percentage for some caches: (TotalSize-Size)/TotalSize.



Measuring Cache Performance


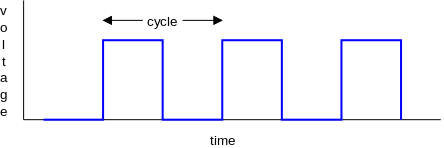
osc-traces

Clocks, Cycles. Rates. and Times


A clock on a computer is an electronic signal.
  If you plot a clock with the horizontal axis time and the vertical
  axis voltage, the result is a square wave as shown on the right.


A cycle is the period of the square
  wave generated by the clock.


We shall assume the clock is a perfect square wave with all periods
  equal.


Note: I added interludes because I realize that CS
  students have little experience in these performance
  calculations.



Interlude on Solving Rate and Time Equations


    
  
  1. A cycle (or clock cycle) is the time for the
    clock to go from one transition from low to high voltage to the
    next such transition.
    2. 
  
  2. Herz means CPS, i.e., cycles per second.
    It is a rate (like MPH) not a
    time.
    So a clock rate of 50 Hz means 50 cycles per second, which also
    means 50 cycles = 1 second or 1 cycle = 1/50 second.
    3. 
  
  3. Continuing with the same example 1 cycle = 2*10-2
    sec. = 20*10-3 sec. = 20ms = 20,000*10-6 sec
    = 20,000us = 20*106*10-9 =
    20 million ns.
    4. 
  
  4. KHz is kilohertz = 1,000Hz.
    MHz is megahertz = 106Hz; GHz is gigahertz =
    109Hz.
    5. 
  
  5. Question: Which takes longer 1GHz or
    10MHz?
    
    Answer: Nonsense!
    Hz is rate NOT time.
    6. 
  
  6. Question: Which takes longer one cycle at 1GHz
    or one cycle at 10MHz
    
    Answer: 1GHz means 109 cycles = 1
    sec; so 1 cycle = 10-9 sec.
    10MHz means 10*106 cycles = 1 sec; so 1 cycle =
    0.1*10-6 sec = 10-7 sec.
    So a cycle at 10MHz takes 100 times as long as a cycle at
    1GHz.
    7. 
  
  7. Question: At a rate of 2GHz, how long is one
    cycle?
    
    Answer: 2GHz means 2*109 cycles = 1
    second.
    Hence 1 cycle = 0.5*10-9sec = 0.5ns
    8. 
  
  8. Question: What megahertz clock has a 300ns
    cycle time?
    
    Answer: 300ns cycle time means 1 cycle = 300ns =
    300*10-9 sec.
    So 1 sec = (1/300)*109 cycles = (10/3)*106
    cycles = 3.33MHz.
    9. 




Interlude on Averages Given Base Plus Extra


    
  
  1. Question: In
    2/5 of the cases X=A, in 3/5 of the cases X=B.
    What is the average X?
    
    Answer: (2/5)A + (3/5)B = (2A + 3B) / 5
    2. 
  
  2. Question:
    30% of cases X=A; the rest X=B.
    What is the average X?
    
    Answer: Average X =(30/100)A + (70/100)B
    3. 
  
  3. Question:
    p% of the cases X=A; rest X=B.
    What is the average X?
    
    Answer:
    Average X = (p/100)A + ((100-p)/100)B
    4. 
  
  4. Question:
    p% of the cases X=A+E; rest X=A (E stands for extra).
    What is the average X?
    
    Answer:
    Average X = (p/100)(A+E) + ((100-p)/100)A
    = (p/100)A + (p/100)E + ((100-p)/100)A
    = (100/100)A + (p/100)E = A + (p/100)E
    5. 
  
  5. Question:
    Base cost is 13; 17% of the cases have an extra cost of E.
    What is the average cost?
    
    Answer:
    Average cost = 13 + (17/100)E = 13 + .17E
    6. 
  
  6. CPI means cycles per instruction.
    Base CPI means the CPI when all references hit in the cache.
    Question:Base CPI = 13; 17% of refs miss cache
    with a penalty of 8 cycles.
    What is the overall CPI?
    
    Answer:
    Overall CPI = 13 + .17(8) = 14.36 cycles.
    7. 




Start Lecture #25
 


Remark: I typed in the example we did last time on
  the board.
  The final answer became 20316.
  I think I had 10316 last time.



Instruction and Data Caches


Modern processors have several caches.
  We shall study just two, the instruction cache and the data cache,
  normally called the I-Cache and D-Cache.


Every instruction that the computer executes has to be fetched from
  memory and the I-Cache is used for such references.
  So the I-cache is accessed once for every instruction.

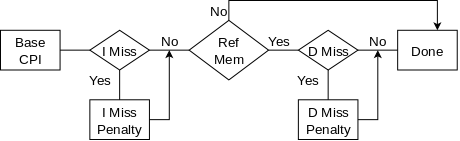
cache-I+D

In contrast only some instructions access the memory for data.
  The most common instructions making such accesses are
  the load and store instructions.
  For example the C assignment statement

        y = x + 1;

  generates a load to fetch the value of x and a store to
  update the value of y.
  There is also an add that does not reference memory.
  The diagram on the right shows all the possibilities
  If both caches have a miss, the misses are processed one at a
  time because there is only one central memory.



An Example


We assume separate instruction and data caches.


Do the following performance example on the board.
  It would be an appropriate final exam question.



A lower base (i.e. miss-free) CPI makes misses appear more
  expensive since waiting a fixed amount of cycles for the
  memory corresponds to losing more instructions if the CPI
  is lower.


A faster CPU (i.e., a faster clock) makes misses appear more
  expensive since waiting a fixed amount of time for the memory
  corresponds to more cycles if the clock is faster (and hence more
  instructions since the base CPI is the same).



Start Lecture #26
 


A Second Example



 Homework:
  Consider a system that has a miss-free CPI of 2, a D-cache miss rate
  of 5%, an I-cache miss rate of 2%, has 1/3 of the instructions
  referencing memory, and has a memory that gives a miss penalty of 20
  cycles.


    
  
  1. What is the CPI?
    2. 
  
  2. If the clock rate is 1.5GHz, how many instructions per second
    does the system execute.
    3. 
  
  3. What would be the CPI if the memory was double speed, but
    the CPU+caches remained the same as the original?
    4. 
  
  4. What would be the CPI if the memory remained the
    same as the original but the CPU+cache were double speed.
    5. 
  
  5. How fast would the CPU+cache have to be so that
    the system, with the original memory, was twice as fast as the
    original?
    6. 




Note:
  Larger caches typically have higher hit rates but
  longer hit times.



Virtual Address Caches vs Physical Address Caches



Virtual and Physical Addresses


We have been a little casual about memory addresses.
  When you write a program you view the memory addresses as starting
  at a fixed location, probably 0.
  In OS we study this topic extensively.
  Here I will give a very abbreviated treatment.



Monoprogramming

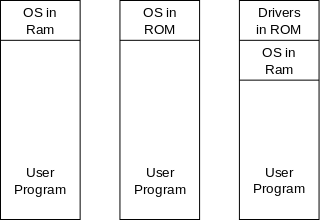
monoprogramming

Way back when (say 1950s), the picture on the right was
  representative of computer memory.
  Each tall box is the memory of the system.
  Three variants of the OS location are shown, but we can just use the
  one on the left.


Note that there is only one user program in the system so, we can
  imagine that it starts at a fixed location (zero if we like).


Using the appropriate technical terms we note that the
  virtual address, i.e., the addresses in the
  program, are equal to the physical addresses, i.e.,
  the address in the actual memory (i.e., the RAM).



Simplest Multiprogramming

MFT

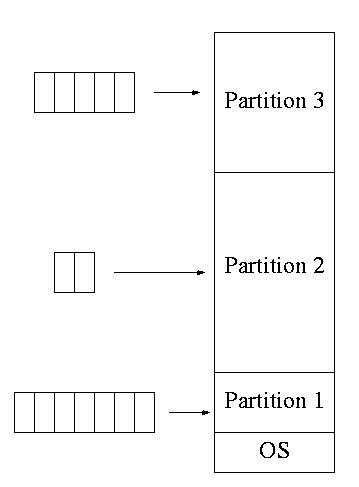
The diagram on the right illustrates the memory layout for
  multiple jobs running on a very early IBM multiprogramming system
  entitled MFT (multiprogramming with a fixed number of tasks).


When the system was booted (which took a number of minutes) the
  division of the memory into a few partitions was established.
  One job at a time was run in each partition, so the diagrammed
  configuration would permit 3 jobs to be running at once.
  That is it supported a multiprogramming level of 3.


If we ignore the OS or move it to the top of memory instead of the
  bottom, we can say that the job in partition 1 starts in location 0
  of the RAM, i.e., it logical addresses (the addresses in the
  program) are equal to its physical addresses (the addresses in the
  RAM).


However, for the other partitions, this situation does not hold.
  For example assume two copies of job J are running, one copy in
  partition 1 and another copy in partition 2.
  Since the jobs are the same, all the logical addresses are the same.
  However, every physical address in partition 2 is greater than every
  physical address in partition 1.


Specifically, equal logical addresses in the two copies differ by
  exactly the size of partition 1.



Multiprogramming Via Swapping


The picture below shows a swapping system.
  Each tall box represents the entire memory at a given point in time.
  The leftmost box represents boot time when only the OS is resident
  (blue shading represent free memory).
  Subsequent boxes represent successively later points in time


The first snapshot after boot time shows three processes A, B, and
  C running.
  Then B finishes and D starts.
  Note the blue hole where B used to be.


The system needs to run E but each of the two holes is two small.
  In response the system moves C and D so that E can fit.
  Then F temporarily preempts C (C is swapped out then swapped
  back in).
  Finally D shrinks and E expands.


In summary, not only does each process have its own set of
  physical addresses, but, even for a given process, the physical
  addresses change over time.

MVT
  

Paging

mapping-pages     
paging

Now it gets crazy.


The moving of processes is an expensive operation.
  Part of the cause for this movement is that, in a swapping system,
  the process must be contiguous in physical memory.


As a remedy the (virtual) memory of the process is divided into
  fixed size regions called pages and the physical memory is divided
  into fixed sized regions called page frames or simply frames.


All pages are the same size; all frames are the same size; and the
  page size equals the frame size.
  So every page fits perfectly in any frame.


The pages are indiscriminately placed in frames without trying to
  keep consecutive pages in consecutive frames.
  The mapping from pages to frames is indicated in the diagram by the
  arrows.


But this can't work!
  Programs are written under the assumption that, in the absent of
  branches, consecutive instructions are executed consecutively.
  In particular, after executing the last instruction in page 4, we
  should execute the first instruction in page 5.
  But page 4 is in frame 0 and the last instruction in frame 0 is
  followed immediately by the first instruction in frame 1, which is
  the first instruction in page 3.


In summary the program has to be executed in the order given by
  its pages, not by its frames.


This where the page table is used.
  Before fetching the next instruction or data item, its virtual
  address is converted into the corresponding physical address as
  follows.
  The virtual address divided into the page number and offset.
  As we did with caches, we divide the virtual address by the page size
  and look at the quotient and remainder.
  The former is the page number and the latter the offset in the page.
  We look up the page number p# in the page table to find the
  corresponding frame number f# and apply the same offset we
  calculated.



 Demand Paging


The final step is that, in modern systems, it is no longer true
  that the entire program is in memory at all times.
  All pages are on disk.
  Some pages are, in addition, in frames as indicated above, but for
  others the page table simply lists that the page is not
  resident.


A program reference to a non-resident page is called a page fault
  and triggers much OS activity.
  Specifically, an unused frame must be found (often by evicting its
  current resident) and the referenced page must be read from the disk
  into this newly available frame.


If the above sounds familiar, that is not surprising.
  For the caching described in 201, the SRAM acts as a small/fast
  cache of the big/slow DRAM.
  For the demand paging just described the DRAM acts as a small/fast
  cache of the big/slow disk.



Start Lecture #27
 


Virtual Address Caches vs Physical Address Caches


Now that we understand the difference between virtual and physical
  address, we can discuss the trade-off between caching based on
  each.
  We will only consider the paging system mentioned above.
  The demand paging system is similar, but more complicated.
  The methods before paging are no longer in active use.



Advantage of Virtual Addressed Caches: Speed


The address from the program itself is the virtual address, the
  system then translates it to the physical address as described
  above.
  Thus with a virtual address based cache, the cache lookup can begin
  right away; whereas, with a physical address based cache, the cache
  lookup must be delayed until the translation to physical address
  has completed.



Advantage of Physical Addressed Caches: No Aliasing


Many concurrently running processes will have the same virtual
  addresses (for example all processes might start at virtual address
  zero).
  However, all these virtual address zeros are different physical
  address and represent parts of different programs.
  Hence they must be cached separately.
  But to a straightforward virtual address cache the virtual address
  zeros would all be assigned the same cache slot.
  Instead the virtual address caching scheme adds complexity to the
  cache hardware to distinguish identical
  virtual address issued by different processes.



Cache Review



Do Another CPI Example



Material on Cache Size and Number of Bits from Lecture #23



Start Lecture #28
 


Reviewed caches again and answer students' questions.



As requested I wrote out another example.
  Here it is.




Extra: One More Problem


At the end of the last class I was asked to do another problem with
   sizes.
   In particular finding which address bits are the tag and which are
   the cache index.



Extra.1: Basic Assumptions

 
In this class we will always make the following assumptions with
   regard to caches.

 
    
   
  1. All addresses are 32 bits.
    2. 
   
  2. The machine is byte addressable, so the 32-bit address
     specifies a byte.
    3. 
   
  3. All references from the process to memory (and hence to the
     cache) are for a single 4-byte word
    4. 
 


One conclusion is that the low-order (i.e., the rightmost) two
  bits of the 32 bit address specifies the byte in the word and hence
  are not used by the cache (which always supplies the entire
  word).



Extra.2: The Cache in the Example


We will use the following cache.


    
  
  1. The size (not the total size) is 256KB.
    2. 
  
  2. The blocksize is 8 words.
    3. 
  
  3. The set size is 2 (i.e., we have a 2-way set associative
    cache).
    4. 




Extra.3: The General Procedure For Assigning the Address Bits


I use a three step procedure.


    
  
  1. Find which bits of a 32-bit memory address, give the MBN,
    or Memory Block Number.
    2. 
  
  2. Find the number of sets in the cache NS.
    3. 
  
  3. Divide MBN by NS and look at the quotient Q and remainder
    R.
    4. 




Extra.4: The Problem to be Solved


For the cache just described


    
  
  1. Which address bits contain the tag?
    2. 
  
  2. How big is each tag?
    3. 
  
  3. How many lines (i.e., sets, i.e., rows) are in the cache?
    4. 
  
  4. What is the total size of the cache?
    5. 




Extra.5: Solving the Problem


We will use the three step procedure mentioned in Extra.2.



Extra.5.1: Finding MBN, the Memory Block Number

extra-problem-1

The top picture shows the 32-bit address.


The rightmost 2 bits give the byte in word, which we don't use
  since we are interested only in the entire word not a specific byte
  in the word.
  That is shown in the second picture.
  Note that there are 4 = 22 bytes in the word.
  The exponent 2 is why we need 2 address bits.


The next 3 bits from the right give the word-in-block.
  There are 8 words in the block (see Extra.2) and
  8=23 so we need 3 bits.

The remaining 27 bits are the MBN.


Extra.5.2: Finding NS, the Number of Sets


You might prefer the abbreviation NCS (number of cache sets).
  I often don't add the word cache because only caches have sets, but
  neither term is standard so use whichever you prefer.


    
  
  1. The cache has 256KB = 218 bytes.
    This is given above in Extra.2.
    2. 
  
  2. 218 bytes is 216 4-byte words.
    3. 
  
  3. 216 words is 213 8-word blocks.
    4. 
  
  4. 213 blocks is 212 2-block sets.
    5. 



So NS = 212, which answers question 3 of Extra.4



Extra.5.3: Dividing to Find the Cache Row (Set) and Tag

extra-problem-2

The MBN is 27 bits and NS is 212.


Dividing a 27-bit number by a 12-bit number gives a
  (27-12)-bit quotient and a 12-bit remainder.


(This last statement is analogous to the more familiar statement
  that dividing a 5-digit number by 100=102 gives a
  (5-2)-digit quotient and a 2-digit remainder.
  To divide a 5 digit
  number by 100, you don't use a calculator, you just chop off the
  rightmost 2 digits as the remainder and remaining (5-2) digits form
  the quotient.
  Example 54321/100 equals 543 with a remainder of 21.)


The remainder is the cache set (the row in a diagram of the cache).
  It is shown in green.
  In blue we see the quotient, which is the tag.


So to answer questions 1 and 2.
   The high-order 15 (blue) bits form the 15-bit tag.



The Total Size of the Cache.


In the cache each 8-word block comes with a 15-bit tag and a 1-bit
  valid flag.
  Each of these cells (I don't know if they have a name) thus
  contains 8 32-bit words + 16 bits.
  (I realize 16 bits is 2 bytes but often the number of bits is not
  always a
  multiple of 8.)
  So each cell is 8*32+16 bits.
  There are 2 cells in each set and 212 sets in the cache
  so the total size of the cache is.


    212 × 2 × (8×32 + 16) bits






















































What follows is NOT Part of the 2018-19 Course




  Chapter T-1: Introduction to Computer Organization and Assembler Language



Homework: Read
  Tanenbaum chapter 1 (T-1 above stands for Tanenbaum 1).



Remark: Everyone with a Windows laptop should
  install cygwin as follows (I don't run windows so cannot test this
  procedure; apparently it worked well last semester).


    
  
  1. Browse http://www.cygwin.com
    2. 
  
  2. Click on install now.
    3. 
  
  3. Where you are asked to select packages, choose devel
    and then check that the box in the bin column next to
    gcc is checked.
    This will ensure that the gcc compiler is included.
    4. 
  
  4. Also in devel, select make.
    5. 
  
  5. Finally select editor and choose emacs.
    There are other editors available if you /prefer.
    6. 



Remark: If you have a linux laptop (or dual
  boot linux), you are set.
  The gcc on linux supports both variants of assembler syntax for the
  x86 CPU.
  We will be using the Intel syntax.


Remark: The mac story is interesting.


    
  
  1. Download XCode from the
      
        Apple Developer Connection
      .
  
    2. 
  
  2. Pick up Carbon Emacs
    here.
    3. 
  
  3. Now the fun.
    The version of gcc on the Mac does not use the same assembler
    syntax (the intel syntax) that nearly everyone else uses.
    You can fairly easily translate from the (ATT) syntax used to
    the Intel syntax.
    4. 
  
  4. Our machine i5.nyu.edu does not use an intel cpu (instead it
    uses a SUN sparc), but I am getting the mac users accounts on a
    departmental linux box, where you can select the intel
    syntax.
    5. 
  
  5. You can also install windows or Linux under MacOS; the gcc
    under Linux or cygwin supports the Intel syntax.
    6. 






Remark: Midterm exams returned.


If you did not read the mailing list, please read my comment on the
  exam and midterm (letter) grades.
  You can find it off the course home page (announcements).



Remark:
  Some comments on catDiff from the midterm.


    
  
  1. Many forgot to allocate space for various strings.
    The maximum penalty (no allocations) was -3.
    2. 
  
  2. Several had trouble with this construct
    
          char *str1 = "something";
      char *str2 = str1;
    
    
    They said char *str2 = *str1; 
    I can see why as it looks symmetric.
    Remember you are declaring str2 not *str2.
    3. 




Remark: Preview on final project.


You will be writing a (trivial) video game.
  For now, install the graphics library and put up a picture
  (find a *.bmp file).
  Here is the installation procedure


    
  
  1. Browse libsdl.org.
    2. 
  
  2. Click on the SDL 1.2 link on the left column.
    Note where the file is downloaded.
    3. 
  
  3. If necessary, move the file to your home directory.
    On Cygwin, your home directory is c:\cygwin\home\yourname).
    4. 
  
  4. In the shell (under cygwin) type
    tar -xvfz SDL-1.2.14.tar.gz.
    5. 
  
  5. Type cd  SDL-1.2.14
    6. 
  
  6. Type ./configure
    
    If this fails try ./configure CC=/usr/bin/gcc-3 CXX=/usr/bin/g++-3
    7. 
  
  7. Type make
    8. 
  
  8. Type sudo make install.
    
    If this fails try simply make install
    
    If both fail, try $@ make install
    
    You may be asked for your password (for your computer, not for an
    NYU machine).
    If you run as administrator, I don't believe you will be asked.
    9. 
  
  9. Type cd test
    10. 
  
  10. Type ./configure
    
    If this fails try ./configure CC=/usr/bin/gcc-3 CXX=/usr/bin/g++-3
    11. 
  
  11. Type make
    12. 
  
  12. Type ./testsprite
    13. 
  
  13. Gasp, in awe.
    14. 



Here is a windows/cygwin tip from Prof. Goldberg.
  Be sure that the name of your home directory does not have a space
  in it.
  For example, if your name is Joe Smith, be sure that your home
  directory on cygwin is not "c:\cygwin\home\joe smith", but rather
  something like "c:\cygwin\home\joe_smith".
  The SDL configure function gets confused by spaces in a directory
  name.
  If cygwin has created your home directory name with a space, change
  the name of the directory using Windows.
  Then, create an environment variable called HOME and set it to
  c:\cygwin\home\joe_smith, except with joe_smith
  replaced by the actual name of your home directory.
  To set an environment variable in Windows, go to

  Start->Control Panel->System->Advanced->Environment Variables.
  It should be obvious from there.


Let me call the subdirectory SDL-1.2.14 the sdl
  directory.
  In there you will find a README file containing the web address of a
  wiki about the library
  Browse that wiki and follow the guide.
  I had never used any of this before and within 20 minutes I had a
  picture up.



Chapter T-2: Computer Systems Organization


Some diagrams of the overall structure of a computer system are in
  section 1.3 of
  
    my OS class notes
  




T-2.1: Processors


The processor (or CPU, Central Processing Unit) performs the
  computations on data.
  The data enter and leave the system via I/O devices and are stored
  in the memory (the last part is over simplified as you will learn in
  OS, but it is good enough for us).



T-2.1.1: CPU Organization


Simple processors have (had?) three basic components, a register
  file, an ALU (Arithmetic Logic Unit), and a control unit.
  Oversimplified, the control unit fetches the instructions and
  determines what needs to be done, the data to be processed is often
  the registers (which can be accessed much faster than
  central memory) and the ALU performs the operation (e.g.,
  multiply).


In addition to the (assembly-language) programmer-visible registers
  mentioned above, the CPU contains several internal registers, two of
  which are the PC (Program Counter, a.k.a. ILC or LC), which
  contains the address of the next instruction to execute and the
  Instruction Register (IR), which contains (a copy of) the
  current instruction.



T-2.1.2: Instruction Execution


There are three parts to executing an instruction: obtain the
  instruction, determining what it needs to do, and doing it.
  Repeatedly performing these three steps for all the instructions in a
  program, is normally referred to as the
  fetch-decode-execute cycle.

In slightly more detail, the CPU executes the following program.

    
  
  1. Fetch the next instruction into the IR.
    2. 
  
  2. Update the PC.
    3. 
  
  3. Determine the type of the instruction.
    4. 
  
  4. If memory is referenced, determine the address.
    5. 
  
  5. Fetch the referenced word, if needed, into a register.
    6. 
  
  6. Execute the instruction.
    7. 
  
  7. Repeat.
    8. 




Architecture vs. Micro-Architecture


The architecture is the instruction set, i.e., the
  (assembly-language) programmer's view of the computer.


The micro-architecture is the design of the computer, it is the
  architect's/designer's/engineer's view of the system.


The interesting case is when you have a computer family,
  e.g., the IBM 360 or 370 line, the x86 microprocessor architecture,
  which has several different implementations, with different
  microarchitectures.



T-2.1.3: RISC vs. CISC


Reduced Instruction Set Computer versus Complex Instruction Set
  Computer.
  Clear implementation advantages for RISC.
  But CISC has thrived!
  Intel found an excellent RISC implementation of most of the very
  CISC x86.



T-2.1.4: Design Principles for Modern Computers


The RISC design principles below are generally agreed to be
  favorable, but are not absolute.
  For example backwards-compatibility with previous systems,
  force compromises.






Remark: I mentioned the wrong guide last
  time.
  The notes are now correct.




  
T-2.1.5: Instruction Level Parallelism

  
Skipped.


  
T-2.1.6: Processor-Level Parallelism

  
Skipped.





T-2.2: Primary Memory



T-2.2.1: Bits


Abbreviates binary digit, which is rather contradictory.



T-2.2.2: Memory Addresses


The smallest addressable unit of memory is called a
  cell.
  Recently, for nearly all computers, a cell is an 8-bit unit called a
  byte (or octet).
  Bytes are grouped into words, which form the units on which
  most instructions operate.



T-2.2.3: Byte Ordering


This has caused decades of headaches.


Memory is addressed in bytes.
  But we also need larger units, e.g., a 4-byte word.
  If memory contains a big collection of bytes, the bytes are stored
  in address 0, 1, 2, 3, etc.
  If memory contains a big collection of words, the words are stored
  in address 0, 4, 8, 12, etc.
  So far no problem.


Consider a 32-bit integer stored in a (4-byte) word.
  If the integer has the value 5 then the bit string will be
  00000000|00000000|00000000|00000101.
  So the lower order byte of the integer is 00000101 and the three
  high order bytes are each 00000000.
  Still no problem.


Let's assume this is the first word in memory, i.e., the one with
  address 0.
  It contains 4 bytes: 0, 1, 2, and 3.
  We are closing in on the problem.


Which of those four bytes is the low order byte of the word.
  Answer from IBM: byte 3 (IBM machines are big endian.
  Answer from Intel: byte 0 (Intel processors are little
  endian.


Either answer makes sense and if you stay on one machine, there is
  no problem at all since either system is consistent.
  But let try to move data from one machine to another.


Say we have an integer containing 5 (as above) and a
  4-byte character string "ABC" stored on an IBM machine.
  The layout is


  00000000  00000000  00000000  00000101     A     B     C    00000000
     0         1         2         3         4     5     6       7



The ABC are expressed in bits, but the specific bit string
  is not important.

  The last byte of all 0s is ...

  the ascii null ending the string.


We send these 8 bytes via ethernet to an Intel machine where we
  again store them starting at location 0, and get the same layout as
  above.
  However, byte 3 is now the most-significant (rather than the
  least-significant) byte.
  Gack.
  The integer 5 has become 5*(256)3!


If the internet software reverses every set of four bytes, we fix
  the integer, but screw up the string.



T-2.2.4: Error-Correcting Codes


The Hamming Distance between two equal-length bit strings
  is the number of bits in which they differ.
  If you arrange that all legal bit strings have Hamming distance at
  least 2 from each other than you can detect any
  1-bit error.
  This explains parity.


More generally if all legal bit strings have Hamming distance at
  least d+1, then you can detect any d-bit error
  since changing d bits of a legal string cannot reach another
  legal string.


To enable correction of errors you need greater
  Hamming distances: specifically Hamming distance 2d+1 is
  needed to enable correction of d bits.
  This is not too hard to see.
  If you have a valid string and change d bits, the result
  is at distance from the original valid string and at least distance
  d+1 from any other valid string (since the valid strings
  are at least 2d+1 apart.


The harder part is designing the code.
  That is, given n, assume you are storing and fetching
  n data bits at a time, how many extra check bits
  must be stored and what must they be in order that all the resulting
  strings are at least distance d apart?


The book gives Hamming's method, but we are skipping the algorithm
  and are content with just one fact.



  If the size of the data word is 2k (i.e., the number of
  bits in a word is 2k), then k+1 check
  bits are necessary and sufficient to obtain a code that can
  correct all single-bit errors and can detect all double-bit
  errors.



For example if we are dealing with bytes, k is 3 so 4
  check bits are required; a heavy overhead (4 check bits for every
  8 data bits).
  If we are only transporting 64-bit words, k is 6 and 7
  check bits are required, which is a much milder overhead.





Remark: Term Project assigned.
  Due in three weeks, 27 apr 2010



T-2.2.5: Cache Memory


The ideal memory is



Commodity memory is big, slow, cheap, and possible.


Caches are small, fast, cheap enough because they are small, and
  possible.


Concentrating on the first two criteria we can build
  big and slow and we can build small and fast, but we
  want big and fast.
  This is where the idea of caching comes in.


A cache is small and fast.
  A significant portion of its speed is because it is close to the CPU
  and clearly if an object is big its (average or worst-case) distance
  from another object can't be small.
  For example, no matter where you park a car you can't have all (or
  half) of it within a foot of a given point.


The idea of caching is that we arrange (somehow) for almost all of
  the important data to be in the small, fast cache and use the
  big and slow memory to hold the rest (actually it holds all the
  data).


Since the portion of memory that is important changes with time,
  caches exchange data with memory as the program executes.


With clever algorithms for choosing which data to exchange with
  memory, surprisingly small caches can service a great deal of the
  memory activity of the processor.


There is no reason to stop with just one cache
  level.
  Today it is common to have a tiny, blistering-fast level-1 cache
  connected to a small, real-fast level-2 cache connected to a
  medium-size, fast level-3 cache connected to huge, slow memory.


This same issue of a small, fast red-memory supporting a large,
  slow blue-memory is studied in Operating Systems (202).
  In the OS setting, the small and fast memory is our big and slow
  central memory and the big and slow OS memory is a disk.
  Unfortunately, nearly all the terminology in the OS case (demand
  paging) is different from the terminology in the computer design
  case (caching).



T2.2.6: Memory Packaging and Types



T-2.3: Secondary Memory



T-2.3.1: Memory Hierarchies


The example of multiple cache levels, can be carried further.
  The processor registers are smaller and faster than a cache.
  As mentioned disks are bigger and slower than central memory,
  and robotic-accessed, tape storage is bigger and slower than a disk.
  Again the goal is to use smarts to approximate the impossible
  big and fast and cheap storage.



T-2.3.2: Magnetic Disks


Disks are covered in OS (202) so we will just define some terms
  (plus I demo'ed a bunch of disks last class).



Homework: 19.



T-2.3.2: Floppy Disks


Demoed last class.




  
T-2.3.4: Ide Disks

  
Describes the specific protocol, cabling, and speed.


  
T-2.3.5: Scsi Disks

  
Describes the specific protocol, cabling, and speed.


  
T-2.3.6: RAID

  
Done in OS (202).


  
T-2.3.7: CD-ROMs

  
Done in OS (202).
    Just one comment, unlike magnetic disks CD-ROMs and friends do not
    have circular tracks; instead the data spirals out from the
    center.


  
T-2.3.8: CD-Recordables (CD-R)

  
Done in OS (202).


  
T-2.3.9: CD Rewritables (CD-RW)

  
Done in OS (202).


  
T-2.3.10: DVD

  
Done in OS (202).


  
T-2.3.11: Blu-Ray

  
Done in OS (202).





T-2.4: Input/Output



T-2.4.1: Buses


Last class I demoed a computer main board
  (a.k.a. motherboard, system board, or mobo) and
  showed the slots where a controller would plug it.


I brought in an ethernet controller that fit onto the PCI bus
  of the main board.
  The different busses (PCI, PCIe, SCSI, ATA, etc) describe the wiring
  and protocols used to connect the different controllers to the CPU.



T-2.4.2: Terminals



Keyboards


Done in 202



CRT Monitors


Obsolete.



Flat Panel Displays


Very important, but a little too much engineering-oriented for us
  to cover.
  You might want to read it for you own curiosity.



Video RAM


One value per pixel on the screen.
  These values together are often called a bit map.
  In fact systems often contain several but maps to enable fast
  switching.



T-2.4.3: Mice


Covered in 202.




  
T-2.4.4: Printers


  
Monocrome Printers


  
Color Printers


  
T-2.4.5: Telecommunications Equipment


  
Modems


  
Digital Subscriber Lines (DSL)


  
Internet over Cable


  
T-2.4.6: Digital Cameras





T-2.4.7: Character Codes



ASCII



Unicode



T-2.5: Summary


Read.



Chapter T3: The Digital Logic Level


This is the bottom of the abstraction hierarchy.



T-3.1: Gates and Boolean Algebra



T-3.1.1: Gates




  
(Bipolar) Transitors and the Device Level

  transistor
  nand-nor
  
When the Base is high (positive voltage, say 5 volts,
    a digital 1) the transistor turns on, i.e., acts
    like a wire and the Collector is pulled down to ground
    (zero volts, a digital zero).

  
When the Base is low (zero volts, a digital zero), the transistor
    turns off, i.e., acts like an open circuit.
    Thus the collector is essentially the same as the voltage supply
    +Vcc; it is a digital one.

  
Summary, when the base is zero, the collector is one; and vice
    versa.
    That is, viewing the base as the input and the collector as the
    output.
    The logic function f having the property that
    f(0)=1 and f(1)=0 is called an inverter.

  
NAND and NOR
 
  

    NAND and NOR   
    The diagram on the right shows two additional logic functions
    built from transistors.
    These logic functions take two arguments and are called
    NAND (not and) and NOR (not OR)
    respectively.





Ignoring the above, which is one level below what we are studying,
  we define 5 logic gates by the truth tables given below their
  diagrams.


  gates



  NOT Truth Table
  
AX

  
01

  
10





  NAND Truth Table
  
ABX

  
001

  
011

  
101

  
110





  NOR Truth Table
  
ABX

  
001

  
010

  
100

  
110





  AND Truth Table
  
ABX

  
000

  
010

  
100

  
111





  OR Truth Table
  
ABX

  
000

  
011

  
101

  
111





  XOR Truth Table
  
ABX

  
000

  
011

  
101

  
110






Homework: Using truth
  tables prove DeMorgans Laws


  NOT(A AND B) = (NOT A) OR (NOT B)
  NOT(A OR B) = (NOT A) AND (NOT B)



Homework
  Show that all Boolean functions with two inputs (and one output) can
  be generated by just using NAND.
  This can be done two ways.


    
  
  1. Draw all the possible truth tables and for each draw a circuit
    with just NAND that generates that same truth table.
    2. 
  
  2. Show how to get NOT, AND, and OR from just NAND and then show
    how any truth table can be generated from NOT, AND, and OR,
    3. 



The book does method 2 in section 3.1.3.
  You should do method 1.
  How many truth tables are there?





Remark: The honors supplement has been added to
  the final project.




  Jumped to Chapter T-5 (for assembler part of term project)





T-3.1.2: Boolean Algebra


Using truth tables, we can prove various formulas such as
  DeMorgan's Laws from the last homework.
  From these laws we can prove other laws.


Standard notation is to use + for OR, * for AND, and ⊕ for
  XOR (exclusive or).
  As in regular algebra the * is often dropped.


From these formulas, and algebraic manipulation we can get other
  formulas.
  This is called Boolean algebra (named after George Boole).


For example (I am using ' to signify NOT),
  you use truth tables to prove both distributive laws


  A(B+C) = AB + AC       * has higher precedence than +
  A+(BC) = (A+B)(A+C)    looks wrong but is correct



and then calculate


  A+(A'B)  =  (A+A')(A+B)      NOT has higher precedence than + or *
           =  (1)(A+B)         1 is the constant function (true)
           =  A+B              1 is the * identity (truth table)




T-3.1.3: Implementation of Boolean Functions


There is a standard procedure to generate any Boolean function
  using just AND, NOT, and OR.
  I did an example of this last time.
  Here is the general procedure.


    
  
  1. Write the truth table.
    2. 
  
  2. Generate rails with each input and its complement.
    3. 
  
  3. Use an AND for each set of inputs with a 1 in the result
    column of the truth table.
    4. 
  
  4. Wire the ANDs to a final OR
    5. 




T-3.1.4: Circuit Equivalence


As we have seen the same truth table can result from different
  Boolean formulas and hence from different circuits.
  Naturally, circuit designers might prefer one over the other
  (faster, less heat, smaller, etc.





T-3.2: Basic Digital Logic Circuits



T-3.2.1: Integrated Circuits


I showed a discrete circuit last time as well as a Pentium II main
  board containing many integrated circuits.
  Initially these circuits had only a few components; now they have
  millions.



T-3.2.2: Combinational Circuits


These are circuits in which the outputs are uniquely determined by
  the inputs.

  Isn't this always true?

  Certainly not!
  Some circuits have memory (i.e., RAM).
  If you give a ram an input of (12,read) the output is the last value
  that was stored in 12.
  So you need to know more than (12,read) to know the answer;
  you need to know the history.


4-way mux

Multiplexors (Muxes)


Have 2n inputs plus n select inputs.
  The select inputs are read as a binary value and thus specify a
  number from 0 to 2n.
  This number is used to select one of the inputs to be the output.


Construct on the board an equivalent circuit with ANDs and ORs in
  three ways:


    
  
  1. Construct the truth table (64 rows!) and write the sum of
    products form, one product (6-input AND) for each row and
    a gigantic 64-way OR.
    Just start this, don't finish it.
    2. 
  
  2. A simpler (more clever) two-level logic solution.
    Four ANDS (one per input), each gets one of the inputs and both
    select lines with appropriate bubbles.
    The four outputs go into a 4-way OR.
    3. 
  
  3. Construct a 2-input mux (using the clever solution).
    Then construct a 4-input mux using a tree of three 2-input
    muxes.
    One select line is used for the two muxes at the base of the
    tree, the other is used at the root.
    4. 




Decoders (and Encoders)


Imagine you are writing a program and have 32 flags, each of which
  can be either true or false.
  You could declare 32 variables, one per flag.
  If permitted by the programming language, you would declare each
  variable to be a bit.
  In a language like C, without bits, you might use a single 32-bit
  int and play with shifts and masks to store the 32 flags in this one
  word.


In either case, an architect would say that you have these flags
  fully decoded.
  That is, you can detect the value of any combination of the
  bits.


Now imagine that for some reason you know that, at all
  times, exactly one of the flags is true and the
  other are all false.
  Then, instead of storing 32 bits, you could store a 5-bit integer
  that specifies which of the 32 flags is true.
  This is called fully encoded.


A 5-to-32 decoder converts an encoded 5-bit signal into 32
  signals with exactly one signal true.


A 32-to-5 encoder does the reverse operations.
  Note that the output of an encoder is defined
  only if exactly one input bit is
  set (recall set means true).



The diagram on the right shows a 3-to-8 decoder.



The truth table for an 8-3 encoder has 256 rows; for a 32-5 decoder
  we need 4 billion rows.


There is a better way!
  Make use of the fact that we can assume
  exactly one input is true.


For each output bit, OR the inputs that set this bit.
  For example the low-order output of an 8-3 is the OR of input bits
  1,3,5,7.




  
Comparators


  
Programable Logic Arrays (PLAs)





T-3.2.3: Arithmetic Circuits



Shifters


Do you want to rotate/0-fill/sign-extend?


Do you want to shift left or right?


Use muxes to give all the choices you want.
  The operation forms the select lines.



Adders


Draw a half adder (AND and XOR) that takes two inputs and produces
  two outputs, the sum and the Carry-out.


adder

Full Adder



  Full Adder   
  Really we want a full adder that has three inputs (A, B, Carry-in)
  and produces two outputs (Sum, Carry-out).
  The Sum equals the total number of 1s in A, B, and Ci is odd.
  The Carry-out is at least two of A, B, and Ci are 1.


The diagram above uses logic formulas for Sum and Carry-out
  equivalent to the definitions just given (see homework just
  below).


Homework: 








T-3.2.4: Clocks


clock

The period is also called the cycle time.
  The number of cycles per second/hour/day/etc is called the frequency.
  So a clock with a 2 nanosecond cycle time has a frequency of 1/2 a
  gigahertz or 500 megahertz (one hertz is one cycle per second).



T-3.3: Memory


s-r latch

T-3.3.1: Latches


The only unclocked memory we will use is a so called S-R latch
  (S-R stands for Set-Reset).


When we define latch below to be a
  level-sensitive, clocked memory, we will see that the S-R latch is
  not really a latch.


The circuit for an S-R latch is on the right.
  Note the following properties.




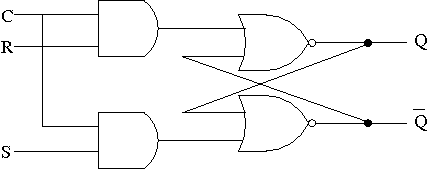
s-r latch clocked

Clocked SR Latches


The clocked version on the right has the property that the values
  of S and R are only relevant when the clock is high (i.e., true not
  false).
  This is sometimes convenient, but we will not use it.
  Instead we will use the important D-latch that we describe next that
  is very similar.



Clocked D Latches

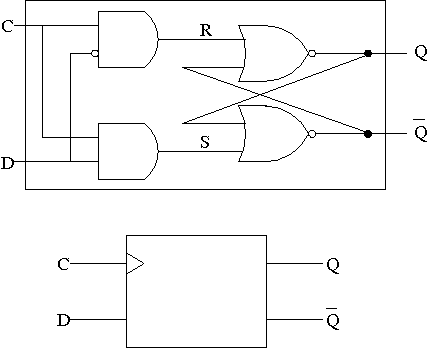
d latch

The D stands for data.


The extra inverter (the bubble on the top left) and the rewiring
  prevents R and S from both being 1.


Specifically, there are three cases.


    
  
  1. When the clock is low (false), both R and S are false and, as
    we saw before, Q and Q' remain unchanged.
    2. 
  
  2. When the clock is high and D is high, Q becomes true and Q'
    false.
    3. 
  
  3. When the clock is high and D is low, Q becomes fales and Q'
    becomes true.
    4. 



The summary is that, when the clock is asserted, the latch takes on
  the value of D, which is then held while the clock is low.
  The value of D is latched when the clock is high and held while the
  clock is low.


The smaller diagram shows how the latch is normally drawn.


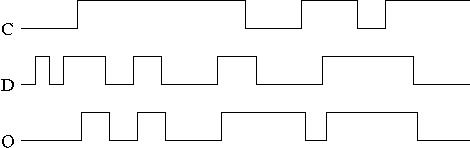
d-latch operation

In the traces to the right notice how the output follows the input
  when the clock is high and remains constant when the clock is low.
  We assume the stored value was initially low.





Remark: Grishman did 4-bit adders and subtracters.
  If you wish (on line) pictures, you can look at my
  
    architecture notes.
  




T-3.3.2: Flip-Flops


D or Master-Slave Flip-flop


This structure was our goal.
  It is an edge-triggered, clocked memory.
  The term edge-triggered means that values change at edges of the
  clock, either the rising edge or the falling edge.
  The edge at which the values change is called the active edge.

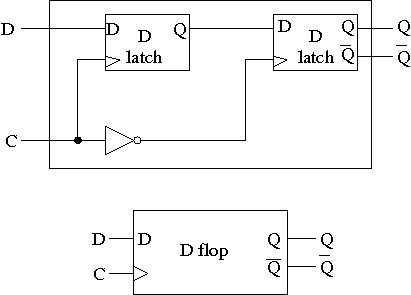
d-flop

The circuit for a D flop is on the right.
  It has the following properties.


d-flop operation

The picture on the right is for a master-slave flip-flop.
  Note how much less wiggly the output is in this picture than before
  with the transparent latch.
  As before we are assuming the output is initially low.


Homework:
  In the D-flop diagram, move the inverter to the other latch, i.e.,
  the inverted clock goes to the left latch and the positive clock
  goes to the right.
  What has changed in the D-flop?


Homework:
  Which code better describes a flip-flop and which a latch?


  repeat {
      while (clock is low) {do nothing}
      Q=D
      while (clock is high) {do nothing}
  } until forever


  repeat {
      while (clock is high) {Q=D}
  } until forever





  R-type datapath
  
Show how to make a register out of FFs (easy just use a bunch).

  
Show how to make a register file out of registers.
    Not too hard use a BIG mux.

  
Describe how to write a register.
    Actually the trick is how to not write a
    register.
    Recall that the constituent FFs are written at every falling edge.
    The idea is to introduce a signal that is ANDed with the clock to
    eliminate edges you don't want (this takes some care).

  
Then the diagram on the right shows the basic workings of a
    register based ADD (or SUB or OR or AND)

  
    add regA,regB,regC
  








  
Chapter T-4: The Microarchitecture Level







Chapter T-5: The Instruction Set Architecture Level


Remark: We jump ahead (out of order)
  so that I can cover enough x86 assemble language for you to do the
  assembler portion of the project.
  I am not following Tanenbaum's order here as the goal is just x86.


Remark: I believe
  
    this reference
  
  is a good resource for x86 assembly programming.



T-5.1: Overview of the ISA Level




  
5.1.1: Properties of the ISA Level


  
5.1.2: Memory Models


  
5.1.3: Registers


  
5.1.4: Instructions





T-5.1.5: Overview of the Pentium 4 ISA Level


In order to maintain compatibility with previous, long-out-of-date
  members of the x86 processor family, modern members can execute in
  three modes.


    
  
  1. Real Mode:
    The processor acts just like a
    1979 8088, the processor used in the original PC.
    If any program screws up, the machine crashes.
    
    
      If Intel had designed human beings, it would have put in a bit
      that made them revert back to chimpanzee mode (most of the
      brain disabled, no speach, sleeps in trees, eats mostly
      bananas, etc.)
    
    
    While perhaps humorous (Tanenbaum certainly writes well) the quote
    does hide the tremendous user advantages of having a new computer
    that can still execute old (often awful) programs, in particular
    old games, which were notorious for not being clean.
    2. 
  
  2. Virtual 8086/8088 mode: Now if a program crashes
    the OS is notified, rather than having the machine crash.
    I am not sure why (indeed, if) real mode is still needed, i.e.,
    why virtual 8086 mode did not simply replace it.
    3. 
  
  3. Protected mode: This is the mode we will study
    and is the mode used by all modern operating systems and
    applications.
    4. 




Registers on the x86


We will mainly use the 32-bit registers, their names begin with E
  standing for extended.
  They extended the 16-bit registers of early members of the family.

The four main registers are EAX, EBX, ECX, and EDX.
  Each is 32 bits.
  We will make most use of EAX, which is the main arithmetic register.
  Also functions returning a single word, return this in EAX.


  mov   EAX   ECX
  mov   EAX   [EBX]
  mov   EAX   [EBX+4]



If an address is in any one of these four the contents of that
  address can be specified as an operand for an instruction.
  Also an offset can be added.
  For example the first instruction on the right simply copies (the
  contents of) ECX into EAX.
  The second instruction does a de-reference.
  If EBX contains 1000, the contents of memory location 1000 is loaded
  into EAX.
  Finally, the last instruction would load the contents of 1004 into
  EAX (again assuming EBX contains 1000).

As you can see from the sheet I handed out and from Tanenbaum's
  figure 5-3, these registers contain named 16-bit and 8-bit subsets.

The two registers ESI and EDI are mostly used for the hardware
  string manipulation instructions.
  I don't think you will need those instructions, but you can also use
  ESI and EDI to hold other values (scratch storage).

The EBP register is normally used to hold the frame pointer FP,
  that will be described below.
  The ESP is the stack pointer (again described below).




  
5.1.6: Overview of the UltraSPARC III ISA Level


  
5.1.7: Overview of the 8051 ISA Level




  
5.2: Data Types




  
T-5.2.1: Numeric Data Types


  
T-5.2.2: Nonnumeric Data Types





T-5.2.3: Data Types on the Pentium 4 (x86)


The x86 architecture supports signed and unsigned integers of three
  sizes.
  
    
    
  1. 8 bit (one byte): used for ascii characters (C char).
    
  2. 16 bit (two bytes): used for unicode characters and for 16-bit
      integers (C short int).
    
  3. 32 bit (4 bytes): used for integers (C int).
  


There is also support for 32-bit and 64-bit floating point, which
  are used for C float and double respectively.

Finally, there is support for 8-bit BCD (binary coded decimal),
  which is not used in C.




  
T-5.2.4: Data types on the UltraSPARC III


  
T-5.2.5: Data types on the Java Virtual Machine





T-5.2A: Argument Passing from C to Assembler on x86


This is not from the book.

Since you will be writing an assembler subroutine called by a C
  program and your subroutine might call another C program, we need to
  understand how arguments, the return address, and the returned value
  are passed from caller to callee.
  The short answer is via the stack.

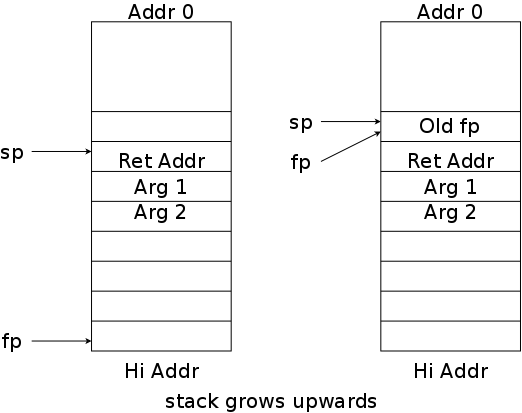
stack1

Each routine places its local variables on the stack, a region of
  memory that grows and shrinks during execution.
  (We are ignoring variables created via malloc as they are not
  allocated on the stack.)
  Due to the lifo nature of calls and returns, stack allocation works
  perfectly for such variables.

As shown in the diagrams, the stack starts at a high address and
grows towards location zero

Each routine uses a region of the stack called its
  stack frame or simply frame.
  The C convention (really the C-compiler convention) is that the
  frame is specified by two pointers: the frame pointer fp,
  which points to the beginning (bottom) of the frame, and the stack
  pointer sp that points to the current end (top) of the
  frame.
  As the routing places more information on the stack, sp
  moves (towards 0) to enlarge the stack.
  As the routine removes entries at the top of the stack,
  sp again moves (in this case away from 0).

In the left diagram the currently running procedure has just called
  another procedure.
  The caller has pushed the arguments onto the stack (in reverse
  order) and then pushed the return address (actually the call
  instruction did the last part).
  Also the caller has saved EAX, ECX, and EDX if necessary (these are
  referred to as caller-save registers).



    .intel_syntax noprefix
.globl add2
add2:   push    ebp
    mov ebp, esp
    mov eax, DWORD PTR [ebp+12]
    add eax, 1
    push    eax
    call    g
    add esp, 4 # undo the push
    pop ebp
    ret
#include <stdio.h>
int main(int argc, char *argv[]) {
    int i;
    for (i=0; i<10; i++)
    printf("i is %d and add2(1,i) is %d\n",
           i, add2(1,i));
    return 0;
}
int g(int x) {
    return x * x;
}
// Local Variables:
// compile-command: "cc -O add2.c add2.s \
// -mpreferred-stack-boundary=2; ./a.out"
// End:



We are the callee and first must set fp to the bottom of
  OUR frame (it is currently the bottom of the
  caller's frame).
  We also must save the current value of fp so that when we
  return to the caller, we can restore fp to the bottom of
  the caller's frame.

That is, we want to move from the left diagram to the right one.
  The first two assembler statements on the right do exactly this.
  The register EBP holds the current fp (I believe B is for
  base, the fp points to the base of the current stack).
  The register ESP holds sp.

The purpose of the program is to compute
  (x+1)2 for x between 0 and 10.
  The main program calls us with two arguments, the first is unused (I
  wanted to illustrate the order the arguments appear on the stack)
  the second is the value to be operated on.

We want to move the second argument to EAX for processing.
  This will overwrite whatever the caller had in EAX, but recall that
  it is one of the caller-saved registers (mentioned above) so we do
  not have to save it.
  How do we reference the second parameter?
  It is in the caller's stack frame, the one below ours.
  Since the stack grows towards zero, going backwards means increasing
  the fp.

Why is it 12 to go back only 3, and what is the DWORD PTR
  nonsense?
  The 12 is easy: 3 words equals 12 bytes.

The DWORD PTR is because a pointer (in this case
  ebp) can point to a byte, a 2-byte word, or a 4-byte
  doubleword.
  We think of 32-bit words, but the x86 family started out with 16-bit
  machines and it shows.

Next we add 1.
  Note that x86 is a 2-operand architecture, you can compute
  x=xOPy or x=yOPx but not x=yOPz.

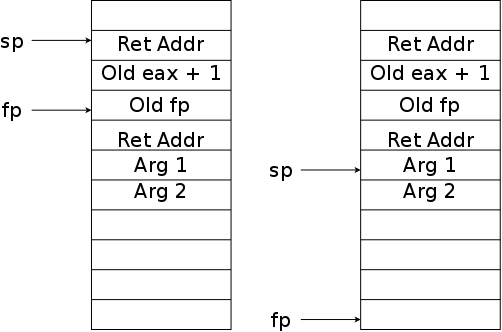
stack2

Now that we have x+1 we want to call a function to do the
  squaring.
  Thus, we are now the caller.

You might think that we need to save EAX since it is a caller-save
  register, but the value it contains is the first argument of the new
  callee so when we push that argument, we have saved EAX as well.
  We then issue the call instruction.

The function g, like all functions, returns its result in
  EAX.
  As it happens that value is the result we are charged with returning
  as well.
  Thus we just leave it there and return to our caller.




But wait, we have messed up the pointers to the stack!
  Hence, the end of our routine restores them before returning.
  The first diagram on the right shows the stack just after we have
  called g(), but before g() has executed.

When g executes ret, sp is lowered one
  word.
  We we execute add, sp is lowered again, returning
  us to the right stack in the previous diagram.
  The pop gives us the left stack in the previous diagram.
  Finally, our ret restores the stack to 2nd on the right,
  which is same as it was before main program called us.

Note that the values above sp are still there but the
  space would be reused if main() called another routine.







5.3: Instruction Formats




  
5.3.1: Design Criteria for Instruction Formats


  
5.3.2: Expanding Opcodes





5.3.3: The Pentium II (x86) Instruction Formats


Very complicated as is clear from looking at Figure 5-14 and
  reading the accompanying text.
  This makes it difficult for the hardware designer, which is not our problem.

It also makes the assembly language somewhat irregular.
  Specifically, it is not true that the 8 main registers
  EAX, EBX, ECX, EDX, ESI, EDI, ESP, EDP can be used
  interchangeably, certain instructions can use certain registers.



  
5.3.4: The UltraSPARC II Instruction Formats


  
5.3.5: The JVM Instruction Formats





T-5.4: Addressing



T-5.4.1: Addressing Modes


Most instructions have one or more operands, each of which is
  specified by a corresponding field in the instruction.
  It is the addressing mode that determines how the operand is
  determined given the address field.


T-5.4.2: Immediate Addressing


In this, the simplest form, the address field is not an address at
  all but is the operand.
  In this case we say the instruction has an immediate operand,
  because it can be determined immediately from the instruction
  (without requiring and additional memory reference).


T-5.4.3: Direct Addressing


Almost as simple, and better fitting the name address field, is for
  the address field to contain the address of the operand.
  So if the address field is 12, the operand is the contents of
  the 32-bit word (or 64-bit word, or 16-bit word, or 8-bit byte)
  specified by location 12.


T-5.4.4: Register Addressing


In this mode the operand is the register specified by the address
  field.
  So if the address field is 12 the operand is the contents of the
  register with address 12 (normally called simply register 12).
  This mode is very common and very fast.


T-5.4.5: Register Indirect Addressing


Using the terminology of C (and other high-level languages).
  This mode is just the de-reference operator applied to the previous
  mode.
  So if the address field is 12 the operand is determined by a two
  step process: first register 12 is examined.
  Say its value is 22888.
  Then the operand is the contents of the word (or byte, etc)
  specified by location 12.


T-5.4.6 Indexed Addressing


In this addressing mode, two values are used to determine the
  address: one is a used to specify a register and the second is a
  constant that is added to the contents of the register.
  The resulting sum is use as a memory address, the contents of which
  is the operand.

Why is this useful and why is it called indexed?
  Consider
  
    for (i=0; i<10; i++)
        A[i] = 0;
  

  and assume that the array A is global (so that its address is known
  before the program begins execution).

What is the address referred to by A[i]?

  It is the address of A[0] plus 4 times the value
  of i.
  The former is a constant (let's say it is 1280) and we use a
  register for the latter so the assembler loop would have body
  
    DWORD PTR mov [1280+EAX], 0     // X is the address of A[0], a known constant
    add EAX, 4
  

  Note that EAX is serving as the index i in the C
  code.
  Hence the name, indexed addressing.


T-5.4.7: Based-Indexed Addressing


If one register is good, two are better (or at least more general).
  In this mode, the contents of two registers are added to a constant.
  Consider again
  
    for (i=0; i<10; i++)
        A[i] = 0;
  

  but this time assume the array A is on the stack.
  Specifically assume A[0] is 1000 bytes below SP
  the top of the stack.
  Register ESP typically holds SP so the loop body
  in assembler would be
  
    mov DWORD PTR [ESP+EAX+1000], 0
    add EAX, 4
  




  
T-5.4.8: Stack Addressing


  
Reverse Polish Notation


  
Evaluation of Reverse Polish Notation Formulas


  
T-5.4.9: Addressing Modes for Branch Instructions


  
T-5.4.10: Orthogonality of Opcodes and Addressing Modes





T-5.4.11: The Pentium 4 Addressing Modes


The x86 is quite irregular: not all addressing modes are available
  for all instructions and not all registers can be used for all
  addressing modes.

The machine has both 16-bit and 32-bit flavors of operations, we
  are only studying the 32-bit versions.

The x86 is a two operand machine, but at most one operand can be a
  memory location.

The x86 supports immediate, direct, register, register indirect,
  indexed, and based-index.
  Based-index uses an extra byte of instruction call the SIB (Scale,
  Index, Base), which specifies not only both the base and index
  registers, but a scale of 1, 2, 4, or 8 that is multiplied with the
  index register, which permits that register to represent the number
  of bytes, (16-bit) words, double words, or quad words the effective
  address is displaced from the base.

I do not understand why Tanenbaum does not consider addresses using
  SIB to be employing based-index mode.




  
T-5.4.12: The UltraSPARC Addressing Modes


  
T-5.4.13: The 8051 Addressing Modes


  
T-5.4.14: Discussion of Addressing Modes


  
T-5.6: Flow of Control


  
T-5.7: A Detailed Example: The Towers of Hanoi


  
T5.8: The IA-64 Architecture and the Itanium2


  
T5.6: Summary









Appendix TA: Binary Numbers



T-A.1: Finite Precision Numbers


In mathematics, integers have infinite precision.
  That is, we uses as many digits as are needed, without limit.

Some software systems offer this as well (up to the memory limits
  of the computer).
  However, we will be looking at the native hardware support for
  integers (we will not do floating point, which is a little more
  complicated).
  On most systems you can buy today, the normal integer is 32 bits or
  64 bits.
  That means you write integers using 32 bits (or 64 buts, but we will
  concentrate on 32-bit systems).
  If an integer requires more than 32 bits it cannot be expressed
  using the native hardware representation of integers.

This possibility of a number not being expressible leads to
  anomalies, such as overflow.
  We will learn the representation shortly, but for the moment note
  that the largest integer expressible in the native 32-bit system is
  231-1=2,147,483,647.
  Thus
  
    (2,000,000,000-1,000,000,000)+1,000,000,000 ≠
    (2,000,000,000+1,000,000,000)-1,000,000,000
  

  Specifically, the first computation yields the mathematically
  correct answer of 2,000,000,000; whereas, the second gives no answer
  since an overflow occurs during the addition.



T-A.2: Radix Number Systems


We write our numbers in the radix-10 system.
  That is the digits read from the right tell you how many 1s,
  how many 10s, how many 100s, etc.
  Note that 1=100, 10=101, 100=102,
  etc.
  (Some ancient civilizations used other radices—or radixes.)

Almost all computers use radix 2; that is what we shall use.
  So the bits (sometimes called binary digits) from
  right to left tell you how many 1s, 2s, 4s, 8s, etc., where
  1=20, 2=21, 4=22, 8=23,
  etc.



A.3: Conversion from one Radix to Another


It is very easy to convert from radix 2 to any radix
  2n.
  You simply group n of the bits together to form a single
  digit in radix 2n.

Do this on the board for octal (radix 8=23) and
  hexadecimal (radix 16=24).



Converting from Binary to Decimal


You can simply follow the definition.
  For the binary number ABCDEFG (each letter is a bit),
  the decimal equivalent is
  
    A×26+B×25...+F×21+G×20 = A×128+B×64...+F×2+G
  

  Less work is to evaluate the equivalent expression
  
    G+2×(F+2×(E+2×(D+2×(C+2×(B+2×A)))))
  

  from right to left
  (start with A, double it and add B, double the sum and add C, ....



Converting from Decimal to Binary


Take the remainders obtained with successive divisions by two.

For example, take 103.
  
    
    
  1. Dividing 103 by two gives a quotient Q=51 and a remainder R=1.
      This says the low order bit is 1.
    
  2. Next divide the quotient 51 by 2 and get Q=25 & R=1.
      So the low order is now 11.
    
  3. Dividing 25 by 2 gives Q=12 & R=1; low order is 111.
    
  4. Dividing 12 by 2 gives Q=6 & R=0; low order is 0111.
    
  5. Dividing 6 by 2 gives Q=3 & R=0; low order is 00111.
    
  6. Dividing 3 by 2 gives Q=1 & R=1; low order is 10111.
    
  7. Dividing 1 by 2 gives Q=0 & R=1; low order is 10111.
  




Homework: 1, 2, 3


T-A.4: Negative Binary Numbers


There are several schemes for representing binary numbers; we will
  study the one that is used on essentially all modern machines:
  two's complement.

Although we are interested in 32-bit systems, let's use 4 bits in
  this section since it will ease our task when we do arithmetic and
  draw pictures.
  There is basically no difference between n-bit and m-bit systems
  providing n and m are least 3.



How Many Positive Values and How Many Negative Values


With 4 bits, we can express 16 numbers.
  One of these bit pattern must be used for zero, leaving 15 for
  positive and negative.
  Thus we cannot achieve the ideal of using all 16 values, having
  exactly one representation for each expressible value, and having
  the same number of positive and negative values.
  So we must give up one of these ideals.
  Possibilities include
  
    
    
  1. Having two (or more) different representations for some
      values.
    
  2. Having at least one bit pattern declared illegal.
    
  3. Having a different number of positive and negative values.
  


Possibility 1 has been done (in this very building!).
  The CDC 6600, then the fastest computer in the world, used one's
  complement arithmetic, which has two expressions for zero
  (0000 and 1111).

Also one could use the bottom three bits to express 0-7 and declare
  the top bit as the sign so both 0000 and 1000 would be zero.

I don't know of a machine that ever did possibility 2.

The third possibility dominates and that is what we will study.



A Conceptual Understanding of Twos Complement


This text (and many others) just tells you how to do it (take the
  ordinary (bitwise) complement (called the one's complement) and then
  add 1 to get the two's complement.

That sound too much like instructions to Merlin for my liking.
  So I will try to explain why it is done.

Recall we have zero and 15 additional numbers to split among the
  positive and negative values.
  Seven will be positive and eight negative.
  It will become clear later why we don't have 8 positive and seven
  negative.

Good news.
  The values from 0-7 are expressed as you would expect:

  0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111.

  The high order bit gives the sign and the bottom n-1=4-1=3 bits
  gives the magnitude.

Bad news.
  The value -3 is not just the value for three with the sign bit 1.

Let's begin.

Note that the number 16 in binary is 10000, it is the first number
  that cannot be expressed in 4 bits.
  If we chop off the high bit (normally called HOB, high-order
  bit), 16 becomes 0.
  Said mathematically 16 mod 16 is 0.

Now what about -3?
  The definition of -3 is that it is the (unique) number that, when
  added to 3, gives 0.
  Instead of demanding to get 0 when added, we loosen the requirement
  to say that we want a number that, when added to 3, gives 0 mod 16.

There are lots of them: 13+3=16, which is 0 mod 16;
  29+3=32, which also is 0 mod 16.
  But there is only one number in the range 0-15 that has this
  property, and those are precisely the numbers expressible in 4 bits.

Mathematically we are simply taking -3 mod 16.

So, for us -3 is the 4-bit representation of 13, which is 1101.
  If we simply add and throw away the 5th bit we see that 13+3 is
  indeed 0: 1101+0011=10000, which becomes 0000 when we throw away bit
  5.

Recall that we define -n to be the number, which when added to n
  gives 16, i.e. we just express -n as (-n) mod 16.
  This is all for n between 1 and 7.

The properties of mod permit us to prove the normal laws of inverses.
  For example, the inverse of n+m is
  
    -(n+m) mod 16 = (-n)+(-m) mod 16 = [(-n) mod 16] + [(-m) mod 16]
  

  which is precisely the inverse of n plus the inverse of m.

OK, but how do you calculate inverses on the computer.
  For our 4-bit system, do we calculate the inverse of 3 by
  evaluating -3 mod 16?
  With a 32-bit system, do we calculate the inverse of 1,000,000 by
  evaluating -1,000,000 mod 232?

There is indeed an easier way.
  Recall that to find the inverse of 3 we needed to find the number
  with the property that when added to 3 we get 16.

Written in 4-bit binary we want the number that when added to 0011
  gives us 10000 (I know that is 5-bits).

Let's ask a different question.
  What is the number that when added to 0011, gives 1111.
  That is easy, look at 0011 and take the complement, 1100.
  Then between the original and the complement each bit position has
  exactly one 1 so the sum is clearly 1111.
  (This number 1100 is called the one's complement).

Since we really wanted to get 10000 not just 1111, we need to add
  one.
  This gives 1101, which is indeed the two's complement of 0011.

So the rule is:
  Take the bitwise complement and add 1, just as all the text books
  say.
  So for 4-bit numbers using two's complement arithmetic, -0011 is
  1101.
  Said more simply -3 is 1101 in 4-bit 2's complement arithmetic.



Negating Negative Numbers and the Lack of Ideal Behavior


It is not too hard to see that this same procedure works when the
  original number is negative.
  Lets try -(-3).
  We already know -3 is 1101.
  Complementing gives 0010 and adding 1 gives 0011.
  Success.

Addition works too.
  Compute -2=-0010=1101+1=1110; (-2)+(-3)=1101+1110=11011 toss the HOB
  and the answer is 1011.
  Is this really -5?
  Does 1011+0100 give 16?
  Yes!

Is -(1011) equal to 5?
  Take the complement and add 1: 0100+1=0101=5.

Now the sad news.
  (-4)+(-4)=1100+1100=11000 toss the HOB and get 1000, which actually
  is -8 but the complement is 0111+1=1000 which is not 8.
  Remember we can't have the same number of positives as negatives.
  So the range for 4-bit two's complement is -8,-7,...0,...6,7.



T-A.5: Binary Arithmetic


Tanenbaum does both one's complement and two's complement
  arithmetic.
  We will just do the latter.
  As we indicated above you simply add the two's complement numbers
  with no thought of signs or compliments.
  If you add two n-bit numbers you might get an (n+1)-bit number,
  i.e., you might get a carry-out of the high order bit.
  But the rule is simple, toss it!



Subtraction


The rule is the same as what you learned in elementary school,
  a-b=a+(-b).
  That is you invert (take the two's complement) the b and
  add.
  For example 5-3 is (0101)-(0011)=(0101)+(1101)=10010 toss the HOB
  and get 0010 which is 2.

Homework: 7.


Overflow


Unfortunately, although the above does describe (part of)
  the hardware, it doesn't always give the correct answer.
  As a simple example, with our 4-bit system we can express -8...7,
  but if you add 5+6 you should get 11.
  We cannot possibly get 11 since we can't express
  11.
  Similarly if you add (-5)+(-6), you should get -11, which again we
  cannot even express.

When the result falls outside the expressible range,
  an overflow has occurred.

When you add numbers of opposite sign overflow is impossible (the
  result is between the two original numbers).

As we have seen, subtracting numbers of the same sign is the same
  as adding numbers of opposite sign so again overflow is impossible.

When you add numbers of the same sign (or subtract numbers of the
  opposite sign) overflow is possible.
  The question is, When does it occur?.

The answer is simple to state but not so simple to explain (you
  need to analyze several cases): An overflow occurs if and only if
  the carry into the HOB does not equal the carry out from the HOB.

Homework: 9.