Operating Systems

Start Lecture #6

Lab 2 (Scheduling) Discussion

Show the detailed output

1. In FCFS see the affect of A, B, C, and I/O
2. In RR see how the cpu burst is limited.
3. Note the intital sorting to ease finding the tie breaking process.
4. Note show random.
5. Comment on how to do it: (time-based) discrete-event simulation (DES).
   1. DoBlockedProcesses()
   2. DoRunningProcesses()
   3. DoCreatedProcesses()
   4. DoReadyProcesses()
6. For processor sharing need event-based DES.

2.5 Classical IPC Problems

2.5.0 The Producer-Consumer (or Bounded Buffer) Problem

We did this previously.

2.5.1 The Dining Philosophers Problem

A classical problem from Dijkstra

• 5 philosophers sitting at a round table
• Each has a plate of spaghetti
• There is a fork between each two
• Need two forks to eat

What algorithm do you use for access to the shared resource (the forks)?

• The obvious solution (pick up right; pick up left) deadlocks.
• Big lock around everything serializes.
• Good code in the book.

The purpose of mentioning the Dining Philosophers problem without giving the solution is to give a feel of what coordination problems are like. The book gives others as well. The solutions would be covered in a sequel course. If you are interested look, for example here.

Homework: 45 and 46 (these have short answers but are not easy). Note that the second problem refers to fig. 2-20, which is incorrect. It should be fig 2-46.

2.5.2 The Readers and Writers Problem

As in the producer-consumer problem we have two classes of processes.

• Readers, which can work concurrently.
• Writers, which need exclusive access.

The problem is to

1. prevent 2 writers from being concurrent.
2. prevent a reader and a writer from being concurrent.
3. permit readers to be concurrent when no writer is active.
4. (perhaps) insure fairness (e.g., freedom from starvation).

Variants

• Writer-priority readers/writers.
• Reader-priority readers/writers.

Solutions to the readers-writers problem are quite useful in multiprocessor operating systems and database systems. The easy way out is to treat all processes as writers in which case the problem reduces to mutual exclusion (P and V). The disadvantage of the easy way out is that you give up reader concurrency. Again for more information see the web page referenced above.

2.5B: Summary of 2.3 and 2.5

We began with a subtle bug (wrong answer for x++ and x--) and used it to motivate the Critical Section Problem for which we provided a (software) solution.

We then defined (binary) Semaphores and showed that a Semaphore easily solves the critical section problem and doesn't require knowledge of how many processes are competing for the critical section. We gave an implementation using Test-and-Set.

We then gave an operational definition of Semaphore (which is not an implementation) and morphed this definition to obtain a Counting (or Generalized) Semaphore, for which we gave NO implementation. I asserted that a counting semaphore can be implemented using 2 binary semaphores and gave a reference.

We defined the Producer-Consumer (or Bounded Buffer) Problem and showed that it can be solved using counting semaphores (and binary semaphores, which are a special case).

Finally we briefly discussed some classical problems, but did not give (full) solutions.

2.7 Summary

Skipped, but you should read.

Chapter 6 Deadlocks

Remark: Deadlocks are closely related to process management so belong here, right after chapter 2. It was here in 2e. A goal of 3e is to make sure that the basic material gets covered in one semester. But I know we will do the first 6 chapters so there is no need for us to postpone the study of deadlock.

A deadlock occurs when every member of a set of processes is waiting for an event that can only be caused by a member of the set.

Often the event waited for is the release of a resource.

In the automotive world deadlocks are called gridlocks.

• The processes are the cars.
• The resources are the spaces occupied by the cars

For a computer science example consider two processes A and B that each want to print a file currently on a CD-ROM Drive.

1. A has obtained ownership of the printer and will release it after getting the CD Drive and printing one file.
2. B has obtained ownership of the CD drive and will release it after getting the printer and printing one file.
3. A tries to get ownership of the drive, but is told to wait for B to release it.
4. B tries to get ownership of the printer, but is told to wait for A to release it.

Bingo: deadlock!

6.1 Resources

A resource is an object granted to a process.

6.1.1 Preemptable and Nonpreemptable Resources

Resources come in two types

1. Preemptable, meaning that the resource can be taken away from its current owner (and given back later). An example is memory.
2. Non-preemptable, meaning that the resource cannot be taken away. An example is a printer.

The interesting issues arise with non-preemptable resources so those are the ones we study.

The life history of a resource is a sequence of

1. Request
2. Allocate
3. Use
4. Release

Processes request the resource, use the resource, and release the resource. The allocate decisions are made by the system and we will study policies used to make these decisions.

6.1.2 Resource Acquisition

A simple example of the trouble you can get into.

• Two resources and two processes.
• Each process wants both resources.
• Use a semaphore for each. Call them S and T.
• If both processes execute
  P(S); P(T); --- V(T); V(S)
  all is well.
• But if one executes instead
  P(T); P(S); -- V(S); V(T)
  disaster! This was the printer/CD example just above.

Recall from the semaphore/critical-section treatment last chapter, that it is easy to cause trouble if a process dies or stays forever inside its critical section. We assumed processes do not do this. Similarly, we assume that no process retains a resource forever. It may obtain the resource an unbounded number of times (i.e. it can have a loop forever with a resource request inside), but each time it gets the resource, it must release it eventually.

6.2 Introduction to Deadlocks

Definition: A deadlock occurs when a every member of a set of processes is waiting for an event that can only be caused by a member of the set.

Often the event waited for is the release of a resource.

6.2.1 (Necessary) Conditions for Deadlock

The following four conditions (Coffman; Havender) are necessary but not sufficient for deadlock. Repeat: They are not sufficient.

1. Mutual exclusion: A resource can be assigned to at most one process at a time (no sharing).
2. Hold and wait: A processing holding a resource is permitted to request another.
3. No preemption: A process must release its resources; they cannot be taken away.
4. Circular wait: There must be a chain of processes such that each member of the chain is waiting for a resource held by the next member of the chain.

One can say If you want a deadlock, you must have these four conditions.. But of course you don't actually want a deadlock, so you would more likely say If you want to prevent deadlock, you need only violate one or more of these four conditions..

The first three are static characteristics of the system and resources. That is, for a given system with a fixed set of resources, the first three conditions are either always true or always false: They don't change with time. The truth or falsehood of the last condition does indeed change with time as the resources are requested/allocated/released.

6.2.2 Deadlock Modeling

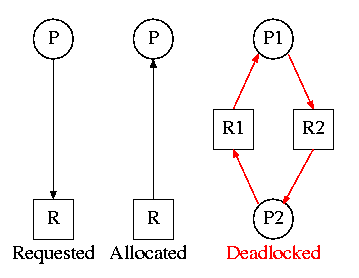
On the right are several examples of a Resource Allocation Graph, also called a Reusable Resource Graph.

• The processes are circles.
• The resources are squares.
• An arc (directed line) from a process P to a resource R signifies that process P has requested (but not yet been allocated) resource R.
• An arc from a resource R to a process P indicates that process P has been allocated resource R.

Homework: 5.

Consider two concurrent processes P1 and P2 whose programs are.

    P1                   P2
    request R1           request R2
    request R2           request R1
    release R2           release R1
    release R1           release R2
  

On the board draw the resource allocation graph for various possible executions of the processes, indicating when deadlock occurs and when deadlock is no longer avoidable.

There are four strategies used for dealing with deadlocks.

1. Ignore the problem
2. Detect deadlocks and recover from them
3. Prevent deadlocks by violating one of the 4 necessary conditions.
4. Avoid deadlocks by carefully deciding when to allocate resources.

6.3 Ignoring the problem—The Ostrich Algorithm

The put your head in the sand approach.

• If the likelihood of a deadlock is sufficiently small and the cost of avoiding a deadlock is sufficiently high it might be better to ignore the problem. For example, if each PC deadlocks once per 10 years, the one reboot may be less painful that the restrictions needed to prevent it.
• Clearly not a good philosophy for nuclear missile launchers or patient monitoring systems for cardiac care units.
• For embedded systems (such as the two examples above) the programs run are fixed in advance so many of the issues that occur in systems like linux or windows (such as many processes wanting to fork at the same time) don't occur.

6.4 Detecting Deadlocks and Recovering From Them

6.4.1 Detecting Deadlocks with Single Unit Resources

Consider the case in which there is only one instance of each resource.

• Thus a request can be satisfied by only one specific resource.
• In this case the 4 necessary conditions for deadlock are also sufficient.
• Remember we are making an assumption (single unit resources) that is often invalid. For example, many systems have several printers and a request is given for a printer not a specific printer. Similarly, one can have many CD-ROM drives.
• So the problem comes down to finding a directed cycle in the resource allocation graph. Why?
  Answer: Because the other three conditions are either satisfied by the system we are studying, or are not in which case deadlock is not a question. That is, conditions 1,2,3 are static conditions on the system in general not conditions on the state of the system right now.

To find a directed cycle in a directed graph is not hard. The algorithm is in the book. The idea is simple.

1. For each node in the graph do a depth first traversal to see if the graph is a DAG (directed acyclic graph), building a list as you go down the DAG (and pruning it as you backtrack back up).
2. If you ever find the same node twice on your list, you have found a directed cycle, the graph is not a DAG, and deadlock exists among the processes in your current list.
3. If you never find the same node twice, the graph is a DAG and no deadlock exists (right now).

The searches are finite since there are a finite number of nodes and you stop if you hit a node twice.

6.4.2 Detecting Deadlocks with Multiple Unit Resources

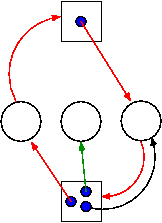
This is more difficult.

• The figure on the right shows a resource allocation graph with multiple unit resources.
  
  
• Each unit is represented by a dot in the box.
  
  
• Request edges are drawn to the box since they represent a request for any dot in the box.
  
  
• Allocation edges are drawn from the dot to represent that this unit of the resource has been assigned (but all units of a resource are equivalent and the choice of which one to assign is arbitrary).
  
  
• Note that there is a directed cycle in red, but there is no deadlock. Indeed the middle process might finish, erasing the green arc and permitting the blue dot to satisfy the rightmost process.
  
  
• The book gives an algorithm for detecting deadlocks in this more general setting. The idea is as follows.
  1. look for a process that might be able to terminate. That is, a process all of whose request arcs can be satisfied by resources the manager has on hand right now.
  2. If one is found, pretend that it does terminate (erase all its arcs), and repeat step 1.
  3. If any processes remain, they are deadlocked.
  
  
• We will soon do in detail an algorithm (the Banker's algorithm) that has some of this flavor.
  
  
• The algorithm just given makes the most optimistic assumption about a running process: it will return all its resources and terminate normally. If we still find processes that remain blocked, they are deadlocked.
  
  
• In the bankers algorithm we make the most pessimistic assumption about a running process: it immediately asks for all the resources it can (details later on can). If, even with such demanding processes, the resource manager can insure that all process terminates, then we can insure that deadlock is avoided.

6.4.3 Recovery from deadlock

Recovery through Preemption

Perhaps you can temporarily preempt a resource from a process. Not likely.

Recovery through Rollback

Database (and other) systems take periodic checkpoints. If the system does take checkpoints, one can roll back to a checkpoint whenever a deadlock is detected. You must somehow guarantee forward progress.

Recovery through Killing Processes

Can always be done but might be painful. For example some processes have had effects that can't be simply undone. Print, launch a missile, etc.

Remark: We are doing 6.6 before 6.5 since 6.6 is easier and I believe serves as a good warm-up.

6.6: Deadlock Prevention

Attack one of the Coffman/Havender conditions.

6.6.1 Attacking the Mutual Exclusion Condition

The idea is to use spooling instead of mutual exclusion. Not possible for many kinds of resources.

6.6.2 Attacking the Hold and Wait Condition

Require each processes to request all resources at the beginning of the run. This is often called One Shot.

6.6.3 Attacking the No Preemption Condition

Normally not possible. That is, some resources are inherently pre-emptable (e.g., memory). For those, deadlock is not an issue. Other resources are non-preemptable, such as a robot arm. It is often not possible to find a way to preempt one of these latter resources. One exception is if the resource (say a CD-ROM drive) can be virtualized (recall hypervisors).

6.6.4 Attacking the Circular Wait Condition

Establish a fixed ordering of the resources and require that they be requested in this order. So if a process holds resources #34 and #54, it can request only resources #55 and higher.

It is easy to see that a cycle is no longer possible.

Homework: Consider Figure 6-4. Suppose that in step (o) C requested S instead of requesting R. Would this lead to deadlock? Suppose that it requested both S and R.