Operating Systems

Start Lecture #5

Remarks: Lab 2 (scheduling) is available. It is due in 2 weeks.

Theoretical Issues

Considerable theory has been developed.

• NP completeness results abound.
• Much work in queuing theory to predict performance.
• Not covered in this course.

Medium-Term Scheduling

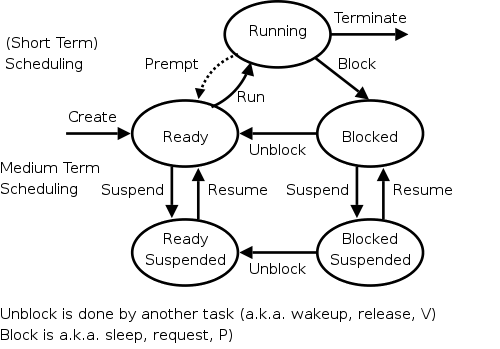
In addition to the short-term scheduling we have discussed, we add medium-term scheduling in which decisions are made at a coarser time scale.

Recall my favorite diagram, shown again on the right. Medium term scheduling determines the transitions from the top triangle to the bottom line. We suspend (swap out) some process if memory is over-committed, dropping the (ready or blocked) process down. We also need resume transitions to return a process to the top triangle.

Criteria for choosing a victim to suspend include:

• How long since previously suspended.
• How much CPU time used recently.
• How much memory does it use.
• External priority (pay more, get swapped out less).

We will discuss medium term scheduling again when we study memory management.

Long Term Scheduling

This is sometimes called Job scheduling.

1. The system decides when to start jobs, i.e., it does not necessarily start them when submitted.
2. Used at many supercomputer sites.

A similar idea (but more drastic and not always so well coordinated) is to force some users to log out, kill processes, and/or block logins if over-committed.

• CTSS (an early time sharing system at MIT) did this to insure decent interactive response time.
• Unix does this if out of memory.
• LEM jobs during the day (Grumman).

Review Homework Assigned Last Time

2.3 Interprocess Communication (IPC) and Coordination/Synchronization

2.3.1 Race Conditions

A race condition occurs when two (or more) processes are about to perform some action. Depending on the exact timing, one or other goes first. If one of the processes goes first, everything works correctly, but if another one goes first, an error, possibly fatal, occurs.

Imagine two processes both accessing x, which is initially 10.

A1: LOAD  r1,x     B1: LOAD  r2,x
A2: ADD   r1,1     B2: SUB   r2,1
A3: STORE r1,x     B3: STORE r2,x

• One process is to execute x := x+1
• The other is to execute x := x-1
• When both are finished x should be 10
• But x := x+1 is not atomic; see the code on the right
• Show in class how we can get 9 or 11!
• Tanenbaum shows how this can lead to disaster for a printer spooler

2.3.2 Critical Regions (Sections)

We must prevent interleaving sections of code that need to be atomic with respect to each other. That is, the conflicting sections need mutual exclusion. If process A is executing its critical section, it excludes process B from executing its critical section. Conversely if process B is executing is critical section, it excludes process A from executing its critical section.

Requirements for a critical section implementation.

1. No two processes may be simultaneously inside their critical section.
   
   
2. No assumption may be made about the speeds or the number of concurrent threads/processes.
   
   
3. No process outside its critical section (including the entry and exit code) may block other processes.
   
   
4. No process should have to wait forever to enter its critical section.
   • I do NOT make this last requirement.
   • I just require that the system as a whole make progress (so not all processes are blocked).
   • I refer to solutions that do not satisfy Tanenbaum's last condition as unfair, but nonetheless correct, solutions.
   • Stronger fairness conditions have also been defined.

2.3.3 Mutual exclusion with busy waiting

We will study only solutions in this class. Note that higher level solutions, e.g., having one process block when it cannot enter its critical are implemented using busy waiting algorithms.

Disabling Interrupts

The operating system can choose not to preempt itself. That is, we could choose not to preempt system processes (if the OS is client server) or processes running in system mode (if the OS is self service). Forbidding preemption for system processes would prevent the problem above where x<--x+1 not being atomic crashed the printer spooler if the spooler is part of the OS.

The way to prevent preemption of kernel-mode code is to disable interrupts. Indeed, disabling (i.e., temporarily preventing) interrupts is often done for exactly this reason.

This is not, however, sufficient for all cases.

• It does not work for user-mode programs. So the Unix print spooler, which is a user-mode program would need another solution.
• We do not want to block interrupts for too long or the system will seem unresponsive.
• Disabling interrupts is insufficient if the system has several processors.
  • The main line can be executing on both processors simultaneously so interrupts are not involved.
  • One processor cannot block interrupts on the other.

Software solutions for two processes

Lock Variables

  Initially P1wants=P2wants=false

  Code for P1                             Code for P2

  Loop forever {                          Loop forever {
     P1wants <-- true         ENTRY          P2wants <-- true
     while (P2wants) {}       ENTRY          while (P1wants) {}
     critical-section                        critical-section
     P1wants <-- false        EXIT           P2wants <-- false
     non-critical-section }                  non-critical-section }

Explain why this works.

But it is wrong!
Why?

Let's try again. The trouble was that setting want before the loop permitted us to get stuck. We had them in the wrong order!

    Initially P1wants=P2wants=false

    Code for P1                             Code for P2

    Loop forever {                          Loop forever {
       while (P2wants) {}       ENTRY          while (P1wants) {}
       P1wants <-- true         ENTRY          P2wants <-- true
       critical-section                        critical-section
       P1wants <-- false        EXIT           P2wants <-- false
       non-critical-section }                  non-critical-section }
  

Explain why this works.

But it is wrong again!
Why?

Strict Alternation

Now let's try being polite and really take turns. None of this wanting stuff.

    Initially turn=1

    Code for P1                      Code for P2

    Loop forever {                   Loop forever {
       while (turn = 2) {}              while (turn = 1) {}
       critical-section                 critical-section
       turn <-- 2                       turn <-- 1
       non-critical-section }           non-critical-section }
  

This one forces alternation, so is not general enough. Specifically, it does not satisfy condition three, which requires that no process in its non-critical section can stop another process from entering its critical section. With alternation, if one process is in its non-critical section (NCS) then the other can enter the CS once but not again.

The first example violated rule 4 (the whole system blocked). The second example violated rule 1 (both in the critical section. The third example violated rule 3 (one process in the NCS stopped another from entering its CS).

In fact, it took years (way back when) to find a correct solution. Many earlier solutions were found and several were published, but all were wrong. The first correct solution was found by a mathematician named Dekker, who combined the ideas of turn and wants. The basic idea is that you take turns when there is contention, but when there is no contention, the requesting process can enter. It is very clever, but I am skipping it (I cover it when I teach distributed operating systems in V22.0480 or G22.2251). Subsequently, algorithms with better fairness properties were found (e.g., no task has to wait for another task to enter the CS twice).

What follows is Peterson's solution, which also combines wants and turn to force alternation only when there is contention. When Peterson's algorithm was published, it was a surprise to see such a simple solution. In fact Peterson gave a solution for any number of processes. A proof that the algorithm satisfies our properties (including a strong fairness condition) for any number of processes can be found in Operating Systems Review Jan 1990, pp. 18-22.

    Initially P1wants=P2wants=false  and  turn=1

    Code for P1                        Code for P2

    Loop forever {                     Loop forever {
       P1wants <-- true                   P2wants <-- true
       turn <-- 2                         turn <-- 1
       while (P2wants and turn=2) {}      while (P1wants and turn=1) {}
       critical-section                   critical-section
       P1wants <-- false                  P2wants <-- false
       non-critical-section }             non-critical-section }
  

The TSL Instruction (Hardware Assist test-and-set)

Tanenbaum calls this instruction test and set lock TSL.

I call it test and set (TAS) and define
TAS(b), where b is a binary variable,
to ATOMICALLY set b←true and return the OLD value of b.

Of course it would be silly to return the new value of b since we know the new value is true.

The word atomically means that the two actions performed by TAS(x), testing (i.e., returning the old value of x) and setting (i.e., assigning true to x) are inseparable. Specifically it is not possible for two concurrent TAS(x) operations to both return false (unless there is also another concurrent statement that sets x to false).

With TAS available, implementing a critical section for any number of processes is trivial.

    loop forever {
        while (TAS(s)) {}  ENTRY
        CS
        s<--false          EXIT
        NCS }
   

2.3.4 Sleep and Wakeup

Remark: Tanenbaum presents both busy waiting (as above) and blocking (process switching) solutions. We present only do busy waiting solutions, which are easier and used in the blocking solutions. Sleep and Wakeup are the simplest blocking primitives. Sleep voluntarily blocks the process and wakeup unblocks a sleeping process. However, it is far from clear how sleep and wakeup are implemented. Indeed, deep inside, they typically use TAS or some similar primitive. We will not cover these solutions.

Homework: Explain the difference between busy waiting and blocking process synchronization.

2.3.5: Semaphores

Remark: Tannenbaum use the term semaphore only for blocking solutions. I will use the term for our busy waiting solutions (as well as for blocking solutions). Others call our solutions spin locks.

P and V and Semaphores

The entry code is often called P and the exit code V. Thus the critical section problem is to write P and V so that

    loop forever
       P
       critical-section
       V
       non-critical-section
  

1. Mutual exclusion.
2. No speed assumptions.
3. No blocking by processes in NCS.
4. Forward progress (my weakened version of Tanenbaum's last condition).

Note that I use indenting carefully and hence do not need (and sometimes omit) the braces {} used in languages like C or java.

A binary semaphore abstracts the TAS solution we gave for the critical section problem.

• A binary semaphore S takes on two possible values open and closed.
• Two operations are supported
• P(S) is

          while (S=closed) {}
          S<--closed     -- This is NOT the body of the while
        

  where finding S=open and setting S<--closed is atomic
• That is, wait until the gate is open, then run through and atomically close the gate
• Said another way, it is not possible for two processes doing P(S) simultaneously to both see S=open (unless a V(S) is also simultaneous with both of them).
• V(S) is simply S<--open

The above code is not real, i.e., it is not an implementation of P. It requires a sequence of two instructions to be atomic and that is, after all, what we are trying to implement in the first place. The above code is, instead, a definition of the effect P is to have.

To repeat: for any number of processes, the critical section problem can be solved by

    loop forever
       P(S)
       CS
       V(S)
       NCS
  

The only solution we have seen for an arbitrary number of processes is the one just above with P(S) implemented via test and set.

Remark: Peterson's solution requires each process to know its process number; the TAS soluton does not. Moreover the definition of P and V does not permit use of the process number. Thus, strictly speaking Peterson did not provide an implementation of P and V. He did solve the critical section problem.

To solve other coordination problems we want to extend binary semaphores.

• With binary semaphores, two consecutive Vs do not permit two subsequent Ps to succeed (the gate cannot be doubly opened).
• We might want to limit the number of processes in the section to 3 or 4, not always just 1.

Both of the shortcomings can be overcome by not restricting ourselves to a binary variable, but instead define a generalized or counting semaphore.

• A counting semaphore S takes on non-negative integer values
• Two operations are supported
• P(S) is

          while (S=0) {}
          S--
        

  where finding S>0 and decrementing S is atomic
• That is, wait until the gate is open (positive), then run through and atomically close the gate one unit
• Another way to describe this atomicity is to say that it is not possible for the decrement to occur when S=0 and it is also not possible for two processes executing P(S) simultaneously to both see the same necessarily (positive) value of S unless a V(S) is also simultaneous.
• V(S) is simply     S++

Counting semaphores can solve what I call the semi-critical-section problem, where you premit up to k processes in the section. When k=1 we have the original critical-section problem.

    initially S=k

    loop forever
       P(S)
       SCS   -- semi-critical-section
       V(S)
       NCS
  

Solving the Producer-Consumer Problem Using Semaphores

Note that my definition of semaphore is different from Tanenbaum's so it is not surprising that my solution is also different from his.

Unlike the previous problems of mutual exclusion, the producer-consumer has two classes of processes

• Producers, which produce items and insert them into a buffer.
• Consumers, which remove items and consume them.

What happens if the producer encounters a full buffer?
Answer: It waits for the buffer to become non-full.

What if the consumer encounters an empty buffer?
Answer: It waits for the buffer to become non-empty.

The producer-consumer problem is also called the bounded buffer problem, which is another example of active entities being replaced by a data structure when viewed at a lower level (Finkel's level principle).

  Initially e=k, f=0 (counting semaphores); b=open (binary semaphore)

  Producer                         Consumer

  loop forever                     loop forever
     produce-item                     P(f)
     P(e)                             P(b); take item from buf; V(b)
     P(b); add item to buf; V(b)      V(e)
     V(f)                             consume-item

• k is the size of the buffer
• e represents the number of empty buffer slots
• f represents the number of full buffer slots
• We assume the buffer itself is only serially accessible. That is, only one operation at a time.
  • This explains the P(b) V(b) around buffer operations
  • I use ; and put three statements on one line to suggest that a buffer insertion or removal is viewed as one atomic operation.
  • Of course this writing style is only a convention, the enforcement of atomicity is done by the P/V.
• The P(e), V(f) motif is used to force bounded alternation. If k=1 it gives strict alternation.

2.3.6 Mutexes

Remark: Whereas we use the term semaphore to mean binary semaphore and explicitly say generalized or counting semaphore for the positive integer version, Tanenbaum uses semaphore for the positive integer solution and mutex for the binary version. Also, as indicated above, for Tanenbaum semaphore/mutex implies a blocking primitive; whereas I use binary/counting semaphore for both busy-waiting and blocking implementations. Finally, remember that in this course our only solutions are busy-waiting.

My Terminology

	Busy wait	block/switch
critical	(binary) semaphore	(binary) semaphore
semi-critical	counting semaphore	counting semaphore

Tanenbaum's Terminology

	Busy wait	block/switch
critical	enter/leave region	mutex
semi-critical	no name	semaphore