Operating Systems

Start Lecture #4

Remark: We shall do section 2.4 before section 2.3 for two reasons.

1. Sections 2.3 and 2.5 are closely related; having 2.4 in between seeks awkward to me.
2. Lab 2 uses material from 2.4 so I don't want to push 2.4 after 2.5.

2.4 Process Scheduling

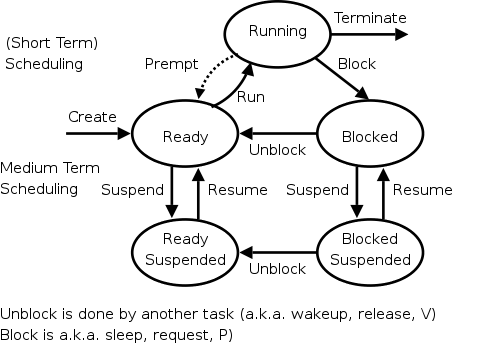
Scheduling processes on the processor is often called processor scheduling or process scheduling or simply scheduling. As we shall see later in the course, a more descriptive name would be short-term, processor scheduling.

For now we are discussing the arcs connecting running↔ready in the diagram on the right showing the various states of a process. Medium term scheduling is discussed later as is disk-arm scheduling.

Naturally, the part of the OS responsible for (short-term, processor) scheduling is called the (short-term, processor) scheduler and the algorithm used is called the (short-term, processor) scheduling algorithm.

2.4.1 Introduction to Scheduling

Importance of Scheduling for Various Generations and Circumstances

Early computer systems were monoprogrammed and, as a result, scheduling was a non-issue.

For many current personal computers, which are definitely multiprogrammed, there is in fact very rarely more than one runnable process. As a result, scheduling is not critical.

For servers (or old mainframes), scheduling is indeed important and these are the systems you should think of.

Process Behavior

Processes alternate CPU bursts with I/O activity, as we shall see in lab2. The key distinguishing factor between compute-bound (aka CPU-bound) and I/O-bound jobs is the length of the CPU bursts.

The trend over the past decade or two has been for more and more jobs to become I/O-bound since the CPU rates have increased faster than the I/O rates.

When to Schedule

An obvious point, which is often forgotten (I don't think 3e mentions it) is that the scheduler cannot run when the OS is not running. In particular, for the uniprocessor systems we are considering, no scheduling can occur when a user process is running. (In the mulitprocessor situation, no scheduling can occur when all processors are running user jobs).

Again we refer to the state transition diagram above.

1. Process creation.
   The running process has issued a fork() system call and hence the OS runs; thus scheduling is possible. Scheduling is also desirable at this time since the scheduling algorithm might favor the new process.
2. Process termination.
   The exit() system call has again transferred control to the OS so scheduling is possible. Moreover, scheduling is necessary since the previously running process has terminated.
3. Process blocks.
   Same as termination.
4. Interrupt received.
   Since the OS takes control, scheduling is possible. When an I/O interrupt occurs, this normally means that a blocked process is now ready and, with a new candidate for running, scheduling is desirable.
5. Clock interrupts are treated next when we discuss preemption and discuss the dotted arc in the process state diagram.

Preemption

It is important to distinguish preemptive from non-preemptive scheduling algorithms.

• Preemption means the operating system moves a process from running to ready without the process requesting it.
• Without preemption, the system implements run until completion, or block (, or yield).
• The preempt arc in the diagram is present for preemptive scheduling algorithms.
• We do not emphasize yield (a solid arrow from running to ready).
• Preemption needs a clock interrupt (or equivalent).
• Preemption is needed to guarantee fairness.
• Preemption is found in all modern general purpose operating systems.
• Even non-preemptive systems can be multiprogrammed (remember that processes do block for I/O).
• Preemption is not cheap.

Categories of Scheduling Algorithms

We distinguish three categories of scheduling algorithms with regard to the importance of preemption.

1. Batch.
2. Interactive.
3. Real Time.

For multiprogramed batch systems (we don't consider uniprogrammed systems, which don't need schedulers) the primary concern is efficiency. Since no user is waiting at a terminal, preemption is not crucial and if it is used, each process is given a long time period before being preempted.

For interactive systems (and multiuser servers), preemption is crucial for fairness and rapid response time to short requests.

We don't study real time systems in this course, but can say that preemption is typically not important since all the processes are cooperating and are programmed to do their task in a prescribed time window.

Scheduling Algorithm Goals

There are numerous objectives, several of which conflict, that a scheduler tries to achieve. These include.

1. Fairness.
   Treating users fairly, which must be balanced against ...
   
   
2. Respecting priority.
   That is, giving more important processes higher priority. For example, if my laptop is trying to fold proteins in the background, I don't want that activity to appreciably slow down my compiles and especially don't want it to make my system seem sluggish when I am modifying these class notes. In general, interactive jobs should have higher priority.
   
   
3. Efficiency.
   This has two aspects.
   • Do not spend excessive time in the scheduler.
   • Try to keep all parts of the system busy.
   
   
4. Low turnaround time
   That is, minimize the time from the submission of a job to its termination. This is important for batch jobs.
   
   
5. High throughput.
   That is, maximize the number of jobs completed per day. Not quite the same as minimizing the (average) turnaround time as we shall see when we discuss shortest job first.
   
   
6. Low response time.
   That is, minimize the time from when an interactive user issues a command to when the response is given. This is very important for interactive jobs.
   
   
7. Repeatability. Dartmouth (DTSS) wasted cycles and limited logins for repeatability.
   
   
8. Degrade gracefully under load.

The Name Game

There is an amazing inconsistency in naming the different (short-term) scheduling algorithms. Over the years I have used primarily 4 books: In chronological order they are Finkel, Deitel, Silberschatz, and Tanenbaum. The table just below illustrates the name game for these four books. After the table we discuss several scheduling policy in some detail.

    Finkel  Deitel  Silbershatz Tanenbaum
    -------------------------------------
    FCFS    FIFO    FCFS        FCFS
    RR      RR      RR          RR
    PS      **      PS          PS
    SRR     **      SRR         **    not in tanenbaum
    SPN     SJF     SJF         SJF
    PSPN    SRT     PSJF/SRTF   SRTF
    HPRN    HRN     **          **    not in tanenbaum
    **      **      MLQ         **    only in silbershatz
    FB      MLFQ    MLFQ        MQ
  

Remark: For an alternate organization of the scheduling algorithms (due to my former PhD student Eric Freudenthal and presented by him Fall 2002) click here.

2.4.2 Scheduling in Batch Systems

First Come First Served (FCFS, FIFO, FCFS, --)

If the OS doesn't schedule, it still needs to store the list of ready processes in some manner. If it is a queue you get FCFS. If it is a stack (strange), you get LCFS. Perhaps you could get some sort of random policy as well.

• Only FCFS is considered.
• Non-preemptive.
• The simplist scheduling policy.
• In some sense the fairest since it is first come first served. But perhaps that is not so fair. Consider a 1 hour job submitted one second before a 3 second job.
• An efficient usage of cpu in the sense that the scheduler is very fast.
• Does not favor interactive jobs.

Shortest Job First (SPN, SJF, SJF, SJF)

Sort jobs by execution time needed and run the shortest first.

This is a Non-preemptive algorithm.

First consider a static situation where all jobs are available in the beginning and we know how long each one takes to run. For simplicity lets consider run-to-completion, also called uniprogrammed (i.e., we don't even switch to another process on I/O). In this situation, uniprogrammed SJF has the shortest average waiting time.

• Assume you have a schedule with a long job right before a short job.
• Consider swapping the two jobs.
• This decreases the wait for the short by the length of the long job and increases the wait of the long job by the length of the short job.
• This decreases the total waiting time for these two.
• Hence decreases the total waiting for all jobs and hence decreases the average waiting time as well.
• Hence, whenever a long job is right before a short job, we can swap them and decrease the average waiting time.
• Thus the lowest average waiting time occurs when there are no short jobs right before long jobs.
• This is uniprogrammed SJF.

The above argument illustrates an advantage of favoring short jobs (e.g., RR with small quantum): The average waiting time is reduced.

In the more realistic case of true SJF where the scheduler switches to a new process when the currently running process blocks (say for I/O), we could also consider the policy shortest next-CPU-burst first.

The difficulty is predicting the future (i.e., knowing in advance the time required for the job or the job's next-CPU-burst).

SJF Can starve a process that requires a long burst.

• This is fixed by the standard technique.
• What is that technique?
  Answer: Priority aging (see below).

Shortest Remaining Time Next (PSPN, SRT, PSJF/SRTF, SRTF)

Preemptive version of above. Indeed some authors call it preemptive shortest job first.

• Permit a process that enters the ready list to preempt the running process if the time for the new process (or for its next burst) is less than the remaining time for the running process (or for its current burst).
• It will never happen that a process already in the ready list will require less time than the remaining time for the currently running process. Why?
  Answer: When the process joined the ready list it would have started running if the current process had more time remaining. Since that didn't happen the currently running job had less time remaining and now it has even less.
• PSPN Can starve a process that requires a long burst.
  • This is fixed by the standard technique.
  • What is that technique?
    Answer: Priority aging (see below).

2.4.3 Scheduling in Interactive Systems

The following algorithms can also be used for batch systems, but in that case, the gain may not justify the extra complexity.

Round Robbin (RR, RR, RR, RR)

• An important preemptive policy.
• Essentially the preemptive version of FCFS.
• The key parameter is the quantum size q.
• When a process is put into the running state a timer is set to q.
• If the timer goes off and the process is still running, the OS preempts the process.
  • This process is moved to the ready state (the preempt arc in the diagram), where it is placed at the rear of the ready list.
  • The process at the front of the ready list is removed from the ready list and run (i.e., moves to state running).
  • Note that the ready list is being treated as a queue. Indeed it is sometimes called the ready queue, but not by me since for other scheduling algorithms it is not accessed in a FIFO manner.
• When a process is created, it is placed at the rear of the ready list.
• Note that RR works well if you have a 1 hr job and then a 3 second job.
• As q gets large, RR approaches FCFS. Indeed if q is larger that the longest time any process will run before terminating or blocking, then RR IS FCFS. A good way to see this is to look at my favorite diagram and note the three arcs leaving running. They are triggered by three conditions: process terminating, process blocking, and process preempted. If the first trigger condition to arise is never preemption, we can erase that arc and then RR becomes FCFS.
• As q gets small, RR approaches PS (Processor Sharing, described next).
• What value of q should we choose?
  • A trade-off
  • A small q makes the system more responsive, a long compute-bound job cannot starve a short job.
  • A large q makes the system more efficient since there is less process switching.
  • A reasonable time for q is a few tens of milliseconds or perhaps a few milliseconds for a fast processor. (millisecond = 1/1000 second and is abbreviated ms). This means every other job can delay your job by at most q (plus the context switch time CS, which is normally less than 1ms). Also the overhead is CS/(CS+q), which is small.
• A student found the following reference for the name Round Robin. A similar, but less detailed, citation can be found in wikipedia.

  The round robin was originally a petition, its signatures arranged in a circular form to disguise the order of signing. Most probably it takes its name from the ruban rond, (round ribbon), in 17th-century France, where government officials devised a method of signing their petitions of grievances on ribbons that were attached to the documents in a circular form. In that way no signer could be accused of signing the document first and risk having his head chopped off for instigating trouble. Ruban rond later became round robin in English and the custom continued in the British navy, where petitions of grievances were signed as if the signatures were spokes of a wheel radiating from its hub. Today round robin usually means a sports tournament where all of the contestants play each other at least once and losing a match doesn't result in immediate elimination.
  
  Encyclopedia of Word and Phrase Origins by Robert Hendrickson (Facts on File, New York, 1997).

Homework: 20, 35.

Homework: Round-robin schedulers normally maintain a list of all runnable processes, with each process occurring exactly once in the list. What would happen if a process occurred more than once in the list? Can you think of any reason for allowing this?

Homework: Give an argument favoring a large quantum; give an argument favoring a small quantum.

Process	CPU Time	Creation Time
P1	20	0
P2	3	3
P3	2	5

Homework:

• Consider the set of processes in the table to the right.
• When does each process finish if RR scheduling is used with q=1, if q=2, if q=3, if q=100?
• First assume (unrealistically) that context switch time is zero.
• Then assume it is .1. Each process performs no I/O (i.e., no process ever blocks).
• All times are in milliseconds.
• The CPU time is the total time required for the process (excluding any context switch time).
• The creation time is the time when the process is created. So P1 is created when the problem begins and P3 is created 5 milliseconds later.
• If two processes have equal priority (in RR this means if they both enter the ready state at the same cycle), we give priority (in RR this means place first on the queue) to the process with the earliest creation time. If they also have the same creation time, then we give priority to the process with the lower number.
• Remind me to discuss this last one in class next time.

Homework: Redo the previous homework for q=2 with the following changes. After process P1 runs for 3ms (milliseconds), it blocks for 2ms. P1 never blocks again. P2 never blocks. After P3 runs for 1 ms it blocks for 1ms. Assume the context switch time is zero. Remind me to answer this one in class next lecture.

Processor Sharing (PS, **, PS, PS)

Merge the ready and running states and permit all ready jobs to be run at once. However, the processor slows down so that when n jobs are running at once, each progresses at a speed 1/n as fast as it would if it were running alone.

• Clearly impossible as stated due to the overhead of process switching.
• Of theoretical interest (easy to analyze).
• Approximated by RR when the quantum is small. Make sure you understand this last point. For example, consider the last homework assignment (with zero context switch time and no blocking) and consider q=1, q=.1, q=.01, etc.
• Show what happens for 3 processes, A, B, C, each requiring 3 seconds of CPU time. A starts at time 0, B at 1 second, C at 2.
• Consider three processes all starting at time 0. One requires 1ms, the second 100ms, the third 10sec (seconds). Compute the total/average waiting time for RR q=1ms, PS, SJF, SRTN, and FCFS. Note that this depends on the order the processes happen to be processed in. The effect is huge for FCFS, modest for RR with modest quantum, and non-existent for PS and SRTN.

Homework: 32.

Variants of Round Robin

1. State dependent RR
   • Same as RR but q is varied dynamically depending on the state of the system.
   • Favor processes holding important resources, for example, non-swappable memory.
   • Perhaps this should be considered medium term scheduling since you probably do not recalculate q each time.
2. External priorities: RR but a user can pay more and get bigger q. That is, one process can be given a higher priority than another. But this is not an absolute priority: the lower priority (i.e., less important) process does get to run, but not as much as the higher priority process.

Priority Scheduling

Each job is assigned a priority (externally, perhaps by charging more for higher priority) and the highest priority ready job is run.

• Similar to External priorities above
• If many processes have the highest priority, use RR among them. Indeed one often groups several priorities into a priority class and employs RR within a class.
• Can easily starve processes, which can be fixed by the standard technique.
• Can have the priorities changed dynamically to favor processes holding important resources (similar to state dependent RR).
• Sometimes a large priority means an important job; sometimes a small priority means an important job.
• Many policies can be thought of as priority scheduling in which we run the job with the highest priority. The different scheduling policies have different notions of priority. For example:
  • FCFS and RR are priority scheduling where the priority is the time last inserted on the ready list.
  • SJF and SRTN are priority scheduling, where the priority of the job is the time it needs to run in order to complete (or complete its current CPU burst).

Priority aging

As a job is waiting, increase its priority; hence it will eventually have the highest priority.

• Starvation means that some process is never run, because it never has the highest priority. It is also called starvation, if process runs for a while, but then is never able to run again, even though it is ready. The formal way to say this is that a system is free of starvation if, No job can remain in the ready state forever.
• Priority aging is the standard technique used to prevent starvation (assuming all jobs terminate or the policy is preemptive).
• There may be many processes with the maximum priority.
• If so, can use FIFO among those with max priority (risks starvation if a job doesn't terminate) or can use RR.
• Can apply priority aging to many policies, in particular to priority scheduling described above.

Homework: 36, 37. Note that when the book says RR with each process getting its fair share, it means Processor Sharing.

Selfish RR (SRR, **, SRR, **)

SRR is a preemptive policy in which unblocked (i.e. ready and running) processes are divided into two classes the Accepted processes, which run RR and the others (perhaps SRR really stands for snobbish RR).

• Accepted process have their priority increase at rate a≥0.
• A new process starts at priority 0; its priority increases at rate b≥0.
• An unaccepted process becomes an accepted process when its priority reaches that of the accepted processes (or when there are no accepted processes).
• Hence, once a process is accepted, it remains accepted until it terminates (or blocks, see below) and all accepted processes have same priority.
• Note that, when the only accepted process terminates (or blocks, see below), all the process with the next highest priority become accepted.

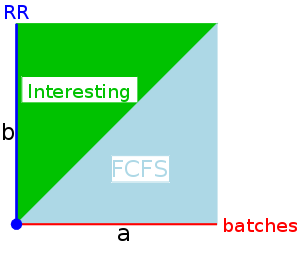
The behavior of SRR depends on the relationship between a and b (and zero).

• If a=0, get RR.
• If a≥b>0, get FCFS.
• If b>a>0, it is interesting.
• If a>b=0, you get RR in batches. This is similar to n-step scan for disk I/O.

It is not clear what is supposed to happen when a process blocks. Should its priority get reset to zero and have unblock act like create? Should the priority continue to grow (at rate a or b)? Should its priority be frozen during the blockage. Let us assume the first case (reset to zero) since it seems the simplest.

Approximating the Behavior of SFJ and PSJF

Recall that SFJ/PSFJ do a good job of minimizing the average waiting time. The problem with them is the difficulty in finding the job whose next CPU burst is minimal. We now learn three scheduling algorithms that attempt to do this. The first algorithm does it statically, presumably with some manual help; the other two are dynamic and fully automatic.

Multilevel Queues (**, **, MLQ, **)

Put different classes of processs in different queues

• Processes do not move from one queue to another.
• Can have different policies on the different queues.
  For example, might have a background (batch) queue that is FCFS and one or more foreground queues that are RR (possibly with different quanta).
• Must also have a policy among the queues.
  For example, might have two queues, foreground and background, and give the first absolute priority over the second
  • Might apply priority aging to prevent background starvation.
  • But might not, i.e., no guarantee of service for background processes. View a background process as a cycle soaker.
  • Might have 3 queues, foreground, background, cycle soaker.
• Another possible inter-queue policy would be have 2 queues, apply RR to each but cycle through the higher priority twice and then cycle through the lower priority queue once.

Multiple Queues (FB, MFQ, MLFBQ, MQ)

As with multilevel queues above we have many queues, but now processes move from queue to queue in an attempt to dynamically separate batch-like from interactive processs so that we can favor the latter.

• Remember that low average waiting time is achieved by SJF and this is an attempt to determine dynamically those processes that are interactive, which means have a very short cpu burst.
• Run processs from the highest priority nonempty queue in a RR manner.
• When a process uses its full quanta (looks a like batch process), move it to a lower priority queue.
• When a process doesn't use a full quanta (looks like an interactive process), move it to a higher priority queue.
• A long process with frequent (perhaps spurious) I/O will remain in the upper queues.
• Might have the bottom queue FCFS.
• Many variants.
  For example, might let process stay in top queue 1 quantum, next queue 2 quanta, next queue 4 quanta (i.e., sometimes return a process to the rear of the same queue it was in if the quantum expires).
  Might move to a higher queue only if a keyboard interrupt occurred rather than if the quantum failed to expire for any reason (e.g., disk I/O).

Shortest Process Next

An attempt to apply sjf to interactive scheduling. What is needed is an estimate of how long the process will run until it blocks again. One method is to choose some initial estimate when the process starts and then, whenever the process blocks choose a new estimate via

    NewEstimate = A*OldEstimate + (1-A)*LastBurst
  

Highest Penalty Ratio Next (HPRN, HRN, **, **)

Run the process that has been hurt the most.

• For each process, let r = T/t; where T is the wall clock time this process has been in system and t is the running time of the process to date.
• If r=2.5, that means the job has been running 1/2.5 = 40% of the time it has been in the system.
• We call r the penalty ratio and run the process having the highest r value.
• We must worry about a process that just enters the system since t=0 and hence the ratio is undefined. Define t to be the max of 1 and the running time to date. Since now t is at least 1, the ratio is always defined.
• HPRN is normally defined to be non-preemptive (i.e., the system only checks r when a burst ends).
• There is an preemptive analogue. That analogue differs from HPRN as follows.
  • When putting a process into the run state compute the time at which it will no longer have the highest ratio and set a timer.
  • When a process is moved into the ready state, compute its ratio and preempt if needed.
• HRN stands for highest response ratio next and means the same thing.
• This policy is yet another example of priority scheduling

Guaranteed Scheduling

A variation on HPRN. The penalty ratio is a little different. It is nearly the reciprocal of the above, namely
   t / (T/n)
where n is the multiprogramming level. So if n is constant, this ratio is a constant times 1/r.

Lottery Scheduling

Each process gets a fixed number of tickets and at each scheduling event a random ticket is drawn (with replacement) and the process holding that ticket runs for the next interval (probably a RR-like quantum q).

On the average a process with P percent of the tickets will get P percent of the CPU (assuming no blocking, i.e., full quanta).

Fair-Share Scheduling

If you treat processes fairly you may not be treating users fairly since users with many processes will get more service than users with few processes. The scheduler can group processes by user and only give one of a user's processes a time slice before moving to another user.

For example, linux has cgroups for a related purpose. The scheduler first schedules across cgroups so if a big job has many processes in the same cgroup, it will not get more time than a small job with just one process.

Fancier methods have been implemented that give some fairness to groups of users. Say one group paid 30% of the cost of the computer. That group would be entitled to 30% of the cpu cycles providing it had at least one process active. Furthermore a group earns some credit when it has no processes active.