V22.0202 Computer Systems Organization
2009-10 Spring
Allan Gottlieb
Tuesdays and Thursdays 11-12:15 Room 101 Ciww

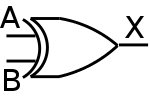
Start Lecture #1

Chapter 0: Administrivia

I start at 0 so that when we get to chapter 1, the numbering will agree with the text.

0.1: Contact Information

0.2: Course Web Page

There is a web site for the course. You can find it from my home page, which is http://cs.nyu.edu/~gottlieb

0.3: Textbook

The course has two texts

0.4: Computer Accounts and Mailman Mailing List

0.5: Grades

Grades are based on the labs, midterm, and the final exam, with each very important. The weighting will be approximately
30%*LabAverage + 30%*MidtermExam + 40%*FinalExam> (but see homeworks below).

0.6: The Upper Left Board

I use the upper left board for lab/homework assignments and announcements. I should never erase that board. Viewed as a file it is group readable (the group is those in the room), appendable by just me, and (re-)writable by no one. If you see me start to erase an announcement, let me know.

I try very hard to remember to write all announcements on the upper left board and I am normally successful. If, during class, you see that I have forgotten to record something, please let me know. HOWEVER, if I forgot and no one reminds me, the assignment has still been given.

0.7: Homeworks and Labs

I make a distinction between homeworks and labs.

Labs are

Homeworks are

0.7.1: Homework Numbering

Homeworks are numbered by the class in which they are assigned. So any homework given today is homework #1. Even if I do not give homework today, the homework assigned next class will be homework #2. Unless I explicitly state otherwise, all homeworks assignments can be found in the class notes. So the homework present in the notes for lecture #n is homework #n (even if I inadvertently forgot to write it to the upper left board).

0.7.2: Doing Labs on non-NYU Systems

You may solve lab assignments on any system you wish, but ...

0.7.3: Obtaining Help with the Labs

Good methods for obtaining help include

  1. Asking me during office hours (see web page for my hours).
  2. Asking the mailing list.
  3. Asking another student, but ...
    Your lab must be your own.
    That is, each student must submit a unique lab. Naturally, simply changing comments, variable names, etc. does not produce a unique lab.

0.7.4: Computer Language Used for Labs

Each lab will indicate the language that must be used.

0.8: A Grade of Incomplete

The rules for incompletes and grade changes are set by the school> and not the department or individual faculty member. The rules set by CAS can be found in <http://cas.nyu.edu/object/bulletin0608.ug.academicpolicies.html>, which states:

The grade of I (Incomplete) is a temporary grade that indicates that the student has, for good reason, not completed all of the course work but that there is the possibility that the student will eventually pass the course when all of the requirements have been completed. A student must ask the instructor for a grade of I, present documented evidence of illness or the equivalent, and clarify the remaining course requirements with the instructor.

The incomplete grade is not awarded automatically. It is not used when there is no possibility that the student will eventually pass the course. If the course work is not completed after the statutory time for making up incompletes has elapsed, the temporary grade of I shall become an F and will be computed in the student's grade point average.

All work missed in the fall term must be made up by the end of the following spring term. All work missed in the spring term or in a summer session must be made up by the end of the following fall term. Students who are out of attendance in the semester following the one in which the course was taken have one year to complete the work. Students should contact the College Advising Center for an Extension of Incomplete Form, which must be approved by the instructor. Extensions of these time limits are rarely granted.

Once a final (i.e., non-incomplete) grade has been submitted by the instructor and recorded on the transcript, the final grade cannot be changed by turning in additional course work.

0.9 Academic Integrity Policy

This email from the assistant director, describes the policy. 

    Dear faculty,

    The vast majority of our students comply with the
    department's academic integrity policies; see

      www.cs.nyu.edu/web/Academic/Undergrad/academic_integrity.html
      www.cs.nyu.edu/web/Academic/Graduate/academic_integrity.html

    Unfortunately, every semester we discover incidents in
    which students copy programming assignments from those of
    other students, making minor modifications so that the
    submitted programs are extremely similar but not identical.

    To help in identifying inappropriate similarities, we
    suggest that you and your TAs consider using Moss, a
    system that automatically determines similarities between
    programs in several languages, including C, C++, and Java.
    For more information about Moss, see:

      http://theory.stanford.edu/~aiken/moss/

    Feel free to tell your students in advance that you will be
    using this software or any other system.  And please emphasize,
    preferably in class, the importance of academic integrity.

    Rosemary Amico
    Assistant Director, Computer Science
    Courant Institute of Mathematical Sciences

Remark: The chapter/section numbers for the material on C, agree with Kernighan and Plauger. However, the material is quite standard so, as mentioned before, if you already own a C book that you like, it should be fine.

Chapter 1: A Tutorial Introduction

Since Java includes much of C, my treatment can be very brief for the parts in common (e.g., control structures).

1.1: Getting Started

Hello World

  #include <stdio.h>
  main() {
    printf("Hello, world\n");
  }

1.2: Variables and Arithmetic Expressions

1.3: The For Statement

1.4 Symbolic Constants

Fahrenheight-Celsius

  #include <stdio.h>
  main() {
    int F, C;
    int lo=0, hi=300, incr=20;

    for (F=lo; F<=hi; F+=incr) {
      C = 5 * (F-32) / 9;
      printf("%d\t%d\n", F, C);
    }
  }

Floating Point Fahrenheight-Celcius

#include <stdio.h>
#define LO 0
#define HI 300
#define INCR 20
main() {
      int F;
      for (F=LO; F<=HI; F+=INCR) {
          printf("%3d\t%5.1f\n", F, (F-32)*(5.0/9.0));
      }
  }

1.5: Character Input and Output

getchar() / putchar()

The simplest (i.e., most primitive form of character I/O is getchar() and putchar(), which read and print a single character.

1.5.1: File Copying

File copy is conceptually trivial: getchar() a char and then putchar() the char until eof. The code is on the right and does require some comment despite is brevity. 

#include <stdio.h>
main() {
    int c;
    while ((c = getchar()) != EOF)
    putchar(c);
}

Homework: Write a (C-language) program to print the value of EOF. (This is 1-7 in the book but I realize not everyone will have the book so I will type them in.)

Homework: (1-9) Write a program to copy its input to its output, replacing each string of one or more blanks by a single blank.

1.5.2: Character Counting

1.5.3: Line Counting

1.5.4: Word Counting

The Unix wc Program

The Unix wc program prints the number of characters, words, and lines in the input. It is clear what the number of characters means. The number of lines is the number of newlines (so if the last line doesn't end in a newline, it doesn't count). The number of words is less clear. In particular, what should be the word separators?

#include <stdio.h>
#define WITHIN   1
#define OUTSIDE  0
main() {
  int c, num_lines, num_words, num_chars, within_or_outside;
  within_or_outside = OUTSIDE; /* C doesn't have Boolean type */
  num_lines = num_words = num_chars = 0;
  while ((c = getchar()) != EOF) {
    ++num_chars;
    if (c == '\n')
      ++num_lines;
    if (c == ' ' || c == '\n' || c == '\t')
      within_or_outside = OUTSIDE;
    else if (within_or_outside == OUTSIDE) { /* at beginning word */
      ++num_words;
      within_or_outside = WITHIN;
    }
  }
  printf("%d %d %d\n", num_lines, num_words, num_chars);
}

Homework: (1-12) Write a program that prints its input one word per line.

Start Lecture #2

Lecture given by Prof. Hull

1.6: Arrays

We are hindered in our examples because we don't know how to input anything other than characters and don't want to write the program to convert a string of characters into an integer or (worse) a floating point number.

Mean and Standard Deviation

#include <stdio.h>
#define N  10   /* imagine you read in N */
#define MAXN  1000
main() {
  int i;
  float x, sum=0, mu;
  for (i=0; i<N; i++) {
    x = i;  /* imagine you read in X[i] */
    sum += x;
  }
  mu = sum / N;
  printf("The mean is %f\n", mu);
}

#include <stdio.h>
#define N  10   /* imagine you read in N */
#define MAXN  1000
main() {
  int i;
  float x[MAXN], sum=0, mu;
  for (i=0; i<N; i++) {
    x[i] = i;  /* imagine you read in X[i] */
  }
  for (i=0; i<N; i++) {
    sum += x[i];
  }
  mu = sum / N;
  printf("The mean is %f\n", mu);
}

#include <stdio.h>
#include <math.h>
#define N  5   /* imagine you read in N */
#define MAXN  1000
main() {
  int i;
  double x[MAXN], sum=0, mu, sigma;
  for (i=0; i<N; i++) {
    x[i] = i;  /* imagine you read in x[i] */
    sum += x[i];
  }
  mu = sum / N;
  printf("The mean is %f\n", mu);
  sum = 0;
  for (i=0; i<N; i++) {
      sum += pow(x[i]-mu,2);
  }
  sigma = sqrt(sum/N);
  printf("The standard deviation is %f\n", sigma);
}

I am sure you know the formula for the mean (average) of N numbers: Add the number and divide by N. Call the mean μ

The standard deviation is the RMS of the deviations-from-the-mean, it is called σ. That is, σ = sqrt(Σ((Xi-&mu)2)/N). (For technical reasons, sometimes we divide by N-1 not N.)

The first program on the right is the natural program to read in N then read N number and compute the mean of the latter, with one problem. We don't know how to read numbers.

So I faked it by having N a symbolic constant and making x[i]=i.

<soapbox>
You would presumably not write the second version, with a gratuitous array. It takes more space, is (a little) longer, is slower, and is more complicated. However, in 202 students want to write it when doing my linker lab. There is an instinct to use a three step procedure for all assignments:

  1. Read everything in.
  2. Do the computation.
  3. Print the answers.

But that is silly if you only need the value once as in this example.
</soapbox>.

The last example is a good use of arrays for computing the standard deviation using the RMS formula above. We do need to keep the values around after computing the mean so that we can compute the deviations and from them the standard deviation.

Note that, unlike Java, no use of new (or the C analogue malloc()) appears. Arrays declared as in this program have a lifetime of the routine in which they are declared. Specifically sum and x are both allocated when main is called and are both freed when main is finished.

Note the declaration int x[N]. In C, to declare something complicated, you say what has to be done to get one of the primitive types.

In C if we have int X[10]; then writing X in you program is the same as writing &A[0]. & is the address of operator. More on this later when we discuss pointers.

1.7: Functions

#include <stdio.h>
// Determine letter grade from score
// Demonstration of functions
char letter_grade (int score) {
  if      (score >= 90) return 'A';
  else if (score >= 80) return 'B';
  else if (score >= 70) return 'C';
  else if (score >= 60) return 'D';
  else                  return 'F';
}  // end function letter_grade
char letter_grade2 ( int score ) {
  switch ( score ) {  // yes, this is an awful case statement!
    case 90 : case 91 : case 92 : case 93 : case 94 :
    case 95 : case 96 : case 97 : case 98 : case 99 :
    case 100 : return 'A'; break;

    default : return 'F'; break;
  } // end switch score
} // end function letter_grade2
main() {
  int  quiz;
  char grade;
  quiz = 95;
  grade = letter_grade( quiz );
  printf(" \n for a score of %3d the grade is %c\n ", quiz, grade);
  quiz = 75;
  grade = letter_grade2( quiz );
  printf(" \n for a score of %3d the grade is %c\n ", quiz, grade);
} // end main

#include <stdio.h>
// Demo of Arrays
// Create random numbers, average and sort them
#define maxelements 50
void sort ( int stuff [], int max ) {
  int temp;
  int x,
  for (x=0; x<(max-1); x++)   {
    for (y=0; y<(max-(x+1)); y++) {
      if (stuff[y] < stuff[y+1]) {
        temp       = stuff[y];
        stuff[y]   = stuff[y+1];
        stuff[y+1] = temp;
      } // end if stuff
    } // end for y
  } // end for x
} // end function sort
float avg ( int stuff [], int max ) {
  int sum;
  int x;
  sum = 0;
  for (x = 0; x < max; x++)
    sum = sum + stuff[x];
  return (sum / max);
}
main() {
  int table[maxelements];
  int  x;
  float average;
  for (x = 0; x < maxelements; x++)
    table[x] = rand();
  for (x = 0; x < maxelements; x++)
    printf(" the element in position %3d is %3d \n", x, table[x]);
  average = avg( table, maxelements );
  printf(" the average value is %5.1f ", average);
  sort( table, maxelements );
  for (x = 0; x < maxelements; x++)
    printf(" the element in position %3d is %3d \n", x, table[x]);
} // end function main

Start Lecture #3

1.8: Arguments—Call by Value

Remark: All the online material is now associated with V22.0202-002. You should now sign up for the mailing list as shown in lecture 1.

1.9: Character Arrays

Unlike Java, C does not have a string datatype. A string in C is an array of chars. String operations like concatenate and copy (assignment) become functions in C. Indeed there are a number of standard library routines for string.

The most common implementation of strings in C is null terminated. That is, a string of length 5 has 6 characters, the 5 characters in the string and a sixth character = '\0'.

Print Longest Line

#include <stdio.h>
#define MAXLINE 1000
int getLine(char line[], int maxline);
void copy(char to[], char from[]);
int main() {
  int len;
  int max;
  char line[MAXLINE];
  char longest[MAXLINE];
  max = 0;
  while ((len=getLine(line,MAXLINE))>0)
    if (len > max) {
      max = len;
      copy(longest,line);
    }
  if (max>0)
    printf("%s", longest);
  return 0;
}
int getLine(char s[], int lim) {
  int c, i;
  for (i=0; i<lim-1 && (c=getchar())!=EOF && c!='\n'; ++i)
    s[i] = c;
  if (c=='\n') {
    s[i]= c;
    ++i;
  }
  s[i] = '\0';
  return i;
}
void copy(char to[], char from[]) {
  int i;
  i=0;
  while ((to[i] = from[i]) != '\0')
    ++i;
}

This program reads lines from the terminal, converts them to C strings by appending '\0', and prints the longest one found. Pseudo code would be 

    while (more lines)
      if (longest)
        save it and its length

Thus we need the ability to read in a line and save it and write two functions getLine and copy for these tasks (the book uses getline, but that doesn't compile for me since there is a library routine in stdio.h with the same name and different signature). Given these two routines, main is fairly simple, needing only a few small comments.

  1. Note that getLine and copy are declared before main. They are defined later in the file but C requires declare before use so either main would have to come last or the declarations are needed. Since only main uses the routines, the declarations could have been in main but it is common practice to put them outside as shown.
  2. Note %s inside printf. This is used for (null-terminated) strings.
  3. Note that main is declared to return an integer and it does return 0. In unix at least, this is the indication of a successful run.

The for condition in getLine is rather complex. Perhaps it would be clearer if the test were simply i<lim-1 and the rest was done with if-break statments inside the loop.

copy is declared and defined to return void.

Homework: Simplify the for condition as just indicated.


1.10: External Variables and Scope

Solving Quadratic Equations

#include <stdio.h>
#include <math.h>
#define A +1.0   // should read
#define B -3.0   // A,B,C
#define C +2.0   // using scanf()
void solve (float a, float b, float c);
int main() {
  solve(A,B,C);
  return 0;
}
void solve (float a, float b, float c) {
  float d;
  d = b*b - 4*a*c;
  if (d < 0)
    printf("No real roots\n");
  else if (d == 0)
    printf("Double root is %f\n", -b/(2*a));
  else
    printf("Roots are %f and %f\n",
           ((-b)+sqrt(d))/(2*a),
           ((-b)-sqrt(d))/(2*a));
}

#include <stdio.h>
#include <math.h>
#define A +1.0   // should read
#define B -3.0   // A,B,C
#define C +2.0   // using scanf()
void solve();
float a, b, c;   // definition
int main() {
  extern float a, b, c; // declaration
  a=A;
  b=B;
  c=C;
  solve();
  return 0;
}
void solve () {
  extern float a, b, c; // declaration
  float d;
  d = b*b - 4*a*c;
  if (d < 0)
    printf("No real roots\n");
  else if (d == 0)
    printf("Double root is %f\n", -b/(2*a));
  else
    printf("Roots are %f and %f\n",
           ((-b)+sqrt(d))/(2*a),
           ((-b)-sqrt(d))/(2*a));
}

The two programs on the right find the real roots (no complex numbers) of the quadratic equation 

    ax2+bx+c
using the standard technique of first calculating the discriminant 
    d = b2-4ac
These programs deal only with real roots, i.e., when d≥0.

The first program calls a function solve() passing it as arguments the three coeficients a,b,c.

The second program communicates with solve using external (global) variables rather than arguments/parameters.

Remark: I am not assigning lab 1 yet because we haven't resolved the situation with i5.nyu.edu. But when it is resolved lab1 will include some of problems 20-24 on page 34.


Start Lecture #4

Remark: Lab 1 assigned. Due in 2 weeks. See the course home page.

Chapter 2: Types, Operators, and Expressions

2.1: Variable Names

Similar to Java: A variable name must begin with a letter and then can use letters and numbers. An underscore is a letter, but you shouldn't begin a variable name with one since that is conventionally reserved for library routines. Keywords such as if, while, etc are reserved and cannot be used as variable names.

2.2: Data Types and Sizes

C has very few primitive types.

There are qualifiers that can be added. One pair is long/short. Typically short int is abbreviated short and long int is abbreviated long.

long must be at least as big as int, which must be as least as big as short.

There is no short float,  short double,   or  long float. The type long double specifies extended precision.

The qualifiers signed or unsigned can be applied to char or any integer type. They basically determined how the sign bit is interpreted. An unsigned char uses all 8 bits for the integer value and thus has a range of 0–255; whereas, a signed char has an integer range of -128–127.

2.3: Constants

Integer Constants

A normal integer constant such as 123 is an int, unless it is too big in which cast it is a long. But there are other possibilities.

String Constants

Although there are no string variables, there are string constants, written as zero or more characters surrounded by double quotes. A null character '\0' is automatically appended.

Enum Constants

Alternative method of assigning integer values to symbolic names. 

    enum Boolean {false, true}; // false is zero, true is 1
    enum Month {Jan=1, Feb, Mar, Apr, May, Jun, Jul, Aug, Sep, Oct, Nov, Dec};

2.4: Declarations

Perhaps they should be called definitions since space is allocated.

Similar to Java for scalars. 

    int x, y;
    char c;
    double q1, q2;

(Stack allocated) arrays are simpler as the entire array is allocated not just a reference (no new/malloc required). 

    int x[10];

Initializations may be given. 

    int x=5, y[2]={44,6}; z[]={1,2,3};
    char str[]="hello, world\n";

The qualifier const makes the variable read only so it better be initialized in the declaration.

2.5: Arithmetic Operators

Mostly the same as java.

Please do not call % the mod operator, unless you know that the operands are positive.

2.6: Relational and Logical Operators

Again very little difference from Java.

Please remember that && and || are required to be short-circuit operators. That is, they evaluate the right operand only if needed.

2.7: Type Conversion

There are two kinds of conversions: automatic conversion, called coercion, and explicit conversions.

Automatic Conversions

C coerces narrow arithmetic types to wide ones. 

    {char, short} → int → long
    float → double → long double
    long → float   // precision can be lost
  

int atoi(char s[]) {
  int i, n;
  for (i=0; s[i]>='0' && s[i]<='9'; i++)
    n = 10*n + (s[i]-'0');  // assumes ascii
  return n;
}

The program on the right (ascii to integer) converts a character string representing an integer to the integral value.

Unsigned coercions are more complicated; you can read about them in the book.

Explicit Casts

The syntax 

    (type-name) expression
converts the value to the type specified. Note that e.g., (double x) converts the value of x; it does not change x itself.

Homework: 2-3.

2.8: Increment and Decrement Operators

The same as Java.

Remember that x++ or ++x are not the same as x=x+1 because, with the operators, x is evaluated only once, which becomes important when x is itself an expression with side effects. 

    x[i++]++ // increments some (which?) element of an array
    x[i++] = x[i++]+1 // puts incremented value in ANOTHER slot

Homework: 2-4.

2.9: Bitwise Operators

The same as Java

2.10: Assignment Operators and Expressions

  int bitcount (unsigned x) {
    int b;
    for (b=0; x!=0; x>>= 1)
      if (x&01) // octal (not needed)
        b++;
    return b;
  }

The same as Java: += -= *= /= %= <<= >>= &= ^= |=

The program on the right counts how many bits of its argument are 1. Right shifting the unisigned x causes it to be zero-filled. Anding with a 1, gives the LOB (low order bit). Writing 01 indicates an octal constant (any integer beginning with 0; similarly starting with 0x indicates hexadecimal). Both are convenient for specifying specific bits (because both 8 and 16 are powers of 2). Since the constant in this case has value 1, the 0 has no effect.

Homework: 2-10.

2.11 Conditional Expressions

The same as Java: 

    printf("You enrolled in %d course\s.\n", n, n==1 ? "" : "s");

2.12: Precedence and Order of Evaluation


Precedence and Associativity of C Operators
OperatorsAssociativity
() [] -> .left to right
! ~ ++ -- + - * & (type) sizeofright to left
* / %left to right
+ -left to right
<< >>left to right
< <= > >=left to right
== !=left to right
&left to right
^left to right
|left to right
&&left to right
||left to right
?:right to left
= += -= *= /= %= &= ^= |= <<= >>=right to left
,left to right

The table on the right is copied (hopefully correctly) from the book. It includes all operators, even those we haven't learned yet. I certainly don't expect you to memorize the table. Indeed one of the reasons I typed it in was to have an online reference I could refer to since I do not know all the precedences.

Homework: Check the table above for typos and report any on the mailing list.

Not everything is specified. For example if a function takes two arguments, the order in which the arguments are evaluated is not specified.

Also the order in which operands of a binary operator like + are evaluated is not specified. So f() could be evaluated before or after g() in the expression f()+g(). This becomes important if, for example, f() alters a global variable that g() reads.

Chapter 3: Control Flow

3.1: Statements and Blocks

int t[]={1,2};
int main() {
    22;
    return 0;
}

C is an expression language; so 22 and x=33 have values. One simple statement is an expression followed by a semicolon; For example, the program on the right is legal.

As in Java, a group of statements can be enclosed in braces to form a compound statement or block.

3.2: If-Else

Same as Java.

3.3: Else-IF

Same as Java.

3.4: Switch

Same as Java.

3.5: Loops—While and For

#include <ctype.h>
int atoi(char s[]) {
  int i, n, sign;
  for (i=0; isspace(s[i]); i++) ;
  sign = (s[i]=='-' ? -1 : 1);
  if (s[i]=='+' || s[i]=='-')
    i++;
  for (n=0; isdigit(s[i]); i++)
    n = 10*n + (s[i]-'0');
  return sign * n;
}

Same as Java.

The program on the right (ascii to integer) illustrates a number of points.

The Comma Operator

If two expressions are separated by a comma, they are evaluated left to right and the final value is the value of the one on the right. This operator often proves convenient in for statements when two variables are to be incremented. 

    for (i=0; i+j<n; i++,j+=3)

Start Lecture #5

3.6: Loops—Do-While

Same as Java.

3.7: Break and Continue

Same as Java.

3.8: Goto and Labels

The syntax is 

    goto label;
The label has the form of a variable name. A label followed by a colon can be attached to any statement in the same function as the goto. The goto transfers control to that statement.

for (...) {
  for (...) {
    while (...) {
      if (...) goto out;
    }
  }
}
out: printf("Left 3 loops\n");

Note that a break in C (or Java) only leaves one level of looping so would not suffice for the example on the right.

The goto statement was deliberately omitted from Java. Poor use of goto can result in code that is hard to understand and therefore it is rarely used in modern practice.

The goto statement was much more commonly used in the past.

Chapter 4: Functions and Program Structure

4.1 Basics of Functions

Very Simplified Unix grep

The Unix utility grep (Global Regular Expression Print) prints all occurrences of a given string (or more generally a RE) from standard input. A very simplified version is on the right. 

#include <stdio.h>
#define MAXLINE 100
int getline(char line[], int max);
int strindex(char source[], char searchfor[]);
char pattern[]="x y"; // "should" be input
main() {
  char line[MAXLINE];
  int found=0;     // "should" be Boolean
  while (getline(line,MAXLINE) > 0)
    if (strindex(line, pattern) >= 0) {
      printf("%s", line);
      found++;
    }
  return found;
}
int getline(char s[], int lim) {
  int c, i;
  i = 0;
  while (--lim>0 && (c=getchar())!=EOF && c!='\n')
    s[i++] = c;
  if (c == '\n')
    s[i++] = c;
  s[i] = '\0';
  return i;
}
int strindex(char s[], char t[]) {
  int i, j, k;
  for(i=0; s[i]!='\0'; i++) {
    for (j=i,k=0; t[k]!='\0'&&s[j]==t[k]; j++,k++) ;
    if (k>0 && t[k]=='\0')
      return i;
  }
  return -1;
}

The basic program is 

    while there is another line
      if the line contains the string
        print the line

Getting a line and seeing if there is more is getline(); a slightly revised version is on the right. Note that a length of 0 means EOF was reached; an "empty" line still has a newline char '\n' and hence has length 1.

Printing the line is printf().

Checking to see if the string is present is the new code. The choice made was to have it a function strindex() that is given two strings s and t and returns the position (the index in the array) in s where t occurs. Strindex() returns -1 if t does not occur in s.

The program is on the right; some comments follow.

Note that a function definition is of the form 

    return-type function-name
    {
        declaratons and statements
    }
The default return type is int.

The return statement is like Java.

4.2: Functions Returning Non-integers

The book correctly gives all the defaults and explains why they are what they are (compatibility with previous versions of C) It is much simpler to always

  1. Use no defaults when defining a function.
  2. Declare all functions that are used in a file. Have this declaration early, before any function definitions.

4.3: External Variables

A C program consists of external objects, which are either variables or functions.

External vs. Internal

Variables and functions defined outside any function are called external. Variables and functions defined inside a function are called internal.

Standard C does not have internal functions, that is you cannot in C define a function inside another function. In this sense C is not a fully block-structured language (see block structure below).

Defining External Variables

As stated, a variable defined outside functions is external. All subsequent functions in that file will see the definition (unless it is overridden by an internal definition).

These can be used, instead of parameters/arguments to pass information between functions. It is sometimes convenient to not have to repeat a long list of arguments common to several functions, but using external variables has problems as well: It makes the exact information flow harder to deduce when reading the program.

4.4: Scope Rules

The scope rules give the visibility of names in a program. In C the scope rules are fairly simple.

Internal Names (Variables)

Since C does not have internal functions, all internal names are variables. Internal variables can be automatic or static. We have seen only automatic internal variables, and this section will discuss only them. Static internal variables are discussed in section 4.6 below.

An automatic variable defined in a function is visible from the definition until the end of the function (but see block structure, below).

If the same variable name is defined internal to two functions, the variables are unrelated.

Parameters of a function are the same as local variables in this respect.

External Names

  int main(...) {...}
  int value;
  float joe(...) {...}
  float sam;
  int bob(...) {...}

An external name (function or variable) is visible from the point of its definition (or declaration as we shall see below) until the end of that file. In the example on the right main() cannot call joe() or bob(), and cannot use either value or sam. Joe() can call bob(), but not vice versa.

Definitions and Declarations

There can be only one definition of an external name in the entire program (even if the program includes many files). However, there can be multiple declarations of the same name.

An declaration describes a variable (gives its type) but does not allocate space for it. A definition both describes the variable and allocates space for it.

extern int X;
extern double z[];
extern float f(double y);

Thus we can put declarations of a variable X, an array z[], and a function f() at the top of every file and then X and X are visible in every function in the entire program. Declarations of z[] do not give its size since space is not allocated; the size is specified in the definition.

If declarations of joe() and bob() were placed at the top of the previous example, then main() would be able to call them.

If an external variable is to be initialized, the initialization must be put with the definition, not with a declaration. 

#include <stdio.h>
double f(double x);
int main() {
    float y;
    int x = 10;
    printf("x is %f\n",x);
    printf("f(x) is %f\n",f(x));
    return 0;
}
double f(double x) {
    return x;
}
x is 0.000000
f(x) is 10.000000

4.5: Header Files

The code on the right shows how valuable having the types declared can be. The function f() is the identity function. However, main() knows that f() takes a double so the system automatically converts x to a double.

It would be awkward to have to change every file in a big programming project when a new function was added or had a change of signature (types of arguments and return value). What is done instead is that all the declarations are included in a header file.

For now assume the entire program is in one directory. Create a file with a name like functions.h containing the declarations of all the functions. Then early in every .c file write the line 

    #include  "functions.h"
Note the quotes not angle brackets, which indicates that functions.h is located in the current directory, rather than in the standard place that is used for <>.

4.6: Static Variables

The adjective static has very different meanings when applied to internal and external variables. 

  int main(...){...}
  static int b16;
  void sam(...){...}
  double beth(...){...}

If an external variable is defined with the static attribute, its visibility is limited to the current file. In the example on the right b16 is naturally visible in sam() and beth(), but not main(). The addition of static means that if another file has a definition or declaration of b16, with or without static, the two b16 variables are not related.

If an internal variable is declared static, its lifetime is the entire execution of the program. This means that if the function containing the variable is called twice, the value of the variable at the start of the second call is the final value of that variable at the end of the first call.

Static Functions

As we know there are no internal functions in standard C. If an external function is defined to be static, its visibility is limited to the current file (as for static external variables).

4.7: Register Variables

Ignore this section. Register variables were useful when compilers were primitive. Today, compilers can generally decide, better than programmers, which variables should be put in register.

4.8: Block Structure

Standard C does not have internal functions, that is you cannot in C define a function inside another function. In this sense C is not a fully block-structured language. 

  #include <stdio.h>
  int main(void) {
    int x;
    x = 5;
    printf ("The value of the outer x is %d\n", x);
    {
      int x;
      x = 10;
      printf ("The value of the inner x is %d\n", x);
    }
    printf ("The value of the outer x is %d\n", x);
    return 0;
}
The value of the outer x is 5.
The value of the inner x is 10.
The value of the outer x is still 5.

The gcc compiler for C does one to define a function inside another function. These are called nested functions; many consider this gcc extension to be evil.

Of course C does have internal variables; we have used them in almost every example. That is, most functions we have written (and will write) have variables defined inside them.

Also C does have block structure with respect to variables. This means that inside a block (remember that is a bunch of statements surrounded by {}) you can define a new variable with the same name as the old one. The lifetime of the new variable is just the lifetime of this execution of the block. The program on the right produces the output shown.


Start Lecture #6

Remark: Must do 4.5 (skipped last time by mistake).

Homework: Write a C funcion int odd (int x) that returns 1 if x is odd and returns 0 if x is even. Can you do it without an if statement?

4.9: Initialization

Default Initialization

Static and external variables are, by default, initialized to zero. Automatic, internal variables (the only kind left) are not initialized by default.

Initializing Scalar Variables

  int x=4;
  int y=x-1;

As in Java, you can write int X=5-2;. For external or static scalars, that is all you can do.

For automatic, internal scalars the initialization expression can involve previously defined values as shown on the right (even function calls are permitted).

Initializing Arrays

  int BB[8] = {4,9,2}
  int AA[] = {3,5,12,7};
  char str[] = "hello";
  char str[] = {'h','e','l','l','o','\0'}

You can initialize an array by giving a list of initializers as shown on the right.

4.10: Recursion

The same as Java

4.11: The C Preprocessor

Normally, before the compiler proper sees your program, a utility called the C preprocessor is invoked to include files and perform macro substitutions.

4.11.1: File Inclusion

  #include <filename>
  #include "filename"

We have already discuss both forms of file inclusion. In both cases the file mentioned is textually inserted at the point of inclusion. The difference between the two is that the first form looks for filename in a system-defined standard place; whereas, the second form first looks in the current directory.

4.11.2: Macro Substitution

  #define MAXLINE 20
  #define MAX(A,B) (A>B ?(A) : (B))
  #undef getchar

We have already used examples of macro substitution similar to the first line on the right. The second line, which illustrates a macro with arguments is more interesting.

Without all the parentheses on the RHS, the macro would be legal, but would (sometimes) give the wrong answers. Why?
Ans: Consider 3+MAX(X+Y,Z-W)

Note that macro substitution is not the same as a function call (with standard call-by-value or call-by-reference semantics). Consider MAX(x++,5). It may increment x twice. If you know call-by-name from algol 60 fame, you will now see where it came from.

We probably will not use the third form. It is used to un-define a macro from a library so that you can write another version.

There is some fancy stuff involving # in the RHS. See the book for details; I do not intend to use it.

4.11.3: Conditional Inclusion

  #if integer-expr
  #elif integer-expr
  ...
  #elif integer-expr
  #else
  #endif

The C-preprocessor has a very limited set of control flow items. On the right we see how the familiar 

    if cond1 then / else if cond2 then / ... / else if condn then / end if
construct is written. The individual conditions are simple integer expressions consisting of integers, some basic operators and little else. Perhaps the most useful additions are the preprocessor functions defined(name), which evaluates to 1 (true) if name has been #define'd, and the ! operator, which converts true to false and vice versa.


  #if !defined(HEADER22)
  #define HEADER22
  // The contents of header22.h
  // goes here
  #endif

We can use defined(name) as shown on the right to ensure that a header file, in this case header22.h, is included only once.

You might ask how could a header file be included more than once unless a programmer by mistake wrote the same #include statement twice? One possibility is a that a user file joe.c might include two systems headers h1.h and h2.h each of which includes h3.h.

Two other directives ifdef and ifndef test whether a name has been defined. Thus the first line of the previous example could have been written ifndef HEADER22. 

  #if SYSTEM == MACOS
    #define HDR macos.h
  #elsif SYSTEM == WINDOWS
    #define HDR windows.h
  #elsif SYSTEM == LINUX
    #define HDR linux.h
  #else
    #define HDR empty.h
    #define MSG System not known
  #endif
  #include HDR

On the right we see a slightly longer example of the use of preprocessor directives. Assume that the name SYSTEM has been set to the name of the system on which the current program is to be run (not compiled). Then the code shown includes an appropriate header and, if the SYSTEM is not one for which the program is designed to be run defines MSG.


Chapter 5: Pointers and Arrays

  public class X {
    int A;
    public static void main(String args[]) {
      int i1=1;
      int i2=2;
      i2 = i1;
      i1 = 3;
      System.out.println("i2 is " + i2);
      X x1 = new X();
      X x2 = new X();
      x2 = x1;
      x1.A = 3;
      System.out.println("x2.A is " + x2.A);
    }
  }

Much of the material on pointers has no explicit analogue in Java; it is there kept under the covers. If in Java you have an Object obj;, then obj is actually what C would call a pointer. The technical term is that Java has reference semantics for all objects. In C this will all be quite explicit

To give an example, look at the Java snippet on the right. The first part works with integers. We define 2 integers; initialize both; set the second to the first; change the first; and print the second. Naturally, the second has its initial value of the first, namely 1.

The second part deals with X's, a trivial with just one data component, an integer. What we do is: define 2 X's; initialize both; set the second to the first; change the first; and print the second. The result is different! The second has the altered value of the first, namely 3.

This is on i5 for demo.

5.1: Pointers and Addresses

You will learn in 202, that the OS finagles memory in ways that would make Bernie Madoff smile. But, in large part thanks to those shenanigans, user programs can have a simple view of memory. For us C programmers, memory is just a large array of consecutively numbered addresses.

The machine model we will use in this course is that the fundamental unit of addressing is a byte and a character (a char) exactly fits in a byte. Other types like short, int, double, float, long take more than one byte but always a consecutive range of bytes.

l-values and r-values

One consequence of our memory model is that associated with int x=5 are two numbers. The first number is the address of the location in which x is stored. The second number is the value stored in that location; in this case that value is 5. The first number, the address, is often called the l-value; the second number, the contents, is often called the r-value. Why?

Consider x = x + 1; To evaluate the RHS we need to add 5 to 1. In particular, we need the value contained in the memory location assigned to x, i.e., we need 5. Since this is what is needed to evaluate a RHS it is called the r-value.

We compute 6=5+1. Where should we put it? We look at the LHS and see that we put it into x; that is, into the memory location assigned to x. Since it is the location that is needed when evaluating a LHS, that is called the l-value.

The Unary Operators & and *

As we have just seen, when a variable appears on the LHS, its l-value or address is used. What if we want the address of a variable that appears on the RHS; how do we get it?

In a language like Java the answer is simple; we don't.

In C we used the unary operator & and write p=&x; to assign the address of x to p. After executing this statement we say that p points to x or p is a pointer to x.

The unary operator does the reverse action. When * is applied to a pointer, it gives the value of the object (object is used in the English not OO sense) pointed. The * operator is called the dereferencing or indirection operator.

Consider the code sequence on the right. The first line we have seen before; the second is new. Recall that in a C declaration, all the doodads around a variable name tell you what you must do the variable to get the base type at the beginning of the line. Thus the second line says that if you dereference ip you get an integer. Common parlance is to say ip is an integer pointer (which is why we often use the name ip. Similarly, jp is another integer pointer.

  int x=1, y=2, z[10];
  int *ip, *jp;
  ip = &x;
  y = *ip;
  *ip = 0;
  ip = &z[0];
  *ip = 0;
  jp = ip;
  *jp = 1;

At this point both ip and jp are uninitialized. The next line sets ip to the l-value, i.e., the address, of x. Note that the types are correct, both ip and &x are pointers to an int.

The next line sets y equal to 1. Make sure you understand this. Slowly, ip at this time points to x, * does the dereference so *ip is x. Since we are on the RHS, we take the contents not the address of x and get 1.

The next line sets x=0;. The RHS is clearly 0. Where do we put this zero; look at the LHS. Slowly, ip at this time points to x, * does the dereference so *ip is x. Since we are on the LHS, we take the address and not the contents of x and hence we put 0 in the address that is the address of x. That is, we put 0 in x.

The next line changes ip; it now points to z[0]. The next line sets z[0]=0;

Pointers can be used without the deferencing operator. The next line sets jp to ip. Since ip at this time points to z[0], jp does as well. Hence the next line sets z[0]=1;

Start Lecture #7

  ip = &x;
  *ip = *ip + 10;
  y = *ip + 1;
  *ip += 1;
  ++*ip;
  (*ip)++;
  *ip++;

The first line on the right re-establishes ip as a pointer to x so the second line increments x by 10 and the next line sets y=x+1;.

The next line increments x by 1 as does the following line (because the unary operators ++ and * are right associative).

The next line also increments x, but the last line does not. By right associativity we see that the increment precedes the dereference, but the full story awaits section 5.4 below.

5.2: Pointers and Function Arguments

  void bad_swap(int x, int y) {
    int temp;
    temp = x;
    x = y;
    y = temp;
  }

The program on the right is what a FORTRAN programer just learning C (or Java) would write. It is supposed to swap its two arguments but fails due to call by value semantics for function calls in C. That is, when a user writes swap(A,B) the values of A and B are transmitted, A and B are not changed.

But programs that change their arguments are useful!

Actually, what is useful is to be able to change the value of variables used in the arguments and that distinction is the key. Just because we want to swap the values of A and B, doesn't mean the arguments have to be exactly A and B.

  void swap(int *px, int *py) {
    int temp;
    temp = *px;
    *px = *py;
    *py = temp;
  }

The program on the right has two parameters x and y each of which is a pointer to an integer (*px and *py are the integers). Since C is a call-by-value language, changes to the parameters, which are the pointers x and y would not result in changes to the corresponding arguments. But the program on the right doesn't change the pointers at all, just the values that they point to.

Since the parameters are pointers to integers, so must be the arguments. A typical call to this function would be swap(&A,&B).

swap

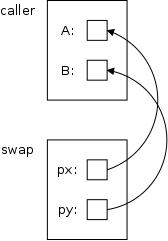
Understanding how this call results in A receiving the value previously in B and B receiving the value previously in A is very important.

On the right is pictorial explanation from the book. A has a certain address. The call swap(&A,&B) places the address of A into the first parameter, which is px. Thus the value of px is the address of A, which is indicated by the arrow. Similarly for B and py.

Homework: Write rotate3(A,B,C) that sets A to the old value of B, sets B to old C, and C to old A.

Homework: Write plusminus(x,y) that sets x to old x + old y and sets y to old x - old y.

5.2A: A Larger Example—getch(), ungetch(), and getint()

#include <stdio.h>
#define BUFSIZE 100
char buf[BUFSIZE];
int  bufp = 0;
int getch(void) {
  return (bufp>0) ? buf[--bufp] : getchar();
}
void ungetch(int c) {
  if (bufp >= BUFSIZE)
    printf("ungetch: too many chars\n");
  else
    buf[bufp++] = c;
}

#include <stdio.h>
#include <ctype.h>
int  getch(void);
void ungetch(int);
int getint(int *pn) {
  int c, sign;
  while (isspace(c=getch())) ;
  if (!isdigit(c) && c!=EOF && c!='+' && c!='-') {
    ungetch(c);
    return 0;
  }
  sign = (c=='-') ? -1 : 1;
  if (c=='+' || c=='-')
    c = getch();
  for (*pn = 0; isdigit(c); c=getch())
    *pn = 10 * *pn + (c-'0');
  *pn *= sign;
  if (c != EOF)
    ungetch(c);
  return c;
}

The program pair getch() and ungetch generalize getchar() by supporting the notion of unreading a character, i.e., having the effect of pushing back several already read characters.

Also shown is getint(), which reads an integer from standard input (stdin) using getch() and ungetch().

getint() returns the integer as a parameter (using a pointer of course). The value of the function itself gives the status, zero means the next characters do not form an integer, EOF (which is negative) means end of file, positive means an integer has been found. The idea is 

    Skip blanks
    Check for legality
    Determine sign
    Evaluate number
      one digit at a time

Note some corner cases

If, in real life, you were asked to produce a getint() function you would have three tasks.

  1. Write, in precise English, what is to happen in all cases.
  2. Write a C program implementing this specification.
  3. Get the C syntax right.
The third is clearly the easiest task. I suspect that the first is the hardest.

5.3: Pointers and Arrays

In C pointers and arrays are closely related. As the book says

Any operation that can be achieved by array subscripting can also be done with pointers.
The authors go on to say
The pointer version will in general be faster but, at least to the uninitiated, somewhat harder to understand.
The second clause is doubtless correct; but perhaps not the first. Remember that the 2e was written in 1988 (1e in 1978). Compilers have improved considerably in the past 20+ years and, I suspect, would turn out equally fast code for many of the subscripted versions.

int a[5], *pa
int i, x;
pa = &a[0];

x = *pa;
x = *(pa+1);
x = a[0];
x = *a;
x = a[i];
x = *(a+i);

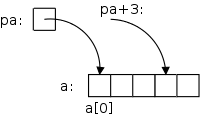
array-ptr

On the far right we see some code involving pointers and arrays. After the first three lines are executed we get the diagram shown. pa is a pointer to the first element of the array a.

The next line sets x=a[0]; the line after that sets x=a[1].

Then we explicitly set x=a[0];; the line after that has the same effect! That is because in C a has the same value as &a[0].

Similarly, the next two lines form a pair having the same effect.

Array Name vs Pointer to First Element

int mystrlen(char *s) {
  int n;
  for (n=0; *s!='\0'; s++,n++);
  return n;
}

char str[50], *pc;
// calculate str and pc
mystrlen(pc);
mystrlen(str);
mystrlen("Hello, world.");

The code on the right shows how well the C pointers, arrays, and strings mesh. What a tiny program to find the length!

Also note the ways it can be called: The first call shown exactly matches the function declaration. The second matches as well, when we remember that an array name has the same value as a pointer to the first value. Finally, the third is like the second since a string is a character array.

Start Lecture #8

Lecture given by Prof. Ralph Grishman

Some Basic Pointer Examples

The next few sections present some simple examples using pointers. Several were written in class with the students.

Value Versus Address

#include <stdio.h>
int x, *p;
int main () {
  p = &x;
  x = 12;
  printf ("p = %d\n", p);
  p++;
  printf ("p = %d\n", p);
  printf ("*p = %d\n", *p);
}

The example on the right illustrates well the difference between a variable, in this case x, and its address &x. The first value printed is the address of x. This is not 12. Instead it is (probably) some large number.

A compiler warning occurs since in (modern) C, integers (%d) and pointers (&x) are not the same type.

Incrementing p does not increment x. Instead, the result is that p points to the next integer after x. In this program there is no further integer after x, so the result is unpredictable. If, instead of x, we had p point to A[7] for some integer array A, then the last line would have printed the value of A[8] and the penultimate line would have printed the address of A[8].

include <stdio.h>
int mystrlen (char *s);
int main () {
  char stg[] = "hello";
  printf ("The string %s has %d characters\n",
          stg, mystrlen(stg));
}
int mystrlen (char *s) {
  int i;
  for (i = 0; s[i] != '\0'; i++);
  return i;
}

#include <stdio.h>
int mystrlen (char s[]);
int main () {}   // unchanged
int mystrlen (char s[]) {
  int i = 0;
  while (*s++ != '\0') i++;
  return i;
}

String Length with Arrays and Pointers

On the right we show two versions of the string length function: The first version uses array notation for the string; the second uses pointer notation. The main() program is identical in the two versions so is shown only once. Note how very close the two string length functions are; another illustration of the similarity of arrays and pointers in C.

In the second version we encounter a common C idiom *s++. First note that the precedence of the operators is such that *s++ is the same as *(s++). That is, we are moving (incrementing) the pointer and examining what it now points at. We are not incrementing a part of the string. Specifically, we are not executing (*s)++;

Note that the two declarations 

    int mystrlen (char *s)
    int mystrlen (char s[])
are the same. They are used 4 times in the two versions of string length.

Changing any of them to the other form does not change the meaning of the program.

#include <stdio.h>
void changeltox (char*);
int main () {
  char stg[] = "hello";
  changeltox (stg);
  printf ("The string is now %s\n", stg);
}
void changeltox (char *s) {
  while (*s != '\0') {
    if (*s == 'l')
      *s = 'x';
    s++;
  }
}

Simple Substitution

The program on the right simply loops through the input string and replaces each occurence of l with x.

The while loop and increment of s could have been combined into a for loop. This version is written in pointer style.

Homework: Rewrite changeltox() to use array style and a for loop.


Start Lecture #9

String Copy

void mystrcpy (char *s, char *t) {
  while ((*s++ = *t++) != '\0');
}

Check out the ONE-liner on the right. Note especially the use of standard idioms for marching through strings and for finding the end of the string.

Slick!

But scary, very scary! Why?
Because there is no length check. If the character array s (or equivalently the block of characters s points to) is smaller than the character array t points to, then the copy will overwrite whatever happens to be located right after the array s.

Array Name Vs Pointer to First Element (Continued)

Although arrays and pointers are closely related, there is a difference between an array name like a, and a pointer that happens to point to the first element like pa. The latter is a variable that can be assigned to; whereas a or equivalently &a[0] is just a value.

The last paragraph might make you worry that the 2nd and 3rd calls above are illegal since they pass an array name and the corresponding parameter s is assigned to. However, all is well since C is call-by-value and the assignment to a parameter does not effect the argument.

Using int *A vs int A[] As a Parameter

double f(int *a);
double f(int a[]);

The two lines on the right are equivalent, when used as a function declaration (or as the head line of a function definition). The authors say they prefer the first. For me it is not so clear cut. In strlen() above I prefer char *s as written. However, if I were writing an inner product routine (a.k.a dot product), I would write 

    double dotprod(double A[], B[], C[])
since I think of dot product as operating on vectors.

Passing Part of an Array: f(A+6), i.e., f(&A[6]) and p[-2], i.e., *(p-2) 

void f(int *p) {
  printf("legal? %d\n", p[-2]);
}
int main(){
  int A[20];
  // calculate all of A
  f(A+6);
  return 0;
}

In the code on the right main() calculates the values for an integer array and then passes only part of it to f. Remembering that A+6 means (&A[0])+6, which is &A[6], we see that f() receives a pointer to the 7th element of the array A.

With call by value, we know that f() cannot change the value of the pointer in main(). But f() can use this pointer to reference or change all the values of A, include those before A[6].

It naturally would be illegal for f() to reference (or worse change) p[-9].

5.4: Address Arithmetic

A crucially important point is that pa+3, does not simply add three to the address stored in pa. Instead, it increments pa so that it points 3 integers further forward (since pa is a pointer to an integer). If pc is a pointer to a character, then pc+3 increments pc so that it points 3 characters forward.

#define ALLOCSIZE 15000
static char allocbuf[ALLOCSIZE];
static char *allocp = allocbuf;
char *alloc(int n) {
  if (allocbuf+ALLOCSIZE-allocp >= n) {
    allocp += n;
    return allocp-n;
  } else
    return 0;
}
void afree (char *p) {
  if (p>=allocbuf && p<allocbuf+ALLOCSIZE)
    allocp = p;
}

On the right is a primitive storage allocator and freer. When alloc(n) is called, with an integer argument n, it returns a pointer to a block of n characters.

When afree(p) is called with the pointer returned by alloc(), it resets the state of alloc()/afree() to what it was before the call to alloc().

A strong assumption is made that calls to alloc()/afree() are made in a stack-like manner. These routines would be useful for managing storage for C automatic, local variables. They are far from general. The real routines malloc()/free() are considerably more complicated.

Since pointers, not array positions are communicated to users of alloc()/afree(), these users do not need to know anything about the array, which is kept under the covers via static. alloc

The tricky (elegant? beautiful?) part is the if in alloc().

Notes

Using the Allocator

Remark: Much of this was presented by Prof. Grishman in the previous lecture.

These examples are interesting in their own right, beyond showing how to use the allocator.

#include <stdio.h>
int changeltox (char*);
void mystrcpy (char *s, char *t);
char *alloc(int n);
int main () {
  char stg[] = "hello";
  char* stg2 = alloc(6);
  mystrcpy (stg2, stg);
  changeltox (stg);
  printf ("The string is now %s\n", stg);
  printf ("String2 is now %s\n", stg2);
}

Making Changes in a New String

We have already written a program to change one character to another in a given string.

The code in this section first copies the string (using mystrcpy(), a one liner presented last time) and then makes changes in the copy. Thus, at the end, we have two versions of the string: the before and the after.

As expected the output is 

    The string is now hexxo
    String2 is now hello

Messing Up

Recall the danger warning given with the code for mystrcpy(char *x, char *y): The code copies all the characters in t (i.e., up to '\0') to s ignoring the current length of s. Thus, if t is longer than the space allocated for s, the copy will overwrite whatever happens to be stored right after s.

#include <stdio.h>
int changeltox (char*);
void mystrcpy (char *s, char *t);
char *alloc(int n);
int main () {
  char stg[] = "hello";
  char* stg2 = alloc(2);
  char* stg3 = alloc(6);
  mystrcpy (stg2, stg);
  printf ("String2 is now %s\n", stg2);
  printf ("String3 is now %s\n", stg3);
  mystrcpy (stg3, stg);
  changeltox (stg);
  printf ("The string is now %s\n", stg);
  printf ("String2 is now %s\n", stg2);
  printf ("String3 is now %s\n", stg3);
}

The example on the right illustrates the danger. When the code on the right is compiled with the code for changeltox(), mystrcpy(), and alloc(), the following output occurs. 

    String2 is now hello
    String3 is now llo
    The string is now hexxo
    String2 is now hehello
    String3 is now hello

What happened?

The string in stg contains the 5 characters in the word hello plus the ascii null '\0' to end the string. (The array stg has 6 elements so the string fits perfectly.)

The major problem occurs with the first execution of mystrcpy() because we are copying 6 characters into a string that has only room for 2 characters (including the ascii null). This executes flawlessly copying the 6 characters to an area of size 6 starting where stg2 points. These 6 locations include the 2 slots allocated to stg2 and then the next for locations. In general it is hard to tell what has been overwritten, but in this case it is easy since we know how alloc() works. The excess 4 characters are written into the first 4 slots of stg3.

mess

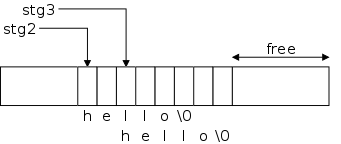
When we print stg2 we see no problem! A string pointer just tells where the string starts, it continues up to the ascii null. So stg2 does have all of hello. Since stg3 points 2 characters after stg2 the string is just the substring of stg2 starting at the third character.

The second mystrcpy copies the six(!) characters in the string hello to the 6 bytes starting at the location pointed to by stg3. Since the string stg2 includes the location pointed to by stg3, both stg2 and stg3 are changed.

The changeltox() execution works as expected.

Pointer Comparison

If pointers p and q point to elements of the same array, then comparisons using <, <=, ==, !=, >, and >= all work as expected.

Any pointer can be compared to 0 via == and !=.

If pointers p and q do not point to members of the same array, the value returned by comparisons is undefined, with one exception: p pointing to an element of an array and q pointing to the first element past the array.

Pointer Subtraction

Again we need p and q pointing to elements of the same array. In that case, if p<q, then p-q+1 equals the number of elements from p to q (including the elements pointed to by p and q.

5.5: Character Pointers and Functions

As we know C does not have string variables, but does have string constants. This arrangement sometimes requires care to avoid errors.

char amsg[]="hello"; vs char *msgp="hello";

  char amsg[] = "hello";
  char *msgp = "hello";
  int main () {...}

Let's see if we can understand the following rules, which can appear strange at first glance.

  1. amsg (a character pointer) cannot be changed, but both *(amsg+2) (an 'l') and amsg[2] can be changed.
  2. msgp (a character pointer) can be changed, but both *(msgp+2) (an 'l') and msgp[2] cannot be changed.
A key to understanding these rules, which really are just consequences of rules we already know, is that "hello" is a constant.

An Even Slicker String Copy

  void mystrcpy (char *s, char *t) {
    while (*s++ = *t++) ;
  }

The previous version of this program tested if the assignment did not return the character '\0' and that character has the value 0 (a fact about ascii null). However checking if something is not 0 is the same (in C) as asking if it is true. Finally, testing if something is true is the same as just testing the something. The C rules can seem cryptic, but they are consistent.


Start Lecture #10

Slick String Length Using Pointer Substraction

int mystrlen(char *s) {
  char *p = s;
  while (*p)
    p++;
  return p-s;
}

The code on the right applies the technique used to get the slicker string copy to the related function string length. It also use pointer subtraction. Note that when the return is executed, p points just after the string (i.e., the character array) and s points to its beginning. Thus the difference gives the length.

String Comparison

int mystrcmp(char *s, char *t) {
  for (; *s == *t; s++,t++)
    if (*s == '\0')
      return 0;
  return *s - *t;
}

We next produce a string comparison routing that is to return a negative integer if the string s is lexicographically before t, zero if they are equal, and a positive integer if s is lexicographically after t.

The loop takes care of equal characters; it returns 0 if we have reached the end of the strings.

If the loop concludes, we have found the first difference. A key is that if one string has ended, its character ('\0') is smaller then the other string's character. This is another ascii fact (ascii null is zero the rest are positive).

I tried to produce a version usingwhile(*s++ == *t++), but that failed since the loop body and the post loop code would be dealing with the subsequent character. It could have been forced to work if I used a bunch of constructions like *(s-1), but that would have been ugly.

Homework: 5-5 (just do strncpy). These kinds of routines are not scary (and hence the world has not ended).

5.6: Pointer Arrays; Pointers to Pointers

For the moment forget that C treats pointers and arrays almost the same. For now just think of a character pointer as another data type.

So we can have an array of 9 character pointers, e.g., char *A[9]. We shall see fairly soon that this is exactly how some systems (e.g. Unix) store command line arguments.

#include <stdio.h>
int main() {
  char *STG[3] = { "Goodbye", "cruel", "world" };
  printf ("%s %s %s.\n", STG[0], STG[1], STG[2]);
  STG[1] = STG[2] = STG[0];
  printf ("%s %s %s.", STG[0], STG[1], STG[2]);
  return 0;
}

Goodbye cruel world.
Goodbye Goodbye Goodbye.

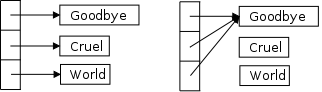
The code on the right defines an array of 3 character pointers, each of which is initialized to a string. The first printf() has no surprises. But the assignment statement should fail since we allocated space for three strings of sizes 8, 6, and 6 and now want to wind up with three strings each of size 8 and we didn't allocate any additional space.

However, it works perfectly and the resulting output is shown as well. What happened? How can space for 8+6+6 characters be enough for 8+8+8?

The reason is that we do not have three strings of size 8. Instead we have one string of size 8, with three character pointers pointing to it.

The picture on the right shows a before and after view of the array and the strings. goodbye

This suggests and interesting possibility. Imagine we wanted to sort long strings alphabetically (really lexicographically). Not to get bogged down in the sort itself assume it is a simple interchange sort that loops and, if a pair is out of order, it executes a swap, which is something like 

    temp = x;
    x = y;
    y = temp;

If x, y, and temp are (varying size, long) strings then we have some issues to deal with.

  1. It is expensive to do the three assignments if the strings are very long.
  2. If one of the strings is longer than the space allocated for another, we either overwrite something else (and potentially end the world) or refuse the copy and hence not complete the sort.

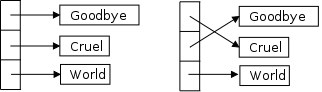
sortstrings

Both of these issues go away if we maintain an array of pointers to the strings. If the string pointed to by A[i] is out of order with respect to the string pointed to by A[j], we swap the (fixed size, short) pointers not the strings that they point to.

This idea is illustrated on the right.

#include <stdio.h>
void sort(int n, char *C[n]) {
  int i,j;
  char *temp;
  for (i=0; i<n-1; i++)
    for (j=i+1; j<n; j++)
      if (mystrcmp(C[i],C[j]) > 0) {
        temp = C[i];
        C[i] = C[j];
        C[j] = temp;
      }
}
int main() {
  char *STG[] = {"hello", "99", "3", "zz", "best"};
  int i,j;
  for (i=0; i<5; i++)
    printf ("STG[%i] = \"%s\"\n", i, STG[i]);
  sort(5,STG);
  for (i=0; i<5; i++)
    printf ("STG[%i] = \"%s\"\n", i, STG[i]);
  return 0;
}

Putting all the pieces together, the code on the right, plus the mystrcmp() function above, produces the following output. 

    STG[0] = "hello"
    STG[1] = "99"
    STG[2] = "3"
    STG[3] = "zz"
    STG[4] = "best"
    STG[0] = "3"
    STG[1] = "99"
    STG[2] = "best"
    STG[3] = "hello"
    STG[4] = "zz"

Note the first line of the sort function, in particular the n in char C[n]. This is an addition made to C in 1999 (the language is called sometimes called C-99 to distinguish it from C-89 or ansii-C as described in our text, and K&R-C as described in the first edition of our text). Our text would write C[] instead of C[n].

You might question if the output is indeed sorted. For example, we remember that ascii '3' is less than ascii '9', and we know that in ascii 'b'<'h'<'z', but why is '9'<'b'?

Well, I don't know why it is, but it is. That is, in ascii the digits do in fact come before the letters.

5.7: Multi-dimensional Arrays

void matmul(int n, int k, int m, double A[n][k],
     double B[k][m], double C[n][m]) {
  int i,j,l;
  for (i=0; i<n; i++)
    for (j=0; j<m; j++) {
      C[i][j] = 0.0;
      for (l=0; l< k; l++)
    C[i][j] += A[i][l]*B[l][j];
    }
}

C does have normal multidimensional arrays. For example, the code on the right multiplies two matrices. 

int A[2][3] = { {5,4,3}, {4,4,4} };
int B[2][3][2] = { { {1,2}, {2,2}, {4,1} },
                   { {5,5}, {2,3}, {3,1} } };

Multidimensional arrays can be initialized. Once you remember that a two-dimensional array is a one-dimensional array the syntax for initialization is not surprising.

(C, like most modern languages uses row-major ordering so the last subscript varies the most rapidly.)

5.8: Initialization of Pointer Arrays

char *monthName(int n) {
  static char *name[] = {"Illegal",
    "Jan", "Feb", "Mar", "Apr",
    "May", "Jun", "Jul", "Aug",
    "Sep", "Oct", "Nov", "Dec"};
  return (n<1 || n>12) ? name[0] : name[n];
}

The initialization syntax for an array of pointers follows the general rule for initializing an array: Enclose the initial values inside braces. How do we write an initial value for a pointer?
Ans: We remember that an array is just a pointer to the first element.

Looking at the code on the right we see this principle in action. I believe the most common usage is for an array of character pointers as in the example.

5.9: Pointers vs. Multi-dimensional Arrays

int  A[3][4];
int *B[3];

Consider the two declarations on the right. They look different, but both A[2][3] and B[2][3] are legal (at least syntactically). The real story is that they most definitely are different. In fact Java arrays have a great deal in common with the 2nd (pointer) form in C.

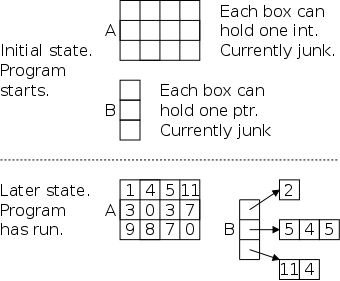
pointer array
  1. The declaration int A[3][4]; allocates space for 12 integers, which are stored consecutively so that A[i][j] is the (4*i+j)th integer stored (counting from zero). With the simple declaration written, none of the integers is initialized, but we have seen how to initialized them.

  2. The declaration int *B[3]; allocates space for NO integers. It does allocate space for 3 pointers (to integers). The pointers are not initialized so they currently point to junk. The program must somehow arrange for each of them to point to an group of integers (and must figure out when the group ends). An important point is that the groups may have different lengths. The technical jargon is that we can have a ragged array as shown in the bottom of the picture.

The diagram shows integers, but the more common usage is for characters. In that case the ragged array is an array of differing length strings. We have see two examples of this. The monthName program just above and the Goodbye Cruel World diagrams in section 5.6.


Start Lecture #11

5.10: Command-line Arguments

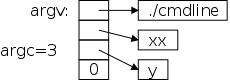
cmdline

On the right is a picture of how arguments are passed to a (Unix) command. Each main() program receives two arguments an integer, normally called argc for argument count, and an array of character pointers, normally called argv for argument vector.

The diagram shows argv as an array and the code below treats it that way as well. As always, an array name is also a pointer to the first element. If you view argv as a pointer, then you would draw a box for it with an arrow pointing to the array. The book pictures it that way.

#include <stdio.h>
int main(int argc, char *argv[argc]) {
  int i;
  printf("My name is %s.\n", argv[0]);
  printf("I was called with %d argument%s\n",
         argc-1, (argc==2) ? "" : "s");
  for (i=1; i<argc; i++)
    printf("Argument #%d is %s.\n", i, argv[i]);
 }

sh-4.0$ cc -o cmdline cmdline.c
sh-4.0$ ./cmdline
My name is ./cmdline.
I was called with 0 arguments.
sh-4.0$ ./cmdline x
My name is ./cmdline.
I was called with 1 argument.
Argument #1 is x.
sh-4.0$ ./cmdline xx y
My name is ./cmdline.
I was called with 2 arguments.
Argument #1 is xx.
Argument #2 is y.
sh-4.0$ ./cmdline -o cmdline cmdline.c
My name is ./cmdline.
I was called with 3 arguments.
Argument #1 is -o.
Argument #2 is cmdline.
Argument #3 is cmdline.c.
sh-4.0$ cp cmdline mary-joe
sh-4.0$ ./mary-joe -o cmdline cmdline.c
My name is ./mary-joe.
I was called with 3 arguments.
Argument #1 is -o.
Argument #2 is cmdline.
Argument #3 is cmdline.c.

Since the same program can have multiple names (more on that later), argv[0], the first element of the argument vector, is a pointer to a character string containing the name by which the command was invoked. Subsequent elements of argv point to character strings containing the arguments given to the command. Finally, there is a NULL pointer to indicate the end of the pointer array.

The integer argc gives the total number of (valid) pointers, including the pointer to the name of the command. Thus, the smallest possible value for argc is 1 and argc is 3 for the picture drawn above.

The code on the right shows how a program can access its name and any arguments it was called with.

Having both a count (argc) and a trailing NULL pointer (argv[argc]==NULL) is redundant, but convenient. The code I wrote treats argv as an array. It loops through the array using the count as an upper bound. Another style would use something like 

    while (*argv)  printf("%s\n", (*argv++));
which treats argv as a pointer and terminates when argv points to NULL.

The second frame on the right shows a session using the code directly above it.

  1. First, we show how to compile a C program and not have the result called a.out.
  2. Next we run the resulting program with differing numbers of arguments. Note the use of the conditional expression to get singular and plural correct.
  3. Finally, we show one way (via copying the executable) that the same program can have more than one name. We could have renamed/moved the executable as well. Another way would have been to recompile the program giving a different file name after -o (or not using -o and getting a.out). In 202 you will learn two other ways (hard and soft links).

Simple Application of Command Line Arguments

Now we can get rid of some symbolic constants that should be specified at run time.

Here are some before and after examples. The code on the left uses symbolic constants; on the right we use command line arguments

Fahrenheight to Celcius

#include <stdio.h>
#define LO 0
#define HI 300                  #include <stdio.h>
#define INCR 20                 #include <stdlib.h>
main() {                        int main (int argc, char *argv[argc]) {
  int F;                          int F;
  for (F=LO; F<=HI; F+=INCR)      for (F=atoi(argv[1]); F<=atoi(argv[2]); F+=atoi(argv[3]))
    printf("%3d\t%5.1f\n", F,       printf("%3d\t%5.1f\n", F,
           (F-32)*(5.0/9.0));              (F-32)*(5.0/9.0));
}                                 return 0;
                                }
  1. Note that now main() is specified correctly; it returns an integer and has the complicated argument structure we just described. As written on the left the program terminates abnormally (it doesn't return 0).
  2. Note the use of atoi() to convert the ascii (character) form of the numerical inputs into integers.

Solving Quadratic Equations

#include <stdio.h>
#include <math.h>
#define A +1.0   // should read                #include <stdio.h>
#define B -3.0   // A,B,C                      #include <math.h>
#define C +2.0   // using scanf()              #include <stdlib.h>
void solve (float a, float b, float c);        void solve (float a, float b, float c);
int main() {                                   int main(int argc, char *argv[argc]) {
  solve(A,B,C);                                  solve(atof(argv[1]), atof(argv[2]),
                                                       atof(argv[3]));
  return 0;                                      return 0;
}                                              }
void solve (float a, float b, float c) {       void solve (float a, float b, float c) {
  float d;                                       float d;
  d = b*b - 4*a*c;                               d = b*b - 4*a*c;
  if (d < 0)                                     if (d < 0)
    printf("No real roots\n");                     printf("No real roots\n");
  else if (d == 0)                               else if (d == 0)
    printf("Double root is %f\n", -b/(2*a));       printf("Double root is %f\n", -b/(2*a));
  else                                           else
    printf("Roots are %f and %f\n",                printf("Roots are %f and %f\n",
           ((-b)+sqrt(d))/(2*a),                          ((-b)+sqrt(d))/(2*a),
           ((-b)-sqrt(d))/(2*a));                         ((-b)-sqrt(d))/(2*a));
}                                              }
  1. Again main() now specified correctly. When we had main() we said don't check the arguments. Now we specify them correctly.
  2. This time we need atof() since the arguments are floating point. 
#include <stdio.h>
#include <ctype.h>
int main (int argc, char *argv[argc]) {
  int c, makeUpper=0;
  if (argc > 2)
    return argc;
  if (argc == 2)
    if (strcmp(argv[1], "-toupper")){
      printf("Argument %s is illegal.\n", argv[1]);
      return -1;
    }
    else
      makeUpper=1;
  while ((c = getchar()) != EOF)
    if (!isdigit(c)) {
      if (isalpha(c) && makeUpper)
	c = toupper(c);
      putchar(c);
    }
  return 0;
}

Specifying Options

Often a leading minus sign (-) is used for optional command line arguments. The program on the right removes all digits from the input. If it is given the argument -toupper it also converts all letters to upper case using the toupper() library routine.

Demo this function on ajglap.cs.nyu.edu.

Homework: Combine the entab and detab functions by writing a function tab that has one argument 

    tab -en   # performs like entab
    tab -DE   # performs like detab
Use a reasonable default for tab width. No need to support the user specifying the tab width, i.e., always use the default value.

5.11: Pointers to Functions

#include <ctype.h>
#include <string.h>
#include <stdio.h>
// Simple program to illustrate function pointers
int digitToStar(int c);   // Convert all digits to *
int letterToStar(int c);  // Convert all letters to *
int main (int argc, char *argv[argc]) {
  int c;
  int (*funptr)(int c);
  if (argc != 2)
    return argc;
  if (strcmp(argv[1],"digits")==0)
    funptr = &digitToStar;
  else if (strcmp(argv[1],"letters")==0)
    funptr = &letterToStar;
  else
    return -1;
  while ((c=getchar())!=EOF)
    putchar((*funptr)(c));
  return 0;
}
int digitToStar(int c) {
  if (isdigit(c))
    return '*';
  return c;
}
int letterToStar(int c) {
  if (isalpha(c))
    return '*';
  return c;
}

In C you can do very little with functions, mostly define them and call them (and take their address, see what follow).

However, pointers to functions (called function pointers) are real values.

  1. A function can return a function pointer.
  2. You can declare variables that hold function pointers.
  3. You can have an array of function pointers.
  4. You can have a structure with function pointer components.
  5. A function can take a function pointer argument.
  6. etc

The program on the right is a simple demonstration of function pointers. Two very simple functions are defined.

The first function, digitToStar() accepts an integer (representing a character) and return an integer. If the argument is a digit, the value returned is (the integer version of) '*'. Otherwise the value returned is just the unchanged value of the argument.

Similarly letterToStar() convert a letter to '*' and leaves all other characters unchanged.

The star of the show is funptr. Read its declaration carefully: The variable funptr is the kind of thing that, once de-referenced, is the kind of thing that, once given an integer, is an integer.

So it is a pointer to something. That something is a function from integers to integers.

The main program checks the (mandatory) argument. If the argument is "digits", funptr is set to the address of digitToStar(). If the argument is "letters", funptr is set to the address of letterToStar().

Then we have a standard getchar()/putchar() loop with a slight twist. The character (I know it is an integer) sent to putchar() is not the naked input character, but instead is the input character processed by whatever function funptr points to. Note the "*" in the call to putchar().

Note: C permits abbreviating &function-name to function-name. So in the program above we could say 

    funptr = digitToStar;
    funptr = letterToStar;
instead of 
    funptr = &digitToStar;
    funptr = &letterToStar;
I don't like that abbreviation so I don't use it. Others do like it and you may use it if you wish.

One difference between a function pointer and a function is their size. A big function is big, a small function is small, and an enormous function is enormous. However all function pointers are the same size. Indeed, all pointers in C are the same size. This makes them easier for the system to deal with.

5.12: Complicated Declarations

We are basically skipping this section. It shows some examples more complicated than we have seen (but are just more of the same—one example is below). The main part of the section presents a program that converts C definition to/from more-or-less English equivalents.

Here is one example of a complicated declaration. It is basically the last one in the book with function arguments added. 

    char (*(*f[3])(int x))[5]

Remembering that *f[3] (like *argv[argc] is an array of pointers not a pointer to an array, we can unwind the above to.

The variable f is an array of size three of pointers.

Remembering that *(g)(int x) = *g(int x) is a function returning a pointer and not a pointer to a function, we can further unwind the monster to.

The variable f is an array of size three of pointers to functions taking an integer and returning a pointer to an array of size five of characters.

One more (the penultimate from the book). 

    char (*(f(int x))[5])(float y)

The function f takes and integer and returns a pointer to an array five pointers to functions taking a real and returning a character.


Start Lecture #12

Chapter 6: Structures

For a Java programmer, structures are basically classes and objects without methods.

Section 6.1: Structure Basics

#include <math.h>
struct point {
  double x;
  double y;
};
struct rectangle {
  struct point ll;
  struct point ur;
} rect1;
double f(struct point pt);
struct point mkPoint(double x, double y);
struct point midPoint(struct point pt1,
                      struct point pt2);
main() {
  struct point pt1={40.,20.}, pt2;
  pt2 = pt1;
  rect1.ll = pt2;
  pt1.x += 1.0;
  pt1.y += 1.0;
  rect1.ur = pt1;
  rect1.ur.x += 2.;
  return 0;
}















double dist (struct point pt) {
  return sqrt(pt.x*pt.x+pt.y*pt.y);
}
struct point midpoint(struct point pt1,
                      struct point pt2){
  // return (pt1 + pt2) / 2;  too bad
  struct point pt;
  pt.x = (pt1.x+pt2.x) / 2;
  pt.y = (pt1.y+pt2.y) / 2;
  return pt;
}
struct point mkPoint(double x, double y) {
  // return {x, y};  too bad, not C
  struct point pt;
  pt.x = x;
  pt.y = y;
  return pt;
}
void mvToOrigin(struct rectangle *r){
  (*r).ur.x = (*r).ur.x - (*r).ll.x;
  r->ur.y = r->ur.y - r->ll.y;
  r->ll.y = 0;
  r->ll.x = 0;
}

On the right we see some simple structure declarations. They should very familiar from your experience with Java.

  1. The top definition defines the struct point type. This is similar to defining a class without methods.
  2. The next definition defines both a new type struct rectangle and a variable of this type. Note that a previously define struct can be used.
  3. The third definition illustrates an initialization. Note that there are no structure constants so you can not write 
            pt1 = {40.20};
    as an executable statement.
  4. We see in the executable statements that one can assign a point to a point as well as assigning to each component.
  5. Since the rectangle rect1 is composed of points, which are in turn composed of doubles, we can assign a point to a point component of a rectangle and can assign a double to a double component of a point component of a rectangle.

I think that, if a Java program had equivalent classes rectangle and point and objects pt1, pt2, and rect1, these same executable statements would be legal.

6.2: Structures and Functions

Functions can take structures as parameters, but is that a good idea? Should we instead use the components as parameters or perhaps pass a pointer to the structure? For example, if the function main above wishes to pass pt1 to another function f, should we write.

  1. f(pt1)
  2. f(pt1.x, pt1.y)
  3. f(&pt1)
Naturally, the declaration of f will be different for the three cases.

  1. f(pt1)
    This form is the most natural for a function that computes a value where the parameter is though of as a point, not just as two real numbers. For example the distance from the origin dist(pt).
  2. f(pt1.x, pt1.y)
    Consider two possible applications.
  3. f(&pt1)
    There are at least two common applications.

Homework: Write two versions of mkRectangle, one that accepts two points, and one that accepts 4 real numbers.

6.3: Arrays of Structures (and Structures of Arrays)

#define MAXVAL 10000
#define ARRAYBOUND (MAXVAL+1)
int G[ARRAYBOUND];
int P[ARRAYBOUND];

struct gameValType {
  int G[ARRAYBOUND];
  int P[ARRAYBOUND];
} gameVal;

struct gameValType {
  int G;
  int P;
} gameVal[ARRAYBOUND];

#define NUMEMPLOYEES 250
struct employeeType {
  int id;
  char gender;
  double salary;
} employee[NUMEMPLOYEES] = {
  { 32, 'M', 1234. },
  { 18, 'F', 1500. }
};

Consider the following game. Take a positive integer N. If it is even, replace it by N/2; if odd, by 3N+1; if 1, stop. So we get, for example,
7 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1.

It is an open problem if all positive integer eventually get to 1. This has been checked for MANY numbers. Let G[i] be the number of rounds of the game needed to get 1. G[1]=0, G[2]=1, G[7]=16.

Factoring into primes is fun too. So let P[N] be the number of distinct prime factors of N. P[2]=1, P[16]=1, P[12]=2 (define P[1]=0).

This leads to two arrays as shown on the right in the top frame.

We might want to group them together and not use up the variable names G and P as in the second frame. This is an array of structures. In this frame the number of distinct prime factors of 763 would be stored in gameVal.P[763].

In the third frame we grouped together the values for the two games. This is an array of structures. In this frame the number of distinct prime factors of 763 would be stored in gameVal[763].P.

If we had a database with employeeID, gender, and salary, we might use the array of structures in the fourth frame. Note the initialization. The inner {} are not needed, but I believe they make the code clearer.

The sizeof and sizeof() Operators

How big is the employee array of structures? How big is employeeType?

C provides two versions of the sizeof unary operator to answer these questions.

These functions are not trivial and indeed the answers are system dependent ... for two reasons.

  1. Certain primitive types (e.g., int) may have different sizes in different systems.
  2. The alignment requirements may be different.

Example: Assume char requires 1 byte, int requires 4, and double requires 8. Let us also assume that each type must be aligned on an address that is a multiple of its size and that a struct must be aligned on an address that is a multiple of 8.

So the data in struct employeeType requires 4+1+8=13 bytes. But three bytes of padding are needed between gender and salary so the size of the type is 16.

Homework: How big is each version of sizeof(struct gameValType)? How big is sizeof employee?

6.4: Pointers to Structures

The program on the right illustrates well the use of pointers to structures and also serves as a good review of many C concepts. The overall goal is to read text from the console and count the occurrence of C keywords (such as break, if, etc.). At the end print out a list of all the keywords that were present and how many times each occurred.

#include <stdio.h>
#include <ctype.h>
#include <string.h>
#define MAXWORDLENGTH 50
struct keytblType {
  char *keyword;
  int  count;
} keytbl[] = {
  { "break", 0 },
  { "case", 0 },
  { "char", 0 },
  { "continue", 0 },
  // others
  { "while", 0 }
};
#define NUMKEYS (sizeof keytbl / sizeof keytbl[0])
int getword(char *, int); // no vars
struct keytblType *binsearch(char *);
int main (int argc, char *argv[argc]) {
  char word[MAXWORDLENGTH];
  struct keytblType *p;
  while (getword(word,MAXWORDLENGTH) != EOF)
    if (isalpha(word[0]) &&
	((p=binsearch(word)) != NULL))
      p->count++;
  for (p=keytbl; p<keytbl+NUMKEYS; p++)
    if (p->count > 0)
      printf("%4d %s\n", p->count, p->keyword);
  return 0;
}
struct keytblType *binsearch(char *word) {
int cond;
  struct keytblType *low = &keytbl[0];
  struct keytblType *high =  &keytbl[NUMKEYS];
  struct keytblType *mid;
  while (low < high) {
    mid = low + (high-low) / 2;
    if ((cond = strcmp(word, mid->keyword)) < 0)
      high = mid;
    else if (cond > 0)
      low = mid+1;
    else
      return mid;
  }
  return NULL;
}

The function getword() is not shown. Its parameters are a buffer (i.e., a pointer to a character) and the size of the buffer. It reads the next word from the console into the buffer (limited by the size of the buffer; the world does not end). A word is either a string of letters and digits beginning with a letter or a single non-white-space character. The idea is that it places into the buffer the next token in a program written in C. The (integer) return value is either the first character in the buffer or EOF.

Now lets examine the code on the right.

  1. The first interesting item is keytbl, the table of keywords. It is an array of struct keytblType; each entry of the array contains string and an integer.
  2. The initialization of keytbl is interesting. Each string is set to a C keyword and each count is initialized to zero. The size of the array is determined by the initialization and the next line cleverly determines that size. The entries are initialized in alphabetical order, which permits the use of a binary search to find an entry.
  3. The main program contains two loops: The first computes the counts and the second outputs the results.
    1. The first loop calls getword() and terminates on receiving EOF. The word is looked up in the keytbl using binsearch. The value returned by binsearch is either a pointer to the table entry found or NULL if the word is not a keyword (i.e., is not in the table). If the word is found the corresponding count is incremented.
      I don't believe the isalpha() test is needed since, if the character is not a letter, binsearch will return NULL; it is presumably there save a useless search.
    2. The second loop traverses the table and prints out all entries with non-zero counts. Note the test used in the for statement and remember that the increment p++ increments p by enough so that it points to the next entry.
  4. As I suspect you know, a binary search is quite efficient (its running time is logarithmic in the size of the table) and very easy to get wrong (< vs. <=, mid vs. mid-1 vs. mid+1, etc.). The only real difference between this one and the one I hope you saw in 102, is that the code on the right is pointer based not array based. This explains the mysterious code to set mid to the midpoint between high and low. But, other than that oddity, I find it striking how array-like the code looks. That is, the manipulations of the pointers could just as well be manipulating indices.

Start Lecture #13

6.5: Self-referential Structures

tree node

Consider a basic binary tree with each node containing just an integer an pointers to the left and right subtrees. Looking at the diagram on the right suggests a structure with three components: left, right, and value. The first two refer to other tree nodes and the third is an integer.

struct bad {
  struct bad left;
  int value;
  struct bad right;
};
struct treenode_t {
  struct treenode_t *left;
  int value;
  struct treenode_t *right;
};

Since trees are recursive data structures you might expect some sort of recursive structure. Consider struct bad defined on the right. (You might be fancier and have a struct tree, which contains a struct root, which has an integer value and two struct tree's).

But struct bad and its fancy friends are infinite data structures. Some languages permit infinite structures providing you never try to materialize more than a finite piece. But C is not one of those languages so for us struct bad is bad!

Instead, we use struct treenode_t also on the right (names like treenode_t are a shorter and very commonly used alternative to names like treenodeType).

Be sure you understand why struct treenode_t is finite and corresponds exactly to the picture above it.

struct s {
  int val;
  struct t *pt;
};
struct t {
  double weight;
  struct s *ps;
};

Mutually Referential/Recursive Structures

What if you have two structure types that need to reference each other. You cannot have a struct s contain a struct t if the struct t contains a struct s.

Once again pointers come to the rescue as illustrated on the right. Neither structure is infinite. A struct s contains one integer and one pointer. A struct t contains one double and one pointer.

Lab 2: 2d-Structures

Instead of trees, lab 2, uses a different 2-dimensional structure, a linked list of linked lists.

Although the lab is not in final form and has not yet been assigned, it is in good enough shape for us to study to learn how to used linked structures.

Malloc()

As you know, in Java objects (including arrays) have to be created via the new operator. We have seen that in C this is not always needed: you can declare a struct rectangle and then declare several rectangles.

However, this doesn't work if you want to generate the rectangles during run time. When you are writing lab 2, you don't know how many 2d nodes or 1d nodes will be needed.

So we need a way to create an object during run time. In C this uses the library function malloc(), which takes one argument, the amount of space to be allocated. The function malloc() returns a pointer to this space.

Since malloc() is not part of C, but is instead just a library routine, the compiler does not treat it specially (unlike the situation with new, which is part of Java). Since malloc() is just an ordinary function, and we want it to work for dynamic objects of any type (e.g., an int, a char *, a struct treenode, etc), and there is no way to pass a type to a function, two questions arise.

  1. How do we arrange that the space returned by malloc() meets the alignment requirements of the object we desire?
  2. How do we arrange that the pointer returned by malloc() is a pointer to the correct type.

The alignment question is the easier. We just have malloc() return space aligned on the most stringent requirement. So, if double requires 8-byte alignment, and all structures require 16-byte alignment, and all other data types require 4-byte alignment, then malloc() always returns space aligned on a 16-byte boundary (i.e., the address is a multiple of 16).

Ensuring type correctness is not so easy. Specifically, malloc() returns a void *, which means it is a pointer that must be explicitly coerced to the correct type. For example, the code supplied with lab 2 contains. 

    struct node2d *p2d;
    p2d = (struct node2d *) malloc(sizeof(struct node2d));

Link to Lab 2

6.6: Table Lookup

Skipped

6.7: Typedef

Instead of declaring pointers to trees via 

    struct treenode *ptree;
we can write 
    typedef struct treenode *Treeptr;
    Treeptr ptree;
Thus treeptr is a new name for the type struct treenode *. As another example, instead of 
    char *str1, *str2;
We could write 
    typedef char *String;
    String str1, str2;

Note that this does not give you a new type; it just gives you a new name for an existing type. In particular str1 and str2 are still pointers to characters even if declared as a String above.

A common convention is to capitalize the a typedef'ed name.

6.8: Unions

Saving Space by Sharing Memory between 2 or More Variables

struct something {
  int x;
  union {
    double y;
    int z;
  }
}

Traditionally union was used to save space when memory was expensive. Perhaps with the recent emphasize on very low power devices, this usage will again become popular. Looking at the example on the right, y and z would be assigned to the same memory locations. Since the size allocated is the larger of what is needed the union takes space max(sizeof(double),sizeof(int)) rather than sizeof(double)+sizeof(int) if a union was not done.

It is up to the programmer to know what is the actual variable stored. The union shown cannot be used if y and z are both needed at the same time.

It is risky since there is no checking done by the language.

Meeting Alignment Constraints

A union is aligned on the most severe alignment of its constituents. This can be used in a rather clever way to meet a requirement of malloc().

As we mentioned above when discussing malloc(), it is sometimes necessary to force an object to meet the most severe alignment constraint of any type in the system. How can we do this so that if we move to another system where a different type has the most severe constraint, we only have to change one line? 

struct something {
  int x;
  struct something *p;
  // others
} obj;

// assume long most severely aligned
typedef long Align
union something {
  struct dummyname {
    int x;
    union something *p;
    // others
  } s;
  Align dummy;
}
typedef union something Something;

Say struct something, as shown in the top frame on the right, is the type we want to make most severely aligned.

Assume that on this system the type long has the most severe alignment requirement and look at the bottom frame on the right.

The first typedef captures the assumption that long has the most severe alignment requirement on the system. If we move to a system where double has the most severe alignment requirement, we need change only this one line. The name Align was chosen to remind us of the purpose of this type. It is capitalized since one common convention is to capitalize all typedefs.

The variable dummy is not to be used in the program. Its purpose is just to force the union, and hence s to be most severely aligned.

In the program we declare an object say obj to be of type Something (with a capital S) and use obj.s.x instead of obj.x as in the top frame. The result is that we know the structure containing x is most severely aligned.

See section 8.7 if you are interested.

6.9: Bit Fields

Skipped

Chapter 7: Input and Output

7.1: Standard Input and Output

getchar() and putchar()

#include <stdio.h>
int main (int argc, char *argv[argc]) {
  int c;
  while ((c = getchar()) != EOF)
    if (putchar(c) == EOF)
      return EOF;
  return 0;
}

This pair form the simplest I/O routines. The function getchar() takes no parameters and returns an integer. This integer is the integer value of the character read from stdin or is the value of the symbolic parameter EOF (normally -1), which is guaranteed not the be the integer value of any character.

The function putchar() takes one integer parameter, the integer value of a character. The character is sent to stdout and is returned as the function value (unless there is an error in which case EOF is returned.

The code on the right copies the standard input (stdin), which is usually the keyboard, to the standard output (stdout), which is usually the screen.

Homework: 7.1.

Formatted Output—printf

We have already seen printf(). A surprising characteristic of this function is that it has a variable number of arguments. The first argument, called the format string, is required. The number of remaining arguments depends on the value of the first argument. The function returns the number of characters printed, but that is not so often used. Technically its declaration is 

    int printf(char *format, ...);

The format string contains regular characters, which are just sent to stdout unchanged and conversion specifications, each of which determines how the value of the next argument is to be printed.

The conversion specification begins with a %, which is optionally followed by some modifiers, and ends with a conversion character.

We have not yet seen any modifiers but have see a few conversion characters, specifically d for an integer (i is also permitted), c for a single character, s for a string, and f for a real number.

There are other conversion characters that can be used, for example, to get real numbers printed using scientific notation. The book gives a full table.

There are a number of modifiers to make the output line up and look better. For example, %12.4f means that the real number will be printed in 12 columns (or more if the number is too big) with 4 digits after the decimal point. So, if the number was 36.3 it would be printed as ||||||36.300 where I used | to represent a blank. Similarly -1000. would be printed as |||-1000.000. These two would line up nicely if printed via 

    printf("%12.4f\n%12.4f\n\n", 36.3, -1000.);


Start Lecture #14

Remark: Midterm will be tues after vacation. Practice midterm will be available next week.

A Relative of printf(): sprintf()

The function 

    int sprintf(char *string, char *fmt, ...);
is very similar to printf(). The only difference is that, instead of sending the output to stout (normally the screen), sprintf() assigns it to the first argument specified.
    char outString[50];
    int d = 14;
    sprintf(outString, "The value of d is %d\n", d);
For example, the code snippet on the right results in the first 23 characters (assuming I counted correctly) of outString containing The value of d is 14 \n\0 while the remaining 27 characters of outString continue to be uninitialized.

Since the system cannot in general check that the first argument is big enough, care is needed by the programmer, for example checking that the returned value is no bigger than the size of the first argument. Even better use snprintf(), which like strncpy(), guarantees than no more than n bytes will be assigned (n is an additional parameter to strncpy).

7.3: Variable-length Argument Lists

As we mentioned, printf() takes a variable number of arguments. But remember printf() is not special, it is just a library function, not an object define by the language or known to the compiler. That is you can write a C program with declaration 

    int myfunction(int x, float y, char *z, ...)
and it will have three named arguments and zero or more unnamed arguments.

There is some magic needed to get the unnamed arguments. The magic is needed by the author of the function; not by a user of the function.

7.4: Formatted Input—scanf

This function is to printf() as putchar() is to getchar(). As with printf(), scanf() accepts one required argument (a format string) and a variable number of additional arguments. Since this is an input function, the additional arguments give the variables into which input data is to be placed.

Consider the code fragment shown on the top frame to the right and assume that the user enters on the console the lines shown on the bottom frame.

int n;
double x;
char str[50];
scanf("%d  %lf  %s %20s", &n, &x, str);

22 37.5
no-blanks-here

A Relative of scanf(): sscanf()

The function 

    int sscanf(char *string, char *fmt, ...);
is very similar to scanf(). The only difference is that, instead of getting the input from stdin (normally the keyboard), sscanf() gets it from the first argument specified.

7.5: File Access

So far all our input has been from stdin and all our output has been to stdout (or from/to a string for scanf()/sprintf).

What if we want to read and write a file?
As I mentioned in class you can use the redirection operators of the command interpreter (the shell), namely < and >, to have stdin and/or stdout refer to a file.

But what if you want to input 2 or more files?

Opening and Closing Files; File Pointers

Before we can specify files in our C programs, we need to learn a (very) little about the file pointer.

Before a file can be read or written, it must be opened. The library function fopen() is given two arguments, the name of the file and the mode; it returns a file pointer.

Consider the code snippet on the right. The type FILE is defined in <stdio.h>. We need not worry about how it is defined.

  FILE *fp1, *fp2, *fp3, *fp4;
  FILE *fopen(char *name, char *mode);
  fp1 = fopen("cat.c", "r");
  fp2 = fopen("../x", "a");
  fp3 = fopen("/tmp/z", "w");
  fp4 = fopen("/tmp/q", "r+");
  1. The file cat.c in the current directory is opened for reading and some information about this file is recorded in *fp1.
  2. The file x in the parent directory is opened for appending; x is created if it doesn't exist
  3. The file z in /tmp is opened for writing. Previous contents of z are lost.
  4. The file q in /tmp is opened for reading and/or writing. (When mixing reads and writes, care is needed.)

After the file is opened, the file name is no longer used; subsequent commands (reading, writing, closing) use the file pointer.

The function fclose(FILE *fp) breaks the connection established by fopen().

getc()/putc(): The File Versions of getchar()/putchar()

Just as getchar()/putchar() are the basic one-character-at-a-time functions for reading and writing stdin/stdout, getc()/putc() perform the analogous operations for files (really for file pointers). These new functions naturally require an extra argument, the file pointer to read from or write to.

Since stdin/stdout are actually file pointers (they are constants not variables) we have the definitions 

    #define getchar()    getc(stdin)
    #define putchar(c)   putc((c), stdout)

I think this will be clearer when we do an example, which is our next task.

An Example cat.c

#include <stdio.h>
main (int argc, char *argv[argc]) {
  FILE *fp;
  void filecopy(FILE *, FILE *);
  if (argc == 1) // NO files specified
    filecopy(stdin, stdout);
  else
    while(--argc > 0)  // argc-1 files
      if((fp=fopen(*++argv, "r")) == NULL) {
	printf ("cat: can't open %s\n", *argv);
	return 1;
      } else {
	filecopy(fp, stdout);
	fclose(fp);
      }
  return 0;
}
void filecopy (FILE *ifp, FILE *ofp) {
  int c;
  while ((c = getc(ifp)) != EOF)
    putc(c, ofp);
}

The name cat is short for catenate, which is short for concatenate :-).

If cat is given no command line arguments (i.e., if argc=1), then it just copies stdin to stdout. This is not useless: for one thing remember < and >.

If there are command line arguments, they must all be the names of existing files. In this case, cat concatenates the files and writes the result to stdout. The method used is simply to copy each file to stdout one after the other.

The copyfile() function uses the standard getc()/putc() loop to copy the file specified by its first argument ifp (input file pointer) to the file specified by its second argument. In this application, the second argument is always stdout so copyfile() could have been simplified to take only one argument and to use putchar().

Note the check that the call to fopen() succeeded; a very good idea.

Note also that cat uses very little memory, even if concatenating 100GB files. It would be an unimaginably awful design for cat to read all the files into some ENORMOUS character array and then write the result out to stdout.

7.6: Error Handling—Stderr and Exit (and Ferror())

Stderr

A problem with cat is that error messages are written to the same place as the normal output. If stdout is the screen, the situation would not be too bad since the error message would occur at the end. But if stdout were redirected to a file via >, we might not notice the message.

Since this situation is common there are actually three standard file pointers defined: In addition to stdin and stdout, the system defines stderr. Although the name suggests that it is for errors and that is indeed its primary application, stderr is really just another file pointer, which (like stdout) defaults to the screen).

Even if stdout is redirected by the standard > redirection operator, stderr will still appear on the screen.

There is syntax to redirect stderr, which can be used if desired.

Exit()

As mentioned previously a command should return zero if successful and non-zero if not. This is quite easy to do if the error is detected in the main() routine itself.

What should we do if main() has called joe(), which has called f(), which has called g(), and g() detects an error (say fopen() returned NULL)?

It is easy to print an error message (sent to stderr, now that we know about file pointers). But it is a pain to communicate this failure all the way back to main() so that main() can return a non-zero status.

Exit() to the rescue. If the library routine exit(n); is called, the effect is the same as if the main() function executed return n. So executing exit(0) terminates the command normally and executing exit(n) with n>0 terminates the command and gives a status value indicating an error.

Ferror()

The library function 

    int ferror(FILE *fp);
returns non-zero if an error occurred on the stream fp; For example, if you opened a file for writing and sometime during execution the file system became full and a write was unsuccessful, the corresponding call to ferror() would return non-zero.

7.7: Line Input and Output (fgets() and fputs())

The standard library routine 

    char *fgets(char *line, int maxchars, FILE *fp)
reads characters from the file fp and stores them plus a trailing '\0' in the string line. Reading stops when a newline is encountered (it is read and stored) or when maxchars-1 characters have been read (hence, counting the trailing '\0', at most maxchars will be stored).

The value returned by fgets is line; on end of file or error, NULL is returned instead.

The standard library routine 

    int fputs(char *line, FILE *fp)
writes the string line to the file fp. The trailing '\0' is not written and line need not contain a newline. The return value is zero unless an error occurs in which case EOF is returned.

Start Lecture #15

Remark: Give password for homework solutions.

7.8: Miscellaneous Functions

A laundry list. I typed them all in to act as convenient reference. Let me know if you find any errors.

The integer type size_t

This subsection represents a technical point; for this class you can replace size_t by int.

Consider the return type of strlen(), which the length of the string parameter. It is surely some kind of integral type but should it be short int, int, long int or one of the unsigned flavors of those three?

Since lengths cannot be negative, the unsigned versions are better since the maximum possible value is twice as large. (On the machines we are using int is at least 32-bits long so even the signed version permits values exceeding two billion, which is good enough for us).

The two main contenders for the type of the return value from strlen() are unsigned int and unsigned long int. Note that long int can be, and usually is, abbreviated as long.

If you make the type too small, there are strings whose length you cannot represent. If you make the type bigger than ever needed, some space is wasted and, in some cases, the code runs slower.

Hence the introduction of size_t, which is defined in stdlib.h.
Each system specifies whether size_t is unsigned int or unsigned long (or something else).

For the same reason that the system-dependent type size_t is used for the return value of strlen, size_t is also used as the return type of the sizeof operator and is used several places below.

7.8.1: String Operations

These are from string.h, which must be #include'd. The versions with n added to the name limit the operation to n characters. In the following table n is of type size_t and c is an int containing a character; s and t are strings (i.e., character pointers, char *); and cs and ct are constant strings (const char *).

In addition to the naming distinction s vs cs, I further indicated which inputs may be modified by writing the string name in red.

CallMeaning
strcat(s,ct) Concatenate ct on to the end of (changing s) and return s.
strncat(s,n,ct) The same but concatenates no more than n characters.
strcmp(cs,ct) Compare s and t lexicographically. Returns a negative, zero, or positive int if s is respectively <, =, or > t
strncmp(cs,ct,n) The same but compares no more than n characters.
strcpy(s,ct) Copy ct to s and return s.
strncpy(s,ct,n) Similar but copies no more than n characters and pads with '\0' if ct has fewer than n characters. The result might NOT be '\0' terminated.
strlen(cs) Returns the length of cs (not including the terminating '\0') as a size_t value.
strchr(cs,c) Returns a pointer to the first c in s or NULL if c is not in cs.
strrchr(cs,c) Returns a pointer to the last c in cs or NULL if c is not in cs.

7.8.2: Character Testing and Conversion

These are from ctype.h, which must be #include'd. All these functions take an integer argument (representing a character or the value EOF) and return an integer.

CallMeaning
isalpha(c) Returns true (non-zero) if (and only if) c is alphabetic. In our locale this means a letter.
isupper(c) Returns true if c is upper case.
islower(c) Returns true if c is lower case.
isdigit(c) Returns true if c is a digit.
isalnum(c) Returns true if isalpha(c) or isdigit(c).
toupper(c) Returns c converted to upper case if c is a letter; otherwise returns c.
tolower(c) Returns c converted to lower case if c is a letter; otherwise returns c.

7.8.3: Ungetc

int ungetc(int c, FILE *fp) pushes back to the input stream the character c. It returns c or EOF if an error was encountered.

Only one character can be pushed back, i.e., it is not safe to call ungetc() twice without an call in between that consumes the first pushed back character.

This function is from stdio.h, which must be #include'd.

7.8.4: Command Execution

The function system(char *s) runs the command contained in the string s and returns an integer status.

The contents of s and the value of the status is system dependent.

#include <stdio.h>
#include <stdlib.h>
int main (int argc, char *argv[argc]) {
    int status;
    printf("Hello.\n");
    status = system("dir; date");
    printf("Goodbye: status %d\n", status);
    return 0;
}

On my system, the program on the right when run in a directory containing only two files x and y produces the following output.

Hello.
x  y
Sun Mar  7 16:05:03 EST 2010
Goodbye: status 0

This function is in stdlib.h, which must be #include'd.

7.8.5: Storage Management

Malloc()

We have already seen 

    void *malloc(size_t n)
which returns pointer to n bytes of uninitialized storage. If the request cannot be satisfied, malloc() returns NULL.

Calloc()

The related function 

    void *calloc(size_t n, size_t size)
returns a pointer to a block of storage adequate to hold an array of n objects each of size size. The storage is initialized to all zeros.

Free()

The function 

    void free (void *p)
is used to return storage obtained from malloc() or calloc().

Remarks

  for (p = head; p != NULL; p = p->next)
      free(p);  
  for (p = head; p != NULL; p = q) {
      q = p-> next;
      free (p);
  1. It is crucial that the pointer argument to free() was obtained by a call to malloc() or calloc() (or realloc(), which we shall not use).
  2. Equally bad is to reference space after free'ing it. For example the code on the top right is buggy since p->next uses the p that has just been free'd. Instead the bottom loop should be used.
  3. The two arguments to calloc() are not silly. You cannot simply multiply them to determine the amount of storage needed due to padding requirements. Indeed, the space needed is system dependent.
  4. The pointers returned by malloc() and calloc are properly aligned, but must be cast to the appropriate type.

7.8.6: Mathematical Functions

These functions are from math.h, which must be #include'd. In addition (at least on on my system and i5.nyu.edu) you must specify a linker option to have the math library linked. If your mathematical program consists of A.c and B.c and the executable is to be named prog1, you would write 

    cc -o prog1 -l m A.c B.c

All the functions in this section have double's as arguments and as result type. The trigonometric functions express their arguments in radians and the inverse trigonometric functions express their results in radians.

CallMeaning
sin(x)sine
cos(x)cosine
atan(x)arctangent
exp(x)exponential ex
log(x) natural logarithm loge(x)
log10(x) common logarithm log10(x)
pow(x,y)xy
sqrt(x)square root, x≥0
fabs(x)absolute value

7.8.7: Random Number Generation

Random number generation (actually pseudo-random number generation) is a complex subject. The function rand() given in the book is an early and not wonderful generator; it dates from when integers were 16 bits. I recommend instead (at least on linux and i5.nyu.edu) 

    long int random(void)
    void srandom(unsigned int seed)

The random() function returns an integer between 0 and RAND_MAX. You can get different pseudo-random sequences by starting with a call to srandom() using a different seed. Both functions are in stdlib.h, which must be #include'd.

On my linux system RAND_MAX (also in stdlib.h) is defined as 231-1, which is also INT_MAX, the largest value of an int. It looks like i5.nyu.edu doesn't define RAND_MAX, but does use the same psuedo-random number generator.

Remark: Let's write some programs/functions.

  1. Write a program (most-vowels) that reads lines and prints the one with the most vowels together with a count of how many vowels it contains.
  2. Write a function (repstr) that accepts a count and a string and returns a newly allocated string containing the concatenation of the original string the specified number of times.
  3. Write a function (mergeint) that merges two sorted arrays of integers A and B into C. The signature is 
            mergeInt(int n, int m, int A[n], int B[m], int C[n+m]);
  4. Think about how to do this for arrays of (varying length) strings.
  5. The 5 -> 16 -> 8 -> 4 -> 2 -> 1 game.
    1. Write a function f giving the next number: f(5)=16; f(1)=4. What should the signature be?
    2. Write a program that repeatedly reads an integer and prints out the generated sequence upto 1.
    3. Modify the previous program to instead accept three arguments, which act like the three parts of a for. The program plays the game for all integers starting at the first argument, incrementing by the third, up to the second.
    4. Modify the previous to accept an optional -b or --brief argument. If present, don't print the sequence, instead just print its length.
    5. Modify the previous to accept an optional -s or --summary argument that prints only the number having the longest sequence and the sequence (OK to re-calculate). If the -b is also present, just print the number and the length of the sequence (not OK to recalculate).

Remark: End of material to be covered on the midterm exam.

Start Lecture #16

Review of solutions to practice midterm.

Wrote a few other programs.

Start Lecture #17

Midterm exam

Start Lecture #18

Chapter T-1: Introduction to Computer Organization and Assembler Language

Homework: Read Tanenbaum chapter 1 (T-1 above stands for Tanenbaum 1).

Remark: Everyone with a Windows laptop should install cygwin as follows (I don't run windows so cannot test this procedure; apparently it worked well last semester).

  1. Browse http://www.cygwin.com
  2. Click on install now.
  3. Where you are asked to select packages, choose devel and then check that the box in the bin column next to gcc is checked. This will ensure that the gcc compiler is included.
  4. Also in devel, select make.
  5. Finally select editor and choose emacs. There are other editors available if you prefer.

Remark: If you have a linux laptop (or dual boot linux), you are set. The gcc on linux supports both variants of assembler syntax for the x86 CPU. We will be using the Intel syntax.

Remark: The mac story is interesting.

  1. Download XCode from the Apple Developer Connection .
  2. Pick up Carbon Emacs here.
  3. Now the fun. The version of gcc on the Mac does not use the same assembler syntax (the intel syntax) that nearly everyone else uses. You can fairly easily translate from the (ATT) syntax used to the Intel syntax.
  4. Our machine i5.nyu.edu does not use an intel cpu (instead it uses a SUN sparc), but I am getting the mac users accounts on a departmental linux box, where you can select the intel syntax.
  5. You can also install window or Linux under MacOS; the gcc under Linux or cygwin supports the Intel syntax.

Start Lecture #19

Remark: Midterm exams returned.

If you did not read the mailing list, please read my comment on the exam and midterm (letter) grades. You can find it off the course home page (announcements).

Remark: Some comments on catDiff from the midterm.

  1. Many forgot to allocate space for various strings. The maximum penalty (no allocations) was -3.
  2. Several had trouble with this construct 
          char *str1 = "something";
      char *str2 = str1;
    They said char *str2 = *str1;  I can see why as it looks symmetric. Remember you are declaring str2 not *str2.

Remark: Preview on final project.

You will be writing a (trivial) video game. For now, install the graphics library and put up a picture (find a *.bmp file). Here is the installation procedure

  1. Browse libsdl.org.
  2. Click on the SDL 1.2 link on the left column. Note where the file is downloaded.
  3. If necessary, move the file to your home directory. On Cygwin, your home directory is c:\cygwin\home\yourname).
  4. In the shell (under cygwin) type tar -xvfz SDL-1.2.14.tar.gz.
  5. Type cd SDL-1.2.14
  6. Type ./configure
    If this fails try ./configure CC=/usr/bin/gcc-3 CXX=/usr/bin/g++-3
  7. Type make
  8. Type sudo make install.
    If this fails try simply make install
    If both fail, try $@ make install
    You may be asked for your password (for your computer, not for an NYU machine). If you run as administrator, I don't believe you will be asked.
  9. Type cd test
  10. Type ./configure
    If this fails try ./configure CC=/usr/bin/gcc-3 CXX=/usr/bin/g++-3
  11. Type make
  12. Type ./testsprite
  13. Gasp, in awe.

Here is a windows/cygwin tip from Prof. Goldberg. Be sure that the name of your home directory does not have a space in it. For example, if your name is Joe Smith, be sure that your home directory on cygwin is not "c:\cygwin\home\joe smith", but rather something like "c:\cygwin\home\joe_smith". The SDL configure function gets confused by spaces in a directory name. If cygwin has created your home directory name with a space, change the name of the directory using Windows. Then, create an environment variable called HOME and set it to c:\cygwin\home\joe_smith, except with joe_smith replaced by the actual name of your home directory. To set an environment variable in Windows, go to
Start->Control Panel->System->Advanced->Environment Variables. It should be obvious from there.

Let me call the subdirectory SDL-1.2.14 the sdl directory. In there you will find a README file containing the web address of a wiki about the library Browse that wiki and follow the guide. I had never used any of this before and within 20 minutes I had a picture up.

Chapter T-2: Computer Systems Organization

Some diagrams of the overall structure of a computer system are in section 1.3 of my OS class notes

T-2.1: Processors

The processor (or CPU, Central Processing Unit) performs the computations on data. The data enter and leave the system via I/O devices and are stored in the memory (the last part is over simplified as you will learn in OS, but it is good enough for us).

T-2.1.1: CPU Organization

Simple processors have (had?) three basic components, a register file, an ALU (Arithmetic Logic Unit), and a control unit. Oversimplified, the control unit fetches the instructions and determines what needs to be done, the data to be processed is often the registers (which can be accessed much faster than central memory) and the ALU performs the operation (e.g., multiply).

In addition to the (assembly-language) programmer-visible registers mentioned above, the CPU contains several internal registers, two of which are the PC (Program Counter, a.k.a ILC or LC), which contains the address of the next instruction to execute and the Instruction Register (IR), which contains (a copy of) the current instruction.

T-2.1.2: Instruction Execution

There are three parts to executing an instruction: obtain the instruction, determining what it needs to do, and doing it. Repeatedly performing these three steps for all the instructions in a program, is normally referred to as the fetch-decode-execute cycle. In slightly more detail, the CPU executes the following program.

  1. Fetch the next instruction into the IR.
  2. Update the PC.
  3. Determine the type of the instruction.
  4. If memory is referenced, determine the address.
  5. Fetch the referenced word, if needed, into a register.
  6. Execute the instruction.
  7. Repeat.

Architecture vs. Micro-Architecture

The architecture is the instruction set, i.e., the (assembly-language) programmer's view of the computer.

The micro-architecture is the design of the computer, it is the architect's/designer's/engineer's view of the system.

The interesting case is when you have a computer family, e.g., the IBM 360 or 370 line, the x86 microprocessor architecture, which has several different implementations, with different microarchitectures.

T-2.1.3: RISC vs. CISC

Reduced Instruction Set Computer versus Complex Instruction Set Computer. Clear implementation advantages for RISC. But CISC has thrived! Intel found an excellent RISC implementation of most of the very CISC x86.

T-2.1.4: Design Principles for Modern Computers

The RISC design principles below are generally agreed to be favorable, but are not absolute. For example backwards-compatibility with previous systems, force compromises.

Start Lecture #20

Remark: I mentioned the wrong guide last time. The notes are now correct.

T-2.1.5: Instruction Level Parallelism

Skipped.

T-2.1.6: Processor-Level Parallelism

Skipped.

T-2.2: Primary Memory

T-2.2.1: Bits

Abbreviates binary digit, which is rather contradictory.

T-2.2.2: Memory Addresses

The smallest addressable unit of memory is called a cell. Recently, for nearly all computers, a cell is an 8-bit unit called a byte (or octet). Bytes are grouped into words, which form the units on which most instructions operate.

T-2.2.3: Byte Ordering

This has caused decades of headaches.

Memory is addressed in bytes. But we also need larger units, e.g., a 4-byte word. If memory contains a big collection of bytes, the bytes are stored in address 0, 1, 2, 3, etc. If memory contains a big collection of words, the words are stored in address 0, 4, 8, 12, etc. So far no problem.

Consider a 32-bit integer stored in a (4-byte) word. If the integer has the value 5 then the bit string will be 00000000|00000000|00000000|00000101. So the lower order byte of the integer is 00000101 and the three high order bytes are each 00000000. Still no problem.

Let's assume this is the first word in memory, i.e., the one with address 0. It contains 4 bytes: 0, 1, 2, and 3. We are closing in on the problem.

Which of those four bytes is the low order byte of the word. Answer from IBM: byte 3 (IBM machines are big endian. Answer from Intel: byte 0 (Intel processors are little endian..

Either answer makes sense and if you stay on one machine, there is no problem at all since either system is consistent. But let try to move data from one machine to another.

Say we have an integer containing 5 (as above) and a 4-byte character string "ABC" stored on an IBM machine. The layout is 

    00000000  00000000  00000000  00000101     A     B     C    00000000
       0         1         2         3         4     5     6       7
The ABC are expressed in bits, but the specific bit string is not important.
The last byte of all 0s is ...
the ascii null ending the string.

We send these 8 bytes via ethernet to an Intel machine where we again store them starting at location 0, and get the same layout as above. However, byte 3 is now the most-significant (rather than the least-significant) byte. Gack. The integer 5 has become 5*(256)3!

If the internet software reverses every set of four bytes, we fix the integer, but screw up the string.

T-2.2.4: Error-Correcting Codes

The Hamming Distance between two equal-length bit strings is the number of bits in which they differ. If you arrange that all legal bit strings have Hamming distance at least 2 from each other than you can detect any 1-bit error. This explains parity.

More generally if all legal bit strings have Hamming distance at least d+1, then you can detect any d-bit error since changing d bits of a legal string cannot reach another legal string.

To enable correction of errors you need greater Hamming distances: specifically Hamming distance 2d+1 is needed to enable correction of d bits. This is not too hard to see. If you have a valid string and change d bits, the result is at distance from the original valid string and at least distance d+1 from any other valid string (since the valid strings are at least 2d+1 apart.

The harder part is designing the code. That is, given n, assume you are storing and fetching n data bits at a time, how many extra check bits must be stored and what must they be in order that all the resulting strings are at least distance d apart?

The book gives Hamming's method, but we are skipping the algorithm and are content with just one fact.

If the size of the data word is 2k (i.e., the number of bits in a word is 2k), then k+1 check bits are necessary and sufficient to obtain a code that can correct all single-bit errors and can detect all double-bit errors.
For example if we are dealing with bytes, k is 3 so 4 check bits are required; a heavy overhead (4 check bits for every 8 data bits). If we are only transporting 64-bit words, k is 6 and 7 check bits are required, which is a much milder overhead.

Start Lecture #21

Remark: Term Project assigned. Due in three weeks, 27 apr 2010

T-2.2.5: Cache Memory

The ideal memory is

Commodity memory is big, slow, cheap, and possible.

Caches are small, fast, cheap enough because they are small, and possible.

Concentrating on the first two criteria we can build big and slow and we can build small and fast, but we want big and fast. This is where the idea of caching comes in.

A cache is small and fast. A significant portion of its speed is because it is close to the CPU and clearly if an object is big its (average or worst-case) distance from another object can't be small. For example, no matter where you park a car you can't have all (or half) of it within a foot of a given point.

The idea of caching is that we arrange (somehow) for almost all of the important data to be in the small, fast cache and use the big and slow memory to hold the rest (actually it holds all the data).

Since the portion of memory that is important changes with time, caches exchange data with memory as the program executes.

With clever algorithms for choosing which data to exchange with memory, surprisingly small caches can service a great deal of the memory activity of the processor.

There is no reason to stop with just one cache level. Today it is common to have a tiny, blistering-fast level-1 cache connected to a small, real-fast level-2 cache connected to a medium-size, fast level-3 cache connected to huge, slow memory.

This same issue of a small, fast red-memory supporting a large, slow blue-memory is studied in Operating Systems (202). In the OS setting, the small and fast memory is our big and slow central memory and the big and slow OS memory is a disk. Unfortunately, nearly all the terminology in the OS case (demand paging) is different from the terminology in the computer design case (caching).

T2.2.6: Memory Packaging and Types

T-2.3: Secondary Memory

T-2.3.1: Memory Hierarchies

The example of multiple cache levels, can be carried further. The processor registers are smaller and faster than a cache. As mentioned disks are bigger and slower than central memory, and robotic-accessed, tape storage is bigger and slower than a disk. Again the goal is to use smarts to approximate the impossible big and fast and cheap storage.

T-2.3.2: Magnetic Disks

Disks are covered in OS (202) so we will just define some terms (plus I demo'ed a bunch of disks last class class).

  • Platter
  • Surface
  • Head
  • Track
  • Sector
  • Cylinder
  • Seek time:
    Average case times are given and often the minimum, which is from one cylinder to the next one.
  • Rotational latency:
    Given as the RPM or given directly in milliseconds.
  • Transfer rate:
    Given directly as MB/sec or indirectly by RPM and track capacity.

    Homework: 19.

    T-2.3.2: Floppy Disks

    Demoed last class.

    T-2.3.4: Ide Disks

    Describes the specific protocol, cabling, and speed.

    T-2.3.5: Scsi Disks

    Describes the specific protocol, cabling, and speed.

    T-2.3.6: RAID

    Done in OS (202).

    T-2.3.7: CD-ROMs

    Done in OS (202). Just one comment, unlike magnetic disks CD-ROMs and friends do not have circular tracks; instead the data spirals out from the center.

    T-2.3.8: CD-Recordables (CD-R)

    Done in OS (202).

    T-2.3.9: CD Rewritables (CD-RW)

    Done in OS (202).

    T-2.3.10: DVD

    Done in OS (202).

    T-2.3.11: Blu-Ray

    Done in OS (202).

    T-2.4: Input/Output

    T-2.4.1: Buses

    Last class I demoed a computer main board (a.k.a motherboard, system board, or mobo) and showed the slots where a controller would plug it.

    I brought in an ethernet controller that fit onto the PCI bus of the main board. The different busses (PCI, PCIe, SCSI, ATA, etc) describe the wiring and protocols used to connect the different controllers to the CPU.

    T-2.4.2: Terminals

    Keyboards

    Done in 202

    CRT Monitors

    Obsolete.

    Flat Panel Displays

    Very important, but a little too much engineering-oriented for us to cover. You might want to read it for you own curiosity.

    Video RAM

    One value per pixel on the screen. These values together are often called a bit map. In fact systems often contain several but maps to enable fast switching.

    T-2.4.3: Mice

    Covered in 202.

    T-2.4.4: Printers

    Monocrome Printers

    Color Printers

    T-2.4.5: Telecommunications Equipment

    Modems

    Digital Subscriber Lines (DSL)

    Internet over Cable

    T-2.4.6: Digital Cameras

    T-2.4.7: Character Codes

    ASCII

    Unicode

    T-2.5: Summary

    Read.

    Chapter T3: The Digital Logic Level

    This is the bottom of the abstraction hierarchy.

    T-3.1: Gates and Boolean Algebra

    T-3.1.1: Gates

    (Bipolar) Transitors and the Device Level

    transistor nand-nor

    When the Base is high (positive voltage, say 5 volts, a digital 1) the transistor turns on, i.e., acts like a wire and the Collector is pulled down to ground (zero volts, a digital zero).

    When the Base is low (zero volts, a digital zero), the transistor turns off, i.e., acts like an open circuit. Thus the collector is essentially the same as the voltage supply +Vcc; it is a digital one.

    Summary, when the base is zero, the collector is one; and vice versa. That is, viewing the base as the input and the collector as the output. The logic function f having the property that f(0)=1 and f(1)=0 is called an inverter.

    NAND and NOR

    NAND and NOR   The diagram on the right shows two additional logic functions built from transistors. These logic functions take two arguments and are called NAND (not and) and NOR (not OR) respectively.


    Ignoring the above, which is one level below what we are studying, we define 5 logic gates by the truth tables given below their diagrams.

    gates

    NOT Truth Table
    AX
    01
    10
    NAND Truth Table
    ABX
    001
    011
    101
    110
    NOR Truth Table
    ABX
    001
    010
    100
    110
    AND Truth Table
    ABX
    000
    010
    100
    111
    OR Truth Table
    ABX
    000
    011
    101
    111
    XOR Truth Table
    ABX
    000
    011
    101
    110

    Homework: Using truth tables prove DeMorgans Laws

    Homework Show that all Boolean functions with two inputs (and one output) can be generated by just using NAND. This can be done two ways.

    1. Draw all the possible truth tables and for each draw a circuit with just NAND that generates that same truth table.
    2. Show how to get NOT, AND, and OR from just NAND and then show how any truth table can be generated from NOT, AND, and OR,
    The book does method 2 in section 3.1.3. You should do method 1. How many truth tables are there?

    Start Lecture #22

    Remark: The honors supplement has been added to the final project.

    Jumped to Chapter T-5 (for assembler part of term project)

    Lecture #23 continued

    T-3.1.2: Boolean Algebra

    Using truth tables, we can prove various formulas such as DeMorgan's Laws from the last homework. From these laws we can prove other laws.

    Standard notation is to use + for OR, * for AND, and ⊕ for XOR (exclusive or). As in regular algebra the * is often dropped.

    From these formulas, and algebraic manipulation we can get other formulas. This is called Boolean algebra (named after George Boole).

    For example (I am using ' to signify NOT), you use truth tables to prove both distributive laws 

        A(B+C) = AB + AC       * has higher precedence than +
    A+(BC) = (A+B)(A+C)    looks wrong but is correct
    and then calculate 
        A+(A'B)  =  (A+A')(A+B)      NOT has higher precedence than + or *
             =  (1)(A+B)         1 is the constant function (true)
             =  A+B              1 is the * identity (truth table)

    T-3.1.3: Implementation of Boolean Functions

    There is a standard procedure to generate any Boolean function using just AND, NOT, and OR. I did an example of this last time. Here is the general procedure.

    1. Write the truth table.
    2. Generate rails with each input and its complement.
    3. Use an AND for each set of inputs with a 1 in the result column of the truth table.
    4. Wire the ANDs to a final OR

    T-3.1.4: Circuit Equivalence

    As we have seen the same truth table can result from different Boolean formulas and hence from different circuits. Naturally, circuit designers might prefer one over the other (faster, less heat, smaller, etc.

    Start Lecture #24

    T-3.2: Basic Digital Logic Circuits

    T-3.2.1: Integrated Circuits

    I showed a discrete circuit last time as well as a Pentium II main board containing many integrated circuits. Initially these circuits had only a few components; now they have millions.

    T-3.2.2: Combinational Circuits

    These are circuits in which the outputs are uniquely determined by the inputs.
    Isn't this always true?
    Certainly not! Some circuits have memory (i.e., RAM). If you give a ram an input of (12,read) the output is the last value that was stored in 12. So you need to know more than (12,read) to know the answer; you need to know the history.

    4-way mux

    Multiplexors (Muxes)

    Have 2n inputs plus n select inputs. The select inputs are read as a binary value and thus specify a number from 0 to 2n. This number is used to select one of the inputs to be the output.

    Construct on the board an equivalent circuit with ANDs and ORs in three ways:

    1. Construct the truth table (64 rows!) and write the sum of products form, one product (6-input AND) for each row and a gigantic 64-way OR. Just start this, don't finish it.
    2. A simpler (more clever) two-level logic solution. Four ANDS (one per input), each gets one of the inputs and both select lines with appropriate bubbles. The four outputs go into a 4-way OR.
    3. Construct a 2-input mux (using the clever solution). Then construct a 4-input mux using a tree of three 2-input muxes. One select line is used for the two muxes at the base of the tree, the other is used at the root.

    Decoders (and Encoders)

    Imagine you are writing a program and have 32 flags, each of which can be either true or false. You could declare 32 variables, one per flag. If permitted by the programming language, you would declare each variable to be a bit. In a language like C, without bits, you might use a single 32-bit int and play with shifts and masks to store the 32 flags in this one word.

    In either case, an architect would say that you have these flags fully decoded. That is, you can detect the value of any combination of the bits.

    Now imagine that for some reason you know that, at all times, exactly one of the flags is true and the other are all false. Then, instead of storing 32 bits, you could store a 5-bit integer that specifies which of the 32 flags is true. This is called fully encoded.

    A 5-to-32 decoder converts an encoded 5-bit signal into 32 signals with exactly one signal true.

    A 32-to-5 encoder does the reverse operations. Note that the output of an encoder is defined only if exactly one input bit is set (recall set means true).

    The diagram on the right shows a 3-to-8 decoder.

    The truth table for an 8-3 encoder has 256 rows; for a 32-5 decoder we need 4 billion rows.

    There is a better way! Make use of the fact that we can assume exactly one input is true.

    For each output bit, OR the inputs that set this bit. For example the low-order output of an 8-3 is the OR of input bits 1,3,5,7.

    Comparators

    Programable Logic Arrays (PLAs)

    T-3.2.3: Arithmetic Circuits

    Shifters

    Do you want to rotate/0-fill/sign-extend?

    Do you want to shift left or right?

    Use muxes to give all the choices you want. The operation forms the select lines.

    Adders

    Draw a half adder (AND and XOR) that takes two inputs and produces two outputs, the sum and the Carry-out.

    adder
    Full Adder

    Full Adder   Really we want a full adder that has three inputs (A, B, Carry-in) and produces two outputs (Sum, Carry-out). The Sum equals the total number of 1s in A, B, and Ci is odd. The Carry-out is at least two of A, B, and Ci are 1.

    The diagram above uses logic formulas for Sum and Carry-out equivalent to the definitions just given (see homework just below).

    Homework:

    Jump to T-A for Lecture #25

    Start Lecture #26 (Prof. Grishman)

    T-3.2.4: Clocks


    clock

    The period is also called the cycle time. The number of cycles per second/hour/day/etc is called the frequency. So a clock with a 2 nanosecond cycle time has a frequency of 1/2 a gigahertz or 500 megahertz (one hertz is one cycle per second).

    T-3.3: Memory

    s-r latch

    T-3.3.1: Latches

    The only unclocked memory we will use is a so called S-R latch (S-R stands for Set-Reset).

    When we define latch below to be a level-sensitive, clocked memory, we will see that the S-R latch is not really a latch.

    The circuit for an S-R latch is on the right. Note the following properties.


    s-r latch clocked

    Clocked SR Latches

    The clocked version on the right has the property that the values of S and R are only relevant when the clock is high (i.e., true not false). This is sometimes convenient, but we will not use it. Instead we will use the important D-latch that we describe next that is very similar.


    Clocked D Latches

    d latch

    The D stands for data.

    The extra inverter (the bubble on the top left) and the rewiring prevents R and S from both being 1.

    Specifically, there are three cases.

    1. When the clock is low (false), both R and S are false and, as we saw before, Q and Q' remain unchanged.
    2. When the clock is high and D is high, Q becomes true and Q' false.
    3. When the clock is high and D is low, Q becomes fales and Q' becomes true.

    The summary is that, when the clock is asserted, the latch takes on the value of D, which is then held while the clock is low. The value of D is latched when the clock is high and held while the clock is low.

    The smaller diagram shows how the latch is normally drawn.


    d-latch operation

    In the traces to the right notice how the output follows the input when the clock is high and remains constant when the clock is low. We assume the stored value was initially low.

    Start Lecture #27

    Remark: Grishman did 4-bit adders and subtracters. If you wish (on line) pictures, you can look at my architecture notes.

    T-3.3.2: Flip-Flops

    D or Master-Slave Flip-flop

    This structure was our goal. It is an edge-triggered, clocked memory. The term edge-triggered means that values change at edges of the clock, either the rising edge or the falling edge. The edge at which the values change is called the active edge. d-flop

    The circuit for a D flop is on the right. It has the following properties.

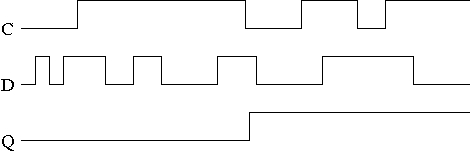
    d-flop operation

    The picture on the right is for a master-slave flip-flop. Note how much less wiggly the output is in this picture than before with the transparent latch. As before we are assuming the output is initially low.

    Homework: In the D-flop diagram, move the inverter to the other latch, i.e., the inverted clock goes to the left latch and the positive clock goes to the right. What has changed in the D-flop?

    Homework: Which code better describes a flip-flop and which a latch? 

        repeat {
        while (clock is low) {do nothing}
        Q=D
        while (clock is high) {do nothing}
    } until forever
    or 
        repeat {
        while (clock is high) {Q=D}
    } until forever

    R-type datapath

    Show how to make a register out of FFs (easy just use a bunch).

    Show how to make a register file out of registers. Not too hard use a BIG mux.

    Describe how to write a register. Actually the trick is how to not write a register. Recall that the constituent FFs are written at every falling edge. The idea is to introduce a signal that is ANDed with the clock to eliminate edges you don't want (this takes some care).

    Then the diagram on the right shows the basic workings of a register based ADD (or SUB or OR or AND) 

          add regA,regB,regC

    Lecture #22 Continued

    Chapter T-4: The Microarchitecture Level


    Chapter T-5: The Instruction Set Architecture Level

    Remark: We jump ahead (out of order) so that I can cover enough x86 assemble language for you to do the assembler portion of the project. I am not following Tanenbaum's order here as the goal is just x86.

    Remark: I believe this reference is a good resource for x86 assembly programming.

    T-5.1: Overview of the ISA Level

    5.1.1: Properties of the ISA Level

    5.1.2: Memory Models

    5.1.3: Registers

    5.1.4: Instructions

    T-5.1.5: Overview of the Pentium 4 ISA Level

    In order to maintain compatibility with previous, long-out-of-date members of the x86 processor family, modern members can execute in three modes.

    1. Real Mode: The processor acts just like a 1979 8088, the processor used in the original PC. If any program screws up, the machine crashes.
      If Intel had designed human beings, it would have put in a bit that made them revert back to chimpanzee mode (most of the brain disabled, no speach, sleeps in trees, eats mostly bananas, etc.)
      While perhaps humorous (Tanenbaum certainly writes well) the quote does hide the tremendous user advantages of having a new computer that can still execute old (often awful) programs, in particular old games, which were notorious for not being clean.
    2. Virtual 8086/8088 mode: Now if a program crashes the OS is notified, rather than having the machine crash. I am not sure why (indeed, if) real mode is still needed, i.e., why virtual 8086 mode did not simply replace it.
    3. Protected mode: This is the mode we will study and is the mode used by all modern operating systems and applications.

    Registers on the x86

    We will mainly use the 32-bit registers, their names begin with E standing for extended. They extended the 16-bit registers of early members of the family.

    The four main registers are EAX, EBX, ECX, and EDX. Each is 32 bits. We will make most use of EAX, which is the main arithmetic register. Also functions returning a single word, return this in EAX.

      mov   EAX   ECX
  mov   EAX   [EBX]
  mov   EAX   [EBX+4]

    If an address is in any one of these four the contents of that address can be specified as an operand for an instruction. Also an offset can be added. For example the first instruction on the right simply copies (the contents of) ECX into EAX. The second instruction does a de-reference. If EBX contains 1000, the contents of memory location 1000 is loaded into EAX. Finally, the last instruction would load the contents of 1004 into EAX (again assuming EBX contains 1000).

    As you can see from the sheet I handed out and from Tanenbaum's figure 5-3, these registers contain named 16-bit and 8-bit subsets.

    The two registers ESI and EDI are mostly used for the hardware string manipulation instructions. I don't think you will need those instructions, but you can also use ESI and EDI to hold other values (scratch storage).

    The EBP register is normally used to hold the frame pointer FP, that will be described below. The ESP is the stack pointer (again described below).

    5.1.6: Overview of the UltraSPARC III ISA Level

    5.1.7: Overview of the 8051 ISA Level

    5.2: Data Types

    T-5.2.1: Numeric Data Types

    T-5.2.2: Nonnumeric Data Types

    T-5.2.3: Data Types on the Pentium 4 (x86)

    The x86 architecture supports signed and unsigned integers of three sizes.

    1. 8 bit (one byte): used for ascii characters (C char).
    2. 16 bit (two bytes): used for unicode characters and for 16-bit integers (C short int).
    3. 32 bit (4 bytes): used for integers (C int).

    There is also support for 32-bit and 64-bit floating point, which are used for C float and double respectively.

    Finally, there is support for 8-bit BCD (binary coded decimal), which is not used in C.

    T-5.2.4: Data types on the UltraSPARC III

    T-5.2.5: Data types on the Java Virtual Machine

    T-5.2A: Argument Passing from C to Assembler on x86

    This is not from the book.

    Since you will be writing an assembler subroutine called by a C program and your subroutine might call another C program, we need to understand how arguments, the return address, and the returned value are passed from caller to callee. The short answer is via the stack.

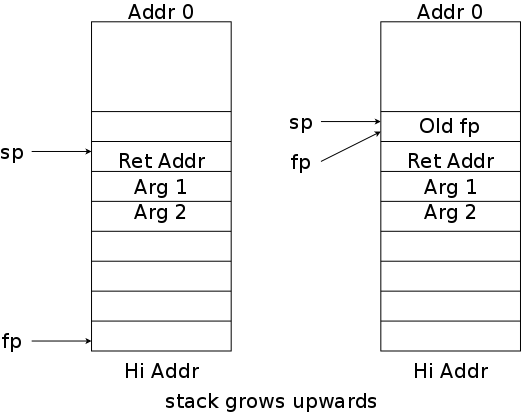
    stack1

    Each routine places its local variables on the stack, a region of memory that grows and shrinks during execution. (We are ignoring variables created via malloc as they are not allocated on the stack.) Due to the lifo nature of calls and returns, stack allocation works perfectly for such variables.

    As shown in the diagrams, the stack starts at a high address and grows towards location zero

    Each routine uses a region of the stack called its stack frame or simply frame. The C convention (really the C-compiler convention) is that the frame is specified by two pointers: the frame pointer fp, which points to the beginning (bottom) of the frame, and the stack pointer sp that points to the current end (top) of the frame. As the routing places more information on the stack, sp moves (towards 0) to enlarge the stack. As the routine removes entries at the top of the stack, sp again moves (in this case away from 0).

    In the left diagram the currently running procedure has just called another procedure. The caller has pushed the arguments onto the stack (in reverse order) and then pushed the return address (actually the call instruction did the last part). Also the caller has saved EAX, ECX, and EDX if necessary (these are referred to as caller-save registers). 

    	.intel_syntax noprefix
.globl add2
add2:	push	ebp
	mov	ebp, esp
	mov	eax, DWORD PTR [ebp+12]
	add	eax, 1
	push	eax
	call	g
	add	esp, 4 # undo the push
	pop	ebp
	ret
#include <stdio.h>
int main(int argc, char *argv[]) {
    int i;
    for (i=0; i<10; i++)
	printf("i is %d and add2(1,i) is %d\n",
           i, add2(1,i));
    return 0;
}
int g(int x) {
    return x * x;
}
// Local Variables:
// compile-command: "cc -O add2.c add2.s \
// -mpreferred-stack-boundary=2; ./a.out"
// End:

    We are the callee and first must set fp to the bottom of OUR frame (it is currently the bottom of the caller's frame). We also must save the current value of fp so that when we return to the caller, we can restore fp to the bottom of the caller's frame.

    That is, we want to move from the left diagram to the right one. The first two assembler statements on the right do exactly this. The register EBP holds the current fp (I believe B is for base, the fp points to the base of the current stack). The register ESP holds sp.

    The purpose of the program is to compute (x+1)2 for x between 0 and 10. The main program calls us with two arguments, the first is unused (I wanted to illustrate the order the arguments appear on the stack) the second is the value to be operated on.

    We want to move the second argument to EAX for processing. This will overwrite whatever the caller had in EAX, but recall that it is one of the caller-saved registers (mentioned above) so we do not have to save it. How do we reference the second parameter? It is in the caller's stack frame, the one below ours. Since the stack grows towards zero, going backwards means increasing the fp.

    Why is it 12 to go back only 3, and what is the DWORD PTR nonsense? The 12 is easy: 3 words equals 12 bytes.

    The DWORD PTR is because a pointer (in this case ebp) can point to a byte, a 2-byte word, or a 4-byte doubleword. We think of 32-bit words, but the x86 family started out with 16-bit machines and it shows.

    Next we add 1. Note that x86 is a 2-operand architecture, you can compute x=xOPy or x=yOPx but not x=yOPz.

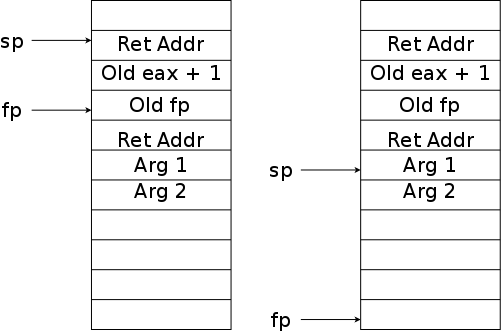
    stack2

    Now that we have x+1 we want to call a function to do the squaring. Thus, we are now the caller.

    You might think that we need to save EAX since it is a caller-save register, but the value it contains is the first argument of the new callee so when we push that argument, we have saved EAX as well. We then issue the call instruction.

    The function g, like all functions, returns its result in EAX. As it happens that value is the result we are charged with returning as well. Thus we just leave it there and return to our caller.

    Start Lecture #23

    But wait, we have messed up the pointers to the stack! Hence, the end of our routine restores them before returning. The first diagram on the right shows the stack just after we have called g(), but before g() has executed.

    When g executes ret, sp is lowered one word. We we execute add, sp is lowered again, returning us to the right stack in the previous diagram. The pop gives us the left stack in the previous diagram. Finally, our ret restores the stack to 2nd on the right, which is same as it was before main program called us.

    Note that the values above sp are still there but the space would be reused if main() called another routine.

    5.3: Instruction Formats

    5.3.1: Design Criteria for Instruction Formats

    5.3.2: Expanding Opcodes

    5.3.3: The Pentium II (x86) Instruction Formats

    Very complicated as is clear from looking at Figure 5-14 and reading the accompanying text. This makes it difficult for the hardware designer, which is not our problem.

    It also makes the assembly language somewhat irregular. Specifically, it is not true that the 8 main registers EAX, EBX, ECX, EDX, ESI, EDI, ESP, EDP can be used interchangeably, certain instructions can use certain registers.

    5.3.4: The UltraSPARC II Instruction Formats

    5.3.5: The JVM Instruction Formats

    T-5.4: Addressing

    T-5.4.1: Addressing Modes

    Most instructions have one or more operands, each of which is specified by a corresponding field in the instruction. It is the addressing mode that determines how the operand is determined given the address field.

    T-5.4.2: Immediate Addressing

    In this, the simplest form, the address field is not an address at all but is the operand. In this case we say the instruction has an immediate operand, because it can be determined immediately from the instruction (without requiring and additional memory reference).

    T-5.4.3: Direct Addressing

    Almost as simple, and better fitting the name address field, is for the address field to contain the address of the operand. So if the address field is 12, the operand is the contents of the 32-bit word (or 64-bit word, or 16-bit word, or 8-bit byte) specified by location 12.

    T-5.4.4: Register Addressing

    In this mode the operand is the register specified by the address field. So if the address field is 12 the operand is the contents of the register with address 12 (normally called simply register 12). This mode is very common and very fast.

    T-5.4.5: Register Indirect Addressing

    Using the terminology of C (and other high-level languages). This mode is just the de-reference operator applied to the previous mode. So if the address field is 12 the operand is determined by a two step process: first register 12 is examined. Say its value is 22888. Then the operand is the contents of the word (or byte, etc) specified by location 12.

    T-5.4.6 Indexed Addressing

    In this addressing mode, two values are used to determine the address: one is a used to specify a register and the second is a constant that is added to the contents of the register. The resulting sum is use as a memory address, the contents of which is the operand.

    Why is this useful and why is it called indexed? Consider 

        for (i=0; i<10; i++)
        A[i] = 0;
    and assume that the array A is global (so that its address is known before the program begins execution).

    What is the address referred to by A[i]?
    It is the address of A[0] plus 4 times the value of i. The former is a constant (let's say it is 1280) and we use a register for the latter so the assembler loop would have body 

        DWORD PTR mov [1280+EAX], 0     // X is the address of A[0], a known constant
    add EAX, 4
    Note that EAX is serving as the index i in the C code. Hence the name, indexed addressing.

    T-5.4.7: Based-Indexed Addressing

    If one register is good, two are better (or at least more general). In this mode, the contents of two registers are added to a constant. Consider again 

        for (i=0; i<10; i++)
        A[i] = 0;
    but this time assume the array A is on the stack. Specifically assume A[0] is 1000 bytes below SP the top of the stack. Register ESP typically holds SP so the loop body in assembler would be 
        mov DWORD PTR [ESP+EAX+1000], 0
    add EAX, 4

    T-5.4.8: Stack Addressing

    Reverse Polish Notation

    Evaluation of Reverse Polish Notation Formulas

    T-5.4.9: Addressing Modes for Branch Instructions

    T-5.4.10: Orthogonality of Opcodes and Addressing Modes

    T-5.4.11: The Pentium 4 Addressing Modes

    The x86 is quite irregular: not all addressing modes are available for all instructions and not all registers can be used for all addressing modes.

    The machine has both 16-bit and 32-bit flavors of operations, we are only studying the 32-bit versions.

    The x86 is a two operand machine, but at most one operand can be a memory location.

    The x86 supports immediate, direct, register, register indirect, indexed, and based-index. Based-index uses an extra byte of instruction call the SIB (Scale, Index, Base), which specifies not only both the base and index registers, but a scale of 1, 2, 4, or 8 that is multiplied with the index register, which permits that register to represent the number of bytes, (16-bit) words, double words, or quad words the effective address is displaced from the base.

    I do not understand why Tanenbaum does not consider addresses using SIB to be employing based-index mode.

    T-5.4.12: The UltraSPARC Addressing Modes

    T-5.4.13: The 8051 Addressing Modes

    T-5.4.14: Discussion of Addressing Modes

    T-5.6: Flow of Control

    T-5.7: A Detailed Example: The Towers of Hanoi

    T5.8: The IA-64 Architecture and the Itanium2

    T5.6: Summary

    Lecture #23 Continues with T-3.1.2

    Start Lecture #25

    Appendix TA: Binary Numbers

    T-A.1: Finite Precision Numbers

    In mathematics, integers have infinite precision. That is, we uses as many digits as are needed, without limit.

    Some software systems offer this as well (up to the memory limits of the computer). However, we will be looking at the native hardware support for integers (we will not do floating point, which is a little more complicated). On most systems you can buy today, the normal integer is 32 bits or 64 bits. That means you write integers using 32 bits (or 64 buts, but we will concentrate on 32-bit systems). If an integer requires more than 32 bits it cannot be expressed using the native hardware representation of integers.

    This possibility of a number not being expressible leads to anomalies, such as overflow. We will learn the representation shortly, but for the moment note that the largest integer expressible in the native 32-bit system is 231-1=2,147,483,647. Thus 

        (2,000,000,000-1,000,000,000)+1,000,000,000 ≠
    (2,000,000,000+1,000,000,000)-1,000,000,000
    Specifically, the first computation yields the mathematically correct answer of 2,000,000,000; whereas, the second gives no answer since an overflow occurs during the addition.

    T-A.2: Radix Number Systems

    We write our numbers in the radix-10 system. That is the digits read from the right tell you how many 1s, how many 10s, how many 100s, etc. Note that 1=100, 10=101, 100=102, etc. (Some ancient civilizations used other radices—or radixes.)

    Almost all computers use radix 2; that is what we shall use. So the bits (sometimes called binary digits) from right to left tell you how many 1s, 2s, 4s, 8s, etc., where 1=20, 2=21, 4=22, 8=23, etc.

    A.3: Conversion from one Radix to Another

    It is very easy to convert from radix 2 to any radix 2n. You simply group n of the bits together to form a single digit in radix 2n.

    Do this on the board for octal (radix 8=23) and hexadecimal (radix 16=24).

    Converting from Binary to Decimal

    You can simply follow the definition. For the binary number ABCDEFG (each letter is a bit), the decimal equivalent is 

        A×26+B×25...+F×21+G×20 = A×128+B×64...+F×2+G
    Less work is to evaluate the equivalent expression 
        G+2×(F+2×(E+2×(D+2×(C+2×(B+2×A)))))
    from right to left (start with A, double it and add B, double the sum and add C, ....

    Converting from Decimal to Binary

    Take the remainders obtained with successive divisions by two.

    For example, take 103.

    1. Dividing 103 by two gives a quotient Q=51 and a remainder R=1. This says the low order bit is 1.
    2. Next divide the quotient 51 by 2 and get Q=25 & R=1. So the low order is now 11.
    3. Dividing 25 by 2 gives Q=12 & R=1; low order is 111.
    4. Dividing 12 by 2 gives Q=6 & R=0; low order is 0111.
    5. Dividing 6 by 2 gives Q=3 & R=0; low order is 00111.
    6. Dividing 3 by 2 gives Q=1 & R=1; low order is 10111.
    7. Dividing 1 by 2 gives Q=0 & R=1; low order is 10111.

    Homework: 1, 2, 3

    T-A.4: Negative Binary Numbers

    There are several schemes for representing binary numbers; we will study the one that is used on essentially all modern machines: two's complement.

    Although we are interested in 32-bit systems, let's use 4 bits in this section since it will ease our task when we do arithmetic and draw pictures. There is basically no difference between n-bit and m-bit systems providing n and m are least 3.

    How Many Positive Values and How Many Negative Values

    With 4 bits, we can express 16 numbers. One of these bit pattern must be used for zero, leaving 15 for positive and negative. Thus we cannot achieve the ideal of using all 16 values, having exactly one representation for each expressible value, and having the same number of positive and negative values. So we must give up one of these ideals. Possibilities include

    1. Having two (or more) different representations for some values.
    2. Having at least one bit pattern declared illegal.
    3. Having a different number of positive and negative values.

    Possibility 1 has been done (in this very building!). The CDC 6600, then the fastest computer in the world, used one's complement arithmetic, which has two expressions for zero (0000 and 1111).

    Also one could use the bottom three bits to express 0-7 and declare the top bit as the sign so both 0000 and 1000 would be zero.

    I don't know of a machine that ever did possibility 2.

    The third possibility dominates and that is what we will study.

    A Conceptual Understanding of Twos Complement

    This text (and many others) just tells you how to do it (take the ordinary (bitwise) complement (called the one's complement) and then add 1 to get the two's complement.

    That sound too much like instructions to Merlin for my liking. So I will try to explain why it is done.

    Recall we have zero and 15 additional numbers to split among the positive and negative values. Seven will be positive and eight negative. It will become clear later why we don't have 8 positive and seven negative.

    Good news. The values from 0-7 are expressed as you would expect:
    0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111.
    The high order bit gives the sign and the bottom n-1=4-1=3 bits gives the magnitude.

    Bad news. The value -3 is not just the value for three with the sign bit 1.

    Let's begin.

    Note that the number 16 in binary is 10000, it is the first number that cannot be expressed in 4 bits. If we chop off the high bit (normally called HOB, high-order bit), 16 becomes 0. Said mathematically 16 mod 16 is 0.

    Now what about -3? The definition of -3 is that it is the (unique) number that, when added to 3, gives 0. Instead of demanding to get 0 when added, we loosen the requirement to say that we want a number that, when added to 3, gives 0 mod 16.

    There are lots of them: 13+3=16, which is 0 mod 16; 29+3=32, which also is 0 mod 16. But there is only one number in the range 0-15 that has this property, and those are precisely the numbers expressible in 4 bits.

    Mathematically we are simply taking -3 mod 16.

    So, for us -3 is the 4-bit representation of 13, which is 1101. If we simply add and throw away the 5th bit we see that 13+3 is indeed 0: 1101+0011=10000, which becomes 0000 when we throw away bit 5.

    Recall that we define -n to be the number, which when added to n gives 16, i.e. we just express -n as (-n) mod 16. This is all for n between 1 and 7.

    The properties of mod permit us to prove the normal laws of inverses. For example, the inverse of n+m is 

        -(n+m) mod 16 = (-n)+(-m) mod 16 = [(-n) mod 16] + [(-m) mod 16]
    which is precisely the inverse of n plus the inverse of m.

    OK, but how do you calculate inverses on the computer. For our 4-bit system, do we calculate the inverse of 3 by evaluating -3 mod 16? With a 32-bit system, do we calculate the inverse of 1,000,000 by evaluating -1,000,000 mod 232?

    There is indeed an easier way. Recall that to find the inverse of 3 we needed to find the number with the property that when added to 3 we get 16.

    Written in 4-bit binary we want the number that when added to 0011 gives us 10000 (I know that is 5-bits).

    Let's ask a different question. What is the number that when added to 0011, gives 1111. That is easy, look at 0011 and take the complement, 1100. Then between the original and the complement each bit position has exactly one 1 so the sum is clearly 1111. (This number 1100 is called the one's complement).

    Since we really wanted to get 10000 not just 1111, we need to add one. This gives 1101, which is indeed the two's complement of 0011.

    So the rule is: Take the bitwise complement and add 1, just as all the text books say. So for 4-bit numbers using two's complement arithmetic, -0011 is 1101. Said more simply -3 is 1101 in 4-bit 2's complement arithmetic.

    Negating Negative Numbers and the Lack of Ideal Behavior

    It is not too hard to see that this same procedure works when the original number is negative. Lets try -(-3). We already know -3 is 1101. Complementing gives 0010 and adding 1 gives 0011. Success.

    Addition works too. Compute -2=-0010=1101+1=1110; (-2)+(-3)=1101+1110=11011 toss the HOB and the answer is 1011. Is this really -5? Does 1011+0100 give 16? Yes!

    Is -(1011) equal to 5? Take the complement and add 1: 0100+1=0101=5.

    Now the sad news. (-4)+(-4)=1100+1100=11000 toss the HOB and get 1000, which actually is -8 but the complement is 0111+1=1000 which is not 8. Remember we can't have the same number of positives as negatives. So the range for 4-bit two's complement is -8,-7,...0,...6,7.

    T-A.5: Binary Arithmetic

    Tanenbaum does both one's complement and two's complement arithmetic. We will just do the latter. As we indicated above you simply add the two's complement numbers with no thought of signs or compliments. If you add two n-bit numbers you might get an (n+1)-bit number, i.e., you might get a carry-out of the high order bit. But the rule is simple, toss it!

    Subtraction

    The rule is the same as what you learned in elementary school, a-b=a+(-b). That is you invert (take the two's complement) the b and add. For example 5-3 is (0101)-(0011)=(0101)+(1101)=10010 toss the HOB and get 0010 which is 2.

    Homework: 7.

    Overflow

    Unfortunately, although the above does describe (part of) the hardware, it doesn't always give the correct answer. As a simple example, with our 4-bit system we can express -8...7, but if you add 5+6 you should get 11. We cannot possibly get 11 since we can't express 11. Similarly if you add (-5)+(-6), you should get -11, which again we cannot even express.

    When the result falls outside the expressible range, an overflow has occurred.

    When you add numbers of opposite sign overflow is impossible (the result is between the two original numbers).

    As we have seen, subtracting numbers of the same sign is the same as adding numbers of opposite sign so again overflow is impossible.

    When you add numbers of the same sign (or subtract numbers of the opposite sign) overflow is possible. The question is, When does it occur?.

    The answer is simple to state but not so simple to explain (you need to analyze several cases): An overflow occurs if and only if the carry into the HOB does not equal the carry out from the HOB.

    Homework: 9.

    Back to T-3.2.4 for Lecture #26