Operating Systems

Start Lecture #6

Chapter 6 Deadlocks

Remark: Deadlocks are closely related to process management so belong here, right after chapter 2. It was here in 2e. A goal of 3e is to make sure that the basic material gets covered in one semester. But I know we will do the first 6 chapters so there is no need for us to postpone the study of deadlock.

A deadlock occurs when every member of a set of processes is waiting for an event that can only be caused by a member of the set.

Often the event waited for is the release of a resource.

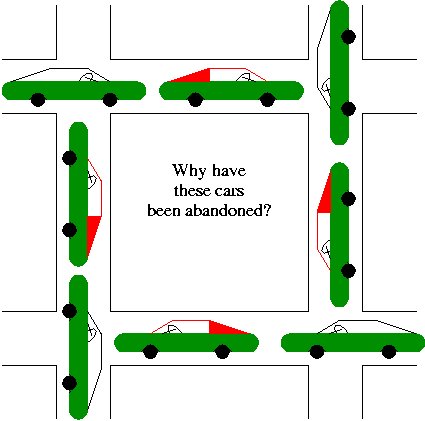
In the automotive world deadlocks are called gridlocks.

• The processes are the cars.
• The resources are the spaces occupied by the cars

For a computer science example consider two processes A and B that each want to print a file currently on a CD-ROM Drive.

1. A has obtained ownership of the printer and will release it after getting the CD Drive and printing one file.
2. B has obtained ownership of the CD drive and will release it after getting the printer and printing one file.
3. A tries to get ownership of the drive, but is told to wait for B to release it.
4. B tries to get ownership of the printer, but is told to wait for A to release it.

Bingo: deadlock!

6.1 Resources

A resource is an object granted to a process.

6.1.1 Preemptable and Nonpreemptable Resources

Resources come in two types

1. Preemptable, meaning that the resource can be taken away from its current owner (and given back later). An example is memory.
2. Non-preemptable, meaning that the resource cannot be taken away. An example is a printer.

The interesting issues arise with non-preemptable resources so those are the ones we study.

The life history of a resource is a sequence of

1. Request
2. Allocate
3. Use
4. Release

Processes request the resource, use the resource, and release the resource. The allocate decisions are made by the system and we will study policies used to make these decisions.

6.1.2 Resource Acquisition

A simple example of the trouble you can get into.

• Two resources and two processes.
• Each process wants both resources.
• Use a semaphore for each. Call them S and T.
• If both processes execute
  P(S); P(T); --- V(T); V(S)
  all is well.
• But if one executes instead
  P(T); P(S); -- V(S); V(T)
  disaster! This was the printer/CD example just above.

Recall from the semaphore/critical-section treatment last chapter, that it is easy to cause trouble if a process dies or stays forever inside its critical section. We assume processes do not do this. Similarly, we assume that no process retains a resource forever. It may obtain the resource an unbounded number of times (i.e. it can have a loop forever with a resource request inside), but each time it gets the resource, it must release it eventually.

6.2 Introduction to Deadlocks

Definition: A deadlock occurs when a every member of a set of processes is waiting for an event that can only be caused by a member of the set.

Often the event waited for is the release of a resource.

6.2.1 (Necessary) Conditions for Deadlock

The following four conditions (Coffman; Havender) are necessary but not sufficient for deadlock. Repeat: They are not sufficient.

1. Mutual exclusion: A resource can be assigned to at most one process at a time (no sharing).
2. Hold and wait: A processing holding a resource is permitted to request another.
3. No preemption: A process must release its resources; they cannot be taken away.
4. Circular wait: There must be a chain of processes such that each member of the chain is waiting for a resource held by the next member of the chain.

One can say If you want a deadlock, you must have these four conditions.. But of course you don't actually want a deadlock, so you would more likely say If you want to prevent deadlock, you need only violate one or more of these four conditions..

The first three are static characteristics of the system and resources. That is, for a given system with a fixed set of resources, the first three conditions are either always true or always false: They don't change with time. The truth or falsehood of the last condition does indeed change with time as the resources are requested/allocated/released.

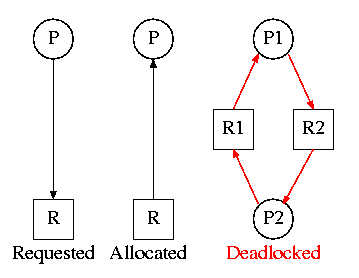
6.2.2 Deadlock Modeling

On the right are several examples of a Resource Allocation Graph, also called a Reusable Resource Graph.

• The processes are circles.
• The resources are squares.
• An arc (directed line) from a process P to a resource R signifies that process P has requested (but not yet been allocated) resource R.
• An arc from a resource R to a process P indicates that process P has been allocated resource R.

Homework: 5.

Consider two concurrent processes P1 and P2 whose programs are.

    P1                   P2
    request R1           request R2
    request R2           request R1
    release R2           release R1
    release R1           release R2
  

On the board draw the resource allocation graph for various possible executions of the processes, indicating when deadlock occurs and when deadlock is no longer avoidable.

There are four strategies used for dealing with deadlocks.

1. Ignore the problem
2. Detect deadlocks and recover from them
3. Prevent deadlocks by violating one of the 4 necessary conditions.
4. Avoid deadlocks by carefully deciding when to allocate resources.

6.3 Ignoring the problem—The Ostrich Algorithm

The put your head in the sand approach.

• If the likelihood of a deadlock is sufficiently small and the cost of avoiding a deadlock is sufficiently high it might be better to ignore the problem. For example, if each PC deadlocks once per 10 years, the one reboot may be less painful that the restrictions needed to prevent it.
• Clearly not a good philosophy for nuclear missile launchers or patient monitoring systems for cardiac care units.
• For embedded systems (such as the two examples above) the programs run are fixed in advance so many of the issues that occur in systems like linux or windows (such as many processes wanting to fork at the same time) don't occur.

6.4 Detecting Deadlocks and Recovering From Them

6.4.1 Detecting Deadlocks with Single Unit Resources

Consider the case in which there is only one instance of each resource.

• Thus a request can be satisfied by only one specific resource.
• In this case the 4 necessary conditions for deadlock are also sufficient.
• Remember we are making an assumption (single unit resources) that is often invalid. For example, many systems have several printers and a request is given for a printer not a specific printer. Similarly, one can have many CD-ROM drives.
• So the problem comes down to finding a directed cycle in the resource allocation graph. Why?
  Answer: Because the other three conditions are either satisfied by the system we are studying, or are not in which case deadlock is not a question. That is, conditions 1,2,3 are static conditions on the system in general not conditions on the state of the system right now.

To find a directed cycle in a directed graph is not hard. The algorithm is in the book. The idea is simple.

1. For each node in the graph do a depth first traversal to see if the graph is a DAG (directed acyclic graph), building a list as you go down the DAG (and pruning it as you backtrack back up).
2. If you ever find the same node twice on your list, you have found a directed cycle, the graph is not a DAG, and deadlock exists among the processes in your current list.
3. If you never find the same node twice, the graph is a DAG and no deadlock exists (right now).

The searches are finite since there are a finite number of nodes.

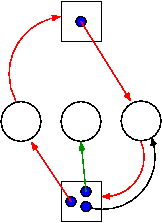
6.4.2 Detecting Deadlocks with Multiple Unit Resources

This is more difficult.

• The figure on the right shows a resource allocation graph with multiple unit resources.
  
  
• Each unit is represented by a dot in the box.
  
  
• Request edges are drawn to the box since they represent a request for any dot in the box.
  
  
• Allocation edges are drawn from the dot to represent that this unit of the resource has been assigned (but all units of a resource are equivalent and the choice of which one to assign is arbitrary).
  
  
• Note that there is a directed cycle in red, but there is no deadlock. Indeed the middle process might finish, erasing the green arc and permitting the blue dot to satisfy the rightmost process.
  
  
• The book gives an algorithm for detecting deadlocks in this more general setting. The idea is as follows.
  1. look for a process that might be able to terminate. That is, a process all of whose request arcs can be satisfied by resources the manager has on hand right now.
  2. If one is found, pretend that it does terminate (erase all its arcs), and repeat step 1.
  3. If any processes remain, they are deadlocked.
  
  
• We will soon do in detail an algorithm (the Banker's algorithm) that has some of this flavor.
  
  
• The algorithm just given makes the most optimistic assumption about a running process: it will return all its resources and terminate normally. If we still find processes that remain blocked, they are deadlocked.
  
  
• In the bankers algorithm we make the most pessimistic assumption about a running process: it immediately asks for all the resources it can (details later on can). If, even with such demanding processes, the resource manager can insure that all process terminates, then we can insure that deadlock is avoided.

6.4.3 Recovery from deadlock

Recovery through Preemption

Perhaps you can temporarily preempt a resource from a process. Not likely.

Recovery through Rollback

Database (and other) systems take periodic checkpoints. If the system does take checkpoints, one can roll back to a checkpoint whenever a deadlock is detected. You must somehow guarantee forward progress.

Recovery through Killing Processes

Can always be done but might be painful. For example some processes have had effects that can't be simply undone. Print, launch a missile, etc.

Remark: We are doing 6.6 before 6.5 since 6.6 is easier and I believe serves as a good warm-up.

6.6 Deadlock Prevention

Attack one of the Coffman/Havender conditions.

6.6.1 Attacking the Mutual Exclusion Condition

The idea is to use spooling instead of mutual exclusion. Not possible for many kinds of resources.

6.6.2 Attacking the Hold and Wait Condition

Require each processes to request all resources at the beginning of the run. This is often called One Shot.

6.6.3 Attacking the No Preemption Condition

Normally not possible. That is, some resources are inherently pre-emptable (e.g., memory). For those, deadlock is not an issue. Other resources are non-preemptable, such as a robot arm. It is often not possible to find a way to preempt one of these latter resources. One exception is if the resource (say a CD-ROM drive) can be virtualized (recall hypervisors).

6.6.4 Attacking the Circular Wait Condition

Establish a fixed ordering of the resources and require that they be requested in this order. So if a process holds resources #34 and #54, it can request only resources #55 and higher.

It is easy to see that a cycle is no longer possible.

Homework: Consider Figure 6-4. Suppose that in step (o) C requested S instead of requesting R. Would this lead to deadlock? Suppose that it requested both S and R.

6.5 Deadlock Avoidance

Let's see if we can tiptoe through the tulips and avoid deadlock states even though our system does permit all four of the necessary conditions for deadlock.

An optimistic resource manager is one that grants every request as soon as it can. To avoid deadlocks with all four conditions present, the manager must be smart not optimistic.

6.5.1 Resource Trajectories

We plot progress of each process along an axis. In the example we show, there are two processes, hence two axes, i.e., planar. This procedure assumes that we know the entire request and release pattern of the processes in advance so it is not a practical solution. I present it as it is some motivation for the practical solution that follows, the Banker's Algorithm.

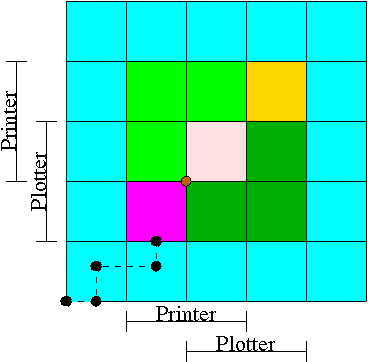
• We have two processes H (horizontal) and V.
• The origin represents them both starting.
• Their combined state is a point on the graph.
• The parts where the printer and plotter are needed by each process are indicated.
• The dark green is where both processes have the plotter and hence execution cannot reach this point.
• Light green represents both having the printer; also impossible.
• Pink is both having both printer and plotter; impossible.
• Gold is possible (H has plotter, V has printer), but the system can't get there.
• The upper right corner is the goal; both processes have finished.
• The brown dot is ... (cymbals) deadlock. We don't want to go there.
• The cyan is safe. From anywhere in the cyan we have horizontal and vertical moves to the finish point (the upper right corner) without hitting any impossible area.
• The magenta interior is very interesting. It is
  • Possible: each processor has a different resource.
  • Not deadlocked: each processor can move within the magenta.
  • Deadly: deadlock is unavoidable. You will hit a magenta-green boundary and then will no choice but to turn and go to the brown dot.
• The cyan-magenta border is the danger zone.
• The dashed line represents a possible execution pattern.
• With a uniprocessor no diagonals are possible. We either move to the right meaning H is executing or move up indicating V is executing.
• The trajectory shown represents.
  1. H excuting a little.
  2. V excuting a little.
  3. H executes; requests the printer; gets it; executes some more.
  4. V executes; requests the plotter.
• The crisis is at hand!
• If the resource manager gives V the plotter, the magenta has been entered and all is lost. Abandon all hope ye who enter here—Dante.
• The right thing to do is to deny the request, let H execute move horizontally under the magenta and dark green. At the end of the dark green, no danger remains, both processes will complete successfully. Victory!
• This procedure is not practical for a general purpose OS since it requires knowing the programs in advance. That is, the resource manager, knows in advance what requests each process will make and in what order.

Homework: All the trajectories in Figure 6-8 are horizontal or vertical. Is is possible for a trajectory to be a diagonal.

Homework: 11, 12.

6.5.2 Safe States

Avoiding deadlocks given some extra knowledge.

• Not surprisingly, the resource manager knows how many units of each resource it had to begin with.
  
  
• Also it knows how many units of each resource it has given to each process.
  
  
• It would be great to see all the programs in advance and thus know all future requests, but that is asking for too much.
  
  
• Instead, when each process starts, it announces its maximum usage. That is each process, before making any resource requests, tells the resource manager the maximum number of units of each resource the process can possible need. This is called the claim of the process.
  • If the claim is greater than the total number of units in the system the resource manager kills the process when receiving the claim (or returns an error code so that the process can make a new claim).
  • If during the run the process asks for more than its claim, the process is aborted (or an error code is returned and no resources are allocated).
  • If a process claims more than it needs, the result is that the resource manager will be more conservative than need be and there will be more waiting.

Definition: A state is safe if there is an ordering of the processes such that: if the processes are run in this order, they will all terminate (assuming none exceeds its claim and assuming each would terminate if all its requests are granted).

Recall the comparison made above between detecting deadlocks (with multi-unit resources) and the banker's algorithm (which stays in safe states).

• The deadlock detection algorithm given makes the most optimistic assumption about a running process: it will return all its resources and terminate normally. If we still find processes that remain blocked, they are deadlocked.
  
  
• The banker's algorithm makes the most pessimistic assumption about a running process: it immediately asks for all the resources it can (i.e., up to its initial claim). If, even with such demanding processes, the resource manager can assure that all process terminates, then we can ensure that deadlock is avoided.

In the definition of a safe state no assumption is made about the running processes. That is, for a state to be safe, termination must occur no matter what the processes do (providing each would terminate if run alone and each never exceeds its claims). Making no assumption on a process's behavior is the same as making the most pessimistic assumption.

Remark: When I say pessimistic I am speaking from the point of view of the resource manager. From the manager's viewpoint, the worst thing a process can do is request resources.

Give an example of each of the following four possibilities. A state that is

1. Safe and deadlocked—not possible.
   
   
2. Safe and not deadlocked—a trivial is example is a graph with no arcs.
   
   
3. Not safe and deadlocked—easy (any deadlocked state).
   
   
4. Not safe and not deadlocked—interesting.

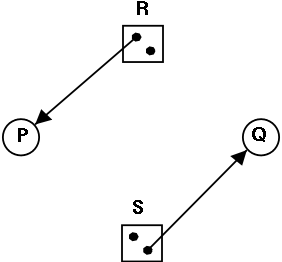Is the figure on the right safe or not?

• You can NOT tell until I give you the initial claims of the process.
  
  
• Please do not make the unfortunately common exam mistake to give an example involving safe states without giving the claims. So if I ask you to draw a resource allocation graph that is safe or if I ask you to draw one that is unsafe, you MUST include the initial claims for each process. I often, but not always, ask such a question and every time I have done so, several students forgot to give the claims and hence lost points.
  
  
• For the figure on the right, if the initial claims are:
  P: 1 unit of R and 2 units of S (written (1,2))
  Q: 2 units of R and 1 units of S (written (2,1))
  the state in the figure is NOT safe.
  
  
• But if the initial claims are instead:
  P: 2 units of R and 1 units of S (written (2,1))
  Q: 1 unit of R and 2 units of S (written (1,2))
  the state in the figure IS safe.
  
  
• Explain why this is so.

A manager can determine if a state is safe.

• Since the manager know all the claims, it can determine the maximum amount of additional resources each process can request.
• The manager knows how many units of each resource it has left.

The manager then follows the following procedure, which is part of Banker's Algorithms discovered by Dijkstra, to determine if the state is safe.

1. If there are no processes remaining, the state is safe.
   
   
2. Seek a process P whose maximum additional request for each resource type is less than what remains for that resource type.
   • If no such process can be found, then the state is not safe.
   • If such a P can be found, the banker (manager) knows that if it refuses all requests except those from P, then it will be able to satisfy all of P's requests. Why?
     Ans: Look at how P was chosen.
   
   
3. The banker now pretends that P has terminated (since the banker knows that it can guarantee this will happen). Hence the banker pretends that all of P's currently held resources are returned. This makes the banker richer and hence perhaps a process that was not eligible to be chosen as P previously, can now be chosen.
   
   
4. Repeat these steps.
   
   

Example 1

Consider the example shown in the table on the right.

A safe state with 22 units of one resource

process	initial claim	current alloc	max add'l
X	3	1	2
Y	11	5	6
Z	19	10	9
Total		16
Available		6

• One resource type R with 22 unit.
• Three processes X, Y, and Z with initial claims 3, 11, and 19 respectively.
• Currently the processes have 1, 5, and 10 units respectively.
• Hence the manager currently has 6 units left.
• Also note that the max additional needs for the processes are 2, 6, and 9 respectively.
• So the manager cannot assure (with its current remaining supply of 6 units) that Z can terminate. But that is not the question.
• This state is safe.
  1. Use 2 units to satisfy X; now the manager has 7 units.
  2. Use 6 units to satisfy Y; now the manager has 12 units.
  3. Use 9 units to satisfy Z; done!

Example 2

This example is a continuation of example 1 in which Z requested 2 units and the manager (foolishly?) granted the request.

An unsafe state with 22 units of one resource

process	initial claim	current alloc	max add'l
X	3	1	2
Y	11	5	6
Z	19	12	7
Total		18
Available		4

• Currently the processes have 1, 5, and 12 units respectively.
• The manager has 4 units.
• The max additional needs are 2, 6, and 7.
• This state is unsafe
  1. X is the only process whose maximum additional request can be satisfied at this point.
  2. So use 2 unit to satisfy X; now the manager has 5 units.
  3. Y needs 6 and Z needs 7 and we can't guarantee satisfying either request.
• Note that we were able to find a process (X) that can terminate, but then we were stuck. So it is not enough to find one process. We must find a sequence of all the processes.

Remark: An unsafe state is not necessarily a deadlocked state. Indeed, for many unsafe states, if the manager gets lucky all processes will terminate successfully. Processes that are not currently blocked can terminate (instead of requesting more resources up to their initial claim, which is the worst case and is the case the manager prepares for). A safe state means that the manager can guarantee that no deadlock will occur (even in the worst case in which processes request as much as permitted by their initial claims.)

6.5.3 The Banker's Algorithm (Dijkstra) for a Single Resource

The algorithm is simple: Stay in safe states. For now, we assume that, before execution begins, all processes are present and all initial claims have been given. We will relax these assumptions very soon.

In a little more detail the banker's algorithm is as follows.

• Before execution begins, ensure that the system is safe. That is, check that no process claims more than the manager has. If not, then the offending process is trying to claim more of some resource than exists in the system has and hence cannot be guaranteed to complete even if run by itself. You might say that it can become deadlocked all by itself. The only thing the manager can do is to refuse to acknowledge the existence of the offending process.
  
  
• When the manager receives a request, it pretends to grant it, and then checks if the resulting state is safe. If it is safe, the request is really granted; if it is not safe the process is blocked (that is, the request is held up).
  
  
• When a resource is returned, the manager (politely thanks the process and then) checks to see if the first pending requests can be granted (i.e., if the result would now be safe). If so the pending request is granted. Whether or not the request was granted, the manager checks to see if the next pending request can be granted, etc.

Homework: 16.

6.5.4 The Banker's Algorithm for Multiple Resources

At a high level the algorithm is identical to the one for a single resource type: Stay in safe states.

But what is a safe state in this new setting?

The same definition (if processes are run in a certain order they will all terminate).

Checking for safety is the same idea as above. The difference is that to tell if there are enough free resources for a processes to terminate, the manager must check that for all resource types, the number of free units is at least equal to the max additional need of the process.

Homework: Consider a system containing a total of 12 units of resource R and 24 units of resource S managed by the banker's algorithm. There are three processes P1, P2, and P3. P1's claim is 0 units of R and 12 units of S, written (0,12). P2's claim is (8,15). P3's claim is (8,20). Currently P1 has 4 units of S, P2 has 8 units of R, P3 has 8 units of S, and there are no outstanding requests.

1. What is the largest number of units of S that P1 can request at this point that the banker will grant?
2. If P2 instead of P1 makes the request, what is the largest number of units of S that the banker will grant?
3. If P3 instead of P1 or P2 makes the request, what is the largest number of units of S that the banker will grant?

Remark: Remind me to go over this one next time.

Limitations of the Banker's Algorithm

• Often users don't know the maximum requests a process will make. They can estimate conservatively (i.e., use big numbers for the claim) but then the manager becomes very conservative.
  
  
• New processes arriving cause a problem (but not so bad as Tanenbaum suggests).
  • The process's claim must be less than the total number of units of the resource in the system. If not, the process is not accepted by the manager.
  • Since the state without the new process is safe, so is the state with the new process! Just use the process order the banker had originally and put the new process at the end.
  • Insuring fairness (starvation freedom) needs a little more work, but isn't too hard either (once an hour stop taking new processes until all current processes finish).
  
  
• A resource can become unavailable (e.g., a CD-ROM drive might break). This can result in an unsafe state and deadlock.

Homework: 22, 25, and 30. There is an interesting typo in 22. A has claimed 3 units of resource 5, but there are only 2 units in the entire system. Change the problem by having B both claim and be allocated 1 unit of resource 5.