Operating Systems

Start Lecture #18

Remark: Here is a better explanation of the problematic exam question.

Multiprogramming with Variable Partitions

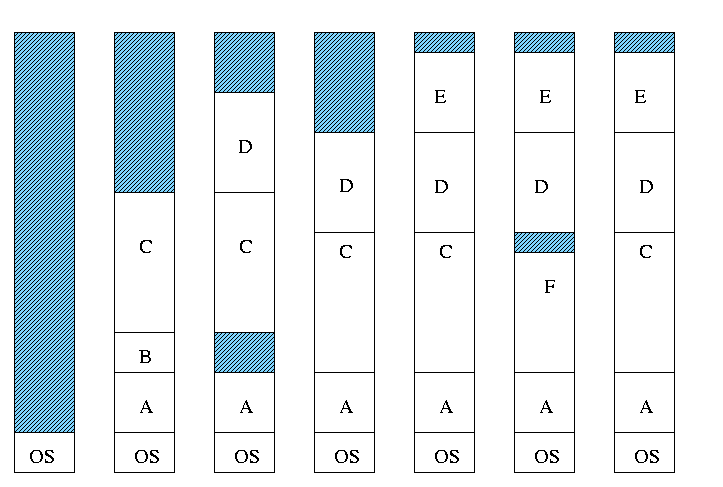
Both the number and size of the partitions change with time.

• OS/MVT (multiprogramming with a varying number of tasks).
  
  
• Also early PDP-10 OS.
  
  
• A process still has only one segment (as with MFT). That is, the virtual address space is contiguous.
  
  
• The physical address is also contiguous, that is, the process is stored as one piece in memory.
  
  
• The job can be of any size up to the size of the machine and the job size can change with time.
  
  
• A single ready list.
  
  
• A job can move (might be swapped back in a different place).
  
  
• This is dynamic address translation (during run time).
  
  
• Must perform an addition on every memory reference (i.e. on every address translation) to add the start address of the partition (the base register).
  
  
• Called a DAT (dynamic address translation) box by IBM.
  
  
• Eliminates Internal Fragmentation, which is defined to be unusable space within a process.
  • Find a region the exact right size.
  • Not quite true, can't get a piece with 108755 bytes. Would get say 108760. But internal fragmentation is much reduced compared to MFT. Indeed, we say that internal fragmentation has been eliminated.
  
  
• Introduces external fragmentation, i.e., holes outside any region of memory assigned to a process.
  
  
• What do you do if no hole is big enough for the request?
  • Can compactify
    • Transition from bar 3 to bar 4 in diagram below.
    • This is expensive.
    • Not suitable for real time (MIT ping pong).
  • Can swap out one process to bring in another, e.g., bars 5-6 and 6-7 in the diagram.
  
  
• There are never two more holes than processes. Why?
  • Because next to a process there might be a process or a hole but next to a hole there must be a process.
  • So can have runs of processes, but not of holes.
  • If after a process one is equally likely to have a process or a hole, you get about twice as many processes as holes.
  
  
• Base and limit registers are used.
  • Storage keys would not good since compactifying or moving would require changing many keys.
  • Storage keys might need a fine granularity to permit the boundaries to move by small amounts (to reduce internal fragmentation). Hence many keys would need to be changed.

Homework: A swapping system eliminates holes by compaction. Assume a random distribution of holes and data segments, assume the data segments are much bigger than the holes, and assume a time to read or write a 32-bit memory word of 10ns. About how long does it take to compact 128 MB? For simplicity, assume that word 0 is part of a hole and the highest word in memory conatains valid data.

3.2.3 Managing Free Memory

MVT Introduces the Placement Question

That is, which hole (partition) should one choose?

• There are various algorithms for choosing a hole including best fit, worst fit, first fit, circular first fit, quick fit, and Buddy.
  • Best fit doesn't waste big holes, but does leave slivers and is expensive to run.
  • Worst fit avoids slivers, but eliminates all big holes so a big job will require compaction. Even more expensive than best fit (best fit stops if it finds a perfect fit).
  • Quick fit keeps lists of some common sizes (but has other problems, see Tanenbaum).
  • Buddy system
    • Round request to next highest power of two (causes internal fragmentation).
    • Look in list of blocks this size (as with quick fit).
    • If list empty, go higher and split into buddies.
    • When returning coalesce with buddy.
    • Do splitting and coalescing recursively, i.e. keep coalescing until can't and keep splitting until successful.
    • See Tanenbaum (look in the index) or an algorithms book for more details.
  
  
• A current favorite is circular first fit, also known as next fit.
  • Use the first hole that is big enough (first fit) but start looking where you left off last time.
  • Doesn't waste time constantly trying to use small holes that have failed before, but does tend to use many of the big holes, which can be a problem.
  
  
• Buddy comes with its own implementation. How about the others?

Homework: Consider a swapping system in which memory consists of the following hole sizes in memory order: 10K, 4K, 20K, 18K 7K, 9K, 12K, and 15K. Which hole is taken for successive segment requests of

1. 12K
2. 10K
3. 9K

Memory Management with Bitmaps

Divide memory into blocks and associate a bit with each block, used to indicate if the corresponding block is free or allocated. To find a chunk of size N blocks need to find N consecutive bits indicating a free block.

The only design question is how much memory does one bit represent.

• Big: Serious internal fragmentation.
• Small: Many bits to store and process.

Memory Management with Linked Lists

Instead of a bit map, use a linked list of nodes where each node corresponds to a region of memory either allocated to a process or still available (a hole).

• Each item on list gives the length and starting location of the corresponding region of memory and says whether it is a hole or Process.
• The items on the list are not taken from the memory to be used by processes.
• The list is kept in order of starting address.
• Merge adjacent holes when freeing memory.
• Use either a singly or doubly linked list.

MVT also introduces the Replacement Question

That is, which victim should we swap out?

This is an example of the suspend arc mentioned in process scheduling.

We will study this question more when we discuss demand paging in which case we swap out only part of a process.

Considerations in choosing a victim

• Cannot replace a job that is pinned, i.e. whose memory is tied down. For example, if Direct Memory Access (DMA) I/O is scheduled for this process, the job is pinned until the DMA is complete.
• Victim selection is a medium term scheduling decision
  • A job that has been in a wait state for a long time is a good candidate.
  • Often choose as a victim a job that has been in memory for a long time.
• Another question is how long should it stay swapped out.
• For demand paging, where swaping out a page is not as drastic as swapping out a job, choosing the victim is an important memory management decision and we shall study several policies.

1. So far the schemes presented so far have had two properties:
   1. Each job is stored contiguously in memory. That is, the job is contiguous in physical addresses.
   2. Each job cannot use more memory than exists in the system. That is, the virtual addresses space cannot exceed the physical address space.
   
   
2. Tanenbaum now attacks the second item. I wish to do both and start with the first.
   
   
3. Tanenbaum (and most of the world) uses the term paging to mean what I call demand paging. This is unfortunate as it mixes together two concepts.
   1. Paging (dicing the address space) to solve the placement problem and essentially eliminate external fragmentation.
   2. Demand fetching, to permit the total memory requirements of all loaded jobs to exceed the size of physical memory.
   
   
4. Most of the world uses the term virtual memory as a synonym for demand paging. Again I consider this unfortunate.
   1. Demand paging is a fine term and is quite descriptive.
   2. Virtual memory should be used in contrast with physical memory to describe any virtual to physical address translation.

** (non-demand) Paging

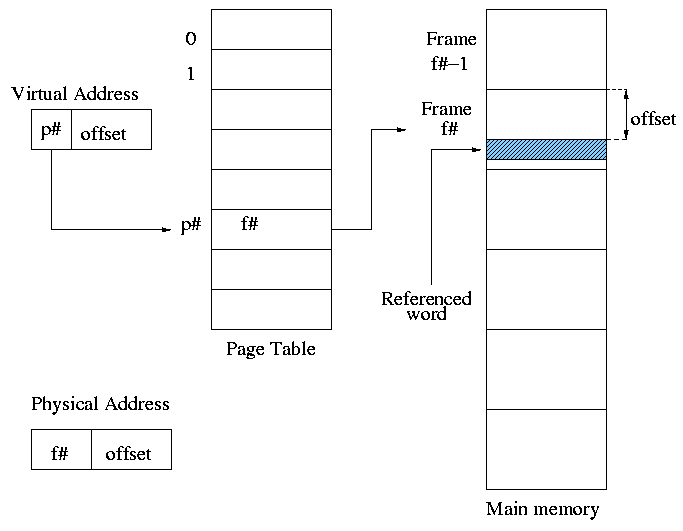
Simplest scheme to remove the requirement of contiguous physical memory.

• Chop the program into fixed size pieces called pages, which are invisible to the user. Tanenbaum sometimes calls pages virtual pages.
  
  
• Chop the real memory into fixed size pieces called page frames or simply frames.
  
  
• The size of a page (the page size) = size of a frame (the frame size).
  
  
• Sprinkle the pages into the frames.
  
  
• Keep a table (called the page table) having an entry for each page. The page table entry or PTE for page p contains the number of the frame f that contains page p.

Example: Assume a decimal machine with page size = frame size = 1000.
Assume PTE 3 contains 459.
Then virtual address 3372 corresponds to physical address 459372.

Properties of (non-demand) paging (without segmentation).

• The entire process must be memory resident to run.
• No holes, i.e., no external fragmentation.
• If there are 50 frames available and the page size is 4KB than any job requiring ≤ 200KB will fit, even if the available frames are scattered over memory.
• Hence (non-demand) paging is useful.
• Indeed, it was used (but no longer).
• Introduces internal fragmentation approximately equal to 1/2 the page size for every process (really every segment).
• Can have a job unable to run due to insufficient memory and have some (but not enough) memory available. This is not called external fragmentation since it is not due to memory being fragmented.
• Eliminates the placement question. All pages are equally good since don't have external fragmentation.
• The replacement question remains.
• Since page boundaries occur at random points and can change from run to run (the page size can change with no effect on the program—other than performance), pages are not appropriate units of memory to use for protection and sharing. But if all you have is a hammer, everything looks like a nail. Segmentation, which is discussed later, is sometimes more appropriate for protection and sharing.
• Virtual address space remains contiguous.

Address translation

• Each memory reference turns into 2 memory references
  1. Reference the page table
  2. Reference central memory
• This would be a disaster!
• Hence the MMU caches page#→frame# translations. This cache is kept near the processor and can be accessed rapidly.
• This cache is called a translation lookaside buffer (TLB) or translation buffer (TB).
• For the above example, after referencing virtual address 3372, there would be an entry in the TLB containing the mapping 3→459.
• Hence a subsequent access to virtual address 3881 would be translated to physical address 459881 without an extra memory reference. Naturally, a memory reference for location 459881 itself would be required.

Choice of page size is discuss below.

Homework: Using the page table of Fig. 3.9, give the physical address corresponding to each of the following virtual addresses.

1. 20
2. 4100
3. 8300