Operating Systems

Start Lecture #13

6.3 Ignoring the problem—The Ostrich Algorithm

The put your head in the sand approach.

• If the likelihood of a deadlock is sufficiently small and the cost of avoiding a deadlock is sufficiently high it might be better to ignore the problem. For example, if each PC deadlocks once per 10 years, the one reboot may be less painful that the restrictions needed to prevent it.
• Clearly not a good philosophy for nuclear missile launchers or patient monitoring systems for cardiac care units.
• For embedded systems (such as the two examples above) the programs run are fixed in advance so many of the issues that occur in systems like linux or windows (such as many processes wanting to fork at the same time) don't occur.

6.4 Detecting Deadlocks and Recovering From Them

6.4.1 Detecting Deadlocks with Single Unit Resources

Consider the case in which there is only one instance of each resource.

• Thus a request can be satisfied by only one specific resource.
• In this case the 4 necessary conditions for deadlock are also sufficient.
• Remember we are making an assumption (single unit resources) that is often invalid. For example, many systems have several printers and a request is given for a printer not a specific printer. Similarly, one can have many CD-ROM drives.
• So the problem comes down to finding a directed cycle in the resource allocation graph. Why?
  Answer: Because the other three conditions are either satisfied by the system we are studying, or are not in which case deadlock is not a question. That is, conditions 1,2,3 are static conditions on the system in general not conditions on the state of the system right now.

To find a directed cycle in a directed graph is not hard. The algorithm is in the book. The idea is simple.

1. For each node in the graph do a depth first traversal to see if the graph is a DAG (directed acyclic graph), building a list as you go down the DAG (and pruning it as you backtrack back up).
2. If you ever find the same node twice on your list, you have found a directed cycle, the graph is not a DAG, and deadlock exists among the processes in your current list.
3. If you never find the same node twice, the graph is a DAG and no deadlock exists (right now).

The searches are finite since there are a finite number of nodes.

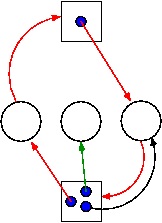
6.4.2 Detecting Deadlocks with Multiple Unit Resources

This is more difficult.

• The figure on the right shows a resource allocation graph with multiple unit resources.
  
  
• Each unit is represented by a dot in the box.
  
  
• Request edges are drawn to the box since they represent a request for any dot in the box.
  
  
• Allocation edges are drawn from the dot to represent that this unit of the resource has been assigned (but all units of a resource are equivalent and the choice of which one to assign is arbitrary).
  
  
• Note that there is a directed cycle in red, but there is no deadlock. Indeed the middle process might finish, erasing the green arc and permitting the blue dot to satisfy the rightmost process.
  
  
• The book gives an algorithm for detecting deadlocks in this more general setting. The idea is as follows.
  1. look for a process that might be able to terminate. That is, a process all of whose request arcs can be satisfied by resources the manager has on hand right now.
  2. If one is found, pretend that it does terminate (erase all its arcs), and repeat step 1.
  3. If any processes remain, they are deadlocked.
  
  
• We will soon do in detail an algorithm (the Banker's algorithm) that has some of this flavor.
  
  
• The algorithm just given makes the most optimistic assumption about a running process: it will return all its resources and terminate normally. If we still find processes that remain blocked, they are deadlocked.
  
  
• In the bankers algorithm we make the most pessimistic assumption about a running process: it immediately asks for all the resources it can (details later on can). If, even with such demanding processes, the resource manager can insure that all process terminates, then we can insure that deadlock is avoided.

6.4.3 Recovery from deadlock

Recovery through Preemption

Perhaps you can temporarily preempt a resource from a process. Not likely.

Recovery through Rollback

Database (and other) systems take periodic checkpoints. If the system does take checkpoints, one can roll back to a checkpoint whenever a deadlock is detected. You must somehow guarantee forward progress.

Recovery through Killing Processes

Can always be done but might be painful. For example some processes have had effects that can't be simply undone. Print, launch a missile, etc.

Remark: We are doing 6.6 before 6.5 since 6.6 is easier and I believe serves as a good warm-up.

6.6 Deadlock Prevention

Attack one of the Coffman/Havender conditions.

6.6.1 Attacking the Mutual Exclusion Condition

The idea is to use spooling instead of mutual exclusion. Not possible for many kinds of resources.

6.6.2 Attacking the Hold and Wait Condition

Require each processes to request all resources at the beginning of the run. This is often called One Shot.

6.6.3 Attacking the No Preemption Condition

Normally not possible. That is, some resources are inherently pre-emptable (e.g., memory). For those, deadlock is not an issue. Other resources are non-preemptable, such as a robot arm. It is often not possible to find a way to preempt one of these latter resources. One exception is if the resource (say a CD-ROM drive) can be virtualized (recall hypervisors).

6.6.4 Attacking the Circular Wait Condition

Establish a fixed ordering of the resources and require that they be requested in this order. So if a process holds resources #34 and #54, it can request only resources #55 and higher.

It is easy to see that a cycle is no longer possible.

Homework: Consider Figure 6-4. Suppose that in step (o) C requested S instead of requesting R. Would this lead to deadlock? Suppose that it requested both S and R.

6.5 Deadlock Avoidance

Let's see if we can tiptoe through the tulips and avoid deadlock states even though our system does permit all four of the necessary conditions for deadlock.

An optimistic resource manager is one that grants every request as soon as it can. To avoid deadlocks with all four conditions present, the manager must be smart not optimistic.

6.5.1 Resource Trajectories

We plot progress of each process along an axis. In the example we show, there are two processes, hence two axes, i.e., planar. This procedure assumes that we know the entire request and release pattern of the processes in advance so it is not a practical solution. I present it as it is some motivation for the practical solution that follows, the Banker's Algorithm.

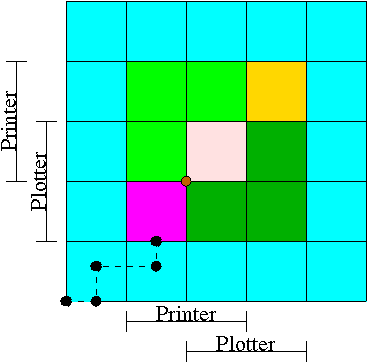
• We have two processes H (horizontal) and V.
• The origin represents them both starting.
• Their combined state is a point on the graph.
• The parts where the printer and plotter are needed by each process are indicated.
• The dark green is where both processes have the plotter and hence execution cannot reach this point.
• Light green represents both having the printer; also impossible.
• Pink is both having both printer and plotter; impossible.
• Gold is possible (H has plotter, V has printer), but the system can't get there.
• The upper right corner is the goal; both processes have finished.
• The brown dot is ... (cymbals) deadlock. We don't want to go there.
• The cyan is safe. From anywhere in the cyan we have horizontal and vertical moves to the finish point (the upper right corner) without hitting any impossible area.
• The magenta interior is very interesting. It is
  • Possible: each processor has a different resource.
  • Not deadlocked: each processor can move within the magenta.
  • Deadly: deadlock is unavoidable. You will hit a magenta-green boundary and then will no choice but to turn and go to the brown dot.
• The cyan-magenta border is the danger zone.
• The dashed line represents a possible execution pattern.
• With a uniprocessor no diagonals are possible. We either move to the right meaning H is executing or move up indicating V is executing.
• The trajectory shown represents.
  1. H excuting a little.
  2. V excuting a little.
  3. H executes; requests the printer; gets it; executes some more.
  4. V executes; requests the plotter.
• The crisis is at hand!
• If the resource manager gives V the plotter, the magenta has been entered and all is lost. Abandon all hope ye who enter here—Dante.
• The right thing to do is to deny the request, let H execute move horizontally under the magenta and dark green. At the end of the dark green, no danger remains, both processes will complete successfully. Victory!
• This procedure is not practical for a general purpose OS since it requires knowing the programs in advance. That is, the resource manager, knows in advance what requests each process will make and in what order.

Homework: All the trajectories in Figure 6-8 are horizontal or vertical. Is is possible for a trajectory to be a diagonal.

Homework: 11, 12.

6.5.2 Safe States

Avoiding deadlocks given some extra knowledge.

• Not surprisingly, the resource manager knows how many units of each resource it had to begin with.
  
  
• Also it knows how many units of each resource it has given to each process.
  
  
• It would be great to see all the programs in advance and thus know all future requests, but that is asking for too much.
  
  
• Instead, when each process starts, it announces its maximum usage. That is each process, before making any resource requests, tells the resource manager the maximum number of units of each resource the process can possible need. This is called the claim of the process.
  • If the claim is greater than the total number of units in the system the resource manager kills the process when receiving the claim (or returns an error code so that the process can make a new claim).
  • If during the run the process asks for more than its claim, the process is aborted (or an error code is returned and no resources are allocated).
  • If a process claims more than it needs, the result is that the resource manager will be more conservative than need be and there will be more waiting.

Definition: A state is safe if there is an ordering of the processes such that: if the processes are run in this order, they will all terminate (assuming none exceeds its claim and assuming each would terminate if all its requests are granted).

Recall the comparison made above between detecting deadlocks (with multi-unit resources) and the banker's algorithm (which stays in safe states).

• The deadlock detection algorithm given makes the most optimistic assumption about a running process: it will return all its resources and terminate normally. If we still find processes that remain blocked, they are deadlocked.
  
  
• The banker's algorithm makes the most pessimistic assumption about a running process: it immediately asks for all the resources it can (i.e., up to its initial claim). If, even with such demanding processes, the resource manager can assure that all process terminates, then we can ensure that deadlock is avoided.

In the definition of a safe state no assumption is made about the running processes. That is, for a state to be safe, termination must occur no matter what the processes do (providing each would terminate if run alone and each never exceeds its claims). Making no assumption on a process's behavior is the same as making the most pessimistic assumption.

Remark: When I say pessimistic I am speaking from the point of view of the resource manager. From the manager's viewpoint, the worst thing a process can do is request resources.

Give an example of each of the following four possibilities. A state that is

1. Safe and deadlocked—not possible.
   
   
2. Safe and not deadlocked—a trivial is example is a graph with no arcs.
   
   
3. Not safe and deadlocked—easy (any deadlocked state).
   
   
4. Not safe and not deadlocked—interesting.

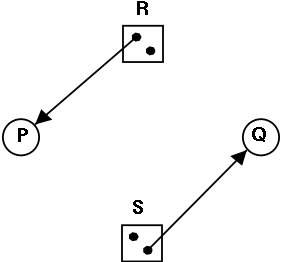Is the figure on the right safe or not?

• You can NOT tell until I give you the initial claims of the process.
  
  
• Please do not make the unfortunately common exam mistake to give an example involving safe states without giving the claims. So if I ask you to draw a resource allocation graph that is safe or if I ask you to draw one that is unsafe, you MUST include the initial claims for each process. I often, but not always, ask such a question and every time I have done so, several students forgot to give the claims and hence lost points.
  
  
• For the figure on the right, if the initial claims are:
  P: 1 unit of R and 2 units of S (written (1,2))
  Q: 2 units of R and 1 units of S (written (2,1))
  the state in the figure is NOT safe.
  
  
• But if the initial claims are instead:
  P: 2 units of R and 1 units of S (written (2,1))
  Q: 1 unit of R and 2 units of S (written (1,2))
  the state in the figure IS safe.
  
  
• Explain why this is so.