Operating Systems

Start Lecture #8

Remark: Midterm grades are based only on lab1, which is a very small part of the final grade.

3.4 Page Replacement Algorithms (PRAs)

These are solutions to the replacement question. Good solutions take advantage of locality when choosing the victim page to replace.

1. Temporal locality: If a word is referenced now, it is likely to be referenced in the near future.
   This argues for caching referenced words, i.e. keeping the referenced word near the processor for a while.
2. Spatial locality: If a word is referenced now, nearby words are likely to be referenced in the near future.
   This argues for prefetching words around the currently referenced word.
3. Temporal and spacial locality are lumped together into locality: If any word in a page is referenced, each word in the page is likely to be referenced. So it is good to bring in the entire page on a miss and to keep the page in memory for a while.

When programs begin there is no history so nothing to base locality on. At this point the paging system is said to be undergoing a cold start.

Programs exhibit phase changes in which the set of pages referenced changes abruptly (similar to a cold start). An example would occurs in your linker lab when you finish pass 1 and start pass 2. At the point of a phase change, many page faults occur because locality is poor.

Pages belonging to processes that have terminated are of course perfect choices for victims.

Pages belonging to processes that have been blocked for a long time are good choices as well.

Random PRA

A lower bound on performance. Any decent scheme should do better.

3.4.1 The Optimal Page Replacement Algorithm

Replace the page whose next reference will be furthest in the future.

• Also called Belady's min algorithm.
• Provably optimal. That is, no algorithm generates fewer page faults.
• Unimplementable: Requires predicting the future.
• Good upper bound on performance.

3.4.2 The Not Recently Used (NRU) PRA

Divide the frames into four classes and make a random selection from the lowest nonempty class.

0. Not referenced, not modified.
1. Not referenced, modified.
2. Referenced, not modified.
3. Referenced, modified.

Assumes that in each PTE there are two extra flags R (for referenced; sometimes called U, for used) and M (for modified, often called D, for dirty).

NRU is based on the belief that a page in a lower priority class is a better victim.

• If a page is not referenced, locality suggests that it probably will not referenced again soon and hence is a good candidate for eviction.
• If a clean page (i.e., one that is not modified) is chosen to evict, the OS does not have to write it back to disk and hence the cost of the eviction is lower than for a dirty page.

Implementation

• When a page is brought in, the OS resets R and M (i.e. R=M=0).
• On a read, the hardware sets R.
• On a write, the hardware sets R and M.

We again have the prisoner problem: We do a good job of making little ones out of big ones, but not as good a job on the reverse. We need more resets. Therefore, every k clock ticks, the OS resets all R bits.

Why not reset M as well?
Answer: If a dirty page has a clear M, we will not copy the page back to disk when it is evicted, and thus the only accurate version of the page will be lost!

I suppose one could have two M bits one accurate and one reset, but I don't know of any system (or proposal) that does so.

What if the hardware doesn't set these bits?
Answer: The OS can uses tricks.

We ignore the tricks and assume the hardware does set the bits.

3.4.3 FIFO PRA

Simple but poor since the usage of the page is ignored.

Belady's Anomaly: Can have more frames yet generate more faults. An example is given later.

The natural implementation is to have a queue of nodes each pointing to a resident page (i.e., pointing to a frame).

• When a page is loaded, a node referring to the page is appended to the tail of the queue.
• When a page needs to be evicted, the head node is removed and the page referenced is chosen as the victim.

3.4.4 Second chance PRA

Similar to the FIFO PRA, but altered so that a page recently referenced is given a second chance.

• When a page is loaded, a node referring to the page is appended to the tail of the queue. The R bit of the page is cleared.
• When a page needs to be evicted, the head node is removed and the page referenced is the potential victim.
• If the R bit is unset (the page hasn't been referenced recently), then the page is the victim.
• If the R bit is set, the page is given a second chance. Specifically, the R bit is cleared, the node referring to this page is appended to the rear of the queue (so it appears to have just been loaded), and the current head node becomes the potential victim.
• What if all the R bits are set?
• We will move each page from the front to the rear and will arrive at the initial condition but with all the R bits now clear. Hence we will remove the same page as fifo would have removed, but will have spent more time doing so.
• Might want to periodically clear all the R bits so that a long ago reference is forgotten (but so is a recent reference).

3.4.5 Clock PRA

Same algorithm as 2nd chance, but a better implementation for the nodes: Use a circular list with a single pointer serving as both head and tail.

Let us begin by assuming that the number of pages loaded is constant.

• So the size of the node list in 2nd chance is constant.
• Use a circular list for the nodes and have a pointer pointing to the head entry. Think of the list as the hours on a clock and the pointer as the hour hand. (Hence the name clock PRA.)
• Since the number of nodes is constant, the operation we need to support is replace the oldest, unreferenced page by a new page.
• Examine the node pointed to by the (hour) hand. If the R bit of the corresponding page is set, we give the page a second chance: clear the R bit, move the hour hand (now the page looks freshly loaded), and examine the next node.
• Eventually we will reach a node whose corresponding R bit is clear. The corresponding page is the victim.
• Replace the victim with the new page (may involve 2 I/Os as always).
• Update the node to refer to this new page.
• Move the hand forward another hour so that the new page is at the rear.

Thus, when the number of loaded pages (i.e., frames) is constant, the algorithm is just like 2nd chance except that only the one pointer (the clock hand) is updated.

How can the number of frames change for a fixed machine? Presumably we don't (un)plug DRAM chips while the system is running?

The number of frames can change when we use a so called local algorithm—discussed later—where the victim must come from the frames assigned to the faulting process. In this case we have a different frame list for each process. At times we want to change the number of frames assigned to a given process and hence the number of frames in a given frame list changes with time.

How does this affect 2nd chance?

• We now have to support inserting a node right before the hour hand (the rear of the queue) and removing the node pointed to by the hour hand.
• The natural solution is to double link the circular list.
• In this case insertion and deletion are a little slower than for the primitive 2nd chance (double linked lists have more pointer updates for insert and delete).
• So the trade-off is: If there are mostly inserts and deletes, and granting 2nd chances is not too common, use the original 2nd chance implementation. If there are mostly replacements, and you often give nodes a 2nd chance, use clock.

LIFO PRA

This is terrible! Why?
Ans: All but the last frame are frozen once loaded so you can replace only one frame. This is especially bad after a phase shift in the program as now the program is references mostly new pages but only one frame is available to hold them.

3.4.6 Least Recently Used (LRU) PRA

When a page fault occurs, choose as victim that page that has been unused for the longest time, i.e. the one that has been least recently used.

LRU is definitely

1. Implementable: The past is knowable.
2. Good: Simulation studies have shown this.
3. Difficult. Essentially the system needs to either:
   • Keep a time stamp in each PTE, updated on each reference and scan all the PTEs when choosing a victim to find the PTE with the oldest timestamp.
   • Keep the PTEs in a linked list in usage order, which means on each reference moving the corresponding PTE to the end of the list.

Homework: 28, 22.

A hardware cutsie in Tanenbaum

A clever hardware method to determine the LRU page.

• For n pages, keep an nxn bit matrix.
• On a reference to page i, set row i to all 1s and column i to all 0s.
• At any time the 1 bits in the rows are ordered by inclusion. I.e. one row's 1s are a subset of another row's 1s, which is a subset of a third. (Tanenbaum forgets to mention this.)
• So the row with the fewest 1s is a subset of all the others and is hence least recently used.
• This row also has the smallest value, when treated as an unsigned binary number. So the hardware can do a comparison of the rows rather than counting the number of 1 bits.
• Cute, but still impractical.

3.4.7 Simulating (Approximating) LRU in Software

The Not Frequently Used (NFU) PRA

Keep a count of how frequently each page is used and evict the one that has been the lowest score. Specifically:

• Include a counter (and reference bit R) in each PTE.
• Set the counter to zero when the page is brought into memory.
• Every k clocks, perform the following for each PTE.
  1. Add R to the counter.
  2. Clear R.
• Choose as victim the PTE with lowest count.

The Aging PRA

NFU doesn't distinguish between old references and recent ones. The following modification does distinguish.

• Include a counter (and reference bit, R) in each PTE.
• Set the counter to zero when the page is brought into memory.
• Every k clock ticks, perform the following for each PTE.
  1. Shift the counter right one bit.
  2. Insert R as the new high order bit of the counter.
  3. Clear R.
• Choose as victim the PTE with lowest count.

Aging does indeed give more weight to later references, but an n bit counter maintains data for only n time intervals; whereas NFU maintains data for at least 2ⁿ intervals.

Homework: 24, 33.

3.4.8 The Working Set Page Replacement Algorithm (Peter Denning)

The working set policy

The goals are first to specify which pages a given process needs to have memory resident in order for the process to run without too many page faults and second to ensure that these pages are indeed resident.

But this is impossible since it requires predicting the future. So we again make the assumption that the near future is well approximated by the immediate past.

We measure time in units of memory references, so t=1045 means the time when the 1045th memory reference is issued. In fact we measure time separately for each process, so t=1045 really means the time when this process made its 1045th memory reference.

Definition: w(k,t), the working set at time t (with window k) is the set of pages referenced by the last k memory references ending at reference t.

The idea of the working set policy is to ensure that each process keeps its working set in memory.

• Allocate |w(t,k)| frames to each process. This number differs for each process and changes with time.
• On a fault, evict a page not in the working set. But it is not easy to find such a page quickly. Indeed determining w(t,k) precisely is quite time consuming and difficult. It is never done in real systems.
• If a process is suspended and swapped out; the working set then can be used to say which pages should be brought back when the process is resumed.

Homework: Describe a process (i.e., a program) that runs for a long time (say hours) and always has a working set size less than 10. Assume k=100,000 and the page size is 4KB. The program need not be practical or useful.

Homework: Describe a process that runs for a long time and (except for the very beginning of execution) always has a working set size greater than 1000. Again assume k=100,000 and the page size is 4KB. The program need not be practical or useful.

The definition of Working Set is local to a process. That is, each process has a working set; there is no system wide working set other than the union of all the working sets of each process.

However, the working set of a single process has effects on the demand paging behavior and victim selection of other processes. If a process's working set is growing in size, i.e., w(t,k) is increasing as t increases, then we need to obtain new frames from other processes. A process with a working set decreasing in size is a source of free frames. We will see below that this is an interesting amalgam of local and global replacement policies.

Interesting questions concerning the working set include:

1. What value should be used for k?
   Experiments have been done and k is surprisingly robust (i.e., for a given system, a fixed value works reasonably for a wide variety of job mixes).
2. How should we calculate w(t,k)?
   Hard to do exactly so ...

... Various approximations to the working set, have been devised. We will study two: Using virtual time instead of memory references (immediately below), and Page Fault Frequency (part of section 3.5.1). In 3.4.9 we will see the popular WSClock algorithm that includes an approximation of the working set as well as several other ideas.

Using Virtual Time

Instead of counting memory referenced and declaring a page in the working set if it was used within k references, we keep track of time, which the system does anyway, and declare a page in the working set if it was used in the past τ seconds. Note that the time is measured only while this process is running, i.e., we are using virtual time.

1. Add a field time of last use to the PTE. The procedure for setting this field is in item 3 below.
2. Clear the reference R bit every m milliseconds and set it on every reference, the latter is done by the hardware.
3. To choose a victim when a page fault occurs, we proceed as follows (also setting the time of last use field). Scan the page table one PTE at a time (actually we are only interested in resident pages so we would rather look at the page frame table).
   • If the R bit is 1, the page is in the working set so set the time of last use to the current (virtual) time. (We are assuming τ seconds is bigger than m milliseconds.)
   • If the R bit is 0 and the last use was more than τ seconds ago, the page is not in the working set and is evicted (but we keep scanning).
   • If the R bit is 0 but the last use is less than τ seconds ago, the page is in the working set so is not evicted.
   • If no page was chosen for eviction, evict the LRU page.

3.4.9 The WSClock Page Replacement Algorithm

The WSClock algorithm combines aspects of the working set algorithm and the clock implementation of second chance.

Like clock we create a circular list of nodes with a hand pointing to the next node to examine. There is one such node for every resident page of this process; thus the nodes can be thought of as a list of frames or a kind of inverted page table.

Like working set we store in each node the referenced and modified bits R and M and the time of last use. R and M are cleared when the page is read in. R is set by the hardware on a reference and cleared periodically by the OS (perhaps at the end of each page fault or perhaps every m milliseconds). M is set by the hardware on a write. We indicate below the setting of the time of last use and the clearing of M.

We use virtual time and declare a page old if its last reference is more than τ seconds in the past. Other pages are declared young (i.e., in the working set).

As with clock, on every page fault a victim is found by scanning the list starting with the node indicated by the clock hand.

• If R=1, the page has been recently referenced. R is set to 0, the time of last use is set to now, and the hand advances.
• If R=0 and M=1, clear M, (schedule an I/O to) write the dirty page, and advance the hand.
• If R=M=0 and the page is young, advance the hand.
• If R=M=0 and the page is old, this is our victim; done.

It is possible to go all around the clock without finding a victim. In that case

• If writes were scheduled on old pages, one of these will become the victim once it becomes clean.
• If no writes were scheduled, we will never find a victim (since nothing will change) so pick a page at random (or perhaps the oldest of the young pages).
• If only young pages are scheduled for writing, no old victim will be chosen so we will need to again pick a page at random (if every page is dirty, we must wait for one to become clean).

An alternative treatment of WSClock, including more details of its interaction with the I/O subsystem, can be found here.

3.4.10 Summary of Page Replacement Algorithms

3.4.A Belady's Anomaly

Consider a system that has no pages loaded and that uses the FIFO PRU.
Consider the following reference string (sequences of pages referenced).

    0 1 2 3 0 1 4 0 1 2 3 4
  

If we have 3 frames this generates 9 page faults (do it).

If we have 4 frames this generates 10 page faults (do it).

Theory has been developed and certain PRA (so called stack algorithms) cannot suffer this anomaly for any reference string. FIFO is clearly not a stack algorithm. LRU is.

Repeat the above calculations for LRU.

3.5 Design Issues for (Demand) Paging Systems

3.5.1 Local vs Global Allocation Policies

A local PRA is one is which a victim page is chosen among the pages of the same process that requires a new frame. That is the number of frames for each process is fixed. So LRU for a local policy means the page least recently used by this process. A global policy is one in which the choice of victim is made among all pages of all processes.

• Of course we can't have a purely local policy, why?
  Answer: A new process has no pages and, even if we didn't restrict the frame needed to a local one for the first page loaded, the process would remain with only one page.
• Perhaps wait until a process has been running a while before restricting it to existing frames or give the process an initial allocation of frames based on the size of the executable.

In general a global policy seems to work better. For example, consider LRU. With a local policy, the local LRU page might have been more recently used than many resident pages of other processes. A global policy needs to be coupled with a good method to decide how many frames to give to each process. By the working set principle, each process should be given |w(k,t)| frames at time t, but this value is hard to calculate exactly.

If a process is given too few frames (i.e., well below |w(k,t)|), its faulting rate will rise dramatically. If this occurs for many or all the processes, the resulting situation in which the system is doing very little useful work due to the high I/O requirements for all the page faults is called thrashing.

An approximation to the working set policy that is useful for determining how many frames a process needs (but not which pages) is the Page Fault Frequency (PFF) algorithm.

• For each process keep track of the page fault frequency, which is the number of faults divided by the number of references.
• Actually, must use a window or a weighted calculation since you are interested in the recent page fault frequency.
• Actually, it is too expensive to calculate the number of references so, as above, we approximate this by the amount of (virtual) time.
• If the PFF is exceptionally low, free some of this processes frames (e.g., limit victim selection to this process for a while).
• If the PFF is too high, allocate more frames to this process. Either
  1. Raise its number of frames if using a local policy; or
  2. Bar its frames from eviction (for a while) and use a global policy.
• What if there are not enough frames in the entire system?
  Answer: Reduce the MPL as we now discuss.

3.5.2 Load Control

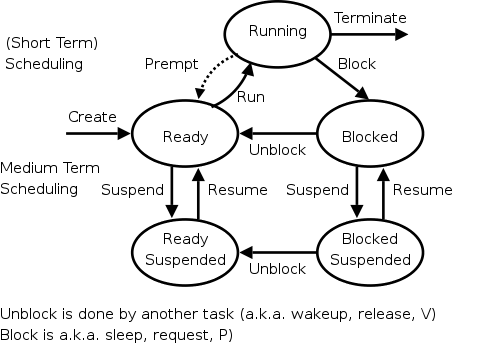
To reduce the overall memory pressure, we must reduce the multiprogramming level (or install more memory while the system is running, which is not possible with current technology). That is, we have a connection between memory management and process management. These are the suspend/resume arcs we saw way back when and are shown again in the diagram on the right.

When the PFF (or another indicator) is too high, we choose a process and suspend it, thereby swapping it to disk and releasing all its frames. When the frequency gets low, we can resume one or more suspended processes. We also need a policy to decide when a suspended process should be resumed even at the cost of suspending another.

This is called medium-term scheduling. Since suspending or resuming a process can take seconds, we clearly do not perform this scheduling decision every few milliseconds as we do for short-term scheduling. A time scale of minutes would be more appropriate.