Compilers

Start Lecture #8

Remark: Midterm grades are based on labs 1 and 2. Note that this is only ~25% of the final grade.

Chapter 5: Syntax-Directed Translation

Homework: Read Chapter 5.

Again we are redoing, more formally and completely, things we briefly discussed when breezing over chapter 2.

Recall that a syntax-directed definition (SDD) adds semantic rules to the productions of a grammar. For example to the production T → T / F we might add the rule

    T.code = T1.code || F.code || '/'
  

Rather than constantly copying ever larger strings to finally output at the root of the tree after a depth first traversal, we can perform the output incrementally by embedding semantic actions within the productions themselves. The above example becomes

    T → T1 / F { print '/' }
  

Since we are generating postfix, the action comes at the end (after we have generated the subtrees for T₁ and F, and hence performed their actions). In general the actions occur within the production, not necessarily after the last symbol.

For SDD's we conceptually need to have the entire tree available after the parse so that we can run the postorder traversal. (It is postorder since we have a simple S-attributed SDD; we will traverse the parse tree in other orders when the SDD is not S-attributed, and will see situations when no traversal order is possible.)

In some situations semantic actions can be performed during the parse, without saving the tree.

5.1: Syntax-Directed Definitions (SDDs)

Formally, attributes are values (of any type) that are associated with grammar symbols. Write X.a for the attribute a of symbol X. You can think of attributes as fields in a record/struct/object.

Semantic rules (rules for short) are associated with productions and give formulas to calculate attributes of non-terminals in the production.

5.1.1: Inherited and Synthesized Attributes

Terminals can have synthesized attributes (not yet officially defined); these are given to it by the lexer (not the parser). For example the token id might well have the attribute lexeme, where id.lexeme is the lexeme that the lexer converted into this instance of id. There are no rules in an SDD giving attribute values to terminals. Terminals do not have inherited attributes (to be defined shortly).

A nonterminal B can have both inherited and synthesized attributes. The difference is how they are computed. In either case the computation is specified by a rule associated with the production at a node N of the parse tree.

Definition: A synthesized attribute of a nonterminal B is defined at a node N where B is the LHS of the production associated with N. The attribute can depend on only (synthesized or inherited) attribute values at the children of N (the RHS of the production) and on inherited attribute values at N itself.

The arithmetic division example above was synthesized.

Production	Semantic Rules
L → E $	L.val = E.val
E → E1 + T	E.val = E1.val + T.val
E → E1 - T	E.val = E1.val - T.val
E → T	E.val = T.val
T → T1 * F	T.val = T1.val * F.val
T → T1 / F	T.val = T1.val / F.val
T → F	T.val = F.val
F → ( E )	F.val = E.val
F → num	F.val = num.lexval

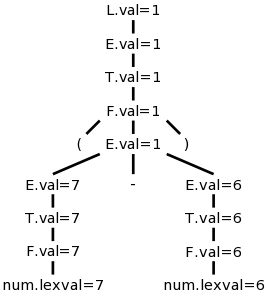
Example: The SDD at the right gives a left-recursive grammar for expressions with an extra nonterminal L added as the start symbol. The terminal num is given a value by the lexer, which corresponds to the value stored in the numbers table for lab 2.

Draw the parse tree for 7+6/3 on the board and verify that L.val is 9, the value of the expression.

This example uses only synthesized attributes.

Definition: An SDD with only synthesized attributes is called S-attributed.

For these SDDs all attributes depend only on attribute values at the children.
Why?
Answer: The other possibility (depending on values at the node itself) involves inherited attributes, which are absent in an S-attributed SDD.

Thus, for an S-attributed SDD, all the rules can be evaluated by a single bottom-up (i.e., postorder) traversal of the annotated parse tree.

Inherited attributes are more complicated since the node N of the parse tree with which the attribute is associated (and which is also the natural node to store the value) does not contain the production with the corresponding semantic rule.

Definition: An inherited attribute of a nonterminal B at node N, where B is the LHS of the production, is defined by a semantic rule of the production at the parent of N (where B occurs in the RHS of the production). The value depends only on attributes at N, N's siblings, and N's parent.

Note that when viewed from the parent node P (the site of the semantic rule), the inherited attribute depends on values at P and at P's children (the same as for synthesized attributes). However, and this is crucial, the nonterminal B is the LHS of a child of P and hence the attribute is naturally associated with that child. It is normally stored there and is shown there in the diagrams below.

We will soon see examples with inherited attributes.

Definition: Often the attributes are just evaluations without side effects. In such cases we call the SDD an attribute grammar.

5.1.2: Evaluating an SDD at the Nodes of a Parse Tree

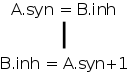
If we are given an SDD and a parse tree for a given sentence, we would like to evaluate the annotations at every node. Since, for synthesized annotations parents can depend on children, and for inherited annotations children can depend on parents, there is no guarantee that one can in fact find an order of evaluation. The simplest counterexample is the single production A→B with synthesized attribute A.syn, inherited attribute B.inh, and rules A.syn=B.inh and B.inh=A.syn+1. This means to evaluate A.syn at the parent node we need B.inh at the child and vice versa. Even worse it is very hard to tell, in general, if every sentence has a successful evaluation order.

All this not withstanding we will not have great difficulty because we will not be considering the general case.

Annotated Parse Trees

Recall that a parse tree has leaves that are terminals and internal nodes that are non-terminals.

Definition: A parse tree decorated with attributes, is called an annotated parse tree. It is constructed as follows.

Each internal node corresponds to a production. The node is labeled with the LHS of the production. If there are no attributes for the LHS in this production, we leave the node as it was (I don't believe this is a common occurrence). If there are k attributes for the LHS, we replace the LHS in the parse tree by k equations. The LHS of the equation is the attribute and the right hand side is its value.

Note that the annotated parse tree contains all the information of the original parse tree since we (either leave the node alone—if the LHS had no attributes or) replace the non-terminal A labeling the LHS with a series of equations A.attr=value.

We computed the values to put in this tree for 7+6/3 and on the right is (7-6).

Homework: 1

Why Have Inherited Attributes?

Inherited attributed definitely make the situation more complicated. For a simple example, recall the circular dependency above involving A.syn and B.inh. But we do need them.

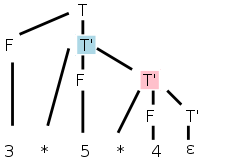
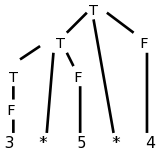
Consider the following left-recursive grammar for multiplication of numbers, and the parse tree on the right for 3*5*4.

    T → T * F
    T → F
    F → num
  

It is easy to see how the values can be propagated up the tree and the expression evaluated.

When doing top-down parsing, however, we need to avoid left recursion. Consider the grammar below, which is the result of removing the left recursion. Again its parse tree is shown on the right. Try not to look at the semantic rules for the moment.

Production	Semantic Rules	Type
T → F T'	T'.lval = F.val	Inherited
	T.val = T'.tval	Synthesized
T' → * F T1'	T'1.lval = T'.lval * F.val	Inherited
	T'.tval = T'1.tval	Synthesized
T' → ε	T'.tval = T'.lval	Synthesized
F → num	F.val = num.lexval	Synthesized

Where on the tree should we do the multiplication 3*5 since there is no node that has 3 and * and 5 as children?

The second production is the one with the *, so that is the natural candidate for the multiplication site. Make sure you see that this production (for the * in 3*5) is associated with the blue-highlighted node in the parse tree. The right operand (5) can be obtained from the F that is the middle child of this T'. F gets the value from its child, the number itself; this is an example of the simple synthesized case we have already seen, F.val=num.lexval (see the last semantic rule in the table).

But where is the left operand? It is located at the sibling of T' in the parse tree, i.e., at the F immediately to T's left (we shall see the significance that the sibling is to the left; it is not significant that it is immediately to the left). This F is not mentioned in the production associated with the T' node we are examining.
So, how does T' get F.val from its sibling?
Answer: The common parent, in this case T, can get the value from F and then our node can inherit the value from its parent.
Bingo! ... an inherited attribute. This can be accomplished by having the following two rules at the node T.
    T.tmp   = F.val (synthesized)
    T'.lval = T.tmp (inherited)

Since we have no other use for T.tmp, we combine the above two rules into the first rule in the table.

Now lets look at the second multiplication (3*5)*4, where the parent of T' is another T'. (This is the normal case. When there are n multiplies, n-1 have T' as parent and only one has T).

The pink-highlighted T' is the site for the multiplication. However, it needs as left operand, the product 3*5 that its parent can calculate. So we have the parent (another T' node, the blue one in this case) calculate the product and store it as an attribute of its right child namely the pink T'. That is the first rule for T' in the table.

We have now explained the first, third, and last semantic rules. These are enough to calculate the answer. Indeed, if we trace it through, 60 does get evaluated and stored in the bottom right T', the one associated with the ε-production. Our remaining goal is to get the value up to the root where it represents the evaluation of this term T and can be combined with other terms to get the value of a larger expression.

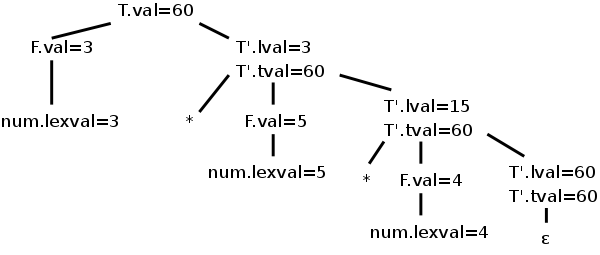
Going up is easy, just synthesize. I named the attribute tval, for term-value. It is generated at the ε-production from the lval attribute and propagated back up. At the T node it is called simply val. At the right we see the annotated parse tree for this input.

Homework: Extend this SDD to handle the left-recursive, more complete expression evaluator given earlier in this section. Don't forget to eliminate the left recursion first.

It clearly requires some care to write the annotations.

Another question is how does the system figure out the evaluation order, assuming one exists? That is the subject of the next section.

Remark: Consider the identifier table. The lexer creates it initially, but as the compiler performs semantic analysis and discovers more information about various identifiers, e.g., type and visibility information, the table is updated. One could think of this as some sort of inherited/synthesized attribute pair that during each phase of analysis is pushed down and back up the tree. However, it is not implemented this way; the table is made a global data structure that is simply updated. The compiler writer must ensure manually that the updates are performed in an order respecting any dependences.

5.2: Evaluation Orders for SDD's

5.2.1: Dependency Graphs

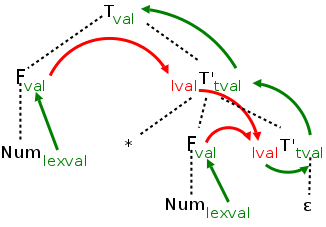
The diagram on the right illustrates a great deal. The black dotted lines comprise the parse tree for the multiplication grammar just studied when applied to a single multiplication, e.g. 3*5.

Each synthesized attribute is shown in green and is written to the right of the grammar symbol at the node where it is defined.

Each inherited attribute is shown in red and is written to the left of its grammar symbol where its value is assigned. Note that this value is defined by semantic rule at the parent of this node.

Each green arrow points to the synthesized attribute calculated from the attribute at the tail of the arrow. These arrows either go up the tree one level or stay at a node. That is because a synthesized attribute can depend only on the node where it is defined and that node's children. The computation of the attribute is associated with the production at the node at its arrowhead. In this example, each synthesized attribute depends on only one other attribute, but that is not required.

Each red arrow points to the inherited attribute calculated from the attribute at the tail. Note that, at the lower right T' node, two red arrows point to the same attribute. This indicates that the common attribute at the arrowheads, depends on both attributes at the tails. According to the rules for inherited attributes, these arrows either go down the tree one level, go from a node to a sibling, or stay within a node. The computation of the attribute is associated with the production at the parent of the node at the arrowhead.

5.2.2: Ordering the Evaluation of Attributes

The graph just drawn is called the dependency graph. In addition to being generally useful in recording the relations between attributes, it shows the evaluation order(s) that can be used. Since the attribute at the head of an arrow depends on the on the one at the tail, we must evaluate the head attribute after evaluating the tail attribute.

Thus what we need is to find an evaluation order respecting the arrows. This is called a topological sort. The rule is that the needed ordering can be found if and only if there are no (directed) cycles. The algorithm is simple.

1. Choose a node having no incoming edges
2. Delete the node and all outgoing edges.
3. Repeat

If the algorithm succeeds in deleting all the nodes, then the deletion order is a suitable evaluation order and there were no directed cycles.

The topological sort algorithm is non-deterministic (Choose a node) and hence there can be many topological sort orders.

Homework: 1.

5.2.3: S-Attributed Definitions

Given an SDD and a parse tree, performing a topological sort constructs a suitable evaluation order or announces that no such order exists.

However, it is very difficult to determine, given just an SDD, whether no parse trees have cycles in their dependency graphs. That is, it is very difficult to determine if there are suitable evaluation orders for all parse trees. Fortunately, there are classes of SDDs for which a suitable evaluation order is guaranteed, and which are adequate for our needs.

As mentioned above an SDD is S-attributed if every attribute is synthesized. For these SDDs all attributes are calculated from attribute values at the children since the other possibility, the tail attribute is at the same node, is impossible since the tail attribute must be inherited for such arrows. Thus no cycles are possible and the attributes can be evaluated by a postorder traversal of the parse tree.

5.2.4 L-Attributed Definitions

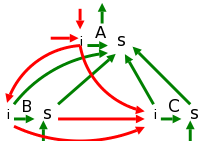
Unfortunately, it is hard to live without inherited attributes. For example, we need them for top-down parsing of expressions. Fortunately, our needs can be met by a class of SDDs called L-Attributed definitions for which we can easily find an evaluation order.

Case 2c must be handled specially whenever it occurs. We will try to avoid it.

The top picture to the right illustrates the other cases and suggests why there cannot be any cycles.

The picture immediately to the right corresponds to a fictitious R-attributed definition. One reason L-attributed definitions are favored over R, is the left to right ordering in English. See the example below on type declarations and also consider the grammars that result from eliminating left recursion.

We shall see that the key property of L-attributed SDDs is that they can be evaluated with two passes over the tree (an euler-tour order) in which we evaluate the inherited attributes as we go down the tree and the synthesized attributes as we go up. The restrictions L-attributed SDDs place on the inherited attributes are just enough to guarantee that when we go down we have all the values needed for the inherited attributes of the child.

Evaluating L-Attributed Definitions

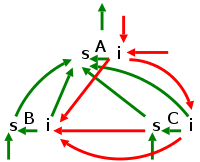
The table on the right shows a very simple grammar with fairly general, L-attributed semantic rules attached. Compare the dependencies with the general case shown in the (red-green) picture of L-attributed SDDs above.

The picture below the table shows the parse tree for the grammar in the table. The triangles below B and C represent the parse tree for X and Y. The dotted and numbered arrow in the picture illustrates the evaluation order for the attributes; it will be discussed shortly.

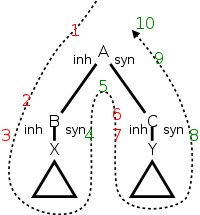
The rules for calculating A.syn, B.inh, and C.inh are shown in the table. The attribute A.inh would have been set by the parent of A in the tree; the semantic rule generating A.inh would be given with the production at the parent. The attributes X.syn and Y.syn are calculated at the children of B and C respectively. X.syn can depend of X.inh and on values in the triangle below X; similarly for Y.syn.

The picture to the right shows that there is an evaluation order for L-attributed definitions (again assuming no case 2c). We just need to follow the (Euler-tour) arrow and stop at all the numbered points. As in the pictures above, red signifies inherited attributes and green synthetic. Specifically, the evaluations at the numbered stops are

1. A is invoked (viewing the traversal as a program) and is passed its inherited attributes (A.inh in our case, but of course there could be several such attributes), which have been evaluated at its parent.
2. B is invoked by A and is given B.inh, which A has calculated. In programming terms: A executes
       call B(B.inh)
   where the argument has been evaluated by A. This argument can depend on A.inh since the parent of A has given A this value.
3. B calls its first child (in our example X is the only child) and passes to the child the child's inherited attributes. In programming terms: B executes
       call X(X.inh)
4. The child returns, passing back to B the synthesized attributes of the child. In programming terms: X executes
       return X.syn
   In reality there could be more synthesized attributes, there could be more children, the children could have children, etc.
5. B returns to A passing back B.syn, which can depend on B.inh (given to B by A in step 2) and X.syn (given to B by X in the previous step).
6. A calls C giving C its inherited attributes, which can depend on A.inh (given to A, by A's parent), B.inh (previously calculated by A in step 2), and B.syn (given to A by B in step 5).
7. C calls its first child, just as B did.
8. The child returns to C, just as B's child returned to B.
9. C returns to A passing back C.syn, just as B did.
10. A returns to its parent passing back A.syn, which can depend on A.inh (given to A by its parent in step 1), B.inh calculated by A in step 2, B.syn (given to A by B in step 5), C.inh (calculated by A in step 6), and C.syn (given to A by C in step 9).

More formally, do a depth first traversal of the tree and evaluate inherited attributes on the way down and synthetic attributes on the way up. This corresponds to a an Euler-tour traversal. It also corresponds to a call graph of a program where actions are taken at each call and each return

The first time you visit a node (on the way down), evaluate its inherited attributes (in programming terms, the parent evaluates the inherited attributes of the children and passes them as arguments to the call). The second time you visit a node (on the way back up), you evaluate the synthesized attributes (in programming terms the child returns the value to the parent).

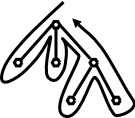
The key point is that all attributes needed will have already been evaluated. Consider the rightmost child of the root in the diagram on the right.

1. Inherited attributes (which are evaluated on the first, i.e., downward, pass): An inherited attribute depends only on inherited attributes from the parent and on (inherited or synthesized) attributes from left siblings.
   • The parent will have already been evaluated on the downward pass before the current child so the parent's inherited attributes will have already been evaluated.
   • The left children have already had both passes done so all their attributes will have been evaluated.
2. Synthesized attributes (which are evaluated on the second, i.e., upward pass): A synthesized attribute depends only on (inherited or synthesized) attributes of its children and on its own inherited attributes.
   • The children have already had both passes so all their attributes have been evaluated.
   • The node itself has already had its first (downward) pass so has had its inherited attributes evaluated.

Homework: 3(a-c).

5.2.5: Semantic Rules with Controlled Side Effects

When we have side effects such as printing or adding an entry to a table we must ensure that we have not added a constraint to the evaluation order that causes a cycle.

For example, the left-recursive SDD shown in the table on the right propagates type information from a declaration to entries in an identifier table.

The function addType adds the type information in the second argument to the identifier table entry specified in the first argument. Note that the side effect, adding the type info to the table, does not affect the evaluation order.

Draw the dependency graph on the board. Note that the terminal ID has an attribute called entry (given by the lexer) that gives its entry in the identifier table. The non-terminal L can be considered to have (in addition to L.type) a dummy synthesized attribute, say AddType, that is a place holder for the addType() routine. AddType depends on the arguments of addType(). Since the first argument is from a child, and the second is an inherited attribute of this node, we have legal dependences for a synthesized attribute.

Thus we have an L-attributed definition.

Homework: For the SDD above, give the annotated parse tree for

    INT a,b,c
  

5.3: Applications of Syntax-Directed Translations

5.3.1: Construction of Syntax Trees

Recall that a syntax tree (technically an abstract syntax tree) contains just the essential nodes. For example, 7+3*5 would have one + node, one *, and the three numbers. Lets see how to construct the syntax tree from an SDD.

Assume we have two functions Leaf(op,val) and Node(op,c1,...,cn), that create leaves and interior nodes respectively of the syntax tree. Leaf is called for terminals. Op is the label of the node (op for operation) and val is the lexical value of the token. Node is called for non-terminals and the ci's are pointers to the children.

Production	Semantic Rules	Type
E → T E'	E.node=E'.syn	Synthesized
	E'node=T.node	Inherited
E' → + T E'1	E'1.node=new Node('+',E'.node,T.node)	Inherited
	E'.syn=E'1.syn	Synthesized
E' → - T E'1	E'1.node=new Node('-',E'.node,T.node)	Inherited
	E'.syn=E'1.syn	Synthesized
E' → ε	E'.syn=E'.node	Synthesized
T → ( E )	T.node=E.node	Synthesized
T → ID	T.node=new Leaf(ID,ID.entry)	Synthesized
T → NUM	T.node=new Leaf(NUM,NUM.val)	Synthesized

The upper table on the right shows a left-recursive grammar that is S-attributed (so all attributes are synthesized).

Try this for x-2+y and see that we get the syntax tree.

When we eliminate the left recursion, we get the lower table on the right. It is a good illustration of dependencies. Follow it through and see that you get the same syntax tree as for the left-recursive version.

Remarks:

1. You probably did/are-doing/will-do some variant of new Node and new Leaf for lab 3. When processing a production
   1. Create a parse tree node for the LHS.
   2. Call subroutines for RHS symbols and connect the resulting nodes to the node created in i.
   3. Return a reference to the new node so the parent can hook it into the parse tree.
2. It is the lack of a call to new in the third and fourth productions (of the first, left recursive, grammar) that causes the (abstract) syntax tree to be produced rather than the parse (concrete syntax) tree.
3. Production compilers do not produce a parse trees; rather they produce syntax trees. The syntax tree is smaller, and hence more (space and time) efficient for subsequent passes that walk the tree. The parse tree is (I believe) slightly easier to construct as you don't have to decide which nodes to produce; you simply produce them all.
4. We could, but will not, have a lab 3.5 that takes in the parse tree generated by lab 3 and produces an abstract syntax tree using an SDD as illustrated by the table above.

5.3.2: The Structure of a Type

This course emphasizes top-down parsing (at least for the labs) and hence we must eliminate left recursion. The resulting grammars often need inherited attributes, since operations and operands are in different productions. But sometimes the language itself demands inherited attributes. Consider two ways to declare a 3x4, two-dimensional array. (Strictly speaking, these are one-dimensional arrays of one-dimensional arrays.)

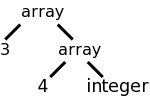
    array [3] of array [4] of int    and     int[3][4]
  

Assume that we want to produce a tree structure like the one the right for either of the array declarations on the left. The tree structure is generated by calling a function array(num,type). Our job is to create an SDD so that the function gets called with the correct arguments.

Production	Semantic Rule
A → ARRAY [ NUM ] OF A1	A.t=array(NUM.val,A1.t)
A → INT	A.t=integer
A → REAL	A.t=real

For the first language representation of arrays (found in Ada and in lab 3), it is easy to generate an S-attributed (non-left-recursive) grammar based on
A → ARRAY [ NUM ] OF A | INT | REAL
This is shown in the upper table on the right.

On the board draw the parse tree and see that simple synthesized attributes above suffice.

Production	Semantic Rules
T → B C	T.t=C.t
	C.b=B.t
B → INT	B.t=integer
B → REAL	B.t=real
C → [ NUM ] C1	C.t=array(NUM.val,C1.t)
	C1.b=C.b
C → ε	C.t=C.b

For the second language representation of arrays (the C-style), we need some smarts (and some inherited attributes) to move the int all the way to the right. Fortunately, the result, shown in the table on the right, is L-attributed and therefore all is well.

Note that, instead of a third column stating whether the attribute is synthesized or inherited, I have adopted the convention of drawing the inherited attribute definitions with a pink background.

Also note that this is not necessary. That is, one can look at a production and the associated semantic rule and determine if the attribute is inherited or synthesized.
How is this done?
Answer: If the attribute being defined (i.e., the one on the LHS of the semantic rule) is associated with the nonterminal on the LHS of the production, the attribute is synthesized. If the attribute being defined is associated with a nonterminal on the RHS of the production, the attribute is inherited.

Homework: 1.