Compilers

Start Lecture #1

Chapter 0: Administrivia

I start at Chapter 0 so that when we get to chapter 1, the numbering will agree with the text.

0.1: Contact Information

• <my-last-name> AT nyu DOT edu (best method)
• http://cs.nyu.edu/~gottlieb
• 715 Broadway, Room 712
• 212 998 3344

0.2: Course Web Page

There is a web site for the course. You can find it from my home page listed above.

• You can also find these lecture notes on the course home page. Please let me know if you can't find it.
• The notes are updated as bugs are found or improvements made.
• I will also produce a separate page for each lecture after the lecture is given. These individual pages might not get updated as quickly as the large page.

0.3: Textbook

The course text is Aho, Lam, Sethi, and Ullman: Compilers: Principles, Techniques, and Tools, second edition

• Available in bookstore.
• We will cover most of the first 8 chapters (plus some asides).
• The first edition is a descendant of the classic Principles of Compiler Design.
• Independent of the titles, each of the books is called The Dragon Book, due to the cover picture.

0.4: Computer Accounts and Mailman Mailing List

• You are entitled to a computer account on one of the departmental sun machines. If you do not have one already, please get it asap.
• Sign up for the Mailman mailing list for the course. You can do so by clicking here
• If you want to send mail just to me, use the address given above, not the mailing list.
• Questions on the labs should go to the mailing list. You may answer questions posed on the list as well. Note that replies are sent to the list.
• I will respond to all questions; if another student has answered the question before I get to it, I will confirm if the answer given is correct.
• Please use proper mailing list etiquette.
  • Send plain text messages rather than (or at least in addition to) html.
  • Use the Reply command to contribute to the current thread, but NOT to start another topic.
  • If quoting a previous message, trim off irrelevant parts.
  • Use a descriptive Subject: field when starting a new topic.
  • Do not use one message to ask two unrelated questions.
  • Do NOT make the mistake of sending your completed lab assignment to the mailing list. This is not a joke; several students have made this mistake in past semesters.

0.5: Grades

Your grade will be a function of your final exam and laboratory assignments (see below). I am not yet sure of the exact weightings for each lab and the final, but the final will be roughly half the grade (very likely between 40% and 60%).

0.6: The Upper Left Board

I use the upper left board for lab/homework assignments and announcements. I should never erase that board. If you see me start to erase an announcement, please let me know.

I try very hard to remember to write all announcements on the upper left board and I am normally successful. If, during class, you see that I have forgotten to record something, please let me know. HOWEVER, if I forgot and no one reminds me, the assignment has still been given.

0.7: Homeworks and Labs

I make a distinction between homeworks and labs.

Labs are

• Required.
• Due several lectures later (date given on assignment).
• Graded and form part of your final grade.
• Penalized for lateness.
• Most often are computer programs you must write.

Homeworks are

• Optional.
• Due the beginning of the Next lecture.
• Not accepted late.
• Mostly from the book.
• Collected and returned.
• Able to help, but not hurt, your grade.

0.7.1: Homework Numbering

Homeworks are numbered by the class in which they are assigned. So any homework given today is homework #1. Even if I do not give homework today, the homework assigned next class will be homework #2. Unless I explicitly state otherwise, all homeworks assignments can be found in the class notes. So the homework present in the notes for lecture #n is homework #n (even if I inadvertently forgot to write it to the upper left board).

0.7.2: Doing Labs on non-NYU Systems

You may solve lab assignments on any system you wish, but ...

• You are responsible for any non-nyu machine. I extend deadlines if the nyu machines are down, not if yours are.
• Be sure test your assignments to the nyu systems. In an ideal world, a program written in a high level language like Java, C, or C++ that works on your system would also work on the NYU system used by the grader. Sadly this ideal is not always achieved despite marketing claims to the contrary. So, although you may develop you lab on any system, you must ensure that it runs on the nyu system assigned to the course.
• If somehow your assignment is misplaced by me and/or a grader, we need a to have a copy ON AN NYU SYSTEM that can be used to verify the date the lab was completed.
• When you complete a lab and have it on an nyu system, email the lab to the grader and copy yourself on that message. This email must come from your CIMS account. Keep the copy until you have received your grade on the assignment. The systems support staff can retrieve your mail from their logs given your copy and from that we can verify the dates. I realize that I am being paranoid about this. It is rare for labs to get misplaced, but they sometimes do and I really don't want to be in the middle of an I sent it ... I never received it debate. Thank you.

0.7.3: Obtaining Help with the Labs

Good methods for obtaining help include

1. Asking me during office hours (see web page for my hours).
2. Asking the mailing list.
3. Asking another student, but ...
4. ... Your lab must be your own.
   That is, each student must submit a unique lab. Naturally, simply changing comments, variable names, etc. does not produce a unique lab. See the Academic Integrity Policy below.

0.7.4: Computer Language Used for Labs

You may write your lab in Java, C, or C++. Other languages may be possible, but please ask in advance. I need to ensure that the TA is comfortable with the language.

0.8: A Grade of Incomplete

The rules for incompletes and grade changes are set by the school and not the department or individual faculty member. The rules set by GSAS state:

The assignment of the grade Incomplete Pass(IP) or Incomplete Fail(IF) is at the discretion of the instructor. If an incomplete grade is not changed to a permanent grade by the instructor within one year of the beginning of the course, Incomplete Pass(IP) lapses to No Credit(N), and Incomplete Fail(IF) lapses to Failure(F).

Permanent grades may not be changed unless the original grade resulted from a clerical error.

0.9: An Introductory Compiler Course with a Programming Prerequisite

0.9.1: An Introductory Course ...

I do not assume you have had a compiler course as an undergraduate, and I do not assume you have had experience developing/maintaining a compiler.

If you have already had a compiler class, this course is probably not appropriate. For example, if you can explain the following concepts/terms, the course is probably too elementary for you.

• Parsing
• Lexical Analysis
• Syntax analysis
• Register allocation
• LALR Grammar

0.9.2: ... with a Programming Prerequisite

I do assume you are an experienced programmer. There will be non-trivial programming assignments during this course. Indeed, you will write a compiler for a simple programming language.

I also assume that you have at least a passing familiarity with assembler language. In particular, your compiler may need to produce assembler language, but probably it will produce an intermediate language consisting of 3-address code. We will also be using addressing modes found in typical assemblers. We will not, however, write significant assembly-language programs.

0.10: Academic Integrity Policy

The CS policy on academic integrity, which applies to all graduate courses in the department, can be found here . A recent email from Rosemary Amico may also be of interest

    Dear faculty,

    The vast majority of our students comply with the
    department's academic integrity policies; see

      www.cs.nyu.edu/web/Academic/Undergrad/academic_integrity.html
      www.cs.nyu.edu/web/Academic/Graduate/academic_integrity.html

    Unfortunately, every semester we discover incidents in
    which students copy programming assignments from those of
    other students, making minor modifications so that the
    submitted programs are extremely similar but not identical.

    To help in identifying inappropriate similarities, we
    suggest that you and your TAs consider using Moss, a
    system that automatically determines similarities between
    programs in several languages, including C, C++, and Java.
    For more information about Moss, see:

      http://theory.stanford.edu/~aiken/moss/

    Feel free to tell your students in advance that you will be
    using this software or any other system.  And please emphasize,
    preferably in class, the importance of academic integrity.

    Rosemary Amico
    Assistant Director, Computer Science
  

An Interlude from Chapter 2

I present this snippet from chapter 2 here (it appears where it belongs as well), since it is self-contained and is needed for lab number 1, which I wish to assign today.

2.3.4: (depth-first) Tree Traversals

When performing a depth-first tree traversal, it is clear in what order the leaves are to be visited, namely left to right. In contrast there are several choices as to when to visit an interior (i.e. non-leaf) node. The traversal can visit an interior node

1. Before visiting any of its children.
2. Between visiting its children.
3. After visiting all of its children.

I do not like the book's pseudocode as I feel the names chosen confuse the traversal with visiting the nodes. I prefer the pseudocode below, which uses the following conventions.

• Comments are introduced by -- and terminate at the end of the line (as in the programming language Ada).
  
  
• Indenting is significant so begin/end or {} are not used (from the programming language family B2/ABC/Python)

    traverse (n : treeNode)
        if leaf(n)                      -- visit leaves once; base of recursion
           visit(n)
        else                            -- interior node, at least 1 child
           -- visit(n)                  -- visit node PRE visiting any children
           traverse(first child)        -- recursive call
           while (more children remain) -- excluding first child
               -- visit(n)              -- visit node IN-between visiting children
               traverse (next child)    -- recursive call
           -- visit(n)                  -- visit node POST visiting all children
  

Note the following properties

1. As written, with the last three visit()s commented out, only the leaves are visited and those visits are in left to right order.
   
   
2. If you uncomment just the first (interior node) visit, you get a preorder traversal, in which each node is visited before (i.e., pre) visiting any of its children.
   
   
3. If you uncomment just the last visit, you get a postorder traversal, in which each node is visited after (i.e., post) visiting all of its children.
   
   
4. If you uncomment only the middle visit, you get an inorder traversal, in which the node is visited (in-) between visiting its children.
   
   Inorder traversals are normally defined only for binary trees, i.e., trees in which every interior node has exactly two children. Although the code with only the middle visit uncommented works for any tree, we will, like everyone else, reserve the name inorder traversal for binary trees. In the case of binary search trees (everything in the left subtree is smaller than the root of that subtree, which in tern is smaller than everything in the corresponding right subtree) an inorder traversal visits the values of the nodes in (numerical) order.
   
   
5. If you uncomment two of the three visits, you get a traversal without a name.
   
   
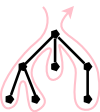6. If you uncomment all of the three visits, you get an Euler-tour traversal.
   
   To explain the name Euler-tour traversal, recall that an Eulerian tour on a directed graph is one that traverses each edge once. If we view the tree on the right as undirected and replace each edge with two arcs, one in each direction, we see that the pink curve is indeed an Eulerian tour. It is easy to see that the curve visits the nodes in the order of the pseudocode (with all visits uncommented).
   
   Normally, the Euler-tour traversal is defined only for a binary tree, but this time I will differ from convention and use the pseudocode above to define Euler-tour traversal for all trees.
   
   Note the following points about our Euler-tour traversal.
   • A node with k children is visited k+1 times. The diagram shows nodes with 0, 1, 2, and 3 children.
   • In a binary tree, a leaf is visited once and an interior node is visited three times. This is one of the standard definitions of an Euler-tour traversal for a binary tree.
   • The other standard definition has all nodes visited 3 times. For a leaf the three visits are in succession. Modifying the pseudocode to obtain this definition simply requires replacing the leaf visit with
         visit(n); visit(n); visit(n)

Do the Euler-tour traversal for the tree in the notes and then for a binary tree.

Lab 1 assigned. See the home page.

Roadmap of the Course

1. Chapter 1 touches on all the material.
   
   
2. Chapter 2 constructs (the front end of) a simple compiler.
   
   
3. Chapters 3-8 fill in the (considerable) gaps, as well as the presenting the beginnings of the compiler back end.
   
   

I always spend too much time on introductory chapters, but will try not to. I have said this before.

Chapter 1: Introduction to Compiling

Homework Read chapter 1.

1.1: Language Processors

A Compiler is a translator from one language, the input or source language, to another language, the output or target language.

Often, but not always, the target language is an assembler language or the machine language for a computer processor.

Note that using a compiler requires a two step process to run a program.

1. Execute the compiler (and possibly an assembler) to translate the source program into a machine language program.
2. Execute the resulting machine language program, supplying appropriate input.

This should be compared with an interpreter, which accepts the source language program and the appropriate input, and itself produces the program output.

Sometimes both compilation and interpretation are used. For example, consider typical Java implementations. The (Java) source code is translated (i.e., compiled) into bytecodes, the machine language for an idealized virtual machine, the Java Virtual Machine or JVM. Then an interpreter of the JVM (itself normally called a JVM) accepts the bytecodes and the appropriate input, and produces the output. This technique was quite popular in academia, with the Pascal programming language and P-code.

Homework: 1, 2, 4

Remark: Unless otherwise stated, homeworks are from the book and specifically from the end of the second level section we are discussing. Even more specifically, we are in section 1.1, so you are to do the first, second, and fourth problem at the end of section 1.1. These three problems are numbered 1.1.1, 1.1.2, and 1.1.4 in the book.

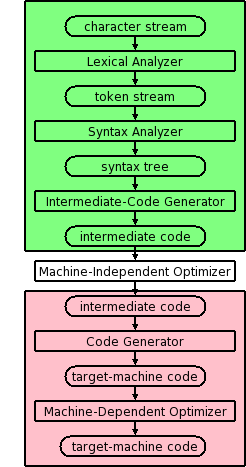
1.2: The Structure of a Compiler

Modern compilers contain two (large) parts, each of which is often subdivided. These two parts are the front end, shown in green on the right and the back end, shown in pink.

The front end analyzes the source program, determines its constituent parts, and constructs an intermediate representation of the program. Typically the front end is independent of the target language.

The back end synthesizes the target program from the intermediate representation produced by the front end. Typically the back end is independent of the source language.

This front/back division very much reduces the work for a compiling system that can handle several (N) source languages and several (M) target languages. Instead of NM compilers, we need N front ends and M back ends. For gcc (originally abbreviating Gnu C Compiler, but now abbreviating Gnu Compiler Collection), N=7 and M~30 so the savings are considerable.

Multiple Phases

The front and back end are themselves each divided into multiple phases. Conceptually, the input to each phase is the output of the previous. Sometime a phase changes the representation of the input. For example, the lexical analyzer converts a character stream input into a token stream output. Sometimes the representation is unchanged. For example, the machine-dependent optimizer transforms target-machine code into (hopefully improved) target-machine code.

The diagram is definitely not drawn to scale, in terms of effort or lines of code. In practice, the optimizers dominate.

Conceptually, there are three phases of analysis with the output of one phase the input of the next. Each of these phases changes the representation of the program being compiled. The phases are called lexical analysis or scanning, which transforms the program from a string of characters to a string of tokens; syntax analysis or parsing, which transforms the program into some kind of syntax tree; and semantic analysis, which decorates the tree with semantic information.

Note that the above classification is conceptual; in practice more efficient representations may be used. For example, instead of having all the information about the program in the tree, tree nodes may point to symbol table entries. Thus the information about the variable counter is stored once and pointed to at each occurrence.

1.2.1: Lexical Analysis (or Scanning)

The character stream input is grouped into meaningful units called lexemes, which are then mapped into tokens, the latter constituting the output of the lexical analyzer. For example, any one of the following C statements

    x3 = y + 3;
    x3  =   y   +   3   ;
    x3   =y+ 3  ;
  

    x 3 = y + 3;
  

A token is a <token-name,attribute-value> pair. For example

1. The lexeme x3 would be mapped to a token such as <id,1>. The name id is short for identifier. The value 1 is the index of the entry for x3 in the symbol table produced by the compiler. This table is used gather information about the identifiers and to pass this information to subsequent phases.
2. The lexeme = would be mapped to the token <=>. In reality it is probably mapped to a pair, whose second component is ignored. The point is that there are many different identifiers so we need the second component, but there is only one assignment symbol =.
3. The lexeme y is mapped to the token <id,2>
4. The lexeme + is mapped to the token <+>.
5. The lexeme 3 is somewhat interesting and is discussed further in subsequent chapters. It is mapped to <number,something>, but what is the something. On the one hand there is only one 3 so we could just use the token <number,3>. However, there can be a difference between how this should be printed (e.g., in an error message produced by subsequent phases) and how it should be stored (fixed vs. float vs. double). Perhaps the token should point to the symbol table where an entry for this kind of 3 is stored. Another possibility is to have a separate numbers table.
6. The lexeme ; is mapped to the token <;>.

Note that non-significant blanks are normally removed during scanning. In C, most blanks are non-significant. That does not mean the blanks are unnecessary. Consider

    int x;
    intx;
  

Note that we can define identifiers, numbers, and the various symbols and punctuation without using recursion (compare with parsing below).

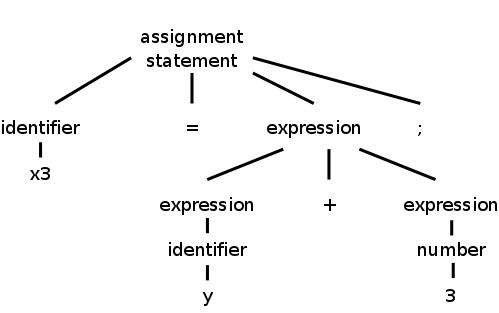
1.2.2: Syntax Analysis (or Parsing)

Parsing involves a further grouping in which tokens are grouped into grammatical phrases, which are often represented in a parse tree. For example

    x3 = y + 3;
  

This parsing would result from a grammar containing rules such as

    asst-stmt → id = expr ;
    expr      → number
              |  id
              |  expr + expr
  

Note the recursive definition of expression (expr). Note also the hierarchical decomposition in the figure on the right.

The division between scanning and parsing is somewhat arbitrary, in that some tasks can be accomplished by either. However, if a recursive definition is involved, it is considered parsing not scanning.

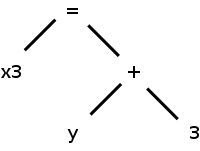
Often one uses a simpler tree called the syntax tree (more properly the abstract syntax tree) with operators as interior nodes and operands as the children of the operator. The syntax tree on the right corresponds to the parse tree above it. We expand on this point later.

1.2.3: Semantic Analysis

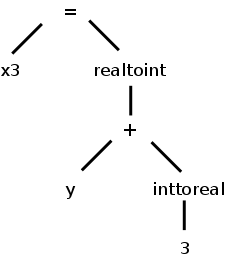
There is more to a front end than simply syntax. The compiler needs semantic information, e.g., the types (integer, real, pointer to array of integers, etc) of the objects involved. This enables checking for semantic errors and inserting type conversion where necessary.

For example, if y was declared to be a real and x3 an integer, we need to insert (unary, i.e., one operand) conversion operators inttoreal and realtoint as shown on the right.

In this class we will use three-address-code for our intermediate language; another possibility that is used is some kind of syntax tree.

1.2.4: Intermediate code generation

Many compilers internally generate intermediate code for an idealized machine. For example, the intermediate code generated would assume that the target has an unlimited number of registers and that any register can be used for any operation. This is similar to a machine model with no registers, but which permits operations to be directly performed on memory locations. Another common assumption is that machine operations take (up to) three operands: two source and one target.

With these assumptions of a machine with an unlimited number of registers and instructions with three operands, one generates three-address code by walking the semantic tree. Our example C instruction would produce

    temp1 = inttoreal(3)
    temp2 = y + temp1
    temp3 = realtoint(temp2)
    x3 = temp3
  

We see that three-address code can include instructions with fewer than 3 operands.

Sometimes three-address code is called quadruples because one can view the previous code sequence as

    inttoreal temp1 3     --
    add       temp2 y     temp1
    realtoint temp3 temp2 --
    assign    x3    temp3 --
  

    operation  target source1 source2
  

1.2.5: Code optimization

This is a very serious subject, one that we will not really do justice to in this introductory course. Some optimizations, however, are fairly easy to understand.

1. Since 3 is a constant, the compiler can perform the int to real conversion and replace the first two quads with

   	add       temp2 y    3.0
         

2. The last two quads can be combined into

   	realtoint x3    temp2
         

In addition to optimizations performed on the intermediate code, further optimizations can be performed on the machine code by the machine-dependent back end.

1.2.6: Code generation

Modern processors have only a limited number of register. Although some processors, such as the x86, can perform operations directly on memory locations, we will for now assume only register operations. Some processors (e.g., the MIPS architecture) use three-address instructions. We follow this model. Other processors permit only two addresses; the result overwrites one of the sources. Using three-address instructions restricted to registers (except for load and store instructions, which naturally must also reference memory), code something like the following would be produced for our example, after first assigning memory locations to x3 and y.

    LD   R1,  y
    LD   R2,  #3.0        // Some would allow constant in ADD
    ADDF R1,  R1, R2      // add float
    RTOI R2,  R1          // real to int
    ST   x3,  R2
  

1.2.7: Symbol-Table Management

The symbol table stores information about program variables that will be used across phases. Typically, this includes type information and storage locations.

A possible point of confusion: the storage location does not give the location where the compiler has stored the variable. Instead, it gives the location where the compiled program will store the variable.

1.2.8: The Grouping of Phases into Passes

Logically each phase is viewed as a separate pass, i.e., a program that reads input and produces output for the next phase. The phases thus form a pipeline. In practice some phases are combined into a pass.

For example one could have the entire front end as one pass.

The term pass is used to indicate that the entire input is read during this activity. So two passes, means that the input is read twice. A grayed out (optional) portion of the notes above discusses 2-pass approaches for both assemblers and linkers. If we implement each phase separately and possibly use multiple passes for some of them, the compiler will perform a large number of I/O operations, an expensive undertaking.

As a result, techniques have been developed to reduce the number of passes. We will see in the next chapter how to combine the scanner, parser, and semantic analyzer into one program or phase. Consider the parser. When it needs to input the next token, rather than reading the input file (presumably produced by the scanner), the parser calls the scanner instead. At selected points during the production of the syntax tree, the parser calls the intermediate-code generator which performs semantic analysis as well as generating a portion of the intermediate code.

For pedagogical reasons, we will not be employing this technique. That is to ease the programming and understanding, we will use a compiler design that performs more I/O than necessary. Naturally, production compilers do not do this. Thus your compiler will consist of separate programs for the scanner, parser, and semantic analyzer / intermediate code generator. Indeed, these will likely be labs 2, 3, and 4.

1.2.9: Compiler-construction tools

Originally, compilers were written from scratch, but now the situation is quite different. A number of tools are available to ease the burden.

We will mention tools that generate scanners and parsers. This will involve us in some theory: regular expressions for scanners and context-free grammars for parsers. These techniques are fairly successful. One drawback can be that they do not execute as fast as hand-crafted scanners and parsers.

We will also see tools for syntax-directed translation and automatic code generation. The automation in these cases is not as complete.

Finally, there is the large area of optimization. This is not automated; however, a basic component of optimization is data-flow analysis (how values are transmitted between parts of a program) and there are tools to help with this task.

Pedagogically, a problem with using the tools is that your effort shifts from understanding how a compiler works to how the tool is used. So instead of studying regular expressions and finite state automata, you study the flex man pages and user's guide.

1.6: Programming Language Basics

Skipped. This is covered in our Programming Languages course, which is a prerequisite for the Compilers course.

Remark: You should be able to do the exercises in this section (but they are not assigned).

Chapter 2: A Simple Syntax-Directed Translator

Homework: Read chapter 2.

The goal of this chapter is to implement a very simple compiler. Really we are just going as far as the intermediate code, i.e., the front end. Nonetheless, the output, i.e. the intermediate code, does look somewhat like assembly language.

How is it possible to do this in just one chapter?
What is the rest of the book/course about?

In this chapter there is

1. A simple source language.
2. A target close to the source.
3. No optimization.
4. No machine-dependent back end.
5. No tools.
6. Little theory.

The material will be presented too fast for full understanding: Starting in chapter 3, we slow down and explain everything.

Sometimes in chapter 2, we only show some of the possibilities (typically omitting the hard cases) and don't even mention the omissions. Again, this is corrected in the remainder of the course.

A weakness of my teaching style is that I spend too long on chapters like this. I will try not to make that mistake this semester, but I have said that before.

2.1: Introduction

We will be looking at the front end, i.e., the analysis portion of a compiler.

The syntax describes the form of a program in a given language, while the semantics describes the meaning of that program. We will learn the standard representation for the syntax, namely context-free grammars also called BNF (Backus-Naur Form).

We will learn syntax-directed translation, where the grammar does more than specify the syntax. We augment the grammar with attributes and use this to guide the entire front end.

The front end discussed in this chapter has as source language infix expressions consisting of digits, +, and -. The target language is postfix expressions with the same components.

For example, the compiler will convert 7+4-5 to 74+5-. Actually, our simple compiler will handle a few other operators as well.

We will tokenize the input (i.e., write a scanner), model the syntax of the source, and let this syntax direct the translation all the way to three-address code, our intermediate language.

2.2: Syntax Definition

2.2.1: Definition of Grammars

This will be done right in the next two chapters.

A context-free grammar (CFG) consists of

1. A set of terminals (tokens produced by the lexer).
2. A set of nonterminals.
3. A set of productions (rules for transforming nonterminals). These are written
       LHS → RHS
   where the LHS is a single nonterminal (that is why this grammar is context-free) and the RHS is a string containing nonterminals and/or terminals.
4. A specific nonterminal designated as start symbol.

Example:

    Terminals: 0 1 2 3 4 5 6 7 8 9 + -
    Nonterminals: list digit
    Productions:
        list → list + digit
        list → list - digit
        list → digit
        digit → 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
    Start symbol: list
  

We use | to indicate that a nonterminal has multiple possible right hand side. So

    A → B | C
  

    A → B
    A → C
  

If no start symbol is specifically designated, the LHS of the first production is the start symbol.

2.2.2: Derivations

Watch how we can generate the string 7+4-5 beginning with the start symbol, applying productions, and stopping when no productions can be applied (because only terminals remain).

    list → list - digit
         → list - 5
         → list + digit - 5
         → list + 4 - 5
         → digit + 4 - 5
         → 7 + 4 - 5
  

This process of applying productions, starting with the start symbol and ending when only terminals are present is called a derivation and we say that the final string has been derived from the initial string (in this case the start symbol).

The set of all strings derivable from the start symbol is the language generated by the CFG

• It is important that you see that this context-free grammar generates precisely the set of infix expressions with single digits as operands (so 25 is not allowed) and + and - as operators.
• The way you get different final expressions is that you make different choices of which production to apply. There are 3 productions you can apply to list and 10 you can apply to digit.
• The result cannot have blanks since blank is not a terminal.
• The empty string is not possible since, starting from list, we cannot get to the empty string. If we wanted to include the empty string, we would add the production
  list → ε
• The idea is that the input language to the compiler is approximately the language generated by the grammar. It is approximate since I have ignored the scanner.

Given a grammar, parsing a string (of terminals) consists of determining if the string is in the language generated by the grammar. If it is in the language, parsing produces a derivation. If it is not, parsing reports an error.

The opposite of derivation is reduction. Given a production, the LHS produces or derives the RHS (a derivation) and the RHS is reduced to the LHS (a reduction).

Ignoring errors for the moment, parsing a string means reducing the string to the start symbol or equivalently deriving the string from the start symbol.

Homework: 1a, 1c, 2a-c (don't worry about justifying your answers).

Remark: Since we are in section 2.2 these questions are in section 2.2.7, the last subsection of section 2.2.

2.2.3: Parse trees

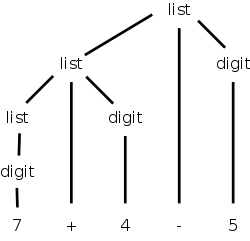
While deriving 7+4-5, one could produce the Parse Tree shown on the right.

You can read off the productions from the tree. For any internal (i.e., non-leaf) tree node, its children give the right hand side (RHS) of a production having the node itself as the LHS.

The leaves of the tree, read from left to right, is called the yield of the tree. We say that this string is derived from the (nonterminal at the) root, or is generated by the root, or can be reduced to the root. The tree on the right shows that 7+4-5 can be derived from list.

Homework: 1b

2.2.4: Ambiguity

An ambiguous grammar is one in which there are two or more parse trees yielding the same final string. We wish to avoid such grammars.

The grammar above is not ambiguous. For example 1+2+3 can be parsed only one way; the arithmetic must be done left to right. Note that I am not giving a rule of arithmetic, just of this grammar. If you reduced 2+3 to list you would be stuck since it is impossible to further reduce 1+list (said another way it is not possible to derive 1+list from the start symbol).

Remark:
The following is a wrong proof of ambiguity. Consider the grammar
S → A B
A → x
B → x
This grammar is ambiguous because we can derive the string x x in two ways
S → A B → A x → x x
S → A B → x B → x x
WRONG!!
There are indeed two derivations, but they have the same parse tree!
End of Remark.

Homework: 3 (applied only to parts a, b, and c of 2)

2.2.5: Associativity of operators

Our grammar gives left associativity. That is, if you traverse the parse tree in postorder and perform the indicated arithmetic you will evaluate the string left to right. Thus 8-8-8 would evaluate to -8. If you wished to generate right associativity (normally exponentiation is right associative, so 2**3**2 gives 512 not 64), you would change the first two productions to

  list → digit + list
  list → digit - list

Draw in class the parse tree for 7+4-5 with this new grammar.

2.2.6: Precedence of operators

We normally want * to have higher precedence than +. We do this by using an additional nonterminal to indicate the items that have been multiplied. The example below gives the four basic arithmetic operations their normal precedence unless overridden by parentheses. Redundant parentheses are permitted. Equal precedence operations are performed left to right.

  expr   → expr + term | expr - term | term
  term   → term * factor | term / factor | factor
  factor → digit | ( expr )
  digit  → 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

Do the examples 1+2/3-4*5 and (1+2)/3-4*5 on the board.

Note how the precedence is enforced by the grammar; slick!